初二上学期数学难题

经典难题（一）1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥C O．求证：CD＝GF．（初二）2、已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝15度求证：△PBC是正三角形．（初二）3、如图，已知四边形ABCD、A1B1C1D1都是正方形，A2、B2、C2、D2分别是AA 1、BB1、CC1、DD1的中点．求证：四边形A2B2C2D2是正方形．（初二）4、已知：如图，在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN＝∠F．经典难题（二）1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC于M．（1）求证：AH＝2OM；（2）若∠BAC＝600，求证：AH＝AO．（初二）2、设MN是圆O外一直线，过O作OA⊥MN于A，自A引圆的两条直线，交圆于B、C及D、E，直线EB及CD分别交MN于P、Q．求证：AP＝AQ．（初二）3、如果上题把直线MN由圆外平移至圆内，则由此可得以下命题：设MN是圆O的弦，过MN的中点A任作两弦BC、DE，设CD、EB分别交MN于P、Q．求证：AP＝AQ．（初二）4、如图，分别以△ABC的AC和BC为一边，在△ABC的外侧作正方形ACDE和正方形CBFG，点P是EF的中点．求证：点P到边AB的距离等于AB的一半．（初二）经典难题（三）1、如图，四边形ABCD为正方形，DE∥AC，AE＝AC，AE与CD相交于F．求证：CE＝CF．（初二）2、如图，四边形ABCD为正方形，DE∥AC，且CE＝CA，直线EC交DA延长线于F．求证：AE＝AF．（初二）3、设P是正方形ABCD一边BC上的任一点，PF⊥AP，CF平分∠DCE．求证：PA＝PF．（初二）4、如图，PC切圆O于C，AC为圆的直径，PEF为圆的割线，AE、AF与直线PO 相交于B、D．求证：AB＝DC，BC＝AD．（初三）经典难题（四）1、已知：△ABC是正三角形，P是三角形内一点，PA＝3，PB＝4，PC＝5．求：∠APB的度数．（初二）2、设P是平行四边形ABCD内部的一点，且∠PBA＝∠PDA．求证：∠PAB＝∠PCB．（初二）3、设ABCD为圆内接凸四边形，求证：AB·CD＋AD·BC＝AC·BD．（初三）4、平行四边形ABCD中，设E、F分别是BC、AB上的一点，AE与CF相交于P，且AE＝CF．求证：∠DPA＝∠DPC．（初二）经典难题（五）1、设P是边长为1的正△ABC内任一点，L＝PA＋PB＋PC，求证：√3≤L＜2．2、已知：P是边长为1的正方形ABCD内的一点，求PA＋PB＋PC的最小值．3、P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC＝3a，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝80度，D、E分别是AB、AC上的点，∠DCA ＝30度，∠EBA＝20度，求∠BED的度数．答案经典难题（一）4.如下图连接AC并取其中点Q，连接QN和QM，所以可得∠QMF=∠F，∠QNM=∠D EN和∠QMN=∠QNM，从而得出∠DEN＝∠F。

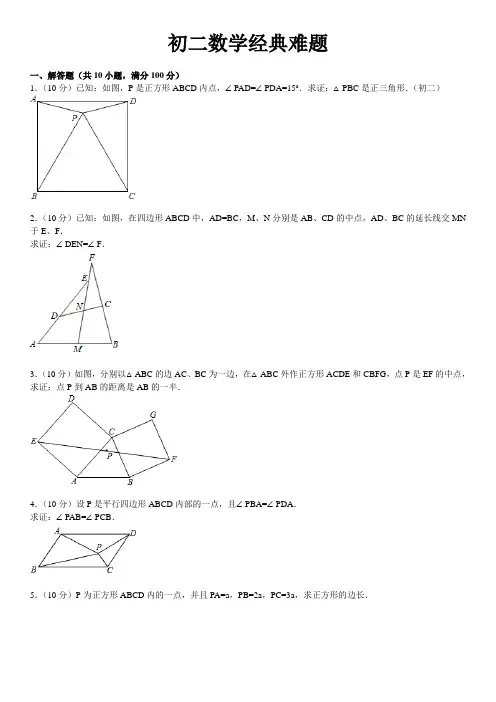
初二数学经典难题一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）2．（10分）已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN 于E、F．求证：∠DEN=∠F．3．（10分）如图，分别以△ABC的边AC、BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半．4．（10分）设P是平行四边形ABCD内部的一点，且∠PBA=∠PDA．求证：∠PAB=∠PCB．5．（10分）P为正方形ABCD内的一点，并且PA=a，PB=2a，PC=3a，求正方形的边长．6．（10分）一个圆柱形容器的容积为V立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管2倍的大水管注水．向容器中注满水的全过程共用时间t分．求两根水管各自注水的速度．7．（10分）（2009•郴州）如图1，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P（﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．（1）写出正比例函数和反比例函数的关系式；（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．8．（10分）（2008•海南）如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在线段BC上，且PE=PB．（1）求证：①PE=PD；②PE⊥PD；（2）设AP=x，△PBE的面积为y．①求出y关于x的函数关系式，并写出x的取值范围；②当x取何值时，y取得最大值，并求出这个最大值．9．（10分）（2010•河南）如图，直线y=k1x+b与反比例函数（x＞0）的图象交于A（1，6），B（a，3）两点．（1）求k1、k2的值．（2）直接写出时x的取值范围；（3）如图，等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为12时，请判断PC和PE的大小关系，并说明理由．10．（10分）（2007•福州）如图，已知直线y=x与双曲线交于A，B两点，且点A的横坐标为4．（1）求k的值；（2）若双曲线上一点C的纵坐标为8，求△AOC的面积；（3）过原点O的另一条直线l交双曲线于P，Q两点（P点在第一象限），若由点A，B，P，Q为顶点组成的四边形面积为24，求点P的坐标．初二数学经典难题参考答案与试题解析一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）考点：正方形的性质；全等三角形的判定与性质；等边三角形的性质；等边三角形的判定。

初二数学难题30道1. 解析几何：在直角坐标系中，点A(2, 3)，点B(1, 2)，求线段AB的中点坐标。

2. 代数方程：解方程 2x + 5 = 3x 4。

3. 函数问题：给定函数 f(x) = x^2 2x + 1，求 f(3) 的值。

4. 不等式求解：解不等式 5x 2 > 3。

5. 平行四边形：已知平行四边形ABCD，AB = 6cm，BC = 8cm，求对角线AC的长度。

6. 解析几何：在直角坐标系中，点A(1, 2)，点B(3, 4)，求线段AB的长度。

7. 代数方程：解方程 3x^2 4x + 1 = 0。

8. 函数问题：给定函数 g(x) = 2x + 3，求 g(2) 的值。

9. 不等式求解：解不等式 2x 5 < 1。

10. 平行四边形：已知平行四边形ABCD，AB = 7cm，BC = 9cm，求对角线BD的长度。

11. 解析几何：在直角坐标系中，点A(4, 5)，点B(2, 1)，求线段AB的长度。

12. 代数方程：解方程 4x^2 9x + 2 = 0。

13. 函数问题：给定函数 h(x) = x^3 3x^2 + 2x，求 h(1) 的值。

14. 不等式求解：解不等式3x + 4 ≤ 7。

15. 平行四边形：已知平行四边形ABCD，AB = 8cm，BC = 10cm，求对角线AC的长度。

16. 解析几何：在直角坐标系中，点A(3, 2)，点B(1, 1)，求线段AB的中点坐标。

17. 代数方程：解方程 5x 3 = 2x + 7。

18. 函数问题：给定函数 f(x) = x^2 + 4x + 4，求 f(0) 的值。

19. 不等式求解：解不等式4x 8 ≥ 2。

20. 平行四边形：已知平行四边形ABCD，AB = 9cm，BC = 11cm，求对角线BD的长度。

21. 解析几何：在直角坐标系中，点A(2, 3)，点B(1, 4)，求线段AB的长度。

22. 代数方程：解方程 6x^2 5x 1 = 0。

初二数学难题目练习题1. 一个长方体的长、宽、高分别是a、b、c米，它的表面积是多少？解析：一个长方体有六个面，每个面的面积等于对应边长的乘积。

所以该长方体的表面积为2ab + 2ac + 2bc 平方米。

2. 如果一条蛇爬行的速度是每小时3米，那么它爬行1440米需要多长时间？解析：根据速度等于距离除以时间公式，时间等于距离除以速度。

所以蛇爬行1440米需要 1440 ÷ 3 = 480小时。

3. 若x + 5 = 9，那么x的值是多少？解析：将已知条件代入方程，得到x + 5 = 9. 使用逆运算，将5从等式两边减去，得到x = 9 - 5 = 4，所以x的值为4。

4. 一个三角形的两边分别为5厘米、12厘米，夹角为60度，求第三边的长度。

解析：根据余弦定理可以求得第三边的长度。

c^2 = a^2 + b^2 - 2ab* cosC，将已知条件代入公式，得到c^2 = 5^2 + 12^2 - 2 * 5 * 12 *cos60°。

计算后得到c^2 = 169，所以第三边的长度为平方根的169，即13厘米。

5. 若7x + 1 = 29，那么x的值是多少？解析：将已知条件代入方程，得到7x + 1 = 29. 使用逆运算，将1从等式两边减去，得到7x = 29 - 1 = 28. 再将等式两边除以7，得到x = 28 ÷ 7 = 4，所以x的值为4。

6. 如果一个圆的半径为5厘米，求它的周长和面积。

解析：圆的周长等于2πr，面积等于πr^2。

所以这个圆的周长等于2 * 3.14 * 5 = 31.4厘米，面积等于3.14 * 5^2 = 78.5平方厘米。

7. 若3x - 2 = 7，那么x的值是多少？解析：将已知条件代入方程，得到3x - 2 = 7. 使用逆运算，将2从等式两边加上，得到3x = 7 + 2 = 9. 再将等式两边除以3，得到x = 9 ÷3 = 3，所以x的值为3。

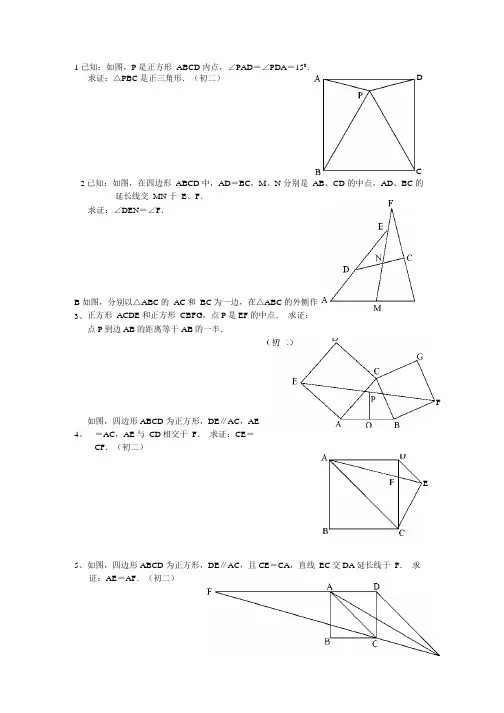
1 已知：如图，P 是正方形 ABCD 内点，∠PAD ＝∠PDA ＝150．2 已知：如图，在四边形 ABCD 中，AD ＝BC ，M 、N 分别是 AB 、CD 的中点，AD 、BC 的延长线交 MN 于 E 、F ．求证：∠DEN ＝∠F ．B 如图，分别以△ABC 的 AC 和 BC 为一边，在△ABC 的外侧作正方形 ACDE 和正方形 CBFG ，点P 是EF 的中点． 求证：点P 到边AB 的距离等于AB 的一半．如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与 CD 相交于 F ． 求证：CE ＝CF ．（初二）E5、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线 EC 交DA 延长线于 F ． 求证：AE ＝AF ．（初二） 求证：△PBC 是正三角形．（初二）3、4、 DCF6、设P 是正方形ABCD 一边BC 上的任一点，PF⊥AP，求证：PA＝PF．（初二）PC＝5．7、已知：△ABC 是正三角形，P 是三角形内一点，PA＝3，PB＝4，求：∠APB 的度数．（初二）C 8、设P 是平行四边形ABCD 内部的一点，且∠ PBA ＝∠ PDA ．求证：∠PAB＝∠PCB．（初二）9、已知：P是边长为1的正方形ABCD 内的一点，10、P 为正方形ABCD 内的一点，并且PA＝a，PB＝2a，PC=3a 正方形的边长．1.如图 1，已知△ABC，∠ACB=90°，分别以 AB、BC 为边向外作△ABD 与且DA=DB ， BE=EC ，若∠ADB=∠BEC=2∠ABC，连接 DE 交 AB 于点 F ，试探究线段 DF 与EF 的数量关系，并加以证明。

B3：如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.（1）当AB≠AC时，证明四边形ADFE为平行四边形；（2） 当AB = AC 时，顺次连结A 、D 、F 、E 四点所构成的图形有哪4：如图，已知△ABC 是等边三角形，D 、E 分别在边 BC 、AC CD=CE ，连结 DE 并延长至点 F ，使 EF=AE ，连结AF 、BE B 和 CF 。

初二数学上册一二册难题1先化简再求值其中x 是不等式组的整数解2. 若△ABC 三边a 、b 、c 满足a2＋b2＋c2＝ab ＋bc ＋ca ．判断△ABC 的形状3. 若3=a x ,4=b x 5=c x 求c b a x 22+-4.观察下列图形（每幅图中最小的三角形都是全等的），请写出第n个图中最小的三角形的个数（）5.根据下列5个图形及相应点的个数的变化规律，试猜测第n个图中有( ) 个点6观察下列图形，则第n个图形中三角形的个数是（）7如图，已知等腰梯形ABCD中，AD∥BC,AC⊥BD，AC=8，求梯形ABCD的面积8如下图，AB=AC，点D在BC上，以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC且∠ADC=∠AEC求证：∠BAC+∠BCE=180°9四边形ABCD中，∠A＝60°，∠B＝∠D＝90°，AB＝200m，CD＝100m，求AD、BC的长。

10如图，ΔABC 和ΔBDE 是等边三角形，D 在AE 延长线上。

求证：BD+DC=AD11已知，如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P。

（1）求证：△ABE≌△CAD；（2）若BQ⊥AD于Q，PQ=6，PE=2，求AD的长12如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．①求证：△ABE≌△CBD；②若∠CAE=30°，求∠BDC的度数13如图，在直角梯形ABCD中，AD∥BC，∠A＝90º，AB＝AD，DE⊥CD 交AB于E，DF平分∠CDE交BC于F，连接EF．证明：CF＝EF14兴发服装店老板用4500元购进一批某款T恤衫，由于深受顾客喜爱，很快售完，老板又用4950元购进第二批该款式T恤衫，所购数量与第一批相同，但每件进价比第一批多了9元．（1）第一批该款式T恤衫每件进价是多少元？（2）老板以每件120元的价格销售该款式T恤衫，当第二批T恤衫售出五分之四时，出现了滞销，于是决定降价促销，若要使第二批的销售利润不低于650元，剩余的T 恤衫每件售价至少要多少元？（利润=售价﹣进价）15我市某学习机营销商经营某品牌A、B两种型号的学习机．用10000元可进货A型号的学习机5个，B型号的学习机10个；用11000元可进货A型号的学习机10个，B型号的学习机5个．（1）求A、B 两种型号的学习机每个分别为多少元？（2）若该学习机营销商销售1个A型号的学习机可获利120元，销售1个B型号的学习机可获利90元，该学习机营销商准备用不超过30000元购进A、B两种型号的学习机共40个，且这两种型号的学习机全部售出后总获利不低于4440元，问有几种进货方案？这几种进货方案中，该学习机营销商将这些型号的学习机全部售出后，获利最大的是哪种方案？最大利润是多少？16几个小伙伴打算去德州看音乐演出，他们准备用180元钱购买门票．下面是两个小伙伴的对话：小红说：如果今天去看演出，我们每人一张票，正好会差一张票的钱．小明说：过两天就是“儿童节”了，那时候去看演出，票价会打六折，我们每人一张票，还能剩36元钱呢！根据对话的内容，请你求出小伙伴们的人数17长方体的长为15 cm，宽为10 cm，高为 20 cm，点B离点C 5 cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是多少？18.2013年4月20日，雅安发生7.0级地震，某地需550顶帐蓬解决受灾群众临时住宿问题，现由甲、乙两个工厂来加工生产．已知甲工厂每天的加工生产能力是乙工厂每天加工生产能力的1.5倍，并且加工生产240顶帐蓬甲工厂比乙工厂少用4天．①求甲、乙两个工厂每天分别可加工生产多少顶帐蓬？②若甲工厂每天的加工生产成本为3万元，乙工厂每天的加工生产成本为2.4万元，要使这批救灾帐蓬的加工生产总成本不高于60万元，至少应安排甲工厂加工生产多少天？19甲乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工；若甲、乙共同整理20分钟后，乙单独整理需要20分钟才完工。

1，某大型超市从生产基地购进一批水果，运输过程中质量损失5%，假设不计超市其他费用。

(1)如果超市在进价的基础上提高5%作为售价,那么请你通过计算说明超市是否亏本;
(2)如果超市至少要获得20%的利润,那么这种水果的售价最低应提高百分之几?(结果精确到0.1%)
,2. 如右图，一只蚂蚁从点O 出发，在扇形OAB 的边缘沿着O B A O ---的路线匀速爬行一周，设蚂蚁的爬行时间为t ，蚂蚁与O 点的距离为s ，则s 关于t 的函数图象大致是（ ）
A. B. C. D. 3. 如图，等边ABC ∆中，点D 、E 分别在边AB ， BC 上，把BDE ∆沿直线DE 翻折，使点B 落在'B
处，'DB 、'EB 分别与边AC 交于点F 、G 。

若o ADF 80=∠，则=∠EGC ▲ o
4．将直线42+-=x y 向上平移2个单位，所得直线解析式是，将直线42+-=x y 向右平移2个单位，所得直线的解析式是
5. 一次函数6+=kx y 的图象经过第三象限，且它与两条坐标轴构成的直角三角形面积等于9，则=k 。

6．如图，直线5+-=x y 与坐标轴交于点A 、B ，
在线段AB 上（不包括端点）任取一点P ，过点P
分别作x PM ⊥轴，y PN ⊥轴，则长方形PMON
的周长为 。

7．如图，在x 轴上有五个点，它们的横坐标分别
为1，2，3，4，5，过这些点作x 轴的垂线与三
A
A
D B C
E 'B
F
G O M N P A B x
y
条直线ax y =，x a y )1(+=，x a y )2(+=相交， 则阴影面积是 。

初二上册数学必考难题一、三角形相关难题例：在△ABC 中，AB = 8，AC = 6，AD 是中线，求 AD 的取值范围。

解析：延长 AD 至点 E，使 AD = DE，连接 BE。

因为 AD 是中线，所以 BD = CD。

在△ADC 和△EDB 中，AD = DE，∠ADC = ∠EDB，CD = BD，所以△ADC ≌△EDB （SAS），则 BE = AC = 6。

在△ABE 中，AB - BE < AE < AB + BE，即 8 - 6 < 2AD < 8 + 6，所以 1 < AD < 7。

二、全等三角形证明难题例：已知，如图，AB = AC，AD = AE，∠1 = ∠2。

求证：△ABD ≌△ACE。

证明：因为∠1 = ∠2，所以∠1 + ∠CAD = ∠2 + ∠CAD，即∠BAD = ∠CAE。

在△ABD 和△ACE 中，AB = AC，∠BAD = ∠CAE，AD = AE，所以△ABD ≌△ACE （SAS）。

三、一次函数应用难题例：某工厂现有甲种原料 360 千克，乙种原料 290 千克，计划利用这两种原料生产 A、B 两种产品共 50 件。

已知生产一件 A 产品需要甲种原料 9 千克，乙种原料 3 千克；生产一件 B 产品需要甲种原料 4 千克，乙种原料 10 千克。

设生产 x 件 A 产品，求 x 的取值范围。

解析：生产 x 件 A 产品，则生产（50 - x）件 B 产品。

根据题意可得：9x + 4(50 - x) ≤ 360 3x + 10(50 - x) ≤ 290解第一个不等式：9x + 200 - 4x ≤ 360，5x ≤ 160，x ≤ 32解第二个不等式：3x + 500 - 10x ≤ 290，-7x ≤ -210，x ≥ 30所以 x 的取值范围是 30 ≤ x ≤ 32。

四、整式乘法与因式分解难题例：分解因式：x^4 - 18x^2 + 81解析：begin{align}x^4 - 18x^2 + 81 =(x^2 - 9)^2 =(x + 3)^2(x - 3)^2end{align}五、分式计算与应用难题例：已知(x/y) = (3/4)，求(x + y/y)的值。

初二数学难题带答案（上学期）一、选择题（每小题3分，共30分）1. 如图，△ ABD^A CDB下面四个结论中，不正确的是（）A.A ABC ffiA CDB的面积相等B . △ABD ffiA CDB的周长相等C.Z A+Z ABD=Z C+Z CBD D AD// BC 且AD= BC,第1 题图）, 第2题图）, 第3题图）, 第4题图）2. 如图，小强利用全等三角形的知识测量池塘两端M N的距离，如果△ PQ3△NMO则只需测出其长度的线段是（）A. POB. PQC. MOD. MQ3.如图，BE±AC于点D,且AD= CD BD= ED,则Z ABC= 54°，则Z E=（） A. 25° B. 27° C. 30° D. 45°4. （2014?南昌）如图，AB// DE AC// DF, AO DF,下列条件中不能判断△ ABC^△DEF的是（）A. AB= DEB.Z B=Z EC. EF= BCD. E F // BC5. 如图，Z 1 = Z 2，Z 3=Z 4，则下面结论中错误的是（）A.A ADC^A BCD B △ABD^A BAC C △ABO^A COD D △AOD^ BOC ,第5题图）, 第6题图）, 第7题图）6. 如图，在△ ABC中, A吐AC,点E, F是中线AD上的两点，则图中可证明为全等三角形的有（）A. 3对B . 4对C . 5对D . 6对7. 如图，在△ ABC中, Z ACB= 90°，沿CD折叠△ CBD使点B恰好落在AC边上的点E处，若Z A= 22°，则Z BDC等于（）A 44°B 60°C 67°D 77°8. 如图，DEIBC于点E,且BE= CE AB+ AO 15,则厶ABD的周长为（） A．15 B．20 C．25 D．309. 如图，AB丄B C, BE!AC, Z 1 = Z 2, AD= AB 则（）A.Z 1 = Z EFDB. BE= ECC. BF- DF= CDD. FD// BC,第8题图）, 第9题图）, 第10题图）10 .如图，在△ ABC中, AD是Z BAC的平分线，DEI AC于E, DF! AB于F,且FB= CE则下列结论：①DE= DF,②AE=AF,③BD= CD④AD!BC.其中正确的个数有（）A. 1个B . 2个C . 3个D . 4个二、填空题（每小题3分，共24分）1 1 .在厶ABC中, A吐8, AO6,贝U BC边上的中线AD的取值范围是12.若厶ABC^A EFG 且Z B= 60°,Z FGE-Z E= 56°，则Z A= _______________度．13 .如图，A吐DB Z ABD=Z CBE请你添加一个适当的条件______________ 使厶ABC^A DBE.（只需添加一个即可）14. 如图，A吐AC AD= AE / BAG=/ DAE / 1= 25°,/ 2 = 30°，则/ 3= ,第13题图） , 第14 题图） , 第15 题图） , 第16题图） , 第17题图）15. 如图，在Rt△ ABC中,/ AC= 90°, BC= 2 cm, CDLAB,在AC上取一点E,使EC= BC,过点E作EF±AC交CD的延长线于点F,若EF= 5 cm,则AE= cm.16. 如图，在Rt△ ABC中,/ C= 90°, AC= 10 cm, BC= 5 cm, —条线段PQ=AB P, Q两点分别在线段AC和AC的垂线AX上移动，则当AF= __________ 时，才能使厶ABC ffiA APQ全等.17. 如图，已知△ ABC中,/ ABC / ACB的角平分线交于点O,连接AO并延长交BC于D, OH L BC于H,若/ BA（= 60° , OH= 5 cm ,则/ BAD= _____ ，点O到AB的距离为________ cm.18. 已知点A, B的坐标分别为（2 , 0）, （2 , 4）,以A, B , P为顶点的三角形与△ ABO全等,写出一个符合条件的点P的坐标：三、解答题（共66 分）19. （6 分）如图,在厶ABC^P^ DCE中 , AB// DC A吐DC BC= CE 且点B, C,E 在一条直线上.求证：/ A=/ D.20. （8 分）如图，点B在射线AE上 , / CAE=Z DAE / CBE=Z DBE求证：AC = AD.21. （10分）如图,E是/ AOB的平分线上一点,EC丄OA EDLOB垂足为C, D,连接CD交OE于 F.求证：（1）OC= OD （2）DF = CF.22. （10 分）如图,在Rt△ ABC中 , / AC= 90°，点D, F分别在AB AC上 , CF= CB连接CD将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.（1）求证：△ BCD^A FCE⑵若EF/ CD求/ BD C的度数.23. （10 分）如图AB=DC AD=BC DE=BF 求证：BE=DF.24. （10分）如图,已知：/ B=/ C= 90° , M是BC的中点,DM平分/ ADC. 求证：（1）AM 平分/ DAB；（2）AD= AB＋CD.25. （12分）如图,在/ AOB的两边OA OB上分别取OM= ON / OM=/ OND DN 和EM相交于点C, CD= CE.求证：点C在/ AO B的平分线上.第12 章检测题参考答案1. C2.B3.B4.C5.C6.D7.C8.A9.D 10.D 11.1 v AD< 712.32 13. /C=/ E 14.55° 15. 3 16.5 cm 或10 cm 17.30°；518. (0 4)或(4 0)或(4 4)( 答其中一个即可)19. v AB// DC, •••/ B=/ DCE又：A吐DC BC= CE , /•△ ABC^ADCE(SAS) •••/ A=/ D20. v/ CBE=Z DBE •- 180°-/ CB= 180°—/ DBE 即/ AB(=Z ABD 在厶ABC?3ABD中, / CA=/ DAE AB= AB / AB(=/ ABD •△ABC^A ABD(ASA) • AC= AD21. (1) v EC L OA EDL OB •/ OC=/ OD= 90°,在厶OCE ffiA ODE中, /Ed EDO / CO旨/ DOE OE= OE :. △ OCE^ ODE(AAS) /• 0C= OD (2) 在厶COF ffiA DOF中, OC= OD / CO昌/ DOE OF= OF, :. △ COF^A DOF(SAS)二DF= CF22. (1) vZ ACB= 90°, / DCE= 90°, /-Z ACB-Z AC亠/DCE-Z ACD 即/ BC亠/ FCE在厶 BCD ffiA FCE中,BO CF, Z BCD^Z FCE DC= CE •/△BCD ◎△ FCE(SAS)(2) v EF// CD /Z E=Z D CE= 90°, /Z BDC=Z E= 90°23. 连接BD.v AD= BC A吐CD BD= BD ABD^A CDB(SSS) , /Z ADB=Z DBC /•180°—Z ADB= 180°-Z DBC /Z BDE=Z DBF 在厶BDE ffiA DBF 中,DE=BF, Z BD吕Z DBF DB= BD BDE^A DBF(SAS) / BE= DF24. (1)过M作MH L AD于H , v DIM平分Z ADC MCL DC MH L AD, / CM= HM 又v BM= CM / MHh BM v MHL AD, MBL AB / AM平分Z DAB (2) vZ CDMk Z HDM/Z CM匡Z HMD 又v DC L MC DHL MH / DC= DH 同理：AB= AH, v AD =DH^AH, / AD= AB+ CD25. 在△MOE^A NOD中, Z OM EZ OND OM= ON Z MO EZ NOD /△MO專△NOD(ASA) / OD= OE v CD= CE OC E OC / △OCI^A OCE(SSS) /Z DOC =Z EOC即C在Z AOB的平分线上以上资料来源可靠，专业可信，将助您更好的提升办公效率。

数学八年级上册第一章难题一、三角形三边关系难题1. 题目：已知三角形的两边长分别为3和5，第三边的长为整数，则第三边的长可能是多少？解析：根据三角形三边关系，两边之和大于第三边，两边之差小于第三边。

设第三边为x，则5 3<x<5+3，即2<x<8。

因为x为整数，所以x可能是3、4、5、6、7。

2. 题目：一个三角形的三条边长分别为x、2x 1、5x 3，求x的取值范围。

解析：同样根据三边关系可得：(2x 1)+x>5x 3，3x 1>5x 3，2>2x，x < 1；(2x 1)+(5x 3)>x，7x 4>x，6x>4，x>2/3；x+(5x 3)>2x 1，6x 3>2x 1，4x>2，x>1/2。

综合可得1/2 < x < 1。

二、三角形内角和与外角难题1. 题目：在△ABC中，∠A=∠B +∠C，求∠A的度数。

解析：因为三角形内角和为180°，即∠A+∠B+∠C = 180°，又因为∠A = ∠B+∠C，所以2∠A=180°，∠A = 90°。

2. 题目：如图，在△ABC中，∠ACD是△ABC的外角，∠ACD = 120°，∠A=70°，求∠B的度数。

解析：因为∠ACD是外角，根据三角形外角性质，∠ACD = ∠A+∠B。

已知∠ACD = 120°，∠A = 70°，则∠B=∠ACD ∠A = 120° 70° = 50°。

3. 题目：在△ABC中，∠ABC的平分线与∠ACB的外角平分线相交于点D，∠A = 50°，求∠D的度数。

解析：设∠ACB的外角为∠ACE。

根据三角形外角性质，∠ACE=∠A + ∠ABC。

因为BD平分∠ABC，CD平分∠ACE，所以∠DCE = 1/2∠ACE，∠DBC = 1/2∠ABC。

8年级上册数学难题试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 若一个三角形的两边分别为8cm和10cm，且这两边的夹角为60°，则这个三角形的周长为多少cm？A. 16cmB. 26cmC. 28cmD. 36cm2. 下列哪一个数是无理数？A. √9B. √16C. √3D. √13. 若一个等腰三角形的底边长为10cm，腰长为13cm，则这个三角形的面积是多少cm²？A. 60cm²B. 78cm²C. 84cm²D. 90cm²4. 下列哪一个数是合数？A. 11B. 13C. 15D. 175. 若一个等边三角形的边长为6cm，则这个三角形的面积是多少cm²？A. 9√3cm²B. 18√3cm²C. 27√3cm²D. 36√3cm²二、判断题（每题1分，共5分）1. 任何两个等边三角形都是全等的。

（）2. 任何两个等腰直角三角形都是相似的。

（）3. 若一个三角形的两边分别为5cm和12cm，则这个三角形一定不是直角三角形。

（）4. 任何两个等腰三角形都是相似的。

（）5. 若一个三角形的周长为20cm，且其中一边长为8cm，则这个三角形一定是锐角三角形。

（）三、填空题（每题1分，共5分）1. 若一个等腰三角形的底边长为8cm，腰长为10cm，则这个三角形的面积是______cm²。

2. 若一个直角三角形的两个直角边分别为3cm和4cm，则这个三角形的斜边长为______cm。

3. 若一个等边三角形的边长为a，则这个三角形的面积是______a²。

4. 若一个等腰三角形的底边长为b，腰长为c，则这个三角形的面积是______b²。

5. 若一个直角三角形的斜边长为c，一直角边长为a，则另一直角边长为______。

四、简答题（每题2分，共10分）1. 简述勾股定理的内容。

数学八年级上册难题一、三角形全等证明难题题目1：已知：如图，在△ABC中，AD是∠BAC的平分线，M是BC的中点，过M作ME∥AD 交BA延长线于E，交AC于F。

求证：BE = CF。

解析：1. 延长FM至N，使MN = FM，连接BN。

因为M是BC中点，所以BM = CM。

在△BMN和△CMF中，BM = CM，∠BMN = ∠CMF（对顶角相等），MN = MF。

根据SAS（边角边）定理，可得△BMN≌△CMF。

所以∠N = ∠CFM，BN = CF。

2. 因为AD平分∠BAC，所以∠BAD = ∠CAD。

又因为ME∥AD，所以∠BAD = ∠AEF，∠CAD = ∠AFE。

从而∠AEF = ∠AFE，所以AE = AF。

3. 因为∠CFM = ∠AFE，∠AEF = ∠N，所以∠N = ∠AEF。

所以BE = BN。

又因为BN = CF，所以BE = CF。

二、等腰三角形性质与判定难题等腰三角形一腰上的高与另一腰的夹角为30°，腰长为a，求其底边上的高。

解析：1. 分两种情况讨论：当等腰三角形为锐角三角形时：因为一腰上的高与另一腰的夹角为30°，所以顶角为60°。

此等腰三角形为等边三角形，底边上的高公式。

当等腰三角形为钝角三角形时：一腰上的高与另一腰的夹角为30°，则顶角的外角为30°，顶角为150°。

底角为15°，设底边上的高为公式，腰长为公式。

根据三角函数关系，公式。

而公式。

所以公式。

三、整式乘法与因式分解难题题目3：已知公式、公式、公式是△ABC的三边，且满足公式，求证：△ABC是等边三角形。

1. 对公式进行变形处理。

等式两边同时乘以2，得到公式。

进一步变形为公式。

2. 因为一个数的平方是非负的，要使公式成立。

则公式，公式，公式。

即公式，公式，公式。

所以△ABC是等边三角形。

初二数学经典难题(带答案与解析)1. 一位农夫要过一条河，他只有一艘小船，船只能支持他和一件物品的重量。

他需要把他自己，一只狼，一只绵羊和一束青菜都安全地运送到对岸。

但是，他不能让狼和绵羊在船上单独相处，因为狼会吃掉绵羊，而他也不能把青菜留在对岸，因为狼会吃掉青菜。

请问，农夫应该如何安全地将这些物品都运送到对岸？答案:农夫的运输过程，可以分为3个阶段:第一次船过去，农夫把绵羊放在岸边，然后把狼和青菜带到对岸。

第二次船会回来，这一次农夫只带绵羊回对岸，留下狼和青菜。

第三次船过去，农夫把青菜放在岸边，把狼带到对岸，然后返回把绵羊也带到对岸。

解析:这是一个相当著名的数学难题，考验玩家的逻辑思维和解决问题的能力。

农夫需要分别带着“绵羊、狼、青菜”三个物品过河，但是船只能支撑一人和一样物品的质量。

如果让“狼”单独和“绵羊”在一起，绵羊就会被吃掉，如果让“青菜”单独和“狼”在一起，青菜就会被吃掉。

怎么办呢？我们需要一步一步来想象这个过程。

首先，农夫需要把狼在非常安全的状态下到对岸。

所以，他需要先把绵羊放在岸边，然后带上狼和青菜一起过河。

这样，在对岸靠岸后，他可以先把青菜放在岸边，回来把狼送过去，并且把青菜留在对岸。

最后再回到原来的岸边，带上绵羊将其送往对岸即可。

这样，农夫就能够安全地将三个物品都运送到了对岸，而他没有违反任何规则。

这个问题是一个“二进制数学问题”，要求玩家发挥他们的逻辑思维和判断能力，找出最好的解决方案。

2. 一支队伍从A地出发向北行走360英里后到达B地，并停留了5天。

然后他们又向北行走280英里，到达C地，他们在C地停留了10天。

然后他们又向北行走400英里，到达D地。

他们在D地停留了15天，然后再向北前进60英里就到达他们的终点E地。

请问他们总共行走的距离以及他们在路途上平均每天行走的距离是多少？答案:他们总共行走的距离是: 1100 英里。

他们在路途上平均每天行走的距离是: 22 英里。

1,某大型超市从生产基地购进一批水果，运输过程中质量损失5%，假设不计超市其他费用.(1）如果超市在进价的基础上提高5％作为售价，那么请你通过计算说明超市是否亏本；（2）如果超市至少要获得20％的利润，那么这种水果的售价最低应提高百分之几?(结果精确到0.1％)解：假设水果总质量m,进价为p,那么运输后出去质量损失水果质量为（1—5%)m = 0.95m （1） 成本为 mp,销售额 0。

95m ＊(1+5％）p = 0.95*1.05mp = 0.9975mp 〈 mp 所以赔本(2) 假设售价提高x%，因为要获得20%的利润，所以销售额为 (1+20％)mp = 1.2mp 实际销售额 0.95m*(1+x%)p = 1.2mp 0。

95 * (1+x ％) = 1.2x% = 1.2/0.95 — 1 = (1。

2 - 0。

95) / 0.95 =0。

25/0。

95 = 25/95 = 5/19 = 0。

263 = 26.3%,2. 如右图，一只蚂蚁从点O 出发，在扇形OAB 的边缘沿着O B A O ---的路线匀速爬行一周，设蚂蚁的爬行时间为t ,蚂蚁与O 点的距离为s ，则s 关于t 的函数图象大致是（ ▲ C ）A 。

B 。

C 。

D 。

3。

如图,等边ABC ∆中,点D 、E 分别在边AB ，BC 上，把BDE ∆沿直线DE 翻折，使点B 落在'B处，'DB 、'EB 分别与边AC 交于点F 、G 。

若oADF 80=∠，则=∠EGC ▲80° o4．将直线42+-=x y 向上平移2个单位，所得直线解析式是 y=—2x+6 ,将直线OABO t s O t s O t s O tsA DBCE'B FG42+-=x y 向右平移2个单位，所得直线的解析式是y=—2x+8。

5. 一次函数6+=kx y 的图象经过第三象限,且它与两条坐标轴构成的直角三角形面积等于9，则=k 2 ▲ 。

初二上册数学练习题难题数学练习题是学习数学的重要组成部分，通过练习，我们可以巩固所学的知识，提高解题能力。

在初二上册数学学习中，难题是让我们感到困扰的一部分，以下将介绍一些初二上册数学练习题中的难题，并提供解题思路和方法。

一、整数运算的难题在初二上册的数学练习题中，整数运算是一个重要的考点。

有时，我们会遇到一些复杂的整数运算题目，让我们感到困惑。

例如：难题1：计算$(-3) \times (-2) \times (-4)$。

对于这道题目，我们可以使用整数乘法的法则来解答。

根据法则，两个负数相乘的结果是正数。

所以，$(-3) \times (-2) \times (-4) = 3\times 2 \times 4 = 24$。

因此，答案为24。

难题2：计算$(-5) \div 2$。

在这道题目中，我们需要知道整数除法的规则。

当一个负数除以一个正数时，商的符号为负数。

所以，$(-5) \div 2 = -\frac{5}{2}$。

因此，答案为$-\frac{5}{2}$。

通过掌握整数运算的法则，我们可以更好地解决这类难题。

二、代数方程的难题初二上册的数学中，代数方程是一个重要的内容，也是一个容易出现难题的部分。

例如：难题1：解方程$2x + 5 = 3x - 1$。

对于这道题目，我们可以通过移项和合并同类项的方式来解决。

首先，我们将3x和2x合并，得到$5 = x - 1$。

然后，我们将x移到等号的左边，得到$x = 5 + 1$。

因此，答案为x = 6。

难题2：解方程$3(x - 4) = 2 - 2x$。

在这道题目中，我们需要注意分配律的运用。

首先，我们将3乘以括号内的表达式，得到$3x - 12 = 2 - 2x$。

然后，我们将-2x移到等号的左边，得到$3x + 2x = 2 + 12$。

最后，我们将x的系数相加，得到$5x = 14$。

因此，答案为x = $\frac{14}{5}$。

通过掌握代数方程的解题方法，我们可以更好地解决这类难题。