梁丽杰建筑力学第五章习题解

PA M eA 9549 n 120 9549 Nm 300 3819.6N m 3.82kN m
M eB 0.95kN m
M eC 1.27kN m
M eD 1.59kN m
第5章 扭转杆的强度计算
（2）计算扭矩 1 1 2 2
截面1-1：
Mx 0
T2 WP2 14 106 MPa 71.3MPa π 1003 16
比较上述结果，该轴最大切应力位于BC段内任一截面的 边缘各点处，即该轴最大切应力为τmax=71.3MPa。
第5章 扭转杆的强度计算
圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力 圆轴的扭转试件可分别用Q235钢、铸铁等材料做成， 扭转破坏试验是在扭转试验机上进行。试件在两端外力偶
T1 M eB 0
T1 M eB 0.95kN m
截面2-2：
Mx 0
T1
T2 M eB M eA 0
T2 M eA M eB 2.87kN m
T2
第5章 扭转杆的强度计算
3
截面3-3：
Mx 0
T3 M eD 0
3
T3 M eD 1.59kN m
式中：[σC]为材料的许用挤压应力，可查有关设计手册。
注意：若两个相互挤压构件的材料不同，应对挤压强度 小的构件进行计算。
第5章 扭转杆的强度计算
挤压强度条件在工程中同样可以解决三类问题。 但工程中构件产生单纯挤压变形的情况较少，挤压强
度的计算问题往往是和剪切强度计算同时进行。
第5章 扭转杆的强度计算
第5章 扭转杆的强度计算
当挤压面为平面时，挤压计算面积与挤压面面积相等。

目录
第五章 杆件的内力\杆件拉（压）时的内力
解 (1)求支座反 A 力。由杆AD的平衡 x 方程∑Fx=0，可求得 支座反力FD=18 kN。 (2)求横截面1－1、2－2、3－3上的轴力。由于在横截 面B和C上作用有外力，须将杆分为AB、BC、CD三段。
应用截面法，假想地沿1 －1横截面把杆截开，取受力 较简单的右段为研究对象（如图），列出平衡方程 ∑Fx=0，F1－FN1=0 得 FN1= F1 =20 kN
目录
第五章 杆件的内力\杆件拉（压）时的内力
若取右段为研究对象，同样可求得轴力F ＝ FN （如 图），但其方向与用左段求出的轴力方向相反。
为了使两种算法得到的同一截面上的轴力不仅数值相 等，符号相同，规定轴力的正负号如下：当轴力的方向与 横截面的外法线方向一致时，杆件受拉伸长，轴力为正； 反之，杆件受压缩短，轴力为负。 在计算轴力时，通常未知轴力按正向假设。若计算结 果为正，则表示轴力的实际指向与所设指向相同，轴力为 拉力；若计算结果为负，则表示轴力的实际指向与所设指 向相反，轴力为压力。
目录
第五章 杆件的内力\杆件拉（压）时的内力
同理，取2－2横 截面的右段为研究对 象，列出平衡方程
x
得
∑Fx=0，F1＋ F2 －FN2=0 FN2= F1－F2=8 kN ∑Fx=0，FN3＋ FD =0 FN3= －FD= － 18 kN
取3－3横截面的左段为研究对象，列出平衡方程 得
式中，FN3为负值，说明FN3的指向与假设的方向相反，即 FN3为压力。
5－2－1 外力偶矩的计算
工程中作用于传动轴上的外力偶矩往往不是直接给 出的，而是给出轴所传递的功率和轴的转速。它们之间的 换算关系为 ｛Me｝N· m=9549

M DB
2
6qa B
0
D
N DB 0
QDB 0
M DB 2qa
N N
轴力：杆轴切线方向
伸长为正
Q
Q
剪力：杆轴法线方向
顺时针方向为正
弯矩: 应力对形心力矩之和
M
M
弯矩图画在受拉一侧
建筑力学
dFQ dFN dM FQ , qy , q x dx dx dx
梁上 无外力 均布力作用 集中力作用 (q向下) 情况 处(FP向下) 斜直 剪力图 水平线 线( ) 一般 抛物 弯矩图 为斜 线( 直线 下凸) 为 零 处 有 极 值 集中力 偶M作 用处 铰处
q P
C
Q
B C
A
q P
D C XC
q
XC
YC
YC XD (b)
Q
B YB A XA YA
(c)
建筑力学
刚架的内力分析及内力图的绘制
①分段：根据荷载不连续点、结点分段。 ②定形：根据每段内的荷载情况，定出内力图 的形状。 ③求值：由截面法或内力算式，求出各控制截 面的内力值。 ④画图：画M图时，将两端弯矩竖标画在受拉侧， 连以直线，再叠加上横向荷载产生的简支梁的 弯矩图。Q，N 图要标 ＋，－号；竖标大致成 比例。
依题意： M B M C
\MB
1 1 ql 2 q (l x ) x qx 2 2 2 16 l 0 .125 l 8
展开上式，得： x
与简支梁相比，多跨静定梁的跨中弯矩值 较小，省材料，但构造复杂。
建筑力学
§13-2 静定平面刚架
静定平面刚架的组成特点及类型
一、平面刚架结构特点： 刚架是由梁和柱以刚性结点相连组成，优点 是将梁柱形成一个刚性整体，结构刚度较大，内 力分布较均匀合理，便于形成大空间。 图（a）是车站雨蓬，图（b）是多层多跨 房屋，图（c）是具有部分铰结点的刚架。

1kW = 1000N· m/s = 1.36PS（马力）
二、扭转内力—扭矩T 以图示圆轴扭转的力学模型为例，用截面法，以m-m截面将轴截分为两段。 取其左段列力偶平衡方程可得 m Me Me Mx(F)=0: T-Me=0 T=Me A B m T为截面的内力偶矩，称为扭 Me T 矩。同理，也可取右段求出截面 A 扭矩。 Mx(F)=0: Me-T' =0 T'=Me 图d为截面扭矩的正负规定。 Me T
解：1、计算各段的轴力。 Fx 0 AB段
FN 1 F1 0 FN 1 10KN
BC段
F
x
0
FN 2 F2 F1 0 FN 2 10KN
CD段
F
x
0
FN3
F4 FN 3 0 FN 3 25kN
F4
2、绘制轴力图。
FN kN
产生轴向拉伸或压缩的杆件称为轴向拉杆或压杆。
轴向拉压的受力特点：外力的作用线与杆的轴线重合。
轴向拉压的变形特点：沿轴线方向伸长或缩短。
力学模型如图
F
轴向拉伸，对应的力称为拉力。
F
F
轴向压缩，对应的力称为压力。
F
如图所示屋架中的弦杆、牵引桥的拉索和桥塔等均为拉 压杆。
工程实例一
轴向压缩构件
工程实例二
1. 轴向拉伸和压缩
2. 剪切 3. 扭转 4. 弯曲
1. 轴向拉伸和压缩
如果在直杆的两端各受到一个外力F的作用， 且二者的大小相等、方向相反、作用线与杆件的轴 线重合，那么杆的变形主要是沿轴线方向的伸长或
缩短，这种变形称为轴向拉伸或压缩。
2. 剪切
如果直杆上受到一对大小相等、方向相反、作

dA 2 y dz 2 R2 Z 2dz
于是求得
Sy
z dA
A
R
z
O
2
R2 z2 dz 2 R3 3
2R3
zc
Sy A
3 πR2
4R 3π
2
图5-6
5. 2. 3 组合图形的面积矩计算
当图形是由若干个简单图形（如矩形、圆形和三角形等）组合而成时， 这类图形称为组合图形。由于简单图形的面积及其形心位置均为已知，而且 由面积矩的定义可知，组合图形对某一轴的面积矩等于其各简单图形对该轴 面积矩的代数和，即
5.1.2 物体重心的坐标公式
1. 重心坐标的一般公式
设有一物体，如图5-1所示。重心 c 坐 标为(xc，yc，zc)，物体的容重为 γ，总体积 为V。将物体分割成许多微小体积 ΔVi，每 个微小体积所受的重力 PGi Vi ， 其作 用点坐标(xi，yi，zi)。整个物体所受的重力
为 PG PGi 。
n
xc
A1x1c A2x2c An xnc A1 A2 An
Ai xic
i 1 n
Ai
i 1
n
yc
A1 y1c A2 y2c An ync A1 A2 An
Ai yic
i 1 n
Ai
i 1
(5-6)
【例5-1】试求图5-2 所示 Z 形平面图形的形心。
解：将Z 形图形视为由三个矩形图形组合而成，以 c1 、c2 、c3 分别表示 这些矩形的形心。取坐标系如图5-2 所示，各矩形的面积和形心坐标为
5. 2. 2 面积矩与形心的关系
由平面图形的形心坐标公式 (5-4) 和面积矩的定义可得
yc
A

边界条件(这里也就是支座处的约束条件)的示例如 下图所示。
建筑力学
若由于梁上的荷载不连续等原因使得梁的弯矩方程
需分段写出时，各段梁的挠曲线近似微分方程也就不同。
而对各段梁的近似微分方程积分时，都将出现两个积分 常数。要确定这些积分常数，除利用支座处的约束条件 外，还需利用相邻两段梁在交界处的连续条件。这两类 条件统称为边界条件。
建筑力学
在图示坐标系中，挠度w向下为正，向上为负；
顺时针转向的转角q为正，逆时针转向的转角q为负。
建筑力学
§5-2 梁的挠曲线近似微分方程及其积分（了解）
一ห้องสมุดไป่ตู้ 挠曲线近似微分方程的导出 在§4-4中曾得到等直梁在线弹性范围内纯弯曲情况
下中性层的曲率为
M EI 1
这也就是位于中性层内的挠曲线的曲率的表达式。

以x为自变量进行积分得：
q lx 2 x 3 EIw C1 2 2 3 q lx 3 x 4 EIw C1 x C2 2 6 12
建筑力学
该梁的边界条件为 在 x=0 处 w=0，
在 x=l 处 w=0
lx 2 x 3 EIw F 2 6 C1 x C2 该梁的边界条件为：在 x=0 处 w 0，w =0
于是得
C1 0，C2 0
建筑力学
从而有
转角方程
Fxl Fx2 q w EI 2 EI
Fx2l Fx3 挠曲线方程 w 2 EI 6 EI
建筑力学
当全梁各横截面上的弯矩
可用一个弯矩方程表示时(例如
图中所示情况)有
EI w M x d x C1

前述可知，按几何组成体系可分为： 几何不变体系、几何可变体系及瞬变体系。
从静力学方面探讨：
一、几何可变体系 对于几何可变体系，在任意荷载作用下一般不能
维持平衡而发生运动，因此无静力学解答。
11kN
A
B
二、几何不变体系 A、有多余约束的几何不变体系
q
X1
X2
X3
X4
结论： 有多余约束的几何不变体系 ——超静定结构的几何组成特征。
几何不变体系： 不考虑材料应变条件下，体系受到任意荷载作用 其位置、几何形状保持不变。
二、 瞬变体系
瞬变体系：某一瞬时可以产生微小运动，然后就不能继续运 动的体系。
瞬变体系
5.2 平面体系的自由度、联系的概念
一、自由度 自由度: 确定体系空间位置所需的独立坐标数，
或体系运动时可以独立改变的几何参数的数目。
A
B
(a)
附属部分
基本部分
(b)
附属部分
基本部分
(c)
例题：分析体系的几何组成
加二元体 减二元体
(a)
(b)
(c)
例题：分析体系的几何组成
EF
C
D
C
C
D
A
B
A
BA
B
EF
C
D
A
B
例题：分析体系的几何组成
C
B
D
I
II
A
III
利用规则进行几何组成分析的注意事项：
（1）体系只用三根不全交于一点也不全平行的支座链杆与基础 相连，只需对体系本身作几何组成分析。
其中：m---刚片数; h ---单铰数; r ---支座链杆数 如遇复铰：相当于（n-1）个单铰。

四川建筑职业技术学院
§5－2 杆件的变形形式
5－ 2 － 1 基本变形
轴向拉伸和压缩 剪切
基本变形
扭转 弯曲
四川建筑职业技术学院
轴向拉伸和压缩： 受力特点:直杆的两端各受到一个外力F的作用，且二者的
大小相等、方向相反，作用线与杆件的轴线重合 。
变形特点: 沿轴线方向的伸长或缩短。
(a) 轴向拉伸
弯矩图绘在梁的受拉侧，而不须标明正负号。 此法称为内力方程法，这是绘制内力图的基本方法。
四川建筑职业技术学院
例5－4 绘制图所示简支梁的剪力图和弯矩图。 解 （1）求支座反力。 FA= FB=
ql 2
（2）列剪力方程和弯矩方程
FS ( x) FA qx ql qx 2
（0＜x＜l ) （0≤x≤l）
力F作用的C处，剪力图出现
向下的突变，突变值等于集中 力的大小。
四川建筑职业技术学院
由弯矩方程知，两段梁的 弯矩图均为斜直线，但两
直线的斜率不同，在C处
形成向下凸的尖角。
四川建筑职业技术学院
(b) 轴向压缩
四川建筑职业技术学院
剪切： 受力特点:直杆受到一对大小相等、方向相反、作用线平行
且相距很近的外力沿垂直于杆轴线方向作用 。
变形特点:杆件的横截面沿外力的方向发生相对错动 。
四川建筑职业技术学院
扭转： 受力特点:直杆的两端各受到一个外力偶Me的作用，且二者
的大小相等、转向相反，作用面与杆件的轴线垂直 。
实际情况：组成构件材料的各个晶粒是各向异性的。
理论分析：材料在任何一个方向的力学性能均可用于其他 方向。 说明：构件内所含微粒的数目极多，在构件内的排列又是 极不规则的，在宏观的研究中固体的性质并不显示方向的差

第五章 空间任意力系5.1解：cos 45sin 60 1.22x F F KN ==o ocos45cos600.7y F F KN ==o osin 45 1.4z F F KN ==o 6084.85x z M F mm KN mm ==⋅5070.71y z M F mm KN mm ==⋅ 6050108.84z x y M F mm F mm KN mm =+=⋅5.2 解：21sin cos sin x F F F αβα=- 1cos cos y F F βα=-12sin cos z F F F βα=+12sin cos x z M F a aF aF βα==+1sin y M aF β= 121cos cos sin cos sin z y x M F a F a aF aF aF βααβα=-=---5.3解：两力F 、F ′能形成力矩1M1502M Fa KN m ==⋅ 11cos 45x M M =o 10y M = 11sin 45z M M =o1cos 4550x M M KN m ==⋅o 11sin 4550100z z M M M M KN m =+=+=⋅o22505C z x M M M KN m =+=⋅63.4α=o90β=o26.56γ=o5.4 如图所示，置于水平面上的网格，每格边长a = 1m ，力系如图所示，选O 点为简化中心，坐标如图所示。

已知：F 1 = 5 N ，F 2 = 4 N ，F 3 = 3 N ；M 1 = 4 N·m，M 2 = 2 N·m，求力系向O 点简化所得的主矢'R F 和主矩M O 。

题5.4图解：'1236R F F F F N =+-=方向为Z 轴正方向21232248x M M F F F N m =++-=⋅ 1123312y M M F F F N m =--+=-⋅2214.42O y x M M M N m =+=⋅56.63α=o 33.9β=-o 90γ=o5.5 解：120,cos30cos300AxBx X F F T T =+++=∑o o 210,sin30sin300Az Bz Z F F T T W =+-+-=∑o o120,60cos3060cos301000zBx M T T F =---=∑o o 120,3060sin3060sin301000xBz M W T T F =-+-+=∑o o 21110,0yMWr T r T r =+-=∑20.78,13Ax Az F KN F KN =-= 7.79, 4.5Bx Bz F KN F KN == 1210,5T KN T KN ==5.6题5.6图2a ，AB 长为2b ，列出平衡方程并求解0Bz F =100Az F N =5.7xyzBAFF 140cm60cm40cm20c m20cmBxF BzF AzF AxF题5.7图解：10,0AxBx X F F F =++=∑0,0AzBz Z F F F =++=∑10,1401000zBx M F F =--=∑10,20200yM F F =-=∑ 0,401000xBz MF F =+=∑320,480Ax Az F N F N ==-1120,320Bx Bz F N F N =-=-800F N =5.8题5.8图解：G 、H 两点的位置对称于y 轴BG BH F F =0,sin 45cos60sin 45cos600BGBH Ax X F F F =-++=∑o o o o 0,cos45cos60cos45cos600BGBH Ay Y F F F =--+=∑o o o o 0,sin60sin600Az BG BH Z F F F W =---=∑o o 0,5sin 45cos605sin 45cos6050xBG BH MF F W =+-=∑o o o o 28.28,0,20,68.99BG BH Ax Ay Az F F KN F F KN F KN ===== 5.95.10。

34
图 5.11
35Biblioteka 图 5.12365.4.2 静定梁的三种基本形式 作用在梁上的荷载通常有三种，即：集中荷载 F、分布荷载 q和集中力偶 M。这三种荷载在上一 篇中均作过讨论。 在平面弯曲中，我们要研究的静定梁有三种基 本形式，即：简支梁、外伸梁和悬臂梁，见图5.11 。这三种形式的静定梁，我们在上一篇中也都均作 过讨论。
25
图 5.6
26
图 5.7
27
5.3.2 扭转轴内力———扭矩的计算 对于机械上的轴而言，作用于轴上的外力偶 Te往往不是直接给出的，给出的经常是轴所传送的 功率 P 和轴的转速 n。根据动力学知识，可以导出 Te、P 和 n的关系如下：
28
图 5.8
29
5.3.3 扭转轴的内力图 若作用于扭转轴上的外力偶矩超过两个，则在 杆件的各横截面上，扭矩一般不尽相同。这时往往 用扭矩图表示扭矩沿杆件轴线的变化情况。关于扭 矩图的绘制，我们通过下面的例题来说明。 例5.2 如图5.9所示的传动轴，轴的转速为 300r/min，主动轮 A输入的功率 PA=60kW，两个 被动轮B、C输出的功率分别为PB=20kW、 PC=40kW。作其扭矩图。
15
图 5.2
16
1）轴力 N：分布内力系的与杆件轴线相重合 的合力。 2）扭矩 T：分布内力系的作用平面与横截面 平行的合力偶矩。
17
3）剪力 V：分布内力系的相切于截面的合力 。 4）弯矩 M：分布内力系的作用平面与横截面 垂直的合力偶矩。
18
在本章中要经常用到截面法求内力，为了便于 学习，我们把其计算步骤归纳如下： 第一步 欲求哪个截面的内力，就沿该截面假想地 把构件分成两部分，选任意一个截离体为研究对象 ，并弃去另一截离体； 第二步 用作用于截面上的内力代替弃去部分 对留下部分的作用； 第三步 对研究对象列平衡方程，解方程确定未知 的内力。

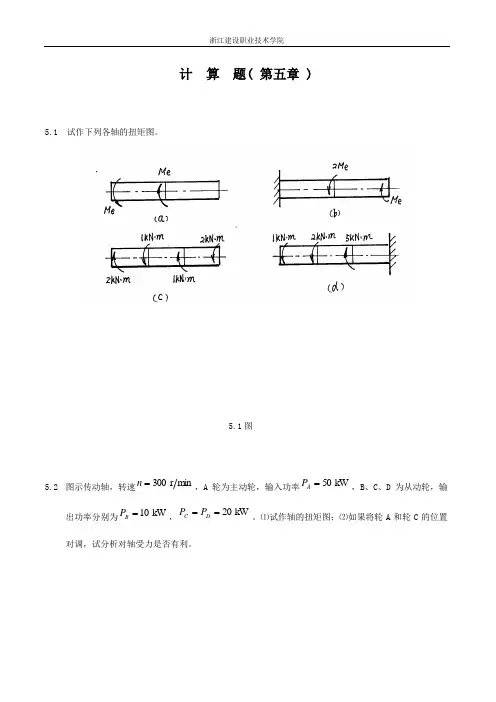
计算题( 第五章 ) 5.1 试作下列各轴的扭矩图。

5.1图5.2图示传动轴，转速m inr300=n，A轮为主动轮，输入功率kW50=AP，B、C、D为从动轮，输出功率分别为kW10=BP，kW20==DCPP。

⑴试作轴的扭矩图；⑵如果将轮A和轮C的位置对调，试分析对轴受力是否有利。

题5.2图 题5.3图5.3 T 为圆轴横截面上的扭矩，试画出截面上与T 对应的切应力分布图。

5.4 图示圆截面空心轴，外径mm 40=D ，内径mm 20=d ，扭矩m kN 1⋅=T ，试计算mm 15=ρ的A 点处的扭转切应力A τ以及横截面上的最大和最小的扭转切应力。

题5.4图5.5 一直径为mm 90的圆截面轴，其转速为m in r 45，设横截面上的最大切应力为MPa 50，试求所传递的功率。

5.6 将直径mm 2=d ，长m 4=l 的钢丝一端嵌紧，另一端扭转一整圈，已知切变模量GPa 80=G ，求此时钢丝内的最大切应力m ax τ。

5.7 某钢轴直径mm 80=d ，扭矩m kN 4.2⋅=T ，材料的许用切应力[]MPa 45=τ，单位长度许用扭转角[]m )(5.0 =θ，切变模量GPa 80=G ，试校核此轴的强度和刚度。

5.8 阶梯形圆轴直径分别为d1=40mm ，d2=70mm ，轴上装有三个皮带轮，如图所示。

已知由轮3输入的功率为N3=3kW ，轮1输出的功率为N1=13kW ，轴作匀速转动，转速n=200r/min ，材料的许用切应力[]MPa 60=τ，GPa 80=G ，许用扭转角[]m 2=θ＝。

试校核轴的强度和刚度。

题5.8图5.9 一钢轴受扭矩m kN 2.1⋅=T ，许用切应力[]MPa 50=τ，许用扭转角[]5.0 =θ，切变模量GPa 80=G ，试选择轴的直径。

5.10 桥式起重机题 5.10图所示。

若传动轴传递的力偶矩m kN M e ⋅=08.1，材料的许用切应力[]MPa 40=τ，GPa 80=G ，同时规定=][θ0.5°/m 。

624435-2e 解：先后取4、5、3、6、2结点为研究对象，受力如图所示。

4结点：⎩⎨⎧=-=→⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+⎪⎭⎫ ⎝⎛⨯--=+⎪⎭⎫ ⎝⎛⨯--→⎩⎨⎧=⨯--=⨯--→⎪⎩⎪⎨⎧==∑∑kN kN 316.30232202323210cos 0sin 10045432243452243434543N N N N N N N N X Y αα 5结点：⎩⎨⎧-===→⎩⎨⎧=--=-→⎪⎩⎪⎨⎧==∑∑kN kN130100455456535654NN N N N N Y X3结点：3432353432363432363635343236320cos cos cos 0sin sin sin 00222 1.580 4.74X N N N N N N Y N N N N N N N N N αααααα⎧=--=⎧⎪→→⎨⎨+-+==⎩⎪⎩--=⎧⎪⎪=⎧⎪→⎨⎨+-+==-⎩⎪⎪⎪⎩∑∑kN kN 6结点：656367676263620cos 0 4.501sin 0 1.500X N N N N N N N Y αα⎧=+-==⎧⎧⎪→→⎨⎨⎨---==-=⎩⎩⎪⎩∑∑kN kN2结点：23212723212726232127232127260cos cos cos 0sin sin sin 0002240X N N N N N N N Y N N N N N N N ααβααβ⎧=--=⎧⎪→→⎨⎨-++==⎩⎪⎩⎧-=⎪⎪⎪⎪⎨⎪++=⎪⎪⎪⎩∑∑2127 6.321.803N N =-⎧→⎨=⎩kN kN(a)方法二：内力分量法，先后研究4、5、3、6、2结点（1）4结点：43434345434543450101 3.1603Y Y Y NN X N X NX⎧=--==-=-⎧⎧⎧⎪→→→⎨⎨⎨⎨--==-==⎩⎩⎩⎪⎩∑∑kNkN由比例：434322/3X Y==，知：434545453.1633N X N X=-=-=-=，。

10
FB=7q l/8
(e)
A
ql q ql
2
A
B l A FQ 图 B
B
q l /2
2
ql M图
2
【解】悬臂梁可以不必求支座反力，可从右向左计算。 (1)定控制点B、C、A (2)计算控制点剪力，按规律连线，得FQ图 FQB左=0，FQA右=ql , AB段上有均布荷载，FQ图为向下斜直线。 (3)计算控制点弯矩，按规律连线，得M图 MB=ql2 , MA=ql2 - ql×l/2=ql2/2, AB段上有均布荷载，M图为 向下凹的抛物线。
12
(g)
C
F=qa q A a 2a FA=3qa/2
qa
q
C A
qa/2 B qa/2 qa FQ 图 E
0.5qa D C A 0.5qa M图
D
0.5qa
D 2a
B a FB=3qa/2
E
B
E
【解】结构对称，荷载对称，则反力和M图对称，FQ图反对称。 (1)求支座反力 FA=3qa/2, FB=3qa/2 (2)定控制点A、C、D (3)计算控制点剪力，按规律连线，得FQ图 FQC右=0， FQA左=-qa ; 从A左到A右跨过集中力FA,FQ图向上突变， FQA右= FQA左+FA=qa/2, FQD左= FQA右=qa/2,AD段无荷载，FQ图水平 线；从D左到D右跨过集中力F, FQ图向下突变，FQD右=-qa/2。 (4)计算控制点弯矩，按规律连线，得M图 MC=0，MA=-qa2/2,CA段均布荷载，M图向下凹抛物线； MD=-qa ×5a/2+FA×2a=-5qa2/2+6qa2/2=qa/2, AD段无荷载， FQ为正值，M图为向下斜直线。

1.已知一剪支梁如图所示，荷载P1=24KN，P2=80KN，求梁跨中截面E处的剪力Q E和弯矩M E。

解（1）求支反力，梁上无水平力，故只有垂直方向支反力V A和V B。

假设支应力的方向如图所示。

由平衡条件∑M A=0 V B•4－P1•1－P2•2.5=0V B=1/4(24•1＋80•2.5)=56KN∑M B=0 V A•4－P1•3－P2•1.5=0V A=1/4(24•3+80•1.5)=48KN用∑My=0校核V A＋V B－P1－P2=48＋56-24-80=0校核结果表明支反力计算无误。

（2）用截面法求剪力Q E和弯矩M E用截面法在截面E处切开，考察左段梁的平衡，并假设Q E和M E均为正值，如图b所示。

由∑y=0V A－P1－Q E=0Q E= V A－P1=48－24=24KN∑M E =0M E－V A•2＋P1•1=0M E= V A•2－P1•1=48•2－24•1=72KN•M得到的QE和ME 均为正值，说明假设方向对,E截面上的剪力QE和弯矩ME 均为正值。

2.简支梁受均布力q和集中力偶ME=ql2/4的作用，如图a所示。

求C截面的剪力和弯矩。

解（1）支反力此题求支反力时可用叠加法求较为方便，即分别求出在q和M E单独作用时梁的支反力，然后求其代数和：V A=ql/2+M E/L= ql/2+ ql2/4=3ql/4V B= ql/2-M E/L= ql/4再由∑y=0校核V A＋V B－ql=3ql/4+ ql/4－ql=0上式表明支反力计算无误。

在求C截面的内力时，因为C截面作用有集中力偶M E，故C截面稍左面和稍右面的内力可能不同，现分别计算如下：（2）求C截面稍左截面处的剪力Q C左和弯矩M C左，如图b由∑y=0Q C左－V A+ qL/2=0故Q C左= V A－qL/2= 3ql/4－ql/2= ql/4由∑M C=0M C左－V A L/2+ qL/2·L/4=0故M C左= V A L/2－qL/2·L/4= 3qL/4·L/2－qL/2·L/4= ql2/4（3）求C截面稍右截面处的剪力Q C右和弯矩M C右由∑y=0Q C右－V A+ qL/2=0故Q C左= V A－qL/2= 3ql/4－ql/2= ql/4由∑M C=0M C右－V A L/2+ qL/2·L/4+=0故M C左= V A L/2－qL/2·L/4= 3qL/4·L/2－qL/2·L/4= ql2/43.简支梁作用均布荷载q，如图所示。

（3）、桁架：各杆中只有轴力，且各杆截面和各杆 轴力沿杆长一般为常数。
kP N NP N N Pl ds EA EA (5 - 16)
（4）、组合结构：一些杆件主要受弯，一些杆件只 有轴力。
kP MMP N N Pl ds EI EA (5 - 17)
注:
1、公式（5-13）为结构由于荷载作用引起的位移计算公式。 2、正负号：⊿kP 若为正值，则所求位移与虚拟状态中单位力P =1 的方向相同，反之为负。 3、位移计算问题转化为两种状态下的内力计算问题。 其中外力功恰好等于所求位移。 4、单位荷载法不仅可以用来计算结构的线位移，也可以用来计算结 构其他性质的位移。只要求虚拟状态中的单位力为与所求位移相对应的 广义单位荷载即可(P207:图5-13)。
例1
简支梁的位移计算。 求图示简支梁中点C的竖向 位移⊿CV 和截面B的转角φB。 解： 1、求C点的竖向位移
A x l/2
q
x C
ql/2
⊿CV
l/2
φB
B ql/2
虚拟状态如图：
实际状态 MP=q(lx-x2) /2 虚拟状态 M= x / 2
P=1
A 1/2 x C 1/2 B
(因对称，只计算一半)
同一体系： A Pi
i j
B
A
i
j
B
力状态 i
⊿ij
位移状态 j
计算虚功时，从第 i 个状态取力，从第 j个状态取位移。
虚功：
Tij Pi ij
4、内力的虚功 （变形虚功）
可以由任意原因引起 P2 M q ds q A C Q+dQ N+dN M+dM ds D B v ds D A’ C’ C’’ A ds C

第五章 梁地变形测试练习1. 判断改错题5-1-1 梁上弯矩最大地截面,挠度也最大,弯矩为零地截面,转角亦为零. （ ） 5-1-2 两根几何尺寸、支承条件完全相同地静定梁,只要所受荷栽相同,则两梁所对应地截面地挠度及转角相同,而与梁地材料是否相同无关. （ ） 5-1-3 悬臂梁受力如图所示,若A 点上作用地集中力P 在A B 段上作等效平移,则A 截面地转角及挠度都不变. （ ） 5-1-4 图示均质等直杆（总重量为W ）,放置在水平刚性平面上,若A 端有一集中力P 作用,使A C 部分被提起,C B 部分仍与刚性平面贴合,则在截面C 上剪力和弯矩均为零. （ ）5-1-5 挠曲线近似微分方程不能用于求截面直梁地位移. （ ） 5-1-6 等截面直梁在弯曲变形时,挠度曲线地曲率最大值发生在转角等于零地截面处.（ ） 5-1-7两简支梁地抗刚度E I 及跨长2a 均相同,受力如图所示,则两梁跨中截面地挠度不等而转角是相等地. （ ） 5-1-8 简支梁在图示任意荷载作用下,截面C 产生挠度和转角,若在跨中截面C 又加上一个集中力偶M 0作用,则梁地截面C 地挠度要改变,而转角不变. ( )5-1-9 一铸铁简支梁,在均布载荷作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面地应力及变形均相同. （ ） 5-1-10 图示变截面梁,当用积分法求挠曲线方程时,因弯矩方程有三个,则通常有6个积分常量. （ ）题5-1-3图题5-1-4图题5-1-8图题5-1-7图题5-1-9图2．填空题5-2-1 挠曲线近似微分方程EIx M x y )()("-= 地近似性表现在 和 . 5-2-2 已知图示二梁地抗弯度E I 相同,若使二者自由端地挠度相等,则=21P P .5-2-3 应用叠加原理求梁地变形时应满足地条件是： . 5-2-4 在梁地变形中挠度和转角之间地关系是 . 5-2-5 用积分法求图示地外伸梁（B D 为拉杆）地挠曲线方程时,求解积分常量所用到地边界条件是 ,连续条件是 .5-2-6 用积分法求图示外伸梁地挠曲线方程时,求解积分常量所用到边界条件是 ,连续条件是 .5-2-7 图示结构为 次超静定梁.5-2-8 纯弯曲梁段变形后地曲率与外力偶矩M 地关系为 ,其变形曲线为 曲线. 5-2-9 两根E I 值相同、跨度之比为1：2地简支梁,当承受相同地均布荷载q 作用时,它们地挠度之比为 .5-2-10 当梁上作用有均布荷载时,其挠曲线方程是x 地 次方程.梁上作用有集中力时,挠曲线方程是x 地 次方程.梁上作用有力偶矩时,挠曲线方程是x 地 次方程.5-2-11 图示外伸梁,若A B 段作用有均布荷载,B C 段上无荷载,则A B 段挠曲线方程是x 地 次方程；B C 段挠曲线方程是x 地 次方程.5-2-12 减小梁变形地主要途径有： , , .题5-2-2图题5-2-7图题5-2-6图xC 题5-2-11图5-2-13 已知梁地挠度曲线方程为)3(6)(2x l EIPx x y -=,则该梁地弯矩方程为 . 5-2-14 梁地变形中,挠度和截面弯矩M 地关系是 ,挠度和截面剪力Q 地关系是 . 5-2-15 为使图示A B 段地挠曲线为一直线,则x = .5-2-16 要使图示简支梁地挠曲线地拐点位于距A 端l /3处,则M 1:M 2= .5-2-17 图示静定梁,其B D 上无荷载作用,若已知B 截面地挠度y B ,则C 截面地挠度y C = ,D 截面地转角θD = .3．选择题5-3-1 简支梁长为l ,跨度中点作用有集中力P ,则梁地最大挠度f =( ) （E I =常量）A .EI Pl 483B .EI Pl 484C .EI Pl 38455D .EIPl 335-3-2 悬臂梁长为l ,梁上作用有均布荷载q ,则自由端截面地挠度为. ( )A .EI ql 64B .EI ql 63C .EI ql 84D .EIql 835-3-3 两梁尺寸及材料均相同,而受力如图示,则两梁地A ． 弯矩相同,挠曲线形状不相同B ． 弯矩相同,挠曲线形状相同C ． 弯矩不相同,挠曲线形状不相同D ． 弯矩不相同,挠曲线形状相同5-3-4 图示(a )、(b )两梁,长度、截面尺寸及约束均相同,图(a )梁地外力偶矩作用在C 截面,图(b )梁地外力偶矩作用在B 支座地右作侧,则两梁A B 段地内力和弯曲变形地比较是 ( ).A .内力相同,变形不相同B ．内力及变形均相同C ．内力及变形均不相同D ．内力不相同,变形相同5-3-5 当用积分法求图示梁地挠度曲线方程时,在确定积分常量地四个条件中,除x =0,题5-2-17图2 题5-2-16图题5-2-15图题5-3-4图C 0 (a )(b )题5-3-3图θA =0;x =0,y A =0外,另两个条件是 ( ) .A ．（y c ）左= (y c )右,（θC ）左=（θC ）右B ．（y c ）左= (y c )右,y B =0C ．y C =0,y B =0D ．y B =0,θC =05-3-6 图示简支梁在分布荷载q （x ）=f （x ）作用下,梁地挠度曲线方程为⎰⎰++-=,)()(D Cx dxdx x M x EIy ,其中,积分常量 ( ).A .0,0==D CB .0,0≠=DC C .0,0≠≠D C D .0,0=≠D C5-3-7 挠曲线方程中地积分常梁主要反映了 A ． 对近似微分方程误差地修正 B ． 剪力对变形地影响 C ． 约束条件对变形地影响D ． 梁地轴向位移对变形地影响5-3-8 图示悬臂梁在B 、C 两截面上各承受一个力偶矩作用,两力偶矩大小相等,转向相反,使梁产生弯曲变形.B 截面地变形为 ( ). A ．0,0≠=θy B . 0,0=≠θyC ．0,0≠≠θyD .0,0==θy5-3-9 图示简支梁受集中力作用,其最大挠度f 发生在（ ）. A ．集中力作用处 B .跨中截面 C ．转角为零处 D .转角最大处5-3-10 两简支梁E I 及l 均相同,作用荷载如图所示.跨中截面C 分别产生挠度y C 和转角θC ,则两梁C 点地挠度及两梁C 点地转角有 （ ）. A ．θC 相等,y C 不相等 B .θC 不相等,y C 相等 C ．θC 和 都不相等 D .θC 和y C 都相等4．计算题题5-3-5图B题5-3-6图题5-3-8图题5-3-10图5-4-1 试画出图示各梁挠曲线地大致形状.5-4-2 一简支梁承受图示分布荷载q =K x 2（K 为已知）,试求此梁地挠曲线方程（设E I =常量）. 5-4-3 已知图示梁地带积分常量地挠曲线方程为)2()2(2412163)210(12163)(2222423222221111312121l x lD x C l x q x ql x ql EIy x D x C x ql x ql x EIy ≤≤++-+-=≤≤++-=试求方程中地积分常量.5-4-4 试用叠加法求图示梁B 点地挠度和转角.（E I =常量）5-4-5 外伸梁受图示荷载作用,试求C 截面地挠度和A 截面地转角.（E I =常量.）5-4-6 矩形截面梁A B 地抗弯刚度为E I ,受力如图示.试问B 端支座向上抬高Δ为多少时,梁地A 截面地弯矩和C 截面地弯矩绝对值相等.（材料地抗拉与抗压性能相同）5-4-7 图示弯曲地钢板梁A B ,截面为矩形,宽度为b ,高度为h ,钢板放在刚硬地面上时原有曲率半径为ρ,在两端受力P 作用使其平直,则将有均布压力作用于刚硬地面C -C 上.已知刚梁E （弹性模量）,试求所需地P 力及其在压平时梁内地最大正应力.5-4-8 长度为l 、抗弯刚度为E I 地悬臂梁A B ,受均布荷载q 作用而弯曲时,与半径为r 地刚性圆柱面接触,如图所示.试求当梁上某一段A C 与刚性圆柱面在C 点接触（假设C 点与梁左端(a )(c )(f )(b ) (d ) (e ) 题5-4-1图 题5-4-4图 B 题5-4-3图 x 题5-4-6图 题5-4-5图 题5-4-7图CA 地距离为x ）时,B 点地挠度. 5-4-9 单位长度重量为q 、抗弯刚度为E I 地矩形截面钢条,放置在水平刚性面上,刚条地一端伸出水平面一小段CD ,如图所示.若伸出长度为a ,试求刚条翘起而不与水平面接触地C D 段地长度b .5-4-10 超静定梁如图所示,A B 段内作用有均布荷载q ,当C 支座向下沉陷EIql 964=∆时,试求梁地反力.5-4-11矩形截面悬臂梁如图所示,梁长为l ,在沿其截面高度h 承受非均匀加热,设梁顶部温度改变为t 1,底部温度改变为t 2,且t 2>t 1.温度沿截面高度呈线形改变.材料地线膨胀系数为a ,弹性模量为E ,由于不均匀受热而使梁发生弯曲变形,当梁地悬臂端施加偶矩M 0时,能使梁展直.问应施加多大地外力偶矩?5-4-12 悬臂梁A B 和C D 地自由端处用拉杆B C 相连,受力如图所示,若A B 梁和C D 梁地抗弯刚度E I 相等,试求在下列两种情况下C 点地挠度. (1) 当B C 杆为刚性杆,即E A = 时； (2) 当B C 杆长为2l ,2lEI EI =时.5-4-13 A B 与B C 两梁铰接于B ,如图所示.已知两梁地抗弯度相等,P =40k N /m ,,试求B 点地约束力.8题5-4-10图 题5-4-9图题5-4-11图 2 题5-4-12图25-4-14 悬臂梁和简支梁材料和截面均相同.已知E 及未受力前A B 梁B 点与C D 梁中点之间地间隙Δ（垂直距离）,如图所示,当受P 力后A B 梁在B 点地挠度大于Δ,试求各梁地支座反力.5-4-15 具有初始挠度地A B 梁如图所示,梁地E I 和l 均为已知.当梁上作用有三角形分布荷载时（q 0已知）,梁便呈直线形状.试求梁地初始挠曲线方程.5-4-16 试根据对称性求图示梁地挠曲线方程.E I =常量5-4-17 两端固定地等截面梁,梁上作用一外力偶矩M 0 ,如图所示.欲使在固定端A 地反力偶矩M A 为零,则力偶矩M 0应作用在梁上何位置？（即x =？）测试练习解答1． 判断改错题5-1-1 ×.挠度和转角不仅与弯矩有关,而且与边界位移条件也有关,例如,当悬臂梁自由端作用有集中力P 时,自由端地M =0,但挠度和转角都是最大值. 5-1-2 ×.凡弹性变形均与材料地弹性模量值有关.5-1-3 √.外力在研究地梁段以外,用等效力系代替不影响研究段地内力及变形. 5-1-4 ×.在C 截面上弯矩为零而剪力不为力零. 5-1-5 ×.可以用于变截面梁,只是分母中地I z 不同. 5-1-6 ×.根据,)()("1EI x M x y =±=ρ可知曲率ρ1最大值应在M 最大地截面处（E I =常量时）.5-1-7 √.若将2q 分解成正对称和反对称两组,就可明显看出,在正对称地q 作用下C 点有挠度,转角等于零.5-1-8 ×.在C 截面加上一力偶矩后C 截面地挠度不变,而转角改变.5-1-9 ×.应力不同,变形相同.因为变形只与I z 有关,而T 形截面无论┬是┴还是,其惯性矩I z 是相等地.而应力不仅与I z 有关而且还与y m a x （上下边缘到中性轴地距离）有关,┬这种方法地最大拉应力比┴这种方法地最大拉应力要大.q 题5-4-15图题5-4-13图l /2 题5-4-14图题5-4-9解图8题5-4-17图题5-4-16图 q a 2/25-1-10 ×弯矩方程式有三个,但积分时要分成四段,因截面改变处要分段. 2．填空题5-2-1 忽略剪力Q 地影响；1)(1'≈+y5-2-2 8.因33231)2(3a a P EI a P =,所以8)2(3321==aa P P 5-2-3 小变形及材料为线弹性 5-2-4 )()('x x y θ= 5-2-5 ;,0,0BD B A l y l x y x ∆====5-2-6AA A AB A y y y y ))(,)()(;0,02121====θθ5-2-7 二次 5-2-8EIM±=ρ1；圆弧线 5-2-9 1：16.因16/1384)2(5/384)(544=EIl q EI l q 5-2-10 4；3；2 5-2-11 4；15-2-12合理安排受力,减小M ；减小l ；加大E I5-2-13 )()(x l P x M -= 5-2-14 EIx Q x y EIx M x y )()(;)()('''"-=-= 5-2-15 l -a 5-2-16 1/2 5-2-17 a y y B C 2/21=3．选择题5-3-1 A 5-3-2 C 5-3-3 A 5-3-4 B 5-3-5 B 5-3-6 D 5-3-7 C 5-3-8 D 5-3-9 C 5-3-10 B 4 计算题5-4-2 梁地挠曲线方程为（1） 求分布荷载地合力 ⎰==tKl dx x q P 033)(求合力作用点到点地距离：l P x dx x q d t43)(0=⋅=⎰（2） 求反力：443,12433Kl P R Kl P R B A ==== （3） 列43)(3xKx x R x M A ⋅-⋅= （4） 代入EI x M y )("-=中并积分,由边界条件确定0,905=-=D Kl C 所以 )45(360)(5523l x x l EIKxx y --=5-4-3 （1）边界条件：,0,011'1===θy x 解出01=C,0,011==y x ,解出01=D（2）连续光滑条件：,)()(,22'1'21C C y y l x x ===解出 02=C ,)()(,22121C C y y lx x ===,解出02=D5-4-4 （1）只有q 作用时,EIql y EI ql q B q B 8)(,6)(43==θ （2）只有P =q l 作用时:22)2(3)2(2)()()(,2)2())(232lEI l P EI l P l y y EIlP P C P C P B P C P B ⋅+=⋅+===θθθ（3）然后两者叠加：EI ql P B q B B 247)()(3=+=θθθEI ql y P B q B B 4811)()(4=+=θθ5-4-5 （1）只有2021ql M =作用时,())(2)(,)(3)(0000↑⋅=↵=ly EIl M M B MC M A θθ（2）只有q 作用时,EI lql q A 6)81()(2⋅=θ(EIl q lEI l ql y q C 8)2(23)81()(42+⋅⋅=（3）叠加：)(3845)()(,487)()(4300↑=+==+=EIqly y y EIql q C M C C q A M A A θθθ 5-4-6 （1）将B 约束解除,用反力R B 代替. （2）由A 、C 两截面地弯拒绝对值相等可列方程l R l P l R B B -=221,解出)(3↑=P R B （3）在 P 和3PR B =作用下,求B 点地挠度. )(1443]22)2(3)2([3323负号表示向上EIPl EI l R l EI l P EI l P B -=-⋅+=∆5-4-7 这是一个求变形和应力地综合题. （1） 求压力P ：依题意,当两端加上力P 后使其平直且在C -C 面上产生均布压力q ,因此可以将其简化为两端铰支地简支梁,其反力均为P ,C -C 面上地均布压力lPq 2=. （2） 简支梁在均布压力q 作用下中点地挠度等于δ,δ=EIql 38454,解出3)(516l h Eb P δ= (3) δδ2max max 2max 524,81l EhW M ql M z ===5-4-8 当q =0 时,A B 梁上没有外力,梁轴线平直,A 端曲率为零.当荷载q 由0增加,到q 0时,梁A 端地弯矩为2021l q -,A 端曲率rA 11=ρ,即有 2022,21)(1rl EIq EIlq EI x M r ==-=得当0q q ≥ 时,梁上某一段A C 与刚性面接触,C 点端曲率为,)(211)(12EIx l q r x -==ρ解得 qrEIl x 2-= (2) B 点地挠度包括三部分,即 321)()()(B B B B y y y y ++=① (y B )1 为C 点地挠度221)2(212)(qrEI l r r x y B -==② (y B )2为C 点地转角引起B 点地挠度qrEIqr EI l r y B 2)2(1)(2-=③ (y B )3为C D 段当作悬臂梁在q 作用下B 点地挠度 2432)(8)(qrEI x l EL q y B =-=④ 以上三种挠度叠加,即为点B 地挠度)(212l qrEI r y B -=5-4-9 由于A B 段平直,所以B 点地弯矩、转角及挠度均等于零.B 点和C 点与刚性平面接触,简化为铰支座,则B C D 端简化为外伸臂梁.在该梁上作用有均布荷载q (自重)但要满足0=B θ地条件,如图（a ）所示.求θB 时,可取B C为简支梁,而C D 上地均布力向C 点平移得一集中力q a 和一力偶矩2021qa M =,如图（b ）所示.根据θ=0地条件求解b ,即 06)21(2)()(230=⋅-=+=EIb qa EI qbM B q B B θθθ解出 a b 2=5-4-10 这是一个在外力作用及有支座位移下地一次超静定问题.将C 约束解除,用约束力RCq a 2/2代替,成为基本结构.变形协调条件是EIql y C 964-=∆=（向上）.在q 和R C 共同作用下求出EI l R EI ql y C C 2434834-= ,并将其代入变形协调方程,解出)(121↑=ql R C ,然后根据平衡方程求出R A 、R B 即 ).(85),(2411↓=↓=ql R ql R B A , . 5-4-11 梁在不均匀温度地变化下,发生弯曲和伸长变形,由于t 2>t 1,所以轴线以上伸长少,而轴线以下伸长大,使梁发生凸向下地弯曲变形,B 点有向上地挠度,设为(ΔB ) t .在梁地自由端上作用力偶矩M 0 后,能使变形展直,B 点又回到原水平位置,设M 0作用下B 点地挠度为0)(M B ∆.由(ΔB ) t = 0)(M B ∆,变形条件可以解出M 0值.其中EIl M h l t t a M B t B 2)(,2)()(202120=∆-=∆,代入变形条件中解得hEIt t a M )(120-=.5-4-12 （1）当杆B C 地E A = 时,杆不变形,将B C 杆切短,用R B C 代替其约束,取基本结构.变形协调条件为y B =y c (↓) ,解出EIPl EI l R y y PR BC B C BC 9653,32533====则 . （2）当2lEAEA =时,杆B C 有伸长变形,同样将B C 杆切段,用R B C 代替,取基本结构.这时地变形协调条件为 EIl R EA l R l l y y BC BC BC BC B C 22,3=⋅=∆∆+= ,解出 EIPl y P R C BC33625,5653==.5-4-13 这是一个二次超静定问题.若不计杆地轴向变形,则结构无水平约束力,将该问题简化为B 铰只有一个垂直约束力为未知数地结构.在B 铰处切断,用约束力R B 代替,取出基本结构,并根据B 点地变形协调条件建立补充方程(y B )A B =(y B )B C⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯+⨯=⨯-⨯=2223234)(,3484)(23444EI P EI P EI R y EIR EI q y B BCB B ABB 代入变形协调方程求出 R =8.75k N5-4-14 因为A B 梁点地挠度大于Δ,因此在P 作用下A B 梁与C D 梁共同受力,成了一次超静定问题.若将两梁拆开,约束反力R 分别作用在梁上,则成为基本结构.变形协调方程为∆+=CD B AB B y y )()(将 EIRl y EI l R P y CD B ABB 48)(,3)()(33=-= ,代入变形协调方程解出∆-=317481716lEIP R ,并由平衡条件求个梁地约束反力, .)(,,2l R P M R P R RR R A A D C -=-=== 5-4-15 （1）将A 端地约束反力用M A 、R A 表示； （2）列出弯矩方程30206121)(x q lx q x R M x M A A +-+= （3）代入挠曲线近似微分方程并积分；(4)根据A 端地位移边界条件求出 C =0,D =0 ;(5)根据B 端地边界条件,即 x =l 时,M =0 （即 y ” =0）；x =l 时,y B =0解出l q R l q M A A 02052,151=-= ； (6)最后地出初始挠度曲线方程 )584(120322320x lx x l l lEIx q y +-+--= . 5-4-16 结构为对称,而外力M 0为反对称.若将结构取出一半（如取左边一半）,则成为A 端为固定端、C 端为铰支座地单跨超静定梁.在C 截面上作用有力偶矩20M ,A C 段地长度为2l.只要解出A C 梁地挠度方程即可,C B 段地挠度曲线与A C 段组成反对称地挠度曲线,)2(41)(3020x lM x M EI x y --=. 5-4-17 若不计梁A B 地轴向变形,这是一个二超静定问题.将A 固定端解除用约束反力R A 、M A =0,代替,并由A 点地θA =0、y =0地变形条件建立两个补充方程,并令M A =0,求出3lx =.。