电磁场与电磁波基础(第6章)..

第一章习题解答【习题1.1解】222222222222222222222222222222222222cos cos cos cos cos cos 1xx x y z yx y z z x y z x y z x y z x y z x y z x y z x y z 矢径r 与轴正向的夹角为，则同理，矢径r 与y 轴正向的夹角为，则矢径r 与z 轴正向的夹角为，则可得从而得证a a b b g g a b g =++=++=++++=++++++++++==++ 【习题1.2解】924331329(243)54(9)(243)236335x y z x y z x y z x y z x y z x y z x y z x y z A B e e e e e e e e e A B e e e e e e e e e A B e e e e e e A B +=--+-+=-+=----+=---∙=--∙-+=+-=⨯（）（）－（）(9)(243)19124331514x y z x y z x y z x y ze e e e e e e e e e e e =--⨯-+=---=--+【习题1.3解】已知,38,x y z x y z A e be ce B e e e =++=-++ （1）要使A B ⊥，则须散度 0A B =所以从 1380A B b c =-++=可得：381b c +=即只要满足3b+8c=1就可以使向量错误！未找到引用源。

和向量错误！未找到引用源。

垂直。

（2）要使A B ，则须旋度 0A B ⨯= 所以从1(83)(8)(3)0138xy zx y z e e e A B b c b c e c e b e ⨯==--+++=-可得 b=-3，c=-8 【习题1.4解】已知129x y z A e e e =++，x y B ae be =+，因为B A ⊥，所以应有0A B ∙= 即()()1291290xy z x y ee e ae be a b ++∙+=+= ⑴又因为 1B =; 所以221=； ⑵由⑴，⑵ 解得 34,55a b =±=【习题1.5解】由矢量积运算规则123233112()()()x y zx y z x x y y z ze e e A Ca a a a z a y e a x a z e a y a x e xyzB e B e B e B =?=-+-+-=++取一线元：x y z dl e dx e dy e dz =++则有xy z xyz e e e dlB B B dx dy dzB ?=则矢量线所满足的微分方程为 x y zd x d y d z B B B == 或写成233112()dx dy dzk a z a y a x a z a y a x==---＝常数 求解上面三个微分方程：可以直接求解方程，也可以采用下列方法k xa a y a a z a d z a a x a a y a d y a a z a a x a d =-=-=-323132132231211)()()( （1）k x a y a z zdzz a x a y ydy y a z a x xdx =-=-=-)()()(211332 （2）由（1）（2）式可得)()(31211y a a x a a k x a d -=)()(21322z a a x a a k y a d -= （3）)()(32313x a a y a a k z a d -= )(32xy a xz a k xdx -=)(13yz a xy a k ydy -= （4）)(21xz a yz a k zdz -=对（3）（4）分别求和0)()()(321=++z a d y a d x a d 0)(321=++z a y a x a d0=++zdz ydy xdx 0)(222=++z y x d所以矢量线方程为1321k z a y a x a =++ 2222k z y x =++【习题1.6解】已知矢量场222()()(2)x y z A axz x e by xy e z z cxz xyz e =++++-+- 若 A 是一个无源场 ，则应有 div A =0即： div A =0y x zA A A A x y z∂∂∂∇⋅=++=∂∂∂ 因为 2x A axz x =+ 2y A by xy =+ 22z A z z cxz xyz =-+- 所以有div A =az+2x+b+2xy+1-2z+cx-2xy =x(2+c)+z(a-2)+b+1=0 得 a=2, b= -1, c= - 2 【习题1.7解】设矢径 r的方向与柱面垂直，并且矢径 r到柱面的距离相等（r ＝a ） 所以，2sssr ds rds a ds a ah πΦ===⎰⎰⎰＝22a h π=【习题1.8解】已知23x y φ=,223y z A x yze xy e =+而 A A A A rot⨯∇+⨯∇=⨯∇=φφφφ)()(2222(6)3203xy zx y ze e e A xy x y e y e xyze x y z x yz xy ∂∂∂∇⨯==--+∂∂∂ 2223[(6)32]x y z A x y xy x y e y e xyze φ∴∇⨯=--+又y x z y x e x e xy ze y e x e 236+=∂∂+∂∂+∂∂=∇φφφφ 232233222630918603xy z x y z e e e A xyx x y e x y e x y ze x yz xy φ∇⨯==-+所以222()3[(6)32]x y z rot A A A x y xy x y e y e xyze φφφ=∇⨯+∇⨯=--+ +z y x e z y x e y x e y x 2332236189+-=]49)9[(3222z y x e xz e y e x x y x+--【习题1.9解】已知 222(2)(2)(22)x y zA y x z e x y z e x z y z e =++-+-+ 所以()()1144(22)0xyzyy x x z z x y z x yzx y z A A A A A A rot A A x y z y z z x x y A A A xz xz y y e e ee e e e e e ∂∂⎛⎫⎛⎫∂∂∂∂∂∂∂⎛⎫=∇⨯==-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭-++-+-=由于场A 的旋度处处等于0，所以矢量场A 为无旋场。

教案课程: 电磁场与电磁波内容: 第6章自由空间的电磁波课时:4学时教师：刘岚。

）线、γ射线等也都是电磁波，科学研究证明电磁波是一个大家族。

所有这些电磁波仅在波长λ（或频率f ）上有所差别，而在本质上完全相同，且波长不同的电磁波在真空中的传播速度都是8001/310c εμ=≈⨯（m/s ）。

因为波的频率和波长满足关系式f c λ⋅=，所以频率不同的电磁波在真空中具有不同的波长。

电磁波的频率愈高，相应的波长就越短。

无线电波的波长最长（频率最低），而γ射线的波长最短（频率最高）。

目前人类通过各种方式已产生或观测到的电磁波的最低频率为2210f Hz -=⨯，其波长为地球半径的3510⨯倍，而电磁波的最高频率为2510f Hz =，它来自于宇宙的γ射线。

为了对各种电磁波有个全面的了解，人们按照波长或频率的顺序把这些电磁波排列起来，这就是电磁波谱。

多媒体课件展示：电磁波谱图电磁波谱无线电波微波红外线可见光紫外线X 射线伽马射线可见光: 红 | 橙 | 黄 | 绿 | 蓝 | 靛 | 紫由于辐射强度随频率的减小而急剧下降，因此波长为几百千米（105米）的低频电磁波强度很弱，通常不为人们注意。

实际使用的无线电波是从波长约几千米（频率为几百千赫）开始：波长3000米～50米（频率100千赫～6兆赫）的属于中波段；波长50米～10米（频率6兆赫～30兆赫）的为短波；波长10米～1厘米（频率30兆赫～3万兆赫）甚至达到1毫米（频率为3×105兆赫）以下的为超短波（或微波）。

有时按照波长的数量级大小也常出现米波，分米波，厘米波，毫米波等名称。

中波和短波用于无线电广播和通信，微波用于电视和无线电定位技术（雷达）。

可见光的波长范围很窄，大约在7600～4000（在光谱学中常采用埃（）作长度单位来表示波长，1＝10～8厘米）、从可见光向两边扩展，波长比它长的称为红外线，波长大约从7600直到十分之几毫米。

红外线的热效应特别显著；波长比可见光短的称为紫外线，它的波长为50～4000，它有显著的化学效应和荧光效应。

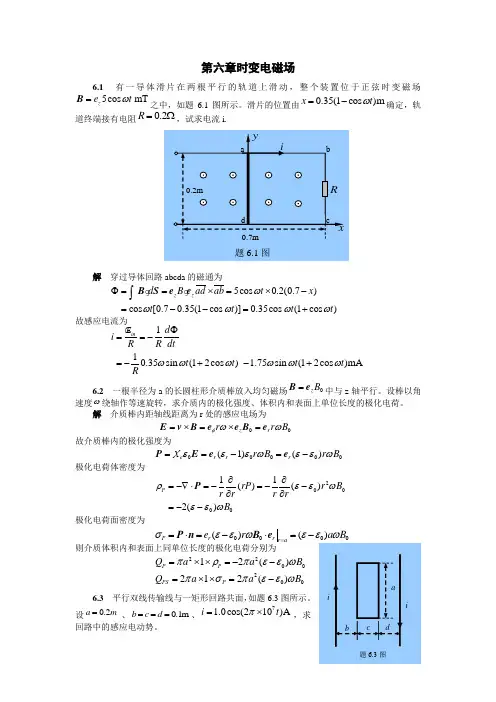
第六章时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动，整个装置位于正弦时变磁场5cos mT z e t ω=B 之中，如题6.1图所示。

滑片的位置由0.35(1cos )m x t ω=-确定，轨道终端接有电阻0.2R =Ω，试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰ B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。

设棒以角速度ω绕轴作等速旋转，求介质内的极化强度、体积内和表面上单位长度的极化电荷。

解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面，如题6.3图所示。

设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯，求回路中的感应电动势。

第6章　均匀平面波的反射与透射一、判断题电磁波垂直入射至两种媒质分界面时，反射系数与透射系数之间的关系为ρτ1＋＝。

（ ）ρτ【答案】√二、填空题电磁波从理想介质1垂直向理想介质2入射，介质1和2的本征阻抗分别为30Ω和70Ω，则分界面处的反射系数Γ和透射系数τ分别是_______，_______。

【答案】0.4；1.4三、简答题1．简述平面电磁波在媒质分界面处的反射现象和折射现象满足的斯耐尔（Snell ）定律；并具体说明什么条件下发生全反射现象，什么是临界角，给出临界角的计算公式。

答：（1）斯耐尔（Snell ）定律：①反射线和折射线都在入射面内；②反射角等于入射角，即；r i θθ=③折射角的正弦值与入射角的正弦值之比等于入射波所在的媒质的折射率与折射波所在媒质的折射率之比，即，式中sin sin ii n n ττθθ=n =（2）全反射现象：①理想导体全反射。

在电磁波入射到理想导体表面时，由理想导体表面切向电场为零的条件，反射系数为±1，称为理想导体全反射现象；②理想介质全反射。

当电磁波由光密介质入射到光疏介质时，由于，根据斯耐12n n >尔定律有。

当入射角增加到某一个角度时，折射角就可能等于。

因此，i τθθ>i θπ2c θ<τθπ2在时，就没有向介质2内传播的电磁波存在，即发生全反射现象。

c θθ>能使的入射角称为临界角，有：π2τθ=c θ21sin c n n θ==2．什么是电磁波在媒质分界面的全反射现象和全折射现象？什么是临界角和布儒斯特角？一个任意极化波由空气斜入射到一介质界面，以什么角度入射才能使反射波为线极化波？说明原因。

答：（1）当电磁波由光密介质入射到光疏介质时，由于，根据斯耐尔定律有12n n >。

当入射角增加到某一个角度时，折射角就可能等于。

因此，在i τθθ>i θπ2C θ＜τθπ2时，就没有向介质2内传播的电磁波存在，即发生全反射现象。

第6章　均匀平面波的反射与透射（一）思考题6.1 试述反射系数和透射系数的定义，它们之间存在什么关系？答：（1）反射波电场振幅E rm与入射波电场振幅E im的比值为分界上的反射系数；透射波电场振幅E tm与入射波电场振幅E im的比值为分界面上的透射系数。

（2）反射系数Γ和透射系数τ之间的关系为：6.2 什么是驻波？它与行波有何区别？答：频率和振幅均相同，振动方向一致，传播方向相反的两列波叠加后形成的波叫驻波。

行波在介质中传播时，其波等相面随时间前移，而驻波的波形不向前推进。

6.3 均匀平面波垂直入射到两种理想媒质分界面时，在什么情况下，反射系数大于0？在什么情况下，反射系数小于0？答：均匀平面波垂直入射到两种理想媒质分界时，当时，反射系数Γ＞0；当时，反射系数Γ＜0。

6.4 均匀平面波向理想导体表面垂直入射时，理想导体外面的合成波具有什么特点？答：均匀平面波向理想导体表面入射时，理想导体外面的合成波具有特点如下：合成波电场和磁场的驻波在时间上有的相移，在空间上也错开了且在导体边界上，电场为零。

驻波的坡印廷矢量的平均值为零，不发生电磁能量的传输过程，仅在两个波节之间进行电场能量和磁场能量的交换。

6.5 均匀平面波垂直入射到两种理想媒质分界面时，在什么情况下，分界面上的合成波电场为最大值？在什么情况下，分界面上的合成波电场为最小值？答：当均匀平面波垂直入射到两种理想媒质分界面时，的位置时，分界面上的合成波电场为最大值。

的位置时，分界面上的合成波电场为最小值。

6.6 一个右旋圆极化波垂直入射到两种媒质分界面上，其反射波是什么极化波？答：右旋圆极化。

6.7 试述驻波比的定义，它与反射系数之间有什么关系？答：驻波比的定义是合成波的电场强度的最大值与最小值之比，即6.8 什么是波阻抗？在什么情况下波阻抗等于媒质的本征阻抗？答：在空间任意点，均匀平面波的电场与磁场强度的模值之比称为自由空间的波阻抗，在均匀无耗各向同性的无界媒质中，均匀平面波的电场与磁场的模值之比称为媒质中的阻波抗。

《电磁场与电磁波》课程教学大纲一、课程基本信息课程代码：课程名称：电磁场与电磁波英文名称：Electromagnetic Fields and Electromagnetic Waves课程类别：专业基础课学时：63学分：3适用对象: 电子信息专业考核方式：考试先修课程：大学物理、高等数学与工程数学(包括矢量分析,场论和数理方程等)二、课程简介电磁场与电磁波是通信技术的理论基础，是电子信息专业本科学生的知识结构中重要组成部分。

本课程使学生掌握电磁场的有关定理、定律、麦克斯韦方程等的物理意义及数学表达式。

使学生熟悉一些重要的电磁场问题的数学模型（如波动方程、拉氏方程等）的建立过程以及分析方法。

培养学生正确的思维方法和分析问题的能力，使学生学会用"场"的观点去观察、分析和计算一些简单、典型的场的问题。

为后续课程打下坚实的理论基础。

Electromagnetic Field and Electromagnetic Wave is the theoretical foundation of communication technology, it is one of the most important components of the knowledge structerue for undergraduate students who major in information and electronic. Electromagnetic Field and Electromagnetic Wave make students grasp the theorem and the physical meaning of the Maxwell equations and mathematical expressions. It also make students grasp building method and analyzing method of some important mathematical model (such as wave equation,Laplace equation). This course trains students on the proper ways of thinking and ability to analyze issues, It also provides a solid theoretical foundation for following courses.三、课程性质与教学目的一切电现象，都会产生电磁场，而电磁波的辐射与传播规律，更是一切无线电活动的基础。

《电磁场与电磁波》（陈抗生）习题解答第一章 引言——波与矢量分析1．1.,,/)102102cos(1026300p y v k f E m V x t y y E E 相速度相位常数度，频率波的传播方向，波的幅的方向，，求矢量设解：m /V )x 102t 102cos(10y y E z E y E x E E 26300y 0z 0y 0x矢量E 的方向是沿Y 轴方向，波的传播方向是-x 方向；波的幅度m /V 10E E 3y。

s /m 10102102k V ;102k ;MHZ 1HZ 1021022f 826P 2661．2写出下列时谐变量的复数表示（如果可能的话）)6sin()3sin()()6(cos 1)()5()2120cos(6)()4(cos 2sin 3)()3(sin 8)()2()4cos(6)()1(t t t U t t D t t C t t t A tt I t t V（1）解：4/)z (vj 23234sin j 64cos6e6V 4j（2）解：)2t cos(8)t (I2)z (vj 8e 8I j 2（3）解：）t cos 132t sin 133(13)t (Aj32e13A 2)z ()2t cos(13)t (A 133cos )2(j v则则令 （4）解：)2t 120cos(6)t (Cj 6e6C 2j(5)(6)两个分量频率不同，不可用复数表示1．3由以下复数写出相应的时谐变量])8.0exp(4)2exp(3)3()8.0exp(4)2(1)1(j j C j C jC（1）解：t sin t cos j t sin j t cos )t sin j t )(cos j 1(e )j 1(t jt sin t cos )Ce (RE )t (C t j（2）解：)8.0t cos(4)e e 4(RE )Ce (RE )t (C t j 8.0j t j（3）解：)8.0t (j )2t (j tj 8.0j j tj e 4e3e)e4e3(Ce2得：)t cos(3)8.0t cos(4)8.0t cos(4)2t cos(3)Ce (RE )t (C tj1．4]Re[,)21(,)21(000000B A B A B A B A z j y j x B z j y j x A ，，，求：假定解：1B A B A B A B A z z y y x x0000000000z y x z y x 000z y x 6)B A (RE j)j 21(1j 21j 1z y x B A j 21B A z )j 21(x B z )j 1(y )j 31(x )4j 4(B B B A A A z y x B A得到：则：1．5计算下列标量场的梯度xyzu xy y x u xz yz xy u z y x u z y x u )5(2)4()3(2)2()1(22222222（1）解：u u grad )(22022022022202220222222z z y x y yz x x z xy z z z y x y y z y x x x z y x（2）解：u u grad )(000224z z y y x x(3) 解：u u grad )(000)()()(z x y y z x x z y(4)解：u u grad )(00)22()22(y x y x y x（5）解：u u grad )(000z xy y xz x yz1．6）处的法线方向，，在点（求曲面21122y x z解：梯度的方向就是电位变化最陡的方向令z y x T22则代入锝：将点)2,1,1(22000z y y x x T法线方向与00022z y x同向1．7求下列矢量场的散度，旋度200022000002020265)4()()()3()()()()2()1(z x y yz x A y y x x y x A z y x y z x x z y A z z y y x x A（1）解：zA y A x A A A div zy x)(z y x 2220)(222000z y x z y x z y x A A curl（2）解：div(A)=0curl(A)=0(3)解：div(A)=1+2y022000)12(0)(z x y x yx z y x z y x A A curl(4)解：div(A)=6z002002665)(y x x y x yz z y x z y x A A curl1.11Sh z z r y x S S d A x x A 组成的闭合曲面是由其中，求若矢量场,0,,2220解：由散度定理可得：hr dV dVx x h z r y x V dV A dS A VV s V20222)]([),()(围成的体积为1．12)()()(,,000000B A A B B A z B y B x B B z A y A x A A z y x z y x试证明：假定证明：)(B AzB A B A y B A B A xB A B A B A B A z B A B A y B A B A x B B B A A A z y x x y y x z x x z y z z y x y y x z x x z y z z y z y x zy x)()()()]()()([000000)()()()()()()()(B A A B y B x B A x B z B A z B y B A yA x AB x A z A B z A y A B zB A B A A B A B yB A B A A B A B xB A B A A B A B x y z z x y yz x x y z z x y yz x xy y x y x x y zx y z x z z x y z z y z y y z1．13AA A A A A)()2()()1(证明：（1）证明：证毕右边左边右边左边z A y A x A z A A y A A x A A zA y A x A z z y y x x z A y A x A zA y A x A z A y A x A z y x z z y y x x z y x z y x zy x z y x )()()()(000000000（2）证明：证毕左边右边左边zyx z y x zy xA A A z y x z y x A A A z y x z y x A A A A A z y x z y x A 000000000)(1．14 证明：)()2(0)()1( A（1）证明：证毕)]()()([)(222222000000y z A z x A y x A y z A z x A y x A yA x A z x A z A y z A y A x A A A z y x z y x A x y z x y z xy z x y z zy x（2）证明：证毕0)()(000000zy x z y x z y x z zy y x x第二章 传输线基本理论与圆图2．1710'0.042/'510/'510/'30.5/R m L H m G S mC pF mk Z 市话用的平行双导线，测得其分布电路参数为：求传播常数与特征阻抗。

第6章习题答案6-1 在1=r μ、4=r ε、0=σ的媒质中，有一个均匀平面波，电场强度是)3sin(),(πω+-=kz t E t z E m若已知MHz 150=f ，波在任意点的平均功率流密度为2μw/m 265.0，试求：（1）该电磁波的波数?=k 相速?=p v 波长?=λ波阻抗?=η （2）0=t ，0=z 的电场?)0,0(=E（3）时间经过μs 1.0之后电场)0,0(E 值在什么地方？（4）时间在0=t 时刻之前μs 1.0，电场)0,0(E 值在什么地方？ 解：（1）)rad/m (22πεπμεω===r cfk )m/s (105.1/8⨯==r p c v ε)m (12==kπλ )Ω(60120πεμπη=rr＝（2）∵ 6200210265.02121-⨯===m rm av E E S εεμη∴ (V/m)1000.12-⨯=m E)V/m (1066.83sin)0,0(3-⨯==πm E E（3） 往右移m 15=∆=∆t v z p（4） 在O 点左边m 15处6-8微波炉利用磁控管输出的2.45GHz 频率的微波加热食品，在该频率上，牛排的等效复介电常数)j 3.01(40~-=rε。

求： （1）微波传入牛排的穿透深度δ，在牛排内8mm 处的微波场强是表面处的百分之几？（2）微波炉中盛牛排的盘子是发泡聚苯乙烯制成的，其等效复介电常数=r ε~ )103.0j 1(03.14-⨯-。

说明为何用微波加热时，牛排被烧熟而盘子并没有被毁。

解：（1）20.8mm m 0208.011211212==⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛+==-ωεσμεωαδ%688.20/8/0===--e e E E z δ（2）发泡聚苯乙烯的穿透深度(m)1028.103.1103.01045.22103212213498⨯=⨯⨯⨯⨯⨯⨯⨯=⎪⎭⎫ ⎝⎛===-πμεωεσωμεσαδ可见其穿透深度很大，意味着微波在其中传播的热损耗极小，所以不会被烧毁。

第一章 习题解答1.2给定三个矢量A ，B ，C ： A =x a +2y a -3z a B = -4y a +z aC =5x a -2za求：⑴矢量A 的单位矢量A a ； ⑵矢量A 和B 的夹角AB θ； ⑶A ·B 和A ⨯B⑷A ·（B ⨯C ）和（A ⨯B ）·C ；⑸A ⨯（B ⨯C ）和（A ⨯B ）⨯C解：⑴A a =A A=149A++=（x a +2y a -3z a ）/14⑵cos AB θ=A ·B /A BAB θ=135.5o⑶A ·B =-11, A ⨯B =-10x a -y a -4z a ⑷A ·（B ⨯C ）=-42（A ⨯B ）·C =-42⑸A ⨯（B ⨯C ）=55x a -44y a -11z a（A ⨯B ）⨯C =2x a -40y a +5z a1.3有一个二维矢量场F(r)=x a （-y ）+y a (x)，求其矢量线方程，并定性画出该矢量场图形。

解：由dx/(-y)=dy/x,得2x +2y =c1.6求数量场ψ=ln （2x +2y +2z ）通过点P （1，2，3）的等值面方程。

解：等值面方程为ln （2x +2y +2z ）=c 则c=ln(1+4+9)=ln14 那么2x +2y +2z =141.9求标量场ψ（x,y,z ）=62x 3y +ze 在点P （2，-1，0）的梯度。

解：由ψ∇=x a x ψ∂∂+y a y ψ∂∂+z a zψ∂∂=12x 3y x a +182x 2y y a +ze z a 得ψ∇=-24x a +72y a +z a1.10 在圆柱体2x +2y =9和平面x=0，y=0,z=0及z=2所包围的区域，设此区域的表面为S: ⑴求矢量场A 沿闭合曲面S 的通量，其中矢量场的表达式为A =x a 32x +y a （3y+z ）+z a (3z -x)⑵验证散度定理。

电磁场与电磁波理论(第二版)(徐立勤,曹伟)第6章习题解答(总10页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第6章习题解答已知空气中存在电磁波的电场强度为 ()80cos 6π102πy E e E t z =⨯+V /m试问：此波是否为均匀平面波传播方向是什么求此波的频率、波长、相速以及对应的磁场强度H 。

解：均匀平面波是指在与电磁波传播方向相垂直的无限大平面上场强幅度、相位和方向均相同的电磁波。

电场强度瞬时式可以写成复矢量j 0e kz y E e E -=。

该式的电场幅度为0E ，相位和方向均不变，且0z E e ⋅=⇒z E e ⊥，此波为均匀平面波。

传播方向为沿着z -方向。

由时间相位86π10t t ω=⨯ ⇒ 86π10ω=⨯ 波的频率Hz 1038⨯=f 波数2πk =波长2π 1 m k λ== 相速p 310 m/s v kω==⨯ 由于是均匀平面波，因此磁场为j 0w w1() e kz z x E H e E e Z Z -=-⨯=有一频率为600MHz 的均匀平面波在无界理想介质(r r 4,1εμ==)中沿x +方向传播。

已知电场只有y 分量，初相位为零，且010t t ==s 时，1x =m 处的电场强度值为800kV /m 。

试写出E 和H 的瞬时表达式。

解：根据题意，角频率812π10ω=⨯，r r 0028πk cωωεμεμεμ====，因此 80cos(12π108π)y E e E t x =⨯-由s 10=t ，m 1=x 处的电场强度值为kV/m 800，可以得到kV/m 8000=E8800cos(12π108π) kV/m y E e t x =⨯-根据电场的瞬时表达式可以写出电场的复矢量为j8π800e kV/m x y E e -=波阻抗为()0r w r 060π ΩZ μμμεεε===。