人教版五年级下册《最小公倍数》练习题

4.5.1《最小公倍数》同步练习基础知识达标一、单选题。

1.一个数既有因数2，又有因数3，这个数最小是（）A. 4B. 6C. 82.2□0是2、3、5的公倍数，□里可填（）。

A. 1B. 4C. 6D. 1、4、73.1和25的最小公倍数是（）。

A. 1B. 25C. 5D. 6二、判断题。

1.两个数的积一定是这两个数的公倍数。

（）2.两个数的公倍数一定比这两个数大。

（）3.任何两个相邻的自然数(0除外)的最小公倍数都是它们的积，如11和12的最小公倍数就是132。

（）4.A是B的因数，A、B的最小公倍数是B。

（）三、填空题。

1.4和11的最大公因数是________，最小公倍数是________。

2.数a和数b只有公因数1，它们的最大公因数是________，最小公倍数是________。

3.一次数学竞赛，结果参赛学生中获得一等奖，获得二等奖，获得三等奖，其余获纪念奖，参加竞赛的至少有________名同学。

4.一个数最大的因数是27，这个数是________；一个数最小的倍数是24，这个数是________。

它们最大的公因数是________，最小公倍数是________。

四、求出下面每组数的最大公因数和最小公倍数（1）18和6（2）12和20（3）8和9五、解答题1.五年级部分学生参加植树活动，如果分成3人一组，4人一组，6人一组，都少1人。

五年级最少有多少人参加了植树活动？2.两个数的最大公因数是15，最小公倍数是90，求这两个数分别是多少。

3.学校合唱队的同学可以分成6人一组，也可以分成8人一组，都正好分完。

如果这些学生的总人数在50人以内，可能是多少人？综合能力运用六、李阿姨今天给月季和君子兰同时浇了水，月季每4天浇一次水，君子兰每6天浇一次水，至少多少天以后给这两种花同时浇水？七、一包糖，无论分给8人还是分给12人，都正好平均分完。

这包糖至少有多少颗？答案解析部分一、单选题1.【答案】B【考点】公倍数与最小公倍数【解析】【解答】一个数既有因数2，又有因数3，这个数最小是：2×3=6. 故答案为：B.【分析】一个数既有因数2，又有因数3，说明这个数是2、3的公倍数，2和3是互质数，它们的最小公倍数是它们的乘积，据此列式解答.2.【答案】D【考点】2、5的倍数的特征，3的倍数的特征，最小公倍数的应用【解析】【解答】解：□里可填1、4、7。

《最小公倍数》同步练习语文课本中的文章都是精选的比较优秀的文章,还有不少名家名篇。

如果有选择循序渐进地让学生背诵一些优秀篇目、精彩段落,对提高学生的水平会大有裨益。

现在,不少语文教师在分析课文时,把文章解体的支离破碎,总在文章的技巧方面下功夫。

结果教师费劲,学生头疼。

分析完之后,学生收效甚微,没过几天便忘的一干二净。

造成这种事倍功半的尴尬局面的关键就是对文章读的不熟。

常言道“书读百遍,其义自见”,如果有目的、有计划地引导学生反复阅读课文,或细读、默读、跳读,或听读、范读、轮读、分角色朗读,学生便可以在读中自然领悟文章的思想内容和写作技巧,可以在读中自然加强语感,增强语言的感受力。

久而久之,这种思想内容、写作技巧和语感就会自然渗透到学生的语言意识之中,就会在写作中自觉不自觉地加以运用、创造和发展。

一、单选题单靠“死”记还不行,还得“活”用,姑且称之为“先死后活”吧。

让学生把一周看到或听到的新鲜事记下来,摒弃那些假话套话空话,写出自己的真情实感,篇幅可长可短,并要求运用积累的成语、名言警句等,定期检查点评,选择优秀篇目在班里朗读或展出。

这样,即巩固了所学的材料,又锻炼了学生的写作能力,同时还培养了学生的观察能力、思维能力等等,达到“一石多鸟”的效果。

1.如果a＝2×2×3，b＝2×3×3，那么a和b的最大公因数和最小公倍数分别是（）单靠“死”记还不行,还得“活”用,姑且称之为“先死后活”吧。

让学生把一周看到或听到的新鲜事记下来,摒弃那些假话套话空话,写出自己的真情实感,篇幅可长可短,并要求运用积累的成语、名言警句等,定期检查点评,选择优秀篇目在班里朗读或展出。

这样,即巩固了所学的材料,又锻炼了学生的写作能力,同时还培养了学生的观察能力、思维能力等等,达到“一石多鸟”的效果。

A. 2、36 B. 6、30 C. 6、36 D. 2、2162.有一箱桃子，6个6个地数，刚好数完；8个8个地数，也刚好数完。

19.有三个连续奇数，若中间的奇数是m，则另外两个奇数分别是（）和（）.20. 如果a=2×2×3×c，b=2×3×5×c，a和b的最大公因数是18，那么c是（）。

a和b的最小公倍数是（）。

二、判断。

1、甲数和乙数都是他们的最大公因数的倍数。

（）3.互质数的两个数必须都是质数。

（）4.最小的合数和最小的质数这两个数的公因数只有1. （）5.相邻的两个自然数的公因数不止一个。

（）6.两个数的最大公因数一定比这两个数都小。

（）7.两个合数一定不是互质数。

（）三、选择。

1.有两根绳子，一根长6米，另一根长15米。

要将两根绳子剪成长度一样的短绳而且没有剩余，每根短绳最长是（）米。

A、15B、3C、62. 2、3和5的最小公倍数是（）A、6B、10C、153.所有自然数的公因数是（）。

A、有无数个B、是0C、是1D、没有4. 数a和数b是两个连续的自然数，a和b的最大公因数是（）A、1B、aC、bD、ab5. a=b+1，(a、b为非0自然数，)a和b的最小公倍数是（）。

A、abB、aC、b6. 两个偶数的最小公倍数（）A、一定是奇数B、一定是偶数C、可能是奇数也可能是偶数7. 在a×b=c中，a、b、c是三个不同的自然数，下面说法正确的有( )A、c一定是a的因数B、a一定是b和c的最小公倍数C、c一定是b的因数。

8. 有四个小朋友的年龄是四个连续的自然数，他们年龄的最小公倍数是120，他们中年龄最大的是（）岁。

A、3B、4C、5D、69. 4.8÷0.6=8，4.8是0.6的（）A. 倍数B. 因数C. 8倍10.m是大于0的自然数，n=m+1,那么m和n的最小公倍数是（），最大公因数是（）A. nB. mC. 1D. mn。

习
题
汇
编姓名：
仅供参考，内容可修改
第11课时最小公倍数的应用
一、填空。

1、自然数a是自然数b的5倍，则a和b的最小公倍数是（）。

2、100以内3和5的公倍数中，最大的两位奇数是（），最大的两位偶数是（）。

3、两个不同质数的和是10，他们的最小公倍数是（）。

4、m＝2×3×7 ，n＝2×3×3，m和n全部公有的质因数有（），m和n的最小公倍数是（）。

二.选择题。

1、一个数的（）的个数是无限的。

A.因数
B.倍数
C.最小公倍数
2、34是17和2的（）。

A.因数
B.最大公因数
C.最小公倍数
3、因为60是10的倍数，也是5的倍数，所以60是10和5的（）。

A.最小公倍数
B.公倍数
C.最小公因数
三、解决问题。

1、五（1）班学生做早操，每行12人或16人都正好站成整行，这个班不到50人，这个班究竟有多少人？
2、一块砖长42厘米，宽26厘米，用这样的砖铺成一块正方形地，至少要多少块？
3、有一筐苹果，无论是平均分给8个人，还是平均分给18人，结果都剩下3个，这筐苹果至少有多少个？。

100以内2的倍数：100以内16的倍数：100以内2和16的公倍数：2和16的最小公倍数：二、求下列每组数的最小公倍数。

5和10 4和18 12和11 3和15 3和153和8 10和18 4和19 9和21 2和6三、写出每组分数的两个分母的最小公倍数。

1 10 1 1 11 14 5 13 —和——和——和——和—6 11 8 12 12 15 6 141 1 9 1 1 1 7 21 —和——和——和——和—3 13 8 16 3 13 8 20100以内3的倍数：100以内15的倍数：100以内3和15的公倍数：3和15的最小公倍数：二、求下列每组数的最小公倍数。

5和9 2和20 6和11 11和13 2和62和7 4和14 8和15 9和17 7和14三、写出每组分数的两个分母的最小公倍数。

1 62 1 1 12 1 17 —和——和——和——和—4 7 3 15 4 136 166 1 3 1 6 187 1 —和——和——和——和—5 19 4 32 5 17 8 13100以内4的倍数：100以内10的倍数：100以内4和10的公倍数：4和10的最小公倍数：二、求下列每组数的最小公倍数。

3和9 4和12 12和17 9和19 3和64和10 4和16 8和9 5和15 5和10三、写出每组分数的两个分母的最小公倍数。

1 1 1 11 1 6 1 13 —和——和——和——和—2 9 4 10 14 7 8 124 14 1 1 1 125 1 —和——和——和——和—3 13 8 32 7 134 14100以内5的倍数：100以内7的倍数：100以内5和7的公倍数：5和7的最小公倍数：二、求下列每组数的最小公倍数。

2和10 8和20 18和11 5和13 5和254和7 10和20 20和11 7和21 2和8三、写出每组分数的两个分母的最小公倍数。

5 10 3 13 1 4 7 17 —和——和——和——和—4 9 4 14 85 8 168 20 7 33 1 14 1 1 —和——和——和——和—9 21 8 32 2 13 8 16100以内4的倍数：100以内11的倍数：100以内4和11的公倍数：4和11的最小公倍数：二、求下列每组数的最小公倍数。

最大公因数和最小公倍数这节课主要复习最小公因数和最小公倍数的意义，重点掌握找最大公因数和最小公倍数的方法，利用其解决相应的实际问题。

一、方法：求两个数的最大公因数和最小公倍数，首先判断这几个数是何种关系。

（1）互质数关系：最大公因数是1。

最小公倍数是这两个数的乘积。

（2）倍数关系：最大公因数是较小的数。

最小公倍数是较大的数。

（3）既不是互质数关系又不是倍数关系：用短除法来求。

二、解决实际问题在例1中贝贝用一块长6分米，宽4分米的长方形纸板裁成若干个边长是整分米数的小正方形,裁完后凑巧没有剩余，小正方形的边长最大是多少？可以裁成多少块？把长方形分割成若干个小正方形而且没有剩余，转化成数学问题就是利用因数和倍数关系来解决。

说明小正方形的边长是大正方形边长的因数。

求边长最大是多少，就是求6和4的最大公因数。

我们可以判断这道题中的2个数，可以用短除法来求。

即：最大公因数是2。

裁成的小正方形的边长最大是2厘米。

在典型例题2中明明用一些长6分米.宽4分米的长方形纸板拼成了一个正方形，正方形的边长至少是多少？要用多少块小长方形纸板？（已知每份数，求总数，应用公倍数知识。

如果正方形的边长在20分米至30分米之间，你知道是多少吗？用小正方形拼成一个大正方形，就可以说明大正方形的边长是小正方形边长的倍数。

求大正方形边长至少是多少厘米就是求6和4的最小公倍数。

即：6和4的最小公倍数是12.所以大正方形的边长至少是12厘米。

如果正方形的边长在20——30之间，那么它的边长还可以是24厘米。

即：12、24厘米。

在培优训练中阳光幼儿园买回49块水果糖和29块奶糖，赵老师把两种糖分别平衡分给小班的每位小朋友，结果水果糖多出4块，奶糖少了1块。

小班最多有多少位小朋友？从培优训练1中我们可以通过转化法把这道题转化成我们学过的因数和倍数关系。

从题中我们可以知道水果糖-4块，奶糖+1块就凑巧能平衡分给小朋友们，也就是说45块水果糖和30块奶糖凑巧是小朋友人数的倍数，求最多有多少个小朋友就是求45和30的最大公因数。

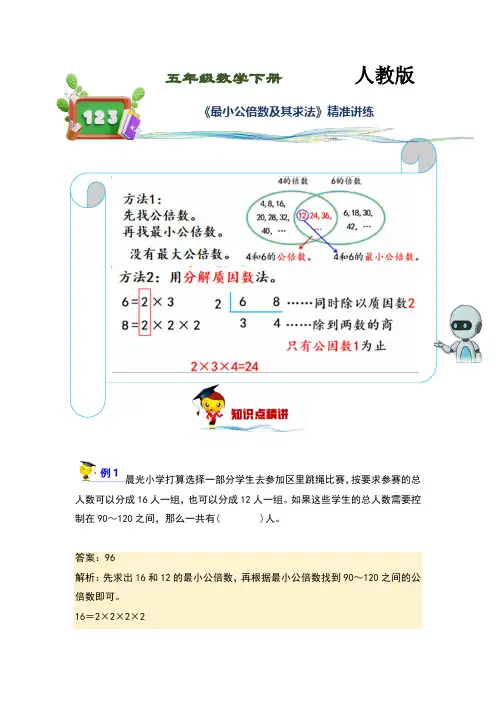
晨光小学打算选择一部分学生去参加区里跳绳比赛，按要求参赛的总人数可以分成16人一组，也可以分成12人一组。

如果这些学生的总人数需要控制在90～120之间，那么一共有( )人。

答案：96解析：先求出16和12的最小公倍数，再根据最小公倍数找到90～120之间的公倍数即可。

16＝2×2×2×2五年级数学下册人教版《最小公倍数及其求法》精准讲练12＝2×2×32×2×2×2×3＝48（人）48×2＝96（人）90＜96＜120所以一共有96人。

用长20cm、宽15cm、高6cm的长方体木块堆成一个正方体，至少需要120块这样的长方体木块。

( )答案：√解析：20cm、15cm、6cm的最小公倍数即为堆成的正方体的棱长。

需要的长方体木块数为堆成的正方体棱长除以20、15、6所得的商的积。

20＝2×2×515＝3×56＝2×320、15、6的最小公倍数为2×2×5×3＝60（60÷20）×（60÷15）×（60÷6）＝3×4×10＝12×10＝120（块）所以原题说法正确；故答案为：√。

A、B两站是某条地铁的两个始发站。

每天早晨从A站开出的首班车是5时整，发车间隔是6分钟。

从B站开出的首班车是5时20分，发车间隔是8分钟。

每天早晨5时（）分会第一次从A、B两站同时开出一列地铁。

A．24 B．36 C．44 D．48答案：B解析：从A站开出的班车的时间分别是5时、5时6分、5时12分、5时18分、5时24分、5时30分、5时36分、5时42分、……；从B站开出的班车的时间分别是5时20分、5时28分、5时36分、……；找出相同的发车时间。

据此解答。

每天早晨5时36分会第一次从A、B两站同时开出一列地铁。

最大公因数与最小公倍数应用题练习1、中心小学五年级学生分为6人一组8人一组或9人一组排队做早操都刚好分完这个年级至少有学生多少人？2、有一堆苹果，8千克一份，9千克一份或10千克一份都会多出3千克，这堆苹果至少有多少千克？3、有24个苹果32个梨。

要分装在盘子里，每盘的苹果和梨的个数相同，最多可以装多少盘？每个盘子里，苹果和梨各多少？4、把37支钢笔。

和38本书。

平均奖给几个学习成绩优秀的学生结果钢笔多出一只，书还缺两本，最多有几个学生成绩优秀的同学？5、数学兴趣小组有24个男同学。

20个女同学。

要分成小组，每个小组男女同学人数分别相同。

最多可以分成多少个小组？每组至少有多少个男同学？多少个女同学？6、两个数的最大公因数为12。

最小公倍数为180。

这两个数不是倍数求这两个数？7、一个数被2除余1。

被3除余2。

被4除余4。

被6除余5。

这个数最小是几？8、甲乙丙三人，早晨在体育场跑步，甲跑完一圈，要3分钟，乙跑完一圈要7分钟丙，跑完一圈要6分钟三人同时从起点出发经过多长时间，三人再次在起点处相遇？9、上一号，9月18号，五年级一班去划船，他们算一下，如果增加1条船正好每船坐6人，如果减少一条船正好每船坐9人，这个班有多少人？10、有一块长方形纸板长24厘米。

宽15厘米。

将这块纸板剪成同样大小的正方形不能有剩余。

每块小正方形的边长最长是多少厘米？可以截成多少块？11、一张长方形纸长96厘米。

宽60厘米。

如果把它截成同样大小且边长都为整厘米的最大正方形。

且保持纸张没有剩余每个正方形的边长是几厘米？每个正方形的面积是多少？可以截多少个这样的正方形？12、已知两数的最大公因数是31，两数的积是5766。

两个分别是多少？13、五一班和五二班两个班的同学去野炊吃饭时，他们三人一个菜碗，四人一个汤碗，他们共用了28个碗，这两个班参加野炊的同学共有多少人？14、王伯伯有三个小孩，老大3天回家一次，老二4天回家一次，老三6天回家一次，这次10月1日一起回家，上一次是几月几日一起回家？15、一路车每隔6分钟一辆，二路车,每隔10分钟一辆，三路车每隔12分钟一辆，在早上八点同时发车后至少再到什么时候又可以同时发车？16、用一个数去除52余4，再用这个数去除40也余4。

五年级数学最大公因数,最小公倍数练习题(含提高)定义：最大公约数：最大公约数.也称最大公因数.最大公因子.指两个或多个整数共有约数中最大的一个·a.b的最大公约数记为（a.b）.同样的.a.b.c的最大公约数记为（a.b.c）.多个整数的最大公约数也有同样的记号·求最大公约数有多种方法.常见的有质因数分解法.短除法.辗转相除法.更相减损法·与最大公约数相对应的概念是最小公倍数.a.b的最小公倍数记为[a.b]·质因数分解法：把每个数分别分解质因数.再把各数中的全部公有质因数提取出来连乘.所得的积就是这几个数的最大公约数·例如：求24和60的最大公约数.先分解质因数.得24=2×2×2×3.60=2×2×3×5.24与60的全部公有的质因数是2.2.3.它们的积是2×2×3=12.所以.（24.60）=12·把几个数先分别分解质因数.再把各数中的全部公有的质因数和独有的质因数提取出来连乘.所得的积就是这几个数的最小公倍数·例如：求6和15的最小公倍数·先分解质因数.得6=2×3.15=3×5.6和15的全部公有的质因数是3.6独有质因数是2.15独有的质因数是5.2×3×5=30.30里面包含6的全部质因数2和3.还包含了15的全部质因数3和5.且30是6和15的公倍数中最小的一个.所以[6.15]=30·短除法：短除法求最大公约数.先用这几个数的公约数连续去除.一直除到所有的商互质为止.然后把所有的除数连乘起来.所得的积就是这几个数的最大公约数·短除法求最小公倍数.先用这几个数的公约数去除每个数.再用部分数的公约数去除.并把不能整除的数移下来.一直除到所有的商中每两个数都是互质的为止.然后把所有的除数和商连乘起来.所得的积就是这几个数的最小公倍数.例如.求12.15.18的最小公倍数·[1]短除法的格式短除法的本质就是质因数分解法.只是将质因数分解用短除符号来进行·短除符号就是除号倒过来·短除就是在除法中写除数的地方写两个数共有的质因数.然后落下两个数被公有质因数整除的商.之后再除.以此类推.直到结果互质为止（两个数互质）·而在用短除计算多个数时.对其中任意两个数存在的因数都要算出.其它没有这个因数的数则原样落下·直到剩下每两个都是互质关系·求最大公因数便乘一边.求最小公倍数便乘一圈·无论是短除法.还是分解质因数法.在质因数较大时.都会觉得困难·这时就需要用新的方法·辗转相除法：辗转相除法是求两个自然数的最大公约数的一种方法.也叫欧几里德算法·这就是辗转相除法的原理·辗转相除法的格式例如.求（319.377）：∵ 319÷377=0（余319）∴（319.377）=（377.319）；∵ 377÷319=1（余58）∴（377.319）=（319.58）；∵ 319÷58=5（余29）.∴（319.58）=（58.29）；∵ 58÷29=2（余0）.∴（58.29）= 29；∴（319.377）=29.可以写成右边的格式·用辗转相除法求几个数的最大公约数.可以先求出其中任意两个数的最大公约数.再求这个最大公约数与第三个数的最大公约数.依次求下去.直到最后一个数为止·最后所得的那个最大公约数.就是所有这些数的最大公约数·更相减损法：也叫更相减损术.是出自《九章算术》的一种求最大公约数的算法.它原本是为约分而设计的.但它适用于任何需要求最大公约数的场合·《九章算术》是中国古代的数学专著.其中的“更相减损术”可以用来求两个数的最大公约数.即“可半者半之.不可半者.副置分母.子之数.以少减多.更相减损.求其等也·以等数约之·”翻译成现代语言如下：第一步：任意给定两个正整数；判断它们是否都是偶数·若是.则用2约简；若不是则执行第二步·第二步：以较大的数减较小的数.接着把所得的差与较小的数比较.并以大数减小数·继续这个操作.直到所得的减数和差相等为止·则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数·其中所说的“等数”.就是最大公约数·求“等数”的办法是“更相减损”法·所以更相减损法也叫等值算法·例1.用更相减损术求98与63的最大公约数·解：由于63不是偶数.把98和63以大数减小数.并辗转相减：98-63=3563-35=2835-28=728-7=2121-7=1414-7=7所以.98和63的最大公约数等于7·这个过程可以简单的写为：（98.63）=（35.63）=（35.28）=（7.28）=（7.21）=（7.14）=（7.7）=7最小公倍数：两个或多个整数公有的倍数叫做它们的公倍数·两个或多个整数的公倍数里最小的那一个叫做它们的最小公倍数·分解质因数法：先把这几个数的质因数写出来.最小公倍数等于它们所有的质因数的乘积（如果有几个质因数相同.则比较两数中哪个数有该质因数的个数较多.乘较多的次数）·比如求45和30的最小公倍数·45=3*3*530=2*3*5不同的质因数是2,3,5·3是他们两者都有的质因数.由于45有两个3.30只有一个3.所以计算最小公倍数的时候乘两个3.最小公倍数等于2*3*3*5=90又如计算36和270的最小公倍数36=2*2*3*3270=2*3*3*3*5不同的质因数是5·2这个质因数在36中比较多.为两个.所以乘两次；3这个质因数在270个比较多.为三个.所以乘三次·最小公倍数等于2*2*3*3*3*5=54020和40的最小公倍数是40[4]公式法：由于两个数的乘积等于这两个数的最大公约数与最小公倍数的积·即（a.b）×[a.b]=a×b·所以.求两个数的最小公倍数.就可以先求出它们的最大公约数.然后用上述公式求出它们的最小公倍数·例如.求[18.20].即得[18.20]=18×20÷（18.20）=18×20÷2=180·求几个自然数的最小公倍数.可以先求出其中两个数的最小公倍数.再求这个最小公倍数与第三个数的最小公倍数.依次求下去.直到最后一个为止·最后所得的那个最小公倍数.就是所求的几个数的最小公倍数·常用结论：在解有关最大公约数.最小公倍数的问题时.常用到以下结论：（1）如果两个自然数是互质数.那么它们的最大公约数是1.最小公倍数是这两个数的乘积·例如8和9.它们是互质数.所以（8.9）=1.[8.9]=72·（2）如果两个自然数中.较大数是较小数的倍数.那么较小数就是这两个数的最大公约数.较大数就是这两个数的最小公倍数·例如18与3.18÷3=6.所以（18.3）=3.[18.3]=18·（3）两个整数分别除以它们的最大公约数.所得的商是互质数·例如8和14分别除以它们的最大公约数2.所得的商分别为4和7.那么4和7是互质数·（4）两个自然数的最大公约数与它们的最小公倍数的乘积等于这两个数的乘积·例如12和16.（12.16）=4.[12.16]=48.有4×48=12×16.即（12.16）× [12.16]=12×16·例1：两个数的最大公因数是15,最小公倍数是90,求这两个数分别是多少？15×1=15,15×6=90；当a1b1分别是2和3时,a.b分别为15×2=30,15×3=45·所以.这两个数是15和90或者30和45·例2：两个自然数的积是360,最小公倍数是120,这两个数各是多少？分析我们把这两个自然数称为甲数和乙数·因为甲.乙两数的积一定等于甲.乙两数的最大公因数与最小公倍数的积·根据这一规律.我们可以求出这两个数的最大公因数是360÷120=3·又因为（甲÷3=a,乙÷3=b)中,3×a×b=120,a和b一定是互质数.所以,a和b可以是1和40,也可以是5和8·当a和b是1和40时.所求的数是3×1=3和3×40=120；当a 和b是5和8时.所求的数是3×5=15和3×8=24·分析甲跑一圈需要600÷3=200秒.乙跑一圈需要600÷4=150秒.丙跑一圈需要600÷2=300秒·要使三人再次从出发点一齐出发.经过的时间一定是200.150和300的最小公倍数·200.150和300的最小公倍数是600,所以.经过600秒后三人又同时从出发点出发·综合练习：一. 填空题·1. 都是自然数.如果.的最大公约数是（）.最小公倍数是（）·2. 甲.乙.甲和乙的最大公约数是（）×（）＝（）.甲和乙的最小公倍数是（）×（）×（）×（）＝（）·3. 所有自然数的公约数为（）·4. 如果m和n是互质数.那么它们的最大公约数是（）.最小公倍数是（）·5. 在4.9.10和16这四个数中.（）和（）是互质数.（）和（）是互质数.（）和（）是互质数·6. 用一个数去除15和30.正好都能整除.这个数最大是（）·7. 两个连续自然数的和是21.这两个数的最大公约数是（）.最小公倍数是（）·8. 两个相邻奇数的和是16.它们的最大公约数是（）.最小公倍数是（）·9. 某数除以3.5.7时都余1.这个数最小是（）·10. 根据下面的要求写出互质的两个数·（1）两个质数（）和（）·（2）连续两个自然数（）和（）·（3）1和任何自然数（）和（）·（4）两个合数（）和（）·（5）奇数和奇数（）和（）·（6）奇数和偶数（）和（）·11.两个数的最大公因数是6.最小公倍数是144.这两个数的和是（）·12.有一个数.同时能被9,10,15整除.满足条件的最大三位数是（）·13.筐里装满了鸡蛋.已知这筐鸡蛋两个两个数多一个.五个五个数仍多一个.那么这筐鸡蛋至少有（）个·14.有336个苹果.252个橘子.210个梨.用这些果品最多可分成若干份同样的礼物.这时在每份礼物中.三种水果各有（）·15.有96多红花和72朵白花扎成花束.如果每个花束里红花的朵数相同.白花的朵数也相同.每个花束至少有（）朵花·二. 判断题·1. 互质的两个数必定都是质数·（）2. 两个不同的奇数一定是互质数·（）3. 最小的质数是所有偶数的最大公约数·（）4. 有公约数1的两个数.一定是互质数·（）5. a是质数.b也是质数..一定是质数·（）三. 直接说出每组数的最大公约数和最小公倍数·26和13（） 13和6（）4和6（） 5和9（）29和87（） 30和15（）13.26和52 （） 2.3和7（）四.求下面每组数的最大公约数和最小公倍数·（三个数的只求最小公倍数）45和60 36和6027和72 76和8042.105和56 24.36和48五.解答题·1.把一张长120厘米.宽80厘米的长方形的纸裁成正方形.不允许剩余.至少能裁多少张？2.已知两个自然数的最大公因数是12.（1）最小公倍数是72.求这两个数的积（2）满足已知条件的自然数有哪几组？3.一筐梨.按每份2个梨分多一个.每份3个梨多两个.每份5个梨多四个.问筐里至少有多少个梨？4.甲乙丙三人环绕操场步行一周.甲要三分钟.乙要四分钟.丙要六分钟.三人同时同地同向出发.当他们三人第一次相遇时.甲乙丙三人分别绕了多少周？5.某港口停着四艘轮船.一天他们同时开出港口.已知甲船每隔两星期回港一次.乙船每隔四星期回港一次.丙船每隔六星期回港一次.丁船八星期回港一次.至少经过几星期后.这四只轮船再次在港口重新会合？6、有一个自然数.被6除余1.被5除余1.被4除余1.这个自然数最小是几？7、一盒钢笔可以平均分给2.3.4.5.6个同学.这盒钢笔最小有多少枝？8、用96朵红花和72朵白花做成花束.如果各花束里红花的朵数相同.白花的朵数也相同.每束花里最少有几朵花？9、从小明家到学校原来每隔50米安装一根电线杆.加上两端的两根一共是55根电线杆.现在改成每隔60米安装一根电线杆.除两端的两根不用移动外.中途还有多少根不必移动？10.每筐梨.按每份两个梨分多1个.每份3个梨分多2个.每份5个梨分4个.则筐里至少有多少个梨？11.学校买来40支圆珠笔和50本练习本.平均奖给四年级三好学生.结果圆珠笔多4支.练习本多2本.四年级有多少名三好学生.他们各得到什么奖品？12.小明.小红.小王一起分17个苹果.小明分得其中的二分之一.小红分得其中的三分之一.小王分得其中的九分之一.问他们每个人分别分得几个苹果？。

一、选择题1. 一筐梨，2个2个拿，3个3个拿，5个5个拿都正好拿完而没有剩余，这筐梨最少应该有（）个。

A．6 B．15 C．30 D．602. 在1，2，…，100，在这100个整数中，能同时被2和3整除的数共有（）。

A．16个B．17个C．18个D．19个3. 小红和爸爸一起去公园散步。

小红绕公园小路走一圈要12分钟，爸爸走一圈要10分钟。

如果他们同时从起点出发沿同方向行走，那么至少要经过（）分钟他们才能在起点再次相遇。

A．10 B．12 C．60 D．1204. 下面正确的有（）句。

①含有字母的式子是方程。

②等式都是方程。

③等式两边同时乘或除以一个小数，等式仍然成立。

④由男生人数比女生的3倍多12人，可以想到“男生人数－女生人数的3倍＝12”。

⑤两个质数相加，得到的和一定是合数。

⑥3和5的公倍数，一定也是15的倍数。

⑦偶数×奇数×奇数＝偶数。

⑧能被5整除的数的特征末尾是5，那么能被3整除的数的特征一定是3。

⑨三角形的面积是S平方米，底边长是a米，则对应的高是（）米。

A．3 B．4 C．5 D．65. 如果A＝2×3×5，B＝2×2×3×5，那么A、B两个数的最小公倍数是（）。

A．15 B．30 C．60二、填空题6. 甲乙两数的最大公约数是3，最小公倍数是30．如果甲数是6，那么乙数是；如果乙数是30，那么甲数是．7. 一个数既是2的倍数，又是5的倍数，这个数最小是( )。

8. （仙游县）有两个自然数，它们的最小公倍数是24，最大公因数是2，它们可能是_______和___ 或___和___．9. 如果三个连续的两位正整数的最大公约数是1，那么最小公倍数的最大值是．10. 甲数是乙数的二分之一，甲数和乙数的最小公倍数是54，甲数是，乙数是．三、解答题11. 曲妍有一袋果冻，无论是平均分给7个人、10个人还是4个人，都剩下1个。