数字信号的基带传输

第五章 数字信号的基带传输基带传输系统频带传输系统（调制传输系统）数字基带信号：没有经过调制的原始数字信号。

（如各种二进制码PCM 码，M ∆码等）数字调制信号：数字基带信号对载波进行调制形成的带通信号。

5.1、基带信号的码型一、数字基带信号的码型设计原则：1． 对传输频带低端受限的信道，线路传输的码型的频谱中应该不含有直流分量；2．信号的抗噪声能力强；3．便于从信号中提取位定时信息；4．尽量减少基带信号频谱中的高频分量，节省传输频带、减小串扰； 5．编译码设备应尽量简单。

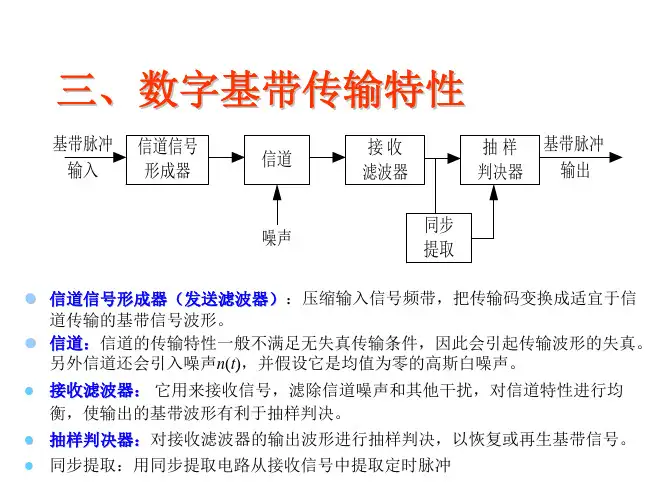
二、数字基带信号的常用码型。

1、单极性不归零码NRZ （Non Return Zero ）脉冲宽度τ等于码元宽度T特点：（1）有直流，零频附近的低频分量一般信道难传输。

（2）收端判决门限与信号功率有关，不方便。

（3）要求传输线一端接地。

（4）不能用滤波法直接提取位定时信号。

2、双极性非归零码（BNRZ ）T =τ，有正负电平特点：不能用滤波直接提取位定时信号。

⎩⎨⎧数字通信系统3、单极性归零码（RZ）τ<T特点：（1）可用滤波法提取位同步信号（2）NRZ的缺点都存在4、双极性归零码（BRZ）特点：（1）整流后可用滤波提取位同步信号（2）NRZ的缺点都不存在5、差分码电平跳变表1，电平不变表0 称传号差分码电平跳变表0，电平不变表1 称空号差分码特点：反映相邻代码的码元变化。

6、传号交替反转码（AMI）τ）归零码表0用零电平表示，1交替地用+1和-1半占空（T5.0=示。

优点：（1）“0”、“1”不等概时也无直流（2）零频附近低频分量小（3）整流后即为RZ码。

缺点：连0码多时，AMI整流后的RZ码连零也多，不利于提取高质量的位同步信号（位同频道抖动大）应用：μ律一、二、三次群接口码型：AMI加随机化。

7、三阶高密度双极性码()3HDBHDB3码编码步骤如下。

①取代变换：将信码中4个连0码用取代节000V或B00V代替，当两个相邻的V码中间有奇数个1码时用000V代替4个连0码，有偶数个1码时用B00V代替4个连0码。

基带传输的三种调制方式在通信领域中，基带传输是指将数字信号直接传输到信道上的一种方式。

为了能够在信道上传输数字信号，需要对其进行调制处理。

基带传输的调制方式有三种：振幅调制（AM）、频率调制（FM）和相位调制（PM）。

下面将逐一介绍这三种调制方式的原理和特点。

1. 振幅调制（AM）振幅调制是将数字信号的振幅与载波的振幅进行调制，以实现信号的传输。

在振幅调制中，载波的频率和相位保持不变，只调制其振幅。

当数字信号为1时，振幅调制会使得载波的振幅增大；当数字信号为0时，振幅调制会使得载波的振幅减小。

通过这种方式，可以将数字信号转换为模拟信号，便于在信道上传输。

振幅调制的优点是实现简单，对信道的要求较低。

然而，由于调制信号是通过改变载波的振幅来传输信息的，因此容易受到噪声的干扰，信号的可靠性较低。

2. 频率调制（FM）频率调制是将数字信号的频率与载波的频率进行调制。

在频率调制中，载波的振幅和相位保持不变，只调制其频率。

当数字信号为1时，频率调制会使得载波的频率增加；当数字信号为0时，频率调制会使得载波的频率减小。

通过这种方式，可以将数字信号转换为模拟信号，便于在信道上传输。

频率调制的优点是抗干扰能力较强，信号的可靠性较高。

然而，频率调制的实现相对复杂，对信道的要求也较高。

3. 相位调制（PM）相位调制是将数字信号的相位与载波的相位进行调制。

在相位调制中，载波的振幅和频率保持不变，只调制其相位。

当数字信号为1时，相位调制会使得载波的相位发生变化；当数字信号为0时，相位调制会使得载波的相位保持不变。

通过这种方式，可以将数字信号转换为模拟信号，便于在信道上传输。

相位调制的优点是调制过程简单，对信道的要求较低。

然而，相位调制容易受到相位偏移和多径效应的影响，导致信号失真。

总结起来，振幅调制、频率调制和相位调制是基带传输中常用的调制方式。

每种调制方式都有其独特的优点和适用场景。

振幅调制简单易实现，适用于对信号可靠性要求不高的场景；频率调制抗干扰能力较强，适用于抗干扰能力要求较高的场景；相位调制实现简单，适用于对信道要求不高的场景。

第5章数字信号的基带传输••••5.1引言5.2数字基带信号波形及其功率谱密度¾数字PAM信号是以脉冲载波的幅度携带数字信息。

5.2.1 数字脉冲幅度调制(PAM)¾MPAM 信号的时域表示式可写为：　()()1,2,...,0i i T ss t ag t i M t T ==≤≤MPAM 信号波形也可表示为另一形式：()()n T s n s t a g t nT ∞=−∞=−∑5.2.2 常用的数字PAM信号波形(码型)1. 单极性不归零码(NRZ)2. 双极性不归零码3. 单极性归零码(RZ)4. 双极性归零码5. 差分码(相对码)6. 多电平的PAM信号波形(MPAM)第5章数字信号的基带传输2 双极性不归零码{}:1110010n b 10n A a A +⎧=⎨−⎩12b t rect T ⎛⎞−⎜⎟⎝⎠0t()T g t 1b T3 单极性归零码(RZ)t()T g t 12b T 1()2T t g t rect τ⎛⎞=−⎜⎟⎝⎠{}:1110010n b②差分译码1n n na b b −=⊕习题5.2（p186)已知信息代码1 1 1 0 0 1 0 1（1）写出相对码（初始值为1）；（2）画出相对码的波形图（单极性矩形不归零码）5.2.3 数字PAM 信号的功率谱密度计算¾如何求PA Ｍ信号的功率谱密度–证明随机过程的平稳性–对于循环平稳过程求其平均自相关函数–通过平均自相关函数求功率谱密度()()n T s n s t a g t nT ∞=−∞=−∑2(1/)22(1/)()()s ssj f T mT a s a m j fmT j ma m P f T R m eR m eeπππ∞−+=−∞∞−−=−∞+==∑∑∵∴P a (f )是f 的周期函数，周期为1/T s 。

其傅氏级数形式为=12()()sj fmT a a m R m eP f π∞−=−∞==∑2()()sj fmT a am P f R m eπ∞−=−∞=∑1/221/2()()sssT j fmT a s a T R m T P f edfπ−=∫系数为[][]{}()()()n n m n n n m n m Cov a a E a E a a E a +++=−⋅−2[][]()[][][]an n m a n n m n n m E a E a R m E a a E a E a σ+++⎧+==⎨⎩设广义平稳随机序列{a n } 是实的且互不相关22200a aam m mm σ⎧+==⎨≠⎩20[][][]0an n m n n m m E a a E a E a m σ++⎧==−=⎨≠⎩例5.2.10二进制信息序列{b n }的取值为＋1或－1，m b =0，方差为1，各符号之间互不相关，序列a n =b n +b n-1(算术加）。