怎样计算弹簧的力

弹簧劲度系数计算公式1. 弹簧劲度系数的定义弹簧劲度系数是指单位长度内弹簧发生单位长度变化时所需的力的大小，也就是用力的大小除以弹簧的伸长（或缩短）量，通常用字母k表示，单位是N/m。

2. 弹簧劲度系数的计算公式弹簧劲度系数的计算公式是：k=F/ΔL其中，k为弹簧劲度系数，F为所用力的大小，ΔL为弹簧伸长（或缩短）的长度。

3. 弹簧劲度系数的测定方法弹簧劲度系数可以通过实验测定获得。

具体操作步骤如下：1. 将弹簧垂直悬挂在支撑物上，并将一端固定。

2. 在弹簧另一端挂上一个钩子，挂上需要测量力的重物，记录下重物的重量。

3. 记录下弹簧的长度、直径、圈数等数据。

4. 用尺量取弹簧受力后的伸长量。

5. 根据公式k=F/ΔL 计算出弹簧劲度系数。

4. 弹簧劲度系数的应用弹簧劲度系数在工程设计中得到了广泛的应用。

例如，根据汽车的重量、挂载位置和所需的行驶舒适性等因素，可以计算出所需要的跳动减缓器的弹簧劲度系数，以此来实现舒适的驾驶体验。

此外，弹簧劲度系数还被应用在各种设置需要回弹的设备中。

例如，弹簧锁、各种开关按钮等等。

5. 弹簧劲度系数与弹性模量的区别弹簧劲度系数和弹性模量都是描述弹性特性的物理量，但是它们的概念和计算方法是不同的。

弹性模量是指单位面积内材料发生单位长度变化时所需的力的大小，而弹簧劲度系数是指单位长度内弹簧发生单位长度变化时所需的力的大小。

6. 弹簧劲度系数的注意事项在测量弹簧劲度系数时，需要注意以下几个方面：1. 测量时需要准确记录弹簧的长度、直径、圈数等数据。

2. 测量时应注意不要超过弹簧的最大变形范围，避免弹簧变形过大而失去弹性。

3. 测量时需要用拉伸试验机或其他专用测量工具，以保证测量结果的准确性。

综上所述，弹簧劲度系数是一个非常重要的物理量，可以在工程设计中发挥重要作用。

通过准确测量弹簧的劲度系数，可以更好地控制和预测弹簧的弹性特性，从而实现更好的使用效果。

物理力弹簧重力的计算公式弹簧的物理力学计算公式包括弹簧力和重力的计算公式。

弹簧力是指当物体挂在弹簧上时，弹簧对物体产生的力，而重力是指物体受到的地球引力。

在物理学中，这两种力都是非常重要的，并且它们的计算公式可以帮助我们更好地理解物体在弹簧上的运动。

首先，我们来看一下弹簧力的计算公式。

弹簧力是指弹簧对物体产生的力，它的大小与弹簧的弹性系数和物体与弹簧的伸长或压缩距离有关。

根据胡克定律，弹簧的弹性力与弹簧的伸长或压缩距离成正比。

因此，弹簧力的计算公式可以表示为：F = -kx。

其中，F表示弹簧力的大小，单位是牛顿（N）；k表示弹簧的弹性系数，单位是牛顿每米（N/m）；x表示物体与弹簧的伸长或压缩距离，单位是米（m）。

负号表示弹簧力的方向与伸长或压缩方向相反。

接下来，我们来看一下重力的计算公式。

重力是指物体受到的地球引力，它的大小与物体的质量和地球的引力加速度有关。

根据牛顿定律，重力的大小可以表示为：F = mg。

其中，F表示重力的大小，单位是牛顿（N）；m表示物体的质量，单位是千克（kg）；g表示地球的引力加速度，单位是米每秒平方（m/s²）。

当物体同时受到弹簧力和重力时，它们的合力可以表示为：F_total = F_spring + F_gravity。

根据上面的计算公式，我们可以得到：F_total = -kx + mg。

这个公式表示了物体在弹簧上受到的合力大小，它包括了弹簧力和重力的影响。

根据这个公式，我们可以计算出物体在弹簧上的运动状态，比如物体的加速度、速度和位移等。

除了计算公式之外，弹簧力和重力还有一些重要的特性。

比如，弹簧力与伸长或压缩距离成正比，而重力与物体的质量成正比。

这些特性可以帮助我们更好地理解物体在弹簧上的运动规律。

总之，弹簧力和重力的计算公式可以帮助我们更好地理解物体在弹簧上的运动。

通过这些公式，我们可以计算出物体受到的合力大小，从而了解物体的运动状态。

同时，弹簧力和重力的特性也可以帮助我们更深入地理解这两种力的本质。

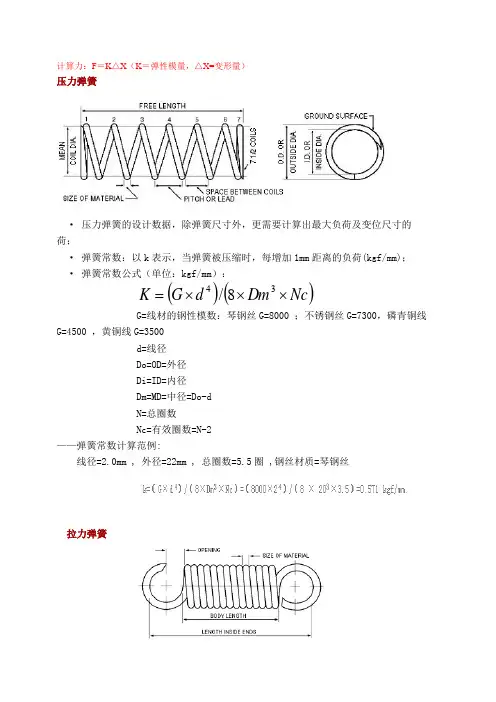
计算力：F ＝K △X （K ＝弹性模量，△X=变形量）压力弹簧· 压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的荷；· 弹簧常数：以k 表示，当弹簧被压缩时，每增加1mm 距离的负荷(kgf/mm)； · 弹簧常数公式（单位：kgf/mm ）：()()Nc Dm d G K ⨯⨯⨯=348/G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300，磷青铜线G=4500 ，黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2——弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝拉力弹簧拉力弹簧的 k值与压力弹簧的计算公式相同·拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

· 初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧· 弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷 (kgf/mm).· 弹簧常数公式（单位：kgf/mm）:()()R4⨯⨯/=1167⨯K⨯pN⨯DmdEE=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。

胡克弹性定律指出，在弹性极限范围内，弹簧的弹性力f 与弹簧的长度x 成正比，即f =-kx，k 是一个物体的质量弹性系数，该系数由材料的性质决定，负号表示弹簧产生的弹性力与其延伸(或压缩)方向相反弹簧常数: 以k 表示，当弹簧被压缩时，载荷(kgf/mm)增加1mm 的距离，弹簧常数公式(单位: kgf/mm) : k = (g d4)/(8dm3 nc) g = 钢丝的刚度模量: 钢琴丝g = 8000; 不锈钢丝g = 7300; 磷青铜丝g = 4500;黄铜丝g = 3500d = 线径= 0d = 外径= id = 内径= md = 中径= do-dn = 转速总数弹簧常数的计算例子: 线径= 2.0 mm，外径= 22 mm，总匝数= 5。

5圈，钢丝材料= 钢琴钢丝k = (gxd4)/(8xdm3xnc) = (8000x24)/(8x203x3.5) = 0.571 kg f/mmpull，张力弹簧的k 值与压力弹簧的k 值相同。

张力弹簧的初始张力: 初始张力等于拉开彼此接近的弹簧所需的力，并发生在弹簧轧制成型之后。

在制作张力弹簧时，由于钢丝材质、线径、弹簧指数、静电现象、油脂、热处理、电镀等的不同，使得各张力弹簧的初始张力不均匀。

因此，在安装各种规格的张力弹簧时，应该预张力到平行弯道之间一定距离的力称为初张力。

初始张力= p-(kxf1) = 最大载荷-(弹簧常数x 拉伸长度)扭转弹簧常数: 以k 表示，当弹簧扭转时，载荷(kgf/m)增加1个扭转角。

弹簧常数(单位: kgf/mm) : k = (exd #)/(1167 xdmxpnxr) e = 钢丝的刚度模量: 钢琴线e = 21000，不锈钢线e = 19400，磷青铜线e =11200,黄铜丝e = 11200d = 线径= 0d = 外径= id = 内径= md = 中径= do-dn = 载荷作用下转臂的总长度= 3.1416。

弹力计算公式压力弹簧初拉力计算F0=〖｛π3.14×d3｝÷(8×D)〗×79mpaF0=｛3.14×(5×5×5)÷(8×33)｝×79=117 kgf1.压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；2.弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；3.弹簧常数公式（单位：kgf/mm）；K=(G×d4)/(8×D3×Nc)G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，60Si2MnA钢丝G=7900，磷青铜线G=4500 ，黄铜线G=3500d=线径(钢丝直径)D=中径N=总圈数Nc=有效圈数F=运动行程(550mm)弹簧常数计算范例：线径=5.0mm , 中径=20mm , 有效圈数=9.5圈,钢丝材质=不锈钢丝K=(G×d4)/(8×D3×Nc)=(7900×54)/(8×203×9.5)=8.12kgf/m m×(F=100)=812 kgf拉力弹簧拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧弹簧常数：以k 表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm)弹簧常数公式（单位：kgf/mm）：K=(E×d4)/(1167×D×p×N×R)E=线材之钢性模数：琴钢丝E=21000，不锈钢丝E=19400 ，磷青铜线E=11200 ，黄铜线E=11200d=线径(钢丝直径)D=中径N=总圈数R=负荷作用的力臂p=3.1416。

弹簧力的计算弹簧力是一个力学中常见的概念，它定义了弹簧接受外力时的反作用力大小。

弹簧力的计算涉及到弹簧的弹性系数、弹簧的伸长或压缩量以及外力的大小，同时也与弹簧的形状和材料有关。

首先，需要明确弹簧力的计算公式。

一般来说，弹簧力可以用胡克定律来计算，即 F = k * x，其中 F 代表弹簧力，k 代表弹性系数，x 代表弹簧的伸长或压缩量。

这个公式说明了弹簧力与伸长或压缩量成正比，而弹性系数则是弹簧的特性之一。

弹性系数取决于弹簧的形状和材料。

不同形状的弹簧有不同的弹性系数计算方法，如圆环弹簧、螺旋弹簧等。

此外，弹簧材料的选择也会影响弹性系数的取值。

常见的弹簧材料有金属材料如钢、铜等，以及非金属材料如橡胶。

对于圆环弹簧，弹性系数 k 的计算可以按照以下公式进行：k = 3 * E * R^4 / (4 * d^3 * n)，其中 E 代表弹簧材料的弹性模量，R 代表弹簧的平均半径，d 为弹簧的线径，n 代表弹簧的匝数。

这个公式显示了弹性系数与弹簧尺寸及材料的关系，也说明了弹性系数的大小对于弹簧力的计算具有重要意义。

螺旋弹簧的弹性系数计算可以使用更为简单的公式：k = (G * d^4) / (8 * D^3 * n)，其中 G 代表弹簧材料的剪切模量，d 代表弹簧线径，D 为弹簧的平均直径，n 表示弹簧的匝数。

这个公式说明了弹性系数与弹簧尺寸及材料的关联，而剪切模量则与弹簧材料的剪切刚度有关。

了解了弹性系数的计算方法，接下来需要考虑弹簧的伸长或压缩量。

通常情况下，伸长或压缩量可以通过直接测量获得，也可以通过应变仪器或力传感器等设备进行测量。

一般而言，弹簧的伸长或压缩量与作用力大小成正比。

通过合理的测量并代入公式中，可以求解弹簧力的大小。

例如，假设我们有一个圆环弹簧，其线径为 0.5 mm，匝数为 10，材料弹性模量为 200 GPa，平均半径为 10 mm，并且伸长了 2 cm。

代入公式，我们可以得到弹性系数 k 的值为 400 N/m，即弹簧力为 800 N。

弹簧的弹力公式
弹簧的弹力公式表明它拥有独特的弹性特性，并且仍然受到弹击
激励，可以从一定程度上恢复到它原来的位置。

这让弹簧能够在多种
结构中使用，以达到减震、稳固和调节作用。

弹簧的弹力公式很复杂，但常见的按照Hooke定律来计算。

Hooke定律指出：当外力作用于一个弹簧时，当前弹簧伸缩量与外力成正比。

其公式表示为：F = -kx，其中：F为外力，k为弹簧在扭结状
态下的刚度系数，x为变形量。

弹性力公式中的刚度系数（k）是弹簧的主要参数，反映了该弹
簧的刚度。

通常而言，受外力作用时，弹簧的伸缩量越大，说明该弹
簧的刚度越高；反之，则说明该弹簧的刚度越低。

此外，弹簧的刚度
还与材料、形状、体积等因素有关，使得改变它们可以调节弹簧的刚度。

弹簧的伸缩量（x）受其刚度系数（k）和外力（F）的影响，且
外力一般表示一定形状的弹簧对应不同伸缩量的外力大小。

通过弹簧
的弹力公式，我们可以了解到，对于特定的弹簧材料和不同的外力，
它们之间存在着唯一的相互关系：弹簧会产生受力而变形，并依据Hooke定律以正比例受力变形。

总之，弹簧的弹力公式看似复杂，但它描述了一个弹簧在扭结状
态下对外力的变形反应，是被广泛应用于减震，稳固和调节结构中的。

要根据应用场景来选择合适的弹簧，以实现减振、稳固和调节的作用。

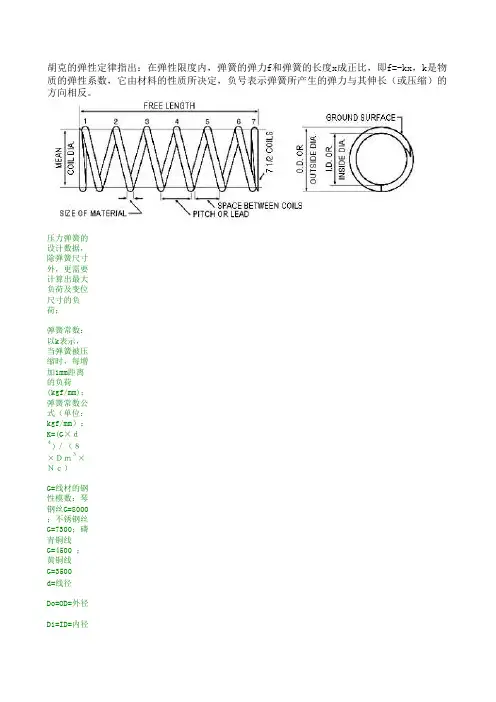
胡克的弹性定律指出：在弹性限度内，弹簧的弹力f和弹簧的长度x成正比，即f=-kx，k是物质的弹性系数，它由材料的性质所决定，负号表示弹簧所产生的弹力与其伸长（或压缩）的方向相反。

压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；弹簧常数公式（单位：kgf/mm）：K=(G×ｄ４)／（８×Ｄｍ３×Ｎｃ）G=线材的钢性模数：琴钢丝G=8000；不锈钢丝G=7300；磷青铜线G=4500 ；黄铜线G=3500d=线径Do=OD=外径Di=ID=内径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm ,外径=22mm, 总圈数=5.5圈 ,钢丝材质=琴钢丝K=(G×ｄ４)／（８×Ｄｍ３×Ｎｃ）＝（８０００×２４）／（８×２０３×３．５）＝０．５７１ｋｇｆ／ｍｍ拉力弹簧拉力弹簧的k值与压力初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm).弹簧常数公式（单位：kgf/mm）:K=(Ｅ×ｄ４)／（１１６７×Ｄｍ×ｐ×Ｎ×Ｒ）拉力弹簧的初张力:初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。

弹簧压力拉力计算弹簧是一种用于储存和释放机械能的弹性元件，广泛应用于机械和工程领域。

在设计和使用弹簧时，计算其压力和拉力是非常重要的。

本文将介绍弹簧压力和拉力的计算方法。

1.弹簧压力的计算方法：弹簧压力是指弹簧在压缩或压摊状态下所受的力。

弹簧的压力可以用胡克定律来计算，胡克定律表示弹簧的变形与所受的力成正比。

1.1一般情况下，弹簧压力的计算公式为：F=k*x其中，F为弹簧受力（压力），k为弹簧的弹性系数，x为弹簧的变形量。

1.2弹簧压力的单位：弹簧的压力一般用牛顿（N）来表示。

1.3弹性系数的计算方法：弹簧的弹性系数可以通过实验或计算得出。

在实验中，可以测量弹簧所受的外力和相应的变形量，然后根据胡克定律计算弹性系数。

在计算中，弹性系数可以通过材料力学性质和弹簧几何参数来确定。

2.弹簧拉力的计算方法：弹簧拉力是指弹簧在拉伸状态下所受的力。

弹簧的拉力可以通过下面的计算方法得出。

2.1一般情况下，弹簧拉力的计算公式为：F=k*x其中，F为弹簧受力（拉力），k为弹簧的弹性系数，x为弹簧的变形量。

2.2弹簧拉力的单位：弹簧的拉力也一般用牛顿（N）来表示。

3.弹簧压力、拉力计算的实例：假设一个弹簧的弹性系数为100N/m，变形量为0.02m，求弹簧的压力和拉力。

根据公式F=k*x，可以计算出弹簧的压力和拉力：压力：F=100N/m*0.02m=2N拉力：F=100N/m*0.02m=2N所以，该弹簧在压缩或拉伸状态下的压力和拉力都为2N。

4.弹簧压力、拉力计算注意事项：4.1在计算弹簧压力和拉力时，需要准确测量弹簧的变形量，以获取正确的结果。

4.2弹簧的弹性系数是一个重要参数，需要根据实际情况选择合适的值。

4.3弹簧的压力和拉力计算仅适用于弹簧的线性变形范围，如果超过线性范围，计算的结果将不准确。

4.4在实际应用中，还需要考虑弹簧的材料性质、弯曲和扭转等因素的影响，以获得更准确的结果。

总结：本文介绍了弹簧压力和拉力的计算方法。

弹簧的力学计算
即胡克定律
其中，F为弹力，k是劲度系数，△x是弹簧形变量
（N/mm）
其中：
G=线材的刚性模数，单位N/mm^2（即切变模量）：碳素弹簧钢丝（如65Mn）以及常用弹簧钢丝79000 ；不锈钢丝71000 ，硅青铜线G=41000 【其他详见机械设计手册（第五版）第三卷P11-10】
d=线径（mm）
Do=OD=外径（mm）
Dm=MD=中径=Do-d（mm）
N=总圈数
Nc=有效圈数=N-2
弹簧常数计算范例: 线径=2.0mm , 外径=22mm , 总圈数=5.5圈,钢丝材质=琴钢丝
在弹性限度内，弹簧的弹力可由F=kX,x为弹簧的伸长的长度；k为劲度系数，表示弹簧的一种属性，它的数值与弹簧的材料，弹簧丝的粗细，弹簧圈的直径，单位长度的匝数及弹簧的原长有关。

在其他条件一定时弹簧越长，单位长度的匝数越多，k值越小。

k还与温度有关，其他条件一定时，温度越低k越大．
两弹簧倔强系数分别为k1，k2。

两弹簧串联后
k串=（k1×k2）/（k1+k2）
两弹簧并联后mg=F1+F2=(K1+K2)X
k并=k1+k2。

弹簧弹力计算公式标准化管理部编码-[99968T-6889628-J68568-1689N]弹力计算公式压力弹簧初拉力计算F0=〖｛π×d 3｝÷(8×D)〗×79mpaF0=｛×(5×5×5)÷(8×33)｝×79=117 kgf1.压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；2.弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；3.弹簧常数公式（单位：kgf/mm）；K=(G×d4)/(8×D3×Nc)G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，60Si2MnA钢丝G=7900，磷青铜线G=4500 ，黄铜线G=3500d=线径(钢丝直径)D=中径N=总圈数Nc=有效圈数F=运动行程(550mm)弹簧常数计算范例：线径=5.0mm , 中径=20mm , 有效圈数=圈 ,钢丝材质=不锈钢丝K=(G×d4)/(8×D3×Nc)=(7900×54)/(8×203×=mm×(F=100)=812 kgf拉力弹簧拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷 (kgf/mm)弹簧常数公式（单位：kgf/mm）：K=(E×d4)/(1167×D×p×N×R)E=线材之钢性模数：琴钢丝E=21000 ，不锈钢丝E=19400 ，磷青铜线E=11200 ，黄铜线E=11200d=线径(钢丝直径)D=中径N=总圈数R=负荷作用的力臂p=。

弹簧力量计算
力=弹簧刚度（kg/mm）*压缩量（mm）
弹簧刚度=线径*刚性模数/(8*旋绕比C的3次方*工作圈数)
工作圈数=总圈数-2
旋绕比C=弹簧中径/线径
弹簧中径=弹簧外径-线径
刚性模数：弹簧钢(常用)8000，不锈钢7000，铜4000
用0.8mm不锈钢丝缠绕外径5.8mm的弹簧，缠绕30圈，总长度80mm，完全压缩到60mm时的压力计算
刚性模数取8000
弹簧中径=5.8-0.8=5mm
旋绕比=5/0.8=6.25
工作圈数=30（为了便于计算）
弹簧刚度=1*8000/(8*6.25^3*30)=0.52
力=0.52*50=26kg
如果弹簧中径增加1mm，则
旋绕比=5/1=5
弹簧刚度=1*8000/(8*5^3*30)=0.047
力=0.047*20=0.94kg
用2.5mm不锈钢丝缠绕外径49.5mm的弹簧，缠绕6圈，总长度70mm，完全压缩到50mm时的压力计算
刚性模数取8000
弹簧中径=49.5-2.5=47mm
旋绕比=47/2.5=18.8
工作圈数=6（为了便于计算）
弹簧刚度=1*8000/(8*18.8^3*6)=0.025
力=0.025*20=0.5kg。

压力弹簧的设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸的负荷;弹簧常数:以k表示,当弹簧被压缩时,每增加1mm距离的负荷(kgf/mm;弹簧常数公式(单位:kgf/mm:K=(G×d4/(8×Dm3×NcG=线材的钢性模数:琴钢丝G=8000 ;不锈钢丝G=7300;磷青铜线G=4500 ;黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝K=(G×d4/(8×Dm3×Nc=(8000×24/(8×203×3.5=0.571kgf/mm拉力弹簧拉力弹簧的 k值与压力弹簧的计算公式相同。

拉力弹簧的初张力:初张力等于适足拉开互相紧贴的弹簧并圈所需的力,初张力在弹簧卷制成形后发生。

拉力弹簧在制作时初张力=P-(k×F1=最大负荷-(弹簧常数×拉伸长度扭力弹簧弹簧常数:以 k 表示,当弹簧被扭转时,每增加1°扭转角的负荷(kgf/mm.弹簧常数公式(单位:kgf/mm: K=(E×d4/(1167×Dm×p×N×RE=线材之钢性模数:琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416后发生。

拉力弹簧在制作时,因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同,使得每个拉力弹簧初始拉力产生不个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时,应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

弹簧拉力的计算公式嘿，咱今天来好好聊聊弹簧拉力的计算公式！在我们的生活中，弹簧这东西可不少见。

就说我前几天收拾房间的时候，发现了一个旧的玩具车，这玩具车的轮子上就有弹簧。

我当时就琢磨，这小小的弹簧到底能产生多大的拉力呢？要搞清楚弹簧拉力的大小，就得知道那个关键的计算公式。

弹簧拉力的计算公式是 F = kx ，这里的 F 表示弹簧的拉力，k 是弹簧的劲度系数，x 则是弹簧的伸长量。

先来说说这个劲度系数 k 。

它就像是弹簧的“性格特点”，不同的弹簧，k 值可不一样。

比如说，那种又粗又大的弹簧，k 值通常就比较大，意味着你得使很大的劲才能让它有明显的伸长；而又细又小的弹簧呢，k 值就小些，轻轻一拉就变长了。

那伸长量 x 呢，就是弹簧被拉伸或者压缩后的长度变化。

比如说，原本弹簧长 10 厘米，你拉了它之后变成 15 厘米，那伸长量就是 5 厘米。

咱们举个例子啊，假如有一个弹簧，它的劲度系数 k 是 50 牛/米，你把它拉长了 0.2 米，那根据公式 F = kx ，拉力 F 就等于 50 乘以 0.2 ，算出来是 10 牛。

再想象一下，如果是在一个物理实验课上，老师给大家一堆不同的弹簧，让同学们自己去测量它们的劲度系数和伸长量，然后计算拉力，那场面肯定特别热闹。

有的同学可能会手忙脚乱地测量，结果还出错；有的同学则会认真仔细，算得又快又准。

在实际生活中，弹簧的应用那可多了去了。

像我们常见的弹簧秤，就是利用弹簧拉力的原理来测量物体的重量。

还有汽车的减震系统，里面也有弹簧，通过弹簧的伸缩来减少路面颠簸带来的震动。

说到这儿，我又想起之前修自行车的时候，发现车座下面的弹簧松了，坐上去老往下塌。

这就是弹簧拉力不够的表现呀，得换个劲度系数合适的弹簧才行。

总之，弹簧拉力的计算公式虽然看起来简单，但是在实际应用中可是非常重要的。

它能帮助我们理解和解决很多与弹簧相关的问题，让我们的生活更加便利和有趣。

不知道您现在对弹簧拉力的计算公式是不是有更清楚的认识啦？。

弹簧⼒值计算公式压⼒弹簧· 压⼒弹簧的设计数据，除弹簧尺⼨外，更需要计算出最⼤负荷及变位尺⼨的负荷；· 弹簧常数：以k表⽰，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；· 弹簧常数公式（单位：kgf/mm）：k =(G×d)/(8×Dm×Nc)G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，磷青铜线G=4500 ，黄铜线G=3500 d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝拉⼒弹簧拉⼒弹簧的 k值与压⼒弹簧的计算公式相同· 拉⼒弹簧的初张⼒：初张⼒等于适⾜拉开互相紧贴的弹簧并圈所需的⼒，初张⼒在弹簧卷制成形后发⽣。

拉⼒弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉⼒弹簧初始拉⼒产⽣不平均的现象。

所以安装各规格的拉⼒弹簧时，应预拉⾄各并圈之间稍为分开⼀些间距所需的⼒称为初张⼒。

· 初张⼒=P-（k×F1）=最⼤负荷-（弹簧常数×拉伸长度）扭⼒弹簧· 弹簧常数：以 k 表⽰,当弹簧被扭转时，每增加1°扭转⾓的负荷 (kgf/mm).· 弹簧常数公式（单位：kgf/mm）:E=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200 ,黄铜线E=11200 d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作⽤的⼒臂p=3.1416。

弹力计算公式压力弹簧初拉力计算F0=〖｛π3.14×d3｝÷(8×D)〗×79mpaF0=｛3.14×(5×5×5)÷(8×33)｝×79=117 kgf1.压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；2.弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；3.弹簧常数公式（单位：kgf/mm）；K=(G×d4)/(8×D3×Nc)G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，60Si2MnA钢丝G=7900，磷青铜线G=4500 ，黄铜线G=3500d=线径(钢丝直径)D=中径N=总圈数Nc=有效圈数F=运动行程(550mm)弹簧常数计算范例：线径=5.0mm , 中径=20mm , 有效圈数=9.5圈,钢丝材质=不锈钢丝K=(G×d4)/(8×D3×Nc)=(7900×54)/(8×203×9.5)=8.12kgf/m m×(F=100)=812 kgf拉力弹簧拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧弹簧常数：以k 表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm)弹簧常数公式（单位：kgf/mm）：K=(E×d4)/(1167×D×p×N×R)E=线材之钢性模数：琴钢丝E=21000，不锈钢丝E=19400 ，磷青铜线E=11200 ，黄铜线E=11200d=线径(钢丝直径)D=中径N=总圈数R=负荷作用的力臂p=3.1416。

弹簧力度计算公式一、背景知识在介绍弹簧力度计算公式之前，我们先了解一些与弹簧力度相关的概念和公式。

1.弹力弹力是指当弹簧发生弹性变形时产生的恢复力。

根据胡克定律，弹力与弹簧位移的关系可以表示为：F=k*x其中，F表示弹力，k表示弹簧的力度或刚度，x表示弹簧的位移。

2.力度或刚度在弹簧力度的定义中，力度或刚度表示弹簧对单位位移的抵抗能力。

一般来说，力度或刚度越大，弹簧的抵抗能力越强。

力度或刚度的单位是牛顿/米（N/m）。

k=F/x其中，k表示力度或刚度，F表示弹力，x表示弹簧的位移。

二、弹簧力度计算公式的应用1.弹簧刚度计算弹簧刚度是指在弹簧受到单位位移时所产生的弹力。

我们可以使用力度计算公式来计算弹簧的刚度。

假设一个弹簧受到100N的力，位移为10mm，则该弹簧的刚度为：2.弹簧设计在机械设计中，我们通常需要选择合适的弹簧来支撑和平衡力的作用。

弹簧设计的关键是选择合适的力度或刚度。

例如，对于一个给定的力和位移要求，可以使用力度计算公式来计算所需的弹簧力度。

然后根据实际情况选择合适的弹簧。

3.弹簧系统分析在弹簧系统的分析中，我们常常需要确定弹簧的力度和位移关系。

通过力度计算公式，可以得到弹簧力度和位移之间的关系。

这对于分析和优化弹簧系统的性能和稳定性非常有帮助。

三、总结弹簧力度计算公式是一种用于计算弹簧力度或刚度的公式。

力度计算公式可以从弹力公式中推导出来，通过该公式，我们可以计算弹簧力度，以满足给定的力学要求。

弹簧力度计算公式广泛应用于工程领域，特别是在机械设计和弹簧选型中。

通过计算弹簧力度，可以确定合适的弹簧尺寸和材料，以满足给定的力学要求。

弹簧力度计算公式是工程师用于设计和分析弹簧系统的重要工具。