高一物理竞赛：第五讲.《万有引力定律》

高中物理竞赛——万有引力定律基础知识点一、考点内容1．万有引力；万有引力定律；万有引力定律的应用。

2．人造地球卫星；宇宙速度。

二、知识结构⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧地球同步卫星地面卫星种类发射与运转三个宇宙速度人造天体（或卫星）开普勒三定律地卫星；自由落体或平抛；近天体质量计算：极地称：与纬度、高度的关系地球附近重力变化规律定律应用 三、复习思路建议分两条主线展开复习，一是万有引力=向心力；另一个是重力=向心力。

由于向心力的表达式有多种形式，表面看来本单元公式多，实际上则只有一个，那就是ma F =。

切实理解好加速度a 的含义至关重要。

复习时应注意做好以下几点：1．万有引力、人造卫星属于现代科技发展的重要领域，所以近年的高考对万有引力、人造卫星的考查是热点。

在学习中要多联系一些现代科技知识，扩大知识面，把这部分知识规律与实际应用联成一体去认识。

2．应用万有引力定律研究天体、人造地球卫星的运动是该部分的重点。

要熟练地应用r Tm r m r v m r Mm G 222224πω===及地球表面附近2r Mm G mg =等公式来求解天体及卫星问题，要熟练地运用比例法解题。

3．要知道卫星的运行速度、发射速度和环绕速度三者的区别，要知道卫星的轨道越高，其运动速度越小，但发射时所需的发射速度却越大。

4．要知道三种宇宙速度都是指发射速度，并了解火箭发射卫星的实际过程，了解一下现代科技。

四、牢固掌握基础知识1、万有引力定律的应用（1）、基本模型：匀速圆周运动（2）、基本方法：一切问题来源于向心力的提供（3）、一条线索：向心力=万有引力=所在位置处的重力（4）、一串公式：=2rMm G = = 以及地球表面附近2地R MmG mg =等公式。

上述式子适用于卫星围绕天体作匀速圆周运动时的情景。

由以上线索和公式可以：A 、估算天体质量B 、估算天体质量C 、求卫星的线速度、角速度、周期r GM v =；3rGM w =；GM r T 32π=。

高一物理万有引力定律课件一、教学内容本节课我们将学习高一物理《万有引力定律》章节。

详细内容包括：万有引力定律的发现历程、万有引力定律的定义及表达式、万有引力常量的测定、以及万有引力定律在实际问题中的应用。

二、教学目标1. 理解万有引力定律的发现历程，了解牛顿在物理学史上的地位。

2. 掌握万有引力定律的表达式，能够运用其解决实际问题。

3. 了解万有引力常量的测定过程，理解其物理意义。

三、教学难点与重点教学难点：万有引力定律的表达式及其应用。

教学重点：万有引力定律的发现历程，万有引力常量的测定。

四、教具与学具准备1. 教具：地球仪、月球仪、万有引力演示仪。

2. 学具：计算器、笔记本、教材。

五、教学过程1. 实践情景引入：通过地球仪和月球仪，展示地球与月球之间的引力现象，引导学生思考引力的本质。

2. 例题讲解：讲解万有引力定律的发现历程，引导学生学习牛顿的科学精神。

3. 知识讲解：（1）万有引力定律的定义及表达式。

（2）万有引力常量的测定过程及意义。

（3）万有引力定律在实际问题中的应用。

（1）地球与月球之间的引力大小。

（2）地球表面物体所受重力与万有引力的关系。

六、板书设计1. 万有引力定律的发现历程。

2. 万有引力定律的表达式。

3. 万有引力常量的测定。

4. 万有引力定律的应用。

七、作业设计1. 作业题目：（1）证明地球表面物体所受重力与万有引力的大小关系。

（2）计算地球与月球之间的引力大小。

2. 答案：（1）证明过程：略。

（2）地球与月球之间的引力大小约为3.52×10^20 N。

八、课后反思及拓展延伸1. 反思：本节课学生对万有引力定律的理解程度，以及在实际问题中的应用能力。

2. 拓展延伸：（1）研究万有引力定律在现代科学中的应用，如人造卫星、航天器等。

（2）了解其他科学家在引力研究方面的贡献，如卡文迪许、爱因斯坦等。

重点和难点解析1. 万有引力定律的表达式及其应用。

2. 万有引力常量的测定。

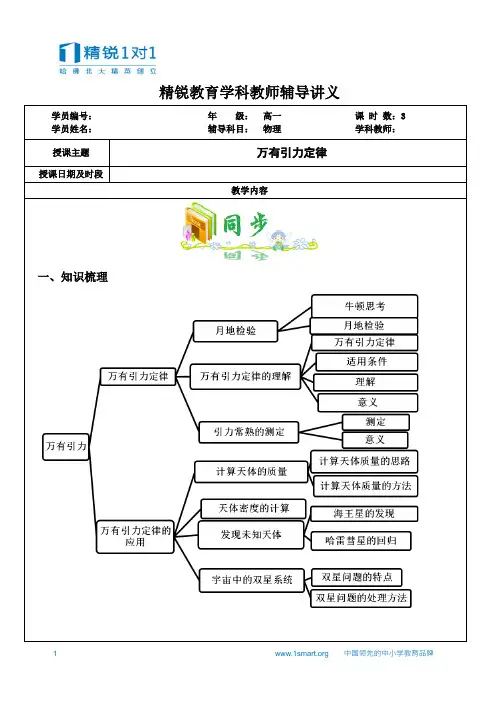
精锐教育学科教师辅导讲义学员编号：年级：高一课时数：3学员姓名：辅导科目：物理学科教师：授课主题万有引力定律授课日期及时段教学内容一、知识梳理二、知识点深化（一）月-地检验 1、牛顿的猜想地球对物体的引力、地球对月球的力及太阳对行星的力可能是同一种性质的力，它们可能遵循相同的规律。

2、检验的思想猜想必须由事实来验证。

由于当时已经能够精确测定地球表面的重力加速度g=9.8m/s 2，也能比较精确地测定月球与地球的距离为60倍地球半径，r=3.8*108m ；月球公转的周期为27.3天。

所以牛顿就想到了月地检验。

3、检验过程如果它们是同一种性质的力，满足同一规律则对于苹果必有： 将苹果放到地面上时（忽略地球自传影响）mg MmGR =2将苹果放到月球轨道上时 ma MmGr=2则向心加速度为srR mga 2322107.2-⨯==而根据实验观测数据T=27.3天，r=3.8*108m ，用公式2322/107.24s m r Ta -⨯==π4、检验的结果地面物体所受地球的引力，月球所受地球的引力，以及太阳与行星间的引力，真的遵循的规律2r MmGF = （二）万有引力定律 1.内容自然界中任何两个物体都是相互吸引的，引力的方向沿两物体的连线，引力的大小F 与这两个物体质量的乘积12m m 成正比，与这两个物体间距离r 的平方成反比。

2.公式：122m m F Gr=，其中G 为万有引力常量，11226.6710/G N m kg -=⨯⋅ 3.适用条件适用于相距很远，可以看作质点的物体之间的相互作用。

质量分布均匀的球体可以认为质量集中于球心，也可以用此公式计算，其中r 为两球心之间的距离。

4、说明（1）普遍性：任何客观存在的物体间都存在着相互作用的吸引力，即“万有引力”（2）相互性：两物体间的万有引力是一对作用力与反作用力，它们的大小相等、方向相反，分别作用在两个物体上。

（3）宏观性：在通常情况下，万有引力非常小，只有在质量巨大的星体间或天体与天体附近的物体间，它的存在才有实际的物理意义，故在分析地球表面的物体受力时，不考虑地面物体间的万有引力，只考虑地球对地面物体的万有引力。

有关高中物理“万有引力定律”的概念
有关高中物理“万有引力定律”的概念如下：
万有引力定律是描述物体之间相互引力的定律，由艾萨克·牛顿在1687年提出。

它表明任何两个物体之间都存在引力，且这个引力与它们质量的乘积成正比，与它们距离的平方成反比。

在高中物理中，万有引力定律通常表示为：F = G * (m1 * m2) / r^2，其中F 是两个物体之间的引力，m1 和m2 分别是两个物体的质量，r 是它们之间的距离，G 是引力常量，其值约为6.67430 × 10^-11 m^3 kg^-1 s^-2。

万有引力定律在天文学中有着重要的应用，它解释了行星轨道运动和天体运动的规律。

此外，万有引力定律也是研究宇宙学和天体物理学等领域的基础。

在高中物理中，学生通常会学习如何使用万有引力定律计算两个物体之间的引力，以及如何使用它来解释一些天体运动的规律。

同时，学生也会学习到万有引力定律的一些特殊情况，例如在地球表面的物体所受的重力可以看作是地球对该物体的万有引力。

总之，万有引力定律是高中物理中的一个重要概念，它描述了物体之间的引力规律，为我们理解天体运动和宇宙结构提供了基础。

高一物理竞赛讲义专题四万有引力定律、引力势能【概念与规律】 1.万有引力定律 （1）公式：2MmF Gr=，其中G=6.67×10-11N ·m 2/kg 2。

（2）适用条件：公示只适用于质点间的相互作用。

当两个物体间的距离远远大于物体本身的尺寸时，物体可视为质点。

均匀球体可视为质点，r 是两球心间的距离。

（3）由万有引力定律可以推出，质量为M 、半径为R 的均匀球壳对球心为r 、质量为m 的质点的万有引力为()()20r R F GMmr R r⎧⎪=⎨⎪⎩ ＞＞ 2.应用万有引力定律解决天体运动问题基本方法：把天体看作是做匀速圆周运动的物体，其所需的向心力由万有引力提供，即()2222222Mm v G m mr m r m f r r r T πωπ⎛⎫==== ⎪⎝⎭在地面上2Mm mg GR =地地。

在空中h 高处()2'Mm mg G R h =+。

物体的重力和地球对该物体的万有引力差别很小，一般可认为二者大小相等。

3.开普勒三定律（1）轨道定律：行星绕太阳做椭圆轨道运动，太阳位于椭圆的一个焦点上。

此定律揭示了太阳系各行星的轨道形状以及太阳和行星的相对位置。

由于行星的椭圆轨道跟圆相似，所以通常把行星轨道作为圆周来处理。

（2）面积定律：行星和太阳之间的连线，在相等的时间内，所扫过的面积相等。

如图所示。

此定律反映了行星速率变化的规律，说明行星在远日点速率最小，在近日点速率最大。

2221111111111111222v S R R t R t R θω===，2222222222222111222v S R R t R t R θω=== 因t 1=t 2，S 1=S 2，故R 1v 1=R 2v 2。

（3）周期定律：行星运动周期的平方和轨道半长轴的立方成正比。

即32R T=常数（此常数只与太阳质量有关）。

此定律阐明了各行星运动周期与其轨道的长半轴的关系。