【八年级数学试题】2018年八年级数学上1.3证明(一)基础训练(浙教版带答案)
- 格式:doc
- 大小:26.00 KB
- 文档页数:4

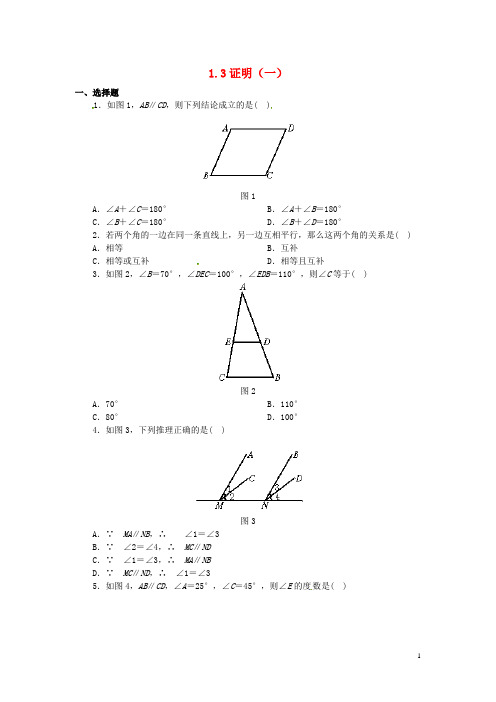
1.3证明(一)一、选择题1.如图1,AB∥CD,则下列结论成立的是( )图1A.∠A+∠C=180°B.∠A+∠B=180°C.∠B+∠C=180°D.∠B+∠D=180°2.若两个角的一边在同一条直线上,另一边互相平行,那么这两个角的关系是( ) A.相等B.互补C.相等或互补D.相等且互补3.如图2,∠B=70°,∠DEC=100°,∠EDB=110°,则∠C等于( )图2A.70°B.110°C.80°D.100°4.如图3,下列推理正确的是( )图3A.∵MA∥NB,∴∠1=∠3B.∵∠2=∠4,∴MC∥NDC.∵∠1=∠3,∴MA∥NBD.∵MC∥ND,∴∠1=∠35.如图4,AB∥CD,∠A=25°,∠C=45°,则∠E的度数是( )图4A.60°B.70°C.80°D.65°二、填空题6.如图5,a∥b,∠1=120°,则∠2=________.图57.如图6,已知AB∥CD,∠1=65°,∠2=45°,则∠ADC=________.图68.如图7,已知∠1=∠2,∠BAD=57°,则∠B=________.图79.如图8,若AB∥EF,BC∥DE,则∠B+∠E=________.图810.如图9,由A测B的方向是________.图9三、解答题11.已知:如图10,AD∥BC,∠B=∠D.求证:AB∥CD.图1012.已知:如图11,∠1=∠B,∠A=32°.求:∠2的度数.图1113.已知:如图12,AD∥BC,∠ABC=∠C,求证:AD平分∠EAC.图1214.如图13,A、B之间是一座山,要修一条铁路通过A、B两地,在A地测得铁路走向是北偏东58°11′.如果A、B两地同时开工开隧道,那么在B地按北偏西多少度施工,才能使铁路隧道在山腹中准确接通?图13参考答案一、1.C 2.C 3.C 4.B 5.B二、6.60°7.110°8.123°9.180°10.南偏东70°三、11.略12.148°13.略14.在B地按北偏西121°49′施工才能使隧道在山腹中准确接通.附:什么样的考试心态最好大部分学生都不敢掉以轻心,因此会出现很多过度焦虑。

第 1 页1.3 证明〔1〕 证明的概念1.如下图,A B∥CD,CE 平分∠BCD,∠B=36°,那么∠DCE 等于〔A 〕 A .18° B.36° C.45° D.54°2.如下图,AB∥CD,EF⊥BD,垂足为 E ,∠1=50°,那么∠2 的度数为〔B 〕 A.50° B.40° C.45° D.25°3.如下图,A B∥C D ,直线 EF 与 AB ,CD 分别交于点 M ,N ,过点 N 的直线 GH与 AB 交于点 P ,那么以下结论中,错误的选项是〔 D 〕A.∠EMB=∠ENDB.∠BMN=∠MNCC.∠CNH=∠BPGD.∠DNG=∠AME4.如下图,直线 l 1∥l 2,且分别与△A B C 的两边 AB ,AC 相交,假设∠A=50°,∠1=35°,那么∠2 的度数为 〔D 〕 A.35° B.65°C.85°D.95°5.如下图,给出了过直线外一点作直线的平行线的方法,其根据是 同位角相等,两直线平行6.如下图,点 E 在 AC 的延长线上,以下四个条件:①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.其中能判断 AB∥CD 的有 3 个.第 2 页7.如下图,AB∥CD∥E F ,假设∠A=30°,∠AFC=15°,那么∠C=15° .【解析】∵AB∥CD,∴∠A=∠A F E=30°.∴∠C F E=∠A FE-∠AFC=15°.∵CD∥EF,∴∠C=∠C F E=15°. 8.下面是一道证明题,李教师已经给同学们讲解了思路,请将过程和理由补充完好:如下图,∠1=∠2,∠A=∠E,求证:AD∥BE.证明:∵∠1=∠2〔〕,∴AC∥ DE 〔 内错角相等,两直线平行 〕.∴∠3= ∠E 〔 两直线平行,内错角相等 〕.又∵∠A=∠E〔 〕,∴∠A= ∠3 〔 等量代换 〕.∴AD∥BE〔 同位角相等,两直线平行 〕.9.完成下面的证明:如下图, BE 平分∠ABD,DE 平分∠BDC,且∠1+∠2=90°.求证:AB∥CD.证明:∵DE 平分∠BDC〔〕,∴∠BDC=2∠1〔 角平分线的定义 〕.∵BE 平分∠ABD 〔〕,∴∠ABD= 2∠2 〔角平分线的定义〕.∴∠BDC+∠ABD=2∠1+2∠2=2〔∠1+∠2〕〔 等量代换 〕.∵∠1+∠2=90°〔〕,∴∠ABD +∠BDC= 180° 〔 等量代换 〕.∴AB∥CD〔 同旁内角互补,两直线平行 〕.10.如下图,AB∥EF,CD⊥EF于点D,假设∠AB C=40°,那么∠BCD 的度数为〔 B 〕A.140°B.130°C.120°D.110°11.如下图,∠AOB的一边OA 为平面镜,∠AOB=37°36′,在OB 上有一点E,从点E 射出一束光线经OA 上一点D 反射,反射光线DC 恰好与OB 平行,那么∠DEB 的度数是〔B〕A.75°36′B.75°12′C.74°36′D.74°12′【解析】如答图所示,过点D作DF⊥A O 交OB于点F.∵入射角等于反射角,∴∠1=∠3.∵CD∥OB,∴∠1=∠2.∴∠2=∠3.在△DOF中,∠ODF=90°,∠AOB=37°36′,∴∠2=90°-37°36′=52°24′.∴在△DEF 中,∠D EB=180°-2∠2=75°12′.应选B.12.如下图,含30°角的直角三角尺DEF 放置在△ABC上,30°角的顶点D 在边AB 上,且D E⊥AB,∠A=50°,BC∥D F,那么∠DNM=40°.【解析】∵DE⊥AB,∴∠A DE=90°.∵∠A=50°,∴∠DNM=90°-50°=40°.13.如图1所示为我们常用的折叠式小刀,刀柄外形是一个梯形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2 所示的∠1与∠2,那么∠1与∠2的度数和是90°.图1图214.如下图,∠BAF=46°,∠ACE=136°,CE⊥CD.求证:CD∥AB.【解析】∵CE⊥CD,∴∠DCE=90°.∵∠ACE=136°,∴∠ACD=360°-136°-90°=134°.∵∠BAF=46°,∴∠BAC=180°-∠BAF=180°-46°=134°.∴∠ACD=∠BAC.∴CD∥AB.15.如下图,点E,F 在直线AB 上,点G 在线段CD 上,ED 与FG 交于点H,∠C=∠EFG,∠CED=∠G HD.〔1〕求证:CE∥GF.〔2〕试判断∠AED与∠D之间的数量关系,并说明理由.〔3〕假如∠EHF=100°,∠D=30°,求∠AEM的度数.【解析】〔1〕∵∠CED=∠GHD,∴CE∥GF.〔2〕∵CE∥GF,∴∠C=∠FGD.∵∠C=∠EFG,∴∠FGD=∠EFG.∴AB∥CD.∴∠AED+∠D=180°.〔3〕∵∠DHG=∠EHF=100°,∠D=30°,∴∠HGD=180°-100°-30°=50°.∵CE∥GF,∴∠C=50°.∵AB∥CD,∴∠AEC=50°.∴∠AEM=180°-50°=130°.16.命题:“两个连续奇数的平方差是8 的倍数〞是真命题还是假命题?假如认为是假命题,请说明理由;如果认为是真命题,请给出证明.【解析】“两个连续奇数的平方差是8 的倍数〞是真命题. 证明:设两个连续奇数为2n+1,2n-1,它们的平方差是〔2n+1〕2-〔2n-1〕2=〔2n+1+2n-1〕〔2n+1-2n+1〕=4n·2=8n.∴两个连续奇数的平方差是8 的倍数.。

1.3证明(2)同步练习【知识盘点】1.三角形的一个外角等于_________的两个内角的和.2.在△ABC中,若∠A:∠B:∠C=1:2:3,则∠C=________.3.在△ABC中,∠B=45°,∠C=72°,那么与∠A相邻的一个外角等于_______.4.如图1所示,△ABC中,D,E分别是AC,BD上的点,且∠A=65°,∠ABD=∠DCE=30•°,则∠BEC的度数是_________.(1) (2) (3) (4)5.按第4题图所示,请你直接写出∠A,∠BEC,∠EDC之间的大小关系,用“<•”号连接____________.6.如图2所示,已知∠BDC=142°,∠B=34°,∠C=28°,则∠A=________.【基础过关】7.如果三角形的一个外角小于和它相邻的内角,则这个三角形是()A.锐角三角形; B.直角三角形; C.钝角三角形; D.都有可能8.若等腰三角形的一个外角为110°,则它的底角为()A.55°B.70°C>55°或70°D.以上答案都不对9.若三角形的三个外角的度数之比为2:3:4,则与之对应的三个内角的度数之比为()A.4:3:2 B.3:2:4 C.5:3:1 D.3:1:510.满足下列条件的△ABC中,不是直角三角形的是()A.∠B+∠A=∠C B.∠A:∠B:∠C=2:3:5C.∠A=2∠B=3∠C D.一个外角等于和它相邻的一个内角11.如图3所示,在△ABC中,∠ABC与∠BAC的平分线相交于点O,若∠BOC=120°,则∠A为()A.30°B.60°C.80°D.100°12.如图所示,在锐角△ABC中,CD和BE分别是AB和AC边上的高,且CD和BE•交于点P,若∠A=50°,则∠BPC的度数是()A.150°B.130°C.120°D.100°【应用拓展】13.如图4所示,点B,D,E,C在同一条直线上,且∠1=∠2,BD=EC,求证:△ABE≌△ACD.14.如图所示,BC⊥ED,垂足为O,∠A=27°,∠D=20°,求∠ACB与∠B的度数.【综合提高】15.如图所示,已知等腰直角三角形ABC中,∠ACB=90°,直线L经过点C,•AD•⊥L,BE⊥L,垂足分别为D,E.(1)证明:△ACD≌△CBE;(2)求证:DE=AD+BE;(3)当直线L经过△ABC内部时,其他条件不变;(2)中的结论还成立吗?如果成立,请给出证明;如果不成立,这时DE,AD,BE有什么关系?证明你的猜想.。
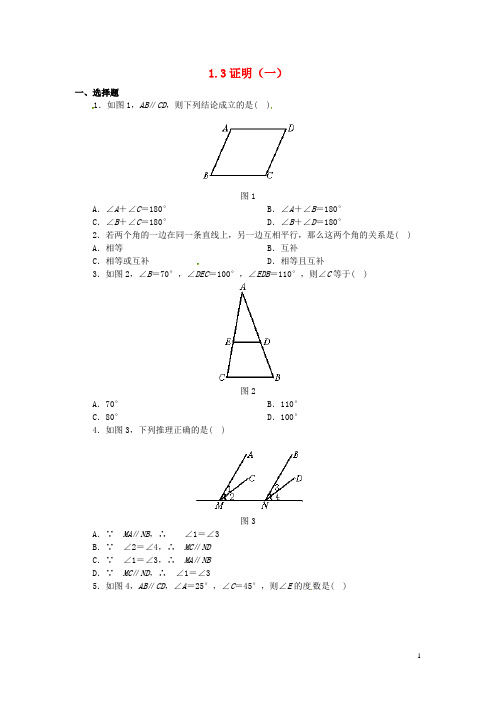
1.3证明(一)一、选择题1.如图1,AB∥CD,则下列结论成立的是( )图1A.∠A+∠C=180°B.∠A+∠B=180°C.∠B+∠C=180°D.∠B+∠D=180°2.若两个角的一边在同一条直线上,另一边互相平行,那么这两个角的关系是( ) A.相等B.互补C.相等或互补D.相等且互补3.如图2,∠B=70°,∠DEC=100°,∠EDB=110°,则∠C等于( )图2A.70°B.110°C.80°D.100°4.如图3,下列推理正确的是( )图3A.∵MA∥NB,∴∠1=∠3B.∵∠2=∠4,∴MC∥NDC.∵∠1=∠3,∴MA∥NBD.∵MC∥ND,∴∠1=∠35.如图4,AB∥CD,∠A=25°,∠C=45°,则∠E的度数是( )图4A.60°B.70°C.80°D.65°二、填空题6.如图5,a∥b,∠1=120°,则∠2=________.图57.如图6,已知AB∥CD,∠1=65°,∠2=45°,则∠ADC=________.图68.如图7,已知∠1=∠2,∠BAD=57°,则∠B=________.图79.如图8,若AB∥EF,BC∥DE,则∠B+∠E=________.图810.如图9,由A测B的方向是________.图9三、解答题11.已知:如图10,AD∥BC,∠B=∠D.求证:AB∥CD.图1012.已知:如图11,∠1=∠B,∠A=32°.求:∠2的度数.图1113.已知:如图12,AD∥BC,∠ABC=∠C,求证:AD平分∠EAC.图1214.如图13,A、B之间是一座山,要修一条铁路通过A、B两地,在A地测得铁路走向是北偏东58°11′.如果A、B两地同时开工开隧道,那么在B地按北偏西多少度施工,才能使铁路隧道在山腹中准确接通?图13参考答案一、1.C 2.C 3.C 4.B 5.B二、6.60°7.110°8.123°9.180°10.南偏东70°三、11.略12.148°13.略14.在B地按北偏西121°49′施工才能使隧道在山腹中准确接通.。
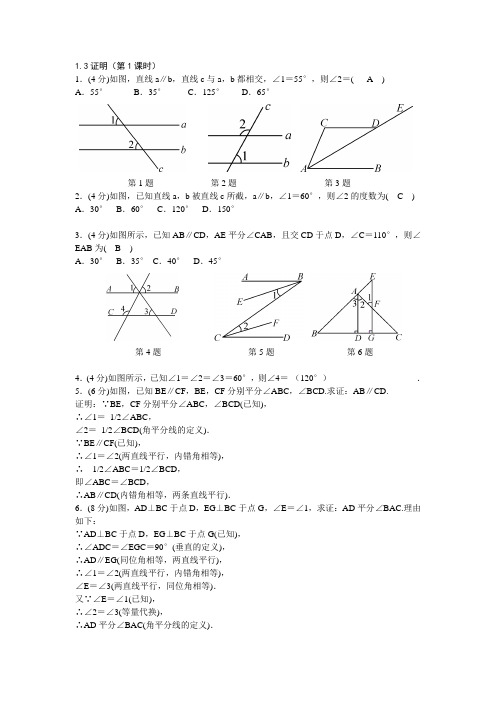
1.3证明(第1课时)1.(4分)如图,直线a∥b,直线c与a,b都相交,∠1=55°,则∠2=(A)A.55°B.35°C.125°D.65°第1题第2题第3题2.(4分)如图,已知直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为(C) A.30°B.60°C.120°D.150°3.(4分)如图所示,已知AB∥CD,AE平分∠CAB,且交CD于点D,∠C=110°,则∠EAB为(B)A.30°B.35°C.40°D.45°第4题第5题第6题4.(4分)如图所示,已知∠1=∠2=∠3=60°,则∠4=(120°).5.(6分)如图,已知BE∥CF,BE,CF分别平分∠ABC,∠BCD.求证:AB∥CD.证明:∵BE,CF分别平分∠ABC,∠BCD(已知),∴∠1=1/2∠ABC,∠2=1/2∠BCD(角平分线的定义).∵BE∥CF(已知),∴∠1=∠2(两直线平行,内错角相等),∴1/2∠ABC=1/2∠BCD,即∠ABC=∠BCD,∴AB∥CD(内错角相等,两条直线平行).6.(8分)如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,求证:AD平分∠BAC.理由如下:∵AD⊥BC于点D,EG⊥BC于点G(已知),∴∠ADC=∠EGC=90°(垂直的定义),∴AD∥EG(同位角相等,两直线平行),∴∠1=∠2(两直线平行,内错角相等),∠E=∠3(两直线平行,同位角相等).又∵∠E=∠1(已知),∴∠2=∠3(等量代换),∴AD平分∠BAC(角平分线的定义).7.(10分)如图,∠1+∠2=180°,∠3=72°,求∠4的度数.(72°)第7题第8题第9题8.(10分)如图,∠B=∠C,AB∥EF.求证:∠BGF=∠C.证明:∵∠B=∠C,∴AB∥CD,∵AB∥EF,∴CD∥EF.∴∠BGF=∠C9.(4分)如图所示,已知直线a∥b,∠1=40°,∠2=60°,则∠3等于(A) A.100°B.60°C.40°D.20°第10题第11题10.(6分)如图,已知AB∥CD,∠B=40°,∠D=40°.求证:BC∥DE.证明:∵AB∥CD,∠B=40°,∴∠B=∠C=40°,又∵∠D=40°,∴∠C=∠D,∴BC∥DE11.(6分)如图,已知AD∥BE,∠1=∠2.求证:∠A=∠E.证明:∵AD∥BE,∴∠A=∠EBC,∵∠1=∠2,∴AC∥DE,∴∠E=∠EBC,∴∠A=∠E12.(8分)如图所示,已知BE是一条直线,∠ABD=∠CDE,BF平分∠ABD,DG平分∠CDE.求证:BF∥DG.证明:∵∠ABD=∠CDE,BF平分∠ABD,DG平分∠CDE,∴1/2∠FBD=1/2∠ABD,∠GDE=∠CDE,∴∠FBD=∠GDE,∴BF∥DG第12题第13题13.(8分)如图,AB∥DE,∠1=∠2,试判断AE与DC的位置关系,并说明理由.解:AE∥DC,理由:∵AB∥DE,∴∠1=∠AED.∵∠1=∠2,∴∠2=∠AED,∴AE∥DC14.(8分)如图所示,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,试判断∠A与∠F的关系,并说明理由.解:∠A=∠F,理由∵∠AGB=∠EHF,∴∠AGB=∠AHC,∴BD∥CE,∴∠ABD=∠C.∵∠C=∠D,∴∠ABD=∠D,∴AC∥DF,∴∠A=∠F第14题第15题15.(10分)如图,已知CD⊥AB,GF⊥AB,∠B=∠ADE.求证:∠1=∠2.证明:∵CD⊥AB,GF⊥AB,∴CD∥GF,∴∠DCB=∠2.∵∠B=∠ADE,∴DE∥BC,∴∠1=∠DCB,∴∠1=∠216.综合应用迁移:某足球比赛中有n个球队(n≥2)进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛?有2个球队时,要进行(2×1)/2 =1场比赛;有3个球队时,要进行(3×2)/2=3场比赛;有4个球队时,要进行 6 场比赛;…;那么有20个球队时,要进行190 场比赛.1.3证明(第2课时)1.(4分)如图,AB∥CD,AD和BC相交于点O,∠A=20°,∠COD=100°,则∠C的度数是(C)A.80°B.70°C.60°D.50°第1题第4题2.(4分)已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于(A) A.40°B.60°C.80°D.90°3.(4分)一个三角形的三个内角的度数之比为2∶3∶7,则这个三角形一定是(D) A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形4.(4分)如图所示,点B,C,D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD =36°,那么∠A=_54°_.5.(4分)阅读下题并填空:已知:△ABC,∠A、∠B、∠C之和为多少?为什么?解:∠A+∠B+∠C=180°.理由:作∠ACD=∠A,并延长BC到点E.∵∠1=∠A(已作),∴AB∥CD(内错角相等,两直线平行),∴∠B=∠2(两直线平行,同位角相等).∵∠ACB+∠1+∠2=180°,∴∠ACB+∠B+∠C=180°(等量代换).第5题第6题第7题6.(8分)如图所示,已知在△ABC中,AD平分∠BAC,BE是高,∠BAC=60°,∠EBC=20°,求∠ADC的度数.(80°)7.(10分)如图,CD是∠ACB的平分线,DE∥BC,∠B=70°,∠ACB=50°,求∠EDC,∠BDC的度数.(25 85)8.(12分)如图,已知在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.(1)求∠DAE的度数.(2)试写出∠DAE与∠C-∠B有何关系?解:(1)∠DAE=10°(2)∠C-∠B=2∠DAE第8题第10题第11题9.(4分)如图所示,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An -1CD的平分线交于点An,设∠A=θ,则(1)∠A1=_θ/2__;(2)∠An=__θ/2n__.10.(8分)小明到工厂去进行社会实践活动时,发现工人生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠A=40°,∠AEC=70°,小明马上运用已学的数学知识得出了∠ECD的度数,你知道他是如何算出来的吗?解:∠ECD=30°11.(8分)在△ABC中,BA平分∠DBC,∠BAC=124°,BD⊥AC于点D,求∠C的度数.解:∠C=22°12.(10分)如图,(1)求证:∠BDC=∠A+∠B+∠C.(2)如果点D与点A分别在线段BC的两侧,猜想∠BDC,∠A,∠B,∠C这4个角之间有怎样的关系,并证明你的结论.解:(1)略(2)猜想:∠BDC+∠C+∠A+∠B=360°,证明略第12题第13题13.(10分)一个零件的形状如图所示,规定∠CAB=90°,∠B,∠C应分别等于32°和21°,检验工人量得∠BDC=148°,就说这个零件不合格,请你运用三角形的有关知识说明此零件不合格的理由.解:不合格.理由:连结AD并延长至E点,∵∠CDE=∠C+∠CAD,∠BDE=∠B +∠BAD,∴∠CDB=∠B+∠C+∠CAB=143°≠148°,∴这个零件不合格14.(10分)如图所示,已知AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD的关系,请你从所得到的关系中任选一个加以说明.解:①∠APC=∠PAB+∠PCD;②∠APC=360°-(∠PAB+∠PCD);③∠APC=∠PAB-∠PCD;④∠APC=∠PCD-∠PAB.证明略。
1.3 证明一、单选题1.如图,有一条直的宽纸带,按图折叠,则∠α的度数等于()A.50 o B.60 o C.75 o D.85 o2.三角形中∠B的平分线和外角的平分线的夹角是().A.60°B.90°C.45°D.135°3.小王、小陈、小张当中有一人做了一件好事,另两人也都知道是谁做了这件事.老师在了解情况时,他们三人分别说了下面几句话:小陈:“我没做这件事.”“小张也没做这件事.”小王:“我没做这件事.”“小陈也没做这件事.”小张:“我没做这件事.”“我也不知道谁做了这件事.”已知他们每人都说了一句假话,一句真话,做好事的人是()A.小王B.小陈C.小张D.不能确定4.下列问题你不能肯定的是()A.一支铅笔和一瓶矿泉水的体积大小问题 B.三角形与矩形的面积关系C.三角形的内角和D.n边形的外角和5.某超市(商场)失窃,大量的商品在夜间被罪犯用汽车运走.三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:(1)罪犯不在甲、乙、丙三人之外;(2)丙作案时总得有甲作从犯;(3)乙不会开车.在此案中,能肯定的作案对象是()A.嫌疑犯乙B.嫌疑犯丙C.嫌疑犯甲D.嫌疑犯甲和丙6.如图,CE是ABC∆的外角ACD∠的平分线,若35∠=( ).∠=,则A∠=,60BACEA.95 B.85 C.75 D.7.如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为()A.60°B.50°C.40°D.30°8.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=A.60°B.120°C.150°D.180°9.如图,下列推理不正确的是( )A.∵AB∥CD,∴∠ABC+∠C=180°B.∵∠1=∠2,∴AD∥BCC.∵AD∥BC,∴∠3=∠4D.∵∠A+∠ADC=180°,∴AB∥CD10.下列推理中,错误的是( )A.因为AB⊥EF,EF⊥CD,所以AB⊥CDB.因为∠α=∠β,∠β=∠γ,所以∠α=∠γC.因为a∥b,b∥c,所以a∥cD.因为AB=CD,CD=EF,所以AB=EF11.下列推理正确的是( )A.∵∠1+∠2=90°,∠2+∠3=90°,∴∠1+∠3=90°B.∵∠1+∠3=90°,∠3+∠2=90°,∴∠1=∠2C.∵∠1与∠2是对顶角,又∠2=∠3,∴∠1与∠3是对顶角D.∵∠1与∠2是同位角,又∠2与∠3是同位角,∴∠1与∠3是同位角12.如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为( )A.4:3:2 B.3:2:4 C.5:3:1 D.3:1:5二、填空题13.如图,直线a b∥,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠α的度数为______.14.现有一个三位数密码锁,已知以下3个条件,可以推断正确的密码是__________.①只有一个号码正确且位置正确②只有两个号码正确且位置都不正确③三个号码都不正确15.如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据___________________________.16.如图,在△ABC中,∠C=90°,∠ABC的平分线与外角∠BAD的平分线的反向延长线交于点F,则∠F=____.17.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=_____.18.在△ABC中,AB≠AC,若用反证法证明∠B≠∠C,应先假设 _____19.为了从500只外形相同的鸡蛋中找到唯一的一只双黄蛋,检查员将这些鸡蛋按1﹣500的顺序排成一列,第一次先从中取出序号为单数的蛋,发现其中没有双黄蛋,他将剩下的蛋的原来位置上又按1﹣250编号(即原来的2号变为1号,原来的4号变成2号,…,原来的500号变成250号).又从中取出新序号为单数的蛋进行检查,任没有发现双黄蛋,…,如此下去,检查到最后的一个是双黄蛋,问这只双黄蛋最初的序号是_____.20.盒子里有甲、乙、丙三种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗乙粒子;不同种类的两颗粒子发生碰撞,会变成第三种粒子,例如一颗甲粒子和一颗乙粒子发生碰撞则变成一颗丙粒子,现有甲粒子6颗,乙粒子4颗,丙粒子5颗,如果经过各种两两碰撞后,只剩下1颗粒子,给出下列结论:①最后一颗粒子可能是甲粒子;②最后一颗粒子一定不是乙粒子;③最后一颗粒子可能是丙粒子.其中正确结论的序号是:_______.21.完成下面的证明过程.已知:如图,∠1和∠D互余,∠C和∠D互余.求证:AB∥CD.证明:∵∠1和∠D互余(已知),∴∠1+∠D=90°(_____________).∵∠C和∠D互余(已知),∴∠C+∠D=90°(_____________),∴∠1=∠C(__________________),∴AB∥CD(________________________).22.如图,点 A,C,F,B 在同一直线上,CD 平分∠ECB,FG∥CD.若∠ECA 为α度,则∠GFB为________度(用关于α的代数式表示).23.如图,是一副三角板叠放的示意图,则∠α=______.24.如图,现给出下列条件:①1B ∠∠=,②25∠∠=,③34∠∠=,④1D ∠∠=,⑤B BCD 180∠∠+=︒.其中能够得到AB//CD 的条件是_______.(只填序号)三、解答题25.观察下列等式:第个等式为:2113323-=⨯第1个等式为:3223323-=⨯第2个等式为:4333323-=⨯第3个等式为:5443323-=⨯....根据上述等式含有的规律,解答下列问题:(1)第5个等式为:是(2)第n 个等式为:是 (用含n 的代数式表示),并证明26.已知△ABC 中,∠ACB=90°,CD 为AB 边上的高,BE 平分∠ABC ,分别交CD 、AC 于点F 、E ,求证:∠CFE=∠CEF .27.当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等.例如:在图①、图②中都有12,34∠=∠∠=∠.设镜子AB 与BC 的夹角ABC α∠=.(1)如图①,若90α=︒,判断入射光线EF 与反射光线GH 的位置关系,并说明理由.(2)如图②,若90180a ︒<<︒,入射光线EF 与反射光线GH 的夹角FMH β∠=.探索α与β的数量关系,并说明理由.(3)如图③,若130α=︒,设镜子CD 与BC 的夹角BCD ∠为钝角,入射光线EF 与镜面AB 的夹角109()0x x ∠=︒<<︒.已知入射光线EF 从镜面AB 开始反射,经过(n n 为正整数,且3n ≤)次反射,当第n 次反射光线与入射光线EF 平行时,请直接写出BCD ∠的度数(可用含x 的代数式表示).答案一、单选题1.C 2.B 3.B 4.B 5.C 6.B7.D8.A 9.C10.A 11.B 12.C二、填空题13.35°14.52015.同旁内角互补,两直线平行16.45°17.540°18.∠B=∠C19.25620.①②③.21.互余的定义;互余的定义;同角的余角相等;内错角相等,两直线平行. 22.90°﹣2α 23.75°24.①②⑤三、解答题25.解:(1)观察等式可知:第5个等式为:6553323-=⨯;故答案为:6553323-=⨯;(2)第n 个等式为:13323n n n +-=⨯,证明:左边1333333(31)23n n n n n n +=-=⨯-=-=⨯=右边∴等式成立. 26.解:根据互余、角平分线及对顶角等相关知识即可得出答案.证明:如图,∵∠ACB =90°,∴∠1+∠3=90°,∵CD ⊥AB ,∴∠2+∠4=90°,又∵BE 平分∠ABC ,∴∠1=∠2,∴∠3=∠4,∵∠4=∠5,∴∠3=∠5,即∠CFE =∠CEF .27.解:()1,EF GH理由如下:在BEG 中,23180,α∠+∠+=︒90,α=︒2390,∴∠+∠=︒12180,34180,12,34FEG EGH ∠+∠+∠=︒∠+∠+∠=︒∠=∠∠=∠, 1234360FEG EGH ∴∠+∠+∠+∠+∠+∠=︒,180FEG EGH ∴∠+∠=,//EF GH ∴;()22180βα=-︒.理由如下:在BEG 中,23180α∠+∠+=23180,α∴∠+∠=︒-12,1MEB ∠=∠∠=∠2,MEB ∴∠=∠22,MEG ∴∠=∠34,4MGB ∠=∠∠=∠3,MGB ∴∠=∠23,MGE ∴∠=∠在MEG 中,180MEG MGE β∠+∠+=︒(0)18MEG MGE β∴=︒-∠+∠180(2223)=-∠+∠(802)123=∠+∠-1802(180)2180αα=︒︒=--- ;()390x ︒+或140︒如图,当夹角为钝角时,根据(2)中的结论,得 ∠FEG=2∠BCD-180°,根据平行线性质,得:∠FEG=∠PAH=2∠NAH=2x ,∴∠BCD=1802902x x ︒+=︒+;如图,当夹角为直角时,根据(1)中的结论,得∠EBC=50°,根据三角形外角性质,得:∴∠BCD=∠EBC+∠BEC=50°+90°=140°.∴∠BCD的度数为90x︒+或140°.。
1.3 证明(一)A组1.如图,下面的推理正确的是(D)A.∵∠1=∠2,∴AB∥CDB.∵∠ABC+∠BCD=180°,∴AD∥BCC.∵AD∥BC,∴∠3=∠4D.∵∠ABC+∠DAB=180°,∴AD∥BC,(第1题)) ,(第2题)) 2.如图,若a∥b,则∠1的度数为(C)A. 90° B. 80°C. 70° D. 60°(第3题)3.如图,下列条件中,能证明AD∥BC的是(D)A.∠A=∠CB.∠B=∠DC.∠B=∠CD.∠C+∠D=180°4.字母a,b,c,d分别代表正方形、线段、正三角形、圆这四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形的连接方式为a⊕c.组合,,,连接,a⊕b,b⊕d,d⊕c(第5题)5.如图,∠1与∠D互余,∠C与∠D互余.求证:AB∥CD.【解】∵∠1与∠D互余,∠C与∠D互余(已知),∴∠1=∠C(同角的余角相等),∴AB∥CD(内错角相等,两直线平行).(第6题)6.如图,直线a∥b,三角形纸板的直角顶点A落在直线a上,两条直线分别交直线b 于B,C两点.若∠1=42°,求∠2的度数.【解】∵直线a∥b,∠1=42°(已知),∴∠ACB=42°(两直线平行,内错角相等).又∵∠BA C=90°(已知),∴∠ABC=180°-∠BAC-∠ACB=48°(三角形的内角和为180°),∴∠2=∠ABC=48°(对顶角相等).(第7题)7.如图,∠1=∠2,∠D=50°,求∠B的度数.【解】∵∠1=∠AGF(对顶角相等),∠1=∠2(已知),∴∠2=∠AGF(等量代换),∴AB∥CD(同位角相等,两直线平行),∴∠B+∠D=180°(两直线平行,同旁内角互补),∴∠B=180°-∠D=180°-50°=130°.B组(第8题)8.如图,已知直线a∥b,直角三角形ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠α的度数为__35°__.【解】过点C作CE∥a.∵a∥b,∴CE∥a∥b,∴∠BCE=∠α,∠ACE=∠β=55°.∵∠ACB=90°,∴∠α=∠BCE=∠ACB-∠ACE=35°.(第9题)9.如图,已知AB∥CD,EF 与AB ,CD 分别相交于点E ,F ,EP ⊥EF ,与∠EFD 的平分线FP 相交于点P ,且∠BEP=50°,则∠EPF 的度数为__70°__.【解】 ∵EP⊥EF,∴∠PEF =90°. 又∵∠BEP=50°,∴∠BEF =∠BEP+∠PEF=140°. ∵AB ∥CD ,∴∠BEF +∠EFD=180°, ∴∠EFD =40°. ∵FP 平分∠EFD,∴∠EFP =12∠EFD=20°.∵∠PEF +∠EFP+∠EPF=180°, ∴∠EPF =70°.10.如图,在△ABC 中,∠ACB =90°,CD ⊥AB ,BE 平分∠ABC,分别交AC ,CD 于点E ,F .求证:∠CEF=∠CFE.(第10题)【解】 ∵BE 平分∠ABC, ∴∠ABE =∠CBE.∵∠ACB =90°,CD ⊥AB ,∴∠CEF +∠CBE=90°,∠DFB +∠ABE=90°, ∴∠CEF =∠DFB. 又∵∠CFE=∠DFB, ∴∠CEF =∠CFE. 11.阅读:如图①,∵CE ∥AB ,∴∠1=∠A,∠2=∠B,∴∠ACD =∠1+∠2=∠A+∠B.这是一个有用的事实,请用这个事实,在图②中的四边形ABCD 内引一条和边平行的直线,求出∠A+∠B+∠C+∠D 的度数.(第11题)(第11题解)【解】 如解图,过点D 作DE∥AB 交BC 于点E ,则∠A+∠ADE=180°,∠B +∠BED =180°.由题意,得∠BED =∠C +∠CDE ,∴∠A +∠B +∠C +∠CDA =(∠A +∠ADE )+(∠CDE +∠C )+∠B =180°+∠BED +∠B =180°+180°=360°.数学乐园12.如图,∠EOF =90°,点A ,B 分别在射线OE ,OF 上移动,连结AB 并延长至点D ,∠DBO 的平分线与∠OAB 的平分线交于点C ,试问:∠AC B 的度数是否随点A ,B 的移动而发生变化?如果保持不变,请说明理由;如果随点A ,B 的移动而发生变化,请给出变化的范围.(第12题)【解】 ∠ACB 的度数不随点A ,B 的移动发生变化.理由如下: ∵BC ,AC 分别平分∠DBO,∠BAO , ∴∠DBC =12∠DBO,∠BAC =12∠BAO.∵∠DBO +∠OBA=180°,∠OBA +∠BAO+∠AOB=180°, ∴∠DBO =∠BAO+∠AOB,∴∠DBO -∠BAO=∠AOB=90°.∵∠DBC +∠ABC=180°,∠ABC +∠ACB+∠BAC=180°, ∴∠DBC =∠BAC+∠ACB, ∴12∠DBO=12∠BAO+∠ACB, ∴∠ACB =12(∠DBO-∠BAO)=12∠AOB=45°.。
第1章 三角形的初步知识1.3 证明第1课时 证明及表述格式基础过关全练知识点 证明1.(2021浙江金华中考)某同学的作业如下框:如图,已知直线l1,l2,l3,l4.若∠1=∠2,则∠3=∠4.请完成下面的说理过程.解:已知∠1=∠2,根据(内错角相等,两直线平行),得l1∥l2.再根据(※),得∠3=∠4.其中※处填的依据是( )A.两直线平行,内错角相等B.内错角相等,两直线平行C.两直线平行,同位角相等D.两直线平行,同旁内角互补2.如图,在下列条件中,不能推理直线a与b平行的是( )A.∠1=∠2B.∠2=∠3C.∠1=∠5D.∠3+∠4=180°3.(2021浙江台州中考)一把直尺与一块直角三角板按如图方式摆放,若∠1=47°,则∠2=( )A.40°B.43°C.45°D.47°4.如图,AB∥CD,EP,FP分别平分∠BEF,∠DFE,则△EPF的形状为 .5.填空(将下面的推理过程及依据补充完整).如图,点E在DF上,点B在AC上,已知∠1=∠2,∠3=∠4,求证:∠A=∠F.证明:∵∠1=∠2(已知),∠2=∠DGF( ),∴∠1=∠DGF,∴BD∥CE( ),∴∠3+∠C=180°( ).又∵∠3=∠4(已知),∴∠4+∠C=180°,∴DF∥AC( ),∴∠A=∠F(两直线平行,内错角相等).能力提升全练6.(2022独家原创)如图,AB∥CD,∠B=∠D,EF与AD,BC的延长线分别交于点E,F.求证:∠DEF=∠F.下面是排乱的证明过程:①∵∠B=∠D,∴∠DCF=∠D,②∴AD∥BF,③∵AB∥CD,④∴∠DCF=∠B,⑤∴∠DEF=∠F.则正确的排列顺序是( )A.①②④③⑤B.④②③①⑤C.③④②①⑤D.③④①②⑤7.(2021浙江台州温岭月考)如图,AB∥CD,BF平分∠ABE,且BF⊥DE,垂足为F,则∠ABE与∠EDC的数量关系是( )A.∠ABE=1∠EDC4B.∠ABE+∠EDC=180°C.∠EDC-1∠ABE=90°2D.∠ABE+1∠EDC=90°28.(2022浙江杭州西湖十三中期中)如图,在△ABC 中,AD平分∠BAC,AE⊥BC,已知∠BAC=2∠B,∠B=4∠DAE,那么∠C的度数为( )A.45°B.60°C.70°D.72°9.(2022浙江杭州余杭三校联考)如图,AB∥CD,∠ABE=∠DCF.求证:∠E=∠F.10.(2021浙江杭州萧山月考)如图,在△ABC中,CD⊥AB于点D,G是BC上一点,过点G 作GF⊥AB于点F,且满足∠B=∠ADE.求证:∠CDE=∠BGF.素养探究全练11.[直观想象]图①是我们常用的折叠式小刀,图②中刀柄外形是一个直角梯形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图②所示的∠1与∠2,则∠1与∠2的度数和为 .图①图②答案全解全析基础过关全练1.C 根据两直线平行,同位角相等,可得∠3=∠4.故选C.2.C 当∠1=∠2时,根据同位角相等,两直线平行可得a ∥b,故A 不符合题意;当∠2=∠3时,根据内错角相等,两直线平行可得a ∥b,故B 不符合题意;当∠1=∠5时,不能得到a ∥b,故C 符合题意;当∠3+∠4=180°时,根据同旁内角互补,两直线平行可得a ∥b,故D 不符合题意.故选C.3.B 如图,∵直尺的两边互相平行,∴可过三角板的直角顶点作直尺两边的平行线,则∠3=∠1=47°,∴∠4=90-∠3=43°,∴∠2=∠4=43°.故选B.4.直角三角形解析 ∵EP,FP 分别平分∠BEF,∠DFE,∴∠PEF=12∠BEF,∠PFE=12∠DFE,∵AB ∥CD,∴∠BEF+∠DFE=180°,∴∠PEF+∠PFE=12∠BEF+12∠DFE=90°,∴∠P=180°-(∠PEF+∠PFE)=90°,∴△EPF 是直角三角形.5.对顶角相等;同位角相等,两直线平行;两直线平行,同旁内角互补;同旁内角互补,两直线平行能力提升全练6.D 证明过程:∵AB ∥CD,∴∠DCF=∠B,∵∠B=∠D,∴∠DCF=∠D,∴AD ∥BF,∴∠DEF=∠F.∴正确的排列顺序为③④①②⑤.故选D.7.C 如图,延长DF交AB于点G.∵AB∥CD,∴∠BGD+∠EDC=180°,即∠BGD=180°-∠EDC,∠ABE,∵BF⊥DE,∴∠BFG=90°,∵BF平分∠ABE,∴∠ABF=12∵∠ABF+∠BFG+∠BGD=180°,∴1∠ABE+90°+(180°-∠EDC)=180°,2整理得∠EDC-1∠ABE=90°.故选C.28.B 设∠DAE=a°,则∠B=4a°,∠BAC=8a°,∴∠C=180°-12a°,∵AE⊥BC,∴∠AEC=90°,∴∠EAC=90°-∠C=12a°-90°,∵AD平分∠BAC,∠BAC=8a°,∴∠DAC=4a°,∵∠DAC-∠EAC=∠DAE,∴4a-(12a-90)=a,解得a=10,∴∠C=180°-12a°=60°.故选B. 9.证明 ∵AB∥CD,∴∠ABC=∠BCD.又∵∠ABE=∠DCF,∴∠ABC-∠ABE=∠BCD-∠DCF,即∠EBC=∠FCB,∴BE∥CF,∴∠E=∠F.10.证明 ∵CD⊥AB,GF⊥AB,∴∠BFG=∠ADC=90°,FG∥CD,∴∠B+∠BGF=90°,∠ADE+∠CDE=90°,∵∠B=∠ADE,∴∠CDE=∠BGF.素养探究全练11.90°解析 如图,延长AE交CD于F,∵AB∥CD,∴∠AFC=∠1.∵∠AEC=90°,∴∠CEF=90°,∴∠2+∠AFC=90°,∴∠1+∠2=90°.。