下载文档原格式
一维对称无限深方势阱的波函数表达式在量子力学中，一维对称无限深方势阱是一种经典的势阱模型，它在研究粒子在受限空间内的运动和能级结构等方面有很好的应用。
对于一维对称无限深方势阱来说，波函数的表达式是非常重要的，它可以帮助我们理解粒子在势阱内的行为以及计算其能级。
1. 势阱模型的基本假设一维对称无限深方势阱模型假设了以下几点：势阱的宽度为a，势阱内部的势能为0，而在势阱外部势能为无穷大，这意味着粒子在势阱内运动自由，在势阱外不能存在。
这是一个理想化的模型，但对于研究粒子在受限空间内的行为却是非常有用的。
2. 薛定谔方程的求解根据薛定谔方程，我们可以求解一维对称无限深方势阱中的波函数。
薛定谔方程的一般形式为：-ħ²/2m * d²Ψ/dx² + V(x)Ψ = EΨ其中，ħ是普朗克常数，m是粒子的质量，V(x)是势能函数，Ψ是波函数，E是能量。
对于无限深方势阱来说，势能函数V(x)在势阱内为0，在势阱外为无穷大，因此薛定谔方程可以简化为：-ħ²/2m * d²Ψ/dx² = EΨ4. 波函数的边界条件在一维对称无限深方势阱中，波函数的边界条件非常明确，因为势能在势阱外为无穷大，粒子无法透过势垒逃逸出去，故波函数在势阱外为0。
而在势阱内部，波函数要满足Ψ(0) = Ψ(a) = 0，这是因为势阱的边界为0。
5. 波函数的表达式根据边界条件，我们可以求解出一维对称无限深方势阱中的波函数表达式。
在势阱内部，波函数的一般形式为：Ψ(x) = Asin(kx) + Bcos(kx)其中，A和B是待定系数，k是波数，根据波函数的边界条件，我们可以求解出波函数的具体形式。
在势阱内部，波函数的波数k为：k = sqrt(2mE) / ħ对于一维对称无限深方势阱，能级是分立的，即E = n²π²ħ² / (2ma²)，其中n为正整数。
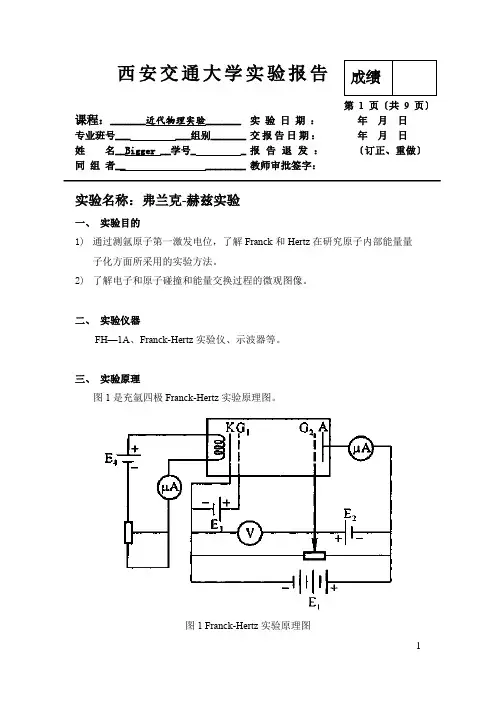
西安交通大学实验报告第 1 页〔共 9 页〕课程：_______近代物理实验_______ 实 验 日 期 ： 年 月 日 专业班号___ ___组别_______ 交报告日期： 年 月 日 姓 名__Bigger __学号_ _ 报 告 退 发 ： 〔订正、重做〕 同 组 者__ ________ 教师审批签字：实验名称：弗兰克-赫兹实验一、 实验目的1) 通过测氩原子第一激发电位，了解Franck 和Hertz 在研究原子内部能量量子化方面所采用的实验方法。
2) 了解电子和原子碰撞和能量交换过程的微观图像。
二、 实验仪器FH—1A 、Franck-Hertz 实验仪、示波器等。
三、 实验原理图1是充氩四极Franck-Hertz 实验原理图。
图1 Franck-Hertz 实验原理图电子与原子的碰撞过程可以用一下方程描述：22221111''2222e e m v MV m v MV E +=++∆ (2.1) 式中：m e ——原子质量； M ——电子质量； v ——电子碰撞前的速度； v ’——电子碰撞后的速度； V ——原子碰撞前的速度； V ’——原子碰撞后的速度； ΔE ——原子碰撞后内能的变化量。
按照波尔原子能级理论，ΔE = 0 弹性碰撞； ΔE = E 1 - E 0 非弹性碰撞；式中：E 0——原子基态能量； E 1——原子第一激发态能量。
电子碰撞前的动能1/2m e v 2 < E 1 - E 0时，电子与原子的碰撞为完全弹性碰撞，ΔE = 0，原子仍然停留在基态。
电子只有在加速电场的作用下碰撞前获得的动能1/2m e v 2 ≥ E 1 - E 0，才能在电子产生非弹性碰撞，使得电子获得某一值〔E 1 - E 0〕的内能从基态跃迁到第一激发态，调整加速电场的强度，电子与原子由弹性碰撞到非弹性碰撞的变化过程将在电流上显现出来。
Franck-Hertz 管即是为此目的而专门设计的。
第一章绪论1. 光电子器件按功能分为哪几类？每类大致包括哪些器件？光电子器件按功能分为光源器件、光传输器件、光控制器件、光探测器件、光存储器件。
光源器件分为相干光源和非相干光源。
相干光源主要包括激光和非线性光学器件等。
非相干光源包括照明光源、显示光源和信息处理用光源等。
光传输器件分为光学元件(如棱镜、透镜、光栅、分束器等等)、光波导和光纤等。
光控制器件包括调制器、偏转器、光开关、光双稳器件、光路由器等。
光探测器件分为光电导型探测器、光伏型探测器、热伏型探测器、各种传感器等。
光存储器件分为光盘(包括CD、VCD、DVD、LD等)、光驱、光盘塔等。
2．谈谈你对光电子技术的理解。
光电子技术主要研究物质中的电子相互作用及能量相互转换的相关技术，以光源激光化，传输波导（光纤）化，手段电子化，现代电子学中的理论模式和电子学处理方法光学化为特征，是一门新兴的综合性交叉学科。
3．谈谈光电子技术各个发展时期的情况。
20世纪60年代，光电子技术领域最典型的成就是各种激光器的相继问世。
20世纪70年代，光电子技术领域的标志性成果是低损耗光纤的实现，半导体激光器的成熟特别是量子阱激光器的问世以及CCD的问世。
20世纪80年代，出现了大功率量子阱阵列激光器；半导体光学双稳态功能器件的得到了迅速发展；也出现了保偏光纤、光纤传感器，光纤放大器和光纤激光器。
20世纪90年代，掺铒光纤放大器(EDFA)问世，光电子技术在通信领域取得了极大成功，形成了光纤通信产业；。
另外，光电子技术在光存储方面也取得了很大进展，光盘已成为计算机存储数据的重要手段。
21世纪，我们正步入信息化社会，信息与信息交换量的爆炸性增长对信息的采集、传输、处理、存储与显示都提出了严峻的挑战，国家经济与社会的发展，国防实力的增强等都更加依赖于信息的广度、深度和速度。
⒋举出几个你所知道的光电子技术应用实例。
如：光纤通信，光盘存储，光电显示器、光纤传感器、光计算机等等。
一维无限深方势阱中粒子动量概率分布引出的问题在量子力学中，无限深方势阱问题是一个简化理想化的问题。
无限正方形势阱是有限大小的正方形势阱。
井内电势为0，井外电势无穷大。
在阱中，粒子可以不受任何力地自由移动。
但是阱壁无限高，粒子完全被约束在阱里。
通过 schr\ddot{o}dinger 方程的解答，明确地呈现出某些量子行为，这些量子行为与实验的结果相符合，然而，与经典力学的理论预测有很大的冲突。
特别令人注目的是，这些量子行为是自然地从边界条件产生的，而非人为勉强添加产生的。
这解答干净利落地展示出，任何类似波的物理系统，自然地会产生量子行为；无限深方势阱问题的粒子的量子行为包括：1.能量的量子化:粒子量子态的本征函数，伴随的能量不是任意的，而只是离散能级谱中的一个能级。
2.基态能量:一个粒子允许的最小能级，称为基态能量，不为零。
3.节点:与经典力学相反，薛定谔方程预言了节点的存在。
这意味着在陷阱的某个地方，发现粒子的概率为零。
这个问题再简单，也能因为能完整分析其薛定谔方程，而导致对量子力学更深入的理解。
其实这个问题也很重要。
无限深正方形势阱问题可以用来模拟许多真实的物理系统，例如直的极细纳米线中导电电子的量子行为。
为了简化问题，本文从一维问题出发，讨论了粒子只在一维空间中运动的问题。
一个粒子束缚于一维无限深方势阱内，阱宽为 l 。
势阱内位势为0，势阱外位势为无限大。
粒子只能移动于束缚的方向（ x 方向）。
一维无限深方势阱的本征函数 \psi_{n} 于本征值 e_{n} 分别为\psi_{n}=\sqrt{\frac{2}{l}}sin(\frac{n\pi x}{l})e_{n}=\frac{n^2 h^2}{8ml^2}其中， n 是正值的整数， h 是普朗克常数， m 是粒子质量。
一维不含时薛定谔方程可以表达为-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}+v(x)\psi(x)= e\psi(x)其中， \psi(x) 是复值的、不含时的波函数， v(x) 是跟位置有关的位势， e 是正值的能量。
