半导体物理第四章
- 格式:pdf
- 大小:2.61 MB
- 文档页数:42










第四章平衡半导体4.0本章概要在上一章中,我们讨论了一般晶体,运用量子力学的概念对其进行了研究,确定了单晶晶格中电子的一些重要特性。
在这一章中,我们将运用这些概念来专门研究半导体材料。
我们将利用导带与价带中的量子态密度函数以及费米-狄拉克分布函数确定导带与价带中电子与空穴的浓度。
另外,我们将在半导体材料中引入费米能级的概念。
注意,本章中所涉及的半导体均处于平衡状态。
所谓平衡状态或者热平衡状态,是指没有外界影响(如电压、电场、磁场或者温度梯度等)作用于半导体上的状态。
在这种状态下,材料的所有特性均与时间无关。
本章目标:(1)推导半导体中热平衡电子浓度和空穴浓度关于费米能级的表达式。
(2)讨论通过在半导体中添加特定杂质原子来改变半导体材料性质的过程。
(3)推导半导体材料中热平衡电子浓度和空穴浓度关于添加到半导体中的掺杂原子浓度的表达式。
(4)求出费米能级的位置,其为添加到半导体中的掺杂原子浓度的函数。
简单说来,本章讨论的重点是:在不掺杂和掺杂的情况下,分别求平衡半导体中电子和空穴的浓度值,以及费米能级位置。
4.1半导体中的载流子我们知道:电流从本质上来说是电荷移动的速率。
在半导体中有两种载流子——电子和空穴——有能力产生电流。
载流子的定义:在物理学中,载流子指可以自由移动的带有电荷的物质微粒,如电子和离子。
如半导体中的自由电子与空穴,导体中的自由电子,电解液中的正、负离子,放电气体中的离子等。
既然半导体中的电流很大程度上取决于导带中电子与价带中空穴的数量,那么我们关心的半导体的一个重要参数就是这些载流子的密度。
联想我们之前学习的知识,我们不难知道电子和空穴的密度与态密度函数、费米-狄拉克分布函数都有关。
在接下来的章节中,我们会从更严谨的数学推导出发,导出电子与空穴的热平衡浓度,定性地讨论这些关系。
4.1.1电子与空穴的热平衡分布导带中电子关于能量的分布,我们可以从允带量子态密度函数乘以量子态被电子占据的概率函数(分布函数)得出。
第四章半导体的导电性
本章学习的内容
1.载流子在电场作用下如何运动,即如何获
得定向运动速度形成电流?
2.半导体的电导率与哪些因素有关,其物理
本质是什么?
载流子的漂移运动迁移率
电导率与迁移率
载流子的散射
两种作用竞争的结果:
1.载流子只在两次散射间作加速运动;
2.每次散射后载流子将失去从电场获得的定向附加速度;平均漂移速度与什么因素有关呢?
平均自由时间:连续两次散射之间时间间隔的平均值。
E 1τ2τ3τi
ττ
载流子在电场作用下时,存在相互矛盾的两种运动:一方面在电场力作用下作加速运动;另一方面载流子不断遭受散射而改变运动方向。
平均自由时间与迁移率
平均自由时间与电导率
载流子的散射
散射机构的本质是破坏晶体周期性势场的附加势
平均自由时间与散射几率
电离杂质散射
散射理论指出电离杂质的散射几率为:
3/2i i P N T −∝(4-19)
i N T 为电离杂质浓度,为温度
电离的杂质会在其附近形成一个库伦势场,经过其附近的载流子将在库伦作用下而改变其运动方向,该作用过程就是电离杂质对载流子的散射作用
晶格振动的散射
¾晶体振动以格波形式存在,格波又分为声学波和光学波,声学波代表原胞质心振动,频率低;而光学波代表原胞内原子间的相对振动,频率高;
¾晶格振动的能量是量子化的,晶格振动的能量子称为声子。
晶格振动对载流子的散射可看作是载流子与声子的碰撞;
¾电子和声子的碰撞也遵循准动量守恒和能量守恒定律。
¾对于硅、锗等单质半导体,起散射作用的主要是声学波;光学波主要在离子性半导体中起重要散射作用。
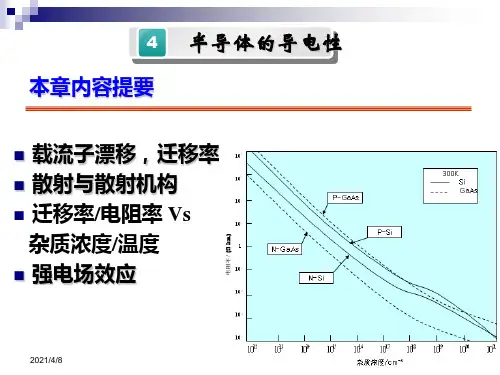
迁移率与杂质和温度的关系
多种散射机构同时存在时的迁移率
300K时锗、硅、砷化镓迁移率与杂质浓度的关系
注:对于补偿半导
决定于施主和受
主浓度之差,但
是迁移率决定于
两种杂质浓度之
和!
电阻率与杂质浓度和温度的关系
ρ
AB段:载流子主要来自杂质电离,它随温度升高而增加,散射以电离杂质为主,迁移率随温度升高而增大;
BC段:杂志全部电离,载流子浓度基本不变,晶格振动散射开始起主导作用,迁移率随温度升高而下降,电阻率增大C段:本征激发为主,随温度升高,载流子数量快速增加,其影响远远超过迁移率变化,电阻下降
习题
作业:
1,2,3
热载流子
硅、锗、砷化镓的平均漂移
速度与电场强度的关系
为与电场无关常数
为与电场无关常数
300K时,随机热运动的平均能量为:
根据电导率的统计理论:
多能谷散射耿氏效应
耿
习题
作业:
7,17,19。