电路理论(四川大学)第二章习题答案..
- 格式:ppt
- 大小:1.95 MB
- 文档页数:36

电路理论习题库+参考答案一、判断题(共100题,每题1分,共100分)1.欧姆定律可表示成U=RI,也可表示成U=-RI,这与采用的参考方向有关。
()A、正确B、错误正确答案:A2.非正弦周期信号分解后的傅里叶级数不一定是一个收敛的无穷三角级数()A、正确B、错误正确答案:B3.由于假定各节点电压的参考极性总是由独立节点指向参考节点,所以,各节点电压在相连电阻中引起的电流总是流出该节点的。
因此,节点电压方程的等式左边是各节点电压引起的流出相应节点的电流,而右边则是电流源和等效电流源注入节点的电流。
()A、正确B、错误正确答案:A4.电阻混联是指电阻连接中,既有串联又有并联()A、正确B、错误正确答案:A5.理想变压器反映阻抗的性质与负载阻抗的性质相反。
()A、正确B、错误正确答案:B6.三相电路是一种特殊类型的复杂电路,因而仍可采用一般复杂电路的分析方法对其进行分析和计算。
()A、正确B、错误正确答案:A7.支路分析法适用于分析支路数较少的电路()A、正确B、错误正确答案:A8.正弦电路中,若串联电路的总电压超前电流(电压、电流取关联参考方向),则此电路一定呈感性。
()A、正确B、错误正确答案:A9.造成系统误差的原因主要是操作者粗心大意。
()A、正确B、错误正确答案:B10.一个线性含源二端网络和其外部负载所构成的电路无唯一解时,此二端网络就可能无等效电源电路()A、正确B、错误正确答案:A11.电工指示仪表准确度的数字越小,表示仪表的准确度越低。
(A、正确B、错误正确答案:B12.对称三相电路Y-Y系统中不管是否含有高次谐波分量,U1=√3U()A、正确B、错误正确答案:B13.工程上将同向耦合状态下的一对施感电流的入端或出端定义为耦合电感的同名端()A、正确B、错误正确答案:A14.三相电路中,对称负载Y接无中线时,发生一相断路故障后,非断开相的相电压降低到电源线电压的一半。
()A、正确B、错误正确答案:A15.RLC串联电路的谐振,电源提供的无功功率为0,电路中无能量交换。

第2章 电路问题习题参考解答2.6 某电源具有线性的外特性,如题2.6所示。
当输出电流为0A 和400mA 时,其端电压分别为1.48V 和1.39V 。
请给出该电源的电压源模型和电流源模型的参数。
解:线性外特性为: S S U U R I =-⎪⎩⎪⎨⎧-==SS 4.048.139.148.1R U 解得:⎪⎩⎪⎨⎧=-==Ω225.04.039.148.148.1SS R V U ⎪⎩⎪⎨⎧===A 58.6Ω225.0SS SS R U I R2.8 考察题2.8图所示几个电路的特点,用最简单的方法计算电路中各个支路的电流、各个元件上的电压和功率。
[提示1 别忘设定电压电流的参考方向];[提示2 充分利用电路中理想电压源和理想电流源的特性和连接特点]; [提示3 注意判断各个元件是消耗还是产生电功率]。
解: (a)A I 2 510 2 = =;1S 24A I I I =+=;510V U Ω=; 4248V U Ω=⨯= 2A 1082V U =-= 244216W P Ω=⨯=; 255220WP Ω=⨯=(消耗功率); 2A 224W P =⨯=(吸收功率); 10V41040W P =⨯=(供出功率);(d ) 416 1.5A 4I I Ω===;6V 22.5A I I ==;电流源模型+_U电压源模型+_5Ω(a)2(d)1.481.392uRCX LX题 2.16 图3339V U Ω=⨯=;3A 693V U =-=-;2A 6212W P =⨯=(供出功率); 3A 339W P =-⨯=-(供出功率); 6V 6 2.515W P =⨯=(供出功率);244 1.59W P Ω=⨯=(消耗功率); 233327W P Ω=⨯=(消耗功率);2.13 已知交流电压V )511000sin(10 +=t u ,交流电流2sin(1000)A 6i t π=+。
试问它们的最大值、有效值、频率、周期、初相位以及两者之间的相位差各是多少。

一、选择题1、如图所示,其节点数、支路数、回路数及网孔数分别为(C )。
A、2、5、3、3B、3、6、4、6C、2、4、6、32、如图所示,I=(B )A。
A、2B、7C、5D、63、如图所示,E=(B )V。
A、3B、4C、—4D、—3/4、如图所示电路中,I1和I2的关系为(C )。
A、I1<I2B、I1>I2C、I1=I2D、不确定5、如图所示,求I1和I2的大小。
解:对于左边节点:I1=10+3+5=18A对于右边节点:I2=10+2-5=7A6、基尔霍夫第一定律的依据是(D )A.欧姆定律B.全电流定律C.法拉第定律D.电荷守恒定¥7、理想电压源和理想电流源间(C )A.有等效变换关系B.没有等效变换关系C.有条件下的等效关系D.无法判定8、下列说法错误的是(D )A.在电路节点处,各支路电流参考方向可以任意设定。
B.基尔霍夫电流定律可以扩展应用于任意假定的封闭面。
C.基尔霍夫电压定律应用于任意闭合路径。
D.∑I=0式中各电流的正负号与事先任意假定的各支路电流方向无关9、实际电压源和电流源模型中,其内阻与理想电压源和电流源之间的正确连接关系是(C)A.理想电压源与内阻串联,理想电流源与内阻串联"B.理想电压源与内阻并联,理想电流源与内阻串联C.理想电压源与内阻串联,理想电流源与内阻并联D.理想电压源与内阻并联,理想电流源与内阻并联10、79.下面的叙述正确的是(B )。
A.理想电压源和理想电流源是不能等效变换的B.理想电压源和理想电流源等效变换后内部是不等效的C.理想电压源和理想电流源等效变换后外部是不等效的D.以上说法都不正确二、填空题1、不能用电阻串、并联化简的电路称为__复杂电路_______。
;2、电路中的_____每一分支_______称为支路,____3条或3条以上支路___所汇成的交点称为节点,电路中__________闭合的电路______________都称为回路。
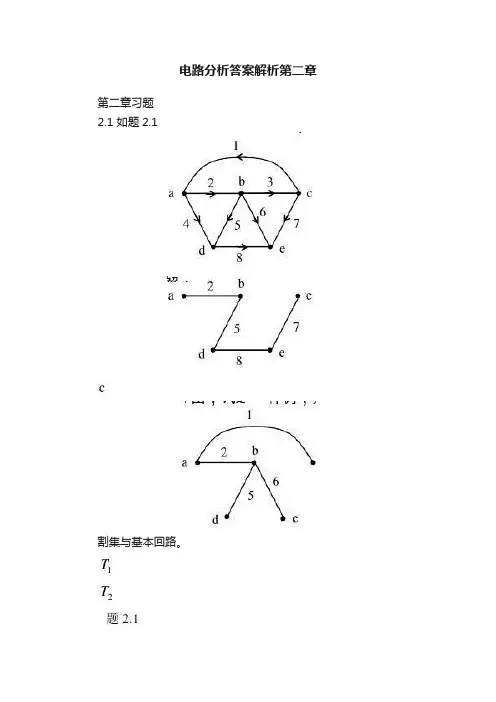
电路分析答案解析第二章第二章习题2.1 如题2.1割集与基本回路。
(a) 树一1T 如图所示。
基本割集为:c1{1,2,4}, c2{1,3,7}, c3{1,3,6,8}, c4{1,3,6,5,4} 基本回路为:l1{5,6,8}, l2{2,4,5}, l3{3,5,8,7}, l4{1,2,5,8,7}(b) 树二2T 如图所示。
基本割集为:c1{4,5,8}, c2{5,7,8}, c3{1,3,7}, c4{4,2,3,7} 基本回路为:l1{2,4,5}, l2{5,6,8}, l3{1,2,3}, l4{1,2,6,7}2.2 题2.2图示电路,求支路电流1I 、2I 、I 解:列两个KVL 回路方程:051)54211=-+++I I I (021)510212=-+++I II (整理为: 45921=+I I 115521=+I I 解得:A I 5.01= A I 1.02-= 而 A I I I 4.0)213-=+-=(2.3 如题2.3图所示电路,已知电流A I 21=解:可列KVL 回路方程: 2I+2+(i-3)R=3已知 i=2A ,代入上式可得:R=3Ω2.4 如题2.4方程求解电流i。
解:10(i-6)+5(0.4i+i)+13i=0解得:i=2A2.5 如题2.5图所示电路,试选一种树,确定基本割集,仅用一个基本割集方程求解电压u程求电压u。
解:①② 选3为参考节点,列方程如下: 52018120124-=-+u u )(已知V u 122-=,代入上式,有: 52012812014-=++u )(解得节点点位: V u 324-=又可知 0124=++u u 得: V u u 201232124=-=--=2.6 如题2.6图所示电路,已知电流A i 21=电压源S u 。
解:列三个网孔方程28)6=-+B A Ri i R (①33)43(-=-+++-C B A i i R Ri ②S C B u i i -=++3)323-(③ 可知: 12==i i B 21==-i i i B A 可得: 32=+=B Ai i由①式可得:283)6=-+R R (解得:Ω=5R 由②式有:33)57(35-=-++?-C i 解得: 0=C i 由③式有: S u -=33- 解得: V u S 6= 根据KVL 有: V i u bc 7432-=--=2.7 如题2.7解该电路的网孔方程。



电路理论习题集电子与电气工程学院电气工程系2013年4月目录第一章电路模型和电路定律 (1)第二章电阻电路的等效变换 (3)第三章电阻电路的一般分析....................................................................... 错误!未定义书签。
第四章电路定理.. (3)第五章一阶电路的时域分析....................................................................... 错误!未定义书签。
第六章相量法 (8)第七章正弦稳态电路的分析....................................................................... 错误!未定义书签。
第八章含有耦合电感的电路....................................................................... 错误!未定义书签。
第九章电路的频率响应............................................................................... 错误!未定义书签。
第十章三相电路 (13)第十一章非正弦周期电流电路................................................................... 错误!未定义书签。
第十二章线性动态电路的复频域分析....................................................... 错误!未定义书签。
第十三章电路方程的矩阵形式................................................................... 错误!未定义书签。
《电路理论(二)》课后作业班级: 学号: 学生姓名:一、储能元件1. 填空(1)电路中的储能元件是指 和 。
(2)电容元件的VCR 满足 (u ,i 为关联参考方向),因此,电容具有 的特性,对于直流电压,电容元件相当于 。
(3)设V u C 0)(=-∞,电容元件在任何时刻t 的储能为 ,只取决于 。
(4)电感元件的VCR 满足 (u ,i 为关联参考方向),因此,电感具有 的特性,对于直流电压,电感元件相当于 。
(5)设V i L 0)(=-∞,电感元件在任何时刻t 的储能为 ,只取决于 。
(6)2A 的电流向2F 的电容充电,已知t =0时刻,V u C 1)0(=,则t =3s 时,)3(C u = 。
二、一阶电路的过渡过程2. 简答:(1)图1所示各电路中是否会出现过渡过程(暂态过程)? (2)总结电路中出现过渡过程(暂态过程)的原因是什么?0)0(=-Cu 0)0(=-C u (a ) (b )(c )三、时间常数3. 填空(1)一阶电路的时间常数τ是零输入响应衰减到初始值的 所需要的时间。
时间常数τ是衡量电路过度过程 的物理量,它取决于电路 ,而与激励无关。
(2)在一阶RL 电路中,时间常数=τ ,若L 不变,R 越大,则换路后过渡过程越 。
(3)在一阶RC 电路中,时间常数=τ ,若C 不变,R 越大,则换路后过渡过程越 。
(4)已知F C R 2,10=Ω=的一阶电路,其时间常数=τ 。
(5)已知H L R 2,10=Ω=的一阶电路,其时间常数=τ 。
(6)已知RL 电路中,Ω==10,2.0R s τ,则电感=L 。
图 1V u C5)0(=-(e )-+10(d )(f )4.(1)一阶电路的时间常数与独立电源 (有关、无关)。
(2)求图2所示电路的时间常数。
四、初始条件5. 什么是换路定律?换路定律的实质是什么?6. 什么是初始值?如何确定一阶电路中的初始值?7. 电路如图3所示,开关闭合前电路已处于稳态,开关在t=0时接通,求电容中的电流的初始值()+0C u 和()+0C i 。
电路分析试题及答案(第⼆章)节点、回路、⽀路分析法:1、如下图所⽰,应⽤节点电压法计算。
已知U s 1=60V ,U s 2=40V ,R 1=6Ω, 23456Ω,求I 1,I 2,I 3,I 4,I 5,I 6的值。
解:114432111111R U U R U R R R R s b a =-+++ 6246541111R U U R U R R R s a b =-???? ??++ U a =U b =24V ;I 1=6A ;I 2=2A ;I 3=4A ;I 4=0A ;I 5=4A ;I 6=-4A ;2、求下图电路的电压U.解:利⽤戴维南等效做,先求ab 两端开路电压:只有24V 的电压源⼯作时: U ‘ab =24/(6+3)=8V ;只有4A 的电流源⼯作时: U ‘‘ab =4×4=16V ; U ab = U ‘ab +U ‘‘ab =24V ;等效电阻R 0=6Ω;U= U ab /(6+2)×2=6V3、计算下图电路中的电压U 1与U 2.解:U 1=8×[4+(6//3)]/[18+4+(6//3)] ×18=36V; U 2=8×18/[18×4+(6//3)] ×3=12V .4、已知下图电路的回路⽅程为2I 1+I 2=4V 和4I 2=8V ,式中各电流的单位为安培。
求:(1)各元件的参数;(2)各电压源供出的功率;(3)改变U和U 的值,使各电阻的功率增加⼀倍。
解:(1)1+ R 3)I 1+R 3I 2+k U 1=Us 1 1+ R 3-k R 1)I 1+R 3I 2 =Us 1-k Us 1R 3I 1 + (R 2+ R 3)I 2+k U 1=Us 2U 1=Us 1- R 1I 1 3-k R 1) I 1+ (R 2+ R 3)I 2+k U 1=Us 2-k Us 1R 1=2Ω, R 2=3Ω, R 3=1Ω, Us 1=8V , Us 1=12V , k =0.5 (2)求解⽅程式,得到:I 1=1A, I 2=2A ,计算各电源功率:Us 1:P 1= Us 1 I 1=8W ; (发出) Us 2:P 2= Us 2 I 2=24W ;(发出) Ucs :Pcs= Ucs (I 1+I 2)=9W ;(吸收)(3)各电源增加2倍,则各电阻上的电流相应增加2倍,即可实现⽬的。
习题22.1选择题(1)C (2)D (3)A (4)C (5)B (6)C2.2简答题(1)因为P 1=100W I s2=-4A所以U s2=50VI 1=10A I r2=5AI A =2-(10-4+5)=-9A(2)11101020111136152020R =+=+=++ 所以i=6020=3 i 1+i 2=330 i 1=15i 2i 2=2i 1i 1=1 i 2 =2i 1’=i 2’i 1’=(60-30)/20=1.5i 1+I=i 1’所以I=0.5A(3) ①有三个电容组成一个网络时有SCU(s)+SCU 1(s)=SC ’U(s)得 C ’=3/2C依次 可得如图所示输入端电容Ci=(n+1)/2(n 为电容所组成的网孔数) ②同理可得 Ri =2/(n+1) (n 为电阻所组成的网孔数)(4) L=L 11+L 22+2 M =16H(5) 设放大器副端电压为U 3 电流为i 2 正端为i 1 从R 1,R 2端流出得电流为i 则有图可得U 3=0, i 1=i 2=001212+=fU U U i R R R =- 所以01212ff R R U U U R R =--R f /R 1=4 R f /R 2=7由此得R 1=2.5K Ω,R 2=10/7(K Ω)(6)设理想变压器输入端线圈电压为U1,输出端线圈电压为U2 有n 1/u 1= n 2/u 2得 u 1=(n 1/n 2)×u 2=3u 2n 1i 1+n 2i 2=0得 i 1=-(1/3)i 2Ri =U/i 1=4i 1+U 1=4+(3U 2)/(-1/3 i 2)=4-9×(-23/3)=73 K Ω2.3(1)LTI ,双向、单调、有源电阻(2)非线性、时变、单调、有源电阻(3)非线性时不变、单调、单向、有源电容(4)非线性、时不变、单向、流控、有源电感(5)非线性、时不变、有向、有源电感、单调(6)非线性、时不变、单调、单向、有源电阻(7)非线性、时不变、压控、单向、无源电(电流)(8)非线性、时不变、单调、单向、有源电容(9)非线性、时不变、单调、有源电阻(10)非线性、时不变、单调、流控、有源电阻(11)非线性、时不变、荷控、有源电容(12)非线性、时不变、单调、有源电阻2.4①2121U ()U ()1 ()()2t t L di t di t dt dt=== ∴元件1 为电感 ②又2L C 1(0)(0)(0)25(0)252C W W W CU =+=+= 故Uc(0)=0,i 1(0)=i 1(t)t =0= -10A.设元件2 为电阻,则(0)(0) 1.5(0)C L U U R i --==Ω ③元件3 为电容,2111()(0)()(1010)0t t C C t U t U i d e e C Cττ--==-+⎰ 由KVL 又可得:Uc(t)=-U L (t)-U R (t)= -10e-t+10e-2t比较两式系数得C=1F .2.52.6(a )P R =34 (w),P v =32 (w),P 1= -2(w ),消耗功率来源于电流源。
第二章电阻电路的等效变换
“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知
12100,2,8s u V R k R k 。
若:(1)38R k ;(2)处开路)33
(R R ;(3)处短路)33(0R R 。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻8
42R k ,。
第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知12100,2,8s u V R k R k ==Ω=Ω。
若:(1)38R k =Ω;(2)处开路)33(R R ∞=;(3)处短路)33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻842R k ==Ω,则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132====V i R u 667.666508222=⨯==(2)当∞=3R ,有03=imA R R u i s 1082100212=+=+=V i R u 80108222=⨯==(3)03=R ,有0,022==u imA R u i s 50210013===2-2 电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如题解图(a )所示。
因此有 32332R R i R i += 32322R R i R R u s+=(2)由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源,如题解图(b )所示。