第3章_液体的表面现象[2016_修正版]

《医学物理学（第3版）》习题解答2009.10部分题解2－10．解：已知 363102525m cm v -⨯==; a P .p 511051⨯= a P .p 521011⨯=()())J (..vp p 110251011105165521=⨯⨯⨯-⨯=-=ω∴-2-11．10-5s第三章 液体的表面现象3-1．解：设由n 个小水滴融合成一个大水滴，释放出的能量为P E ∆。

n 个小水滴的总表面积S 1=24r n ⋅⋅π，大水滴的表面积S 2=42R ⋅π，利用n 个小水滴的体积等于一个大水滴的体积，可求出n 即n ×334r ⋅π=334R ⋅π 所以n ×334r ⋅π=334R ⋅π; ()()936333310102102=⨯⨯==--r R n 个将910个半径为2×310-mm 小水滴融合成一个半径为2mm 的大水滴时，其释放的能量等于表面能的减少，所以 )44()(2221R r n S S E P ⋅-⋅⨯=-=∆ππαα=3612931066.3)10414.3410414.3410(1073----⨯≈⨯⨯⨯-⨯⨯⨯⨯⨯J3-2解：由于肥皂泡非常薄，因此可忽略肥皂泡的厚度，取外内＝R R ＝2d＝0.05m 。

因为肥皂泡有内外两个表面，所以肥皂泡增加的表面积242R S π⨯=∆。

根据SW∆=α可得吹一个直径为10cm 的肥皂泡，需要做的功 4423108105421040---⨯=⨯⨯⨯⨯⨯=∆⋅=ππαS W J 又因为增加表面能等于外力所做的功 W E P =∆ 所以 4108-⨯==∆πW E P J根据拉普拉斯公式，可得球形液面的内外压强差 ＝－外内p p Rα2 由于肥皂泡有内外两个表面，所以其内外压强差 ＝－外内p p 2.3100.510404423=⨯⨯⨯=--R α(P a )3-3．解：根据拉普拉斯公式，可得球形液面的内外压强差 ＝－外内p p Rα2 所以，当肺泡的半径为0.04mm 时，它的内外压强差为＝－外内p p 353100.2100.4104022⨯=⨯⨯⨯=--R α(P a ) 3-4．解：根据拉普拉斯公式可得球形液面的内外压强差 ＝－外内p p Rα2 因为气泡在水下面只有一个球形表面，所以气泡的内外压强差＝－外内p p Rα2 而 h g p p ⋅⋅+ρ0＝外 所以,气泡内的压强 h g p p ⋅⋅+ρ0＝内＋Rα2 即 内p ＝1.013×105＋310×9.8×10＋5331001.2101.010732⨯=⨯⨯⨯--(P a )3=5．解：根据毛细现象的公式 θραcos 2rg h ⋅⋅=由于乙醇能完全润湿玻璃壁，所以接触角O=0θ，故 rg h ⋅⋅=ρα2所以 332107.2221015.08.97911090.32---⨯=⨯⨯⨯⨯⨯=⋅⋅⋅=r g h ρα (N/m)3-6．解：根据毛细现象的公式 θραcos 2rg h ⋅⋅=由于水能完全润湿玻璃壁，所以接触角O =0θ，故 rg h ⋅⋅=ρα2所以 112r g h ⋅⋅=ρα 222r g h ⋅⋅=ρα⎪⎭⎫⎝⎛⨯-⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛-=-=-=∆---3333212121105.11105.018.9101073211222r r g gr gr h h h ραραρα ＝1.99×210-(m)＝1.99(cm)3-7．解：根据毛细现象的公式 θραcos 2rg h ⋅⋅=;由于水能完全润湿毛细管，所以接触角O =0θ，因此水在毛细管中上升的高度为 rg h ⋅⋅=ρα2而管中水柱的高度r g R h ⋅⋅+='ρα223333103.5103.08.91010732103----⨯=⨯⨯⨯⨯⨯+⨯=(m)=5.3(cm) 3-8．解：：根据毛细现象的公式 θραcos 2rg h ⋅⋅=由于水和丙酮能完全润湿毛细管，所以接触角O =0θ，因此水和丙酮在毛细管上升的高度分别为rg h ⋅=水水ρα21 ① rg h ⋅=酮酮ρα22 ②②式除以①式可得酮水水酮ρραα⋅=t h h 12 所以 3332212104.32107310105.2792104.1-⨯=⨯⨯⨯⨯⨯⨯⋅⋅－－－水水酮酮＝＝αρραh h (N/m) 3-9．解：根据毛细现象的公式 θραcos 2rg h ⋅⋅=由于血液在毛细管产生完全润湿现象，所以接触角O =0θ，故 rg h ⋅⋅=ρα2所以,血液表面张力系数3332109.572105.08.91005.11025.22---⨯=⨯⨯⨯⨯⨯⨯=⋅⋅⋅=r g h ρα (N/m)第四章 振动和波动及超声波成像的物理原理4－2.解：已知 kg M 5=；()cm t cos x 44010π+π= （1） 由()cm t cos x 44010π+π=得m cm A 11010-==；)s rad (π=ω40；mk 2=ω； m k 2ω=则)J (.)J (.mA kA E 384394400105160021212122222=π=⨯⨯π⨯=ω==s .T 0504022=ππ=ωπ=； Hz T f 201==； ()()sm 43t 40cos 4s m 4t 40sin 4vπ+ππ=π+ππ-= ()()2222sm 45t 40cos 160s m 4t 40cos 160a π+ππ=π+ππ-=（2） 当s .t 21=时，则()m .cos x 2110254214010--⨯=π+⨯π=；()sm .cos v π=π+⨯ππ=224321404)J (kx E );J (mv E p k 242222220105051600212120852121π=⨯⨯⨯π⨯==π=π⨯⨯==-(或)J (E E E k p 222202040π=π-π=-=)4－3.解：已知cm A 2=；0=t 时，刚好向x 反向传播;πω==250Hz f , 则 s rad π=ω100()ϕ+ω=t cos A x Θ，0=t 时 0=x 则 2πϕ±=又由 ()0sin 〈+-=ϕωωt A v ， 得 2π=ϕ所以，振动方程为 cm 2t 100cos 2x ⎪⎭⎫ ⎝⎛π+π=速度方程为 s cm t sin v ⎪⎭⎫ ⎝⎛π+ππ-=2100200 s m t cos ⎪⎭⎫ ⎝⎛π+ππ=231002 ；s m 2v m π= 加速度方程为 222100200sm t cos a ⎪⎭⎫ ⎝⎛π+ππ-=；22m s m 200a π= 4－4. 解：（１）2A x =时，222121kA kx E p ==； 41218122==kA kAE E p 即势能占总能量的25%，动能占总能量的75% 。

液体的表面张力与液体的表面现象在日常生活中，只要你稍加留意，就会观察到许多与液体表而张力有关的现象。

如草叶上晶莹剔透的露珠，荷叶上滚动着的小水滴，玻璃板上的小水银滴等，它们为什么都是球形或近似球形？这就是因为液体表而张力的作用结果。

当用细管吹岀一个个五彩缤纷的肥皂泡时，在泡膜的表而上就布满了液体表而张力。

用数学可以证明，在体积相同的各种形状的几何体中，球体的表而积最小。

正是由于表而张力的作用，才会出现露珠、小水银滴等都收缩为球形的现象。

你若有机会观察护士给病人输液，你会看到在输液之前，护士总是要把输液管中的空气泡排除干净。

不然的话，若让那些气泡混入人体血管中，任表而张力的作用下，气泡将会阻碍血液的正常流动。

下而就来分析一下液体的表而张力，以及液体表而现象发生的原因。

1表面张力的成因、大小和方向表而张力就是促使液体表而收缩的力。

液体与气体的交界而（属于液体薄层），称为表而层。

在表而层中，液体分子因受到液体内部分子的引力，而有一部分会被拉入液体内，致使表而层液体分子密度小于液内分子密度。

表而层中液体分子的这种布局，使得液体表而层就像一张“绷紧”的橡皮膜，而具有收缩趋势。

表面层一直处在具有收缩趋势的表而张力作用之下。

这里应指岀，液体表而张力与橡皮膜张力在本质上是不同的。

橡皮膜的分子间距会随着膜面积的增大而增大。

而液体表而张力却不受而枳变化的影响，当液体表而层而积增大时，液内分子会自动进入液面来补充，从而维持液而内分子间距不变。

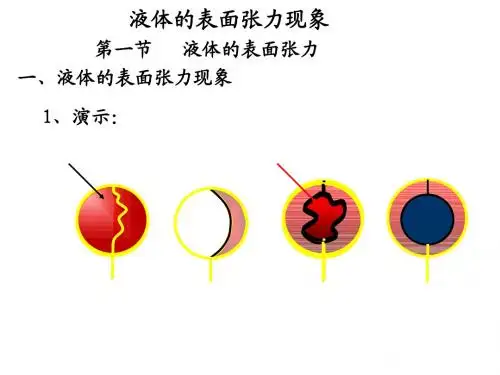
可以用一个很简单的实验，来可说明表而张力的存在。

取一段铜丝制成一个直径约5〜&•加的圆环，在环上跨系一根细红线（用红线易于观察）。

将环浸入洗洁精溶液再取岀，环上蒙了一层液膜，这时用粉笔头轻触线一侧的液膜，原来自由弯曲的红线则立即被液膜拉向另一侧，成为一段张紧的弧线。

实验表明，液体表而具有收缩到最小而积的趋势。

同时它还表明，表而张力的方向垂直于任一周界线且与液而相切。

理论和实验表明，表而张力的大小，可用如下公式表示：F = aL（单表面层）' F = 2aL（双表而层）上式中，◎称为表而张力系数。