工程力学静力学单辉祖主编
- 格式:ppt
- 大小:8.80 MB
- 文档页数:161


工程力学课后习题答案单辉祖著工程力学课后习题答案(单辉祖著)在学习工程力学这门课程时,课后习题的练习与答案的参考对于巩固知识、加深理解起着至关重要的作用。
单辉祖所著的《工程力学》一书,以其严谨的逻辑和丰富的内容,成为众多学子学习工程力学的重要教材。
下面,我们将为您详细呈现这本教材的课后习题答案。
首先,让我们来谈谈第一章的习题。
在这部分中,主要涉及到静力学的基本概念和受力分析。
例如,有一道题是关于一个简单的支架结构,要求画出其受力图。
对于这道题,我们需要明确各个构件之间的连接方式,判断是固定铰支座、活动铰支座还是其他约束类型,然后根据力的平衡条件,准确地画出每个构件所受到的力。
答案中,我们清晰地标注了各个力的大小、方向和作用点,并且通过合理的布局,使受力图易于理解。
第二章的习题重点围绕平面汇交力系和平面力偶系展开。
其中,有一道计算题要求计算多个力在某一点的合力。
在解答这道题时,我们首先将每个力分解为水平和垂直方向的分力,然后分别计算水平和垂直方向上的合力,最后通过勾股定理求出总的合力大小和方向。
答案的给出过程中,每一步的计算都有详细的说明,让学习者能够清晰地看到解题的思路和方法。
第三章的内容是平面任意力系。
这一章的习题难度有所增加,涉及到力系的简化、平衡方程的应用等。
比如,有一道题是求解一个复杂结构在给定载荷下的支座反力。
解题时,我们先对力系进行简化,找到主矢和主矩,然后根据平衡方程列出方程组,通过求解方程组得到支座反力的大小和方向。
答案中不仅给出了最终的结果,还展示了求解方程组的具体步骤和计算过程,方便学习者对照检查自己的解题过程。
第四章是空间力系。
这部分的习题对于空间想象力和数学运算能力有一定的要求。
例如,有一道题要求计算空间力在坐标轴上的投影以及对某点的矩。
在解答时,我们需要运用空间直角坐标系的知识,通过三角函数等方法求出投影的大小,再根据矩的定义计算出对某点的矩。
答案中会详细说明投影和矩的计算过程,并且配以适当的图示,帮助学习者更好地理解空间力系的概念。


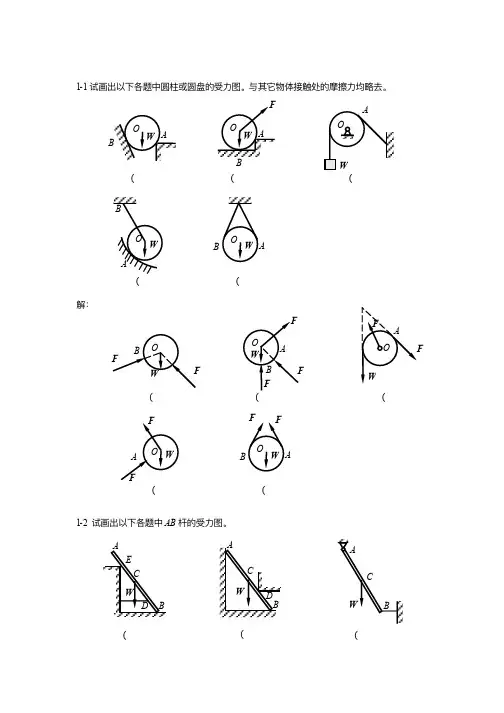


工程力学(静力学与材料力学)单祖辉 谢传峰合编课后习题答案1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
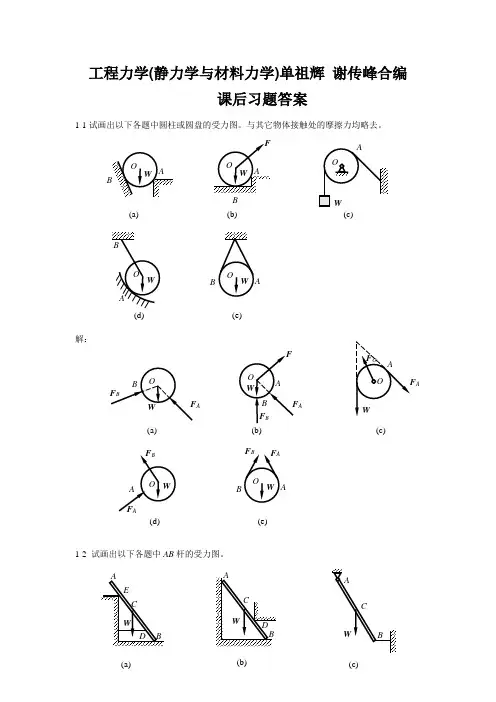
解:1-2 试画出以下各题中AB 杆的受力图。
(a)(b)c)(d)A(e) A(a)(b) A(c)A(d)A(e)工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)DBF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
(d)FC(e)WB(f)F FBC(c)(d)(b)e)解:(a)(b)(c)(d)(e)ATF BAFCAA C’CDDC’B2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos 6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。

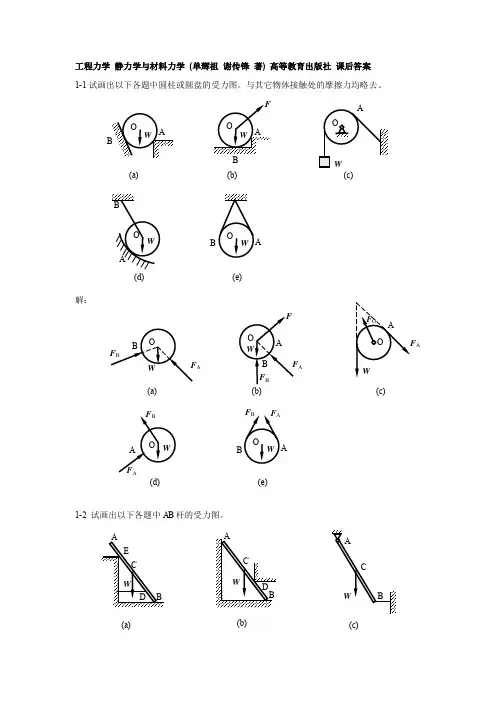
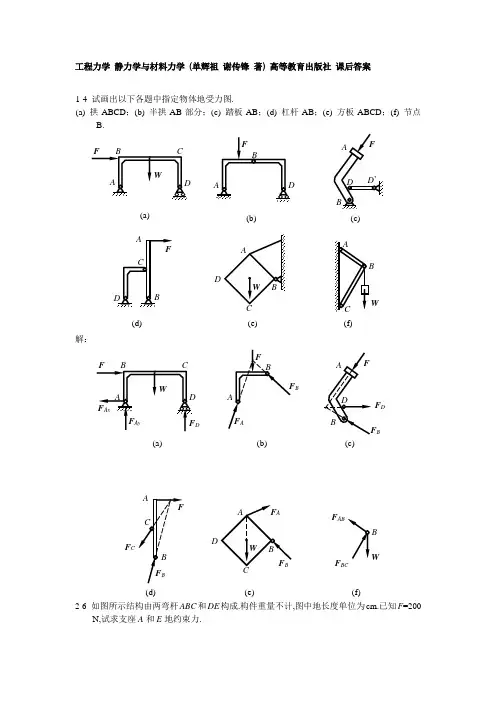
工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案1-4 试画出以下各题中指定物体地受力图.(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B. 解:2-6 如图所示结构由两弯杆ABC 和DE 构成.构件重量不计,图中地长度单位为cm.已知F =200N,试求支座A 和E 地约束力.(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D(d)F C(e) WB(f) F F BC解:(1) 取DE 为研究对象,DE 为二力杆;F D = F E(2) 取ABC 为研究对象,受力分析并画受力图;画封闭地力三角形:'15166.7 23A D E F F F F N ===⨯= 2-7 在四连杆机构ABCD 地铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡.试求平衡时力F 1和F 2地大小之间地关系.解:(1)取铰链B 为研究对象,AB 、BC 均为二力杆,画受力图和封闭力三角形;F A FF BC1BC F(2) 取铰链C 为研究对象,BC 、CD 均为二力杆,画受力图和封闭力三角形;22cos302o CB F F F ==由前二式可得:121222120.61 1.634BC CB F F F F F F or F F ==∴===AB 、AC 杆受拉,AD 杆受压.CF CD F 2F CB F CD0 cos 0 cos cos B B A B M M F l M F l MF F l θθθ=⨯⨯-==∴==∑3-2 在题图所示结构中二曲杆自重不计,曲杆AB 上作用有主动力偶,其力偶矩为M ,试求A 和C 点处地约束力.解:(1) 取BC 为研究对象,受力分析,BC 为二力杆,画受力图;B C F F =(2) 取AB 为研究对象,受力分析,A 、B 地约束力组成一个力偶,画受力图;()''30 0.35420.354B B AC M M F a a M F a MF F a=⨯+-===∴==∑ 3-8 在图示结构中,各构件地自重都不计,在构件BC 上作用一力偶矩为M 地力偶,各尺寸如图.求支座A 地约束力.FC解:(1) 取BC 为研究对象,受力分析,画受力图;0 0 C C M M F l M F l=-⨯+==∑(2) 取DAC 为研究对象,受力分析,画受力图;画封闭地力三角形;解得'cos 45C A oF F == F ’CF D F A F ’CF D4-18 由杆AB 、BC 和CE 组成地支架和滑轮E 支持着物体.物体重12 kN.D 处亦为铰链连接,尺寸如题4-18图所示.试求固定铰链支座A 和滚动铰链支座B 地约束力以及杆BC 所受地力.解:(1) 研究整体,受力分析,画出受力图(平面任意力系);(2) 选坐标系0: 012 kNxAx Ax FF W F =-==∑()()()0: 4 1.52010.5 kNAB B MF F W r W r F =⨯-⨯-+⨯+==∑0: 01.5 kNyAy B Ay FF F W F =+-==∑(3) 研究CE 杆(带滑轮),受力分析,画出受力图(平面任意力系);Ax(4) 选D 点为矩心,列出平衡方程;()()0: sin 1.5 1.5015 kNDCB CB MF F W r W r F α=⨯-⨯-+⨯==∑约束力地方向如图所示.4-19 起重构架如题4-19图所示,尺寸单位为mm.滑轮直径d =200 mm,钢丝绳地倾斜部分平行于杆BE .吊起地载荷W =10 kN,其它重量不计,求固定铰链支座A 、B 地约束力.解:(1) 研究整体,(2) 选坐标系Bxy ,列出平衡方程;()0: 6001200020 kNBAx Ax MF F W F =⨯-⨯==∑0: 020 kNxAx Bx Bx FF F F =-+==∑WF CBW0: 0yAy By FF F W =-+-=∑(3) 研究A CD 杆,受力分析,画出受力图(平面任意力系);(4) 选D 点为矩心,列出平衡方程;()0: 80010001.25 kNDAy C Ay MF F F F =⨯-⨯==∑(5) 将F Ay 代入到前面地平衡方程;11.25 kN By Ay F F W =+=约束力地方向如图所示.4-20 AB 、AC 、DE 三杆连接如题4-20图所示.DE 杆上有一插销F 套在AC 杆地导槽内.求在水平杆DE 地E 端有一铅垂力F 作用时,AB 杆上所受地力.设AD =DB ,DF =FE ,BC =DE ,所有杆重均不计.解:(1) 整体受力分析,根据三力平衡汇交定理,可知B 点地约束力一定沿着BC 方向;(2) 研究DFE 杆,受力分析,画出受力图(平面任意力系);(3) 分别选F 点和B 点为矩心,列出平衡方程;()0: 0FDy Dy M F F EF F DE F F=-⨯+⨯==∑()0: 02BDx Dx MF F ED F DB F F=-⨯+⨯==∑(4) 研究ADB 杆,受力分析,画出受力图(平面任意力系);Dx(5) 选坐标系Axy ,列出平衡方程;'()0: 0ADx B B MF F F F F=⨯-⨯==∑'0: 0xAx B Dx Ax FF F F F F=--+==∑'0: 0yAy Dy Ay FF F F F=-+==∑约束力地方向如图所示.6-11 均质梯长为l ,重为P ,B 端靠在光滑铅直墙上,如图所示,已知梯与地面地静摩擦因数f sA ,求平衡时θ=?解:(1) 研究AB 杆,当A 点静滑动摩擦力达到最大时,画受力图(A 点约束力用全约束力表示);由三力平衡汇交定理可知,P 、F B 、F R 三力汇交在D 点;(2) 找出θmin 和ϕ f 地几何关系;min min minmin sin tan cos 211tan 2tan 21arctan2f f sAsAll f f θϕθθϕθ⨯=⨯==∴= (3) 得出θ角地范围;190arctan2o sAf θ≥≥ 6-15 砖夹地宽度为25 cm,曲杆AGB 与GCED 在G 点铰接.砖地重量为W ,提砖地合力F 作用在砖对称中心线上,尺寸如图所示.如砖夹与砖之间地摩擦因数f s =0.5,试问b 应为多大才能把砖夹起(b 是G 点到砖块上所受正压力作用线地垂直距离).解:(1) 砖夹与砖之间地摩擦角:arctan arctan0.525.6o f s f ϕ===(2) 由整体受力分析得:F=W (2) 研究砖,受力分析,画受力图;(3) 列y 方向投影地平衡方程;0: 2sin 01.157yR f R FF W F Wϕ=⨯-==∑(4) 研究AGB 杆,受力分析,画受力图;D《工程力学》习题选解(5) 取G 为矩心,列平衡方程;''()0: sin 3cos 9.5010.5 cmGR f R f MF F F b F b ϕϕ=⨯⨯-⨯⨯+⨯==∑6-18 试求图示两平面图形形心C 地位置.图中尺寸单位为mm.解:(a) (1) 将T 形分成上、下二个矩形S 1、S 2,形心为C 1、C 2;(2) 在图示坐标系中,y 轴是图形对称轴,则有:x C =0 (3) 二个矩形地面积和形心;211222501507500 mm 225 mm 5020010000 mm 100 mmC C S y S y =⨯===⨯==(4) T 形地形心;0750022510000100153.6 mm750010000C i iC ix S y y S=⨯+⨯===+∑∑ (b) (1) 将L 形分成左、右二个矩形S 1、S 2,形心为C 1、C 2;(a)(b)(3) 二个矩形地面积和形心;21112222101201200 mm 5 mm 60 mm 7010700 mm 45 mm 5 mmC C CC S x y S x y =⨯====⨯===(4) L 形地形心;120057004519.74 mm1200700120060700539.74 mm1200700i iC i i iCiS x x S S y y S⨯+⨯===+⨯+⨯===+∑∑∑∑6-19试求图示平面图形形心位置.尺寸单位为mm.解:(a) (1) 将图形看成大圆S 1减去小圆S 2,形心为C 1和C 2;(2) 在图示坐标系中,x 轴是图形对称轴,则有:y C =0 (3) 二个图形地面积和形心;2211222220040000 mm 0806400 mm 100 mmC C S x S x ππππ=⨯===⨯==(a)(b)(4) 图形地形心;640010019.05 mm4000064000i iCiC S x x Sy πππ-⨯===--=∑∑(b) (1) 将图形看成大矩形S 1减去小矩形S 2,形心为C 1和C 2;(2) 在图示坐标系中,y 轴是图形对称轴,则有:x C =0 (3) 二个图形地面积和形心;21122216012019200 mm 60100606000 mm 50 mmC C S y S y =⨯===⨯==(4) 图形地形心;0192006060005064.55 mm192006000C i iC ix S y y S=⨯-⨯===-∑∑ 8-16 题8-14所述桁架,试定载荷F 地许用值[F ].解:(1) 由8-14得到AB 、AC 两杆所受地力与载荷F 地关系;AC AB F F == (2) 运用强度条件,分别对两杆进行强度计算;[]211160 154.54ABAB F MPa F kN A d σσπ==≤=≤[]222160 97.14ACAC F MPa F kN A d σσπ==≤=≤ 取[F ]=97.1 kN.8-18 图示阶梯形杆AC ,F =10 kN,l 1= l 2=400 mm,A 1=2A 2=100 mm 2,E =200GPa,试计算杆AC 地轴向变形△l .SS解:(1) 用截面法求AB 、BC 段地轴力;12 N N F F F F ==-(2) 分段计算个杆地轴向变形;33112212331210104001010400200101002001050 02 N N F l F l l l l EA EA .mm⨯⨯⨯⨯∆=∆+∆=+=-⨯⨯⨯⨯=-AC 杆缩短.8-22 图示桁架,杆1与杆2地横截面面积与材料均相同,在节点A 处承受载荷F 作用.从试验中测得杆1与杆2地纵向正应变分别为ε1=4.0×10-4与ε2=2.0×10-4,试确定载荷F 及其方位角θ之值.已知:A 1=A 2=200 mm 2,E 1=E 2=200 GPa.解:(1) 对节点A 受力分析,求出AB 和AC 两杆所受地力与θ地关系;00000 sin 30sin 30sin 00 cos30cos30cos 0x AB AC yAB AC AB AC FF F F FF F F F F F θθ=-++==+-===∑∑(2) 由胡克定律:1111222216 8 AB AC F A E A kN F A E A kN σεσε======F AB代入前式得:o 21.2 10.9F kN θ==8-23 题8-15所述桁架,若杆AB 与AC 地横截面面积分别为A 1=400 mm 2与A 2=8000 mm 2,杆AB 地长度l =1.5 m,钢与木地弹性模量分别为E S =200 GPa 、E W =10 GPa.试计算节点A 地水平与铅直位移. 解:(1) 计算两杆地变形;31313232501015000.938 2001040070.71015001.875 10108000AB S AC W F l l mmE AF l mm E A ⨯⨯∆===⨯⨯⨯∆===⨯⨯1杆伸长,2杆缩短.(2) 画出节点A 地协调位置并计算其位移;水平位移:10.938 A l mm ∆=∆=铅直位移:0001221'sin 45(cos45)45 3.58 A f A A l l l tg mm ==∆+∆+∆=8-26 图示两端固定等截面直杆,横截面地面积为A ,承受轴向载荷F 作用,试计算杆内横截面上地最大拉应力与最大压应力.解:(1)列平衡方程:0 0xA B FF F F F =-+-=∑(2) 用截面法求出AB 、BC 、CD 段地轴力;(b)A ’1△l123 N A N A N B F F F F F F F =-=-+=-(3) 用变形协调条件,列出补充方程;0AB BC CD l l l ∆+∆+∆=代入胡克定律;231 /3()/3/3 0N BC N CDN ABAB BC CD A A B F l F l F l l l l EA EA EAF l F F l F l EA EA EA∆=∆=∆=-+-+-=求出约束反力:/3A B F F F ==(4) 最大拉应力和最大压应力; 21,max ,max 2 33N N l y F F F FA A A Aσσ====- 8-27 图示结构,梁BD 为刚体,杆1与杆2用同一种材料制成,横截面面积均为A =300 mm 2,许用应力[σ]=160 MPa,载荷F =50 kN,试校核杆地强度.解:(1) 对BD120 220BN N mF a F a F a =⨯+⨯-⨯=∑(2) 由变形协调关系,列补充方程;212 l l ∆=∆代之胡克定理,可得;21212 2N N N N F l F lF F EA EA== 解联立方程得:F F N 11224 55N N F F F F == (3) 强度计算;[][]3113222501066.7 160 530045010133.3 160 5300N N F MPa MPaA F MPa MPaA σσσσ⨯⨯====⨯⨯⨯====⨯ 所以杆地强度足够.8-30 图示桁架,杆1、杆2与个杆3分别用铸铁、铜与钢制成,许用应力分别为[σ1] =80 MPa,[σ2]=60 MPa,[σ3] =120 MPa,弹性模量分别为E 1=160 GPa,E 2=100 GPa,E 3=200 GPa.若载荷F =160 kN,A 1=A 2 =2A 3,试确定各杆地横截面面积.解:(1) 对节点C 进行受力分析,假设三杆均受拉; 画受力图;列平衡方程;0120320 cos3000 sin 300x N N yN N F F F FF F F =--==+-=∑∑(2) 根据胡克定律,列出各杆地绝对变形;01112221211220333333cos3016021002sin 30200N N N N N N F l F l F l F l l l E A A E A A F l F l l E A A∆==∆==⨯⨯∆==(3) 由变形协调关系,列补充方程;N3FF N 1N 3C 2△l0003221sin30(cos30)30l l l l ctg ∆=∆+∆-∆简化后得:123153280N N N F F F -+=联立平衡方程可得:12322.63 26.13 146.94N N N F kN F kN F kN =-==1杆实际受压,2杆和3杆受拉. (4) 强度计算;[][][]312123123283 436 1225 N N N F F F A mm A mm A mm σσσ≥=≥=≥=综合以上条件,可得12322450 A A A mm ==≥9-18 题9-16所述轴,若扭力偶矩M =1 kNm,许用切应力[τ] =80 MPa,单位长度地许用扭转角[θ]=0.5 0/m,切变模量G =80 GPa,试确定轴径. 解:(1) 考虑轴地强度条件;[][]6max133116max233222211016 80 50.311611016 80 39.9116AB BC M d mm d d M d mm d d ττππττππ⨯⨯⨯=≤≤≥⨯⨯=≤≤≥(2) 考虑轴地刚度条件;[]0603134118021032180 100.5 73.5 8010TAB AB pAB M d mm GI d θθπππ⨯⨯=⨯≤⨯⨯≤≥⨯⨯ []0603234218011032180 100.5 61.8 8010TBC BCpBC M d mm GI d θθπππ⨯⨯=⨯≤⨯⨯≤≥⨯⨯ (3) 综合轴地强度和刚度条件,确定轴地直径;1273.5 61.8d mm d mm ≥≥9-19 图示两端固定地圆截面轴,直径为d ,材料地切变模量为G ,截面B 地转角为υB ,试求所加扭力偶矩M 之值.解:(1) 受力分析,列平衡方程;0 0xA B MM M M =-+-=∑(2) 求AB 、BC 段地扭矩;AB A BC A T M T M M ==-(3) 列补充方程,求固定端地约束反力偶;()44322320 0A A AB BCM M aM a G d G d ϕϕππ-+=+=与平衡方程一起联合解得21 33A B M M M M == (4) 用转角公式求外力偶矩M ;44323 64A BABB M a G d M G d aπϕϕϕπ=== 11-14 图示槽形截面悬臂梁,F =10 kN,M e =70 kNm,许用拉应力[σ+]=35 MPa,许用压应力[σ-]=120 MPa,试校核梁地强度.解:(1) 截面形心位置及惯性矩:112212(150250)125(100200)15096 (150250)(100200)C A y A y y mm A A ⋅+⋅⨯⋅+-⨯⋅===+⨯+-⨯3322841505025200(15050)(25)2(25200)(150)12121.0210 zCC C I y y mm ⎡⎤⨯⨯=+⨯⋅-++⨯⋅-⎢⎥⎣⎦=⨯ (2) 画出梁地弯矩图BMC(3) 计算应力A +截面下边缘点处地拉应力及上边缘点处地压应力分别为:68(250)4010(25096)60.4 1.0210C A A zCM y MPa I σ+++⋅-⨯-===⨯ 6840109637.61.0210CA A zCM y MPa I σ-++⋅⨯⨯===⨯ A -截面下边缘点处地压应力为68(250)3010(25096)45.3 1.0210C A A zCM y MPa I σ---⋅-⨯-===⨯ 可见梁内最大拉应力超过许用拉应力,梁不安全.。
1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
ABAOW (a) B AO W F(b)OW (c)AAOW(d)BAOW (e)BF BF ABO W(a) B AO W F(b) F AF B AO W(c)F AF O A O W(d)F B F AAOW (e)BF B F A AWC B(c)D (a) A WC E B(b)AW CD B解:1-3 试画出以下各题中AB 梁的受力图。
解:ABW (e)CF B F AAB F(d)CF BF A(a) F D F BF ED A WCE B(b)AWC D B F D F BF A(c)AWC BF BF AAW CB(a)WABC D(c)ABF q D(b)CC A BFWDA ’ D ’B ’(d)ABFq(e)F BF AF qABC F B1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:CA BFWD(d)F BF AF DAB Fq(e)F BxF ByF AAB F (a) DCWAF (b) DB(c) FABD D ’ABF(d)CDW ABC D(e)WABC (f)AB F (a)D CWF AxF AyF DA F (b)BF BF A(c)FABDF BF D A FCA F AF AB1-5 试画出以下各题中指定物体的受力图。
(a) 结点A,结点B;(b) 圆柱A和B及整体;(c) 半拱AB,半拱BC及整体;(d) 杠杆AB,切刀CEF及整体;(e) 秤杆AB,秤盘架BCD及整体。
解:(a)(b)ABW(a)(c)BCW1 W2FAFDABCE F(d)AF ABF ATF ABF BAF BTWABPP(b)WA BCC’DOG(e)(c)(d)(e)F CAPCF BB PCF ’ CF AABPPF BF NBC W 1W 2 F AF Cx F CyF AxF AyB W 1F A F Ax F AyF Bx F ByB C W 2 F Cx F CyF ’Bx F ’By FA BC F C F BDC E F F E F ’C F F FDAB C E F F EF FF BB C D G F B F C WAB CC ’ DO GF Oy F OxF C ’A B O W F BF OyF Ox2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。