结构方程模型与偏最小二乘法教学文稿

结构方程模型案例重点讲义资料以下是结构方程模型案例重点讲义资料的主要内容：一、结构方程模型的基本概念1.1结构方程模型的定义和目的1.2结构方程模型的组成部分（潜变量、测量变量、误差项、因果关系）1.3结构方程模型的表示方式（路径图、方程式）二、测量模型的构建2.1潜变量的定义和测量2.2测量模型的评估准则（信度、效度、合理性）2.3验证性因素分析（CFA）的步骤和方法2.4模型修正指标（修正指数、比较指数、适配指数）三、结构模型的构建3.1潜变量间的因果关系的设定3.2结构模型的估计方法（最小二乘估计法、最大似然估计法）3.3结构模型的适配度检验（适配指数、残差、误差修正模型）四、模型分析和解释4.1结构方程模型的参数估计和显著性检验4.2模型拟合程度的评估（拟合指数、误差修正指数、SRMR）4.3预测能力和因果关系的解释4.4结果的解释和可信度评价五、结构方程模型在实际研究中的应用案例5.1教育领域中的结构方程模型应用5.2金融领域中的结构方程模型应用5.3健康领域中的结构方程模型应用5.4社会科学领域中的结构方程模型应用六、结构方程模型案例分析技巧和注意事项6.1结构方程模型数据的准备和处理6.2模型设定和变量选择的技巧6.3数据样本量的要求和样本偏倚的处理6.4模型解释和模型比较的技巧总结：结构方程模型是一种强大的统计分析工具，可以帮助研究人员深入理解和解释潜变量之间的因果关系。

掌握结构方程模型的基本概念和构建步骤，能够为实际研究提供有力的支持。

在使用结构方程模型时，需要注意模型设定和变量选择的合理性，样本量和样本偏倚的问题，以及模型解释和比较的技巧。

随着结构方程模型在不同领域的广泛应用，我们可以看到其在教育、金融、健康和社会科学等领域中的重要作用。

因此，进一步学习和掌握结构方程模型的技巧和方法，对于提高研究质量和推动学科发展具有重要意义。

2平差数学模型与最小二乘原理2.1 参数估计及其最优性质几何模型：包括水准网和平面控制网（包括测角网、测边网、边角网）。

每种几何模型都包含有不同的几何元素，如水准网中包括点的高程、点间的高差，平面网中包含角度、边长、边的坐标方位角以及点的二维或三维坐标等元素。

这些元素都被称为几何量。

在诸多几何量中，有的可以直接测量，有的是间接求出。

几何模型不同，它所需要知道的元素的个数与类型也不同，目标是确定几何模型的唯一性。

1.如图2-1的三角形ABC中，为了确定它的形状，只需要知道三个内角中的任意两个内角的大小就可以了。

它们都是同一类型的元素。

2.要确定该三角形的大小和形状，就必须知道三个不同的元素，即任意的一边两角、任意的两边一角或者是三边。

它们中间都至少包含一条边长该情况包含角度和边长两类元素。

3.要确定该三角形的大小、形状和它在一个特定坐标系中的位置和方向，则必须知道图中15个元素（6个坐标元素，3个内角元素，3个边长元素，3个方位角元素）中的6个不同的元素，这6个元素可以构成更多的组合，至少要包含一个点的坐标和一条边坐标方位角，它们的改变只相当于整个网在坐标系中发生了平移和旋转，并不影响该三角形的内部形状和大小。

如果A、B两点都是已知点，为确定三角形的大小、形状、位置和方向，则只需要任意两个元素就行了，如两角、两边或一边一角等。

我们把能够唯一地确定一个几何模型所必要的元素，称为必要观测元素。

必要观测个数用t表示。

例如，确定三角形的形状，必要观测元素个数t=2；确定三角形的大小和形状，必要观测元素个数t=3；确定三角形的大小、形状、位置和方向，必要观测元素个数t=6。

对于后两种情况，不仅要考虑必要观测元素的个数，还要考虑到元素的类型，否则就无法唯一地确定模型。

必要起算数据个数用d表示，水准网为1，测角网为4，测边网和边角网为3。

观测值个数用n个表示。

当n<t时,显然无法确定模型的解；当n =t 时,则可唯一地确定该模型，但对观测结果中含有的粗差和错误都将无法发现；当n >t 时，能及时发现测量中的粗差和错误，提高观测成果的精度和可靠性。

偏最小二乘法教案一、引言偏最小二乘法（Partial Least Squares，简称PLS）是一种常用的统计分析方法，广泛应用于科学研究和数据分析领域。

本教案旨在介绍偏最小二乘法的基本原理、应用场景以及实际操作过程。

二、偏最小二乘法概述1. 基本原理偏最小二乘法是一种多元统计分析方法，主要用于分析自变量与因变量之间的关系。

它通过对自变量与因变量进行正交变换，得到新的综合变量，使得新变量之间的协方差最大，同时与因变量的相关性也最大。

2. 应用场景偏最小二乘法可以应用于许多领域，如生物医学、化学工程、金融等。

例如，在生物医学领域，可以利用偏最小二乘法对肿瘤等疾病的相关因素进行分析和预测。

三、偏最小二乘法的步骤1. 数据准备首先，需要收集相关的数据，包括自变量和因变量。

确保数据质量，并进行必要的数据预处理。

2. 模型建立在偏最小二乘法中，需要建立自变量与因变量之间的模型。

通过选择合适的模型算法和参数，得到最佳的模型表达。

3. 变量选择与降维在建立模型时，可能会面临自变量过多的问题。

为了简化模型和提高模型的稳定性，可以进行变量选择和降维操作。

4. 模型评估与优化完成模型建立后，需要对模型进行评估与优化。

可以采用交叉验证、拟合度等指标进行评估，并根据评估结果进行相应的调整和优化。

5. 结果解释与应用最后，需要对模型结果进行解释和应用。

可以通过系数分析、相关性分析等方法，理解自变量与因变量之间的关系，并对实际问题进行预测和决策。

四、实例演示1. 数据收集以某企业的销售数据为例，收集相关的自变量（如广告投入、促销活动等）和因变量（如销售额）。

2. 数据预处理对收集到的数据进行预处理，包括数据清洗、数据转换等操作，确保数据的可靠性和一致性。

3. 模型建立选择适当的偏最小二乘法模型算法，建立自变量与因变量之间的关系模型。

4. 变量选择与降维如果自变量较多，可以采用变量选择和降维的方法，减少模型复杂度和提高模型的预测能力。

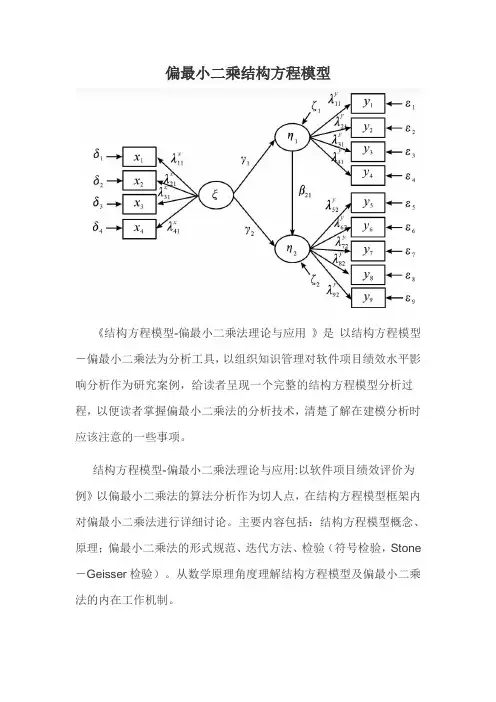
偏最小二乘结构方程模型
《结构方程模型-偏最小二乘法理论与应用》是以结构方程模型－偏最小二乘法为分析工具，以组织知识管理对软件项目绩效水平影响分析作为研究案例，给读者呈现一个完整的结构方程模型分析过程，以便读者掌握偏最小二乘法的分析技术，清楚了解在建模分析时应该注意的一些事项。

结构方程模型-偏最小二乘法理论与应用:以软件项目绩效评价为例》以偏最小二乘法的算法分析作为切人点，在结构方程模型框架内对偏最小二乘法进行详细讨论。

主要内容包括：结构方程模型概念、原理；偏最小二乘法的形式规范、迭代方法、检验（符号检验，Stone －Geisser检验）。

从数学原理角度理解结构方程模型及偏最小二乘法的内在工作机制。

根据偏最小二乘法原理，本书在MATLAB上实现了基于偏最小二乘法的结构方程模型分析软件MS－PLS。

通过假设模型的模拟分析，不仅验证了MS－PLS软件的正确性和有效性，而且从中归纳得到基于两个潜变量的偏最小二乘法数据处理特征。

在顾客满意度应用背景下，本书对偏最小二乘法与层次分析法进行了可比性研究。

不仅通过理论基础与应用背景分析，而且通过多个模型验证了在航空公司顾客满意度模型权重确定上这两种方法具有
可比性。

将人类隐性知识显性化是这两个算法的共同目标，也是算法比较研究的意义所在。

借此，将PLS算法引入群体决策领域并进行了初步探讨。

结构方程估计方法
结构方程模型（SEM）的估计方法主要有三种：协方差分析法、偏最小二乘法和贝叶斯法。

1. 协方差分析法：这种方法认为潜变量间的关系反映在可测变量的协方差关系中，理想的模型产生的协方差结构和真实协方差结构应一致。

因此，这种方法以协方差矩阵的差异作为优化准则。

2. 偏最小二乘法：在考虑潜变量结构的前提下，这种方法认为“最好”的潜变量应该与对应可测变量“最接近”。

其优化准则本质是OLS（最小二乘法）。

3. 贝叶斯法：这种方法对潜变量假定先验，然后用MCMC（马尔科夫链蒙特卡洛）直接对潜变量进行抽样。

当潜变量的样本都有了，结构方程模型也就退化为了一堆回归。

以上内容仅供参考，建议查阅结构方程模型相关书籍获取更多专业信息。

偏最小二乘路径建模（PLS-PM）结构方程一、变量间关系偏最小二乘路径建模（PLS-PM）是一种探索变量间关系的统计方法。

它通过路径图来描述变量之间的因果关系，并使用偏最小二乘回归（PLS）进行模型估计。

PLS-PM适用于变量间存在复杂关系的情境，可以处理多个因变量和自变量，并考虑测量误差和潜在变量的影响。

二、因果关系在PLS-PM中，因果关系是核心概念。

通过路径图，我们可以直观地展示变量之间的因果关系，并根据专业知识或实证数据来构建路径。

在路径图中，箭头表示因果关系，箭头的方向表示因果关系的方向。

通过因果关系，我们可以分析一个变量对另一个变量的影响，以及这种影响是如何传递的。

三、路径图构建构建路径图是PLS-PM的重要步骤。

路径图需要基于理论或实证数据来构建，并遵循一定的原则，如因果关系应该基于理论或实证证据，箭头指向表示因果关系的方向等。

构建路径图时，我们需要确定因变量和自变量，并考虑潜在变量的影响。

路径图可以帮助我们更好地理解变量之间的关系，并为后续的模型估计提供基础。

四、模型估计在PLS-PM中，模型估计使用偏最小二乘回归（PLS）进行。

PLS 是一种广义的线性模型，通过迭代的方式对模型进行拟合，并考虑到测量误差和潜在变量的影响。

在模型估计过程中，我们需要确定合适的模型拟合指标，如R方、Q方等，并对模型的拟合效果进行评估。

五、模型评估模型评估是PLS-PM的重要环节。

我们需要评估模型的拟合效果、预测能力和解释能力。

通过比较模型拟合指标和竞争模型的性能，我们可以判断模型的优劣。

此外，我们还可以使用交叉验证、敏感度分析等方法来评估模型的稳定性。

如果模型拟合效果不理想，我们需要重新审视路径图和模型估计过程，并进行相应的调整。

六、模型应用与拓展模型应用是PLS-PM的目的之一。

我们可以将建立好的模型应用于实际情境中，预测新数据或对未知数据进行解释。

此外，我们还可以将PLS-PM应用于其他相关领域，以探索变量之间的关系。

偏最小二乘结构方程偏最小二乘（Partial Least Squares，简称PLS）是一种常见的结构方程模型方法，用于将多个自变量与一个或多个因变量联系起来，同时考虑自变量之间和因变量之间的相关性。

本文将介绍PLS的原理、步骤和优点，帮助读者更好地了解和使用该方法。

PLS的核心思想是将自变量和因变量的信息映射到几个新的变量（称为潜变量）中，这些变量能够最好地解释自变量和因变量之间的关系。

PLS与传统的最小二乘回归（Linear Regression）方法不同，它能够处理具有多重共线性（Multicollinearity）和高维数（High Dimensionality）的数据集，并且能够发现潜在的非线性关系。

PLS的步骤主要包括以下几个方面：第一步：标准化数据。

将自变量和因变量标准化，使其均值为0，标准差为1，从而消除不同变量之间的量纲差异性。

第二步：选择潜变量数目。

根据样本量和数据结构的特点，确定潜变量的数目，以便更好地表示自变量和因变量之间的关系。

第三步：估计剖面矩阵。

使用PLS算法计算潜变量，估计自变量和因变量之间的相关性，并构建剖面矩阵。

第四步：估计结构方程模型。

使用剖面矩阵和PLS算法，构建能够解释自变量和因变量之间关系的结构方程模型。

PLS方法有以下优点：1. 能够处理多重共线性和高维数的数据集。

2. 能够发现潜在的非线性关系。

3. 能够同时估计自变量和因变量的贡献。

4. 能够将多个自变量结合成一个潜变量，并能够同时处理多个因变量。

总之，PLS是一种优秀的结构方程模型方法，可以帮助研究者更好地探究自变量和因变量之间的关系。

在实际应用中，需要注意选择适当的潜变量数目和确认模型的可靠性，以充分发挥PLS方法的优点。

偏最小二乘法 1.1 基本原理偏最小二乘法（PLS ）是基于因子分析的多变量校正方法，其数学基础为主成分分析。

但它相对于主成分回归（PCR ）更进了一步，两者的区别在于PLS 法将浓度矩阵Y 和相应的量测响应矩阵X 同时进行主成分分解：X=TP+E Y=UQ+F式中T 和U 分别为X 和Y 的得分矩阵，而P 和Q 分别为X 和Y 的载荷矩阵，E 和F 分别为运用偏最小二乘法去拟合矩阵X 和Y 时所引进的误差。

偏最小二乘法和主成分回归很相似，其差别在于用于描述变量Y 中因子的同时也用于描述变量X 。

为了实现这一点，数学中是以矩阵Y 的列去计算矩阵X 的因子。

同时，矩阵Y 的因子则由矩阵X 的列去预测。

分解得到的T 和U 矩阵分别是除去了大部分测量误差的响应和浓度的信息。

偏最小二乘法就是利用各列向量相互正交的特征响应矩阵T 和特征浓度矩阵U 进行回归：U=TB得到回归系数矩阵，又称关联矩阵B ：B=(T T T -1)T TU因此，偏最小二乘法的校正步骤包括对矩阵Y 和矩阵X 的主成分分解以及对关联矩阵B 的计算。

1.2主成分分析主成分分析的中心目的是将数据降维，以排除众多化学信息共存中相互重叠的信息。

他是将原变量进行转换，即把原变量的线性组合成几个新变量。

同时这些新变量要尽可能多的表征原变量的数据结构特征而不丢失信息。

新变量是一组正交的，即互不相关的变量。

这种新变量又称为主成分。

如何寻找主成分，在数学上讲，求数据矩阵的主成分就是求解该矩阵的特征值和特征矢量问题。

下面以多组分混合物的量测光谱来加以说明。

假设有n 个样本包含p 个组分，在m 个波长下测定其光谱数据，根据比尔定律和加和定理有：A n×m =C n×pB p×m如果混合物只有一种组分，则该光谱矢量与纯光谱矢量应该是方向一致，而大小不同。

换句话说，光谱A 表示在由p 个波长构成的p 维变量空间的一组点（n 个），而这一组点一定在一条通过坐标原点的直线上。

结构方程模型的约束最小二乘解与确定性算法1)摘要研究了结构方程模型(SEM)的约束最小二乘解（CLS），从分析SEM的观测方程组入手，发现了这个不定方程组的结构变量与观测变量必须满足的最小二乘关系，在对结构变量有固定模长参数约束的条件下，求出它的一组模长约束最小二乘解（MCLS）。

MCLS 可以作为求解结构方程组的偏最小二乘（PLS）迭代初值。

在求得MCLS以后，在观测方程组中改变模长，使得每个结构变量所对应的与观测变量的路径系数满足配方条件，是更为合理的约束，它可以保证结构变量与所辖的观测变量同质。

尽管观测方程组是不定方程组，但是根据误差平方和最小以及对路径系数的配方约束，使得MCLS求解为合理的确定性算法。

然后再对结构方程组直接求解，也是确定性算法，这就解决了结构方程模型求解的唯一性问题。

关键词：结构方程模型，约束最小二乘解，配方条件，确定性算法MR(2000)主题分类：62H12, 62J05THE CONSTRAINT LEST SQUARE SOLUTION AND DEFINITE ALGORITHM IN STRUCTURALEQUATION MODELAbstractthe constraint least square solution in structural equation model (SEM) has been studied. By analysis of the observation equations in SEM, the least square relationship between each structural variable and its observation variables is find. Adding a constraint with modular length to the structural variables, the modular constraint least square solution (MCLS) for observation equations is obtained. This MCLS can be used as the initial value in PLS iterative process to improve its convergence. Furthermore it is reasonable to change the modular lengths of observation variables so that the path coefficients between the structure variable and its observation variables satisfy prescription conditions. This prescription conditions can guarantee the homogeneity of a structure variable with its observation variables. This algorithm is a determinate algorithm with the least square of errors and prescription conditions for the path coefficients, although the SEM is an indeterminate equations.Keywords:Structural equation models, Constraint least square solution, Prescription conditions, Definite algorithm.2000 Mathematics Subject Classification：62H12, 62J05 ——————————————————————————————1) 国家自然科学基金资助项目（30570611, 60773210）.1. 结构方程模型结构方程模型（SEM）是应用统计领域近来发展迅速的一个分支，广泛应用于心理学、社会学等领域，尤其是顾客满意指数（CSI）分析模型([1][2])。