数列单调性Microsoft Word 文档

高中数学必修五-数列突破点（二）数列的单调性
基础回顾
考点链接
考点一：利用数列的单调性研究最值问题
方法技巧
实战演练
考点二：利用数列的单调性求参数的取值范围
方法技巧
已知数列的单调性求参数取值范围的两种方法
(1)利用数列的单调性构建不等式，然后将其转化为不等式的恒成立问题进行解决，也可通过分离参数将其转化为最值问题处理．
(2)利用数列与函数之间的特殊关系，将数列的单调性转化为相应函数的单调性，利用函数的性质求解参数的取值范围，但要注意数列通项中n的取值范围．
实战演练
全国卷5年真题集中演练。

专题1 数列的单调性微点5 数列单调性的判断方法（五）——递推法12n n nn x x x ++++；112n b ⎛⎫− ⎪⎭⎝，若在k b 与m b m ++−n a (,m n ∈N参考答案：()1122941n a a −−⎛⎫== ⎪⎝⎭⋅⋅+由10a >可得若21a a >，即，解得10a <<即当10a <<，此时数列k由③知∑是递增数列．21c c >>>>，11024， 是单调递增；当10n ≥时3n n++，由此利用错位相减法能求出）问得到m =)N n *∈时，12212333n n nn nnx x x +++++=+++，① 1133n n n n+−+++，② 211111()1111133(11333332313n n n n n n n ++⎡⎤−⎢⎥⎣⎦+++−=−=−−． m ，n ，使T 11m +=+112n ⎫⎛⎫−⎪ ⎪⎭⎝⎭从而求得n t 的最大值，项,然后对{2k k +++=，当9k =时的情况即可求得是等比数列，且各项均为正数，所以112n ⎫⎛⎫−⎪ ⎪⎭⎝⎭11142n ⎫⎛⎫−⎪ ⎪⎭⎝⎭112n ⎫⎛⎫⎛−⎪⎪⎭⎝⎭⎝224848n n n +=+233λ<<，2k k +++=9922−=+， 2019=m b ++，设m b m ++−212222m mm b m ++=++++， 22222m m +++，则2311212222m m T −=++++21111111112222222m m m m m m T ++=+++−=−−=2222222m m mm mb m m m ++++−=+−−=−，22mm+−，N *m ∈， 2122222m m ++++=−−+77922S =−21n b −+++112n ⎛ −+−⎝121n +单调递减，23=−，显然b,a ()3,⎫+∞⎪⎪⎭②，②－①即得()3,⎫+∞⎪⎪⎭考查数列的单调性的判定和最值的求法，意在考查学生对这些知识的理解掌握水平(8n n b ++=256125125()2()()940n n b b b b b b b b b b n n ++−++=+++−++++=−+9,15940,6n n n n +≤≤+≥；）由题知12111(1)(1)(1)222n nA a a a =−−−， 21n +，则111()21(1)(1)(1)22ng n n a a =+−−−， (21)2(22)2n n n n ++3(1)g =都成立，则3a >.。

数列的单调性(1)一个数列{a n }，如果从第2项起，每一项都大于它前面的一项，即a n ＋1>a n ，那么这个数列叫作递增数列．(2)一个数列，如果从第2项起，每一项都小于它前面的一项，即a n ＋1<a n ，那么这个数列叫作递减数列．(3)一个数列，如果从第2项起，有些项大于它的前一项，有些项小于它的前一项，这样的数列叫作摆动数列．(4)如果数列{a n }的各项都相等，那么这个数列叫作常数列．[典例] 已知数列{a n }的通项公式为a n ＝22n －9，画出它的图像，并判断增减性． [解] 图像如图所示，该数列在{1,2,3,4}上是递减的，在{5,6，…}上也是递减的．利用数列的图像判断数列的增减性数列的图像可直观地反映数列各项的变化趋势，从而可判断数列的增减性．[典例] 已知数列{a n }的通项公式a n ＝nn 2＋1，试判断该数列的增减性． [解] a n ＋1－a n ＝n ＋1(n ＋1)2＋1－n n 2＋1 ＝1－n 2－n [(n ＋1)2＋1](n 2＋1). 因为n ∈N ＋，所以1－n 2－n <0，所以a n ＋1－a n <0，即a n ＋1<a n .故该数列为递减数列．应用函数单调性判断数列增减性的方法(1)作差法，将a n ＋1－a n 与0进行比较；(2)作商法，将a n ＋1a n与1进行比较(在作商时，要注意a n <0还是 a n >0)． 1．已知数列{a n }的通项公式a n ＝(n ＋1)⎝⎛⎭⎫1011n (n ∈N ＋)，试问数列{a n }有没有最大项？若有，求最大项和最大项的项数；若没有，说明理由．解：法一：假设数列{a n }中存在最大项．∵a n ＋1－a n ＝(n ＋2)⎝⎛⎭⎫1011n ＋1－(n ＋1)⎝⎛⎭⎫1011n ＝⎝⎛⎭⎫1011n ·9－n 11，当n <9时，a n ＋1－a n >0，即a n ＋1>a n ；当n ＝9时，a n ＋1－a n ＝0，即a n ＋1＝a n ；当n >9时，a n ＋1－a n <0，即a n ＋1<a n .故a 1<a 2<a 3<…<a 9＝a 10>a 11>a 12…，所以数列中有最大项，最大项为第9、10项，且a 9＝a 10＝1010119. 法二：假设数列{a n }中有最大项，并设第k 项为最大项，则⎩⎪⎨⎪⎧ a k ≥a k －1，a k ≥a k ＋1对任意的k ∈N ＋且k ≥2都成立．即⎩⎨⎧ (k ＋1)⎝⎛⎭⎫1011k ≥k ⎝⎛⎭⎫1011k －1，(k ＋1)⎝⎛⎭⎫1011k ≥(k ＋2)⎝⎛⎭⎫1011k ＋1，∴⎩⎨⎧1011(k ＋1)≥k ，k ＋1≥1011(k ＋2)，解得9≤k ≤10.又k ∈N ＋， ∴数列{a n }中存在最大项是第9项和第10项，且a 9＝a 10＝1010119. 题点二：由数列的单调性求参数问题2．已设数列{a n }的通项公式为：a n ＝n 2＋kn (n ∈N ＋)，若数列{a n }是单调递增数列，求实数k 的取值范围 .解：法一：∵数列{a n }是单调递增数列，∴a n ＋1－a n >0(n ∈N ＋)恒成立．又∵a n ＝n 2＋kn (n ∈N ＋)，∴(n ＋1)2＋k (n ＋1)－(n 2＋kn )>0恒成立．即2n ＋1＋k >0.∴k >－(2n ＋1)(n ∈N ＋)恒成立．而n ∈N ＋时，－(2n ＋1)的最大值为－3(n ＝1时)，∴k >－3.即k 的取值范围为(－3，＋∞)．法二：结合二次函数y ＝x 2＋kx 的图像，要使{a n }是递增数列，只要a 1<a 2即可， 即1＋k <4＋2k ，得k >－3，所以k 的取值范围为(－3，＋∞)．题点三：数列与函数的综合应用3．已知函数f (x )＝2x －2－x ，数列{a n }满足f (log 2a n )＝－2n .(1)求数列{a n }的通项公式；(2)证明数列{a n }是递减数列．解：(1)∵f (x )＝2x －2－x ，f (log 2a n )＝－2n ，∴2log 2a n －2－log 2a n ＝－2n ，∴a n －1a n ＝－2n ， ∴a 2n ＋2na n －1＝0，解得a n ＝－n ±n 2＋1. ∵a n >0，∴a n ＝n 2＋1－n ，n ∈N ＋.(2)证明：a n ＋1a n ＝(n ＋1)2＋1－(n ＋1)n 2＋1－n＝n 2＋1＋n(n ＋1)2＋1＋(n ＋1)<1. ∵a n >0，∴a n ＋1<a n ，∴数列{a n }是递减数列．函数思想方法在数列问题中的应用(1)数列的单调性是通过比较{a n }中任意相邻两项a n 与a n ＋1的大小来判定的．某些数列的最大项或最小项问题，可以通过研究数列的单调性加以解决．(2)数列是特殊函数，一定要注意其定义域是N ＋(或它的有限子集)．n n (1)n 为何值时，a n 有最小值？并求出最小值；(2)数列{a n }有没有最大项？若有，求出最大项，若没有说明理由．解：(1)因为a n ＝n 2－21n ＋20＝⎝⎛⎭⎫n －2122－3614，可知对称轴方程为n ＝212＝10.5.又因n ∈N ＋，故n ＝10或n ＝11时，a n 有最小值，其最小值为102－21×10＋20＝－90.(2)由(1)知，对于数列{a n }有：a 1>a 2>…>a 10＝a 11<a 12<…，故数列{a n }没有最大项．。

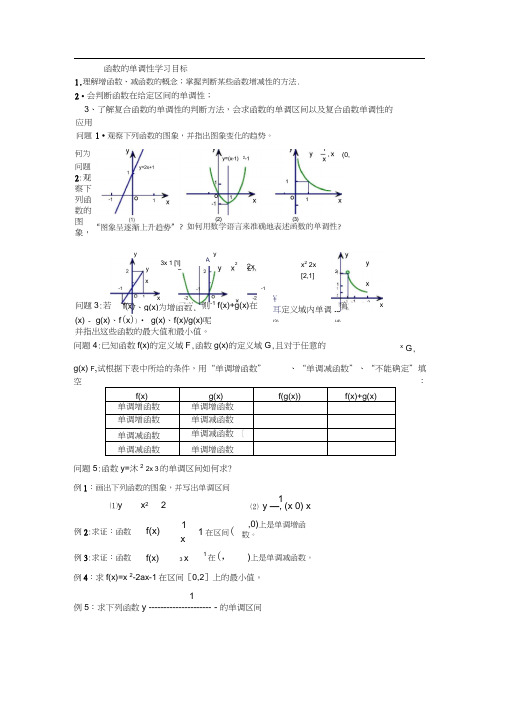
函数的单调性学习目标1.理解增函数、减函数的概念；掌握判断某些函数增减性的方法. 2•会判断函数在给定区间的单调性；3、了解复合函数的单调性的判断方法，会求函数的单调区间以及复合函数单调性的何为 问题2:观察下列函数的图象，并指出这些函数的最大值和最小值。

问题4:已知函数f(x)的定义域F ,函数g(x)的定义域G ,且对于任意的 g(x) F ,试根据下表中所给的条件，用“单调增函数” 、“单调减函数”、“不能确定”填空：f(x) g(x) f(g(x))f(x)+g(x)单调增函数 单调增函数单调增函数 单调减函数单调减函数单调减函数 ［单调减函数单调增函数问题5:函数y=沐2 2x 3的单调区间如何求?例1：画出下列函数的图象，并写出单调区间⑴y例2:求证：函数 x 221⑵ y —, (x 0) x,0)上是单调增函数。

f(x)1x1在区间( 例3:求证：函数 f(x)3x1在(，)上是单调减函数。

例4：求f(x)=x 2-2ax-1在区间［0,2］上的最小值。

1例5：求下列函数y --------------------- - 的单调区间应用问题 1•观察下列函数的图象，并指出图象变化的趋势。

x-、g(x)为增函数, 问题3:若(x) - g(x)、f (x ))• g(x)、f(x)/g(x)呢¥耳定义域内单调to(3)(4)xG ,(0,yy x22x-1则-1 f(x)+g(x)在yA3x 1 ['l]x2x 2 2x [2,1]叩3 2x x2例6:已知二次函数f(x)=x 2-(a-1)x+5在区间2, 上是增函数，求a的取值范围检测：1.函数f(x)= -x2+2ax+1-a在区间［0,1］上有最大值2,求实数a的值1.函数f(x)=ax2+2ax+1在［-3,2］上有最大值4,求a的值。

3.求函数y . x22x 3的单调区间4•已知是定义在1,1上的增函数，且f x 1 f x2 1 ,求x的取值范围。

10．【2012，安徽理21】数列{}n x 满足：2*110,()n n n x x x x c n N +==-++∈（I ）证明：数列{}n x 是单调递减数列的充分必要条件是0c < （II ）求c 的取值范围，使数列{}n x 是单调递增数列．【答案】（I ）详见解析；（II ）当104c <≤时，数列{}n x 是单调递增数列．【解析】（I ）必要条件：当0c <时，21n n n n x x x c x +=-++<⇒数列{}n x 是单调递减数列．充分条件．必要条件：数列{}n x 是单调递减数列22121110x x x x c c x ⇒>=-++⇔<=，得：数列{}n x 是单调递减数列的充分必要条件是0c <． （II ）由（I ）得：0C ≥．①当0c =时，10n a a ==，不合题意；②当0c >时，22132,201x c x x c c x c c =>=-+>=⇔<<2211010n n n n n x x c x x c x x +-=->⇔<<⇔=≤< 22211111()()()(1)n n n n n n n n n n x x x x x x x x x x ++++++-=--+-=--+-当14c ≤时，1211102n n n n n x x x x x +++<≤⇒+-<⇔-与1n nx x +-同号，由212100n n n n x x c x x x x ++-=>⇒->⇔>21lim lim()lim n n n n n n n x x x c x +→∞→∞→∞=-++⇔= 当14c >时，存在N ，使121112N N N N N x x x x x +++>⇒+>⇒-与1N N x x +-异号，与数列{}n x 是单调递减数列矛盾，得：当104c <≤时，数列{}n x 是单调递增数列．12．【2009，安徽理21】首项为正数的数列{n a }满足*21),3(41N n a a n n ∈+=+．(Ⅰ)证明：若1a 为奇数，则对一切2≥n ，n a 都是奇数； (Ⅱ)若对一切*N n ∈，都有n n a a >+1，求1a 的取值范围． 【答案】(Ⅰ) 详见试题解析；(Ⅱ) 101a <<或13a >．．【解析】：（I ）已知1a 是奇数，假设21k a m =-是奇数，其中m 为正整数，则由递推关系得213(1)14k k a a m m ++==-+是奇数．根据数学归纳法，对任何n N +∈，n a 都是奇数．（II ）（方法一）由11(1)(3)4n n n n a a a a +-=--知，1n n a a +>当且仅当1n a <或3n a >．另一方面，若01,k a <<则113014k a ++<<=；若3k a >，则21333.4k a ++>= 根据数学归纳法，1101,01,;33,.n n a a n N a a n N ++<<⇔<<∀∈>⇔>∀∈ 综合所述，对一切n N +∈都有1n n a a +>的充要条件是101a <<或13a >．（方法二）由21213,4a a a +=>得211430,a a -+>于是101a <<或13a >．22111133()(),444n n n n n n n n a a a a a a a a ---++++--=-=因为21130,,4n n a a a ++>=所以所有的n a 均大于0，因此1n n a a +-与1n n a a --同号． 根据数学归纳法，n N +∀∈，1n n a a +-与21a a -同号．因此，对一切n N +∈都有1n n a a +>的充要条件是101a <<或13a >．21.（本题满分13分）解析：（Ⅰ）若2-=λ，则nn n a a a 221-=+， 由21122000n n n n n n n na a a a a a a a ++->⇔->⇔->⇔>，得2>n a 或02<<-n a ，所以只需21>a 或021<<-a .所以实数a的取值范围为(∪)+∞. …………6分 (Ⅱ) 2≥n a 对任意*∈N n 成立的充要条件为4-≥λ.必要性：由22≥a ，解出4-≥λ；（另解：假设221≥+=+nn n a a a λ，得n n a a 222+-≥λ，令21)21(2)(2+--=n a n f ， 2≥n a ，可得：4)(max -=n f ，即有4-≥λ.） …………8分 充分性：数学归纳法证明：4-≥λ时，对一切*∈N n ，2≥n a 成立. 证明：（1）显然1=n 时，结论成立；（2）假设)1(≥=k k n 时结论成立，即2≥k a ，当1+=k n 时，kk k a a a λ+=+21.考察函数xx x f λ+=2)(，),2[+∞∈x ，① 若 04≤≤-λ，由02)('2>-=xx f λ，知)(x f 在区间),2[+∞上单调递增.由假设得kk k a a a λ+=+2124λ+≥2≥.② 若0>λ，对),2[+∞∈x 总有242)(>>+=xx x f λ，则由假设得221>+=+kk k a a a λ.所以，1+=k n 时，结论成立，综上可知：当4-≥λ时，对一切*∈N n ，2≥n a 成立.故2≥n a 对任意*∈N n 成立的充要条件是4-≥λ.13．【2008，安徽理21】设数列{}n a 满足3*010,1,,n n a a ca c c N c +==+-∈其中为实数．（Ⅰ）证明：[0,1]n a ∈对任意*n N ∈成立的充分必要条件是[0,1]c ∈；（Ⅱ）设103c <<，证明：1*1(3),n n a c n N -≥-∈;（Ⅲ）设103c <<，证明：222*1221,13n a a a n n N c++>+-∈-． 【命题立意】本题主要考查等比数列的求和、数学归纳法、不等式的性质，综合运送知识分析问题和解决问题的能力．本小题满分13分．【答案】（I ）详见解析；（II ）详见解析；（Ⅲ）详见解析． 【解析】（Ⅰ）必要性：∵120,1a a c ==-，又∵2[0,1]a ∈，∴011c ≤-≤，即[]0,1c ∈．．充分性：设[]0,1c ∈，对任意*n N ∈用数学归纳法证明[]0,1n a ∈．当1n =时，[]100,1a =∈．假设当n k =时，[]0,1(1)k a k ∈≥，则31111k n a ca c c c +=+-≤+-=，且31110k n a ca c c +=+-≥-≥，[]10,1k a +∈．由数学归纳法知，[]0,1n a ∈对任意*n N ∈成立． (Ⅱ) 设103c <<，当1n =时，10a =，结论成立；当2n ≥时，∵311n n a ca c -=+-，∴3211111(1)(1)(1)n n n n n a c a c a a a -----=-=-++．∵103c <<，由（Ⅰ）知[]10,1n a -∈，∴21113n n a a --++≤且10n a -≥，∴21112113(1)(3)(1)(3)(1)(3)n n n n n a c a c a c a c -----≤-≤-≤≤-=，∴()113,*n n a c n N -≥-∈．(Ⅲ)设103c <<，当1n =时，2120213a c=>--，结论成立；当2n ≥时，由(Ⅱ)知()1130n n a c -≥->，∴21212(1)1[1(3)]12(3)(3)12(3)n n n n n a c c c c ---->-=-+>-， ∴222222112212[(3)(3)(3)]n n n a a a a a n c c c -+++=++>--+++2[1(3)]2111313n c n n c c-=+->+---．。

（师) 研究过数列的有界性、周期性——周期数列都是有界的-—这些都是数列的整体性质，我们再来看看数列的局部性质，比较着函数…（生) 单调性。

(师) 对，单调性.依然是两个问题:什么是数列的单调性？怎样去判断数列的单调性？（生）（沉默）（师）不妨举些具体的例子。

(板书）（1) 263,163,126，115，…(2） x_n=2n+3/n（师）你也可以用自己的例子来说明。

(生) 第一个是递减。

(师）为什么是递减?（生）前面的数大，后面的数小。

(师) 前项比后项大,后项比前项小。

（生）对。

（师）但是我们的表述不一样，有区别？（生) (沉默）(师）以及数列中的“…”怎么办？(生A) 也应该比前项小。

(生B) 不一定。

（师）为什么说“不一定”呢？（生B) 因为没有全写出来.（师）如果是一个无穷数列,当然不能全写出来。

(生) (沉默)（师) 第二个数列？或者你自己的例子？（生) （沉默)（师）能不能写出几项来看看？(生) （沉默）（生) 看作函数。

(师) 数列就是函数，是特殊的函数.（生）（沉默）（师）你是想看作怎样的函数？（生) 连续的函数。

(师）什么是“连续的函数”？(生）（沉默）(师) 数列是“不连续的函数”？（生）嗯.（师）所以数列是特殊的函数，我们又找到了数列一个特殊的地方?还是说，与前面讨论数列的有界性差不多？（生）（沉默）（师）我们讨论数列是不是有界,而不讨论它的值域，是什么原因?(生) 定义域。

（师) 数列的特殊似乎总可以归结到它的定义域特殊上去吧。

（生) （沉默）（师）回到刚才的问题上来,你是想看作什么样的函数呢？(生) 定义域大于0.(师）定义域(0,+∞）是吧。

（板书）f（n)=2n+3/n, n∈（0，+∞)(师）你打算怎么用这个函数来说这个数列的单调性呢？(生）对勾函数。

(师）说它是“对勾函数”，你要说明什么？(生) 单调区间。

（师）是什么？(生) 用均值。

(开始算）（师) 你在算什么?(生) 最值。

数列的单调性以及恒成立的问题一、数列的单调性（一）数列的单调性与函数的单调性的区别【例题1】已知()2*n a n n n N λ=+∈是单调递增数列，则λ的取值范围是 【例题2】给定函数y =f (x )的图像在下列图中，并且对任意a 1()0,1∈，由关系a n+1=f (a n )得到a n+1>a n (n *N ∈)，则该函数的图像是（二）a n =f (n )的单调性【例题3】已知{a n }的通项a n =(n 2-1)c n +c n-1(n *N ∈)，其中实数c ≠0，若对一切k *N ∈有a 2k >a 2k-1，求c 的取值范围.【例题4】已知a 1=a ，a n+1=S n +3n，若a n+1≥a n (n *N ∈)，求a 的取值范围.【变式训练】设数列{a n }满足a 1=2，11n n na a a +=+(n *N ∈). （I ）证明：21n a n >+对一切正整数n 成立；（II ）令n b =n *N ∈)，试判断b n 和b n+1的大小，并说明理由.【例题5】已知数列{a n }中，a 1=2，对于任意的p ，q *N ∈，有a p+q =a p +a q . （I ）求数列{a n }的通项公式； （II ）若数列{b n }满足()112121212121n nn n b b b a -=-++-+++，求数列{b n }的通项公式； （III ）若3nn n c b λ=+，是否存在实数λ，使得当n *N ∈时，c n+1>c n 恒成立？【变式训练】设数列{a n }的各项都是正数，且对任意的n *N ∈，都有333212n n a a a S +++=，其中，S n 为数列{a n }的前n 项和.（I ）求证：2112n n n a S a ++=+；（II ）求数列{a n }的通项公式； （III ）设()1312n n a n n b λ-=+-⋅⋅为非零整数，n *N ∈，试确定λ的值，使得对任意的n *N ∈，都有b n+1>b n 成立.（三）a n+1=f (a n )的单调性【知识点】对于迭代数列a n+1=f (a n )，如果有y=f (x )是非递减函数，那么：①若a 1<a 2，则数列{a n }递增；②若a 1=a 2，那么数列{a n }是常数列；③若a 1>a 2，则数列{a n }递减. 特别地，对于迭代数列a n+1=f (a n )，若f (x )是二次函数，则数列单调递增的充要条件是a 1<a 2<a 3，且对于任意的n ≥2，n *N ∈，在[a 2，a n ]上，函数f (x )为单调递增函数.【例题6】已知数列{}n a 满足1a =12且1n a +=n a -2n a （n ∈*N ） （1）证明：112nn a a +≤≤（n ∈*N ）； （2）设数列{}2n a 的前n 项和为n S ，证明112(2)2(1)n S n n n ≤≤++（n ∈*N ）.【变式训练】在数列{}n a 中，13a =，2110n n n n a a a a λμ++++=，()n N +∈（1）若0,2,λμ==-求数列{}n a 的通项公式； （2）若()0001,2,1,k N k k λμ+=∈≥=-证明：010*********k a k k ++<<+++【变式训练】数列{x n }满足：x 1=0，x n+1= -x n 2+x n +c （n *N ∈） （I ）证明：数列{x n }单调递减的充分必要条件是c <0； （II ）求c 的取值范围，使数列{x n }是单调递增数列.二、数列的单调性应用 （一）数列的最值问题【例题7】数列{a n }和数列{b n }满足：①a 1=a<0，b 1=b>0；②当k ≥2时，若a k -1+b k -1≥0，则a k =a k -1，112k k k ab b --+=；若a k -1+b k -1<0，则111,2k k k k k a b a b b ---+==. （1）若a= -1，b=1，求a 2，b 2，a 3，b 3的值；（2）设S n =(b 1 –a 1)+(b 2 –a 2)+…+(b n -a n )，求S n (用a ，b 表示)；（3）若存在n *N ∈，对任意的正整数k ，当2≤k ≤n 时，恒有b k -1>b k 成立，求n 的最大值（用a ，b 表示）.【变式训练】在数列{a n }中，a 1=3，a n b n =a n +2，n =2，3，4，… (I)求a 2，a 3，判断数列{a n }的单调性并证明； (II)求证|a n -2|<1124n a --(n =2，3，4，…)； (III)是否存在常数M ，对任意n ≥2，有b 2b 3…b n ≤M ？若存在，求出M 的值；若不存在，说明理由.（二）数列中的恒成立问题【例题8】如图，在平面直角坐标系xOy 中，设a 1=2，有一组圆心在x 轴的正半轴上的圆A n （n *N ∈）与x 轴的交点分别为A 0(1，0)和A n+1(a n +1，0)，过圆心A n 作x 轴的垂线l n 在第一象限与圆A n 交于点B n (a n ，b n ). （1）求数列{a n }的通项公式；（2）设曲边形A n+1B n B n+1(阴影部分所示)的面积为S n ，若对于任意n *N ∈，12111nm S S S +++≤恒成立，试求实数m 的取值范围.【变式训练】已知数列{}n a 与{}n b 满足()112n n n n a a b b ++-=-，n *∈N .（1）若35n b n =+，且11a =，求数列{}n a 的通项公式；（2）设{}n a 的第0n 项是最大项，即0n n a a >（n *∈N ），求证：数列{}n b 的第0n 项是最大项；（3）设10a λ=<，n n b λ=（n *∈N ），求λ的取值范围，使得{}n a 有最大值M 与最小值m ，且()2,2mM∈-.【课时作业】1、设数列{}n a 的前n 项和12n n S a a =-，且123,1,a a a +成等差数列. （1）求数列{}n a 的通项公式； （2）记数列1{}n a 的前n 项和n T ，求得1|1|1000n T -<成立的n 的最小值.2、设数列{a n }的前n 项和为S n ，已知a 1=a （a ≠3），a n+1=S n +3n，n *N ∈. （I ）设b n =S n -3n，求证：数列{b n }是等比数列，并写出{b n }的通项公式； （II ）若数列{a n }是单调递增数列，求a 的取值范围.3、设数列{a n }的前n 项和为S n ，()24*,n n S a n n N R λλ=+-∈∈，且数列|a n -1|为等比数列.（I ）求实数λ的值，并写出数列{a n }的通项公式； （II ）（i ）判断数列111n n a a ⎧⎫-⎨⎬-⎩⎭（n *N ∈）的单调性；（ii ）设()11n n nb a --=，数列{b n }的前n 项和为T n ，求证：229n T <.4、已知数列{a n }，{b n }中，a 1=1，b n =221111nn n a a a ++⎛⎫-⋅ ⎪⎝⎭，n *N ∈，数列{b n }的前n 项和为S n .（I ）若a n =2n -1，求S n ；（II ）是否存在等比数列{a n }，使得b n+2=S n 对于任意的n *N ∈恒成立？若存在，求出所有满足条件的数列{a n }的通项公式；若不存在，请说明理由. （III ）若{a n }是单调递增数列，求证：S n <2.5、已知数列{a n }的前n 项和为S n ，其中，a 1=1，且1nn nS a a λ+=(n *N ∈). （I ）求常数λ的值，并写出{a n }的通项公式； （II ）记3nn n a b =，数列{b n }的前n 项和为T n ，求最小的正整数k ，使得对任意的n ≥k ，都有3144n T n-<成立.6、数列{a n }，a n ≥0，a 1=0，a n+12+a n+1-1=a n 2（n *N ∈），求证：当n *N ∈时，a n <a n+1.7、【变式训练】设a 1=1，11n a +=（n *N ∈），问：是否存在实数c ，使得a 2n <c <a 2n+1对所有的n *N ∈成立？证明你的结论.8、首项为正数的数列a n 满足：a n+1=()2134n a +. n *N ∈ (I)证明：若a 1为奇数，则对于任意的n ≥2，a n 为奇数； (II)若对于任意的n *N ∈，都有a n+1≥a n ，求a 1的取值范围.。