上海市徐汇区2020-2020年八年级上期末数学试卷含答案解析

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图所示，l是四边形ABCD的对称轴，AD∥BC，现给出下列结论：①AB//CD；②AB=BC；③AB⊥BC；④AO=OC．其中正确的结论有（）A．1个B．2个C．3个D．4个【答案】C【分析】根据轴对称图形的性质，四边形ABCD沿直线l对折能够完全重合，再根据两直线平行，内错角相等可得∠CAD=∠ACB=∠BAC=∠ACD，然后根据内错角相等，两直线平行即可判定AB∥CD，根据等角对等边可得AB=BC，然后判定出四边形ABCD是菱形，根据菱形的对角线互相垂直平分即可判定AO=OC；只有四边形ABCD是正方形时，AB⊥BC才成立．【详解】∵l是四边形ABCD的对称轴，∴∠CAD=∠BAC，∠ACD=∠ACB，∵AD∥BC，∴∠CAD=∠ACB，∴∠CAD=∠ACB=∠BAC=∠ACD，∴AB∥CD，AB=BC，故①②正确；又∵l是四边形ABCD的对称轴，∴AB=AD，BC=CD，∴AB=BC=CD=AD，∴四边形ABCD是菱形，∴AO=OC，故④正确，∵菱形ABCD不一定是正方形，∴AB⊥BC不成立，故③错误，综上所述，正确的结论有①②④共3个．故选：C．2．以下列各组线段为边,能构成直角三角形的是()A．8cm,9cm,10cm B263cmC ．1cm,2cm,3cmD ．6cm,7cm,8cm 【答案】C 【解析】根据勾股定理的逆定理对四组数据进行逐一判断即可．【详解】A ．∵82+92≠102，∴不能构成直角三角形； B ．∵222(2)(3)(6)+≠，∴不能构成直角三角形；C ．∵2221(3)=2+，∴能构成直角三角形；D ．∵62+72≠82，∴不能构成直角三角形．故选C ．【点睛】本题考查了用勾股定理的逆定理判断三角形的形状，即只要三角形的三边满足a 2+b 2=c 2，则此三角形是直角三角形．3．若代数式1x +有意义，则x 必须满足条件（ ）A ．x ≥﹣1B ．x ≠﹣1C ．x ≥1D ．x ≤﹣1【答案】A【分析】根据二次根式中的被开方数必须是非负数列出不等式，解不等式即可．【详解】由题意得，x+1≥0，解得，x≥-1，故选A ．【点睛】本题考查了二次根式有意义的条件，掌握二次根式中的被开方数必须是非负数是解题的关键． 4．《九章算术》中有一道“盈不足术”问题，原文为：今有人共买物，人出八，盈三；人出七，不足四，问人数，物价各几何?设该物品的价格是x 钱，共同购买该物品的有y 人，则根据题意，列出的方程组是（ ） A ．83{74y x y x -=-= B ．83{74y x y y -=-= C ．83{74y x y x -=--=-D ．83{74y x y x -=-=- 【答案】D 【分析】设该物品的价格是x 钱，共同购买该物品的有y 人，由“每人出8钱，则多3钱；每人出7钱，则差4钱”，即可得出关于x ，y 的二元一次方程组，此题得解．【详解】解：根据题意可知，8374y x y x -=⎧⎨-=-⎩ 故答案为：D.此题考查由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键． 5．有五名射击运动员，教练为了分析他们成绩的波动程度，应选择下列统计量中的（ ）A ．方差B ．中位数C ．众数D ．平均数 【答案】A【解析】试题分析：方差是用来衡量一组数据波动大小的量，体现数据的稳定性，集中程度；方差越大，即波动越大，数据越不稳定；反之，方差越小，数据越稳定．故教练要分析射击运动员成绩的波动程度，只需要知道训练成绩的方差即可．故选A.考点：1、计算器-平均数，2、中位数，3、众数，4、方差6．下列代数式中，属于分式的是（ ）A ．5xB ．3xy C ．3x D 【答案】C【分析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式，从而得出答案．【详解】根据分式的定义A ．是整式，答案错误；B ．是整式，答案错误；C ．是分式，答案正确；D ．是根式，答案错误；故选C ．【点睛】本题考查了分式的定义，在解题时要注意分式是形式定义，只要是分母中含有未知数的式子即为分式． 7．下列运算正确的是( )A ．a 2·a 3＝a 6B ．(－a 2)3＝－a 5C ．a 10÷a 9＝a(a≠0)D ．(－bc)4÷(－bc)2＝－b 2c 2 【答案】C【分析】根据同底数幂的乘法、除法、积的乘方和幂的乘方法则进行计算即可．【详解】解：A 、a 2•a 3＝a 5，故A 错误；B 、（﹣a 2）3＝﹣a 6，故B 错误；C 、a 10÷a 9＝a （a ≠0），故C 正确；D 、（﹣bc ）4÷（﹣bc ）2＝b 2c 2，故D 错误；故选：C ．本题考查了同底数幂的乘法、除法、积的乘方和幂的乘方，掌握运算法则是解题的关键．8．在平面直角坐标系中，点A(2,3)与点B 关于y 轴对称，则点B 的坐标为( )A ．(－2,3)B ．(－2, －3)C ．(2, －3)D ．(－3, －2)【答案】A【解析】根据关于y 轴对称的点的横坐标互为相反数，纵坐标不变进行求解即可.【详解】∵点A （2，3）与点B 关于y 轴对称，∴点B 的坐标为（-2，3），故选A.【点睛】本题考查了关于y 轴对称的点的坐标特征，熟练掌握坐标的变化规律是解题的关键.9．如图，在ABC ∆中，4AC =，BC 边上的垂直平分线DE 分别交BC 、AB 于点D 、E ，若AEC ∆的周长是11，则直线DE 上任意一点到A 、C 距离和最小为（ ）A ．28B ．18C ．10D ．7【答案】D 【分析】根据垂直平分线的性质和已知三角形的周长进行计算即可求得结果．【详解】解：∵DE 是BC 的中垂线，∴BE=EC ，则AB=EB+AE=CE+EA ，又∵△ACE 的周长为11，故AB=11−4=1，直线DE 上任意一点到A 、C 距离和最小为1．故选：D ．【点睛】本题考查的是轴对称—最短路线问题，线段垂直平分线的性质（垂直平分线上任意一点到线段两端点的距离相等）有关知识，难度简单．10．如图，已知点A 和直线MN ，过点A 用尺规作图画出直线MN 的垂线，下列画法中错误的是（ ） A ． B ．C．D．【答案】A【分析】根据经过直线外一点作已知直线的方法即可判断．【详解】解：已知点A和直线MN，过点A用尺规作图画出直线MN的垂线，画法正确的是B、C、D选项，不符合题意．A选项错误，符合题意；故选：A．【点睛】本题考查了作图-基本作图，解决本题的关键是掌握经过一点作已知直线的垂线的方法．二、填空题11．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3EC，其中正确的结论是_____（填序号）．【答案】①②③④【分析】根据平行线的性质结合三线合一的性质证明△ABC为等腰三角形，即可得到BD=CD，AD⊥BC，故②③正确；通过△CDE≌△DBF即可得到DE=DF，CE=BF，故①④正确．【详解】∵BC平分∠ABF，∴∠FBC=∠ABC，∵BF∥AC，∴∠FBC=∠ACB，∴∠ACB=∠ABC=∠CBF，∴AC= AB，∴△ABC为等腰三角形，∵AD是△ABC的角平分线，∴DB=DC，故②正确；AD⊥BC，故③正确；在△CDE与△DBF中，ACB CBF CD BDEDC BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴Rt △CDE ≌Rt △BDF （ASA ），∴DE=DF ，故①正确；CE= BF ，∵AE =2BF ，∴AE =2CE ，AC= AE+CE=2CE+CE=3CE ，故④正确；综上，①②③④均正确；故答案为：①②③④．【点睛】本题考查了等腰三角形的判定和性质，全等三角形的判定和性质，平行线的性质，掌握全等三角形的判定和性质是解题的关键．12．若8m a =，2n a =，,m n 为正整数，则2m n a +=___________．【答案】1【分析】根据同底数幂的乘法及幂的乘方的逆运算即可解答．【详解】解：222()m n m n m n a a a a a +=⋅=⋅∵8m a =，2n a =∴22()8232m n a a ⋅=⨯=，故答案为：1．【点睛】本题考查了同底数幂的乘法及幂的乘方的逆运算，解题的关键是熟练掌握同底数幂的乘法及幂的乘方的逆运算．13．三个全等三角形按如图的形式摆放，则123∠+∠+∠=_______________度．【答案】180°【分析】如图所示，利用平角的定义结合三角形内角和性质以及全等三角形性质得出∠4+∠9+∠6=180°，∠5+∠7+∠8=180°，然后进一步求解即可.【详解】如图所示，由图形可得：∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=1803︒⨯=540°，∵三个三角形全等，∴∠4+∠9+∠6=180°，∵∠5+∠7+∠8=180°，∴123∠+∠+∠=540°− 180°− 180°=180°，故答案为：180°.【点睛】本题主要考查了全等三角形性质以及三角形内角和性质，熟练掌握相关概念是解题关键.14．如图，在△ABC中，∠ACB=90°，CD是高，∠A=30°，若AB=20，则BD的长是．【答案】1【详解】试题分析：根据同角的余角相等知，∠BCD=∠A=30°，所以分别在△ABC和△BDC中利用30°锐角所对的直角边等于斜边的一半即可求出BD．解：∵在直角△ABC中，∠ACB=90°，∠A=30°，且CD⊥AB∴∠BCD=∠A=30°，∵AB=20，∴BC=12AB=20×12=10，∴BD=12BC=10×12=1．故答案为1．考点：含30度角的直角三角形．15．已知xy=3，那么y xx yx y______．3【解析】分析：先化简，再分同正或同负两种情况作答．详解：因为xy=3，所以x、y同号，于是原式=当x>0，y>0时，原式；当x<0，y<0时，原式=(故原式.点睛：本题考查的是二次根式的化简求值，能够正确的判断出化简过程中被开方数底数的符号是解答此题的关键.16．已知关于x 的方程4433x m m x x ---=--无解，则m=________． 【答案】－3或1【分析】分式方程去分母转化为整式方程()348m x m +=+，分两种情况：（1）()348m x m +=+无实数根，（2）整式方程()348m x m +=+的根是原方程的增根，分别求解即可.【详解】去分母得：()()434x x m m ---+=-，整理得()348m x m +=+，由于原方程无解，故有以下两种情况：（1）()348m x m +=+无实数根，即30m +=且480m +≠，解得3m =-；（2）整式方程()348m x m +=+的根是原方程的增根， 即4833m m +=+，解得1m =； 故答案为：3m =-或1m =.【点睛】此题考查了分式方程无解的条件，分式方程无解，有两种情况，①整式方程本身无解；②整式方程有解，但使得分式方程的最简公分母为零（即为增根）．17．若分式22x x -+的值为0，则x 的值是 _____． 【答案】1【解析】分式值为零的条件：分子等于零且分母不等于零，由此列出不等式和等式，求解即可. 【详解】∵分式22x x -+的值为0， ∴2020x x ⎧-⎨+≠⎩＝,∴x=1．故答案是：1.【点睛】考查了分式的值为零的条件，解题关键是：分式值为零的条件是分子等于零且分母不等于零．三、解答题18．如图，在ABC ∆中，AD 平分BAC ∠．（1）若P 为线段AD 上的一个点，过点P 作PE AD ⊥交线段BC 的延长线于点E ．①若34B ∠=︒，86ACB ∠=︒，则E ∠=_______︒；②猜想E ∠与B 、ACB ∠之间的数量关系，并给出证明．（2）若P 在线段AD 的延长线上，过点P 作PE AD ⊥交直线BC 于点E ，请你直接写出PED ∠与ABC ∠、ACB ∠的数量关系．【答案】（1）①26︒，②()12E ACB B ∠=∠-∠；（2）()12PED ACB ABC ∠=∠-∠ 【分析】（1）先根据三角形的内角和定理求得BAC ∠的度数，再根据角平分线的定义求得DAC ∠的度数，从而根据三角形的内角和定理即可求出ADC ∠的度数，进一步求得E ∠的度数；（2）根据第（1）小题的思路即可推导这些角之间的关系；（3）同（1）（2）的思路即可得出结论.【详解】（1）①∵34B ∠=︒，86ACB ∠=︒∴180=60BAC B ACB ∠=︒-∠-∠︒∵AD 平分BAC ∠ ∴1302BAD BAC ∠=∠=︒ ∴64PDE B BAD ∠=∠+∠=︒∵PE ⊥AD∴9026E PDE ∠=︒-∠=︒；②数量关系：()12E ACB B ∠=∠-∠， 理由如下：设B x ACB y ∠=∠=，∵AD 平分BAC ∠∴12BAD CAD BAC ∠=∠=∠ ∵180B ACB BAC ∠+∠+∠=∴180CAB x y ∠=︒--∴1(180)2BAD x y ∠=︒-- ∴11(18090())22PDE B BAD x x y x y ∠=∠+∠=︒--=︒+-＋ ∵PE ⊥AD∴90PDE E ∠+∠=︒∴()()()1[]102199022y x y AC x E B B =∠=︒-︒∠-+-=-∠； （2）()12PED ACB ABC ∠=∠-∠， 如下图：设B n ACB m ∠=∠=，∵AD 平分BAC ∠∴12BAD CAD BAC ∠=∠=∠ ∵180B ACB BAC ∠+∠+∠=︒∴180CAB n m ∠=︒--∴()11802BAD n m ∠=︒-- ∴()11118029202PDE ADC B BAD n n m n m ∠=∠=∠∠=+︒--+-=︒＋ ∵PE ⊥AD∴90DPE ∠=︒∴11119090()()2222PDE n m m n ACB B ⎛⎫∠=︒-︒+-=-=∠-∠ ⎪⎝⎭. 【点睛】 本题主要考查了三角形的内角和定理，角平分线定理以及角的和差倍分计算，熟练掌握相关角的计算是解决本题的关键.19．如图所示，已知ABC ∆中，90B ∠=︒，16AB cm =，20AC cm =，P 、Q 是ABC ∆的边上的两个动点，其中点P 从点A 开始沿A B →方向运动，且速度为每秒1cm ，点Q 从点B 开始沿B C A →→方向运动，且速度为每秒2cm ，它们同时出发，设出发的时间为ts ．（1）则BC =____________cm ；（2）当t 为何值时，点P 在边AC 的垂直平分线上？此时CQ =_________?（3）当点Q 在边CA 上运动时，直接写出使BCQ ∆成为等腰三角形的运动时间．【答案】（1）11；（1）t=11.5s 时，13 cm ；（3）11s 或11s 或13.1s【分析】（1）由勾股定理即可得出结论；（1）由线段垂直平分线的性质得到PC= PA=t ，则PB=16-t ．在Rt △BPC 中，由勾股定理可求得t 的值，判断出此时，点Q 在边AC 上，根据CQ=1t-BC 计算即可；（3）用t 分别表示出BQ 和CQ ，利用等腰三角形的性质可分BQ=BC 、CQ=BC 和BQ=CQ 三种情况，分别得到关于t 的方程，可求得t 的值．【详解】（1）在Rt △ABC 中，BC 2222212016AC AB =-=-=(cm)．故答案为：11；（1）如图，点P 在边AC 的垂直平分线上时，连接PC ，∴PC= PA=t ，PB=16-t ． 在Rt △BPC 中，222BC BP CP +=，即2221216)t t +-=（， 解得：t=252． ∵Q 从B 到C 所需的时间为11÷1=6(s)，252＞6， ∴此时，点Q 在边AC 上，CQ=25212132⨯-=(cm)；（3）分三种情况讨论：①当CQ=BQ 时，如图1所示，则∠C=∠CBQ ．∵∠ABC=90°，∴∠CBQ+∠ABQ=90°，∠A+∠C=90°，∴∠A=∠ABQ ，∴BQ=AQ ，∴CQ=AQ=10，∴BC+CQ=11，∴t=11÷1=11(s)．②当CQ=BC 时，如图1所示，则BC+CQ=14，∴t=14÷1=11(s)．③当BC=BQ 时，如图3所示，过B 点作BE ⊥AC 于点E ，则BE 121648205AB BC AC ⋅⨯===， ∴CE 2222483612()55BC BE =-=-==7.1． ∵BC=BQ ，BE ⊥CQ ，∴CQ=1CE=14.4，∴BC+CQ=16.4，∴t=16.4÷1=13.1(s)．综上所述：当t为11s或11s或13.1s时，△BCQ为等腰三角形．【点睛】本题考查了勾股定理、等腰三角形的性质、方程思想及分类讨论思想等知识．用时间t表示出相应线段的长，化“动”为“静”是解决这类问题的一般思路，注意方程思想的应用．20．如图1，在△ABC和△ADE中，∠BAC＝∠EAD，AB＝AC，AD＝AE，连接CD、AE交于点F．（1）求证：BE＝CD．（2）当∠BAC＝∠EAD＝30°，AD⊥AB时（如图2），延长DC、AB交于点G，请直接写出图中除△ABC、△ADE以外的等腰三角形．【答案】（1）见解析；（2）△ACF是等腰三角形，△ADG是等腰三角形，△DEF是等腰三角形，△ECD是等腰三角形．【分析】（1）由“SAS”可证△ACD≌△ABE，可得BE＝CD；（2）如图2，图形中有四个等腰三角形：分别是①△ACF是等腰三角形，②△ADG是等腰三角形，③△DEF 是等腰三角形；④△ECD是等腰三角形；根据已知角的度数依次计算各角的度数，根据两个角相等的三角形是等腰三角形得出结论．【详解】解：（1）如图1，∵∠BAC＝∠EAD，∴∠BAC+∠CAE＝∠EAD+∠CAE，即∠BAE＝∠CAD，且AB＝AC，AD＝AE，∴△ACD≌△ABE（SAS）∴BE＝CD；（2）如图2，①∵∠BAC＝∠EAD＝30°，∴∠ABC＝∠ACB＝∠AED＝∠ADE＝75°，由（1）得：∠ACD＝∠ABC＝75°，∠DCE＝∠BAC＝30°，∵AD⊥AB，∴∠BAD＝90°，∴∠CAE＝30°，∴∠AFC＝180°﹣30°﹣75°＝75°，∴∠ACF＝∠AFC，∴△ACF是等腰三角形，②∵∠BCG＝∠DCE＝30°，∠ABC＝75°，∴∠G＝45°，在Rt△AGD中，∠ADG＝45°，∴△ADG是等腰三角形，③∠EDF＝75°﹣45°＝30°，∴∠DEF＝∠DFE＝75°，∴△DEF是等腰三角形；④∵∠ECD＝∠EDC＝30°，∴△ECD是等腰三角形．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的判定，三角形内角和定理，灵活运用这些性质进行推理是本题的关键．21．今年，长沙开始推广垃圾分类，分类垃圾桶成为我们生活中的必备工具．某学校开学初购进A型和B 型两种分类垃圾桶，购买A型垃圾桶花费了2500元，购买B型垃圾桶花费了2000元，且购买A型垃圾桶数量是购买B型垃圾桶数量的2倍，已知购买一个B型垃圾桶比购买一个A型垃圾桶多花30元．（1）求购买一个A型垃圾桶、B型垃圾桶各需多少元？（2）由于实际需要，学校决定再次购买分类垃圾桶，已知此次购进A型和B型两种分类垃圾桶的数量一共为50个，恰逢市场对这两种垃圾桶的售价进行调整，A型垃圾桶售价比第一次购买时提高了8%，B型垃圾桶按第一次购买时售价的9折出售，如果此次购买A型和B型这两种垃圾桶的总费用不超过3240元，那么此次最多可购买多少个B型垃圾桶？【答案】（1）购买一个A型垃圾桶、B型垃圾桶分别需要50元和80元；（2）此次最多可购买1个B型垃圾桶．【分析】（1）设一个A型垃圾桶需x元，则一个B型垃圾桶需（x+1）元，根据购买A型垃圾桶数量是购买B品牌足球数量的2倍列出方程解答即可；（2）设此次可购买a个B型垃圾桶，则购进A型垃圾桶（50-a）个，根据购买A、B两种垃圾桶的总费用不超过3240元，列出不等式解决问题．【详解】（1）设购买一个A型垃圾桶需x元，则购买一个B型垃圾桶需(30)x+元．由题意得：25002000230x x=⨯+．解得：50x=．经检验50x=是原分式方程的解．∴3080x+=．答：购买一个A型垃圾桶、B型垃圾桶分别需要50元和80元．（2）设此次购买a 个B 型垃圾桶，则购进A 型垃圾桶(50)a -个，由题意得：50(18%)(50)800.93240a a ⨯+-+⨯≤．解得30a ≤．∵a 是整数，∴a 最大为1．答：此次最多可购买1个B 型垃圾桶．【点睛】本题考查一元一次不等式与分式方程的应用，正确找出等量关系与不等关系是解决问题的关键． 22．在数学活动课上,李老师让同学们试着用角尺平分 AOB ∠(如图所示),有两组．同学设计了如下方案:方案①:将角尺的直角顶点P 介于射线 ,OA OB 之间,移动角尺使角尺两边相同的刻度位于 ,OA OB 上,且交点分别为,M N ,即PM PN =,过角尺顶点P 的射线OP 就是AOB ∠的平分线．方案②:在边 ,OA OB 上分别截取OM ON =,将角尺的直角顶点P 介于射线 ,OA OB 之间,移动角尺使角尺两边相同的刻度与点,M N 重合,即PM PN =,过角尺顶点P 的射线OP 就是AOB ∠的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行，请说明理由．【答案】方案①不可行，理由见解析；方案②可行，证明见解析．【分析】通过画图可分析到：方案①中判定PM=PN 并不能判断PO 就是∠AOB 的角平分线，关键是缺少△OPM ≌△OPN 的条件，只有“边边”的条件；方案②中△OPM 和△OPN 是全等三角形（三边相等），则∠MOP=∠NOP ，所以OP 为∠AOB 的角平分线；【详解】如图可得，方案①不可行.因为只有, OP OP PM PN ==,不能判断OPM OPN ∆∆≌.不能得到AOP BOP ∠=∠,所以不能判定OP 就是AOB ∠的平分线.方案②可行.在OPM ∆和OPN ∆中，OM ON PM PN OP OP =⎧⎪=⎨⎪=⎩()OPM OPN SSS ∴∆∆≌AOP BOP ∴∠=∠.OP ∴就是AOB ∠的平分线.【点睛】考核知识点：全等三角形的判定和性质.理解全等三角形的判定和性质是关键.23．如图，在□ABCD 中，AC 交BD 于点O ，点E ，点F 分别是OA ，OC 的中点。

A．4B．2C．8D．6
7．下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（ ）
A．甲和乙B．乙和丙C．甲和丙D．只有丙
8．如果 +ax+1是一个完全平方公式，那么a的值是（）
A．2B．－2C．±2D．±1
9．如图，已知∠ACB＝∠DBC，添加以下条件，不能判定△ABC≌△DCB的是（ ）
故答案选：D.
【点睛】
本题考查的知识点是作图—基本作图,坐标与图形性质,角平分线的性质，解题的关键是熟练的掌握作图—基本作图,坐标与图形性质,角平分线的性质作图—基本作图,坐标与图形性质,角平分线的性质.
2．D
解析：D
【解析】
【分析】
先用x表示出增加2名同学前和增加后每人分摊的车费钱，再根据增加后每人比原来少摊了3元钱车费列出方程即可.
C．3∠A=2∠1+∠2D．3∠A=2（∠1+∠2）
12．已知一个多边形的内角和为1080°，则这个多边形是（ ）
A．九边形B．八边形C．七边形D．六边形
二、填空题
13．分解因式： ___________________.
14．－12019＋22020×（ ）2021＝_____________
15．若分式 的值为零，则x的值等于_____．
【详解】
∵BD是△ABC的角平分线，AE⊥BD，
∴∠ABD=∠EBD= ∠ABC= ，∠AFB=∠EFB=90°，
∴∠BAF=∠BEF=90°-17.5°，
∴AB=BE，
∴AF=EF，
∴AD=ED，
∴∠DAF=∠DEF，
∵∠BAC=180°-∠ABC-∠C=95°，
∴∠BED=∠BAD=95°，

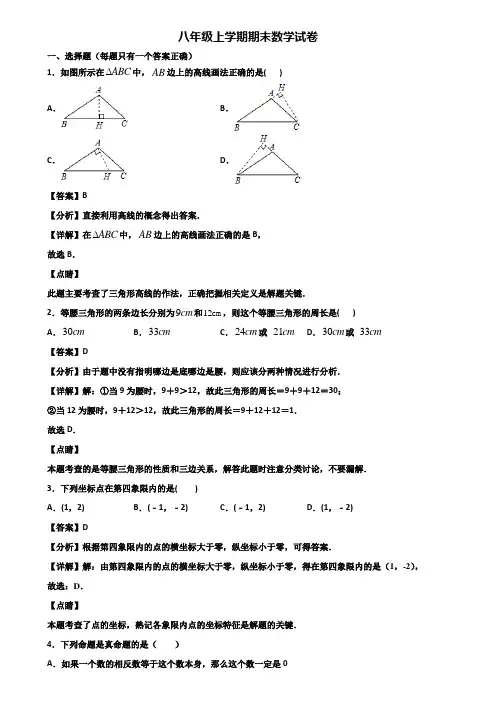
八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）∆中，AB边上的高线画法正确的是( )1．如图所示在ABCA．B．C．D．【答案】B【分析】直接利用高线的概念得出答案．∆中，AB边上的高线画法正确的是B，【详解】在ABC故选B．【点睛】此题主要考查了三角形高线的作法，正确把握相关定义是解题关键．2．等腰三角形的两条边长分别为9cm和12cm，则这个等腰三角形的周长是( )A．30cm B．33cm C．24cm或21cm D．30cm或33cm【答案】D【分析】由于题中没有指明哪边是底哪边是腰，则应该分两种情况进行分析．【详解】解：①当9为腰时，9＋9＞12，故此三角形的周长＝9＋9＋12＝30；②当12为腰时，9＋12＞12，故此三角形的周长＝9＋12＋12＝1．故选D．【点睛】本题考查的是等腰三角形的性质和三边关系，解答此题时注意分类讨论，不要漏解．3．下列坐标点在第四象限内的是( )A．(1，2) B．(﹣1，﹣2) C．(﹣1，2) D．(1，﹣2)【答案】D【分析】根据第四象限内的点的横坐标大于零，纵坐标小于零，可得答案．【详解】解：由第四象限内的点的横坐标大于零，纵坐标小于零，得在第四象限内的是（1，-2），故选：D．【点睛】本题考查了点的坐标，熟记各象限内点的坐标特征是解题的关键．4．下列命题是真命题的是（）A．如果一个数的相反数等于这个数本身，那么这个数一定是0B ．如果一个数的倒数等于这个数本身，那么这个数一定是1C ．如果一个数的平方等于这个数本身，那么这个数一定是0D ．如果一个数的算术平方根等于这个数本身，那么这个数一定是0【答案】A【分析】根据相反数是它本身的数为0；倒数等于这个数本身是±1；平方等于它本身的数为1和0；算术平方根等于本身的数为1和0进行分析即可．【详解】A 、如果一个数的相反数等于这个数本身，那么这个数一定是0，是真命题；B 、如果一个数的倒数等于这个数本身，那么这个数一定是1，是假命题；C 、如果一个数的平方等于这个数本身，那么这个数一定是0，是假命题；D 、如果一个数的算术平方根等于这个数本身，那么这个数一定是0，是假命题；故选A ．【点睛】此题主要考查了命题与定理，关键是掌握正确的命题为真命题，错误的命题为假命题．5．下列命题为假命题的是（ ）A ．三角形三个内角的和等于180°B ．三角形两边之和大于第三边C ．三角形的面积等于一条边的长与该边上的高的乘积的一半D ．同位角相等【答案】D【分析】根据三角形内角和定理对A 进行判断；根据三角形三边的关系对B 进行判断；根据三角形面积公式对C 进行判断；根据同位角的定义对D 进行判断．【详解】A 、三角形三个内角的和等于180°，所以A 选项为真命题；B 、三角形两边之和大于第三边，所以B 选项为真命题；C 、三角形的面积等于一条边的长与该边上的高的乘积的一半，所以C 选项为真命题，D 、两直线平行，同位角相等，所以D 选项为假命题．故选：D ．【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．6．已知ABC ∆的三边长为a b c 、、满足条件4422220a b b c a c -+-=，则ABC ∆的形状为（ ） A ．等腰三角形B ．等腰直角三角形C ．等边三角形D ．等腰三角形或直角三角形【答案】D【分析】把所给的等式4422220a b b c a c -+-=能进行因式分解的要因式分解，整理为非负数相加得0的形式，求出三角形三边的关系，进而判断三角形的形状.【详解】由4422220a b b c a c -+-=,得()()()22222220ab a bc a b +---= ()()()2220a b c a b a b -+-=+ 因为已知ABC ∆的三边长为a b c 、、所以0abc ≠所以222a b c +-=0,或0a b -=,即222+=a b c ,或a b =所以ABC ∆的形状为等腰三角形或直角三角形故选:D【点睛】本题考查了分组分解法分解因式，利用因式分解最后整理成多项式的乘积等于0的形式是解题的关键. 7．若x ，y 的值均扩大为原来的3倍，则下列分式的值保持不变的是（ ）A ．2x x y+- B ．22y x C ．3223y x D ．222()y x y - 【答案】D 【分析】根据分式的基本性质，x ，y 的值均扩大为原来的3倍，求出每个式子的结果，看结果等于原式的即是答案．【详解】根据分式的基本性质，可知若x ，y 的值均扩大为原来的3倍，A 、23233x x x y x y++≠--，错误； B 、22629y y x x≠，错误； C 、3322542273y y x x ≠，错误； D 、()()22221829y y x y x y --＝，正确；故选D ．【点睛】本题考查的是分式的基本性质，即分子分母同乘以一个不为0的数，分式的值不变．此题比较简单，但计算时一定要细心．8．下列实数中最大的是（ ）A ．32B ．πCD ．4-【答案】D【解析】先对四个选项进行比较，再找出最大值.【详解】解：3442π<<<-=， ∴所给的几个数中，最大的数是4-．故选：D ．【点睛】本题考查的是实数的大小，熟练掌握实数是解题的关键.9．华为麒麟990芯片采用了最新的0.000000007米的工艺制程，数0.000000007用科学记数法表示为（ ） A ．9710-⨯B ．8710-⨯C ．90.710-⨯D ．80.710-⨯ 【答案】A【分析】根据科学记数法绝对值小于1的正数也可以利用科学记数法表示，一般形式为10n a -⨯，其中110a ≤<，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】由科学记数法的表示可知，90.000000007=710-⨯，故选：A ．【点睛】科学记数法表示数时，要注意形式10n a -⨯中，a 的取值范围，要求110a ≤<，而且n 的值和原数左边起第一个不为零的数字前面的0的个数一样.10．点P （-2，-3）向左平移1个单位，再向上平移3个单位，则所得到的点的坐标为（ ）A ．（-3，0）B ．（-1，6）C ．（-3，-6）D ．（-1，0） 【答案】A【解析】试题分析：点P （-2，-3）向左平移1个单位后坐标为（-3，-3），（-3，-3）向上平移3个单位后为（-3，0），∴点P （-2，-3）向左平移1个单位，再向上平移3个单位，则所得到的点的坐标为（-3，0），故选A ．考点：坐标的平移二、填空题11．一组数据3，4，x ，6，7的平均数为5.则这组数据的方差是______．【答案】2【分析】先根据平均数的公式121()n x x x x n =+++ 求出x 的值，然后利用方差的公式2222121[()()()]n s x x x x x x n=-+-++- 计算即可． 【详解】∵3，4，x ，6，7的平均数为5，∴346755x ++++= 解得5x =2222221[(35)(45)(55)(65)(75)]25s ∴=⨯-+-+-+-+-= 故答案为：2【点睛】本题主要考查平均数与方差，掌握平均数与方差的求法是解题的关键．12．若分式293x x --的值为0，则x 的值为_______. 【答案】-1【分析】根据分式的值为零的条件可以求出x 的值．【详解】解：根据题意得：29=030x x ⎧-⎨-≠⎩，解得：x=-1．故答案为：-1.【点睛】若分式的值为零，需同时具备两个条件：（1）分子为2；（2）分母不为2．这两个条件缺一不可． 13．分解因式：29y x y -=_____________．【答案】(3)(3)y x x +-．【分析】先提取公因式y ，再对余下的多项式利用平方差公式继续分解．【详解】229(9)(3)(3)y x y y x y x x -=-=+-．故答案为：(3)(3)y x x +-．【点睛】本题考查了用提取公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直至不能分解为止．14．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=_________【答案】135°【分析】易证△ABC≌△BDE，得∠1=∠DBE，进而得∠1+∠3=90°，即可求解．【详解】∵AC=BE，BC=DE，∠ACB=∠BED=90°，∴△ABC≌△BDE（SAS），∴∠1=∠DBE，∵∠DBE+∠3=90°，∴∠1+∠3=90°，∵∠2=12×90°=45°，∴∠1+∠2+∠3=90°+45°=135°．故答案是：135°．【点睛】本题主要考查三角形全等的判定和性质以及直角三角形的性质，掌握SAS判定三角形全等，是解题的关键．15．如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C 向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为．【答案】（﹣2，2）【解析】试题分析：∵直线y=2x+4与y轴交于B点，∴x=0时，得y=4，∴B（0，4）．∵以OB为边在y轴右侧作等边三角形OBC，∴C在线段OB的垂直平分线上，∴C点纵坐标为2．将y=2代入y=2x+4，得2=2x+4，解得x=﹣2．所以C′的坐标为（﹣2，2）．考点：2．一次函数图象上点的坐标特征；2．等边三角形的性质；3．坐标与图形变化-平移．16．△ABC中，AB=15，AC=13，高AD=12，则△ABC的面积为______________．【答案】84或24【解析】分两种情况考虑：①当△ABC为锐角三角形时，如图1所示，∵AD⊥BC，∴∠ADB=∠ADC=90°，在Rt△ABD中，AB=15，AD=12，根据勾股定理得：BD=22-AB AD=9，在Rt△ADC中，AC=13，AD=12，根据勾股定理得：DC=22AC AD-=5，∴BC=BD+DC=9+5=14，则S△ABC=12BC⋅AD=84；②当△ABC为钝角三角形时，如图2所示，∵AD⊥BC，∴∠ADB=90°，在Rt△ABD中，AB=15，AD=12，根据勾股定理得：22-AB AD，在Rt△ADC中，AC=13，AD=12，根据勾股定理得：22AC AD-=5，∴BC=BD−DC=9−5=4，则S△ABC=12BC⋅AD=24.综上，△ABC的面积为24或84.故答案为24或84.点睛：此题考查了勾股定理，利用了分类讨论的数学思想，灵活运用勾股定理是解本题的关键.17．有一程序，如果机器人在平地上按如图所示的步骤行走，那么机器人回到A点处行走的路程是________．【答案】30米【分析】利用多边形的外角和等于360°，可知机器人回到A点时，恰好沿着360°÷24°=15边形的边走了一圈，即可求得路程．【详解】解：2×（360°÷24°）=30米．故答案为30米．【点睛】本题需利用多边形的外角和解决问题．三、解答题18．列二元一次方程组解决问题：某校八年级师生共466人准备参加社会实践活动，现已预备了,A B两种型号的客车共10辆，每辆A种型号客车坐师生49人，每辆B种型号客车坐师生37人，10辆客车刚好坐满，求,A B两种型号客车各多少辆？【答案】A种型号客车8辆，B种型号客车2辆【分析】设A型号客车用了x辆，B型号客车用了y辆，根据两种客车共10辆正好乘坐466人，即可得出关于x，y的二元一次方程组，解之即可得出结论．【详解】设A种型号客车x辆，B种型号客车y辆，依题意，得10 4937466 x yx y+=⎧⎨+=⎩解得82 xy=⎧⎨=⎩答：A种型号客车8辆，B种型号客车2辆.【点睛】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．19．因式分解：（1）﹣3x3y2+6x2y3﹣3xy4（2）9a2（x﹣y）+4b2（y﹣x）【答案】（1）﹣3xy2（x﹣y）2；（2）（x﹣y）（3a+2b）（3a﹣2b）．【分析】（1）原式提取公因式，再利用完全平方公式分解即可；（2）原式变形后，提取公因式，再利用平方差公式分解即可．【详解】解：（1）原式＝﹣3xy2（x2﹣2xy+y2）＝﹣3xy2（x﹣y）2；（2）原式＝（x﹣y）（9a2﹣4b2）＝（x﹣y）（3a+2b）（3a﹣2b）．【点睛】本题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．20．如图，在△ABC中，AB＝AC，AD和BE是高，它们相交于点H，且AE＝BE求证：AH＝2BD【答案】详见解析【分析】由等腰三角形的底边上的垂线与中线重合的性质求得BC=2BD，根据直角三角形的两个锐角互余的特性求知∠1+∠C=90°；又由已知条件AE⊥AC知∠2+∠C=90°，所以根据等量代换求得∠1=∠2；然后由三角形全等的判定定理SAS证明△AEH≌△BEC，再根据全等三角形的对应边相等及等量代换求得AH=2BD 【详解】∵AD是高,BE是高∴∠EBC+∠C=∠CAD+∠C=90°∴∠EBC=∠CAD又∵AE＝BE∠AEH=∠BEC∴△AEH△BEC(ASA)∴AH ＝BC∵AB＝AC，AD是高∴BC=2BD∴AH ＝2BD考点：1 等腰三角形的性质;2 全等三角形的判定与性质21．数学活动课上，同学们探究了角平分线的作法．下面给出三个同学的作法：小红的作法如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再过点O作MN的垂线，垂足为P，则射线OP便是∠AOB的平分线．小明的作法如图，∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C的射线OC便是∠AOB的平分线．小刚的作法如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再分别过点M，N作OA，OB的垂线，交点为P，则射线OP便是∠AOB的平分线．请根据以上情境，解决下列问题(1)小红的作法依据是．(2)为说明小明作法是正确的，请帮助他完成证明过程．证明：∵OM ＝ON ，OC ＝OC ， ，∴△OMC ≌△ONC( )(填推理的依据)(3)小刚的作法正确吗?请说明理由【答案】（1）等腰三角形三线合一定理；（2）CM=CN ，边边边；（3）正确，证明见详解．【分析】（1）利用等腰三角形三线合一定理，即可得到结论成立；（2）利用SSS ，即可证明△OMC ≌△ONC ，补全条件即可；（3）利用HL ，即可证明Rt △OPM ≌Rt △OPN ，即可得到结论成立．【详解】解：（1）∵OM=ON ，∴△OMN 是等腰三角形，∵OP ⊥MN ，∴OP 是底边上的高，也是底边上的中线，也是∠MON 的角平分线；故答案为：等腰三角形三线合一定理；（2）证明：∵OM ＝ON ，OC ＝OC ，CM=CN ，∴△OMC ≌△ONC （边边边）；∴∠MOC=∠NOC ，∴OC 平分∠AOB ；故答案为：CM=CN ，边边边；（3）小刚的作法正确，证明如下：∵PM ⊥OA ，PN ⊥OB ，∴∠OMP=∠ONP=90°，∵OM=ON ，OP=OP ，∴Rt △OPM ≌Rt △OPN （HL ），∴∠MOP=∠NOP ，∴OP 平分∠AOB ；∴小刚的作法正确．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的性质，角平分线的判定，解题的关键是熟练掌握全等三角形的判定和性质，以及等腰三角形的性质进行证明．22．课堂上，老师出了一道题：比较23与23的大小. 小明的解法如下：解：22224-，因为，所以19403->，所以192233->，我们把这种比较大小的方法称为作差法. (1)根据上述材料填空(在横线上填“>”“=”或“<”)：若0a b ->，则a b ；若0a b -=，则a b ；若0a b -<，则a b .(2)利用上述方法比较实数9224-与32的大小. 【答案】 (1)>；=；<；(2)92232-<. 【解析】（1）根据不等式和方程移项可得结论；（2）同理，利用作差法可比较大小．【详解】(1) （1）①若a-b ＞0，则a ＞b ；②若a-b=0，则a=b ；③若a-b ＜0，则a ＜b ；(2)9223922632242444----=-=. 因为93922=<，，所以3220-<，即92232-<. 【点睛】 本题考查了实数大小的比较，根据所给的材料，运用类比的方法解决问题．23．已知：如图180B BCD ∠+∠=，B D ∠=∠，那么E DEF ∠=∠成立吗？为什么？下面是小丽同学进行的推理，请你将小丽同学的推理过程补充完整．解：成立，理由如下：180B BCD ∠+∠=（已知）∴① （同旁内角互补，两条直线平行）B DCE ∴∠=∠（② ）又B D ∠=∠（已知），DCE D ∴∠=∠（等量代换）//AD BE ∴（③ ）【答案】AB∥CD；两直线平行，同位角相等；内错角相等，两直线平行；两直线平行，内错角相等．【分析】根据平行线的判定推出AB∥CD，根据平行线的性质和已知得出∠DCE＝∠D，推出AD∥BE，根据平行线的性质推出即可．【详解】180B BCD∠+∠=，∴AB∥CD（同旁内角互补，两直线平行），∴∠B＝∠DCE（两直线平行，同位角相等），∵∠B＝∠D，∴∠DCE＝∠D，∴AD∥BE（内错角相等，两直线平行），∴∠E＝∠DFE（两直线平行，内错角相等），故答案为：AB∥CD；两直线平行，同位角相等；内错角相等，两直线平行；两直线平行，内错角相等．【点睛】本题考查了对平行线的性质和判定的应用，主要考查学生的推理能力．24．如图1，△ABC是直角三角形，∠C=90°，∠CAB的角平分线AE与AB的垂直平分线DE相交于点E. （1）如图2，若点E正好落在边BC上.①求∠B的度数②证明：BC=3DE（2）如图3，若点E满足C、E、D共线.求证：AD+DE=BC．【答案】（1）①30°，②见解析；（2）见解析.【解析】(1)由∠C=90°，∠CAB的角平分线AE与AB的垂直平分线DE相交于点E，可直接求出∠B的度数.先证明BE=2DE，易得BC=3DE(2) 过点E作EF⊥AC于点F，先证明△ABC是等腰直角三角形△CEF是等腰直角三角形，再证明△ADE≌△AFE（HL）即可.【详解】（1）①∵AE平分∠CAB∴∠CAE=∠DAE又∵ED是AB的垂直平分线∴EA=EB∴∠CAE=∠DAE=∠B 又∵∠C=90°∴∠B=13×90°=30°②∵AE平分∠CAB，且EC⊥AC，ED⊥AB∴EC=ED在Rt△EDB中，∠B=30°∴BE=2DEBC=BE+CE=BE+DE=3DE（2）过点E作EF⊥AC于点F，∵ED是AB的垂直平分线，且C、E、D共线∴CD也是AB的垂直平分线∴CA=CB又∠ACB=90°∴△ABC是等腰直角三角形.∴∠ACD=45°∴△CEF是等腰直角三角形.∴EF=CF∵AE平分∠CAB，且EF⊥AC，ED⊥AB∴EF=ED∴ED=FC在Rt△ADE和Rt△AFE中EF=ED，AE=AE，△ADE≌△AFE（HL）∴AD=AF∴BC=AC=AF+FC=AD+DE.【点睛】本题考查的知识点是角的计算及全等三角形，解题的关键是熟练的掌握角的计算及全等三角形.25．某区为加快美丽乡村建设，建设秀美幸福薛城，对A，B两类村庄进行了全面改建.根据预算，建设一人资金1140万元.(1)建设一个A 类美丽村庄和一个B 类美丽村庄所需的资金分别是多少万元?(2)乙镇3个A 类美丽村庄和6个B 类美丽村庄的改建共需资金多少万元?【答案】（1）建设一个A 类美丽村庄和一个B 类美丽村庄所需的资金分别是120万元、180万元；(2)乙镇3个A 类美丽村庄和6个B 类美丽村庄的改建共需资金1440万元.【解析】（1）设建设一个A 类美丽村庄和一个B 类美丽村庄所需的资金分别是x 、y 万元，根据建设一个A 类美丽村庄和一个B 类美丽村庄共需资金300万元，甲镇建设了2个A 类村庄和5个B 类村庄共投入资金1140万元，列方程组求解；（2）根据（1）求出的值代入求解．【详解】解：(1)设建设一个A 类美丽村庄和一个B 类美丽村庄所需的资金分别是x 万元、y 万元.由题意，得300,251140.x y x y +=⎧⎨+=⎩解得120,180.x y =⎧⎨=⎩ 答：建设一个A 类美丽村庄和一个B 类美丽村庄所需的资金分别是120、180万元.(2)3×120+6×180=1440（万元）.答：乙镇3个A 类美丽村庄和6个B 类美丽村庄的改建共需资金1440万元.【点睛】本题考查了二元一次方程组的应用，解答本题的关键是设出未知数，找出等量关系，列方程组求解．八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．若ABC ∆有一个外角是钝角，则ABC ∆一定是（ ）A ．钝角三角形B ．锐角三角形C ．直角三角形D ．以上都有可能【答案】D【分析】利用三角形的外角和相邻的内角互补即可得出答案．【详解】解：∵三角形的外角和相邻的内角互补，∴若ABC ∆有一个外角是钝角，则△ABC 有一个内角为锐角，∴△ABC 可能是钝角三角形，也可能是锐角三角形，也可能是直角三角形，故答案为：D ．【点睛】本题考查了三角形的内角与外角的性质，解题的关键是熟知三角形的外角和相邻的内角互补的性质． 2．如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β的度数是（ ）A ．180B ．220C ．240D ．300【答案】C 【分析】本题可先根据等边三角形顶角的度数求出两底角的度数和，然后在四边形中根据四边形的内角和为360°，求出∠α+∠β的度数．【详解】∵等边三角形的顶角为60°，∴两底角和=180°-60°=120°；∴∠α+∠β=360°-120°=240°；故选C ．【点睛】本题综合考查等边三角形的性质及三角形内角和为180°，四边形的内角和是360°等知识，难度不大，属于基础题.3．如图，分别以Rt △ABC 的直角边AC ，斜边AB 为边向外作等边三角形△ACD 和△ABE ，F 为AB 的中点，连接DF ，EF ，∠ACB ＝90°，∠ABC ＝30°．则以下4个结论：①AC ⊥DF ；②四边形BCDF 为平行四边形；③DA+DF＝BE ；④ACDBCDES1S6=四边形其中，正确的是（）A．只有①②B．只有①②③C．只有③④D．①②③④【答案】A【分析】根据平行四边形的判定定理判断②，根据平行四边形的性质和平行线的性质判断①，根据三角形三边关系判断③，根据等边三角形的性质分别求出△ACD、△ACB、△ABE的面积，计算即可判断④．【详解】∵∠ACB=90°，∠ABC=30°，∴∠BAC=60°，AC=12AB，∵△ACD是等边三角形，∴∠ACD=60°，∴∠ACD=∠BAC，∴CD∥AB，∵F为AB的中点，∴BF=12AB，∴BF∥CD，CD=BF，∴四边形BCDF为平行四边形，②正确；∵四边形BCDF为平行四边形，∴DF∥BC，又∠ACB=90°，∴AC⊥DF，①正确；∵DA=CA，DF=BC，AB=BE，BC+AC＞AB∴DA+DF＞BE，③错误；设AC=x，则AB=2x，S△ACD2222222333143733342ACDACB ABEBCDESS x S xSx x x====++四边形，，，，④错误，故选：A．【点睛】此题考查平行四边形的判定和性质、等边三角形的性质，掌握一组对边平行且相等的四边形是平行四边形、4．已知23a =+，23b =-，则a 与b 的大小关系为（ ） A ．a b =B ．a b <C ．a b >D ．不能确定【答案】A 【分析】通过“分母有理化”对23+进行化简，进而比较大小，即可得到答案． 【详解】∵23a =+=2323(23)(23)-=-+-，23b =-， ∴a b =．故选A ．【点睛】 本题主要考查二次根式的化简，掌握二次根式的分母有理化，是解题的关键．5．以下四家银行的行标图中，是轴对称图形的有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C 【解析】试题分析：根据轴对称图形的定义可知：第1个行标是轴对称图形；第2个行标不是轴对称图形；第3个行标是轴对称图形；第4个行标是轴对称图形；所以共3个轴对称图形，故选C.考点：轴对称图形6．若关于x 的分式方程3533x m x x +=--无解，则m 的值是（ ） A ．3B ．3-C ．9D ．9- 【答案】D【分析】根据分式方程的增根是使最简公分母为零的值，可得关于m 的方程，根据解方程，可得答案.【详解】解：方程去分母得：()353x x m +-=-，整理得：815x m =-，∴158m x -=， ∵方程无解，∴1538m -=， 解得：m=-9.【点睛】本题考查了分式方程的解，利用分式方程的增根得出关于m 的方程是解题关键．7．下列各组数是勾股数的是（ ）A ．6，7，8B ．1，2，3C ．3，4，5D ．5，5，9【答案】C【分析】直接根据勾股数的概念进行排除选项即可．【详解】A 、2226+7=858≠，故不符合题意；B 、2221+2=53≠，故不符合题意；C 、2223+4=25=5，故符合题意；D 、2225+5=509≠，故不符合题意；故选C ．【点睛】本题主要考查勾股数，熟练掌握勾股数的概念及勾股定理是解题的关键．8．如图所示，在直角三角形ACB 中，已知∠ACB=90°，点E 是AB 的中点，且DE AB ⊥，DE 交AC 的延长线于点D 、交BC 于点F ，若∠D=30°，EF=2，则DF 的长是（ ）A ．5B ．4C ．3D ．2【答案】B 【分析】求出∠B=30°，结合EF=2，得到BF ，连接AF ，根据垂直平分线的性质得到FA=FB=4，再证明∠DAF=∠D ，得到DF=AF=4即可．【详解】解：∵DE ⊥AB ，则在△AED 中，∵∠D=30°，∴∠DAE=60°，在Rt △ABC 中，∵∠ACB=90°，∠BAC=60°，∴∠B=30°，在Rt △BEF 中，∵∠B=30°，EF=2，连接AF ，∵DE 是AB 的垂直平分线，∴FA=FB=4，∠FAB=∠B=30°，∵∠BAC=60°，∴∠DAF=30°，∵∠D=30°，∴∠DAF=∠D ，∴DF=AF=4，故选B ．【点睛】本题考查了垂直平分线的判定和性质，直角三角形的性质，解题的关键是掌握相应定理，构造线段AF ． 9．已知32a =+32b =则a 与b 的关系是( ) A ．a b =B ．1ab =C ．=-a bD ．1ab =- 【答案】C【分析】将a 分母有理化，然后求出a+b 即可得出结论． 【详解】解：()()323223323232a --====-++-∴(()23320a b +=+-= ∴=-a b故选C ．【点睛】 此题考查的是二次根式的化简，掌握分母有理化是解决此题的关键．10．现实世界中，对称现象无处不在，中国的黑体字中有些也具有对称性，下列黑体字是轴对称图形的是（ ）A ．诚B ．信C ．自D ．由【答案】D【分析】根据轴对称图形的概念求解即可．【详解】解：根据轴对称图形的概念可知“由”是轴对称图形，故选：D ．【点睛】本题考查轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．二、填空题11．如图，O 对应的有序数对为（1，3）有一个英文单词的字母顺序对应如图中的有序数对分别为（1，2），（5，1），（5，2），（5，2），（1，3），请你把这个英文单词写出来或者翻译成中文为________．【答案】HELLO【解析】H(1,2),E(5,1),L(5,2),L(5,2),O(1,3)，所以，这个单词为HELLO.故答案为HELLO.12．分析下面式子的特征，找规律，三个括号内所填数的和是 ____________．415+，235+，7＋（ ），15＋（ ），（ ）120+，… 【答案】11.1【分析】分别找到这列算式中的整数部分的规律与分式部分的规律即可求解.【详解】这列算式中的整数部分：1，1，7，15…1×2＋1＝1；1×2＋1＝7；7×2+1＝15；后一个整数是前一个整数的2倍加上1；∴括号内的整数为15×2+1=11，25÷2＝15； 15÷2＝110 验证：110÷2＝120； 要填的三个数分别是：15，110，11，它们的和是：15+110+11=11310=11.1． 故答案为：11.1．【点睛】本题分出整数部分和分数部分，各自找出规律，再根据规律进行求解．13．在△ABC 中，AB ＝AC ，∠B ＝60°，则△ABC 是_______三角形．【答案】等边【分析】由于AB=AC ，∠B=60°，根据有一个角为60°的等腰三角形为等边三角形，判断得出△ABC 为等边三角形即可解决问题．【详解】∵AB=AC ，∠A=60°，∴△ABC 为等边三角形，故答案是：等边．【点睛】本题考查了等边三角形的判定与性质：有一个60°的等腰三角形为等边三角形；三个角都相等，每一个角等于60°．14．如图，直线a 和直线b 被直线c 所截，给出下列条件：①∠1＝∠2；②∠3＝∠6；③∠4+∠7＝180°；④∠5+∠8＝180°．其中能判断a ∥b 的条件是________．【答案】①②③④；【详解】解：①∠1=∠2即同位角相等，能判断a ∥b （同位角相等，两直线平行）；②∠3=∠6为内错角相等，能判断a ∥b ；③易知∠4=∠6，已知∠4+∠7=180°即∠6+∠7=180°能判断a ∥b （同旁内角互补，两直线平行）； ④易知∠5和∠3为对顶角，∠8和∠2为对顶角，故∠5+∠8=180°即∠3+∠2=180°能判断a ∥b （同旁内角互补，两直线平行）；综上可得①②③④可判断a ∥b ．【点睛】本题难度较低，主要考查学生对平行线判定定理知识点的掌握．15．若1003997a =1001999b =21001c =a b c ，，的大小关系用“＜”号排列为 _________．【答案】a ＜b ＜c【分析】利用平方法把三个数值平方后再比较大小即可．【详解】解：∵a 21003997⨯b 21001999⨯，c 2=4004=2000+2×1002，1003×997=1000000-9=999991，1001×999=1000000-1=999999，10022=1．∴a ＜b ＜c ．故答案为：a ＜b ＜c.【点睛】这里注意比较数的大小可以用平方法，两个正数，平方大的就大．此题也要求学生熟练运用完全平方公式和平方差公式．16．已知a 、b 、c 是△ABC 的三边的长，且满足a 2+b 2+c 2=ab+bc+ac ，关于此三角形的形状有下列判断：①是锐角三角形；②是直角三角形；③是钝角三角形；④是等边三角形．其中正确说法的是__________．(把你认为正确结论的序号都填上)【答案】①④【分析】先将原式转化为完全平方公式，再根据非负数的性质得出a=b=c ．进而判断即可．【详解】解：∵a 2+b 2+c 2=ab+bc+ca ，∴2a 2+2b 2+2c 2=2ab+2bc+2ca ，即（a-b ）2+（b-c ）2+（a-c ）2=0，∴a=b=c ，∴此三角形为等边三角形，同时也是锐角三角形．故答案是：①④．【点睛】此题考查了因式分解的应用，根据式子特点，将原式转化为完全平方公式是解题的关键．17．如图，已知12∠=∠ ，45B ∠=︒ 则DCE ∠= _________．【答案】45°【分析】根据三角形外角的性质得出∠ACD=∠2+∠B ，再利用12∠=∠即可求出∠DCE 的度数.【详解】∵∠ACD=∠2+∠B=∠1+∠DCE ，45B ∠=︒∴DCE ∠=45B ∠=︒，故答案为：45°.【点睛】此题考查三角形的外角性质，三角形的外角等于与它不相邻的两个内角的和，熟记性质并熟练运用是解题的关键.三、解答题18．如图所示，在△ABC 中，∠ABC ＝∠ACB ．（1）尺规作图：过顶点A 作△ABC 的角平分线AD ；（不写作法，保留作图痕迹）（2）在AD 上任取一点E ，连接BE 、CE ．求证：△ABE ≌△ACE ．【答案】（1）如图所示,见解析；（2）见解析.【分析】（1）根据角平分线的尺规作图方法即可解答；（2）根据AD 是△ABC 的角平分线，得到∠BAD ＝∠CAD ，再由∠ABC ＝∠ACB 证得AB ＝AC ，即可证明△ABE ≌△ACE （SAS ）．【详解】（1）如图所示：（2）证明：∵AD 是△ABC 的角平分线，∴∠BAD ＝∠CAD ，∵∠ABC ＝∠ACB ，∴AB ＝AC ，∵在△ABE 和△ACE 中AB AC BAE CAE AE AE =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ACE （SAS ）．【点睛】此题考查角平分线的作图方法，角平分线定理的应用，熟记定理内容并熟练应用解题是关键.19．如图1，把一张长方形的纸片ABCD 沿对角线BD 折叠，点C 落在E 处，BE 交AD 于点F.（1）求证：FB=FD;（2）如图2，连接AE ，求证：AE ∥BD;（3）如图3，延长BA ，DE 相交于点G ，连接GF 并延长交BD 于点H ，求证：GH 垂直平分BD ．【答案】（1）证明见解析；（2）证明见解析；（3）证明见解析.【解析】试题分析：(1)根据矩形的性质和折叠的性质可得：AB＝DC=DE，∠BAD＝∠BCD＝∠BED=90°，根据AAS可证△ABF≌△EDF，根据全等三角形的性质可证BF=DF；(2)根据全等三角形的性质可证：FA=FE，根据等边对等角可得：∠FAE=∠FEA，根据三角形内角和定理可证：2∠AEF ＋∠AFE =2∠FBD＋∠BFD =180°，所以可证∠AEF=∠FBD，根据内错角相等，两直线平行可证AE∥BD；(3)根据矩形的性质可证：AD=BC=BE，AB=CD=DE，BD=DB，根据SSS可证：△ABD≌△EDB，根据全等三角形的性质可证：∠ABD=∠EDB，根据等角对等边可证：GB=GD，根据HL可证：△AFG≌△EFG，根据全等三角形的性质可证：∠AGF=∠EGF，所以GH垂直平分BD.试题解析：（1）∵长方形ABCD，∴AB＝DC=DE，∠BAD＝∠BCD＝∠BED=90°，在△ABF和△DEF中，{BAD BED AFB EFD AB DE∠=∠∠=∠=∴△ABF≌△EDF（AAS），∴BF=DF.（2）∵△ABF≌△EDF，∴FA=FE，∴∠FAE=∠FEA，又∵∠AFE=∠BFD，且2∠AEF ＋∠AFE =2∠FBD＋∠BFD =180°，∴∠AEF=∠FBD，∴AE∥BD，（3）∵长方形ABCD，∴AD=BC=BE，AB=CD=DE，BD=DB，∴△ABD≌△EDB（SSS），∴∠ABD=∠EDB，∴GB=GD，在△AFG和△EFG中，∠GAF＝∠GEF=90°，FA=FE，FG＝FG，∴△AFG≌△EFG（HL），∴∠AGF=∠EGF，∴GH垂直平分BD.【方法II】。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，BE=CF ，AE ⊥BC ，DF ⊥BC ，要根据“HL ”证明Rt △ABE ≌Rt △DCF ，则还需要添加一个条件是（ ）A ．AE=DFB ．∠A=∠DC ．∠B=∠CD ．AB= CD【答案】D【分析】根据垂直定义求出∠CFD ＝∠AEB ＝90°，由已知BE CF =，再根据全等三角形的判定定理推出即可．【详解】添加的条件是AB ＝CD ；理由如下： ∵AE ⊥BC ，DF ⊥BC ， ∴∠CFD ＝∠AEB ＝90°， 在Rt △ABE 和Rt △DCF 中，AB CDBE CF =⎧⎨=⎩， ∴Rt ABE Rt DCF ≅ (HL)． 故选：D ． 【点睛】本题考查了全等三角形的判定定理的应用，能灵活运用全等三角形的判定定理进行推理是解此题的关键． 2．实数a b 、在数轴上对应点如图所示，则化简()22b a b a+-- 的结果是（ ）A ．2aB ．2bC ．2b -D ．2a -【答案】B【解析】分析：先根据数轴确定a ，b 的范围，再根据二次根式的性质进行化简，即可解答． 详解：由数轴可得：a ＜0＜b ，a- b ＜0， ()22b a b a -=|b|+| a-b|-| a|,=b-(a-b)+a, =b-a+b+a ， =2b ． 故选B ．点睛：本题考查了实数与数轴，解决本题的关键是根据数轴确定a ，b 的范围．3．某市为解决部分市民冬季集中取暖问题，需铺设一条长4000米的管道，为尽量减少施工对交通造成的影响，施工时“…”，设实际每天铺设管道x 米，则可得方程4000400010x x--＝20，根据此情景，题中用“…”表示的缺失的条件应补为（ ）A ．每天比原计划多铺设10米，结果延期20天完成B ．每天比原计划少铺设10米，结果延期20天完成C ．每天比原计划多铺设10米，结果提前20天完成D ．每天比原计划少铺设10米，结果提前20天完成 【答案】C【解析】由给定的分式方程，可找出缺失的条件为：每天比原计划多铺设10米，结果提前20天完成．此题得解．【详解】解：∵利用工作时间列出方程：4000400020x 10x-=-， ∴缺失的条件为：每天比原计划多铺设10米，结果提前20天完成． 故选：C ． 【点睛】本题考查了由实际问题抽象出分式方程，由列出的分式方程找出题干缺失的条件是解题的关键． 4．关于一次函数123y x =-+，下列结论正确的是（ ） A ．图象过点（3，-1） B ．图象不经过第四象限C ．y 随 x 的增大而增大D ．函数图象与两坐标轴所围成的三角形面积是 6【答案】D【分析】根据一次函数的性质，依次分析各个选项，选出正确的选项即可．【详解】解：A 、令3x =，则13213y =-⨯+=，则图像过点（3，1）；故A 错误；B 、由103k =-<，则一次函数经过第二、四象限，故B 错误； C 、由103k =-<，则y 随 x 的增大而减小；故C 错误；D 、令0x =，则2y =，令0y =，则6x =，则面积为：12662⨯⨯=；故D 正确；故选：D. 【点睛】本题考查了一次函数图象上点的坐标特征和一次函数的性质，正确掌握一次函数的性质是解题的关键．5．下列因式分解中：①()3222x xy x x x y ++=+；②22()()x y x y x y -+=+-；③2244(2)x x x ++=+；④221(1)x x x ++=+；正确的个数为（ ）A ．3个B ．2个C ．1个D ．0个【答案】C【分析】根据因式分解的方法逐个判断即可．【详解】解：①()32221x xy x x x y ++=++，故①错误； ②22()()x y x y x y -+=-+-，故②错误； ③2244(2)x x x ++=+，正确， ④221(1)x x x ++≠+，故④错误， 所以正确的只有③， 故答案为：C ． 【点睛】本题考查了判断因式分解是否正确，掌握因式分解的方法是解题的关键．6．科学家可以使用冷冻显微术以高分辨率测定溶液中的生物分子结构，使用此技术测定细菌蛋白结构的分辨率达到0.22纳米，也就是0.000 000 000 22米．将0.000 000 000 22用科学记数法表示为（ ） A ．0.22×10﹣9 B ．2.2×10﹣10C ．22×10﹣11D ．0.22×10﹣8【答案】B【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为-n a 10⨯，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定． 【详解】解：0.000 000 000 22＝-102.210⨯， 故选：B ． 【点睛】此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．表示时关键要正确确定a 的值以及n 的值．7．等腰三角形的两条边长分别为9cm 和12cm ，则这个等腰三角形的周长是( ) A ．30cm B ．33cmC ．24cm 或 21cmD ．30cm 或 33cm【答案】D【分析】由于题中没有指明哪边是底哪边是腰，则应该分两种情况进行分析． 【详解】解：①当9为腰时，9＋9＞12，故此三角形的周长＝9＋9＋12＝30； ②当12为腰时，9＋12＞12，故此三角形的周长＝9＋12＋12＝1． 故选D ．【点睛】本题考查的是等腰三角形的性质和三边关系，解答此题时注意分类讨论，不要漏解． 8．下列关于分式方程增根的说法正确的是（ ） A ．使所有的分母的值都为零的解是增根 B ．分式方程的解为零就是增根 C ．使分子的值为零的解就是增根 D ．使最简公分母的值为零的解是增根 【答案】D【解析】试题分析：分式方程的增根是最简公分母为零时，未知数的值． 解：分式方程的增根是使最简公分母的值为零的解． 故选D ．考点：分式方程的增根． 9．下列计算正确的是（ ） A ．（a 2）3＝a 5B ．（15x 2y ﹣10xy 2）÷5xy ＝3x ﹣2yC ．10ab 3÷（﹣5ab ）＝﹣2ab 2D ．a ﹣2b 3•（a 2b ﹣1）﹣2＝66b a【答案】B【分析】根据合并同类项、幂的乘方和积的乘方进行计算即可． 【详解】A 、（a 2）3＝a 6，故A 错误；B 、（15x 2y ﹣10xy 2）÷5xy ＝3x ﹣2y ，故B 正确；C 、10ab 3÷（﹣5ab ）＝﹣2b 2，故C 错误；D 、a ﹣2b 3•（a 2b ﹣1）﹣2＝56b a，故D 错误；故选B ． 【点睛】本题考查了整式的混合运算，掌握合并同类项、幂的乘方和积的乘方的运算法则是解题的关键． 10．设,,a b c 是三角形的三边长，且满足222a b c ab bc ca ++=++，关于此三角形的形状有以下判断：①是直角三角形； ②是等边三角形； ③是锐角三角形；④是钝角三角形，其中正确的说法的个数有（ ） A ．1个 B ．2个C ．3个D ．4个【答案】B【分析】先将原式转化为完全平方公式，再根据非负数的性质得出a b c ==．进而判断即可． 【详解】∵222a b c ab bc ca ++=++，∴222222222a b c ab bc ca ++=++， 即()()()2220a b b c a c -+-+-=， ∴a b c ==，∴此三角形为等边三角形，同时也是锐角三角形． 故选：B ． 【点睛】本题考查了因式分解的应用，根据式子特点，将原式转化为完全平方公式是解题的关键． 二、填空题11．小亮用天平称得一个罐头的质量为2.026kg ，近似数2.026精确到0.1是_____． 【答案】2.0【解析】2.026kg ，精确到0. 1即对小数点后的0后边的数进行四舍五入，为2.0， 故答案为2.0.12．已知x 、y |2|0y +=，则24x y -的平方根为________．【答案】3±【分析】利用算术平方根及绝对值的非负性求出x 、y 的值，即可代入求出24x y -的平方根.|2|0y +=， ∴x-1=0，y+2=0， ∴x=1，y=-2， ∴24x y -=1+8=9， ∴24x y -的平方根为3±， 故答案为：3±. 【点睛】此题考查算术平方根及绝对值的非负性，求一个数的平方根，能根据题意求出x 、y 的值是解题关键.132(3)0y +-=_____．【答案】【分析】先根据算术平方根的非负性、偶次方的非负性求出x 、y 根的定义即可得．【详解】由题意得：120,30x y -=-=， 解得12,3x y ==，则1236xy =⨯=， 因此，xy 的平方根是6±，故答案为：6±． 【点睛】本题考查了算术平方根的非负性、平方根等知识点，掌握理解算术平方根的非负性是解题关键． 14．若2(3)|7|0a b -+-=，则以a 、b 为边长的等腰三角形的周长为______． 【答案】17【分析】先根据非负数的性质列式求出a 、b 的值，再分情况讨论求解即可． 【详解】∵2(3)|7|0a b -+-=，∴a －3=0，7－b =0，解得a=3，b=7 ①若a=3是腰长，则底边为7，三角形的三边分别为3、3、7， ∵3+3＜7，∴3、3、7不能组成三角形。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，分别用火柴棍连续搭建等边三角形和正六边形，公共边只用一根火柴棍．如果搭建等边三角形和正六边形共用了2018根火柴，并且等边三角形的个数比正六边形的个数多7，那么连续搭建的等边三角形的个数是（）…………A．291B．292C．293D．以上答案都不对【答案】C【分析】设搭建了x个正三角形，y个正六边形，则搭建正三角形用掉了（2x+1）根火柴棍，搭建正六边形用掉了（5y+1）根火柴棍，根据“搭建正三角形和正六边形共用了2018根火柴棍，并且正三角形的个数比正六边形的个数多7个”，即可得出关于x，y的二元一次方程组，解之即可得出结论．【详解】解：设搭建了x个正三角形，y个正六边形，则搭建正三角形用掉了（2x+1）根火柴棍，搭建正六边形用掉了（5y+1）根火柴棍，依题意，得：721512018 x yx y-=⎧⎨+++=⎩，解得：293286 xy=⎧⎨=⎩．故答案为:C．【点睛】本题考查了二元一次方程组的应用以及规律型：图形的变化类，找准等量关系，正确列出二元一次方程组是解题的关键．2．等腰三角形的一个外角是100°，则它的顶角的度数为（）A．80°B．80°或50°C．20°D．80°或20°【答案】D【分析】根据邻补角的定义求出与外角相邻的内角，再根据等腰三角形的性质分情况解答．【详解】∵等腰三角形的一个外角是100°，∴与这个外角相邻的内角为180°−100°=80°，当80°为底角时，顶角为180°-160°=20°，∴该等腰三角形的顶角是80°或20°.故答案选：D.【点睛】本题考查了等腰三角形的性质，解题的关键是熟练的掌握等腰三角形的性质.3．小明对九（1）、九（2）班（人数都为50人）参加“阳光体育”的情况进行了调查，统计结果如图所示.下列说法中正确的是( )A ．喜欢乒乓球的人数(1)班比(2)班多B ．喜欢足球的人数(1)班比(2)班多C ．喜欢羽毛球的人数(1)班比(2)班多D ．喜欢篮球的人数(2)班比(1)班多【答案】C 【解析】根据扇形图算出（1）班中篮球，羽毛球，乒乓球，足球，羽毛球的人数和（2）班的人数作比较，（2）班的人数从折线统计图直接可看出．【详解】解：A 、乒乓球：(1)班50×16%=8人，(2)班有9人，8<9，故本选项错误；B 、足球：(1)班50×14%=7人，(2)班有13人，7<13，故本选项错误；C 、羽毛球：(1)班50×40%=20人，(2)班有18人，20>18，故本选项正确；D 、篮球：(1)班50×30%=15人，(2)班有10人，15>10，故本选项错误.故选C.【点睛】本题考查扇形统计图和折线统计图，扇形统计图表现部分占整体的百分比，折线统计图表现变化，在这能看出每组的人数，求出(1)班喜欢球类的人数和(2)班比较可得出答案．4．在平面直角坐标系中，点()1,2A -关于x 轴的对称点坐标为（ ）A ．(1,2)-B ． (1,2)C ． (2,1)-D ．(1,2)--【答案】B【分析】根据关于x 轴对称的点的特点：横坐标相同，纵坐标互为相反数即可得出答案．【详解】根据关于x 轴对称的点的特点：横坐标相同，纵坐标互为相反数，可知点()1,2A -关于x 轴的对称点坐标为 (1,2)．故选：B ．【点睛】本题主要考查关于x 轴对称的点的特点，掌握关于x 轴对称的点的特点是解题的关键．5．下列各组数，可以作为直角三角形的三边长的是( )A ．2，3，4B ．7，24，25C ．8，12，20D ．5，13，15【答案】B【解析】试题解析：A、∵22+32≠42，∴不能构成直角三角形；B、∵72+242=252，∴能构成直角三角形；C、∵82+122≠202，∴不能构成直角三角形；D、∵52+132≠152，∴不能构成直角三角形．故选B．=，则AD一定是ABC的（）6．如图，已知BD CDA．角平分线B．高线C．中线D．无法确定【答案】C【分析】根据三角形中线的定义可知．=，所以AD一定是ABC的中线．【详解】因为BD CD【点睛】本题考查三角形的中线，掌握三角形中线的定义是解题的关键．7．已知实数a在数轴上对应的点如图所示，则22（的值等于（）-+a a1)A．2a+1B．-1C．1D．-2a-1【答案】D【解析】先根据数轴判断出a和a+1的正负，然后根据二次根式的性质化简，再合并同类项即可. 【详解】由数轴可知，a<0，a+1>0，22a a+（1)=-a-(a+1)=-a-a-1=-2a-1.故选D.【点睛】本题考查了利用数轴比较式子的大小及二次根式的化简，熟练掌握二次根式的性质是解答本题的关键. 8．若等腰三角形的周长为15cm，其中一边为7cm，则该等腰三角形的底边长为（）A．4cm B．4cm或7cm C．1cm或7cm D．7cm【答案】C【分析】分底为7cm和腰为7cm两种情况进行讨论，再根据三角形的三边关系进行验证．【详解】分两种情况讨论：①当底为7cm时，此时腰长为4cm和4cm，满足三角形的三边关系；②当腰为7cm时，此时另一腰为7cm，则底为1cm，满足三角形的三边关系；综上所述：底边长为1cm或7cm．故选：C．【点睛】本题考查了等腰三角形的性质及三角形的三边关系，分两种情况讨论是解答本题的关键．9．若一个三角形的三个内角的度数之比为1:1:2，则此三角形是()A．锐角三角形B．钝角三角形C．等边三角形D．等腰直角三角形【答案】D【解析】解：设这三个内角度数分别为x、x、2x，则x+x+2x=180°，解得：x=45°，∴2x=90°，∴这个三角形是等腰直角三角形，故选D．10．下列四位同学的说法正确的是()A．小明B．小红C．小英D．小聪【答案】C【分析】根据平方根、立方根、相反数的概念逐一判断即可．【详解】解：9的平方根是±3，故小明的说法错误；-27的立方根是-3，故小红的说法错误；-π的相反数是π，故小英的说法正确，16=416故答案为：C．【点睛】本题考查了平方根、立方根、相反数的概念，掌握上述的概念及基本性质是解题的关键．二、填空题112105的结果是__________________．【答案】1【分析】利用二次根式的计算法则正确计算即可．【详解】解：2102105425⨯⨯÷=== 故答案为：1．【点睛】 本题考查的是二次根式的乘除混合运算，要正确使用计算法则：a b ab ⋅=，a a b b=． 12．计算：(16x 3-8x 2+4x)÷(-2x)=________.【答案】-8x 1+4x-1【分析】直接利用整式除法运算法则计算得出答案．【详解】解：（16x 3-8x 1+4x ）÷（-1x ）=-8x 1+4x-1．故答案为-8x 1+4x-1．【点睛】本题主要考查整式的除法运算，解题关键是正确掌握运算法则． 13．如图，折叠长方形ABCD ，使顶点D 与BC 边上的点F 重合，已知长方形ABCD 的长度为10，宽为8，则DE =______．【答案】1【分析】由长方形ABCD 沿AE 折叠后，D 点恰与BC 边上的F 重合，可得AF ＝AD ＝10，DE ＝EF ，然后设EC ＝x ，则DE ＝EF ＝CD−EC ＝8−x ，首先在Rt △ABF 中，利用勾股定理求得BF 的长，继而可求得CF 的长，然后在Rt △CEF 中，由勾股定理即可求得方程：x 2＋42＝（8−x ）2，解此方程即可求得答案．【详解】∵四边形ABCD 是长方形，∴∠B ＝∠C ＝90︒，AD ＝BC ＝10，CD ＝AB ＝8，∵△ADE 折叠后得到△AFE ，∴AF ＝AD ＝10，DE ＝EF ，设EC ＝x ，则DE ＝EF ＝CD−EC ＝8−x ，∵在Rt △ABF 中，AB 2＋BF 2＝AF 2，∴82＋BF 2＝102，∴BF ＝6，∴CF ＝BC−BF ＝10−6＝4，∵在Rt△EFC中，EC2＋CF2＝EF2，∴x2＋42＝（8−x）2，解得：x＝3，∴DE=1故答案为1．【点睛】此题考查了折叠的性质、矩形的性质以及勾股定理．此题难度适中，注意掌握折叠前后图形的对应关系，注意数形结合思想与方程思想的应用．14．将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合，则∠1的度数为_________度．【答案】1【分析】根据三角形的内角和求出∠2=45°，再根据对顶角相等求出∠3=∠2，然后根据三角形的一个外角等于与它不相邻的两个内角的和计算即可．【详解】解：∵∠2=90°－45°=45°（直角三角形两锐角互余），∴∠3=∠2=45°，∴∠1=∠3+30°=45°+30°=1°．故答案为：1．【点睛】本题考查的是三角形的内角和，三角形外角的性质，熟知三角形的一个外角等于与它不相邻的两个内角的和是解答此题的关键．15．一种病毒的直径为0.000023m，这个数用科学记数法表示为_____．【答案】2.3×10﹣1．【分析】根据“科学记数法的定义”进行分析解答即可.【详解】5=⨯.0.000023 2.310-故答案为5⨯.2.310-【点睛】在把一个绝对值小于1的数用科学记数法表示为10n a ⨯的形式时，我们要注意两点：①a 必须满足：110a ≤<；②n 等于原来的数中从左至右第1个非0数字前面0的个数（包括小数点前面的0）的相反数.16．已知13a a +=，则221a a +的值是__________． 【答案】7【分析】已知等式两边平方，利用完全平方公式展开，变形即可求出所求式子的值．【详解】将13a a +=两边平方得：221()3a a +=， 即：221+2=9a a +， 解得：221a a+＝7， 故填7.【点睛】此题考查了完全平方公式，熟练掌握公式是解本题的关键．17．如图所示的棋盘放置在某个平面直角坐标系内，棋子A 的坐标为（﹣2，﹣3），棋子B 的坐标为（1，﹣2），那么棋子C 的坐标是_____．【答案】 (2,1)【分析】先由点A 、B 坐标建立平面直角坐标系，进而可得点C 坐标．【详解】解：由点A 、B 坐标可建立如图所示的平面直角坐标系，则棋子C 的坐标为（2，1）．故答案为：（2，1）．【点睛】本题考查了坐标确定位置，根据点A 、B 的坐标确定平面直角坐标系是解题关键．三、解答题18．先化简，再求值：（1）(2)(1)(1)+-+-x x x x ，其中x ＝﹣12（2）259123x x x -⎛⎫-÷ ⎪++⎝⎭，其中x ＝﹣1． 【答案】（1）2x+1，0；（2）12x +，1 【分析】（1）原式第一项利用单项式乘以多项式法则计算展开，第二项利用平方差公式化简，将x 的值代入计算即可求出值；（2）先根据分式的混合运算顺序和运算法则化简原式，再将x 的值代入计算可得．【详解】解：（1）原式＝x 2+2x ﹣（x 2﹣1），＝x 2+2x ﹣x 2+1，＝2x+1，当x ＝﹣12时，原式＝2×（﹣12）+1＝﹣1+1＝0； （2）原式＝253()22(3)(3)x x x x x x ++-⋅+++-， ＝3123x x x -⋅+-， ＝12x +， 当x ＝﹣1时，原式＝112-+＝1． 【点睛】此题考查了分式的化简求值，以及整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键． 19．先化简，再求值：（x+3）（x ﹣3）﹣x （x ﹣2），其中x=1．【答案】2x ﹣2，-3【解析】解：原式=x 2﹣2﹣x 2+2x=2x ﹣2．当x=3时，原式=2×3﹣2=﹣3．20．（1）在Rt ABC △中，90ACB ∠=︒，30A ∠=︒（如图1），BC 与AB 有怎样的数量关系？试证明你的结论．（2）图2，在四边形ABCD 中，,AC BD 相于点E ，90DAB CDB ∠=∠=︒，45ABD ∠=︒，30DCA ∠=︒，AB =AE 长．【答案】（1）AB=2BC，证明见解析；（2）3-1．【分析】（1）取AB的中点D，连接DC，得AD=BD=CD，再证明△DBC是等边三角形得BD=BC，从而可证明AB=2BC；（2）过点A作AF⊥BD于点F，先确定∠2及∠3的度数，在Rt△AFB中求出AF，BF；Rt△AEF中，求出EF，AE，在Rt△ABD中求出DB，继而得出DE.【详解】（1）AB=2BC证明：取AB的中点D，连接DC，∵∠ACB=90°，CD为斜边AB上的中线∴AD=BD=CD∴∠A=∠ACD=30°，∠B=∠BCD∴∠ADC=180°-∠A-∠ACD=120°∴∠B=∠BCD=12∠ADC=60°∴△DBC是等边三角形∴BD=BC∴AB=2BD=2BC即AB=2BC（2）过点A作AF⊥BD于点F，∵∠CDB=90°，∠1=30°，∴∠2=∠3=60°，在△AFB 中，∠AFB=90°，∵∠4=45°，，∴在Rt △AEF 中，∠AFE=90°，∴EF=1，AE=2，在△ABD 中，∠DAB=90°，，∴∴．【点睛】本题考查了勾股定理的知识，解答本题的关键是作辅助线构造特殊三角形．21．阅读下列计算过程，回答问题：解方程组2413,43 3.x y x y -=-⎧⎨+=⎩①② 解：①2⨯，得4813x y -=-，③②-③，得510y -=-，2y =．把2y =代入①，得2813x -=-，2813x =-，52x =． ∴该方程组的解是522x y ⎧=⎪⎨⎪=⎩以上过程有两处关键性错误，第一次出错在第_______步（填序号），第二次出错在第________步（填序号），以上解法采用了__________消元法．【答案】（1）；（2）；加减．【分析】逐步分析解题步骤，即可找出错误的地方；本解法采用了加减消元法进行求解.【详解】第一步中，①2⨯，得4813x y -=-，③等式右边没有⨯2，应该为4826x y -=-③第二步中，②-③，得510y -=-，应该为，1129y =，根据题意，得此解法是加减消元法；故答案为：（1）；（2）；加减．【点睛】此题主要考查利用加减消元法解二元一次方程组，熟练掌握，即可解题.22．已知，如图，点A 、D 、B 、E 在同一直线上，AC ＝EF ，AD ＝BE ，∠A ＝∠E ，（1）求证：△ABC ≌△EDF ；（2）当∠CHD ＝120°，求∠HBD 的度数．【答案】（1）详见解析；（2）60°．【分析】（1）根据SAS 即可证明：△ABC ≌△EDF ；（2）由（1）可知∠HDB ＝∠HBD ，再利用三角形的外角关系即可求出∠HBD 的度数．【详解】（1）∵AD ＝BE ，∴AB ＝ED ，在△ABC 和△EDF 中，AC EF A E AB ED =⎧⎪∠=∠⎨⎪=⎩，∴△ABC ≌△EDF （SAS ）；（2）∵△ABC ≌△EDF ，∴∠HDB ＝∠HBD ，∵∠CHD ＝∠HDB+∠HBD ＝120°，∴∠HBD ＝60°．【点睛】本题考查了全等三角形的判定与性质，三角形外角的性质，熟练掌握和灵活运用相关知识是解题的关键． 23．如图，已知M 是AB 的中点，CM=DM ，∠1=∠1．（1）求证：△AMC≌△BMD．（1）若∠1=50°，∠C=45°，求∠B的度数．【答案】（1）详见解析；（1）85°.【解析】（1）根据SAS证明即可；（1）由三角形内角和定理求得∠A，在根据全等三角形对应角相等，即可求得∠B的度数.【详解】（1）∵M是AB的中点，∴AM=BM，∵CM=DM，∠1=∠1∴△AMC≌△BMD（SAS）（1）∵△AMC≌△BMD，∴∠A=∠B，在△ACM中，∠A+∠1+∠C=180°，∴∠A=85°，∴∠B=85° .24．某市对城区部分路段的人行道地砖、绿化带、排水管等公用设施进行全面更新改造，根据市政建设的需要，需在35天内完成工程.现有甲、乙两个工程队有意承包这项工程，经调查知道，乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍，若甲、乙两工程队合作，只需10天完成．（1）甲、乙两个工程队单独完成此项工程各需多少天？（2）若甲工程队每天的工程费用是4万元，乙工程队每天的工程费用是2.5万元，请你设计一种方案，既能按时完工，又能使工程费用最少．【答案】（1）甲工程队单独完成该工程需15天，则乙工程队单独完成该工程需30天；（2）应该选择甲工程队承包该项工程．【分析】（1）设甲工程队单独完成该工程需x天，则乙工程队单独完成该工程需2x天．再根据“甲、乙两队合作完成工程需要10天”，列出方程解决问题；（2）首先根据（1）中的结果，从而可知符合要求的施工方案有三种：方案一：由甲工程队单独完成；方案二：由乙工程队单独完成；方案三：由甲乙两队合作完成．针对每一种情况，分别计算出所需的工程费用．【详解】（1）设甲工程队单独完成该工程需x天，则乙工程队单独完成该工程需2x天.根据题意得：101012x x+=方程两边同乘以2x，得230x=解得：15x=经检验，15x=是原方程的解.∴当15x =时，230x =.答：甲工程队单独完成该工程需15天，则乙工程队单独完成该工程需30天.（2）因为甲乙两工程队均能在规定的35天内单独完成，所以有如下三种方案：方案一：由甲工程队单独完成.所需费用为：41560⨯=（万元）；方案二：由乙工程队单独完成.所需费用为：2.53075⨯=（万元）；方案三：由甲乙两队合作完成.所需费用为：(4 2.5)1065+⨯=（万元）.∵756560>>∴应该选择甲工程队承包该项工程.【点睛】本题考查分式方程在工程问题中的应用．分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．25．如图，Rt ABC ∆中，90C ∠=︒，6AC =，8BC =．（1）用直尺和圆规在边BC 上找一点D ，使D 到AB 的距离等于CD ．（2）AD 是A ∠的________线．（3）计算（1）中线段CD 的长．【答案】（1）画图见解析；（2）平分；（1）1．【分析】（1）作∠A 的角平分线，以点A 为圆心，任意半径画弧，再分别以交点为圆心，大于交点线段长度一半为半径画弧，将交点和点A 连接，与BC 的交点为点D ，根据角平分线的性质即可得到，D 到AB 的距离等于CD ；（2）根据（1）可得，是平分线；（1）设CD x =，作DE AB ⊥于E ，则DE CD x ==，因为直角三角形DEB ，勾股定理列出方程即可求出答案．【详解】解：（1）利用角平分线的性质可得，角平分线的点到角两边距离相等，即作CBA ∠的角平分线，与CB 的交点即为D 点．如图：（2）由（1）可得AD 是A ∠的平分线．故填平分；（1）设CD x =，作DE AB ⊥于E ，则DE CD x ==，90C ∠=︒，6AC =，8BC =，10AB ∴=，1064EB ∴=-=，222DE BE DB +=，()22248x x ∴+=-，3x =，即CD 的长为3．【点睛】本题主要考查了尺规作图，熟练角平分线的画法和性质以及勾股定理是解决本题的关键．八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．下列因式分解正确的是（）A．x2﹣4=（x+4）（x﹣4）B．x2+2x+1=x（x+2）+1C．3mx﹣6my=3m（x﹣6y）D．2x+4=2（x+2）【答案】D【解析】试题分析：A、原式利用平方差公式分解得到结果，即可做出判断；B、原式利用完全平方公式分解得到结果，即可做出判断；C、原式提取公因式得到结果，即可做出判断；D、原式提取公因式得到结果，即可做出判断．解：A、原式=（x+2）（x﹣2），错误；B、原式=（x+1）2，错误；C、原式=3m（x﹣2y），错误；D、原式=2（x+2），正确，故选D点评：此题考查了因式分解﹣运用公式法与提公因式法，熟练掌握因式分解的方法是解本题的关键．2．如图，长方形纸片ABCD中，点E是AD的中点，且AE＝1，BE的垂直平分线MN恰好过C．则长方形的一边CD的长度为（）A．1 B．2C．3D．2【答案】C【分析】本题要依靠辅助线的帮助，连接CE，首先利用线段垂直平分线的性质证明BC=EC．求出EC后根据勾股定理即可求解．【详解】解:如图，连接EC．∵FC垂直平分BE,∴BC=EC (线段垂直平分线的性质)∵点E是AD的中点，AE=1, AD=BC,∴EC=2,利用勾股定理可得22==-=．AB CD2 13故选: C．【点睛】本题考查的是勾股定理、线段垂直平分线的性质以及矩形的性质，本题的关键是要画出辅助线，证明BC=EC 后易求解，本题难度中等．3．已知一个等腰三角形底边的长为5cm，一腰上的中线把其周长分成的两部分的差为3cm，则腰长为（）A．2cm B．8cm C．2cm或8cm D．10cm【答案】B【详解】解：如图，∵BD是△ABC的中线，∴AD=CD，∴两三角形的周长的差等于腰长与底边的差，∵BC=5cm，∴AB-5=3或5-AB=3，解得AB=8或AB=2，若AB=8，则三角形的三边分别为8cm、8cm、5cm，能组成三角形，若AB=2，则三角形的三边分别为2cm、2cm、5cm，∵2+2=4＜5，∴不能组成三角形，综上所述，三角形的腰长为8cm．故选：B．故选B．4．设(2a+3b)2＝(2a﹣3b)2+A，则A＝()A．6ab B．12ab C．0 D．24ab【答案】D【解析】∵(2a+3b)2＝4a 2+12ab+9b 2, (2a-3b)2+A =4a 2-12ab+9b 2+A, (2a+3b)2 =(2a-3b)2+A∴4a 2+12ab+9b 2=4a 2-12ab+9b 2+A,∴A=24ab ;故选D ．5成立的条件是( ) A ．13x > B ．13x ≥ C ．x ＞2 D ．123≤<x 【答案】C【分析】直接利用二次根式的性质得出关于x 的不等式进而求出答案．成立， ∴31020x x -≥⎧⎨->⎩， 解得：x ＞1．故选：C ．【点睛】此题主要考查了二次根式的性质，正确解不等式组是解题关键．6．若分式211x x -+的值为0，则x 应满足的条件是( ) A ．x = -1B ．x ≠ -1C ．x = ±1D ．x = 1【答案】D【分析】将分式方程转换成整式方程，一定要注意分母不为0【详解】由题意得：x 2-1=0 且x+1≠0，解得：x=1，故选D【点睛】求解分式方程是本题的考点，解分式方程时应注意分母不为07．下列运算错误的是（ ）A =B =C =D ．2(2= 【答案】A【分析】根据同类二次根式的合并，二次根式的乘除法则，分别进行各选项的判断即可．【详解】解：A 不是同类二次根式，不能直接合并，故本选项正确；B ，计算正确，故本选项错误；C 、6÷2=3，计算正确，故本选项错误；D 、（-2）2=2，计算正确，故本选项错误；故选A ．【点睛】本题考查了二次根式的加减及乘除运算，解答本题的关键是掌握二次根式的加减及乘除法则． 8．函数21y x =--与5y x =+的图象相交于点,M 则点M 的坐标是（ ）A ．()2,3-B ．()1,1-C ．()1,3-D ．()2,3--【答案】A【分析】把两个函数解析式联立，解方程组，方程组的解是交点的坐标． 【详解】解：由题意得：215y x y x =--⎧⎨=+⎩①② 215,x x ∴--=+解得：2,x =-把2x =-代入②得：3,y =2.3x y =-⎧∴⎨=⎩ 所以交点坐标是()2,3-．故选A ．【点睛】本题考查的是函数的交点坐标问题，解题的关键是转化为方程组问题．9．如图，将点A 0（-2，1）作如下变换：作A 0关于x 轴对称点，再往右平移1个单位得到点A 1，作A 1关于x 轴对称点，再往右平移2个单位得到点A 2，…，作A n －1关于x 轴对称点，再往右平移n 个单位得到点A n （n 为正整数），则点A 64的坐标为（ ）A ．（2078，-1）B ．（2014 ，-1）C ．（2078 ，1）D ．（2014 ，1）【答案】C 【分析】观察不难发现，角码为奇数时点的纵坐标为-1，为偶数时点的纵坐标为1，然后再根据向右平移的规律列式求出点的横坐标即可．【详解】解：由题意得：()()()()()123451,1,1,1,4,1,8,1,13,1A A A A A ----......由此可得角码为奇数时点的纵坐标为-1，为偶数时点的纵坐标为1，故64A 的纵坐标为1，则点64A 的横坐标为()16464212345.. (64220782)+⨯-+++++++=-+=，所以()642078,1A ． 故选C ．【点睛】 本题主要考查平面直角坐标系点的坐标规律，关键是根据题目所给的方式得到点的坐标规律，然后求解即可．10．如图，一副分别含有60︒和45︒角的两个直角三角板，拼成如下图形，其中90C =∠，45BAC ∠=，60EDC ∠=，则BFD ∠的度数是（ ）A ．15°B ．25°C ．30°D ．10°【答案】A 【分析】先由平角的定义求出∠BDF 的度数，根据三角形内角和定理即可得出结论．【详解】解：∵Rt △CDE 中，∠EDC=60°，∴∠BDF=180°-60°=120°，∵∠C=90°，∠BAC=45°，∴∠B=45°，∴∠BFD=180°-45°-120°=15°．故选：A ．【点睛】本题考查的是三角形的内角和，熟知三角形的内角和是解答此题的关键．二、填空题11．如图，50ABC ︒∠=，BD 平分ABC ∠，过D 作//DE AB 交于BC 于点E ，若点F 在射线BA 上，且满足DF DE =，则DFB ∠的度数为_________．【答案】130︒或50︒【分析】如图所示符合题目条件的有F ，F′两种情况，当在点F 位置时，可证的△BFD ≌△BED ，根据50ABC ︒∠=，即可得出∠BED=∠DFB=130°，当在点F′时，FD=D F′，根据第一种情况即可求解.【详解】解：如图所示当在点F 位置时∵BD 平分ABC ∠，由图形的对称性可知△BFD ≌△BED∴∠BED=∠DFB∵50ABC ︒∠=，//DE AB∴=50ABC DEC ∠=∠︒∴∠BED=∠DFB=130°当在点F′时由①知，FD=D F′，∠DFA=∠F F′D=50°综上所述：DFB ∠的度数为130︒或50︒故答案为：130︒或50︒.【点睛】本题主要考查的是等腰三角形的判定及其性质定理的应用问题，灵活运用有关定理来分析、判定、推理和解答是解题的关键.12．若分式22x x -+的值为0，则x 的值是 _____． 【答案】1【解析】分式值为零的条件：分子等于零且分母不等于零，由此列出不等式和等式，求解即可. 【详解】∵分式22x x -+的值为0，∴2020 xx⎧-⎨+≠⎩＝,∴x=1．故答案是：1.【点睛】考查了分式的值为零的条件，解题关键是：分式值为零的条件是分子等于零且分母不等于零．13．在平面直角坐标系中，已知一次函数y=x−1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1_____y2（填“＞”，“＜”或“=”）【答案】＜【分析】根据k=1结合一次函数的性质即可得出y=x﹣1为单调递增函数，再根据x1＜x1即可得出y1＜y1，此题得解．【详解】∵一次函数y=x﹣1中k=1，∴y随x值的增大而增大．∵x1＜x1，∴y1＜y1．故答案为＜．14．如图，直线483y x=+与x轴，y轴分别交于点A，点B，P是OB上的一点，若将PAB∆沿AP折叠，使点B恰好落在x轴上的点B'处，则直线AP的表达式是_________．【答案】y=12x+3.【分析】由直线483y x=+即可得到A(-6，0)，B(0，8)，再根据勾股定理即可得到P(0，3)，利用待定系数法即可得到直线AP的表达式．【详解】令0x=，则8y=，令0y=，则6x=-，由直线483y x=+与x轴，y轴交点坐标为：A(-6，0)，B(0，8)，∴AO=6，BO=8，∴22226810AB AO BO++=，由折叠可得AB'=AB=10，B'P=BP，∴OB'= AB'- AO 1064=-=，设P(0，y )，则OP=y ，B'P=BP=8y -，∵Rt △POB'中，PO 2+B'O 2=B'P 2，∴y 2+42=(8y -)2，解得：3y =，∴P(0，3)，设直线AP 的表达式为y kx b =+，则603k b b -+=⎧⎨=⎩， 123k b ⎧=⎪⎨⎪=⎩， ∴直线AP 的表达式是132y x =+． 故答案为：132y x =+． 【点睛】本题是一次函数与几何的综合题，考查了待定系数法求解析式及折叠问题．解题时，常常设要求的线段长为x ，然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．15．已知直角三角形的两边长分别为3、1．则第三边长为________．【答案】4【解析】试题分析：已知直角三角形两边的长，但没有明确是直角边还是斜边，因此分两种情况讨论： ①长为3的边是直角边，长为3=；②长为3、35；∴或4．考点：3．勾股定理；4．分类思想的应用．16．如图，已知ABC ∆中，5AC AB ==，3BC =，DE 垂直平分AB ，点D 为垂足，交AC 于点E ．那么EBC ∆的周长为__________．【答案】8【分析】先根据线段垂直平分线的性质得出AE=BE ，再根据AB=AC 即可得出AC 的长，进而得出结论．【详解】AB 的垂直平分线交AC 于点E ，垂足为点D ，AE BE ∴=，BE CE AE CE AC ∴+=+=，AB AC =，5AB =，3BC =，EBC ∴∆的周长()538BE CE BC AC BC =++=+=+=．故答案为：8．【点睛】本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．17．已知等腰三角形两边长为5、11，则此等腰三角形周长是_________________________．【答案】1【分析】根据等腰三角形腰的情况分类讨论，然后根据三角形的三边关系进行取舍，即可求出等腰三角形周长．【详解】解：若等腰三角形的腰长为5时∵5＋5＜11∴5、5、11构不成三角形，舍去；若等腰三角形的腰长为11时∵5＋11＞11∴5、11、11能构成三角形此时等腰三角形周长是5＋11＋11=1故答案为：1．【点睛】此题考查的是已知等腰三角形的两边求周长，掌握三角形的三边关系、等腰三角形的定义、分类讨论的数学思想是解决此题的关键．三、解答题18．如图，D ，E 分别是等边三角形ABC 边BC 、AC 上的一点，且BD CE =，连接AD 、BE 相交于点O ．（1）求证：ABD BCE ∆∆≌；（2）求AOE ∠的度数．【答案】（1）见解析；（2）60AOE =︒∠【分析】（1）根据等边三角形的性质，三条边都相等、三个内角都是60︒，即可根据边角边定理判定出ABD BCE ∆∆≌．（2）根据全等三角形的性质、三角形的外角定理进行转化即可得出AOE ∠的度数．【详解】（1）证明：∵ABC ∆是等边三角形∴AB BC =，ABC C ∠=∠在ABD ∆和BCE ∆中AB BC ABD C BD CE =⎧⎪∠=∠⎨⎪=⎩∴()ABD BCE SAS ∆∆≌（2）解：∵ABD BCE ∆∆≌∴CBE BAD ∠=∠∵60CBE ABE ABC ∠+∠=∠=︒∴60AOE BAD ABE ∠=∠+∠=︒【点睛】本题考查了等边三角形的性质、全等三角形的判定以及性质、三角形的外角定理等知识点，较为基础．19．先化简再求值：2344111a a a a a -+⎛⎫-+÷ ⎪++⎝⎭，再从0，-1，2中选一个数作为a 的值代入求值． 【答案】22+-a a，当0a =时，原式=1 【分析】先通分去括号，因式分解，变除为乘，约分得最简分式，然后确定a 不能取的数值，可取的值代入运算即可． 【详解】解：2344111a a a a a -+⎛⎫-+÷ ⎪++⎝⎭ 23(1)(1)(2)+11a a a a a --+-=÷+ 2(2+)(2)11(2)a a a a a -+=⋅+-22a a+=- ∵1,2a ≠-∴当0a =时，原式=20120+=-． 【点睛】本题考查了分式的化简求值，熟知相关运算是解题的关键．20．如图①，△ABC 是等边三角形，点P 是BC 上一动点（点P 与点B 、C 不重合），过点P 作PM ∥AC 交AB 于M ，PN ∥AB 交AC 于N ，连接BN 、CM ．（1）求证：PM+PN ＝BC ；（2）在点P 的位置变化过程中，BN ＝CM 是否成立？试证明你的结论；（3）如图②，作ND ∥BC 交AB 于D ，则图②成轴对称图形，类似地，请你在图③中添加一条或几条线段，使图③成轴对称图形（画出一种情形即可）．【答案】（1）见解析；（2）结论成立，理由见解析；（3）见解析【分析】（1）先证明△BMP ，△CNP 是等边三角形，再证明△BPN ≌△MPC ，从而PM=PB ，PN=PC ，可得PM+PN ＝BC ；（2）BN ＝CM 总成立，由（1）知△BPN ≌△MPC ，根据全等三角形的性质可得结论；（3）作ND ∥BC 交AB 于N ，作ME ∥BC 交AC 于M ，作EF ∥AB 交BC 于F ，连接DF 即可．【详解】（1）证明：∵△ABC 是等边三角形，∴AB ＝BC ，∠ABC ＝∠ACB ＝60°，∵PM ∥AC ，PN ∥AB ，∴∠BPM ＝∠ACB ＝60°，∠CPN ＝∠ABC ＝60°，∴△BMP ，△CNP 是等边三角形，∴∠BPM ＝∠CPN ＝60°，PN=PC ，PN=PC ，∴∠BPN ＝∠MPC ，∴△BPN ≌△MPC ，∴PM=PB ，PN=PC ，∵BP+PC ＝BC ，∴PM+PN ＝BC;（2）BN ＝CM 总成立，理由：由（1）知△BPN ≌△MPC ，∴BN ＝CM ；（3）解：如图③即为所求．作ND ∥BC 交AB 于N ，作ME ∥BC 交AC 于M ，作EF ∥AB 交BC 于F ，连接DF ，作直线AH ⊥BC 交BC 于H ，同（1）可证△AND ，△AME ，△BPM ，△CEF 都是等边三角形，∴D 与N ，M 与E ，B 与C 关于AH 对称.∴BM=CE ，∴BM=CF ，∴P 与F 关于AH 对称，∴所做图形是轴对称图形.【点睛】本题属于三角形综合题，考查了等边三角形的性质与判定，全等三角形的判定和性质，轴对称图形的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．21．某校为了丰富学生的校园生活，准备购进一批篮球和足球．其中篮球的单价比足球的单价多40元，用1500元购进的篮球个数与900元购进的足球个数相等．（1）篮球和足球的单价各是多少元？（2）该校打算用1000元购买篮球和足球，问恰好用完1000元，并且篮球、足球都买有的购买方案有哪几种？【答案】详见解析【分析】（1）首先设足球单价为x 元，则篮球单价为（x+40）元，根据题意可得等量关系：1500元购进的篮球个数=900元购进的足球个数，由等量关系可得方程150090040x x=+，再解方程可得答案； （2）设恰好用完1000元，可购买篮球m 个和购买足球n 个，根据题意可得篮球的单价×篮球的个数m+足球的单价×足球的个数n=1000，再求出整数解即可．【详解】（1）设足球单价为x 元，则篮球单价为（x+40）元，由题意得：150090040x x=+，。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，在ABC ∆中，AB AD DC ==，40BAD ∠=︒，则C ∠的度数为( )A ．30B ．35︒C ．40︒D ．45︒【答案】B 【分析】根据等腰三角形两底角相等求出∠B ＝∠ADB ，根据等边对等角可得∠C ＝∠CAD ，然后利用三角形内角和定理列式进行计算即可解答．【详解】∵AB ＝AD ，∠BAD ＝40°∴∠B ＝12（180°－∠BAD ）＝12（180°－40°）＝70° ∵AD ＝DC∴∠C ＝CAD在△ABC 中，∠BAC ＋∠B ＋∠C ＝180°即40°＋∠C ＋∠C ＋70°＝180°解得：∠C ＝35°故选：B【点睛】本题主要考查等腰三角形的性质：等角三角形两底角相等、等边对等角，掌握等腰三角形的性质是解题的关键．2．在坐标平面上有一个轴对称图形，其中A （3，﹣52）和B （3，﹣112）是图形上的一对对称点，若此图形上另有一点C （﹣2，﹣9），则C 点对称点的坐标是（ ）A ．（﹣2，1）B ．（﹣2，﹣32）C ．（﹣32，﹣9）D ．（﹣2，﹣1） 【答案】A【分析】先利用点A 和点B 的坐标特征可判断图形的对称轴为直线y=-4，然后写出点C 关于直线y=-4的对称点即可．【详解】解：∵A （3，﹣5）和B （3，﹣11）是图形上的一对对称点，∴点A 与点B 关于直线y ＝﹣4对称，∴点C （﹣2，﹣9）关于直线y ＝﹣4的对称点的坐标为（﹣2，1）．故选：A ．【点睛】本题考查了坐标与图形的变化，需要注意关于直线对称：关于直线x=m 对称，则两点的纵坐标相同，横坐标和为2m ；关于直线y=n 对称，则两点的横坐标相同，纵坐标和为2n ．3．在ΔABC 中，AB 3=，AC 5=，第三边BC 的取值范围是( )A ．10BC 13<<B ．4BC 12<< C ．3BC 8<<D ．2BC 8<<【答案】D【分析】已知两边，则第三边的长度应是大于两边的差而小于两边的和，这样就可求出第三边的边长的取值范围．【详解】∵AB=3，AC=5，∴5-3<BC<5+3，即2<BC<8，故选D.【点睛】考查了三角形三边关系，一个三角形任意两边之和大于第三边，任意两边之差小于第三边．熟练掌握三角形的三边关系是解题关键.4．如图，△ABC 中，点D 在BC 延长线上，则下列结论一定成立的是（ ）A ．∠1＝∠A+∠BB ．∠1＝∠2+∠AC ．∠1＝∠2+∠BD ．∠2＝∠A+∠B【答案】A 【分析】根据三角形外角性质逐一判断即可得答案．【详解】∵∠1是△ABC 的一个外角，∴∠1＝∠A+∠B ，故A 选项说法一定成立，∠1与∠2+∠A 的关系不确定，故B 选项说法不一定成立，∠1与∠2+∠B 的关系不确定，故C 选项说法不一定成立，∠2与∠A+∠B 的关系不确定，故D 选项说法不一定成立，故选：A ．本题考查三角形外角得性质，三角形的一个外角，等于和它不相邻得两个内角得和；熟练掌握三角形外角性质是解题关键．5．对于一次函数y ＝x ＋1的相关性质，下列描述错误的是（ ）A ．y 随x 的增大而增大；B ．函数图象与x 轴的交点坐标为（1，0）；C ．函数图象经过第一、二、三象限；D ．函数图象与坐标轴围成的三角形面积为12． 【答案】B【分析】由一次函数图像的性质可知：一次函数y ＝x ＋1中，11k b ==，，可判断A 、C ，把00x y ==，分别代入一次函数即可判断B 、D ．【详解】∵一次函数y ＝x ＋1，∴11k b ==，，∴函数为递增函数，∴y 随x 的增大而增大，A 正确；令0y =，得：1x =-， ∴函数图象与x 轴的交点坐标为()10-，， ∴B 不正确；∵11k b ==，，∴函数图象经过第一、二、三象限，∴C 正确；令0x =，得：1y =， ∴函数图象与坐标轴围成的三角形面积为：1122⨯⨯=S=11， ∴D 正确；故选：B ．【点睛】本题考查的是一次函数图象的性质，熟练掌握一次函数图象的性质是解答本题的关键．6．在85 ，3m n ，3x y +，1x ，3a b +中，分式的个数是（ ） A ．1B ．2C ．3D ．4 【答案】C 【解析】解：85，3x y +，的分母中均不含有字母，因此它们是整式，而不是分式． 3m n ，1x ，3a b +分母中含有字母，因此是分式．7．三个等边三角形的摆放位置如图所示，若12120∠+∠=︒，则3∠的度数为（ ）A ．90︒B ．60︒C ．45︒D ．30【答案】B 【分析】先根据图中是三个等边三角形可知三角形各内角均等于60°，用123∠∠∠，，表示出中间三角形的各内角，再根据三角形的内角和即可得出答案．【详解】解：如图所示，图中三个等边三角形，∴1806031203ABC ∠=︒-︒-∠=︒-∠，1806011201BAC ∠=︒-︒-∠=︒-∠，1806021202ACB ∠=︒-︒-∠=︒-∠，由三角形的内角和定理可知：180ABC BAC ACB ∠+∠+∠=︒，即1203+12011202180︒-∠︒-∠+︒-∠=︒，又∵12120∠+∠=︒，∴360∠=︒，故答案选B ．【点睛】本题考查等边三角形的性质及三角形的内角和定理，熟悉等边三角形各内角均为60°是解答此题的关键． 8．如图，射线OA 平分角，AB OM ⊥于点B ，AC ON ⊥于点C ，若130BOC ∠=︒，则BAC ∠=（ ）A ．70︒B ．60︒C ．50︒D ．40︒可求解．【详解】解：∵AB OM ⊥于点B ，AC ON ⊥于点C ，∠∠=90ABO ACO ∴=︒，130BOC ∠=︒，360-90-90-130=50∴∠=︒︒︒︒︒BAC ；故选：C ．【点睛】本题考查的是四边形的内角和，这里要注意到⊥构造的是90°的角即可求解本题．9．如图，△ABC 中，AC ＝BC ，AC 的垂直平分线分别交AC ，BC 于点E ，F ．点D 为AB 边的中点，点M 为EF 上一动点，若AB ＝4，△ABC 的面积是16，则△ADM 周长的最小值为（ ）A ．20B ．16C ．12D ．10【答案】D 【分析】连接CD ，CM ，由于△ABC 是等腰三角形，点D 是BA 边的中点，故CD ⊥BA ，再根据三角形的面积公式求出CD 的长，再再根据EF 是线段AC 的垂直平分线可知，点A 关于直线EF 的对称点为点C ，故CD 的长为AM ＋MD 的最小值，由此即可得出结论．【详解】解：连接CD ，CM ．∵△ABC 是等腰三角形，点D 是BA 边的中点，∴CD ⊥BA ，∴S △ABC ＝12BA•CD ＝12×4×CD ＝16，解得CD ＝8， ∵EF 是线段AC 的垂直平分线，∴点A 关于直线EF 的对称点为点C ，∴MA ＝MC ，∵CD≤CM+MD ，∴CD 的长为AM+MD 的最小值，∴△ADM 的周长最短＝（AM+MD ）+AD ＝CD+12BA ＝8+12×4＝8+2＝1． 故选：D ．【点睛】本题考查的是轴对称−最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．10．满足下列条件的是直角三角形的是（ ）A ．4BC =，5AC =，6AB =B ．13BC =，14AC =，15AB = C ．::3:4:5BC AC AB =D ．::3:4:5A B C ∠∠∠= 【答案】C【分析】要判断一个角是不是直角，先要知道三条边的大小，用较小的两条边的平方和与最大的边的平方比较，如果相等，则三角形为直角三角形；否则不是．【详解】A ．若BC=4，AC=5，AB=6，则BC 2+AC 2≠AB 2，故△ABC 不是直角三角形；B.若13BC =，14AC =，15AB =，则AC 2+AB 2≠CB 2，故△ABC 不是直角三角形； C ．若BC ：AC ：AB=3：4：5，则BC 2+AC 2=AB 2，故△ABC 是直角三角形；D ．若∠A ：∠B ：∠C=3：4：5，则∠C ＜90°，故△ABC 不是直角三角形；故答案为：C ．【点睛】本题主要考查了勾股定理的逆定理，如果三角形的三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形就是直角三角形．二、填空题11．下面的图表是我国数学家发明的“杨辉三角”，此图揭示了（a+b ）n （n 为非负整数）的展开式的项数及各项系数的有关规律．请你观察，并根据此规律写出：（a ﹣b ）5=__________．【答案】a 5﹣5a 4b+10a 3b 2﹣10a 2b 3+5ab 4﹣b 5【分析】根据“杨辉三角”，寻找解题的规律：（a+b ）n 的展开式共有（n+1）项，各项系数依次为2n ．根据规律，（a-b ）5的展开式共有6项，各项系数依次为1，-5，10，-10，5，-1，系数和为27，554322345【详解】请在此输入详解！12．化简：1xy x y ++＝_____． 【答案】x【分析】把分子分解因式，然后利用分式的性质化简得出答案．【详解】解：原式＝()11x y y ++＝x ．故答案为：x ．【点睛】本题考查了分式的约分，熟练掌握分式的基本性质是解答本题的关键，本题也考查了因式分解. 13．如图，直线a //b ，∠1=42°，∠2=30°，则∠3=______度．【答案】1【分析】如图，利用三角形的外角，可知∠3=∠2+∠4，由平行知∠1=∠4，则∠3=∠2+∠1即可．【详解】如图， ，∵a ∥b ，∴∠1=∠4，又∵∠3=∠2+∠4，∴∠3=∠2+∠1=30゜+42゜=1゜．故答案为：1．【点睛】本题考查角的度数问题，关键是把∠3转化为∠1与∠2有关的式子表示．14．已知2211221899m n n m +=--，则11m n-的值等于___________． 【答案】29- 【分析】先进行配方计算出m ，n 的值，即可求出11m n-的值.22112218099m n n m +++=- 22112929099m m n n -++++= 221133033m n ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭+ 1130,3033m n +=-= 9,9m n =-=， 则1129m n -=-， 故答案为：29-. 【点睛】本题是对完全平方非负性的考查，熟练掌握配方知识和完全平方非负性是解决本题的关键.15．如果关于x 的二次三项式294x mx -+是完全平方式，那么m 的值是__________．【答案】12±【分析】根据两平方项确定出这两个数，再根据乘积二倍项列式求解即可．【详解】解：∵294x mx -+是完全平方式∴-mx=±2×2•3x ，解得：m=±1．故答案为：±1.【点睛】本题是完全平方公式的考查，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．16．如图，在ABC ∆中，90C =∠，AD 平分CAB ∠，交BC 于点D ，若ADC 60∠=，2CD =，则ABC ∆周长等于__________．【答案】3+6【分析】根据含有30°直角三角形性质求出AD,根据勾股定理求出AC ，再求出AB 和BD 即可.所以30DAC ∠=o所以AD=2CD=4所以AC=22224223AD CD -=-=因为AD 平分CAB ∠，所以CAB ∠=2o DAC 60∠=所以o B BAD 30∠=∠=所以BD=AD=4,AB=2AC=43所以ABC ∆周长=AC+BC+AB=23+43+2+4==63+6故答案为：63+6【点睛】考核知识点：含有30°直角三角形性质，勾股定理；理解直角三角形相关性质是关键.17．如图，以数轴的单位长度线段为边做一个正方形以表示数2的点为圈心，正方形对角线长为半径画半圆，交数轴于点A 和点B ,则点A 表示的数是_________【答案】22-【分析】由图可知，正方形的边长是12，所以点A 表示的数为2减去圆的半径即可求得.22112+=2，则点A 表示的数为22-故答案为22-【点睛】本题主要考查了数轴的基本概念，圆的基本概念以及正方形的性质，根据题意求出边长是解题的关键.三、解答题18．随着智能手机的普及，微信抢红包已成为春节期间人们最喜欢的活动之一，某校七年级（1）班班长对全班50名学生在春节期间所抢的红包金额进行统计，并绘制成了统计图．请根据以上信息回答：（1）该班同学所抢红包金额的众数是______，中位数是______；（2）该班同学所抢红包的平均金额是多少元？（3）若该校共有18个班级，平均每班50人，请你估计该校学生春节期间所抢的红包总金额为多少元？【答案】（1）30，30；（2）32.4元；（3）29160元.【分析】（1）由表提供的信息可知，一组数据的众数是这组数中出现次数最多的数，而中位数则是将这组数据从小到大（或从大到小）依次排列时，处在最中间位置的数，据此可知这组数据的众数，中位数； （2）根据加权平均数的计算公式列式求解即可；（3）利用样本平均数乘以该校总人数即可．【详解】(1)捐款30元的人数为20人，最多，则众数为30，中间两个数分别为30和30，则中位数是30.故答案为30，30；(2)该班同学所抢红包的平均金额是(6×10+13×20+20×30+8×50+3×100)÷50=32.4(元)；(3)18×50×32.4=29160(元).答：估计该校学生春节期间所抢的红包总金额为29160元.【点睛】此题考查加权平均数，中位数，众数，解题关键在于利用统计图中的数据进行计算.19．如图，AB ＝AC ，AD ＝AE.求证：∠B ＝∠C ．【答案】证明见解析.【分析】欲证明∠B ＝∠C ，只要证明△AEB ≌△ADC.【详解】证明：在△AEB 和△ADC 中，AB AC A A =⎧⎪∠=∠⎨，∴△AEB ≌△ADC(SAS)∴∠B ＝∠C.【点睛】本题考查全等三角形的判定和性质，解题的关键是正确寻找全等三角形全等的条件20．先化简，再求值：2112111x x x x +⎛⎫-÷ ⎪-+-⎝⎭，其中x 满足240x -=． 【答案】22x ，12． 【分析】根据分式混合运算的法则把原式进行化简，再求出x 的值代入进行计算即可.【详解】原式11(1)(1)()112x x x x x +-=-⨯-++ 1122x x x x +-=-++ 22x =+ 因为：240x -=2x =当2x =时，原式12=． 【点睛】本题考查分式的化简求值，熟练掌握计算法则是解题关键.21．如图，△ABC 中，∠ACB ＝90°，∠A ＝40°，CD 、BE 分别是△ABC 的高和角平分线，求∠BCD 、∠CEB 的度数．【答案】∠BCD ＝40°，∠CEB ＝65°．【分析】在Rt △ABC 中求得∠ABC=50°，在由CD ⊥AB ，即∠BDC=90°知∠BCD=40°，根据BE 平分∠ABC 知∠CBE=12∠ABC=25°，由∠CEB=90°-∠CBE 可得答案． 【详解】∵在△ABC 中，∠ACB ＝90°，∠A ＝40°，∴∠ABC ＝50°，∵CD ⊥AB ，∴∠BDC ＝90°，∴∠BCD ＝40°，∵BE 平分∠ABC ，∴∠CBE＝12∠ABC ＝25°， ∴∠CEB ＝90°﹣∠CBE ＝65°．【点睛】本题主要考查三角形内角和定理，解题的关键是掌握三角形的内角和定理及角平分线的定义． 22．如图,矩形ABCD 中,点P 是线段AD 上一动点, O 为BD 的中点, PO 的延长线交BC 于Q .(1)求证: OP OQ =;(2)若=8AD cm ,6AB cm =,P 从点A 出发,以l /cm s 的速度向D 运动(不与D 重合).设点P 运动时间为()t s ,请用t 表示PD 的长;并求t 为何值时,四边形PBQD 是菱形.【答案】 (1)证明见解析；(2) PD=8-t ，运动时间为74秒时，四边形PBQD 是菱形． 【分析】(1)先根据四边形ABCD 是矩形，得出AD ∥BC ，∠PDO=∠QBO ，再根据O 为BD 的中点得出△POD ≌△QOB ，即可证得OP=OQ ；(2)根据已知条件得出∠A 的度数，再根据AD=8cm ，AB=6cm ，得出BD 和OD 的长，再根据四边形PBQD 是菱形时，利用勾股定理即可求出t 的值，判断出四边形PBQD 是菱形．【详解】(1)∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠PDO=∠QBO ，又∵O 为BD 的中点，∴OB=OD ，在△POD 与△QOB 中，PDO QBO OD OBPOD QOB ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△POD ≌△QOB ，∴OP=OQ ；(2)PD=8-t ，∵四边形PBQD 是菱形，∴BP=PD= 8-t ，∵四边形ABCD 是矩形，∴∠A=90°，在Rt △ABP 中，由勾股定理得：AB 2+AP 2=BP 2，即62+t 2=(8-t)2，解得：t=74， 即运动时间为74秒时，四边形PBQD 是菱形． 【点睛】本题考查了矩形的性质，菱形的性质，全等三角形的判定与性质，勾股定理等，熟练掌握相关知识是解题关键.注意数形结合思想的运用.23．解方程组：（1）2931x y y x +=⎧⎨-=⎩ （2）41423243x y x y +=⎧⎪-+⎨-=-⎪⎩ 【答案】（1）14x y =⎧⎨=⎩；（2）23x y =⎧⎨=⎩ 【分析】（1）利用加减法消元法和代入消元法求解即可；（2）先把②去分母，然后利用加减法消元法和代入消元法求解即可；【详解】（1）2931x y y x +=⎧⎨-=⎩①②， 由②得31y x ③，③代入①得2(31)9x x ++=，解得1x =，把1x =代入③得314y =+=，∴方程组的解是14x y =⎧⎨=⎩； （2）方程组可化为414346x y x y +=⎧⎨-=-⎩①②， ①+②得48x =，解得2x =，把2x =代入①得2414y +=，解得3y =，∴原方程组的解是23x y =⎧⎨=⎩． 【点睛】本题主要考查了解二元一次方程组，掌握解二元一次方程组是解题的关键.24．雾霾天气持续笼罩我国大部分地区，困扰着广大市民的生活，口罩市场出现热销，小明的爸爸用12000元购进甲、乙两种型号的口罩在自家商店销售，销售完后共获利2700元，进价和售价如表：（1）小明爸爸的商店购进甲、乙两种型号口罩各多少袋？（2）该商店第二次以原价购进甲、乙两种型号口罩，购进甲种型号口罩袋数不变，而购进乙种型号口罩袋数是第一次的2倍，甲种口罩按原售价出售，而效果更好的乙种口罩打折让利销售，若两种型号的口罩全部售完，要使第二次销售活动获利不少于2460元，每袋乙种型号的口罩最多打几折？【答案】（1）购进甲型号口罩300袋，购进乙种型号口罩200袋；（2）每袋乙种型号的口罩最多打9折【解析】（1）设小明爸爸的商店购进甲种型号口罩x 袋，乙种型号口罩y 袋，根据“小明的爸爸用12000元购进甲、乙两种型号的口罩，销售完后共获利2700元”列出方程组，解方程组即可求解；（2）设每袋乙种型号的口罩打m 折，根据“两种型号的口罩全部售完，要使第二次销售活动获利不少于2460元”列出不等式，解不等式即可求解.【详解】（1）设小明爸爸的商店购进甲种型号口罩x 袋，乙种型号口罩y 袋，根据题意可得， 203012000562700x y x y +=⎧⎨+=⎩， 解得：300200x y =⎧⎨=⎩ ， 答：该商店购进甲种型号口罩300袋，乙种型号口罩200袋；（2）设每袋乙种型号的口罩打m 折，由题意可得，300×5+400（0.1m ×36-30）≥2460，解得：m ≥9，答：每袋乙种型号的口罩最多打9折．【点睛】本题考查了二元一次方程组的应用及一元一次不等式的应用，解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的数量关系，列出方程组或不等式求解．25．已知△ABC中，AB＝17，AC＝10，BC边上得高AD=8,则边BC的长为________【答案】21或1【分析】由题意得出∠ADB=∠ADC=10°，由勾股定理求出BD、CD，分两种情况，容易得出BC的长．【详解】分两种情况：①如图1所示：∵AD是BC边上的高，∴∠ADB=∠ADC=10°，22222222=-=-==-=-=BD AB AD CD AC AD17815,1086∴BC=BD+CD=15+6=21；②如图2所示：同①得：BD=15，CD=6，∴BC=BD-CD=15-6=1；综上所述：BC的长为21或1．【点睛】本题考查了勾股定理、分类讨论思想；熟练掌握勾股定理，并能进行推理计算是解决问题的关键．八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，//AB CD ，以点A 为圆心，小于AC 长为半径作弧，分别交AB 、AC 于E 、F 两点，再分别以,E F 为圆心，大于12EF 的长为半径画弧，两弧交于点G ，作射线AG ，交CD 于点H ，若ACD ∠120=︒，则AHD ∠的度数为（ ）A ．150︒B ．115︒C ．120︒D ．160︒【答案】A 【分析】先由平行线的性质得出,180CHA HAB ACD CAB ∠=∠∠+∠=︒，进而可求出CAB ∠的度数，再根据角平分线的定义求出HAB ∠的度数，则CHA ∠的度数可知，最后利用180AHD CHA ∠=︒-∠求解即可．【详解】∵//AB CD∴,180CHA HAB ACD CAB ∠=∠∠+∠=︒120ACD ∠=︒180********CAB ACD ∴∠=︒-∠=︒-︒=︒∵AH 平分CAB ∠1302HAB CAB ∴∠=∠=︒ 30CHA ∴∠=︒180150AHD CHA ∴∠=︒-∠=︒故选：A ．【点睛】本题主要考查平行线的性质和角平分线的画法及定义，掌握平行线的性质和角平分线的画法及定义是解题的关键．2．下列语句是命题的是( )(1)两点之间，线段最短．(2)如果20x >，那么0x >吗?(3)如果两个角的和是90度，那么这两个角互余．(4)过直线外一点作已知直线的垂线．A ．(1)(2)B ．(3)(4)C ．(1)(3)D ．(2)(4)【答案】C【分析】根据命题的定义对四句话进行判断即可．【详解】（1）两点之间，线段最短，它是命题；(2)如果20x >，那么0x >吗?不是命题；（3）如果两个角的和是90度，那么这两个角互余，它是命题；(4)过直线外一点作已知直线的垂线，是作法不是命题．故选C ．【点睛】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．3．在式子1x x +，3x ，a π，2y x 中，分式的个数是( ) A ．1B ．2C ．3D ．4 【答案】B【分析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式． 【详解】3x ，a π分母中均不含有字母，因此它们是整式，而不是分式． 其余两个式子的分母中含有字母，因此是分式．故选：B ．【点睛】本题考查了分式的定义，特别注意π不是字母，是常数，所以a π不是分式，是整式． 4．下列实数为无理数的是（ ）A ．0.101B C ．227 D ．π【答案】D【解析】由题意根据无理数的概念即无理数就是无限不循环小数，进行分析判断可得答案．【详解】解：A 、0.101是有理数，B 是有理数，C 、227是有理数， D 、π是无限不循环小数即是无理数， 故选：D ．【点睛】本题考查的是无理数的概念、掌握算术平方根的计算方法是解题的关键．5．下列各运算中，计算正确的是（ ）A ．()3253a b a b =B ．()325327a a -=C ．624x x x ÷=D ．()333a b a b +=+ 【答案】C【分析】根据积的乘方、同底数幂的除法、多项式的乘法逐项判断即可.【详解】A. ()3263a ba b =，错误； B. ()3263-27a a -=，错误；C. 624x x x ÷=，正确；D. ()32233+33+a a b b b ab a ++=，错误.故选C.【点睛】本题考查积的乘方、同底数幂的除法、多项式的乘法等知识，熟练掌握各计算公式是解题的关键. 6．对于实数a 、b 定义一种运算“※”，规定a ※b =21a b -，如1※3=2113-，则方程x ※（﹣2）=234x x --的解是（ ）A ．4x =B ．5x =C ．6x =D ．7x = 【答案】C【分析】根据定义新运算公式列出分式方程，然后解分式方程即可．【详解】解：∵x ※（﹣2）=234x x-- ∴()212342x xx =---- 解得：x=6经检验：x=6是原方程的解故选C ．【点睛】此题考查的是定义新运算和解分式方程，掌握定义新运算公式和解分式方程的一般步骤是解决此题的关键．7．将长方形纸片按如图所示的方式折叠,BC 、BD 为折痕，若∠ABC=35°,则∠DBE 的度数为A ．55°B ．50°C ．45°D ．60°【答案】A 【分析】根据折叠的性质可知∠ABC=∠A’BC ，∠DBE=∠DBE’，然后根据平角等于180°代入计算即可得出答案．【详解】解：由折叠的性质可知∠ABC=∠A’BC=35°，∠DBE=∠DBE’，∴∠EBE’=180°-∠ABC-∠A’BC=180°-35°-35°=110°，∴∠DBE=∠DBE’=12∠EBE’=12×110°=55°． 故选A ．【点睛】本题考查了折叠的性质和角的计算，熟知折叠后重合的角相等是解决此题的关键．8．在食品包装、街道、宣传标语上随处可见节能、回收、绿色食品、节水的标志，在下列这些示意图标中，是轴对称图形的是（ ） A ． B ． C ． D ．【答案】B【分析】根据轴对称图形的定义即可解答．【详解】根据轴对称图形的定义可知：选项A 不是轴对称图形；选项B 是轴对称图形；选项C 不是轴对称图形；选项D 不是轴对称图形．故选B ．【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合． 9．三个等边三角形的摆放位置如图所示，若12120∠+∠=︒，则3∠的度数为（ ）A ．90︒B ．60︒C ．45︒D ．30【答案】B 【分析】先根据图中是三个等边三角形可知三角形各内角均等于60°，用123∠∠∠，，表示出中间三角形的各内角，再根据三角形的内角和即可得出答案．【详解】解：如图所示，图中三个等边三角形，∴1806031203ABC ∠=︒-︒-∠=︒-∠，1806011201BAC ∠=︒-︒-∠=︒-∠，1806021202ACB ∠=︒-︒-∠=︒-∠，由三角形的内角和定理可知：180ABC BAC ACB ∠+∠+∠=︒，即1203+12011202180︒-∠︒-∠+︒-∠=︒，又∵12120∠+∠=︒，∴360∠=︒，故答案选B ．【点睛】本题考查等边三角形的性质及三角形的内角和定理，熟悉等边三角形各内角均为60°是解答此题的关键． 10．广州市发布2019年上半年空气质量状况，城区PM2.5平均浓度为0.000029克/立方米，0.000029用科学记数法表示为（ ）A ．2.9510-⨯B ．2.9510⨯C ．2.9610-⨯D ．2.9610⨯【答案】A【分析】科学记数法表示较小数时的形式为10n a -⨯ ，其中110a ≤<，n 为正整数，只要找到a,n 即可．【详解】50.000029 2.910-=⨯故选：A ．【点睛】本题主要考查科学记数法，掌握科学记数法的形式是解题的关键．二、填空题11．比较大小：35211【答案】＞ 【分析】根据二次根式的性质，对35、211 【详解】∵3545，211444544， ∴35211故答案是：＞．【点睛】本题主要考查二次根式的性质，掌握二次根式的性质，是解题的关键．12．因式分解：3269a a a -+=_________.【答案】2(3)a a -【分析】利用提取公因式a 和完全平方公式进行因式分解．【详解】3269a a a -+=22(69)(3)a a a a a -+=-【点睛】本题考查了提公因式法与公式法的综合运用，正确应用完全平方公式是解题关键．13．在正整数中，2111111222⎛⎫⎛⎫⎛⎫-=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ 2111111333⎛⎫⎛⎫⎛⎫-=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ 2111111444⎛⎫⎛⎫⎛⎫-=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭利用上述规律，计算2222111111112342019⎛⎫⎛⎫⎛⎫⎛⎫-⨯-⨯-⨯⨯-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭_____． 【答案】10102019【分析】先依据题例用平方差公式展开，再利用乘法分配律交换位置后，相乘进行约分计算即可．【详解】解：2222111111112342019⎛⎫⎛⎫⎛⎫⎛⎫-⨯-⨯-⨯⨯- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=11111111(1)(1)(1)(1)(1)(1)(1)(1)22334420192019+-+-+-+- =11111111(1)(1)(1)(1)(1)(1)(1)(1)23420192342019++++⨯---- =3452020123201823420192342019⨯⨯⨯⨯⨯⨯⨯⨯⨯ =2020122019⨯ =10102019， 故答案为：10102019． 【点睛】 本题考查运用因式分解对有理数进行简便运算．熟练掌握平方差公式是解题关键．14．当x 时，分式11x-有意义．【答案】x≠1【解析】试题分析：分式有意义，则分母x-1≠0，由此易求x的取值范围．试题解析：当分母x-1≠0，即x≠1时，分式11x-有意义．考点：分式有意义的条件．15．如图，一个密封的圆柱形油罐底面圆的周长是10m，高为13m，一只壁虎在距底面1m的A处，C处有食物，壁虎沿油罐的外侧面爬行到C处捕食，它爬行的最短路线长为_____m．【答案】1【分析】根据题意画出圆柱的侧面展开图的平面图形，进而利用勾股定理得出答案．【详解】解：如图所示：由题意可得：AD=5m，CD=12m，则AC=2212513+=(m)，故答案为：1．【点睛】本题主要考查了平面展开图的最短路径问题，正确画出平面图形是解题的关键．161x+有意义，则x的取值范围为_____．【答案】x≥﹣1且x≠1．【解析】根据被开方式是非负数，且分母不等于零列式求解即可. 【详解】解：由题意得：x+1≥0，且x﹣1≠0，解得：x≥﹣1且x≠1，故答案为x≥﹣1且x≠1．【点睛】本题考查了代数式有意义时字母的取值范围，代数式有意义时字母的取值范围一般从几个方面考虑：①当代数式是整式时，字母可取全体实数；②当代数式是分式时，考虑分式的分母不能为0；③当代数式是二次根式时，被开方数为非负数．17．在某次数学测验后，王老师统计了全班50名同学的成绩，其中70分以下的占12%，70～80分的占24%，80～90分的占36%，则90分及90分以上的有__________人．【答案】1【分析】先求出90分及90分以上的频率，然后根据“频数=频率×数据总和”求解．【详解】90分及90分以上的频率为：1-12%-24%-36%=28%，∵全班共有50人，∴90分及90分以上的人数为：50×28%=1(人)．故答案为：1．【点睛】本题考查了频数和频率的知识，解答本题的关键是掌握频数=频率×数据总和．三、解答题18．阅读下列题目的解题过程：已知a、b、c为△ABC的三边，且满足a2c2﹣b2c2=a4﹣b4，试判断△ABC的形状．解：∵a2c2﹣b2c2=a4﹣b4（A）∴c2（a2﹣b2）=（a2+b2）（a2﹣b2）（B）∴c2=a2+b2（C）∴△ABC是直角三角形问：（1）上述解题过程，从哪一步开始出现错误？请写出该步的代号：；（2）错误的原因为：；（3）本题正确的结论为：．【答案】（1）C；（2）没有考虑a=b的情况；（3）△ABC是等腰三角形或直角三角形．【解析】（1）根据题目中的书写步骤可以解答本题；（2）根据题目中B到C可知没有考虑a=b的情况；（3）根据题意可以写出正确的结论．【详解】（1）由题目中的解答步骤可得，错误步骤的代号为：C，故答案为C；（2）错误的原因为：没有考虑a=b的情况，故答案为没有考虑a=b的情况；（3）本题正确的结论为：△ABC是等腰三角形或直角三角形，故答案为△ABC是等腰三角形或直角三角形．【点睛】本题考查因式分解的应用、勾股定理的逆定理，解答本题的关键是明确题意，写出相应的结论，注意考虑问题要全面．19．已知：如图，AB AC =，点D 是BC 的中点，AB 平分DAE ∠，AE BE ⊥.（1）求证：AD AE =；（2）若//BE AC ，试判断ABC ∆的形状，并说明理由.【答案】（1）见解析；（2）△ABC 为等边三角形【分析】（1）根据三线合一定理，得AD ⊥BD ，由角平分线的性质定理，得BE=BD ，即可得到Rt ABE Rt ABD ∆∆≌，即可得到结论；（2）由BE ∥AC ，则∠EAC=∠E=90°，由角平分线的性质，得到∠EAB=∠BAD=∠CAD=30°，则∠BAC ＝60°，即可得到答案.【详解】（1）证明：如图，∵AB=AC ，点D 是BC 中点∴AD ⊥BD∵AB 平分∠DAE ，AE ⊥BE∴BE=BD∴Rt ABE Rt ABD ∆∆≌∴AD=AE ；（2）解：△ABC 为等边三角形∵BE ∥AC∴∠EAC=∠E=90°∵AB=AC ，AD 是中线∴AD 平分∠BAC∵AB 平分∠DAE∴∠EAB=∠BAD=∠CAD=30°∴∠BAC ＝∠BAD+∠CAD ＝60°∵AB ＝AC∴△ABC 是等边三角形.【点睛】本题考查了等边三角形的判定和性质，全等三角形的判定和性质，角平分线的性质定理，解题的关键是熟练掌握所学的知识进行解题.20．如图1，AC BC =，CD CE =，ACB DCE α∠=∠=，AD 、BE 相交于点M ，连接CM ． ()1求证：BE AD =；()2求AMB ∠的度数(用含α的式子表示)；()3如图2，当90α=时，点P 、Q 分别为AD 、BE 的中点，分别连接CP 、CQ 、PQ ，判断CPQ 的形状，并加以证明．【答案】（1）见解析；（2）α；（3）CPQ 为等腰直角三角形，证明见解析.【解析】分析（1）由CA=CB ，CD=CE ，∠ACB=∠DCE=α，利用SAS 即可判定△ACD ≌△BCE ；（2）根据△ACD ≌△BCE ，得出∠CAD=∠CBE ，再根据∠AFC=∠BFH ，即可得到∠AMB=∠ACB=α；（3）先根据SAS 判定△ACP ≌△BCQ ，再根据全等三角形的性质，得出CP=CQ ，∠ACP=∠BCQ ，最后根据∠ACB=90°即可得到∠PCQ=90°，进而得到△PCQ 为等腰直角三角形．详解：()1如图1，ACB DCE α∠=∠=，ACD BCE ∴∠=∠，在ACD 和BCE 中，CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ACD ∴≌()BCE SASBE AD ∴=；()2如图1，ACD ≌BCE ，CAD CBE ∴∠=∠， ABC 中，180BAC ABC α∠+∠=-，180BAM ABM α∴∠+∠=-，ABM ∴中，()180180AMB αα∠=--=；()3CPQ 为等腰直角三角形．证明：如图2，由()1可得，BE AD =， AD ，BE 的中点分别为点P 、Q ，AP BQ ∴=， ACD ≌BCE ，CAP CBQ ∴∠=∠，在ACP 和BCQ 中，CA CB CAP CBQ AP BQ =⎧⎪∠=∠⎨⎪=⎩，ACP ∴≌()BCQ SAS ，CP CQ ∴=，且ACP BCQ ∠=∠，又90ACP PCB ∠+∠=，90BCQ PCB ∴∠+∠=，90PCQ∴∠=，CPQ∴为等腰直角三角形．点睛：本题主要考查了全等三角形的判定与性质，等腰直角三角形的判定以及三角形内角和定理等知识，解题的关键是正确寻找全等三角形解决问题．21．小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示（1）家与图书馆之间的路程为多少m，小玲步行的速度为多少m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．【答案】（1）家与图书馆之间路程为4000m，小玲步行速度为100m/s；（2）自变量x的范围为0≤x≤403；（3）两人相遇时间为第8分钟．【分析】(1)认真分析图象得到路程与速度数据；(2)采用方程思想列出小东离家路程y与时间x之间的函数关系式；(3)两人相遇实际上是函数图象求交点．【详解】解：(1)结合题意和图象可知，线段CD为小东路程与时间函数图象，折现O﹣A﹣B为小玲路程与时间图象则家与图书馆之间路程为4000m，小玲步行速度为（4000-2000）÷（30-10）=100m/s(2)∵小东从离家4000m处以300m/min的速度返回家，则xmin时，∴他离家的路程y=4000﹣300x，自变量x的范围为0≤x≤403，(3)由图象可知，两人相遇是在小玲改变速度之前，∴4000﹣300x=200x解得x=8∴两人相遇时间为第8分钟．故答案为(1)4000，100；(2)y=4000﹣300x，0≤x≤403；(3)第8分钟.【点睛】。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．点M （3，-4）关于y 轴的对称点的坐标是（ ）A ．（3，4）B ．（-3，4）C ．（-3，-4）D ．（-4，3）【答案】C【分析】根据关于y 轴对称点的坐标特点：横坐标互为相反数，纵坐标不变，即点P （x ，y ）关于y 轴的对称点P ′的坐标是（−x ，y ）．【详解】∵点M （3，−4），∴关于y 轴的对称点的坐标是（−3，−4）．故选：C ．【点睛】此题主要考查了关于x 轴、y 轴对称点的坐标特点，熟练掌握关于坐标轴对称的特点是解题关键． 2．已知ABC ∆的三边长分别为a b c 、、，且()()()M a b c a b c a b c =+++---那么( ) A ．0M >B ．0M ≥C ．0M =D ．0M < 【答案】D【分析】根据三角形的三边关系即可求解.【详解】∵ABC ∆的三边长分别为a b c 、、∴a b c ++＞0，a b c +-＞0，a b c --＜0∴()()()M a b c a b c a b c =+++---＜0故选D.【点睛】此题主要考查三角形的三边关系的应用，解题的关键是熟知两边之和大于第三边.3．在平面直角坐标系中，点A （﹣1，2）关于x 轴对称的点B 的坐标为（ ）A ．（﹣1，2）B ．（1，2）C ．（1，﹣2）D ．（﹣1，﹣2） 【答案】D【解析】试题分析：关于x 轴对称的点的坐标特征是横坐标相同，纵坐标互为相反数，从而点A （﹣1，2）关于x 轴对称的点B 的坐标是（﹣1，﹣2）．故选D ．4．如图，点E ，F 在AC 上，AD=BC ，DF=BE ，要使△ADF ≌△CBE ，还需要添加的一个条件是（ ）A ．∠A=∠CB ．∠D=∠BC ．AD ∥BC D ．DF ∥BE【答案】B【分析】利用全等三角形的判定与性质进而得出当∠D=∠B 时，△ADF ≌△CBE ．【详解】当∠D=∠B 时， 在△ADF 和△CBE 中∵AD BC D B DF BE =⎧⎪∠=∠⎨⎪=⎩，∴△ADF ≌△CBE （SAS ）考点：全等三角形的判定与性质．5．如图，将正方形ABCD 的一角折叠，折痕为AE ，点B 落在点B ′处，B AD ∠'比BAE ∠大48︒.设BAE ∠和B AD ∠'的度数分别为x ︒和y ︒，那么x 和y 满足的方程组是()A ．4890y x y x -=⎧⎨+=⎩B ．482y x y x -=⎧⎨=⎩C ．48290x y y x -=⎧⎨+=⎩D ．48290y x y x -=⎧⎨+=⎩【答案】D 【分析】根据由将正方形ABCD 的一角折叠，折痕为AE ，∠B'AD 比∠BAE 大48°的等量关系即可列出方程组.【详解】解：.设BAE ∠和B AD ∠'的度数分别为x ︒和y ︒由题意可得：48290y x y x -=⎧⎨+=⎩故答案为D.【点睛】本题考查了二元一次方程组的应用，根据翻折变换的性质以及正方形的四个角都是直角寻找等量关系是解答本题的关键.6．如图，在▱ABCD 中，AB=2，BC=1．以点C 为圆心，适当长为半径画弧，交BC 于点P ，交CD 于点Q ，再分别以点P ，Q 为圆心，大于12PQ 的长为半径画弧，两弧相交于点N ，射线CN 交BA 的延长线于点E ，则AE 的长是（ ）A ．12B ．1C ．65D ．32【答案】B【解析】分析：只要证明BE=BC 即可解决问题；详解：∵由题意可知CF 是∠BCD 的平分线，∴∠BCE=∠DCE ．∵四边形ABCD 是平行四边形，∴AB ∥CD ，∴∠DCE=∠E ，∠BCE=∠AEC ，∴BE=BC=1，∵AB=2，∴AE=BE-AB=1，故选B ．点睛：本题考查的是作图-基本作图，熟知角平分线的作法是解答此题的关键．7．如图，在ABC ∆中，10AB AC ==，AB 的垂直平分线DE 交AC 于点D ，连接BD ，若BCD 的周长为17，则BC 的长为（ ）A ．6B ．7C ．8D ．9【答案】B 【分析】根据线段垂直平分线的性质可得AD=BD ，AB=2AE ，把△BCD 的周长转化为AC 、BC 的和，然后代入数据进行计算即可得解．【详解】∵DE 是AB 的垂直平分线，∴AD=BD ，AB=2AE=10，∵△BCD 的周长=BD+CD+BC=AD+CD+BC=AC+BC=11，∵AB=AC=10，∴BC=11-10=1．故选：B ．【点睛】此题考查线段垂直平分线的性质．此题比较简单，解题的关键是掌握垂直平分线上任意一点，到线段两端点的距离相等定理的应用．8．小意是一位密码翻译爱好者，在她的密码手册中，有这样一条信息：-a b ，22x y -，x y -，x y +，22a b -，+a b 分别对应下列六个字：泗、我、大、美、爱、水，现将()()222222x y a x y b ---因式分解，结果呈现的密码信息可能是（ ）A ．我爱美B ．我爱水C ．我爱泗水D ．大美泗水 【答案】D【分析】先提取公因式，再利用平方差公式：22()()a b a b a b -=+-进行因式分解，然后根据密码手册即可得．【详解】()()222222x y a x y b ---2222)()(x y a b =--)(()))((a x y x a b b y =+--+由密码手册得，可能的四个字分别为：美、大、水、泗观察四个选项，只有D 选项符合故选：D ．【点睛】本题考查了利用提取公因式和平方差公式进行因式分解，因式分解的方法主要包括：提取公因式法、公式法、十字相乘法、换元法等，熟记各方法是解题关键．9．下列命题中，为真命题的是（ ）A ．直角都相等B ．同位角相等C ．若22a b =，则a b =D ．若a b ＞，则22a b --＞【答案】A【分析】根据直角、同位角的性质，平方与不等式的性质依次分析即可．【详解】A.直角都相等90°，所以此项正确；B.两直线平行，同位角相等，故本选项错误；C.若22a b =，则a b =或=-a b ，故本选项错误；D.若a b ＞，则22a b -<-，本项正确，故选A ．【点睛】本题考查的是命题与定理，熟知各项性质是解答此题的关键．10．甲、乙、丙、丁四人进行射箭测试，每人10次，测试成绩的平均数都是8.9环，方差分别是s甲2＝0.45，s乙2＝0.50，s丙2＝0.55，s丁2＝0.65，则测试成绩最稳定的是（）A．甲B．乙C．丙D．丁【答案】A【分析】根据方差的定义，方差越小数据越稳定即可得出答案．【详解】解：∵s甲2＝0.45，s乙2＝0.50，s丙2＝0.55，s丁2＝0.65，∴S丁2＞S丙2＞S乙2＞S甲2，∴射箭成绩最稳定的是甲；故选：A．【点睛】本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．二、填空题11．如图，数轴上点A、B对应的数分别是1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径作圆弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，当点M在点B的右侧时，点M对应的数是_____．【答案】5【分析】连接OC，根据题意结合勾股定理求得OC的长，即可求得点M对应的数．【详解】如图，连接OC，由题意可得：OB=2，BC=1，则22OC=+=，215故点M 对应的数是：5 ．故答案为5．【点睛】本题考查了勾股定理的应用，根据题意求得OC 的长是解决问题关键．12．等腰三角形的一个外角为100°，则它的底角是______.【答案】80°或50°【分析】等腰三角形的一个外角等于100°，则等腰三角形的一个内角为80°，但已知没有明确此角是顶角还是底角，所以应分两种情况进行分类讨论．【详解】∵等腰三角形的一个外角等于100°，∴等腰三角形的一个内角为80°，当80°为顶角时,其他两角都为50°、50°，当80°为底角时,其他两角为80°、20°，所以等腰三角形的底角可以是50°,也可以是80°.答案为：80°或50°.【点睛】本题考查等腰三角形的性质，当已知角没有明确是顶角还是底角的时候，分类讨论是关键.13．现有一个长方形纸片ABCD ，其中6,10AB AD ==．如图所示，折叠纸片，使点A 落在BC 边上的A '处，折痕为PQ ，当点A '在BC 上移动时，折痕的端点P 、Q 也随之移动．若限定P 、Q 分别在AB 、AD 边上移动，则点A '在BC 边上可移动的最大距离为_________．【答案】1【解析】根据翻折的性质，可得BA ′与AP 的关系，根据线段的和差，可得A ′C ，根据勾股定理，可得A ′C ，根据线段的和差，可得答案．【详解】①当P 与B 重合时，BA ′＝BA ＝6，CA ′＝BC−BA ′＝10−6＝1，②当Q 与D 重合时，由勾股定理，得CA 22A D CD '-8，CA ′最远是8，CA ′最近是1，点A ′在BC 边上可移动的最大距离为8−1＝1，故答案为1．【点睛】本题考查了翻折变换，利用了翻折的性质，勾股定理，分类讨论是解题关键．14．如图，两个三角形全等，则∠α的度数是____【答案】50°【解析】根据全等三角形的对应角相等解答．【详解】∵两个三角形全等，a与c的夹角是50°，∴∠α=50°，故答案是：50°．【点睛】考查的是全等三角形的性质，掌握全等三角形的对应角相等是解题的关键．15．我们知道，三角形的稳定性在日常生活中被广泛运用.要使不同的木架不变形，四边形木架至少要再钉1根木条；五边形木架至少要再钉2根木条；…按这个规律，要使n边形木架不变形至少要再钉______________根木条.（用n表示，n为大于3的整数）【答案】n-3【分析】根据三角形具有稳定性，需要的木条数等于过多边形的一个顶点的对角线的条数．【详解】过n边形的一个顶点可以作（n-3）条对角线，把多边形分成（n-2）个三角形，所以，要使一个n边形木架不变形，至少需要（n-3）根木条固定．故答案为：（n-3）．【点睛】考查了三角形的稳定性以及多边形的对角线的问题，解题关键是将问题转换成把多边形分成三角形的问题．16．已知点M(a，1)与点N(﹣2，b)关于y轴对称，则a﹣b=____．【答案】1．【分析】根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”求出a、b的值，然后计算即可得解．【详解】∵点M（a，1）与点N（-2，b）关于y轴对称，∴a=2，b=1，∴a-b=2-1=1．故答案为：1．【点睛】此题考查关于x轴、y轴对称的点的坐标，解题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数．17．如图所示，已知点A、D、B、F在一条直线上，AC=EF，AD=FB，要使△ABC≌△FDE，还需添加一个条件，这个条件可以是_______．（只需填一个即可）【答案】∠A=∠F（答案不唯一）【详解】要判定△ABC≌△FDE，已知AC=FE，AD=BF，则AB=CF，具备了两组边对应相等，故添加夹角∠A=∠F，利用SAS可证全等；或添加AC∥EF得夹角∠A=∠F，利用SAS可证全等；或添加BC=DE，利用SSS可证全等．三、解答题18．“校园手机”现象越来越受社会的关注．春节期间，小飞随机调查了城区若干名同学和家长对中学生带手机现象的看法，统计整理并制作了如下的统计图：(1) 这次的调查对象中，家长有人；(2) 图2中表示家长“赞成”的圆心角的度数为度；(3)开学后，甲、乙两所学校对各自学校所有学生带手机情况进行了统计，发现两校共有576名学生带手机，且乙学校带手机学生数是甲学校带手机学生数的35，求甲、乙两校中带手机的学生数各有多少？【答案】（1）1；（2）36°；（3）甲：360，乙：216【分析】（1）认为无所谓的有80人，占总人数的20%，据此即可求得总人数；（2）赞成的人数所占的比例是：40400，所占的比例乘以360°即可求解；（3）甲、乙两校中带手机的学生数分别有x、y人，根据两校共有2384名学生带手机，且乙学校带手机的学生数是甲学校带手机学生数的35，即可列方程组，从而求解． 【详解】解：（1）家长人数为 80÷20%=1． （2）表示家长“赞成”的圆心角的度数为40400×360°=36°﹒ （3）设甲、乙两校中带手机的学生数分别有x 、y 人，则由题意有57635x y y x +=⎧⎪⎨=⎪⎩，解得360216x y =⎧⎨=⎩， 即甲、乙两校中带手机的学生数分别有360人，216人﹒【点睛】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．19．已知：如图，在Rt ABC ∆中，90C ∠=︒，30A ∠=︒，（1）作B 的平分线BD ，交AC 于点D ；作AB 的中点E ；（要求：尺规作图，保留作图痕迹，不必写作法和证明）（2）连接DE ，求证：ADE BDE ∆≅∆．【答案】（1）见解析；（2）见解析【分析】（1）①以B 为圆心，任意长为半径画弧，交AB 、BC 于F 、N ，再以F 、N 为圆心，大于12FN 长为半径画弧，两弧交于点M ，过B 、M 画射线，交AC 于D ，线段BD 就是∠B 的平分线；②分别以A 、B 为圆心，大于12AB 长为半径画弧，两弧交于X 、Y ，过X 、Y 画直线与AB 交于点E ，点E 就是AB 的中点；（2）首先根据角平分线的性质可得∠ABD 的度数，进而得到∠ABD ＝∠A ，根据等角对等边可得AD ＝BD ，再加上条件AE ＝BE ，ED ＝ED ，即可利用SSS 证明△ADE ≌△BDE ．【详解】解：（1）作出B 的平分线BD ； 作出AB 的中点E ．（2）证明：160302ABD ∠=⨯︒=︒，30A ∠=︒， ABD A ∴∠=∠，AD BD ∴=，在ADE ∆和BDE ∆中，AE BE ED ED AD BD =⎧⎪=⎨⎪=⎩()ADE BDE SSS ∴∆≅∆．【点睛】此题主要考查了复杂作图，以及全等三角形的判定，关键是掌握基本作图的方法和证明三角形全等的判定方法．20．如图所示，数轴上表示1,3-的对应点分别为A B 、，点B 关于A 点的对称点为C ，设点C 所表示的数为x ．()1写出实数x 的值．()2求(23x 的值． 【答案】（1）23x =-（2）1683+【分析】（1）由点B 关于A 点的对称点为C ，可知A 点为B 、C 两点的中点，根据线段中点的性质求解即可；（2）将x 值代入，计算即可求得答案．【详解】解：（1）数轴上3-的对应点分别为A B 、，点B 关于A 点的对称点为C∴A 点为B 、C 两点的中点31x +=- 解得：23x =--故实数23x =--（2）当23x =--时，()2223(233)(223)1683x -=---=--=+故()231683x -=+．【点睛】 本题考查了实数与数轴、代数式求值，解题的关键是利用线段的中点正确求出x 的值．21．如图，已知ABC ∆是直角三角形，90ACB ∠=︒，//AD BC ，点E 是线段AC 上一点，AE BC =且DE AB ⊥，连接DC.（1）证明：AB ED =.（2）若55B ∠=︒，求CDE ∠的度数.【答案】（1）见解析；（2）10°【分析】（1）证明ABC DEA ∆≅∆即可说明AB ED =；（2）由（1）可得CDA ∆是等腰直角三角形，根据55DEA B ∠=∠=︒可求35EDA ∠=︒，最后CDE CDA EDA ∠=∠-∠即可解答．【详解】解：（1）证明：90ACB ∠=︒，//AD BC ，90EAD ACB ∴∠=︒=∠，90CAB DAB ∴∠+∠=︒，DE AB ∵⊥，90EDA DAB ∴∠+∠=︒，EDA CAB ∴∠=∠， 又BC AE =，()ABC DEA AAS ∴∆≅∆．AB ED ∴=．（2）ABC DEA ∆≅∆，AC DA ∴=，55DEA B ∠=∠=︒，905535EDA ∴∠=︒-︒=︒．AC DA =，90DAC ∠=︒，45CDA ∴∠=︒．∴∠=∠-∠=︒-︒=︒．CDE CDA EDA453510【点睛】本题主要考查了全等三角形的判定和性质，运用全等三角形解决问题时，要注意：（1）全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．（2）在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．22．如图（1），一架云梯AB斜靠在一竖直的墙上，云梯的顶端A距地面15米，梯子的长度比梯子底端B 离墙的距离大5米.（1）这个云梯的底端B离墙多远?（2）如图（2），如果梯子的顶端下滑了8m（AC的长），那么梯子的底部在水平方向右滑动了多少米?【答案】（1）这个云梯的底端B离墙20米；（2）梯子的底部在水平方向右滑动了4米.【解析】（1）由题意得OA=15米，AB-OB=5米，根据勾股定理OA2+OB2=AB2，可求出梯子底端离墙有多远；（2）由题意得此时CO=7米，CD=AB=25米，由勾股定理可得出此时的OD，继而能和（1）的OB进行比较．【详解】解：（1）设梯子的长度为米，则云梯底端B离墙为米。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．若点()1,a y 、()21,a y +在直线2y kx =+上，且12y y >，则该直线所经过的象限是（ ） A ．第一、二、三象限B ．第一、二、四象限C ．第二、三、四象限D ．第四象限【答案】B【分析】通过比较直线上两点的坐标大小，即可判断该一次函数的增减性，从而判断其所经过的象限．【详解】解：在直线2y kx =+上两点()1,a y 、()21,a y +满足：a ＜a ＋1，12y y >∴此函数y 随x 的增大而减小∴k ＜0，∵2＞0∴该直线经过第一、二、四象限故选B ．【点睛】此题考查的是判断直线所经过的象限，掌握一次函数的增减性与各项系数的关系是解决此题的关键． 2．如图，在△ABC 中，点D 是∠ABC 和∠ACB 的角平分线的交点，∠A ＝80°，∠ABD ＝30°，则∠DCB 为（ ）A ．25°B ．20°C ．15°D ．10°【答案】B 【分析】由BD 是∠ABC 的角平分线，可得∠ABC ＝2∠ABD ＝60°；再根据三角形的内角和求得∠ACB ＝40°；再由角平分线的定义确定∠DCB 的大小即可.【详解】解：∵BD 是∠ABC 的角平分线，∴∠ABC ＝2∠ABD ＝2×30°＝60°，∴∠ACB ＝180°﹣∠A ﹣∠ABC ＝180°﹣80°﹣60°＝40°，∵CD 平分∠ACB ，∴∠DCB ＝12∠ACB ＝12×40°＝20°， 故选B ．【点睛】本题考查了三角形的内角和和三角形角平分线的相关知识，解答本题的关键在于所学知识的活学活用.3．如图，等腰直角三角形纸片ABC 中，∠C=90°，把纸片沿EF 对折后，点A 恰好落在BC 上的点D 处，若CE=1，AB=42，则下列结论一定正确的个数是（ ）①2；②BD>CE ；③∠CED+∠DFB=2∠EDF ；④△DCE 与△BDF 的周长相等；A ．1个B ．2个C ．3个D ．4个 【答案】D【分析】利用等腰直角三角形的相关性质运用勾股定理以及对应角度的关系来推导对应选项的结论即可.【详解】解：由2AC=BC=4，则AE=3=DE ，由勾股定理可得2 ①正确； 21>，②正确；由∠A=∠EDF=45°，则2∠EDF=90°，∠CED=90°-∠CDE=90°-（∠CDF-45°）= 135°-∠CDF=135°-（∠DFB+45°）= 90°-∠DFB ，故∠CED+∠DFB=90°=2∠EDF ，③正确；△DCE 的周长2+4，△BDF 的周长222正确的选项有4个，故选：D.【点睛】本题主要考查等腰直角三角形的相关性质以及勾股定理的运用,本题涉及的等腰直角三角形、翻折、勾股定理以及边角关系，需要熟练地掌握对应性质以及灵活的运用.4．下列各数中，能化为无限不循环小数的是( )A ．13B ．15C ．17D ．2π 【答案】D【解析】根据无理数的概念进行选择判断．【详解】解:A.13属于无限循环小数； B.10.25= 属于有限小数； C.17 属于无限循环小数； D.2π属于无限不循环小数． 故选D ．【点睛】本题考查无理数的概念，比较简单．5．--种饮料有大、中、小3种包装，一个中瓶比2个小瓶便宜2角，一个大瓶比一个中瓶加上一个小瓶贵4角，若大、中、小各买1瓶，需要9元6角.设小瓶单价是x 角，大瓶的单价是y 角，可列方程组为（ ）A ．39832x y y x +=⎧⎨-=⎩B ．39832x y y x +=⎧⎨+=⎩C ．29834x y y x +=⎧⎨-=⎩D ．39822x y x y -=⎧⎨+=⎩ 【答案】A【分析】设设小瓶单价为x 角，大瓶为y 角，根据题意列出二元一次方程组，求出方程组的解即可．【详解】解：设小瓶单价为x 角，大瓶为y 角，则中瓶单价为（2x-2）角，可列方程为：39832x y y x +=⎧⎨-=⎩， 故选A.【点睛】本题考查了由实际问题抽象出二元一次方程组，正确得出等量关系是解题关键．6．下列计算中，正确的是（ ）A ．21(3)9--=-B ．428x x x ⋅=C ．2339()a a a ⋅=D ．0(2)1a -= 【答案】C【详解】选项A ， ()23--=21193()=-； 选项B ，426x x x ⋅=；选项C ， ()323639 a a a a a ⋅=⋅=；选项D ，()021a -=，必须满足a-2≠0.故选C.7．若ABC ∆≌DEF ∆，则根据图中提供的信息，可得出x 的值为（ ）A ．30B ．27C ．35D ．40【答案】A【分析】在△ABC 中利用三角形内角和可求得∠A=70°，则可得∠A 和∠D 对应，则EF=BC ，可得到答案．【详解】∵∠B=50°，∠C=60°，∴∠A=70°，∵△ABC ≌△DEF ，∴∠A 和∠D 对应，∴EF=BC=30，∴x=30，故选：A ．【点睛】本题主要考查全等三角形的性质，掌握全等三角形的对应边、对应角相等是解题的关键．8．等腰三角形的一条边长为6，另一边长为13，则它的周长为（ ）A ．25B ．25或32C ．32D ．19【答案】C【解析】因为等腰三角形的两边分别为6和13，但没有明确哪是底边，哪是腰，所以有两种情况，需要分类讨论．【详解】解：当6为底时，其它两边都为13，6、13、13可以构成三角形，周长为32；当6为腰时，其它两边为6和13，6、6、13不可以构成三角形．故选C ．【点睛】本题考查了等腰三角形的性质及三角形三边关系；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论.9．如图，在ABC ∆中，90C ∠=︒，15A ∠=︒，60DBC ∠=︒，1BC =，则AD 的长为（ ）A ．1B ．2C ．3D ．4【答案】B 【分析】根据直角三角形的两个锐角互余，即可求出∠BDC ，然后根据30°所对的直角边是斜边的一半即可求出BD ，再根据三角形外角的性质即可求出∠DBA ，从而得出∠BDA=∠A ，最后根据等角对等边即可求出AD 的长．【详解】解：∵90C ∠=︒，60DBC ∠=︒∴∠BDC=90°－30DBC ∠=︒在Rt △BDC 中，BD=2BC=2∵15A ∠=︒，∠BDC 为△ADB 的外角∴∠DBA=∠BDC －∠A=15°∴∠DBA =∠A∴AD=BD=2故选B ．【点睛】此题考查的是直角三角形的性质、三角形外角的性质和等腰三角形的性质，掌握直角三角形的两个锐角互余、30°所对的直角边是斜边的一半、三角形外角的性质和等角对等边是解决此题的关键．10．解分式方程21211x x =--时，去分母化为一元一次方程，正确的是（ ） A ．x+1＝2（x ﹣1）B ．x ﹣1＝2（x+1）C ．x ﹣1＝2D ．x+1＝2 【答案】D【分析】先确定分式方程的最简公分母，然后左右两边同乘即可确定答案；【详解】解：由题意可得最简公分母为（x+1）（x-1）去分母得：x+1＝2，故答案为D ．【点睛】本题考查了分式方程的解法，解答的关键在于最简公分母的确定.二、填空题11．计算：2(2-=___________．【答案】.【分析】依据完全平方公式222()2a b a ab b -=-+进行计算.【详解】24(372=-=--【点睛】此题考查完全平方公式以及二次根式的混合运算，熟记公式即可正确解答.12．在平面直角坐标系中，O 为坐标原点，已知点A 的坐标是(-2，0)，点B 在y 轴上，若OA=2OB ，则点B 的坐标是______．【答案】（0，1）或（0，-1）【分析】先得出OA 的长度，再结合OA=2OB 且点B 在y 轴上，从而得出答案．【详解】∵点A 的坐标是（-2，0），∴OA=2，又∵OA=2OB ，∴OB=1，∵点B 在y 轴上，∴点B 的坐标为（0，1）或（0，-1），故答案为：（0，1）或（0，-1）．【点睛】本题主要考查了坐标与图形的性质，点到坐标轴的距离与这个点的坐标是有区别的，表现在两个方面：①到x 轴的距离与纵坐标有关，到y 轴的距离与横坐标有关；②距离都是非负数，而坐标可以是负数，在由距离求坐标时，需要加上恰当的符号．13．如图，已知Rt △ABC 中，∠ACB=90°，D 是AB 的中点，CD=2cm ，则AB= cm ．【答案】1．【解析】试题分析：因为Rt △ABC 中，∠ACB=90°，D 是AB 的中点， CD=2cm ，所以AB="2" CD=1． 考点：直角三角形斜边上的中线．14．如图，AD 是ABC 的外角平分线， //AD BC ，若70,C ∠=︒则BAC ∠的度数为__________．【答案】40︒【分析】根据平行线的性质可得∠CAD=∠C ，根据角平分线的定义可得∠EAD=∠CAD ，再根据平角的定义求解即可．【详解】解：∵//AD BC ，70C ∠=︒，∴∠CAD=∠C=70°，∵AD 平分∠CAE ，∴∠EAD=∠CAD=70°，∴∠BAC=180°－∠EAD －∠CAD=40°．故答案为：40°．【点睛】本题考查了平行线的性质和角平分线的定义，属于基本题型，熟练掌握基本知识是解题的关键． 15．已知12x y +=，6-=x y ，则22x y -=__________．【答案】72【分析】利用平方差公式对22x y -变形为()()x y x y +-，即可求解． 【详解】∵12x y +=，6-=x y ，∴()()2212672x y x y x y -=+-=⨯=． 故答案为：72．【点睛】本题主要考查了平方差公式的应用，解题的关键是牢记公式的结构特征和形式．16．已知等腰三角形一个外角的度数为108，则顶角度数为____________.【答案】72︒或36︒【分析】等腰三角形的一个外角等于108，则等腰三角形的一个内角为72°，但已知没有明确此角是顶角还是底角，所以应分两种情况进行分类讨论．【详解】∵一个外角为108，∴三角形的一个内角为72°，当72°为顶角时，其他两角都为54︒、54︒，当72°为底角时，其他两角为72°、36°，所以等腰三角形的顶角为72︒或36︒．故答案为：72︒或36︒【点睛】本题考查了等腰三角形的性质，及三角形内角和定理；在解决与等腰三角形有关的问题，由于等腰所具有的特殊性质，很多题目在已知不明确的情况下，要进行分类讨论，才能正确解题，因此，解决和等腰三角形有关的边角问题时，要仔细认真，避免出错．17．如图,在△ABC 中,AD ⊥BC 于D 点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为__________ .【答案】7.5【解析】试题解析：根据题意,阴影部分的面积为三角形面积的一半,116515,22ABC S BC AD =⋅=⨯⨯=阴影部分面积为：1157.5. 2⨯=故答案为：7.5.三、解答题18．如图，点O是直线AB上的一点，∠COD是直角，OE平分∠BOC．（1）如图（1），若∠AOC=40︒，求∠DOE的度数；（2）如图（2），将∠COD绕顶点O旋转，且保持射线OC在直线AB上方，在整个旋转过程中，当∠AOC 的度数是多少时，∠COE=2∠DOB．【答案】（1）20°；（2）当∠AOC的度数是60°或108°时，∠COE=2∠DOB【分析】（1）依据邻补角的定义以及角平分线的定义，即可得到∠COE的度数，进而得出∠DOE的度数；（2）设∠AOC=α，则∠BOC=180°-α，依据OE平分∠BOC，可得∠COE=12×（180°-α）=90°-12α，再分两种情况，依据∠COE=2∠DOB，即可得到∠AOC的度数．【详解】（1）∵∠AOC=40°，∴∠BOC=140°，又∵OE平分∠BOC，∴∠COE=12×140°=70°，∵∠COD=90°，∴∠DOE=90°-70°=20°；（2）设∠AOC=α，则∠BOC=180°-α，∵OE平分∠BOC，∴∠COE=12×（180°-α）=90°-12α，分两种情况：当OD在直线AB上方时，∠BOD=90°-α，∵∠COE=2∠DOB，∴90°-12α=2（90°-α）， 解得α=60°．当OD 在直线AB 下方时，∠BOD=90°-（180°-α）=α-90°，∵∠COE=2∠DOB ，∴90°-12α=2（α-90°）， 解得α=108°．综上所述，当∠AOC 的度数是60°或108°时，∠COE=2∠DOB ．【点睛】本题考查角的计算以及角平分线的定义的运用，解决问题的关键是画出图形，运用分类思想进行求解． 19．如图，在△ABC 中，D 是BC 边上的一点，AB ＝DB ，BE 平分∠ABC ，交AC 边于点E ，连接DE ．（1）求证：AE ＝DE ；（2）若∠A ＝100°，∠C ＝50°，求∠AEB 的度数．【答案】（1）见解析；（2）65°【分析】（1）根据BE 平分∠ABC ，可以得到∠ABE ＝∠DBE ，然后根据题目中的条件即可证明△ABE 和△DBE 全等，从而可以得到结论成立；（2）根据三角形内角和求出∠ABC ＝30°，根据角平分线的定义求出∠CBE ＝15°，，然后根据外角的性质可以得到∠AEB 的度数．【详解】（1）证明：∵BE 平分∠ABC ，∴∠ABE ＝∠DBE ，在△ABE 和△DBE 中，AB DB ABE DBE BE BE =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△DBE （SAS ），∴AE ＝DE ；（2）∵∠A ＝100°，∠C ＝50°，∴∠ABC ＝30°，∵BE 平分∠ABC ，∴∠ABE ＝∠DBE ，∴∠CBE ＝15°，∴∠AEB ＝∠C+∠CBE ＝50°+15°＝65°．【点睛】本题考查全等三角形的判定与性质、角平分线的定义，以及三角形外角的性质，解答本题的关键是明确题意，利用全等三角形的判定和性质解答．20．观察下列各式：11111122=+-=11111236=+-=111113412=+-= 请你根据上面三个等式提供的信息，猜想：（1=_____________ （2）请你按照上面每个等式反映的规律，写出用n （n 为正整数）表示的等式：______________；（3【答案】（1）1120；（211(1)n n =++；（3）1156，过程见解析 【分析】（1）仿照已知等式确定出所求即可；（2）归纳总结得到一般性规律，写出即可；（3）原式变形后，仿照上式得出结果即可．【详解】解：（1111114520=+-=； 故答案为：1120；（2111111(1)n n n n =+-=+++；故答案为：2211111(1)(1)n n n n ++=+++； （3）225011111149647856+=++= 【点睛】此题是一个阅读题目，通过阅读找出题目隐含条件．总结：找规律的题，都要通过仔细观察找出和数之间的关系，并用关系式表示出来．21．在平面直角坐标系中，一次函数y 23=-x+4的图象与x 轴和y 轴分别交于A 、B 两点．动点P 从点A 出发，在线段AO 上以每秒1个单位长度的速度向点O 作匀速运动，到达点O 即停止运动．其中A 、Q 两点关于点P 对称，以线段PQ 为边向上作正方形PQMN ．设运动时间为秒．如图①．（1）当t=2秒时，OQ 的长度为 ；（2）设MN 、PN 分别与直线y 23=-x+4交于点C 、D ，求证：MC=NC ； （3）在运动过程中，设正方形PQMN 的对角线交于点E ，MP 与QD 交于点F ，如图2，求OF+EN 的最小值．【答案】（1）2；（2）证明见解析；（3）32【分析】（1）解方程得到OA=1，由t=2，于是得到结论；（2）根据AP=PQ=t ，得到OQ=1-2t ，根据正方形的性质得到PQ=QM=MN=PN=t ，求得M （1-2t ，t ），N （1-t ，t ），C （1-32t ，t ），求得CM=（1-32t ）-（1-2t ）=12t ，CN=（1-t ）-（1-32t ）=12t ，于是得到结论； （3）作矩形NEFK ，则EN=FK ，推出当O ，F ，K 三点共线时，OF+EN=OF+FK 的值最小，如图，作OH ⊥QN 于H ，解直角三角形即可得到结论．【详解】（1）在y 23=-x+4中，令y=0，得x=1，∴OA=1． ∵t=2，∴AP=PQ=2，∴OQ=1﹣2﹣2=2．故答案为：2；（2）∵AP=PQ=t ，∴OQ=1﹣2t ．∵四边形PQMN 是正方形，∴PQ=QM=MN=PN=t ，∴M （1﹣2t ，t ），N （1﹣t ，t ），C （132-t ，t ）， ∴CM=（132-t ）﹣（1﹣2t ）12=t ， CN=（1﹣t ）﹣（132-t ）12=t ， ∴CM=CN ；（3）作矩形NEFK ，则EN=FK ．∵OF+EN=OF+FK ，∴当O ，F ，K 三点共线时，OF+EN=OF+FK 的值最小，如图，作OH ⊥QN 于H ，在等腰直角三角形PQN 中，∵PQ=t ，∴QN 2=t ， ∴HN=QN ﹣QH 2=t ﹣（2t ﹣32）=32，∴OF+EN 的最小值为：HE+EN=HN=32．【点睛】本题考查了一次函数的综合题，正方形的性质，矩形的性质，最短路线问题，正确的作出图形是解题的关键．22．如图，已知等腰△ABC 顶角∠A ＝36°．（1）在AC 上作一点D ，使AD ＝BD （要求：尺规作图，保留作图痕迹，不必写作法和证明，最后用黑色墨水笔加墨）；（2）求证：△BCD 是等腰三角形．【答案】（1）见解析；（2）见解析【分析】（1）根据题意作AB 的垂直平分线；（2）根据题意求出∠BDC=∠C=72°，即可证明．【详解】（1）解：如图，点D 为所作，；（2）证明：∵AB＝AC，∴∠ABC＝∠C＝12（180°﹣36°）＝72°，∵DA＝DB，∴∠ABD＝∠A＝36°，∴∠BDC＝∠A+∠ABD＝36°+36°＝72°，∴∠BDC＝∠C，∴△BCD是等腰三角形．【点睛】此题主要考查等腰三角形的性质，垂直平分线的尺规作图方法，以及垂直平分线的性质，解题的关键是熟知等腰三角形的判定与性质．23．某商场第一次用10000元购进某款机器人进行销售，很快销售一空，商家又用2400元第二次购进同款机器人，所购进数量是第一次的2倍，但单价贵了10元．（1）求该商家第一次购进机器人多少个？（2）若所有机器人都按相同的标价销售，要求全部销售完毕的利润率不低于20%(不考虑其他因素)，那么每个机器人的标价至少是多少元？【答案】（1）该商家第一次购进机器人1个；（2）每个机器人的标价至少是140元．【分析】（1）设该商家第一次购进机器人x个，根据“所购进数量是第一次的2倍，但单价贵了10元”列出分式方程解答即可；（2）设每个机器人的标价是y元，根据“全部销售完毕的利润率不低于20%”列出不等式解答即可．【详解】解：（1）设该商家第一次购进机器人x个，依题意得：11000x +10=240002x解得x=1．经检验x=1是原方程的解．答：该商家第一次购进机器人1个．（2）设每个机器人的标价是y元．则依题意得：()()1100024001002001100002400020% y++⨯--≥解得140y≥．答：每个机器人的标价至少是140元．【点睛】本题考查了分式方程与实际问题，不等式与实际问题相结合，解题的关键是找出题中等量关系，列出方程或不等式解答．24．星期天，小明和小芳从同一小区门口同时出发，沿同一路线去离该小区1800米的少年宫参加活动，为响应“节能环保，绿色出行”的号召，两人都步行，已知小明的速度是小芳的速度的1.2倍，结果小明比小芳早6分钟到达，求小芳的速度．【答案】小芳的速度是50米/分钟．【分析】设小芳的速度是x 米/分钟，则小明的速度是1.2x 米/分钟，根据路程÷速度=时间，列出方程，再求解即可．【详解】设小芳的速度是x 米/分钟，则小明的速度是1.2x 米/分钟，根据题意得：1800180061.2x x-= ， 解得：x =50，经检验x =50是原方程的解，答：小芳的速度是50米/分钟．25．先化简：2222421121m m m m m m m ---÷+--+，其中m 从0，1，2中选一个恰当的数求值． 【答案】21m +，2 【分析】原式利用除法法则变形，约分后两项通分并利用同分母分式的减法法则计算得到最简结果，把0m =代入计算即可求出值． 【详解】解：2222421121m m m m m m m ---÷+--+ 222(2)(1)1(1)(1)2m m m m m m m --=-⋅++-- 21m =+ 因为m+10≠ ，m-10≠，m-20≠所以m 1≠- ，m 1≠，m 2≠当0m =时，原式2=．【点睛】此题考查了解分式方程，以及分式的化简求值，熟练掌握运算法则是解本题的关键．八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．下列命题中的假命题是（ ）A ．三角形的一个外角大于内角B ．同旁内角互补，两直线平行C ．21x y =-⎧⎨=⎩是二元一次方程231x y +=-的一个解 D ．方差是刻画数据离散程度的量【答案】A【分析】根据三角形的外角、平行线的判断、二元一次方程的解以及方差即可判断出结果．【详解】解：在三角形内角中大于90°角的外角是一个锐角，故A 选项符合题目要求；同旁内角互补，两直线平行，故B 选项不符合题目要求；21x y =-⎧⎨=⎩是二元一次方程231x y +=-的一个解，故C 选项不符合题目要求； 方差是刻画数据离散程度的量，故D 选项不符合题目要求．故选：A【点睛】本题主要考查的是命题与定理的知识，正确的掌握这些知识点是解题的关键．2．如图，在一个三角形的纸片(ABC ∆)中， 90C ∠=︒，将这个纸片沿直线DE 剪去一个角后变成一个四边形ABED ，则图中12∠+∠的度数为( )A ．180°B ．90C ．270°D ．315°【答案】C 【分析】根据直角三角形与邻补角的性质即可求解.【详解】∵90C ∠=︒∴90EDC DEC ∠+∠=︒∴12∠+∠=180180EDC DEC ︒-∠+︒-∠=()360EDC DEC ︒-∠+∠=36090270︒-︒=︒ 故选C.【点睛】此题主要考查三角形的求解求解，解题的关键是熟知直角三角形与邻补角的性质.3．下列关于8的叙述错误的是（ ） A ．8是无理数B ．283<<C ．数轴上不存在表示8的点D ．面积为8的正方形的边长是8【答案】C【分析】根据无理数的定义、实数比较大小、实数与数轴的关系和正方形的面积公式逐一判断即可．【详解】解：A ．8是无理数，故本选项不符合题意；B ． 283<<，故本选项不符合题意；C ．数轴上存在表示8的点，故本选项符合题意；D ．面积为8的正方形的边长是8，故本选项不符合题意．故选C ．【点睛】此题考查的是实数的相关性质，掌握无理数的定义、实数比较大小、实数与数轴的关系和正方形的面积公式是解决此题的关键．4．活动课上, 小华将两张直角三角形纸片如图放置, 已知AC=8，O 是AC 的中点, △ABO 与△CDO 的面积之比为4:3, 则两纸片重叠部分即△OBC 的面积为（）A ．4B ．6C ．5D ．7【答案】D 【分析】先根据直角三角形的性质可求出OB 、OC 、OA 的长、以及ABO ∆的面积等于OBC ∆的面积，再根据题中两三角形的面积比可得OD 的长，然后由勾股定理可得CD 的长，最后根据三角形的面积公式可得出答案．【详解】在Rt ABC ∆中，908,A C C AB ∠=︒=，O 是AC 的中点142OB OC OA AC ∴==== ABO ∴∆的面积等于OBC ∆的面积ABO ∆与CDO ∆的面积之比为4:3OBC ∴∆与CDO ∆的面积之比为4:3又CD BD ⊥ 11,22O BC CD O S OB CD S OD CD ∆∆∴=⋅=⋅ ::4:3CDO OBC S S OB OD ∆∆∴==，即4:4:3OD =3OD ∴=在Rt CDO ∆中，2222437CD OC OD =-=-=11472722OBC S OB CD ∆∴=⋅=⨯⨯= 故选：D ．【点睛】本题考查了直角三角形的性质（斜边上的中线等于斜边的一半）、勾股定理等知识点，根据已知的面积之比求出OD 的长是解题关键．5．小红同学将自己5月份的各项消费情况制作成扇形统计图(如图)，从图中可看出（ ）A ．各项消费金额占消费总金额的百分比B ．各项消费的金额C ．消费的总金额D ．各项消费金额的增减变化情况【答案】A【分析】读懂题意，从题意中得到必要的信息是解决问题的关键．在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比．因此，【详解】解：从图中可以看出各项消费金额占消费总金额的百分比．故选A ．6．根据下列表述，能确定一个点位置的是（ ）A ．北偏东40°B ．某地江滨路C ．光明电影院6排D ．东经116°，北纬42°【答案】D【分析】逐一对选项进行判断即可.【详解】解：根据题意可得，北偏东40°无法确定位置，故选项A 错误；某地江滨路无法确定位置，故选项B 错误；光明电影院6排无法确定位置，故选项C 错误；东经116°，北纬42°可以确定一点的位置，故选项D 正确，故选：D ．【点睛】本题主要考查确定位置的要素，只有方向和距离都有才可以确定一个点的位置.7．如图，点A ，D ，C ，F 在一条直线上，AB=DE ，∠A=∠EDF ， 下列条件不能判定△ABC ≌△DEF 的是（ ）A ．AD=CFB ．∠BCA=∠FC ．∠B=∠ED ．BC=EF【答案】D 【解析】根据全等三角形的判定方法分别进行分析即可．【详解】AD=CF ，可用SAS 证明△ABC ≌△DEF ，故A 选项不符合题意，∠BCA=∠F ，可用AAS 证明△ABC ≌△DEF ，故B 选项不符合题意，∠B=∠E ，可用ASA 证明△ABC ≌△DEF ，故C 选项不符合题意，BC=EF ，不能证明△ABC ≌△DEF ，故D 选项符合题意，故选D.【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．但是AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．8．如图，在ABC 中，90C ∠=︒，30B ∠=︒，以A 为圆心，任意长为半径画弧分别交AB 、AC 于点M 和N ，再分别以M 、N 为圆心，大于MN 的长为半径画弧，两弧交于点P ，射线AP 交BC 于点D ，则下列说法中：①AD 是BAC ∠的平分线；②60ADC ∠=︒；③点D 在AB 的垂直平分线上；④:1:3DAC ABC S S =．其中正确的个数是（ ）A ．1B ．2C ．3D ．4【答案】D【分析】①连接NP ，MP ，根据SSS 定理可得ANP AMP ≌，故可得出结论；②根据三角形的外角的性质即可得出结论；③先根据三角形内角和定理求出CAB ∠的度数，再由AD 是BAC ∠的平分线得出30BAD CAD ∠=∠=︒，根据BAD B =∠∠可知AD BD =，故可得出结论；④先根据直角三角形的性质得出30CAD ∠=︒，12CD AD =，再由三角形的面积公式即可得出结论． 【详解】解：①证明：连接NP ，MP，在ANP 与AMP 中，AN AM NP MP AP AP =⎧⎪=⎨⎪=⎩， ()ANP AMP SSS ∴△≌△，则CAD BAD ∠=∠，故AD 是BAC ∠的平分线，故此结论正确；②在ABC 中，90C ∠=︒，30B ∠=︒，60CAB ∴∠=︒．AD 是BAC ∠的平分线，1302BAD CAD CAB ∴∠=∠=∠=︒， ∴60ADC BAD B ∠=∠+∠=︒，故此结论正确；③1302BAD CAD CAB ∠=∠=∠=︒， 30BAD B ∴∠=∠=︒，AD BD ∴=，∴点D 在AB 的垂直平分线上，故此结论正确； ④在Rt ACD △中，30CAD ∠=︒，12CD AD ∴=， 1322BC BD CD AD AD AD ∴=+=+=，1124DAC S AC CD AC AD =⋅=⋅△， 11332224ABC S AC BC AC AD AC AD ∴=⋅=⋅=⋅△， :1:3DAC ABC S S ∴=△△，故此结论正确；综上，正确的是①②③④．故选：D．【点睛】本题考查的是角平分线的性质，线段垂直平分线的性质，作图 基本作图等，熟知角平分线的作法是解答此题的关键．9．如图，在下列条件中，不能判定直线a与b平行的是（）A．∠1=∠2 B．∠2=∠3 C．∠3=∠5 D．∠3+∠4=180°【答案】C【详解】解：A．∵∠1与∠2是直线a，b被c所截的一组同位角，∴∠1=∠2，可以得到a∥b，∴不符合题意B．∵∠2与∠3是直线a，b被c所截的一组内错角，∴∠2=∠3，可以得到a∥b，∴不符合题意，C．∵∠3与∠5既不是直线a，b被任何一条直线所截的一组同位角，内错角，∴∠3=∠5，不能得到a∥b，∴符合题意，D．∵∠3与∠4是直线a，b被c所截的一组同旁内角，∴∠3+∠4=180°，可以得到a∥b，∴不符合题意，故选C．【点睛】本题考查平行线的判定，难度不大．10．如图，把一个直角三角尺的直角顶点放在直尺的一边上，若∠1=40°，则∠2=（）A．40°B．50°C．60°D．70°【答案】B【分析】根据两直线平行，同位角相等可得∠3＝∠1，再根据平角等于180°列式计算即可得解．【详解】解：∵直尺对边互相平行，∴∠3＝∠1＝40°，∴∠2＝180°−40°−90°＝50°．故选：B．【点睛】本题考查了平行线的性质，平角的定义，熟记性质并准确识图是解题的关键． 二、填空题11．2(5)=______；33(2)=_____. 【答案】5 2【分析】直接根据乘方与开方是互逆运算即可求解． 【详解】解：2(5)=5；33(2)=2 【点睛】此题主要考查乘方与开方的互逆运算，正确理解乘方与开方的概念是解题关键．12．如图，已知点()0,1A ．规定“把点A 先作关于x 轴对称，再向左平移1个单位”为一次变化．经过第一次变换后，点A 的坐标为_______；经过第二次变换后，点A 的坐标为_____；那么连续经过2019次变换后，点A 的坐标为_______．【答案】(1,1)-- (2,1)- (2019,1)--【分析】根据轴对称判断出点A 关于x 轴对称后的位置，此时横坐标不变，纵坐标互为相反数，然后再向左平移1个单位长度便可得到第一次变换后的点A 的坐标；按照同样的方式可以找到第二次变换后的点A 的坐标；然后再通过比较横纵坐标的数值，可以发现点A 在每一次变换后的规律，即可求出经过2019次变换后的点A 的坐标．【详解】点A 原来的位置（0,1）第一次变换：()()0, 11,1→-→--（0，1），此时A 坐标为(1,1)--； 第二次变换： →→（-1,-1）(-1,1)(-2,1)，此时A 坐标为(2,1)-第三次变换： (2,1)-→→（-2,-1）(-3,-1)，此时A 坐标为(3,1)-- ……第n 次变换：点A 坐标为(,(1))nn --所以第2019次变换后的点A 的坐标为(2019,1)--．故答案为：(1,1)--；(2,1)-；(2019,1)-- 【点睛】本题考查的知识点是轴对称及平移的相关知识，平面直角坐标系中四个象限的点的横、纵坐标的符号是解题中的易错点，必须特别注意.13．已知一个等腰三角形的顶角30°，则它的一个底角等于_____________． 【答案】75°【分析】已知明确给出等腰三角形的顶角是30°，根据等腰三角形的性质及三角形的内角和定理易求得底角的度数．【详解】解：∵等腰三角形的顶角是30°， ∴这个等腰三角形的一个底角=12（180°-30°）=75°． 故答案为：75°． 【点睛】此题考查了等腰三角形的性质及三角形内角和定理，此题很简单，解答此题的关键是熟知三角形内角和定理及等腰三角形的性质．14．用四舍五入法，对3.5952取近似值，精确到0.01，结果为______． 【答案】3.1【分析】根据近似数的精确度把千分位上的数字5进行四舍五入即可． 【详解】解：3.5952≈3.1（精确到0.01）． 故答案为3.1． 【点睛】本题考查近似数和有效数字：经过四舍五入得到的数为近似数；从一个数的左边第一个不是0的数字起到末位数字止，所有的数字都是这个数的有效数字．近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．15．若点(),3P a 在第二象限，且到原点的距离是5，则a =________． 【答案】-4【分析】根据点(),3P a 到原点的距离是5，即可列出关于a 的方程，求出a 值，再根据(),3P a 在第二象限，a ＜0，取符合题意的a 值即可． 【详解】∵点(),3P a 到原点的距离是5 ∴22235a += 解得a=±4又∵(),3P a 在第二象限∴a ＜0 ∴a=-4 故答案为：-4 【点睛】本题考查了坐标到原点的距离求法，以及直角坐标系中不同象限内点的坐标特点． 16．若一组数据4,,5,,7,9x y 的平均数为6，众数为5，则这组数据的方差为__________． 【答案】83【分析】根据平均数的计算公式，可得11x y +=，再根据众数是5，所以可得x,y 中必须有一个5，则另一个就是6，通过方差的计算公式计算即可.【详解】解：∵一组数据4,,5,,7,9x y 的平均数为6，众数为5， ∴,x y 中至少有一个是5，∵一组数据4,,5,,7,9x y 的平均数为6， ∴()4579166x y +++++=， ∴11x y +=，∴,x y 中一个是5，另一个是6，∴这组数据的方差为()()()()()22222846256661[]676963-+-+-+-+-=； 故答案为83． 【点睛】本题是一道数据统计中的综合性题目，涉及知识点较多，应当熟练掌握，特别是记忆方差的计算公式. 17．在人体血液中，红细胞直径约为0.00077cm ，数据0.00077用科学记数法表示为_____．【答案】7.7×10﹣1【解析】分析：绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n ，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定． 详解：0.00077=7.7×10-1， 故答案为7.7×10-1．点睛：本题主要考查用科学记数法表示较小的数，一般形式为a×10-n ，其中1≤|a|＜10，n 为由原数左边起第一个不为零的数字前面的0的个数所决定． 三、解答题18．平面内有四个点A ，B,C ，D ，用它们作顶点可以组成几个三角形？画出图形，并写出存在的三角形．（只写含已知字母的）【答案】详见解析，分别是：△ABC ，△ACD ，△ABD ；。

2020-2020学年上海市徐汇区八年级（上）期末数学试卷一．选择题（本大题共6题，每题2分，满分12分）【下列各题的四个选项中，有且只有一个选项是正确的】1．下列各式中与是同类二次根式的是（）A．B．C．D．2．如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，那么下列结论错误的是（）A．∠A+∠DCB=90°B．∠ADC=2∠B C．AB=2CD D．BC=CD3．如图，点P在反比例函数y=（x＞0）第一象限的图象上，PQ垂直x轴，垂足为Q，设△POQ的面积是s，那么s与k之间的数量关系是（）A．B．C．s=k D．不能确定4．如果y关于x的函数y=（k2+1）x是正比例函数，那么k的取值范围是（）A．k≠0 B．k≠±1 C．一切实数D．不能确定5．如果关于x的一元二次方程（a﹣c）x2﹣2bx+（a+c）=0有两个相等的实数根，其中a、b、c是△ABC的三边长，那么△ABC的形状是（）A．直角三角形B．等腰三角形C．等边三角形D．等腰直角三角形6．下列命题的逆命题是假命题的是（）A．同位角相等，两直线平行B．在一个三角形中，等边对等角C．全等三角形三条对应边相等D．全等三角形三个对应角相等二．填空题（本大题共12题，每题2分，满分24分）7．计算：=．8．函数的定义域是．9．在实数范围内因式分解：x2﹣3x+1=．10．如果f（x）=，那么f（2）=．11．已知变量x和变量x﹣2，那么x﹣2是不是x的函数？你的结论是：（填“是”或“不是”）．12．如果反比例函数y=（k≠0）的图象在每个象限内，y随着x的增大而减小，那么请你写出一个满足条件的反比例函数解析式（只需写一个）．13．在Rt△ABC和Rt△DEF中，∠C=∠F=90°，∠D=30°，AB=DE，EF=BC，如果EF=，那么AC的长是．14．已知关于x的方程x2+mx﹣6=0的一个根为2，那么它的另一个根是．15．如果点A（3，m）在正比例函数图象上，那么点A和坐标原点的距离是．16．某产品原价每件价格为200元，经过两次降价，且每次降价的百分率相同，现在每件售价为162元，那么每次降价的百分率是．17．在一个角的内部（不包括顶点）且到角的两边距离相等的点的轨迹是．18．在△ABC中，AB=AC，MN垂直平分AB分别交AB、BC于M、N．如果△ACN是等腰三角形，那么∠B的大小是．三、简答题（本大题共4题，每题5分，满分20分）19．先化简再计算：（其中ab=9）．20．解方程：（2x﹣3）2=x（x﹣5）+6．21．如图，已知线段a，b，求作：△ABC，使AB=AC=a，BC=b．22．如图，正比例函数y=kx（k≠0）与反比例函数y=﹣的图象交于点A（﹣1，m）和点B．求点B的坐标．四、（本大题共3题，第23、24题每题7分，第25题8分，满分22分）23．如图，在Rt△ABC中，∠C=90°，AC=6，AB=10，DE垂直平分AB，分别交AB、BC 于点D、E．求CE的长．24．某商店从厂家以每件21元的价格购进一批商品，该店可以自行定价，若每件商品售价为a元，则可以卖出（350﹣10a）件；但物价局限定每件商品加价不能超过进价的20%，如果商店计划要赚400元，那么每件商品售价是多少元？25．如图，AD∥BC，∠A=90°，AB=BC，点E是AB的中点，BD=CE．（1）求证：BD⊥CE；（2）联结CD、DE，试判断△DCE的形状，并证明你的结论．五、（本大题共2题，第26题10分，第27题12分，满分22分）26．如图，点B（2，n）是直线y=k1x（k1≠0）上的点，如果直线y=k1x（k1≠0）平分∠yOx，BA⊥x轴于A，BC⊥y轴于C．（1）求k1的值；（2）如果反比例函数y=（k2≠0）的图象与BC、BA分别交于点D、E，求证：OD=OE；（3）在（2）的条件下，如果四边形BDOE的面积是△ABO面积的，求反比例函数的解析式．27．如图1，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，BC=CD．（1）求∠DCB的大小；（2）如图2，点F是边BC上一点，将△ABF沿AF所在直线翻折，点B的对应点是点H，直线HF⊥AB，垂足为G，如果AB=2，求BF的长；（3）如图3，点E是△ACD内一点，且∠AEC=150°，联结DE，请判断线段DE、AE、CE 能否构成直角三角形？如果能，请证明；如果不能，请说明理由．2020-2020学年上海市徐汇区八年级（上）期末数学试卷参考答案与试题解析一．选择题（本大题共6题，每题2分，满分12分）【下列各题的四个选项中，有且只有一个选项是正确的】1．下列各式中与是同类二次根式的是（）A．B．C．D．【考点】同类二次根式．【分析】先化简二次根式，再根据同类二次根式的定义判定即可．【解答】解：A、与不是同类二次根式，B、=3与不是同类二次根式，C、=2与是同类二次根式，D、=3与不是同类二次根式，故选C．【点评】本题考查了同类二次根式，解题的关键是二次根式的化简．2．如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，那么下列结论错误的是（）A．∠A+∠DCB=90°B．∠ADC=2∠B C．AB=2CD D．BC=CD【考点】直角三角形斜边上的中线．【分析】根据直角三角形斜边上的中线性质得出CD=AD=BD，根据等边对等角得出∠DCB=∠B，再逐个判断即可．【解答】解：A、∵在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，∴CD=AD=BD=AB，∴∠DCB=∠B，∵∠ACB=90°，∴∠A+∠B=90°，∴∠A+∠DCB=90°，故本选项错误；B、∵∠DCB=∠B，∠ADC=∠B+∠DCB，∴∠ADC=2∠B，故本选项错误；C、∵在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，∴AB=2CD，故本选项错误；D、根据已知不能推出BC=CD，故本选项正确；故选D．【点评】本题考查了直角三角形斜边上的中线性质，等腰三角形性质的应用，能熟记直角三角形斜边上的中线等于斜边的一半是解此题的关键．3．如图，点P在反比例函数y=（x＞0）第一象限的图象上，PQ垂直x轴，垂足为Q，设△POQ的面积是s，那么s与k之间的数量关系是（）A．B．C．s=k D．不能确定【考点】反比例函数系数k的几何意义．【分析】根据点P在反比例函数图象上结合反比例函数系数k的几何意义就可以求出s与k 之间的数量关系．【解答】解：∵点P是反比例函数y=图象上一点，且PQ⊥x轴于点Q，=|k|=s，∴S△POQ解得：|k|=2s．∵反比例函数在第一象限有图象，∴k=2s．即s=故选：B．【点评】本题考查了反比例函数的性质以及反比例函数系数k的几何意义，解题的关键是根据反比例函数系数k的几何意义找出△POQ面积s与k的关系．4．如果y关于x的函数y=（k2+1）x是正比例函数，那么k的取值范围是（）A．k≠0 B．k≠±1 C．一切实数D．不能确定【考点】正比例函数的定义．【分析】根据正比例函数的定义，列出方程求解即可．【解答】解：∵函数y=（k2+1）x是正比例函数，∴k2+1≠0，∴k取全体实数，故选C．【点评】本题考查了正比例函数的定义，掌握正比例函数的定义：形如y=kx（k≠0）的形式，叫正比例函数．5．如果关于x的一元二次方程（a﹣c）x2﹣2bx+（a+c）=0有两个相等的实数根，其中a、b、c是△ABC的三边长，那么△ABC的形状是（）A．直角三角形B．等腰三角形C．等边三角形D．等腰直角三角形【考点】根的判别式．【分析】由方程有两个相等的实数根以及该方程为一元二次方程，结合根的判别式即可得出关于a、b、c的方程组，解方程组即可得出a2=b2+c2，由此即可得出结论．【解答】解：∵关于x的一元二次方程（a﹣c）x2﹣2bx+（a+c）=0有两个相等的实数根，∴，即，解得：a2=b2+c2且a≠c．又∵a、b、c是△ABC的三边长，∴△ABC为直角三角形．故选A．【点评】本题考查了根的判别式，解题的关键是求出a2=b2+c2．本题属于基础题，难度不大，解决该题型题目时，根据根的个数结合根的判别式得出方程（不等式或不等式组）是关键．6．下列命题的逆命题是假命题的是（）A．同位角相等，两直线平行B．在一个三角形中，等边对等角C．全等三角形三条对应边相等D．全等三角形三个对应角相等【考点】命题与定理．【分析】分别写出原命题的逆命题，然后判断真假即可．【解答】解：A、逆命题为两直线平行，同位角相等，正确，为真命题；B、逆命题为：在一个三角形中等角对等边，正确，是真命题；C、逆命题为：三条边对应相等的三角形全等，正确，是真命题；D、逆命题为：三个角对应相等的三角形全等，错误，为假命题，故选D．【点评】本题考查了命题与定理的知识，解题的关键是能够正确的写出原命题的逆命题，难度不大．二．填空题（本大题共12题，每题2分，满分24分）7．计算：=2．【考点】二次根式的乘除法．【分析】先化简二次根式，再利用二次根式的除法运算法则求出即可．【解答】解：原式=2÷=2，故答案为：2．【点评】此题主要考查了二次根式的除法运算，正确掌握运算法则是解题关键．8．函数的定义域是x≥3．【考点】函数自变量的取值范围；二次根式有意义的条件．【分析】根据二次根式的意义，被开方数是非负数，列不等式求得．【解答】解：根据题意得：2x﹣6≥0，解得x≥3．【点评】当函数表达式是二次根式时，被开方数为非负数．9．在实数范围内因式分解：x2﹣3x+1=．【考点】实数范围内分解因式．【分析】根据x2﹣3x+1=0的解为：x=，根据求根公式的分解方法和特点得出答案．【解答】解：∵x2﹣3x+1=0的解为：x=，∴x2﹣3x+1=（x﹣）（x﹣）．故答案为：（x﹣）（x﹣）．【点评】此题主要考查了实数范围内分解因式，利用求根公式法得出方程的根再分解因式是解决问题的关键．10．如果f（x）=，那么f（2）=．【考点】函数值．【分析】将x=2代入公式，再分母有理化可得．【解答】解：当x=2时，f（2）===，故答案为：．【点评】本题主要考查函数的求值，（1）当已知函数解析式时，求函数值就是求代数式的值；（2）函数值是唯一的，而对应的自变量可以是多个．11．已知变量x和变量x﹣2，那么x﹣2是不是x的函数？你的结论是：是（填“是”或“不是”）．【考点】函数的概念．【分析】根据函数的概念进行判断，自变量与因变量需满足一一对应的关系．【解答】解：∵对于变量x的每一个确定的值，变量x﹣2有且只有一个值与之对应，∴根据函数的概念可知，x﹣2是x的函数．故答案为：是【点评】本题主要考查了函数，解决问题的关键是掌握函数的概念．设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量．12．如果反比例函数y=（k≠0）的图象在每个象限内，y随着x的增大而减小，那么请你写出一个满足条件的反比例函数解析式y=（答案不唯一）（只需写一个）．【考点】反比例函数的性质．【分析】先根据函数的增减性判断出k的符号，进而可得出结论．【解答】解：∵反比例函数y=（k≠0）的图象在每个象限内，y随着x的增大而减小，∴k＞0，∴满足条件的反比例函数解析式可以是y=．故答案为：y=（答案不唯一）．【点评】本题考查的是反比例函数的性质，熟知反比例函数的增减性是解答此题的关键．13．在Rt△ABC和Rt△DEF中，∠C=∠F=90°，∠D=30°，AB=DE，EF=BC，如果EF=，那么AC的长是3．【考点】全等三角形的判定与性质．【分析】先利用含30度的直角三角形三边的关系得到DF=3，然后利用“HL”证明Rt△ABC ≌Rt△DEF，再利用全等三角形的性质得到AC的长．【解答】解：在Rt△DEF中，∵∠F=90°，∠D=30°，∴DF=EF=×=3，在Rt△ABC和Rt△DEF中，，∴Rt△ABC≌Rt△DEF，∴AC=DF=3．故答案为3．【点评】本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．14．已知关于x的方程x2+mx﹣6=0的一个根为2，那么它的另一个根是﹣3．【考点】根与系数的关系．【分析】设方程的另一根为a，由一个根为2，利用根与系数的关系列出关于a的方程，求出方程的解得到a的值，即为方程的另一根．【解答】解：∵方程x2+mx﹣6=0的一个根为2，设另一个为a，∴2a=﹣6，解得：a=﹣3，则方程的另一根是﹣3．故答案为：﹣3．【点评】此题考查了一元二次方程根与系数的关系，一元二次方程ax2+bx+c=0（a≠0），当b2﹣4ac≥0时方程有解，此时设方程的解为x1，x2，则有x1+x2=﹣，x1x2=．15．如果点A（3，m）在正比例函数图象上，那么点A和坐标原点的距离是5．【考点】一次函数图象上点的坐标特征．【分析】先把A（3，m）代入中求出m，从而确定A点坐标，然后利用勾股定理计算点A和坐标原点的距离．【解答】解：把A（3，m）代入得m=×3=4，则点A的坐标为（3，4），所以点A和坐标原点的距离==5．故答案为5．【点评】本题考查了一次函数图象上点的坐标特征：一次函数图象上点的坐标满足其解析式，于是解决此类问题时把已知点的坐标代入解析式求解．16．某产品原价每件价格为200元，经过两次降价，且每次降价的百分率相同，现在每件售价为162元，那么每次降价的百分率是10%．【考点】一元二次方程的应用．【分析】解答此题利用的数量关系是：衬衫原来价格×（1﹣每次降价的百分率）2=现在价格，设出未知数，列方程解答即可．【解答】解：设这种衬衫平均每次降价的百分率为x，根据题意列方程得，200×（1﹣x）2=162，解得x1=0.1，x2=﹣1.9（不合题意，舍去）；答：这种衬衫平均每次降价的百分率为10%．故答案为：10%．【点评】本题考查了一元二次方程在实际生活中的应用，此题列方程得依据是：衬衫原来价格×（1﹣每次降价的百分率）2=现在价格．17．在一个角的内部（不包括顶点）且到角的两边距离相等的点的轨迹是这个角的平分线（除顶点）．【考点】轨迹；角平分线的性质．【分析】根据角平分线上的点到角两边的距离相等进行解答．【解答】解：∵角平分线上的点到角两边的距离相等，∴在∠AOB的内部且到这个角的两边距离相等的点的轨迹是∠AOB的平分线（端点除外），故答案为∠AOB的平分线（端点除外）．【点评】此题考查了点的轨迹问题，要熟悉角平分线的性质是解题的关键．18．在△ABC中，AB=AC，MN垂直平分AB分别交AB、BC于M、N．如果△ACN是等腰三角形，那么∠B的大小是45°或36°．【考点】等腰三角形的性质；线段垂直平分线的性质．【分析】首先根据线段垂直平分线的性质得出NA=NB，即可得到∠B=∠BAN=∠C．然后对△ANC中的边进行讨论，然后在△ABC中，利用三角形内角和定理即可求得∠B的度数．【解答】解：∵MN是AB的中垂线，∴NB=NA．∴∠B=∠BAN，∵AB=AC，∴∠B=∠C．设∠B=x°，则∠C=∠BAN=x°．1）当AN=NC时，∠CAN=∠C=x°．则在△ABC中，根据三角形内角和定理可得：4x=180，解得：x=45，则∠B=45°；2）当AN=AC时，∠ANC=∠C=x°，而∠ANC=∠B+∠BAN，故此时不成立；3）当CA=CN时，∠NAC=∠ANC=．在△ABC中，根据三角形内角和定理得到：x+x+x+=180，解得：x=36．即∠B的度数为45°或36°．故答案为45°或36°．【点评】本题考查了线段垂直平分线的性质，等腰三角形的性质，三角形内角和定理，正确对△ANC的边进行讨论是解题的关键．三、简答题（本大题共4题，每题5分，满分20分）19．先化简再计算：（其中ab=9）．【考点】二次根式的化简求值．【分析】先将题目中的式子化简，然后将ab=9代入即可解答本题．【解答】解：==当ab=9时，原式==．【点评】本题考查二次根式的化简求值，解题的关键是明确如何化简二次根式．20．解方程：（2x﹣3）2=x（x﹣5）+6．【考点】解一元二次方程-公式法．【分析】原方程化为，3x2﹣7x+3=0，找出a，b，c，求出△=b2﹣4ac的值，再代入求根公式即可．【解答】解：原方程化为，3x2﹣7x+3=0；∴△=（﹣7）2﹣4×3×3=13；∴；∴原方程的根是，．【点评】本题考查了用公式法解一元二次方程，找出a，b，c，求出△=b2﹣4ac的值，是解此题的关键．21．如图，已知线段a，b，求作：△ABC，使AB=AC=a，BC=b．【考点】作图—复杂作图．【分析】先作线段BC=b，然后分别以B、C两点为圆心，a为半径画弧，两弧相交于点A，再连结AB、AC，则△ABC满足条件．【解答】解：如图，△ABC为所作．【点评】本题考查了作图﹣复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．22．如图，正比例函数y=kx（k≠0）与反比例函数y=﹣的图象交于点A（﹣1，m）和点B．求点B的坐标．【考点】反比例函数与一次函数的交点问题．【分析】只需把点A的坐标代入反比例函数的解析式，即可求得m，能够根据对称的性质，求得另一个交点B的坐标．【解答】解：由题意，得，∴A（﹣1，2）；又∵2=﹣k，∴k=﹣2，∴y=﹣2x；∴，解得，，∴B（1，﹣2）．【点评】本题利用了待定系数法确定m，k的值，并且用到了过原点的直线与反比例函数图象的两个交点坐标关于原点对称的知识．四、（本大题共3题，第23、24题每题7分，第25题8分，满分22分）23．如图，在Rt△ABC中，∠C=90°，AC=6，AB=10，DE垂直平分AB，分别交AB、BC 于点D、E．求CE的长．【考点】线段垂直平分线的性质．【分析】由在Rt△ABC中，∠C=90°，AC=6，AB=10，根据勾股定理可求得BC的长，又由DE垂直平分AB，可得AE=BE，然后设CE=x，则AE=BE=8﹣x；利用勾股定理即可求得方程x2+62=（8﹣x）2，解此方程即可求得答案．【解答】解：在Rt△ABC中，∠C=90°，∴；∵DE垂直平分AB，分别交AB、BC于点D、E，∴AE=BE；设CE=x，则AE=BE=8﹣x；在Rt△ACE中，∠C=90°，∴CE2+AC2=AE2；即x2+62=（8﹣x）2，解得，即．【点评】此题考查了线段垂直平分线的性质以及勾股定理．注意掌握方程思想的应用是解此题的关键．24．某商店从厂家以每件21元的价格购进一批商品，该店可以自行定价，若每件商品售价为a元，则可以卖出（350﹣10a）件；但物价局限定每件商品加价不能超过进价的20%，如果商店计划要赚400元，那么每件商品售价是多少元？【考点】一元二次方程的应用．【分析】本题的等量关系是商品的单件利润=售价﹣进价．然后根据商品的单价利润×销售的件数=总利润，设商品的售价为a，列出方程求出未知数的值后，根据“物价局限定每次商品加价不能超过进价的20%”将不合题意的舍去，进而求出卖的商品的件数．【解答】解：设每件商品售价是x元，由题意，得（x﹣21）（350﹣10x）=400；化简，得x2﹣56x+775=0；解得x1=25，x2=31；又21×（1+0.2）=25.2，∴x=31不合题意，舍去．答：每件商品售价是25元．【点评】本题考查了一元二次方程的应用．可根据题意列出方程，判断所求的解是否符合题意，舍去不合题意的解．找到关键描述语，找到等量关系准确的列出方程是解决问题的关键．25．如图，AD∥BC，∠A=90°，AB=BC，点E是AB的中点，BD=CE．（1）求证：BD⊥CE；（2）联结CD、DE，试判断△DCE的形状，并证明你的结论．【考点】全等三角形的判定与性质；等腰直角三角形．【分析】（1）由条件可证明Rt△ABD≌Rt△BCE，则可求得∠EFD=90°，可证得结论；（2）过点D作DG⊥BC于G，结合条件可证明△ABD≌△GDB，则可证得BD=CD，结合条件可证得CD=CE，可证明△CDE为等腰三角形．【解答】（1）证明：∵AD∥BC，∴∠A+∠CBE=180°，又∠A=90°，∴∠CBE=90°；∵AB=BC，BD=CE，在Rt△ABD和Rt△BCE中∴Rt△ABD≌Rt△BCE（HL），∴∠D=∠BEC，∵∠D+∠ABD=90°，∴∠BEC+∠ABD=90°，∵∠EFB+∠BEC+∠ABD=180°，∴∠EFB=90°，∴BD⊥CE；（2）解：△DCE是等腰三角形．证明如下：∵Rt△ABD≌Rt△BEC，∴AD=BE，又AB=BC，点E是AB的中点，∴，如图，过点D作DG⊥BC于G，∴∠DGB=90°=∠A，∵AD∥BC，∴∠GBD=∠ADB，在△ABD和△GDB中∴△ABD≌△GDB（AAS），∴；∴DF垂直平分BC，∴BD=CD，又BD=CE，∴CD=CE ， ∴△DCE 是等腰三角形．【点评】本题主要考查全等三角形的判定和性质，掌握全等三角形的判定和性质是解题的关键，即SSS 、SAS 、ASA 、AAS 和HL ．五、（本大题共2题，第26题10分，第27题12分，满分22分）26．如图，点B （2，n ）是直线y=k 1x （k 1≠0）上的点，如果直线y=k 1x （k 1≠0）平分∠yOx ，BA ⊥x 轴于A ，BC ⊥y 轴于C ．（1）求k 1的值；（2）如果反比例函数y=（k 2≠0）的图象与BC 、BA 分别交于点D 、E ，求证：OD=OE ；（3）在（2）的条件下，如果四边形BDOE 的面积是△ABO 面积的，求反比例函数的解析式．【考点】反比例函数综合题．【分析】（1）根据角的平分线的性质，可得B 的横、纵坐标相等，则利用待定系数法即可求得k 1的值；（2）利用k 2表示出D 和E 的坐标，然后利用勾股定理求得OD 和OE 的长，从而判断；（3）S △BOE =S 四边形BDOE ，则S △BOE =S △AOB ，据此即可求得AE 的长，则k 2即可求得．【解答】解：（1）∵直线y=k 1x （k 1≠0）平分∠yOx ，BA ⊥x 轴于A ，BC ⊥y 轴于C ，∴AB=BC ；又B （2，n ），∴AB=BC=2； ∴B （2，2）， ∴2=2k 1， ∴k 1=1．（2）∵反比例函数y=（k 2≠0）的图象与BC 、BA 分别交于点D 、E ，∴D （，2），E （2，）；∴OD==，OE==；∴OD=OE ．（3）由题意，可得△BOD ≌△BOE ， ∴S △BOE =S 四边形BDOE ； 又S 四边形BDOE =S △AOB ，∴S △BOE =S △AOB ，即BEOA=×ABOA ，∴BE=AB=； ∴AE=， ∴E （2，）， ∴=，解得k 2=， ∴y=．【点评】本题考查了反比例函数与正方形的性质的运算，正确求得AE的长是本题的关键．27．如图1，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，BC=CD．（1）求∠DCB的大小；（2）如图2，点F是边BC上一点，将△ABF沿AF所在直线翻折，点B的对应点是点H，直线HF⊥AB，垂足为G，如果AB=2，求BF的长；（3）如图3，点E是△ACD内一点，且∠AEC=150°，联结DE，请判断线段DE、AE、CE 能否构成直角三角形？如果能，请证明；如果不能，请说明理由．【考点】三角形综合题．【分析】（1）只要证明AB=2AC，即可得到∠B=30°，再根据DC=DB即可解决问题．（2）首先证明△ABH是等边三角形，设GF=x，得到BF=2GF=2x，在RT△BFG中利用勾股定理即可解决问题．（3）线段DE、AE、CE能构成直角三角形，如图3中，作∠ECP=60°，截取CP=CE，连接AP、PE，ED，只要证明△DCE≌△ACP即可解决问题．【解答】解：（1）如图1中，在Rt△ABC中，CD是斜边AB上的中线，∴AB=2CD，设CD=x，则AB=2x，BC=x，∴AC===x，∴AC=DC=AB，∴∠B=30°，又CD=BD，∴∠DCB=∠B=30°．（2）如图2中，连接BH．△AHF与△ABF关于直线AF对称，又点B的对应点是点H，∴AH=AB，HF=BF，∵HF⊥AB，∠ABC=30°，∴∠BFG=60°，∴∠FBH=∠FHB=30°；∴∠ABH=60°，∴△ABH是等边三角形，∴BG=AB=1，设GF=x，∴BF=2GF=2x，∴x2+12=（2x）2，解得x=∴BF=．（3）线段DE、AE、CE能构成直角三角形．如图3中，作∠ECP=60°，截取CP=CE，连接AP、PE，ED．∵PC=CE，∠PCE=60°，∴△PCE是等边三角形，∴PE=CE，∠PEC=60°，∵∠B=30°，∴∠BAC=60°，又CD=AD，∴△ACD是等边三角形，∴∠ACD=60°，AC=CD；∴∠ACD﹣∠ACE=∠PCE﹣∠ACE，即∠DCE=∠ACP，在△DCE和△ACP中，，∴△DCE≌△ACP，∴DE=AP，又∠AEC=150°，∴∠AEP=150°﹣60°=90°，∴线段DE、AE、CE能构成直角三角形．【点评】本题考查三角形综合题、全等三角形的判定和性质、等边三角形的性质和判定、勾股定理等知识，解题的关键是灵活应用这些知识解决问题，学会添加辅助线，构造全等三角形，属于中考常考题型．。

徐汇区学年初二年级第一学期期末考试数学试卷（考试时间90分钟，满分100分）一．选择题（本大题共6题，每题3分，满分18分）1. 下列二次根式中，是最简二次根式是（ ）A.B.C.D.2.下列方程中，没有实数根的是（） A.2310x x −−= B.230x x −= C.2210x x −+= D.2230x x −+=3.如果正比例函数图像与反比例函数图像一个交点的坐标为（3，-4），那么另一个交点的坐标为（ ）A.（-3，-4）B.（3，4）C.（−3，4）D.（-4，3）4.满足下列条件的三角形中，不是直角三角形的是（）A.三内角之比为3：4：5B.三边长的平方之比为1：2：3C.三边长之比为7：24：25D.三内角之比为1：2：35.下列命题中，其逆命题是真命题的命题个数有（） （1）全等三角形的对应边相等； （2）对顶角相等；（3）等角对等边；（4）全等三角形的面积相等．A.1个 B.2个 C.3个 D.4个6. 如图所示，在平面直角坐标系xOy 中，点A 、B 、C 为反比例函数y =k x（k ＞0）上不同的三点，连接OA 、OB 、OC ，过点A 作AD ⊥y 轴于点D ，过点B 、C 分别作BE ，CF 垂直x 轴于点E 、F ，OC 与BE 相交于点M ，记△AOD 、△BOM 、四边形CMEF 的面积分别为S 1、S 2、S 3，则（ ） 的的A. S 1=S 2+S 3B. S 2=S 3C. S 3＞S 2＞S 1D. S 1S 2＜S 32二．填空题（本大题共12题，每题2分，满分24分）7. 函数y = ___________________．8. 已知函数y ＝1x x −，当x 时，y ＝_____． 9. 已知0是关于x 的一元二次方程22(1)210m x x m −++−=的一个实数根，则m =______．10. 在实数范围内因式分解：2231x x −−=_________．11. 若1(1,)M y −、21(,)2N y −两点都在函数k y x=的图像上，且1y <2y ，则k 的取值范围是______． 12. 已知正比例函数()0y kx k =≠的图象经过第一、三象限，且经过点（k ，k +2），则k =________．13. 以线段AB 为底边的等腰三角形，它的两底角平分线交点的轨迹是_____．14. 如图，在△ABC 中，∠C =37°，边BC 的垂直平分线分别与AC 、BC 交于点D 、E ，AB =CD ，那么∠A =____°．15. 如图，∠AOE ＝∠BOE ＝15°，EF //OB ，EC ⊥OB ，若EC ＝2，则EF ＝___．16. 如图，梯形ABCD 中，AD ∥BC ，AF ⊥BC 于F ，M 是CD 中点，AM 的延长线交BC 的延长线于E ，AE ⊥AB ，∠B =60°，AF =，则梯形的面积是___．17. 如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在Rt △ABC 中，∠C =90° ，AC =2，若Rt △ABC 是“好玩三角形”，则AB =_______．18. 小华用一张直角三角形纸片玩折纸游戏，如图1，在Rt ABC △中，90ACB ∠=°，30B ∠=°，1AC =．第一步，在AB 边上找一点D ，将纸片沿CD 折叠，点A 落在A ′处，如图2，第二步，将纸片沿CA ′折叠，点D 落在D ¢处，如图3．当点D ¢恰好在原直角三角形纸片的边上时，线段A D ′′的长为__________．三．简答题（第19、20、21、22、23每题6分，24、25每题8分，26题12分）19.2−． 20. 用配方法解方程：2420x x −−=．21. 关于x 的一元二次方程22(2)20x m x +−+=有两个相等的实数根，求m 的值及方程的根． 22. 某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10%，月份的营业额达到633.6万元．求3月份到5月份营业额的平均月增长率．23. 接种疫苗是预防控制传染病最有效手段．甲、乙两地分别对本地各40万人接种新冠病毒疫苗．甲地在前期完成5万人员接种后，甲、乙两地同时以相同速度接种．甲地经过a 天接种后，由于情况变化，接种速度放缓．图中的折线BCD 和线段OA 分别反映了甲、乙两地的接种人数y （万人）与接种时间x (天)之间的函数关系．根据图像所提供的信息回答下列问题的（1）乙地比甲地提前了________天完成疫苗接种工作．（2）试写出乙地接种人数2y（万人）与接种时间x(天)之间的函数解析式______．（3）当甲地放缓接种速度后，每天可接种_______万人．24. 如图，在△ABC中，∠ACB=90°，AC=4，CB=2，点D是AB的中点，点E在AC上，点E、D、F一条直线上，且ED=FD，（1）求证：FB⊥CB；（2）联结CD，若CD⊥EF，求CE的长．25. 在平面直角坐标系中，反比例函数y＝kx（x＞0，k＞0图象上的两点（n，3n）、（n+1，2n）．（1）求n的值；（2）如图，直线l为正比例函数y＝x的图象，点A在反比例函数y＝kx（x＞0，k＞0）的图象上，过点A作AB⊥l于点B，过点B作BC⊥x轴于点C，过点A作AD⊥BC于点D，记△BOC的面积为S1，△ABD的面积为S2，求S1﹣S2的值．26. 如图1所示，已知△ABC 中，∠ACB =90°，BC =2，AC=D 在射线BC 上，以点D 为圆心，BD 为半径画弧交AB 边AB 于点E ，过点E 作EF ⊥AB 交边AC 于点F ，射线ED 交射线AC 于点G ．（1）求证：EA =EG ；（2）若点G 在线段AC BD =x ，FC =y ，求y 关于x 函数解析式并写出定义域； （3）联结DF ，当△DFG 是等腰三角形时，请直接写出BD 长度．的的徐汇区学年初二年级第一学期期末考试数学试卷（考试时间90分钟，满分100分）一．选择题（本大题共6题，每题3分，满分18分）1. 下列二次根式中，是最简二次根式的是（）A.B.C.D.【答案】D【解析】【分析】根据最简二次根式的定义去判断即可．含有分母，不是最简二次根式，故A不符合题意；含有开方不尽的因数，不最简二次根式，故B不符合题意；含有开方不尽的因数，不是最简二次根式，故C不符合题意；是最简二次根式，故D符合题意；故选D．【点睛】本题考查了最简二次根式即被开方数中的每一个因数的指数都小于根指数2，正确理解最简二次根式的定义是解题的关键．2. 下列方程中，没有实数根的是（）是A. 2310x x −−=B. 230x x −=C. 2210x x −+=D. 2230x x −+=【答案】D【解析】 【分析】利用一元二次方程根的判别式，即可求解．【详解】解：A 、()()2341130∆=−−×−=> ，所以方程有两个不相等的实数根，故本选项不符合题意；B 、()234090∆=−−×=>，所以方程有两个不相等的实数根，故本选项不符合题意； C 、()22410∆=−−×=，所以方程有两个相等的实数根，故本选项不符合题意； D 、()224380∆=−−×=−<，所以方程没有的实数根，故本选项符合题意；故选：D【点睛】本题主要考查了一元二次方程根的判别式，熟练掌握二次函数()20y ax bx c a ++≠ ，当240b ac ∆=−> 时，方程有两个不相等的实数根；当240b ac ∆=−= 时，方程有两个相等的实数根；当240b ac ∆=−< 时，方程没有实数根是解题的关键．3. 如果正比例函数图像与反比例函数图像的一个交点的坐标为（3，-4），那么另一个交点的坐标为（ ）A. （-3，-4）B. （3）C. （−3，4）D. （-4，3） 【答案】C【解析】【分析】根据两交点关于原点对称求解．【详解】设正比例函数解析式为y kx =，反比例函数解析式为a y x= ∴联立得a y x y kx = = ，解得2a x k =，x y = =或x y = =− ∴正比例函数和反比例函数交点关于原点对称∴如果正比例函数图像与反比例函数图像的一个交点的坐标为（3，-4），那么另一个交点的坐标为（−3，4）故选：C【点睛】本题考查了反比例函数图象的对称性，联立两函数解析式求交点坐标是常用的方法，也是基本的方法，需熟练掌握，另外，利用对称性求解更简单，且不容易出错．4. 满足下列条件的三角形中，不是直角三角形的是（ ）A. 三内角之比为3：4：5B. 三边长的平方之比为1：2：3C. 三边长之比为7：24：25D. 三内角之比为1：2：3【答案】A【解析】【分析】根据勾股定理逆定理及三角形内角和可直接进行排除选项．【详解】解：A 、由三内角之比为3：4：5可设这个三角形的三个内角分别为3,4,5k k k ，根据三角形内角和可得345180k k k ++=°，所以15k =°，所以这个三角形的最大角为5×15°=75°，故不是直角三角形，符合题意；B 、由三边长的平方之比为1：2：3可知该三角形满足勾股定理逆定理，即1+2=3，所以是直角三角形，故不符合题意；C 、由三边长之比为7：24：25可设这个三角形的三边长分别为7,24,25k k k ，则有()()()22272425k k k +=，所以是直角三角形，故不符合题意； D 、由三内角之比为1：2：3可设这个三角形的三个内角分别为,2,3k k k ，根据三角形内角和可得23180k k k ++=°，所以30k =3×30°=90°，是直角三角形，故不符合题意；故选A ．【点睛】本题主要考查勾股定理逆定理及三角形内角和，熟练掌握勾股定理逆定理及三角形内角和是解题的关键．5. 下列命题中，其逆命题是真命题的命题个数有（ ）（1）全等三角形的对应边相等； （2）对顶角相等；（3）等角对等边； （4）全等三角形的面积相等．A. 1个B. 2个C. 3个D. 4个 【答案】B【解析】【分析】首先写出各个命题的逆命题，再进一步判断真假．【详解】（1）逆命题是：对应边相等的两个三角形全等，正确；（2）逆命题是：相等的角是对顶角，错误；（3）逆命题是：等边对等角，正确；（4）逆命题是：面积相等，两三角形全等，错误．故选：B ．【点睛】本题主要考查了逆命题的定义及真假性，学生易出现只判断原命题的真假，也就是审题不认真，难度适中．6. 如图所示，在平面直角坐标系xOy 中，点A 、B 、C 为反比例函数y =k x（k ＞0）上不同的三点，连接OA 、OB 、OC ，过点A 作AD ⊥y 轴于点D ，过点B 、C 分别作BE ，CF 垂直x 轴于点E 、F ，OC 与BE 相交于点M ，记△AOD 、△BOM 、四边形CMEF 的面积分别为S 1、S 2、S 3，则（ ）A. S 1=S 2+S 3B. S 2=S 3C. S 3＞S 2＞S 1D. S 1S 2＜S 32 【答案】B【解析】【分析】先根据反比例函数的几何意义可得,,AOD BOE COF V V V 的面积都等于2k ，再逐项分析即可得． 【详解】解：由题意得：,,AOD BOE COF V V V 的面积都等于2k ， 123,22EOM k k S S S S =−=∴=V ， A 、1S 与23S S +不一定相等，此项错误；B 、23S S =，此项正确；C 、321S S S =<，此项错误；D 、12222223S S S S S S >==，此项错误；故选：B ．【点睛】本题考查了反比例函数的几何意义，熟练掌握反比例函数的几何意义是解题关键．二．填空题（本大题共12题，每题2分，满分24分）7. 函数y = ___________________．【答案】x ≤2.【解析】【分析】y =2-x≥0，解不等式即可得到所求定义域．【详解】解：y= 可得2-x≥0，解得x≤2.故答案为x≤2.【点睛】本题考查求函数的定义域的问题，解题时应根据函数的解析式，列出使解析式有意义的不等式，从而求出定义域来．8. 已知函数y ＝1x x −，当x 时，y ＝_____．【答案】【解析】【分析】把自变量x 的值代入函数关系式进行计算即可．【详解】解：当x 时，函数y ＝1x x −，故答案为：．【点睛】本题考查了求函数值及分母有理化，理解求函数值的方法及分母有理化是解题关键．9. 已知0是关于x 的一元二次方程22(1)210m x x m −++−=的一个实数根，则m =______．【答案】-1【解析】【分析】根据一元二次方程的二次项系数不等于零可得10m −≠，由0是一元二次方程方程的解，把0x =，代入方程可得210m −=，进而即可解得m 的值．【详解】解：∵0是关于x 的一元二次方程22(1)210m x x m −++−=的一个实数根，∴210m −=，且10m −≠，∴1m =−，故应填-1．【点睛】本题主要考查了一元二次方程中的字母求值问题．10. 在实数范围内因式分解：2231x x −−=_________．【答案】2x x −−【解析】 【分析】结合题意，当231022x x −−=时，通过求解一元二次方程，得231022x x x x −−== ，结合2231231222x x x x −−=−− ，即可得到答案． 【详解】2231231222x x x x −−=−−当231022x x −−=时，得x =∴231022x x x x −−==∴23122x x x x −−=∴22312x x x x −−=故答案为：2x x−− ． 【点睛】本题考查了因式分解和一元二次方程的知识；解题的关键是熟练掌握一元二次方程的性质，从而完成求解．11. 若1(1,)M y −、21(,)2N y −两点都在函数k y x=的图像上，且1y <2y ，则k 的取值范围是______． 【答案】k <0【解析】 【分析】根据112−<−，且1y <2y ，可得y 随x 的增大而增大，即可求解 【详解】解：∵112−<− ，且1y <2y ， ∴y 随x 的增大而增大， ∴0k <故答案为：0k < 【点睛】本题主要考查了反比例函数的图象和性质，熟练掌握对于反比例函数()0k y k x=≠ ，当0k > 时，在每一象限内， y 随x 的增大而减小，当0k < 时，在每一象限内，y 随x 的增大而增大是解题的关键．12. 已知正比例函数()0y kx k =≠的图象经过第一、三象限，且经过点（k ，k +2），则k =________．【答案】2【解析】【分析】先根据正比例函数的图象可得0k >，再将点(,2)k k +代入函数的解析式可得一个关于k 的一元二次方程，解方程即可得．【详解】解：Q 正比例函数()0y kx k =≠的图象经过第一、三象限， 0k ∴>，由题意，将点(,2)k k +代入函数()0y kx k =≠得：22k k =+， 解得2k =或10k =−<（舍去）， 故答案为：2．【点睛】本题考查了正比例函数的图象、一元二次方程的应用，熟练掌握正比例函数的图象特点是解题关键．13. 以线段AB 为底边的等腰三角形，它的两底角平分线交点的轨迹是_____．【答案】线段AB 的垂直平分线（AB 中点除外）【解析】【分析】根据等边对等角，得到两个底角相等，两个底角的一半也是相等的，利用等角对等边，交点到A，B的距离相等，得到结论．【详解】如图，∵CA=CB，∴∠CAB=∠CBA，∵AD，BD分别是∠CAB，∠CBA的平分线，∴12∠CAB=12∠CBA，∴∠DAB=∠DBA，∴D在AB的垂直平分线上，故答案为：线段AB的垂直平分线（AB中点除外）．【点睛】本题考查了等腰三角形的性质，等腰三角形的判定，线段垂直平分线的逆定理，熟练等腰三角形的性质，线段垂直平分线的逆定理是解题的关键．14. 如图，在△ABC中，∠C=37°，边BC的垂直平分线分别与AC、BC交于点D、E，AB=CD，那么∠A=____°．【答案】74【解析】【分析】连接BD，由题意易得BD=CD=AB，然后可得∠DBC=∠C=37°，进而根据三角形外角的性质及等腰三角形的性质可求解．【详解】解：连接BD，如图所示：∵DE垂直平分BC，AB=CD，∴BD=CD=AB，∵∠C=37°，∴∠DBC=∠C=37°，∴∠ADB=2∠C=74°，∵AB=BD，∴∠A=∠ADB=74°，故答案为74．【点睛】本题主要考查线段垂直平分线的性质定理、三角形外角的性质及等腰三角形的性质，熟练掌握线段垂直平分线的性质定理、三角形外角的性质及等腰三角形的性质是解题的关键．15. 如图，∠AOE＝∠BOE＝15°，EF//OB，EC⊥OB，若EC＝2，则EF＝___．【答案】4【解析】【分析】作EG⊥OA于G，根据角平分线的性质得到EG的长度，再根据平行线的性质得到∠OEF＝∠COE＝15°，然后利用三角形的外角和内角的关系求出∠EFG＝30°，利用30°角所对的直角边是斜边的一半解题．【详解】解：作EG⊥OA于G，如图所示：∵EF//OB，∠AOE＝∠BOE＝15°，EC⊥OB，∴∠OEF＝∠COE＝15°，EG＝CE＝2，∵∠AOE＝15°，∴∠EFG＝15°＋15°＝30°，∴EF＝2EG＝4．故答案为：4．【点睛】本题考查了角平分线的性质、平行线的性质、含30°角的直角三角形的性质；熟练掌握角平分线的性质，证出∠EFG＝30°是解决问题的关键．16. 如图，梯形ABCD中，AD∥BC，AF⊥BC于F，M是CD中点，AM的延长线交BC的延长线于E，AE⊥AB，∠B=60°，AF=，则梯形的面积是___．【答案】【解析】【分析】根据已知条件易证△ADM≌△ECM，得S△ADM＝S△ECM，进而得到S梯形＝S△ABE，然后解直角△ABF，求出AB，进而可得AE，根据三角形面积公式求出S△ABE即可．【详解】解：∵AD∥BC，∴∠DAM ＝∠E ，∠D ＝∠ECM ，∵DM ＝CM ，∴△ADM ≌△ECM ，∴S △ADM ＝S △ECM ， ∴S 梯形＝S △ABE ，∵AF ⊥BC ，∠B ＝60°，AF ＝，∴sin60°＝AF AB ， 解得：4AB =，∵AE ⊥AB ，∴AE =∴S △ABE ＝11422AB AE ?创=，即梯形的面积是故答案为：【点睛】本题考查了平行线的性质、全等三角形的判定和性质以及解直角三角形等知识点，求出S 梯形＝S △ABE 是解题关键． 17. 如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在Rt △ABC 中，∠C =90° ，AC =2，若Rt △“好玩三角形”，则AB =_______．或【解析】【分析】分AC 边上的中线BD 等于AC ，BC 边上的中线AE 等于BC 两种情况，根据勾股定理计算．【详解】解：当AC 边上的中线BD 等于AC 时，如图，∵∠C =90°，AC =2，∴CD =1,BD =2∴22222213BC BD CD =−=−=,∴AB =当BC 边上的中线AE 等于BC 时，∵AC 2=AE 2−CE 2，∴BC 2−(12BC )2=22， 解得，BC 2=163，∴AB ===,综上所述，AB AB或【点睛】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2=c 2. 熟练掌握勾股定理是解本题的关键.18. 小华用一张直角三角形纸片玩折纸游戏，如图1，在Rt ABC △中，90ACB ∠=°，30B ∠=°，1AC =．第一步，在AB 边上找一点D ，将纸片沿CD 折叠，点A 落在A ′处，如图2，第二步，将纸片沿CA ′折叠，点D 落在D ¢处，如图3．当点D ¢恰好在原直角三角形纸片的边上时，线段A D ′′的长为__________．【答案】12或2− 【解析】 【分析】因为点D ¢恰好在原直角三角形纸片的边上，所以分为当D ¢落在AB 边上和BC 边上两种情况分析，根据勾股定理求解即可．【详解】解：当D ¢落在AB 边上时，如图（1）：设DD ′交AB 于点E ，由折叠知：60EA D A ′∠=∠=°,ADA D A D ′′′==,DD A E ′′⊥,A C AC ′= 90ACB ∠=°Q ，30B ∠=°，1AC =2,AB BC ∴==设AD x =，则在Rt A ED ′V 中，12A E x ′=在Rt ECB V 中，12EC BC ==A C AC ′=Q112x ∴+=即2x =−．当D ¢落在BC 边上时，如图（2）因为折叠，30,ACD A CD A CD ′′′∠=∠=∠=° ∴ 11,122A D A C AB AC A B AC ′′′′′′===== 12AD A D ′′∴．故答案为：12或2 【点睛】本题考查了轴对称变换，勾股定理，直角三角形中30°的性质，正确的作出图形是解题的关键．三．简答题（第19、20、21、22、23每题6分，24、25每题8分，26题12分）19. 2−．【答案】4+−【解析】 【分析】先根据二次根式的乘法、分母有理化和完全平方公式化简，再计算加减即可．【详解】解：原式15+−+4．【点睛】本题主要考查二次根式的混合运算，解题的关键是掌握二次根式的混合运算顺序和法则． 20. 用配方法解方程：2420x x −−=．【答案】12x =+，22x =【解析】【分析】利用配方法解一元二次方程即可得．【详解】解：2420x x −−=，2x 4x 2−=，24424x x −+=+，2(26)x −=，2x −2x =±即1222x x −【点睛】本题考查了利用配方法解一元二次方程，熟练掌握配方法是解题关键．21. 关于x 的一元二次方程22(2)20x m x +−+=有两个相等的实数根，求m 的值及方程的根．【答案】当16m =时，121x x ==−；当22m =−时，121x x == 【解析】【分析】根据原方程有两个相等的实数根可以得到有关m 的方程，解得m 的值，再代入得到方程的解即可．【详解】∵方程有两个相等的实数根，∴22(2)422412m m m ∆=−−××=−−=0∴126,2m m ==−当16m =时，121x x ==−当22m =−时，121x x == 【点睛】考查了根的判别式的知识，解题的关键是根据根的情况得到方程．当Δ=0时，方程有两个相等的两个实数根；22. 某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10%，月份的营业额达到633.6万元．求3月份到5月份营业额的平均月增长率．【答案】20%【解析】【分析】主要考查增长率问题，一般用增长后的量=增长前的量×（1+增长率），设3月份到5月份营业额的平均增长率是x ，则四月份的营业额是400（1+10%）（1+x ），5月份的营业额是400（1+10%）（1+x ）2，据此即可列方程求解．要注意根据实际意义进行值的取舍．【详解】设月份至月份的营业额的平均月增长率为．依题意，得: 2400(110%)(1)633.6x ++=．整理得: 2(1) 1.44x +=．解得: 120.2, 2.2x x ==−（不合题意，舍去）． 答：月份至月份的营业额的平均月增长率为20%．【点睛】可根据题意列出方程，判断所求的解是否符合题意，舍去不合题意的解．找到关键描述语，找到等量关系准确的列出方程是解决问题的关键．23. 接种疫苗是预防控制传染病最有效的手段．甲、乙两地分别对本地各40万人接种新冠病毒疫苗．甲地在前期完成5万人员接种后，甲、乙两地同时以相同速度接种．甲地经过a 天接种后，由于情况变化，接种速度放缓．图中的折线BCD 和线段OA 分别反映了甲、乙两地的接种人数y （万人）与接种时间x (天)之间的函数关系．根据图像所提供的信息回答下列问题（1）乙地比甲地提前了________天完成疫苗接种工作．（2）试写出乙地接种人数2y （万人）与接种时间x (天)之间的函数解析式______．（3）当甲地放缓接种速度后，每天可接种_______万人．【答案】（1）20 （2）212y x =（3）0.25【解析】【分析】（1）看图像，乙地用80天完成，甲地用100天，时间差即提前天数．（2）乙地接种人数2y （万人）与接种时间x (天)成正比，且过点（80，40），用待定系数法求解即可；为（3）先根据BC 与2y 相同，求得BC 的解析式，确定a 值，再确定CD 的解析式即可．【小问1详解】看图像，乙地用80天完成，甲地用100天，∴提前100-80=20（天），故答案为：20．小问2详解】∵乙地接种人数2y （万人）与接种时间x (天)成正比，∴设2y =mx ，∵函数经过点（80，40），∴40=80m ，解得m =12， ∴2y =12x ， 故答案为：2y =12x ． 【小问3详解】∵2y =12x ， ∴BC y =12x +b ， ∵B （0，5），∴b =5，∴BC y =12x +5， ∴25=12a +5， ∴a =40，∴C （40，25），D （100，40），∴设CD y =kx +n ，∴402510040k n k n += += ， 【解得0.2515k n = =， ∴设CD y =0.25x +15，故答案为：0.25．【点睛】本题考查了正比例函数，一次函数解析式的确定，正确获取图像信息，灵活用待定系数法是解题的关键．24. 如图，在△ABC 中，∠ACB =90°，AC =4，CB =2，点D 是AB 的中点，点E 在AC 上，点E 、D 、F 一条直线上，且ED =FD ，（1）求证：FB ⊥CB ；（2）联结CD ，若CD ⊥EF ，求的长．【答案】（1）见解析 （2）52 【解析】【分析】（1）先证明△ADE ≅△BDF 可得A FBD ∠∠=，再由∠ACB =90°可得∠A +∠ABC =90°，再根据等量代换可得∠FBC =90°即可证明结论；（2）如图：联结CD 、CF ．根据题意可得CF =EF ，设CE =x ，则CF =x ，BF =AE =4-x ，然后根据勾股定理列方程求得x 即可．【小问1详解】（1）证明：∵D 是AB 中点，∴AD =BD在△ADE 与△BDF 中，AD BD ADE BDF ED FD = ∠=∠ =∴△ADE ≅△BDF∴A FBD ∠∠=，AE =BF ．∵∠ACB =90°，∴∠A +∠ABC =90°，∴FBD ∠+∠ABC =90°，即∠FBC =90°，∴FB ⊥CB ．【小问2详解】解：（2）如图：联结CD 、CF ．∵CD ⊥EF ，ED =FD ，∴CF =CE ，设CE =x ，则CF =x ，BF =AE =4-x ，Rt △FBC 中，222BF BC CF +=，∴2222(4x x +−=），∴x =52 ，即CE =52．【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的性质、勾股定理等知识点，正确运用勾股定理列方程成为解答本题的关键．25. 在平面直角坐标系中，反比例函数y ＝k x （x ＞0，k ＞0图象上的两点（n ，3n ）、（n+1，2n ）． （1）求n 的值；（2）如图，直线l为正比例函数y＝x的图象，点A在反比例函数y＝kx（x＞0，k＞0）的图象上，过点A作AB⊥l于点B，过点B作BC⊥x轴于点C，过点A作AD⊥BC于点D，记△BOC的面积为S1，△ABD的面积为S2，求S1﹣S2的值．【答案】（1）2（2）6【解析】【分析】（1）利用反比例函数图象上点的坐标特征得到n•3n＝（n+1）•2n，然后解方程可得n的值；（2）设B（m，m），利用△OBC为等腰直角三角形得到∠OBC＝45°，再证明△ABD为等腰直角三角形，则可设BD＝AD＝t，所以A（m+t，m﹣t），把A（m+t，m﹣t）代入y＝12x中得到m2﹣t2＝12，然后利用整体代入的方法计算S1﹣S2．【详解】解：（1）∵反比例函数y＝kx（x＞0，k＞0图象上的两点（n，3n）、（n+1，2n）．∴n•3n＝（n+1）•2n，解得n＝2或n＝0（舍去），∴n的值为2；（2）反比例函数解析式为y＝12x，设B（m，m），∵OC＝BC＝m，∴△OBC为等腰直角三角形，∴∠OBC＝45°，∵AB⊥OB，∴∠ABO＝90°，∴∠ABC＝45°，∴△ABD为等腰直角三角形，设BD ＝AD ＝t ，则A （m+t ，m ﹣t ），∵A （m+t ，m ﹣t ）在反比例函数解析式为y ＝12x 上， ∴（m+t ）（m ﹣t ）＝12，∴m 2﹣t 2＝12，∴S 1﹣S 2＝2211112222m t −=×＝6． 【点睛】本题考查了反比例函数系数k 的几何意义：在反比例函数y ＝k x（k ≠0）图象中任取一点，过这一个点向x 轴和y 轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．也考查了反比例函数的性质．26. 如图1所示，已知△ABC 中，∠ACB =90°，BC =2，AC =D 在射线BC 上，以点D 为圆心，BD 为半径画弧交AB 边AB 于点E ，过点E 作EF ⊥AB 交边AC 于点F ，射线ED 交射线AC 于点G ．（1）求证：EA =EG ；（2）若点G 在线段AC 延长线上时，设BD =x ，FC =y ，求y 关于x 的函数解析式并写出定义域；（3）联结DF ，当△DFG 是等腰三角形时，请直接写出BD 的长度．【答案】（1）见解析 （2）)12y x =≤<（3）85 【解析】【分析】（1）在BA 上截取BM =BC =2，在Rt △ACB 中，由勾股定理222AC BC AB +=，可得AB =4，进而可得∠A =30°，∠B =60°；由DE =DB ，可证△DEB 是等边三角形，∠BED =60°，由外角和定理得∠BED =∠A +∠G ，进而得∠G =30°，所以∠A =∠G ，即可证EA =EG ；（2）由△DEB 是等边三角形可得BE =DE ，由BD =x ，FC =y ，得BE =x ， DE =x ，AE =AB -BE =4-x ，在Rt △AEF 中，由勾股定理可表示出AF =，把相关量代入FC =AC -AF ，整理即可得y 关于x 的函数解析式；当F 点与C 点重合时，x 取得最小值1，G 在线段AC 延长线上,可知，D 点不能与C 点重合，所以x 最大值小于2，故可得1≤x <2；（3）连接DF ，根据等腰三角形判定定理，有两条边相等的三角形是等腰三角形，分三种情况①当CF CG =时，②当DG FG =时③当DF FG =时，分别计算即可得BD 的长．【小问1详解】如图，BA 上截取BM =BC =2，Rt △ACB 中，∠C =90°∵ACBC =2，∴AB4=∴AM =AB -BM =2，∴CM =BM =AM =2，∴△BCM 是等边三角形，∴∠B =60°，∴∠A =30°，∵DE =DB ，∴△DEB 是等边三角形， 的在∴∠BED=60°，∵∠BED=∠A+∠G，∴∠G=30°∴∠A=∠G，∴EA=EG．【小问2详解】∵△DEB是等边三角形，∴BE=DE设BE=x，则DE=x，AE=AB-BE=4-x ∵∠A=30°，∠AEF=90°，∴EF=12 AF，Rt△AEF中，222AE EF AF+=∴AF=∵FC=AC-AF，∴y=定义域：1≤x<2【小问3详解】连接DF，Rt △ACB 中，∠C =90°∴222AC BC AB +=∵AC BC =2，BD =x ，∴AB =4，EA =EG=4-x ，42DG x =−，2DC x =−，①当CF CG =时，在Rt △DCG 中，∴222DG DC CG =+，222(42)(2)x x =−−+， 解得：14x =（舍去），285x =； ②当DG FG =时，在Rt △DCG 中，∠G =30°，∴DG =2DC ，∴CG )2x ==−∴42)x x −=−+，解之得：x =； ③当DF FG =时，在Rt △DCF 中，22222(2)DF DC CF x =+=−+， ∴22DF FG =， 222(2)2)x x −+−+，解得：x =综上所述：BD 的长为85【点睛】本题主要考查了勾股定理，等腰三角形的判定等有关知识，正确进行分析，熟练掌握和灵活运用相关知识是解题的关键，注意分类思想的运用．。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，为估计池塘岸边A、B 两点的距离，小方在池塘的一侧选取一点O，测得OA＝8 米，OB＝6 米，A、B 间的距离不可能是（）A．12 米B．10 米C．15 米D．8 米【答案】C【解析】试题分析：根据两边之和大于第三边，两边之差小于第三边，AB的长度在2和14之间，故选C．考点：三角形三边关系．A2．如图，将正方形OABC放在平面直角坐标系中，O是原点，点A的坐标为(1，3)，则点C的坐标为()A．(－3，1) B．(－1，3) C．(3，1) D．(－3，－1)【答案】A【解析】试题分析：作辅助线构造出全等三角形是解题的关键，也是本题的难点．如图：过点A作AD⊥x 轴于D，过点C作CE⊥x轴于E，根据同角的余角相等求出∠OAD=∠COE，再利用“角角边”证明△AOD和△OCE全等，根据全等三角形对应边相等可得OE=AD，CE=OD，然后根据点C在第二象限写出坐标即可．∴点C的坐标为（-，1）故选A．考点：1、全等三角形的判定和性质；2、坐标和图形性质；3、正方形的性质．3．已知△ABC的周长是24，且AB=AC，又AD⊥BC，D为垂足，若△ABD的周长是20，则AD的长为() A．6 B．8 C．10 D．12【答案】B【分析】根据三线合一推出BD＝DC，再根据两个三角形的周长进而得出AD的长．【详解】解：∵AB=AC，且AD⊥BC，∴BD=DC=1BC，2∵AB+BC+AC=2AB+2BD=24，∴AB+BD+AD=12+AD=20，解得AD=1．故选：B ．【点睛】本题考查了等腰三角形的性质，做题时应该将已知和所求联系起来，对已知进行灵活运用，从而推出所求． 4．以下列各组线段为边,能构成直角三角形的是 ( )A ．8cm,9cm,10cmB ．2cm,6cm,3cmC ．1cm,2cm,3cmD ．6cm,7cm,8cm【答案】C【解析】根据勾股定理的逆定理对四组数据进行逐一判断即可．【详解】A ．∵82+92≠102，∴不能构成直角三角形；B ．∵222(2)(3)(6)+≠，∴不能构成直角三角形；C ．∵2221(3)=2+，∴能构成直角三角形；D ．∵62+72≠82，∴不能构成直角三角形．故选C ．【点睛】本题考查了用勾股定理的逆定理判断三角形的形状，即只要三角形的三边满足a 2+b 2=c 2，则此三角形是直角三角形．5．如图，AB ∥CD ，∠A+∠E=75º，则∠C 为（ ）A ．60 ºB ．65 ºC ．75 ºD ．80 º【答案】C【解析】如图，∵∠A+∠E=75 º，∴根据三角形内角和等于1800，得∠AFE=105 º．∵∠AFE与∠BFC是对顶角，∴∠AFE=∠BFC=105 º．∵AB∥CD，∴根据平行线的同旁内角互补的性质，得∠C=1800－∠BFC=75 º．故选C．6．如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A的坐标是（a，b），经过第2019次变换后所得的点A的坐标是（）A．（﹣a，b）B．（﹣a，﹣b）C．（a，﹣b）D．（a，b）【答案】A【分析】观察图形，可知每四次对称为一个循环组依次循环，用2019除以4，然后根据商和余数的情况，确定变换后点A所在的象限，即可求解．【详解】解：点A第一次关于x轴对称后在第四象限，点A第二次关于y轴对称后在第三象限，点A第三次关于x轴对称后在第二象限，点A第四次关于y轴对称后在第一象限，即点A回到原始位置，所以，每四次对称为一个循环组依次循环，∵2019÷4＝504余3，∴经过第2019次变换后所得的A点与第三次变换的位置相同，在第二象限，坐标为（﹣a，b）．故选：A．【点睛】键．7．k 、m 、n ===k 、m 、n 的大小关系正确的是（ ）A ．k ＜m=nB ．m=n ＜kC ．m ＜n ＜kD ．m ＜k ＜n 【答案】A【分析】先化简二次根式，再分别求出k 、m 、n 的值，由此即可得出答案．==2k ===5m ===5n =则k m n <=故选：A ．【点睛】本题考查了二次根式的化简，掌握化简方法是解题关键．8．下列命题为假命题的是（ ）A ．三条边分别对应相等的两个三角形全等B ．三角形的一个外角大于与它相邻的内角C ．角平分线上的点到角两边的距离相等D ．有一个角是60的等腰三角形是等边三角形【答案】B【分析】根据全等三角形的判定、三角形外角的性质、角平分线上的性质以及等边三角形的判定得出答案即可．【详解】解：A 、三条边分别对应相等的两个三角形全等，此选项是真命题，故此选项不符合题意； B 、三角形的一个外角大于与它不相邻的任意一个内角，根据三角形外角性质得出，此选项是假命题，故此选项符合题意；C 、角平分线上的点到角两边的距离相等，此选项是真命题，故此选项不符合题意；D 、有一个角是60的等腰三角形是等边三角形，故此选项是真命题，故此选项不符合题意；故选：B ．【点睛】此题主要考查了命题与定理，正确把握三角形外角的性质、角平分线上的性质、等边三角形的判定以及全等三角形的性质是解题关键．9．如图，在Rt ABC ∆中，90C ∠=︒，AD 是BAC ∠的平分线交BC 于点D ．若CD m =，AB n =，30B ∠=︒，那么ABD ∆的面积是( )A．12mn B．mn C．13mn D．2mn【答案】A【分析】作DE⊥AB,由角平分线性质可得DE=ED,再根据三角形的面积公式代入求解即可．【详解】过点D作DE⊥AB交AB于E,∵AD平分∠BAC,∴ED=CD=m,∵AB=n,∴S△ABC=1122AB ED mn⋅=．故选A．【点睛】本题考查角平分线的性质,关键在于通过角平分线的性质得到AB边上高的长度．10．不等式组的解集在数轴上表示为（）A．B．C．D．【答案】C【详解】解：由x≤2得：x≤2．由2-x＜3得：x＞-2．所以不等式组的解集为-2＜x≤2．故选C．【点睛】此题主要考查不等式组的解法及在数轴上表示不等式组的解集．不等式组的解集在数轴上表示的方法：把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．二、填空题11．若P（a﹣2，a+1）在x轴上，则a的值是_____．【答案】﹣1【分析】直接利用x轴上点的坐标特点得出a+1＝0，进而得出答案．【详解】解：∵P（a﹣2，a+1）在x轴上，∴a+1＝0，解得：a＝﹣1．故答案为：﹣1．【点睛】本题主要考查坐标轴上点的特征，掌握坐标轴上点的特征是解题的关键.12．因式分解：3x2-6xy+3y2=______．【答案】3（x﹣y）1【解析】试题分析：原式提取3，再利用完全平方公式分解即可，得到3x1﹣6xy+3y1=3（x1﹣1xy+y1）=3（x﹣y）1．考点：提公因式法与公式法的综合运用13．在一个不透明的盒子中装有n个球，它们有且只有颜色不同，其中红球有3个.每次摸球前，将盒中所有的球摇匀，然后随机摸出一个球，记下颜色后再放回盒中.通过大量重复试验，发现摸到红球的频率稳定在0.06，那么可以推算出n的值大约是__________．【答案】1【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，列出方程求解．【详解】由题意可得，30.06 n=，解得，50n=，经检验n=1是方程的解，故答案为：1．【点睛】本题主要考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：概率=所求情况数与总情况数之比．14．在平面直角坐标系中，点A、B、C的坐标分别为：A（﹣2，1），B（﹣3，﹣1），C（1，﹣1）．若以A，B，C，D为顶点的四边形为平行四边形，那么点D的坐标是_____．【答案】（﹣6，1）或（2，1）或（0，﹣3）【分析】如图，首先易得点D纵坐标为1，然后根据平行四边形性质和全等三角形的性质易得点D横坐标为2；同理易得另外两种情况下的点D的坐标．【详解】解：如图，过点A、D作AE⊥BC、DF⊥BC，垂足分别为E、F，∵以A，B，C，D为顶点的四边形为平行四边形，∴AD∥BC，∵B（﹣3，﹣1）、C（1，﹣1）；∴BC∥x轴∥AD，∵A（﹣2，1），∴点D纵坐标为1，∵▱ABCD中，AE⊥BC，DF⊥BC，易得△ABE≌△DCF，∴CF＝BE＝1，∴点D横坐标为1+1＝2，∴点D（2，1），同理可得，当D点在A点左侧时，D点坐标为（﹣6，1）；当D点在C点下方时，D点坐标为（0，﹣3）；综上所述，点D坐标为（﹣6，1）或（2，1）或（0，﹣3），故答案为：（﹣6，1）或（2，1）或（0，﹣3）.【点睛】本题主要考查了坐标与图形性质和平行四边形的性质，注意要分情况求解．15．如图，在△ABC中，AB=AD=DC，∠BAD=28°，则∠C=______．【答案】38°【解析】首先发现此图中有两个等腰三角形，根据等腰三角形的两个底角相等找到角之间的关系．结合三角形的内角和定理进行计算．【详解】∵AB=AD=DC，∠BAD=28°∴∠B=∠ADB=（180°-28°）÷2=76°．∴∠C=∠CAD=76°÷2=38°．故答案为38°．【点睛】此题主要考查等腰三角形的性质及三角形内角和定理；求得∠ADC=76°是正确解答本题的关键．16．如图，将△ABC沿着AB方向，向右平移得到△DEF，若AE=8，DB=2，则CF=______.【答案】1.【解析】根据平移的性质可得AB=DE，然后求出AD=BE，再求出AD的长即为平移的距离．【详解】∵△ABC沿AB方向向右平移得到△DEF，∴AB=DE，∴AB-DB=DE-DB，即AD=BE，∵AE=8，DB=2，∴AD=（AE-DB）=×（8-2）=1，即平移的距离为1．∴CF=AD=1，故答案为：1【点睛】本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行（或在同一条直线上）且相等，对应线段平行（或在同一条直线上）且相等，对应角相等．1724__________．【分析】根据二次根式 的性质直接化简即可. 【详解】24=|4|4=.故答案为：4.【点睛】此题主要考查了运用二次根式的性质进行化简，注意：2 (0)||0 (0) (0)a a a a a a a ⎧⎪===⎨⎪-⎩＞＜. 三、解答题18．如图，将长方形 ABCD 沿 EF 折叠，使点 D 与点 B 重合．（1）若∠AEB=40°，求∠BFE 的度数；（2）若 AB=6，AD=18，求 CF 的长．【答案】（1）70°； （2）1．【分析】（1）依据平行线的性质可求得∠BFE=∠FED ，然后依据翻折的性质可求得∠BEF=∠DEF ，最后根据平角的定义可求得∠BFE 的度数;（2）先依据翻折的性质得到CF=GF,AB=DC=BG=6，然后设CF=GF=x ，然后在RT △BGF 中，依据勾股定理列出关于x 的方程求解即可．【详解】解：（1）∵AD ∥BC ，∴∠BFE=∠FED ，由翻折的性质可知：∠BEF=∠DEF ，∴∠BFE=∠FED=∠BEF∵∠FED ＋∠BEF ＋∠AEB=110°∴2∠BFE =110°-40°=140°，∴∠BFE=70°;（2）由翻折的性质可知CF=GF,AB=DC=BG=6,设CF=GF=x ，则BF=11-x,在Rt △BGF 中，依据勾股定理可知：BF 2=BG 2+GF 2，即(11-x)2=62+x 2，解得：x=1【点睛】本题考查了翻折的性质及勾股定理，熟练掌握翻折的性质和利用勾股定理解直角三角形是解题的关键． 19．勾股定理是初中数学学习的重要定理之一，这个定理的验证方法有很多，你能验证它吗？请你根据所给图形选择一种方法，画出验证勾股定理的方法，并写出验证过程．【答案】见解析【分析】根据勾股定理的定义及几何图形的面积法进行证明即可得解.【详解】如下图，根据几何图形的面积可知：222211()42422a b ab a b ab ab c +-⨯=++-⨯= 整理得：222a b c +=.【点睛】本题主要考查了勾股定理的推到，熟练掌握面积法推到勾股定理是解决本题的关键.20．在ABC ∆中，90,C AC BC ︒∠==，点D 在射线BC 上（不与点B ，C 重合），连接AD ，将AD 绕点D 顺时针旋转90︒得到DE ，连接BE ．如图，点D 在BC 边上．（1）依题意；补全图；（2）作DF BC ⊥交AB 于点F ，若8,3AC DF ==，求BE 的长；【分析】（1）根据题意，过点D 作DE ⊥AD ，补全图形即可；（2）首先判定ADF EDB ∆∆≌，然后得出AF=BE ，再利用平行线分线段成比例性质得出AF ，即可得出BE.【详解】（1）①补全图形，如图所示：②如图所示：由题意可知,90AD DE ADE ︒=∠=DF BC ⊥90FDB ︒∴∠=ADF EDB ∴∠=∠90,C AC BC ︒∠==45ABC DFB ︒∴∠=∠=DB DF ∴=ADF EDB ∴∆∆≌（SAS ）∴AF=BE在ABC ∆和EDB ∆中，DF ∥AC ， ∴DF BF AC AB= 8,3AC DF ==82,2AB BF ∴==∴52AF AB BF =-=即52BE =【点睛】此题主要考查等腰直角三角形的性质以及全等三角形的判定与性质和平行线分线段成比例的性质，熟练掌握，即可解题.21．已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD 与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC＝3MC，请直接写出DBBC的值．【答案】（1）证明见解析；（2）结论：BD＝2CF．理由见解析；（3）23 DBBC.【分析】（1）欲证明BF=AD，只要证明△BCF≌△ACD即可；（2）结论：BD=2CF．如图2中，作EH⊥AC于H．只要证明△ACD≌△EHA，推出CD=AH，EH=AC=BC，由△EHF≌△BCF，推出CH=CF即可解决问题；（3）利用（2）中结论即可解决问题.【详解】（1）证明：如图1中，∵B E⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BC＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴2233 DB aBC a==．【点睛】本题考查三角形综合题、全等三角形的判定和性质、等腰直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．22．潍坊市某大酒店豪华间实行淡季、旺季两种价格标准，旺季每间比淡季上涨13，下表是去年该酒店豪华间某两天的相关记录．问：旺季每间价格为多少元？该酒店豪华间有多少间？淡季旺季未入住间数12 0【答案】旺季每间为800元，酒店豪华间有50间．【分析】设淡季每间价格为x 元，该酒店有y 间豪华间，则旺季时每间单价为113x ⎛⎫+ ⎪⎝⎭元，根据日总收入＝豪华间的单价×入住的房间数，即可得出关于x ，y 的方程组，解之即可得出结论．【详解】解：设淡季每间价格为x 元，该酒店有y 间豪华间，则旺季时每间单价为113x ⎛⎫+ ⎪⎝⎭元， 根据题意得：()122280011400003x y xy ⎧-=⎪⎨⎛⎫+= ⎪⎪⎝⎭⎩ 解得：60050x y =⎧⎨=⎩ ∴14160080033x ⎛⎫+=⨯= ⎪⎝⎭， 答：旺季每间为800元，酒店豪华间有50间．【点睛】本题考查了二元一次方程组，找准等量关系，正确列出方程组是解题的关键．23．某一项工程，在工程招标时，接到甲、乙两个工程队的投标书，施工一天，需付甲工程队工程款1.5万元，乙工程队工程款1.1万元，工程领导小组根据甲乙两队的投标书测算，可有三种施工方案： （1）甲队单独完成这项工程刚好如期完成；（2）乙队单独完成这项工程要比规定日期多用5天；（3）若甲、乙两队合作4天，余下的工程由乙队单独也正好如期完成．据上述条件解决下列问题：①规定期限是多少天？写出解答过程；②在不耽误工期的情况下，你觉得那一种施工方案最节省工程款?【答案】规定期限1天；方案（3）最节省 【分析】设这项工程的工期是x 天，根据甲队单独完成这项工程刚好如期完成，乙队单独完成这项工程要比规定日期多用5天，若甲、乙两队合做4天，余下的工程由乙队单独做也正好如期完成以及工作量=工作时间×工作效率可列方程求解．再看费用情况：方案（1）、（3）不耽误工期，符合要求，可以求费用，方案（2）显然不符合要求．【详解】解：设规定期限x 天完成，则有：415x x x +=+， 解得x=1．经检验得出x=1是原方程的解；答：规定期限1天．方案（1）：1×1.5=30（万元）方案（2）：25×1.1=27.5（万元 ），方案（3）：4×1.5＋1.1×1=28（万元）．所以在不耽误工期的前提下，选第三种施工方案最节省工程款．所以方案（3）最节省．点睛：本题主要考查分式方程的应用，解题的关键是熟练掌握列分式方程解应用题的一般步骤，即①根据题意找出等量关系②列出方程③解出分式方程④检验⑤作答．注意：分式方程的解必须检验． 24．（1）如图1，AD 是ABC ∆的中线，8,6AB AC ==，求AD 的取值范围，我们可以延长AD 到点M ，使DM AD =，连接BM （如图2所示），这样就可以求出2AD 的取值范围，从而得解，请写出解题过程； （2）在（1）问的启发下，解决下列问题：如图3，AD 是ABC ∆的中线，BE 交AC 于点E ，交AD 于点F ，且AE EF =，求证：AC BF =．【答案】（1）17AD <<；（2）见解析．【分析】（1）延长AD 到点M ，使DM AD =，连接BM ，易证ADC MDB ∆≅∆，从而得BM AC =，根据三角形三边关系，可得214AM <<，进而即可求解；（2）先证ADC MDB ∆≅∆，结合AE EF =，可得BM BF =，结合BM AC =，即可得到结论．【详解】（1）AD DM BD CD ADC MDB ==∠=∠，，，ADC MDB ∴∆≅∆（SAS ）， ∴BM AC =，∴在ABM ∆中， 214AM <<，即：2214AD <<，∴AD 的范围是：17AD <<；（2）延长AD 到点M ，使DM AD =，连接BM ，由（1）知：ADC MDB ∆≅∆，M CAD BM AC ∴∠=∠=，，AE EF =，CAD AFE ∴=∠，MFB AFE ∠=∠，BMF BFM ∴∠=∠，BM BF ∴=，AC BF ∴=．【点睛】本题主要考查三角形全等的判定和性质定理，三角形三边的关系，等腰三角形的性质和判定定理，添加辅助线，构造全等三角形，是解题的关键．25．如图，在平面直角坐标系中，一次函数y kx b =+的图象与x 轴的交点为()30A -,，与y 轴的交点为B ，且与正比例函数43y x =的图象交于点(),4C m ．（1）求m 的值及一次函数y kx b =+的解析式；（2）观察函数图象，直接写出关于x 的不等式43x kx b >+的解集． 【答案】（1）3m =，223y x =+；（2）3x > 【分析】（1）将(),4C m 代入正比例函数43y x =即可求出m ，再将A ，C 坐标代入y kx b =+，求出k ，b 的值，即可得一次函数解析式；（2）观察图像，当正比例函数43y x =在一次函数y kx b =+图象上方时，对应x 的取值范围，即为不等式的解集．【详解】（1）将(),4C m 代入正比例函数43y x =得 443m =，解得3m =， ∴()3,4C将()30A -,，()3,4C 代入y kx b =+得： 3034k b k b -+=⎧⎨+=⎩，解得232k b ⎧=⎪⎨⎪=⎩ ∴一次函数解析式为223y x =+； （2）由图像得，当正比例函数43y x =在一次函数y kx b =+图象上方时，3x >， ∴不等式43x kx b >+的解集为：3x >． 【点睛】本题考查求一次函数解析式，一次函数与不等式的关系，熟练掌握待定系数法求函数解析式，掌握根据交点判断不等式解集是解题的关键．八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．已知关于x的方程33kx x=-的解是正整数，且k为整数，则k的值是（）A．-2 B．6 C．-2或6 D．-2或0或6【答案】C【分析】解分式方程，用含k的代数式表示x．再根据解为正整数、k为整数求出k的值．【详解】解：方程33kx x=-去分母，得9-3x=kx，即kx+3x=9，由题意可知30k+≠∴x=93k+，∵原分式方程的解为正整数，∴k+3=1，3，9，∴k=-2，0，1，∵x≠3，∴93k+≠3，∴k≠0，∴k=-2或1．故选：C．【点睛】本题考查了分式方程的解法．由解为正整数、k为整数确定k的值是解决本题的关键．本题易错，只考虑解为正整数，而忽略x=3时分式无意义．2．下列命题中为假命题的是（）A．两直线平行，内错角相等B．对顶角相等C．两个锐角的和是钝角D．如果a是整数，那么a是有理数【答案】C【分析】根据平行线的性质可判断A项，根据对顶角的性质可判断B项，举出反例可判断C项，根据有理数的定义可判断D项，进而可得答案．【详解】解：A、两直线平行，内错角相等，是真命题，故本选项不符合题意；B、对顶角相等，是真命题，故本选项不符合题意；C、两个锐角的和不一定是钝角，如20°和30°这两个锐角的和是50°，仍然是锐角，所以原命题是假命题，故本选项符合题意；D 、如果a 是整数，那么a 是有理数，是真命题，故本选项不符合题意．故选：C ．【点睛】本题考查了真假命题、平行线的性质、对顶角的性质和有理数的定义等知识，属于基础题型，熟练掌握上述基本知识是解题的关键．3．下列计算正确的是（ ）A B C ．=3 D 【答案】D【解析】解：A 不能合并，所以A 错误；B ==，所以B 错误；C ．=C 错误；D ==D 正确．故选D ．4．下列各式中，相等关系一定成立的是（ ）A ．22()()x y y x -=-B ．2(6)(6)6x x x +-=-C ．222()x y x y +=+D ．6(2)(2)(2)(6)x x x x x -+-=--【答案】A【分析】用平方差公式和完全平方公式分别计算，逐项判断即可.【详解】解：A ．22()()x y y x -=-，故A 正确； B ．应为2(6)(6)36x x x +-=-，故B 错误；C ．应为222()2x y x y xy +=++，故C 错误；D ．应为6(2)(2)(2)(6)x x x x x -+-=--，故D 错误．故选A ．【点睛】本题考查平方差公式及完全平方公式的计算．5．如图，在ABC ∆中，AB AC =，AB 的垂直平分线交AB 于点D ，交AC 于点E ，若76BEC ∠=，则ABC ∠=（ ）A ．70B ．71C ．74D ．76【答案】B 【分析】由垂直平分线的性质可得AE=BE ，进而可得∠EAB=∠ABE ，根据三角形外角性质可求出∠A 的度数，利用等腰三角形性质求出∠ABC 的度数.【详解】∵DE 是AC 的垂直平分线，∴AE=BE ，∴∠A=∠ABE ，∵76BEC ∠=，∠BEC=∠EAB+∠ABE ，∴∠A=76°÷2=38°，∵AB=AC ，∴∠C=∠ABC=（180°-38°）÷2=71°，故选B.【点睛】本题考查线段垂直平分线的性质、等腰三角形的性质及外角性质.线段垂直平分线上的点到线段两端的距离相等；等腰三角形的两个底角相等；三角形的外角定义和它不相邻的两个内角的和，熟练掌握相关性质是解题关键.6．如图，已知S △ABC ＝12，AD 平分∠BAC，且AD⊥BD 于点D ，则S △ADC 的值是( )A ．10B ．8C ．6D ．4【答案】C 【解析】延长BD 交AC 于点E ，则可知△ABE 为等腰三角形，则S △ABD =S △ADE ，S △BDC =S △CDE ，可得出S △ADC =12S △ABC ． 【详解】解：如图，延长BD 交AC 于点E ，∵AD 平分∠BAE ，AD ⊥BD ，∴∠BAD=∠EAD ，∠ADB=∠ADE ，在△ABD 和△AED 中，BAD EAD AD AD BDA EDA ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABD ≌△AED （ASA ），∴BD=DE ，∴S △ABD =S △ADE ，S △BDC =S △CDE ，∴S △ABD +S △BDC =S △ADE +S △CDE =S △ADC ，∴S △ADC =12S △ABC =12×12=6（m 2）， 故答案选C ．【点睛】本题主要考查等腰三角形的判定和性质，由BD=DE 得到S △ABD =S △ADE ，S △BDC =S △CDE 是解题的关键． 7．下列图形中，是轴对称图形且只有三条对称轴的是（ ）A ．B ．C ．D ．【答案】C【解析】首先确定轴对称图形，再根据对称轴的概念，确定对称轴的条数．【详解】解：A 、不是轴对称图形；B 、是轴对称图形，有2条对称轴；C 、是轴对称图形，有3条对称轴；D 、是轴对称图形，有4条对称轴；故选：C ．【点睛】掌握轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．能够熟练说出轴对称图形的对称轴条数．8．某画室分两次购买了相同的素描本，第一次用120元购买了若干本，第二次在同一家商店又购买了240元，这次商家每本优惠4元，结果比上次多买了20本．设第一次买了x本素描本，列方程正确的是（）A．120240420x x-=+B．240120420x x-=+C．120240420x x-=-D．240120420x x-=-【答案】A【分析】根据题意可知第二次买了（x＋20）本素描本，然后根据“第二次购买比第一次购买每本优惠4元”列出分式方程即可．【详解】解：由题意可知：120240420x x-=+故选A．【点睛】此题考查的是分式方程的应用，掌握实际问题中的等量关系是解决此题的关键．9．以下四组数中的三个数作为边长，不能构成直角三角形的是（）A．1B．5，12，13 C．32，42，52D．8，15，17.【答案】C【解析】分别求出两小边的平方和和长边的平方，看看是否相等即可．【详解】A、∵12+2=2，∴以1B、∵52+122=132，∴以5、12、13为边能组成直角三角形，故本选项不符合题意；C、∵92+162≠52，∴以32，42，52为边不能组成直角三角形，故本选项符合题意；D、∵82+152=172，∴8、15、17为边能组成直角三角形，故本选项不符合题意；故选C．【点睛】本题考查了勾股定理的逆定理，能熟记勾股定理的逆定理的内容是解此题的关键，注意：如果三角形的两边的平方和等于第三边的平方，那么这个三角形是直角三角形10．以下问题，不适合用普查的是（）A．旅客上飞机前的安检B．为保证“神州9号”的成功发射，对其零部件进行检查C．了解某班级学生的课外读书时间D．了解一批灯泡的使用寿命【答案】D【分析】根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似解答．【详解】解：旅客上飞机前的安检适合用普查；为保证“神州9号”的成功发射，对其零部件进行检查适合用普查；了解某班级学生的课外读书时间适合用普查；了解一批灯泡的使用寿命不适合用普查．故选D．【点睛】本题考查的是抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．二、填空题11．已知29x mx++是完全平方式，则m=_________．【答案】6±【分析】根据完全平方公式的形式，可得答案．【详解】解：∵x2+mx+9是完全平方式，∴m=2136±⨯⨯=±，故答案为：6±．【点睛】本题考查了完全平方公式，注意符合条件的答案有两个，以防漏掉．12．某射击小组有20人，教练根据他们某次射击的数据绘制成如图所示的统计图，则这组数据的中位数是_____．【答案】7.5【分析】根据中位数的定义先把数据从小到大的顺序排列，找出最中间的数即可得出答案.【详解】解：因图中是按从小到大的顺序排列的，最中间的环数是7环、8环，则中位数是872+=7.5（环）．故答案为：7.5.【点睛】此题考查了中位数．注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求．如果是偶数个则找中间两位数的平均数.13．已知()()2226x my x ny x xy y ++=+-，则22m n mn +的值为_________________________． 【答案】-1【分析】根据多项式乘多项式法则将等式左侧展开，然后利用对应系数法即可求出m ＋n 和mn ，然后将所求多项式因式分解，最后用整体代入法求值即可．【详解】解：∵()()2226x my x ny x xy y ++=+- ∴()222226x m n xy mny x xy y +++=+- ∴m ＋n=2，mn=-622m n mn +=()mn m n +=()62-⨯=-1故答案为：-1．【点睛】此题考查的是多项式乘多项式和因式分解，掌握多项式乘多项式法则和用提公因式法因式分解是解决此题的关键．14．已知点P(a ，b)在一次函数y ＝2x+1的图象上，则2a ﹣b ＝_____．【答案】-1【分析】把P 点的坐标代入，再求出答案即可．【详解】∵点P(a ，b)在一次函数y ＝2x+1的图象上，∴代入得：b ＝2a+1，∴2a ﹣b ＝﹣1，故答案为﹣1．【点睛】本题考查了一次函数图象上点的坐标特征，能得出b=2a+1是解此题的关键．15．如图,已知平面直角坐标系,A 、B 两点的坐标分别为A(2,−3),B(4,−1)．(1)若P(p,0)是x 轴上的一个动点，则△PAB 的最小周长为___________(2)若C(a,0),D(a+3,0)是x 轴上的两个动点，则当a=___________时，四边形ABDC 的周长最短；【答案】2522+ 54 【分析】（1）根据题意，设出并找到B （4，-1）关于x 轴的对称点是B'，其坐标为（4，1），算出AB′+AB 进而可得答案；（2）过A 点作AE ⊥x 轴于点E ，且延长AE ，取A'E=AE ．做点F （1，-1），连接A'F ．利用两点间的线段最短，可知四边形ABDC 的周长最短等于A'F+CD+AB ，从而确定C 点的坐标值．【详解】解：（1）设点B （4，-1）关于x 轴的对称点是B'，可得坐标为（4，1），连接AB′，则此时△PAB 的周长最小，∵AB′=()()222431=25-+--，AB=()()222431=22-+-+，∴△PAB 的周长为2522+，故答案为：2522+；（2）过A 点作AE ⊥x 轴于点E ，且延长AE ，取A'E=AE ．作点F （1，-1），连接A'F ．那么A'（2，3）． 设直线A'F 的解析式为y=kx+b ，则132k b k b -=+⎧⎨=+⎩，解得：45k b =⎧⎨=-⎩， ∴直线A'F 的解析式为y=4x-5，∵C 点的坐标为（a ，0），且在直线A'F 上，∴a=54， 故答案为：54．【点睛】本题考查最短路径问题，同时考查了根据两点坐标求直线解析式，运用解析式求直线与坐标轴的交点等知识．16．已知a+ 1a = ,则a-1a=__________【答案】【解析】通过完全平方公式即可解答.【详解】解：已知a+ 1a = ， 则21(a a +）= 2212a a ⎛⎫++ ⎪⎝⎭=10， 则21a a ⎛⎫- ⎪⎝⎭= 2212a a ⎛⎫+- ⎪⎝⎭=6，故a-1a =. 【点睛】本题考查完全平方公式的运用，熟悉掌握是解题关键.17．分式方程21x -＝31x +的解为_____． 【答案】x=5【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【详解】方程两边同时乘以(x-1)(x+1)，得：2x+2＝3x ﹣3，解得：x ＝5，检验：当x ＝5时(x-1)(x+1)≠0，所以x=5是分式方程的解，故答案为：x ＝5.【点睛】本题考查了解分式方程，利用了转化的思想，熟练掌握解分式方程的方法以及注意事项是解题的关键.解分式方程注意要检验．三、解答题18．某班要购买一批篮球和足球．已知篮球的单价比足球的单价贵40元，花1500元购买的篮球的个数与花900元购买的足球的个数恰好相等．（1）篮球和足球的单价各是多少元？（2）若该班恰好用完1000元购买的篮球和足球，则购买的方案有哪几种？【答案】（1）足球的单价为60元，篮球的单价为100元；（2）学校共有3种购买方案，方案1：购买7个篮球，5个足球；方案2：购买4个篮球，10个足球；方案3：购买1个篮球，15个足球．【分析】（1）设足球的单价为x 元，则篮球的单价为(40)x +元，根据“花1500元购买的篮球的个数与。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，△BAC的外角∠CAE为120°，∠C=80°，则∠B为（）A．60°B．40°C．30°D．45°【答案】B【分析】由三角形的外角性质得出∠CAE=∠B+∠C，即可得出结果．【详解】解：由三角形的外角性质得：∠CAE=∠B+∠C，∴∠B=∠CAE-∠C=120°-80°=40°；故选B．【点睛】本题考查了三角形的外角性质；熟记三角形的外角性质是解决问题的关键．2．等腰三角形是轴对称图形,它的对称轴是( )A．中线B．底边上的中线C．中线所在的直线D．底边上的中线所在的直线【答案】D【分析】根据等腰三角形的三线合一的性质，可得出答案．【详解】解：等腰三角形的对称轴是顶角的角平分线所在直线，底边高所在的直线，底边中线所在直线，A、中线，错误；B、底边上的中线，错误；C、中线所在的直线，错误；D、底边上的中线所在的直线，正确．故选D．【点睛】本题考查了轴对称图形的知识，解答本题的关键是掌握轴对称及对称轴的定义．3．下列各组数中不能作为直角三角形的三边长的是（）A．2，3，5 B．3，4，5 C．6，8，10 D．5，12，13【答案】A【分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形．如果没有这种关系，这个就不是直角三角形．【详解】解：A、22+32 52，不符合勾股定理的逆定理，故错误；B、32+42=52，符合勾股定理的逆定理，故正确；C、62+82=102，符合勾股定理的逆定理，故正确；D、52+122=132，符合勾股定理的逆定理，故正确．故选：A．【点睛】本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．4．如图，数轴上的A、B、C、D四点中，与数﹣3表示的点最接近的是( )A．点A B．点B C．点C D．点D【答案】B-≈-，计算-1.732与-3，-2，-1的差的绝对值，确定绝对值最小即可.【分析】3 1.732-≈-，【详解】3 1.732()1.7323 1.268---≈，()---≈，1.73220.268()---≈，1.73210.732因为0.268＜0.732＜1.268，-表示的点与点B最接近，所以3故选B.5．下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽，其中为中心对称图形的是（）．A．B．C．D．【答案】C【分析】根据中心对称图形定义分析.【详解】A．∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，故此选项错误；B.∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，故此选项错误；C．此图形旋转180°后能与原图形重合，此图形是中心对称图形，故此选项正确；D∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，故此选项错误．故选C ．【点睛】考点：中心对称图形．6．将一组数2，2，6，22，10，…，210，按下列方式进行排列：2，2，6，22，10；23，14，4，32，25；…若2的位置记为（1，2），23的位置记为（2，1），则38这个数的位置记为（ ）A ．（5，4）B ．（4，4）C ．（4，5）D ．（3，5）【答案】B【分析】先找出被开方数的规律，然后再求得38的位置即可．【详解】解：这组数据可表示为：246810，，，，；1214161820，，，，； …∵19×2＝38，∴38为第4行，第4个数字．故选：B ．【点睛】此题考查的是数字的变化规律，找出其中的规律是解题的关键．7．如图，在Rt ABC ∆中，90BCA ∠=︒，CD 是高，BE 平分∠ABC 交CD 于点E ，EF ∥AC 交AB 于点F ，交BC 于点G ．在结论：(1) EFD ∠=BCD ∠；(2) AD CD =；(3)CGEG ；(4) BF BC =中，一定成立的有( )A ．1个B ．2个C ．3个D ．4个【答案】B 【分析】根据两直线平行，同旁内角互补求出∠CGE=∠BCA=90°，然后根据等角的余角相等即可求出∠EFD=∠BCD ；只有△ABC 是等腰直角三角形时AD=CD ，CG=EG ；利用“角角边”证明△BCE 和△BFE 全等，然后根据全等三角形对应边相等可得BF=BC ．【详解】∵EF ∥AC ，∠BCA=90°，∴∠CGE=∠BCA=90°，∴∠BCD+∠CEG=90°，又∵CD 是高，∴∠EFD+∠FED=90°，∵∠CEG=∠FED （对顶角相等），∴∠EFD=∠BCD ，故（1）正确；只有∠A=45°，即△ABC 是等腰直角三角形时，AD=CD ，CG=EG 而立，故（2）（3）不一定成立，错误； ∵BE 平分∠ABC ，∴∠EBC=∠EBF ，在△BCE 和△BFE 中，EFD BCD EBC EBF BE BE ∠∠∠∠⎧⎪⎨⎪⎩＝＝＝，∴△BCE ≌△BFE （AAS ），∴BF=BC ，故（4）正确，综上所述，正确的有（1）（4）共2个．故选：B ．【点睛】本题主要考查了角平分线的性质，全等三角形的判定与性质，直角三角形的性质，等腰直角三角形的性质，综合题，但难度不大，熟记性质是解题的关键．8．如图是由6个完全相同的小正方体组成的立体图形，它的左视图是()A ．B ．C ．D ．【答案】D 【分析】从正面看所得到的图形是主视图，从左面看到的图形是左视图，从上面看到的图象是俯视图．【详解】左视图有2层3列，第一层有3个正方形，第二层有一个正方形；每列上正方形的分布从左到右分别是2，1，1个．故选D ．【点睛】此题主要考查了三视图，关键是把握好三视图所看的方向．属于基础题，中考常考题型．9．已知直线y = kx + b 的图象如图所示，则不等式kx + b > 0的解集是（ ）A ．x > 2B ．x > 3C ．x < 2D ．x < 3【答案】C 【分析】根据函数图象可得当y ＞0时，图象在x 轴上方，然后再确定x 的范围．【详解】直线y ＝kx+b 中，当y ＞0时，图象在x 轴上方，则不等式kx+b ＞0的解集为：x ＜2，故选：C ．【点睛】此题主要考查了一次函数与一元一次不等式，关键是掌握数形结合思想，利用图象可直接确定答案． 10．如图，△ABC 中，∠C＝90°，∠A＝30°，AB ＝12，则BC ＝( )A ．6B ．2C ．3D ．12【答案】A 【详解】∵30°的角所对的直角边等于斜边的一半，1112622BC AB ∴==⨯= , 故选A. 二、填空题11．已知12x y =，则32x y x y ++的值为____． 【答案】1 【分析】根据已知得到12x y =，代入所求式子中计算即可． 【详解】∵12x y =， ∴12x y =，∴1533221152222y y y x y x y y y y ⨯++===++． 故答案为：1．【点睛】 本题考查了求分式的值，利用已知得到12x y =，再整体代入是解题的关键． 12．一次数学活动课上，老师利用“在面积一定的矩形中，正方形的周长最短”这一结论，推导出“式子()10x x x+>的最小值为2”.其推导方法如下:在面积是1的矩形中，设矩形的一边长为x ，则另一边长是1x ，矩形的周长是12x x ⎛⎫+ ⎪⎝⎭；当矩形成为正方形时，就有()10x x x =>，解得1x =，这时矩形的周长124x x ⎛⎫+= ⎪⎝⎭最小，因此()10x x x +>的最小值是2，模仿老师的推导，可求得式子()20x x x +>的最小值是________．【答案】【分析】仿照老师的推导过程，设面积为2的矩形的一条边长为x ，根据x=2x 可求出x 的值，利用矩形的周长公式即可得答案．【详解】在面积为2的矩形中，设一条边长为x ，则另一条边长为2x ， ∴矩形的周长为2（x+2x）， 当矩形成为正方形时，就有x=2x ， 解得：，∴2（x+2x ）， ∴x+2x(x>0)的最小值为故答案为：【点睛】此题考查了分式方程的应用，弄清题意，得出x=2x是解题的关键． 13．如图，ABC ∠的内角平分线BP 与ACB ∠的外角平分线CP 相交于点P ，若29P ∠=︒，则A ∠=____．【答案】58︒【分析】根据角平分线的定义和三角形外角性质然后整理得到∠BAC=2∠P ，代入数据进行计算即可得解．【详解】∵BP 、CP 分别是∠ABC 和∠ACD 的平分线，∴∠ACD=2∠PCD ，∠ABC=2∠PBC ，由三角形的外角性质得，∠ACD=∠BAC+∠ABC ，∠PCD=∠P+∠PBC ，∴∠BAC+∠ABC=∠ACD=2∠PCD ＝2(∠P+∠PBC)= 2∠P+2∠PBC=2∠P+∠ABC ，∴∠BAC=2∠P ，∵∠P=29︒，∴∠BAC=58︒．故答案为：58︒．【点睛】本题考查了三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和，角平分线的定义，熟记性质并准确识图最后求出∠BAC=2∠P 是解题的关键．14．化简：129=_______________． 【答案】3【分析】根据分数指数幂的定义化简即可． 【详解】解：12993== 故答案为：3【点睛】本题主要考查了分数指数幂的意义，熟知分数指数幂意义是解题关键．15．若关于x 的分式方程322x m x x -=--有正数解，则m 的取值范围是______________． 【答案】m 6<且m 2≠【分析】分式方程去分母转化为整式方程，由分式方程有正数解，即可确定出m 的范围．【详解】解：去分母得：x-3(x-1)=m ，解得：x=62m -， ∵分式方程有一正数解，∴62m -＞0，且62m -≠1， 解得：m ＜6且m ≠1，故答案为：m ＜6且m ≠1．【点睛】此题考查了分式方程的解，始终注意分母不为0这个条件．16．如图，△ABC 中边AB 的垂直平分线分别交BC 、AB 于点D 、E ， AE=3cm ，△ADC•的周长为9cm ，则△ABC 的周长是____ ___【答案】15cm【详解】在△ABC 中，边AB 的垂直平分线分别交BC 、AB 于点D 、E ，AE=3cm ，AE=BE ，AD=BD ，△ADC•的周长为9cm ，即AC+CD+AD=9，则△ABC 的周长=AB+BC+AC=AE+BE+BD+CD+AC=AE+BE+AD+CD+AC=6+9=15cm【点睛】本题考查垂直平分线，解答本题的关键是掌握垂直平分线的概念和性质，运用其来解答本题17．若3m n -=，5mn =，则m n +的值为__________． 【答案】29【分析】根据（m ＋n ）2＝（m−n ）2＋4mn ，把m−n ＝3，mn ＝5，解答出即可；【详解】根据（m ＋n ）2＝（m−n ）2＋4mn ，把m−n ＝3，mn ＝5，得，（m ＋n ）2＝9＋20＝29∴m n +=29故答案为29【点睛】本题考查了完全平方公式，熟记完全平方公式及其变形，是正确解答的基础．三、解答题18．（1）计算：22242442 a a a a a a--÷+++（2）先化简，后求值：221221212x x xx x x x x+--⎛⎫-÷⎪--+⎝⎭；其中1x=-【答案】（1）1a；（2）()221x-，12【分析】（1）分式除法，先进行因式分解，然后再将除法转化成乘法进行计算；（2）分式的混合运算，先做小括号里的异分母分式减法，要进行通分，能进行因式分解的先进行因式分解，然后做除法，最后代入求值．【详解】（1）22242442a a aa a a--÷+++()()()()222222a a aa aa+-+=⨯-+1a=；（2）原式()()21221211x x xx x xx⎡⎤+-=-⨯⎢⎥---⎢⎥⎣⎦()222122211x x x xxx x--+=⨯--()221x=-，当1x=-时，原式()221211==--．【点睛】本题考查分式的混合运算，掌握因式分解的技巧，运算顺序，正确计算是解题关键．19．如图，在△ABC中，AB=AC，∠BAC=36°，BD是∠ABC的平分线，交AC于点D，E是AB的中点，连接ED并延长，交BC的延长线于点F，连接AF．求证：（1）EF⊥AB；（2）△ACF为等腰三角形．【答案】（1）见解析；（2）见解析．【分析】（1）依据AB＝AC，∠BAC＝36°，可得∠ABC＝72°，再根据BD是∠ABC的平分线，即可得到∠ABD＝36°，由∠BAD＝∠ABD，可得AD＝BD，依据E是AB的中点，即可得到FE⊥AB；（2）依据FE⊥AB，AE＝BE，可得FE垂直平分AB，进而得出∠BAF＝∠ABF，依据∠ABD＝∠BAD，即可得到∠FAD＝∠FBD＝36°，再根据∠AFC＝∠ACB−∠CAF＝36°，可得∠CAF＝∠AFC＝36°，进而得到AC＝CF．【详解】证明：（1）∵AB＝AC，∠BAC＝36°，∴∠ABC＝∠ABC ＝72°．又∵BD是∠ABC的平分线，∴∠ABD＝36°．∴∠BAD＝∠ABD．∴AD＝BD．又∵E是AB的中点，∴DE⊥AB，即EF⊥AB．（2）∵EF⊥AB，AE＝BE，∴EF垂直平分AB．∴AF＝BF．∴∠BAF＝∠ABF．又∵∠ABD＝∠BAD，∴∠FAD＝∠FBD＝36°．又∵∠ACB＝72°，∴∠AFC＝∠ACB−∠CAF＝36°．∴∠CAF＝∠AFC＝36°．∴AC＝CF，即△ACF为等腰三角形．【点睛】本题考查了等腰三角形的判定与性质，解决问题的关键是熟练掌握并能综合运用等腰三角形的判定与性质，线段垂直平分线的判定与性质，三角形外角的性质．20．一支园林队进行某区域的绿化，在合同期内高效地完成了任务，这是记者与该队工程师的一段对话：如果每人每小时绿化面积相同，请通过这段对话，求每人每小时的绿化面积．【答案】每人每小时的绿化面积为2.5平方米．【分析】设每人每小时的绿化面积为x 平方米．根据对话内容列出方程并解答．【详解】解：设每人每小时的绿化面积为x 平方米． 根据题意，得18018036(62)x x-=+， 方程两边乘以24x ，得1804180372x ⨯-⨯=，解得 2.5x =，检验：当 2.5x =时，24600x =≠，所以，原分式方程的解为 2.5x =，答：每人每小时的绿化面积为2.5平方米．【点睛】本题考查了分式方程的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程求解即可．21．（1）计算：（﹣2a 2b ）2+（﹣2ab ）•（﹣3a 3b ）．（2）分解因式：（a+b ）2﹣4ab ．【答案】（1）10a 4b 1；（1）（a ﹣b ）1．【分析】1）先根据幂的乘方和积的乘方、单项式乘以单项式的运算法则计算，再合并同类项即可； （1）先利用完全平方公式去括号合并同类项，进而利用完全平方公式分解因式即可．【详解】解：（1）原式＝4a 4b 1+6a 4b 1＝10a 4b 1；（1）原式＝a 1+1ab+b 1﹣4ab＝a 1﹣1ab+b 1＝（a ﹣b ）1．【点睛】本题考查整式的运算和完全平方公式分解因式．解题的关键是运用幂的乘方和积的乘方、单项式乘以单项式的运算法则去括号，及熟练运用合并同类项的法则．能够正确应用完全平方公式．22．如图所示，在平面直角坐标系中，已知()0,1A 、()2,0B 、()4,3C ．()1在平面直角坐标系中画出ABC ，则ABC 的面积是______；()2若点D 与点C 关于y 轴对称，则点D 的坐标为______；()3已知P 为x 轴上一点，若ABP 的面积为4，求点P 的坐标．【答案】（1）图详见解析，4；（2） ()4,3-；（3）P 点坐标为：()10,0或()6,0-．【分析】()1直接利用ABC 所在矩形面积减去周围三角形面积进而得出答案；()2利用关于y 轴对称点的性质得出答案；()3利用三角形面积求法得出符合题意的答案．【详解】()1如图所示：ABC 的面积是：111341224234222⨯-⨯⨯-⨯⨯-⨯⨯=； 故答案为4；()2点D 与点C 关于y 轴对称，则点D 的坐标为：()4,3-；故答案为()4,3-；()3P 为x 轴上一点，ABP 的面积为4，8BP ∴=，∴点P 的横坐标为：2810+=或286-=-，故P 点坐标为：()10,0或()6,0-．【点睛】此题主要考查了三角形面积求法以及关于y 轴对称点的性质，正确得出对应点位置是解题关键． 23．如图所示，在平面直角坐标系xOy 中，已知点(1,2)(3,1)(0,1)，，---A B C（1）在图作出ABC 关于y 轴的称图形111A B C △（2）若将ABC 向右移2个单位得到A B C '''，则点A 的对应点A '的坐标是 ．【答案】（1）作图见解析；（2） (1，2)【分析】（1）根据网格结构找出点A 、B 、C 关于y 轴的对称点A 1、B 1、C 1的位置，然后顺次连接即可； （2）根据网格结构找出点A 、B 、C 向右平移2个单位的对应点A′、B′、C′的位置，然后顺次连接即可，再根据平面直角坐标系写出点A′的坐标．【详解】（1）△A 1B 1C 1如图所示；（2）△A′B′C′如图所示，A′（1，2）；【点睛】本题考查了利用轴对称变换作图，利用平移变换作图，熟练掌握网格结构，准确找出对应点的位置是解题的关键．24．计算：（1（2+（38（4）．【答案】（1；（2）（3）2；（4）2 -283．【分析】（1）先化成最简二次根式，然后合并同类二次根式即可; （2）先化成最简二次根式，然后合并同类二次根式即可;（3）根据二次根式的混合运算的法则计算即可;（4）根据二次根式的混合运算的法则计算即可．【详解】解：（1）原式=（2）原式=2+（3）原式=108=2-（4）原式===2 -283【点睛】本题考查二次根式的混合运算，掌握二次根式的化简、二次根式的混合运算法则是解题的关键．25．金堂县在创建国家卫生城市的过程中，经调查发现居民用水量居高不下，为了鼓励居民节约用水，拟实行新的收费标准．若每月用水量不超过12吨，则每吨按政府补贴优惠价m元收费；若每月用水量超过12吨，则超过部分每吨按市场指导价n元收费．毛毛家家10月份用水22吨，交水费59元；11月份用水17吨，交水费1．5元．（1）求每吨水的政府补贴优惠价和市场指导价分别是多少元？（2）设每月用水量为x吨，应交水费为y元，请写出y与x之间的函数关系式；（3）小明家12月份用水25吨，则他家应交水费多少元？【答案】（1）每吨水的政府补贴优惠价和市场指导价分别是2元、3.5元；（2）()()20123.51812x x y x x ⎧≤≤⎪=⎨->⎪⎩；（3）69.5【分析】（1）根据题意列出方程组，求解此方程组即可； （2）根据用水量分别求出在两个不同的范围内y 与x 之间的函数关系，注意自变量的取值范围； （3）根据小明家的用水量判断其在哪个范围内，代入相应的函数关系式求值即可．【详解】解：（1）由题可得()()1222125912171241.5m n m n ⎧+-=⎪⎨+-=⎪⎩， 解得：23.5m n =⎧⎨=⎩， ∴每吨水的政府补贴优惠价和市场指导价分别是2元、3.5元；（2）①当012x ≤≤时，2y x =，②当12x >时，()12212 3.5 3.518y x x =⨯+-⨯=-，综上：()()20123.51812x x y x x ⎧≤≤⎪=⎨->⎪⎩； （3）∵2512>，∴ 3.5251869.5y =⨯-=答：他家应交水费69.5元．【点睛】本题考查了二元一次方程组的应用及一次函数的应用，明确题意正确找出数量关系是解题关键，同时在求一次函数表达式时，此函数是一个分段函数，注意自变量的取值范围．八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．从边长为a 的大正方形纸板中挖去一个边长为b 的小正方形纸板后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（ ）．A ．222()a b a b -=-B ．（a+b ）2=a 2+2ab+b 2C ．222()2a b a ab b -=-+D ．22()()a b a b a b -=+-【答案】D【分析】分别表示出图甲和图乙中阴影部分的面积，二者相等，从而可得答案．【详解】图甲中阴影的面积等于边长为a 的正方形面积减去边长为b 的正方形面积，即22a b -， 图乙中平行四边形底边为(a b +)，高为(a b -)，即面积=()()a b a b +-，∵两个图中的阴影部分的面积相等，即：()()22a b a b a b -=+-． ∴验证成立的公式为：()()22a b a b a b -=+-． 故选：D ．【点睛】本题考查了平方差公式的几何背景，运用不同方法表示阴影部分面积是解题的关键．2．某鞋厂为了了解初中生穿鞋的尺码情况，对某中学八年级（2）班的20名男生进行了调查，统计结果如下表：则这20个数据的中位数和众数分别为（ ） 尺码37 38 39 40 41 42 人数3 4 4 7 1 1A ．4和7B ．40和7C ．39和40D ．39.1和39 【答案】C【分析】根据众数与中位数的定义求解分析．40出现的次数最多为众数，第10、11个数的平均数为中位数．【详解】解：观察图表可知：有7人的鞋号为40，人数最多，即众数是40；中位数是第10、11人的平均数，即39；故选：C．【点睛】本题考查众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数）；众数是数据中出现最多的一个数．3．如图在△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，BE与CD相交于点F，BF=2CE，H是BC边的中点，连接DH与BE相交于点G，下列结论中：①∠A=67.5°；②DF=AD；③BE=2BG；④DH⊥BC 其中正确的个数是（）A．1个B．2个C．3个D．4个【答案】C【分析】根据已知条件得到△BCD是等腰直角三角形，由等腰直角三角形的性质得到BD＝CD，由BE平分∠ABC，得到∠ABE＝22.5°，根据三角形的内角和得到∠A＝67.5°；故①正确；根据余角得到性质得到∠DBF ＝∠ACD，根据全等三角形的性质得到AD＝DF，故②正确；根据BE平分∠ABC，且BE⊥AC于E，得到∠ABE＝∠CBE，∠AEB＝∠CEB＝90°，根据全等三角形的性质得到AE＝CE＝12AC，求得BE⊥AC，由于△BCD是等腰直角三角形，H是BC边的中点，得到DH⊥BC，故④正确；推出DH不平行于AC，于是得到BE≠2BG，故③错误．【详解】解：∵∠ABC＝45°，CD⊥AB于D，∴△BCD是等腰直角三角形，∴BD＝CD，∵BE平分∠ABC，∴∠ABE＝22.5°，∴∠A＝67.5°；故①正确；∵CD⊥AB于D，BE⊥AC于E，∴∠DBF＋∠A＝90°，∠ACD＋∠A＝90°，∴∠DBF＝∠ACD，在△BDF 与△CDA 中90DBF ACD BD CD BDF CDA ∠∠⎨⎪⎩∠⎪∠︒⎧＝＝＝＝，∴△BDF ≌△CDA （ASA ），∴AD ＝DF ，故②正确；∵BE 平分∠ABC ，且BE ⊥AC 于E ，∴∠ABE ＝∠CBE ，∠AEB ＝∠CEB ＝90°，∴在△ABE 与△CBE 中90ABE CBE BE BEAEB CEB ⎧⎪⎨⎪⎩∠∠∠︒＝＝＝＝， ∴△ABE ≌△CBE （ASA ），∴AE ＝CE ＝12AC ， ∵△BCD 是等腰直角三角形，H 是BC 边的中点，∴DH ⊥BC ，故④正确；∴DH 不平行于AC ，∵BH ＝CH ，∴BG≠EG ；∴BE≠2BG ，故③错误．故选：C ．【点睛】本题考查了等腰直角三角形的判定与性质，角平分线的性质，全等三角形的判定与性质，仔细分析图形并熟练掌握各性质是解题的关键．4．如果点（m ﹣1，﹣1）与点（5，﹣1）关于y 轴对称，则m ＝（ ）A ．4B ．﹣4C ．5D ．﹣5【答案】B【分析】根据“关于y 轴对称的点，纵坐标相同，横坐标互为相反数”列出方程求解即可．【详解】解：∵点（m ﹣1，﹣1）与点（5，﹣1）关于y 轴对称，∴m ﹣1＝﹣5，解得m ＝﹣1．故选：B ．【点睛】本题考查了关于y 轴对称的点的坐标特征，掌握关于y 轴对称的点的坐标特征是横坐标互为相反数是解题的关键.5．下列代数式中，属于分式的是（ ）A ．﹣3B ．1xC ．﹣a ﹣bD ．﹣14 【答案】B 【分析】根据分式的定义：形如A B ，A 、B 是整式，B 中含有字母且B 不等于0的式子叫做分式，逐一判断即可．【详解】解：A ．﹣3不是分式，故本选项不符合题意；B ．1x是分式，故本选项符合题意； C ．﹣a ﹣b 不是分式，故本选项不符合题意；D ．﹣14不是分式，故本选项不符合题意． 故选B ．【点睛】此题考查的是分式的判断，掌握分式的定义是解决此题的关键．6．已知分式方程312(1)(2)x k x x x +=++-+的解为非负数，求k 的取值范围（ ） A ．5k ≥B ．1k ≥-C ．5k ≥且6k ≠D ．1k ≥-且0k ≠ 【答案】D【分析】先把分式方程转化为整式方程求出用含有k 的代数式表示的x ，根据x 的取值求k 的范围．【详解】解：分式方程转化为整式方程得，(3)(1)k (1)(2)x x x x +-=+-+解得：k 1x =+解为非负数，则k+10≥，∴k -1≥又∵x≠1且x≠-2，∴k+11k+1-2≠≠，∴k -1≥ ，且k 0≠故选D【点睛】本题考查了分式方程的解，解答本题的关键是先把分式方程转化为整式方程，求出方程的解，再按要求列不等式，解不等式．7．()020202019π-的计算结果是（ ）A ．20202019π-B ．20192018π-C ．0D ．1 【答案】D【解析】根据非零数的零次幂等于1解答即可．【详解】()020202019π-=1．故选D ．【点睛】本题考查了零次幂的意义，熟练掌握非零数的零次幂等于1是解答本题的关键．8．如图所示，在锐角三角形ABC 中，AB ＝8，AC ＝5，BC ＝6，沿过点B 的直线折叠这个三角形，使点C 落在AB 边上的点E 处，折痕为BD ，下列结论：①∠CBD ＝∠EBD ，②DE ⊥AB ，③三角形ADE 的周长是7，④34BCDABD S S =△△，⑤34CD AD =.其中正确的个数有（ ）A ．2B ．3C ．4D ．5【答案】C 【分析】根据翻折变换的性质得到DC=DE ，BE=BC ，BCD BED ∠=∠，根据已知求出AE 的长，根据三角形周长公式计算即可，根据高相等判断34BCD ABD S S =△△ ，根据△BCD ≅△BDE 判断①的对错，根据等高，则面积的比等于底边的比判断⑤．【详解】根据翻折变换的性质得到DC=DE ，BE=BC=6，BCD BED ∠=∠，故DE ⊥AB 错误，即②错误∴△BCD≅△BDE ，∴∠CBD ＝∠EBD,故①正确； ∵AB=8，∴AE=AB-BE=2，△AED 的周长为：AD+AE+DE=AC+AE=7，故③正确；设三角形BCD 的高为h ，则三角形BAD 的高也为h∴116322114822BCD ABD h BC h S S h AB h ⨯⨯⨯⨯==⨯⨯⨯⨯△△＝,故④正确； 当三角形BCD 的高为H ，底边为CD ，则三角形BAD 的高也为H ，底边为AD∴34BCD ABD S C S D AD ==△△，故⑤正确. 故选C.本题考查的是翻折变换的知识涉及了三角形全等、等高等知识点，掌握翻折变换的性质、找准对应关系是解题的关键．9．如图，分别给出了变量y 与x 之间的对应关系，y 不是x 的函数的是( )A ．B ．C ．D ．【答案】B【分析】根据函数的定义判断即可．【详解】A 、C 、D 中y 均是x 的函数，不符合题意；B 中每一个自变量x 对应两个y 值，故y 不是x 的函数，符合题意．故选B ．【点睛】本题考查的是函数的定义，解答本题的关键是熟练掌握函数的定义：对于两个变量x 、y ，x 每取一个值，y 都有唯一的值与之对应；注意要强调“唯一”．10．边长为m ，n 的长方形，它的周长为14，面积为10，则22m n mn +的值为( )A ．35B ．70C ．140D ．280【答案】B【分析】先把所给式子提取公因式mn ，再整理为与题意相关的式子，代入求值即可．【详解】根据题意得：m+n=7，mn=10，∴22=()70m n mn mn m n ++=．故选：B ．本题既考查了对因式分解方法的掌握，又考查了代数式求值的方法，同时还隐含了数学整体思想和正确运算的能力．二、填空题11．若216x mx ++是一个完全平方式，则m=________【答案】±1【分析】利用完全平方公式的结构特征可确定出m 的值．【详解】解：∵多项式222164x mx x mx ++=++是一个完全平方式，∴m ＝±2×1×4，即m ＝±1，故答案为：±1．【点睛】此题考查了完全平方式，熟练掌握完全平方公式的结构特征是解本题的关键．12．已知(x+y+2)2=0，则x y 的值是____． 【答案】13-．【分析】利用平方和算术平方根的意义确定(x+y+2)2⩾040，从而确定x+y+2=0且x−y−4=0，建立二元一次方程组求出x 和y 的值，再代入求值即可．【详解】解：∵(x+y+2)2≥0≥0，且(x+y+2)2=0， ∴(x+y+2)2=0，=0，即2040x y x y ++=⎧⎨--=⎩①② 解得：13x y =⎧⎨=-⎩则13x y =-． 故答案为：13-．【点睛】本题重点考查偶次方和算术平方根的非负性，是一种典型的“0+0=0”的模式题型，需重点掌握；另外此题结合了二元一次方程组的运算，需熟练掌握“加减消元法”和“代入消元法”这两个基本的运算方法． 13．如图，在等边ABC ∆中，10AC =，点O 在线段AC 上，且3AO =，点P 是线段AB 上一点，连接OP ，以O 为圆心，OP 长为半径画弧交线段BC 于一个点D ，连接PD ，如果PO PD =，那么AP 的长是___________．【答案】7【分析】连接OD ，则由DO PO PD ==得到△ADP 是等边三角形，则∠OPD=∠B=∠A=60°，由三角形外角性质，得到∠APD=∠BDP ，则△APO ≌△BDP ，即可得到BP=AO=3，然后求出AP 的长度.【详解】解：连接OD ，∵DO PO PD ==，∴△ADP 是等边三角形，∵△ABC 是等边三角形，∴∠OPD=∠B=∠A=60°，AB=AC=10，∵∠APD=∠APO+∠OPD=∠BDP+∠B ，∴∠APO=∠BDP ，∴△APO ≌△BDP ，∴BP=AO=3，∴AP=AB -BP=103-=7；故答案为：7.【点睛】考查了等边三角形的判定和性质，全等三角形的判定和性质，以及三角形外角性质，解题的关键是熟练掌握所学的知识，正确求出BP 的长度.14．分解因式：3a 2+6a+3=_____．【答案】3（a+1）2【分析】首先提取公因式，然后应用完全平方公式继续分解.【详解】3a 2＋6a ＋3＝()()2232131a a a ++=+． 故答案为()231a +．考点：分解因式．15．如图，在△ABC 中，∠B=60°，AB=12cm ，BC=4cm ，现有一动点P 从点A 出发，以2cm/s 的速度沿射线AB 运动，当点P 运动______s 时，△PBC 为等腰三角形．【答案】4或1【分析】分①当点P 在线段AB 上时，②当点P 在AB 的延长线上时两种情况讨论即可．【详解】解：如图①，当点P 在线段AB 上时，∵∠B=60°，△PBC 为等腰三角形，∴△PBC 是等边三角形，∴PB=PC=BC=4cm ，AP=AB-BP=1cm ，∴运动时间为1÷2=4s ；如图②，当点P 在AB 的延长线上时，∵∠CBP=110°-∠ABC=120°，∴BP=BC=4cm ．此时AP=AB+BP=16cm ，∴运动时间为16÷2=1s ；综上所述，当点P 运动4s 或1s 时，△PBC 为等腰三角形，故答案为：4或1．【点睛】本题主要考了等边三角形的性质和判定，等腰三角形的判定，找全两种情况是解题关键．16()2350a b --=，那么以a b 、边边长的直角三角形的面积为__________．【答案】6或152()2350a b --=得出a b 、的值，再分情况求出以a b 、边边长的直角三角形的面积． ()2350a b --=∴35a b ==，（1）a b 、均为直角边11522S ab == （2）a 为直角边，b 为斜边根据勾股定理得另一直角边4== ∴13462S =⨯⨯= 故答案为：6或152 【点睛】本题考查了三角形的面积问题，掌握勾股定理以及三角形的面积公式是解题的关键．17有意义，则x 的取值范围是__．【答案】x ≥﹣1【分析】根据二次根式有意义的条件可得x+1≥0，再解不等式即可．∴：x+1≥0，解得：x ≥﹣1，故答案为：x ≥﹣1．【点睛】本题考查的知识点为二次根式有意义的条件．二次根式的被开方数是非负数．三、解答题18．已知34(1)(2)12x A B x x x x -=+----，求实数A 和B 的值． 【答案】A ＝1，B ＝1【分析】首先对等式的右边进行通分相加，然后根据分母相同，得到分子相同．根据两个多项式相等，则其同次项的系数应当相等，得到关于A ，B 的方程，进行求解． 【详解】∵34(2)(1)()(2)(1)(2)(1)(2)(1)(2)x A x B x A B x A B x x x x x x --+-++--==------， ∴3x ﹣4＝（A+B ）x+（﹣1A ﹣B ），比较两边分子的系数，3{24A B A B +=--=-， ∴A ＝1，B ＝1．【点睛】掌握分式的加法运算，能够根据两个多项式相等得到关于A ，B 的方程．19．如图，△ABC 是等腰三角形，AB=AC ，点D 是AB 上一点，过点D 作DE ⊥BC 交BC 于点E ，交CA 延长线于点F ．(1)证明：△ADF 是等腰三角形；(2)若∠B=60°，BD=4，AD=2，求EC 的长【答案】（1）见解析；（2）EC=4，理由见解析【分析】（1）由AB=AC ，可知∠B=∠C ，再由DE ⊥BC 和余角的性质可推出∠F=∠BDE ，再根据对顶角相等进行等量代换即可推出∠F=∠FDA ，于是得到结论；（2）由题意根据解直角三角形和等边三角形的性质即可得到结论．【详解】解：（1）AB AC =，B C ∴∠=∠，又DE BC ⊥，90FEC DEB ∴∠=∠=︒，∴90BDE B ∠=︒-∠，90F C ∠=︒-∠，∴BDE F ∠=∠，又BDE ADF ∠=∠，ADF F ∴∠=∠，AF AD ∴=.（2）,60AB AC B =∠=︒，AB BC AC ∴==，又4,2BD AD ==，6AB ∴=，在Rt DEB ∆中，60,4B BD ∠=︒=，122BE BD ∴==， 4EC ∴=.【点睛】本题主要考查等腰三角形的判定与性质和余角的性质以及对顶角的性质等知识点，解题的关键根据相关的。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．某工程对承接了60万平方米的绿化工程，由于情况有变，……，设原计划每天绿化的面积为x万平方米，列方程为606030(120%)xx-=+，根据方程可知省略的部分是（）A．实际工作时每天的工作效率比原计划提高了20%，结果提前30天完成了这一任务B．实际工作时每天的工作效率比原计划提高了20%，结果延误30天完成了这一任务C．实际工作时每天的工作效率比原计划降低了20%，结果延误30天完成了这一任务D．实际工作时每天的工作效率比原计划降低了20%，结果提前30天完成了这一任务【答案】A【解析】根据工作时间=工作总量÷工作效率结合所列分式方程，即可找出省略的条件，此题得解．【详解】解：设原计划每天绿化的面积为x万平方米，∵所列分式方程是606030(120%)xx-=+，∴60(120%)x+为实际工作时间，60x为原计划工作时间，∴省略的条件为：实际工作时每天的工作效率比原计划提高了20%，结果提前30天完成了这一任务.故选：A．【点睛】本题考查了分式方程的应用，根据给定的分式方程，找出省略的条件是解题的关键．2．下列各数，准确数是()A．小亮同学的身高是1.72m B．小明同学买了6支铅笔C．教室的面积是260m D．小兰在菜市场买了3斤西红柿【答案】B【解析】根据准确数与近似数的概念逐一判断即可．【详解】解：A、小亮同学的身高是1.72m，是近似数，故A错误；B、小明同学买了6支铅笔，是准确数，故B正确；C、教室的面积是260m，是近似数，故C错误；D、小兰在菜市场买了3斤西红柿，是近似数，故D错误；故答案为：B．【点睛】本题考查了准确数与近似数的概念，掌握并理解基本概念是解题的关键．3．已知非等腰三角形的两边长分别是2 cm和9 cm,如果第三边的长为整数,那么第三边的长为（）A ．8 cm 或10 cmB ．8 cm 或9 cmC ．8 cmD ．10 cm 【答案】A【解析】根据三角形的三边关系求得第三边的取值范围，再根据第三边为整数即可得出答案． 【详解】解：根据三角形的三边关系，得 7cm ＜第三边＜11cm ， 故第三边为8，1，10， 又∵三角形为非等腰三角形， ∴第三边≠1． 故选：A ． 【点睛】本题主要考查了三角形的三边关系：任意两边之和大于第三边，任意两边之差小于第三边. 4．微信已成为人们的重要交流平台，以下微信表情中，不是轴对称图形的是（ ） A ．B ．C ．D ．【答案】C【解析】根据轴对称的概念作答：如果一个图形沿一条直线对折，直线两旁的部分能互相重合，那么这个图形叫做轴对称图形．【详解】A 、是轴对称图形，故本选项不符合题意； B 、是轴对称图形，故本选项不符合题意； C 、不是轴对称图形，故本选项符合题意； D 、是轴对称图形，故本选项不符合题意． 故选：C ． 【点睛】本题主要考查了轴对称的概念，解题关键是掌握轴对称的概念并能找到对称轴． 5．下列各式运算正确的是( ) A 42=± B ．3553=C 1232=D 11222=【答案】D【分析】计算出各个选项中式子的正确结果，然后对照即可得到哪个选项是正确的． 42=，故选项A 错误； ∵35525=B 错误； 1223=，故选项C 错误； 11222=D 正确；故选D. 【点睛】本题考查二次根式的混合运算，解题的关键是明确二次根式混合运算的计算方法． 6．若x ＜2，化简()22x -＋|3－x|的正确结果是( )A ．－1B ．1C ．2x －5D ．5－2x【答案】D【解析】分析：本题利用绝对值的化简和二次根式()2a a = 的化简得出即可.解析：∵x ＜2，∴()22x -+|3﹣x|=2352x x x -+-=- .故选D.7．如图所示，将矩形纸片ABCD 折叠，使点D 与点B 重合，点C 落在点C '处，折痕为EF ，若122EFC '∠=︒，那么ABE ∠的度数为（ ）A ．24︒B ．32︒C ．30D ．26︒【答案】D【分析】由折叠的性质知：∠EBC ′、∠BC ′F 都是直角，∠BEF=∠DEF ，因此BE ∥C ′F ，那么∠EFC ′和∠BEF 互补，这样可得出∠BEF 的度数，进而可求得∠AEB 的度数，则∠ABE 可在Rt △ABE 中求得． 【详解】解：由折叠的性质知，∠BEF=∠DEF ，∠EBC ′、∠BC ′F 都是直角， ∴BE ∥C ′F ，∴∠EFC ′+∠BEF=180°， 又∵∠EFC ′=122°， ∴∠BEF=∠DEF=58°，∴∠AEB=180°-∠BEF-∠DEF=64°，在Rt △ABE 中，∠ABE=90°-∠AEB=26°． 故选D ． 【点睛】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．8．若()()23x x m -+计算的结果中不含关于字母x 的一次项，则m 的值为（ ）A ．4B ．5C ．6D ．7【答案】C【分析】根据题意，先将代数式()()23x x m -+通过多项式乘以多项式的方法展开，再将关于x 的二次项、一次项及常数项分别合并，然后根据不含字母x 的一次项的条件列出关于x 的方程即可解得． 【详解】()()23x x m -+2662x mx x m =+-- ()2662x m x m =+--∵计算的结果中不含关于字母x 的一次项 ∴60m -= ∴6m = 故选：C 【点睛】本题考查的知识点是多项式乘以多项式的方法，掌握多项式乘法法则，能根据不含一次项的条件列出方程是关键，在去括号时要特别注意符号的准确性． 9．下列各数中是无理数的是（ ）A ．3.14BC D【答案】C【分析】分别根据无理数、有理数的定义即可判定选择项． 【详解】A ．3.14是有限小数，属于有理数；B ，是整数，属于有理数；CD =4，是整数，属于有理数； 故选C ． 【点睛】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数． 10．对于所有实数a ，b ，下列等式总能成立的是（ ）A ．2a b =+ B 22a b =+C a b =+D a b =+【答案】B【详解】解：A、错误，∵2=+a bB 、正确，因为a 2+b 2≥02+b 2； CD，其结果a+b 的符号不能确定． 故选B ． 二、填空题11．在△ABC 中，AB ＝AC ，与∠BAC 相邻的外角为80°，则∠B ＝________． 【答案】40°【分析】根据等边对等角可得∠B=∠C ，然后根据三角形外角的性质可得∠B ＋∠C=80°，从而求出∠B ． 【详解】∵AB ＝AC ， ∴∠B=∠C∵与∠BAC 相邻的外角为80°， ∴∠B ＋∠C=80° 即2∠B=80° ∴∠B=40° 故答案为：40°． 【点睛】此题考查的是等腰三角形的性质和三角形外角的性质，掌握等边对等角和三角形外角的性质是解决此题的关键．12．如果x+1x ＝3，则24233x x x ++的值等于_____ 【答案】122【分析】由x +1x =3得x 2+2+21x =9，即x 2+21x=1，整体代入原式=221331x x ++=221131x x++（），计算可得结论．【详解】解：∵x +1x =3，∴（x +1x ）2=9，即x 2+2+21x =9，则x 2+21x=1． ∵x ≠0，∴原式=221331x x++ =221131x x ++（） =1371⨯+=122． 故答案为122． 【点睛】本题主要考查分式的值，解题的关键是熟练掌握整体代入思想的运用及利用分式的基本性质对分式变形． 13．计算：03(2)2--⋅=____，()()263282a b a b ÷-=_____．【答案】1810532a b - 【分析】根据零指数幂、负整数指数幂的意义可计算03(2)2--⋅，根据积的乘方、以及单项式的除法可计算()()263282a b a b ÷-.【详解】03(2)2--⋅=1×18=18，()()263282a b a b ÷-=()6122642ab a b ÷-=10532a b -.故答案为：18，10532a b - 【点睛】本题考查了零指数幂、负整数指数幂、积的乘方、以及单项式的除法，熟练掌握运算法则是解答本题的关键.14．如图，利用图①和图②的阴影面积相等，写出一个正确的等式_____．【答案】 (a+2)(a ﹣2)＝a 2﹣1【分析】根据图形分别写出图①与图②中阴影部分面积，由阴影部分面积相等得出等式． 【详解】∵图①中阴影部分面积＝(a+2)(a ﹣2)，图②中阴影部分面积＝a 2﹣1， ∵图①和图②的阴影面积相等， ∴(a+2)(a ﹣2)＝a 2﹣1， 故答案为：(a+2)(a ﹣2)＝a 2﹣1． 【点睛】本题考查平方差公式的几何背景，结合图形得到阴影部分的面积是解题的关键． 15．如图，数轴上所表示的不等式的解是________．【答案】1x ≥【分析】根据数轴判断解集即可. 【详解】由图知不等式解集为：1x ≥， 故答案为：1x ≥. 【点睛】本题是对不等式知识的考查，熟练掌握数轴上表示不等式解集是解决本题的关键. 16．已知4y 2+my+1是完全平方式，则常数m 的值是______． 【答案】1或-1【解析】∵1y 2-my+1是完全平方式， ∴-m=±1，即m=±1． 故答案为1或-1.17．在ABC ∆中，将B ，C ∠按如图所示方式折叠，点B ，C 均落于边BC 上一点Q 处，线段MN ，EF 为折痕，若82A ∠=︒，则MQE ∠=______.【答案】82︒【分析】由折叠的性质，得到∠MQN=∠B ，∠EQF=∠C ，由三角形内角和定理，得到∠B+∠C=98°，根据平角的定义，即可得到答案.【详解】解：由折叠的性质，得到∠MQN=∠B ，∠EQF=∠C ， ∵∠A+∠B+∠C=180°， ∴∠B+∠C=180°82-︒=98°， ∴∠MQN+∠EQF=98°， ∴1809882MQE ∠=︒-︒=︒； 故答案为：82︒. 【点睛】本题考查了折叠的性质，三角形内角和定理，以及平角的定义，解题的关键是熟练掌握折叠的性质进行解题. 三、解答题18．如图，ABC ∆为等边三角形，延长BC 到D ，延长BA 到E ， AE BD =，连结EC ，ED ，求证：CE DE=．【答案】详见解析【分析】根据题意首先延长BD至F，使DF=BC，连接EF，得出△BEF为等边三角形，进而求出△ECB≌△EDF，从而得出EC=DE．=，连接EF，如图所示，【详解】解：证明：延长BD至F，使DF BC，为等边三角形，AE BD ABC=∆，，∴=∠=︒BE BF B60∴∆为等边三角形，BEF∴∠=︒，60F∴=∠=∠=︒=，，，BE EF B F BC DF60≌（），ECB EDF SAS∴∆∆∴=．EC ED【点睛】本题主要考查等边三角形的性质与判定以及全等三角形的判定等知识，解决问题的关键是学会添加常用辅助线，构造全等三角形解决问题.19．列方程或方程组解应用题：为了响应“十三五”规划中提出的绿色环保的倡议，某校文印室提出了每个人都践行“双面打印，节约用纸”．已知打印一份资料，如果用A4厚型纸单面打印，总质量为400克，将其全部改成双面打印，用纸将减少一半；如果用A4薄型纸双面打印，这份资料的总质量为160克，已知每页薄型纸比厚型纸轻0.8克，求A4薄型纸每页的质量．（墨的质量忽略不计） 【答案】3.2克．【分析】设A4薄型纸每页的质量为x 克，则A4厚型纸每页的质量为（x+0.8）克，然后根据“双面打印，用纸将减少一半”列方程，然后解方程即可．【详解】解：设A4薄型纸每页的质量为x 克，则A4厚型纸每页的质量为（x+0.8）克，根据题意，得：40016020.8x x=⨯+，解得：x=3.2，经检验：x=3.2是原分式方程的解，且符合题意． 答：A4薄型纸每页的质量为3.2克． 【点睛】本题考查分式方程的应用，掌握题目中等量关系是关键，注意分式方程结果要检验．20．甲、乙两校参加学生英语口语比赛，两校参赛人数相等．比赛结束后，发现学生成绩分别为7分、1分、9分、10分（满分为10分），乙校平均分是1．3分，乙校的中位数是1分．依据统计数据绘制了如下尚不完整的甲校成绩统计表和乙校成绩统计图； 甲校成绩统计表 分数 7分 1分 9分 10分 人数11■1（1）请你将乙校成绩统计图直接补充完整；（2）请直接写出甲校的平均分是 ，甲校的中位数是 ，甲校的众数是 ，从平均分和中位数的角度分析 校成绩较好（填“甲”或“乙”）．【答案】（1）见解析；（2）1.3分，7分，7分，乙【分析】（1）根据乙校的平均分和条形统计图中的数据可以得到得分为1分的学生人数，从而可以将条形统计图补充完整；（2）根据乙校人数和甲校人数相等和统计表中的数据可以计算出甲校得分为9分的学生人数，从而可以计算出甲校的平均分、得到甲校的中位数和众数，以及从平均分和中位数的角度分析哪个学校的成绩较好即可．【详解】解：（1）设乙校得1分的学生有x人，（7×1+1x+9×4+10×5）÷（1+x+4+5）＝1.3，解得，x＝3，即乙校得1分的学生有3人，补充完整的统计图如图所示:（2）甲校得9分的学生有：（1+3+4+5）-（11+0+1）＝1（人），甲校的平均分是：711809110811018⨯+⨯+⨯+⨯+++＝1.3（分），甲校的中位数是7分，众数是7分，对比甲校和乙校的成绩，平均分相同，但乙校的中位数比甲校的大，所以从平均分和中位数的角度分析乙校成绩较好故答案为：1.3分，7分，7分，乙．【点睛】本题主要考查数据分析和条形统计图，掌握平均数，中位数的求法和条形统计图的画法是解题的关键．21．已知：如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DM⊥AB，DN⊥AC，垂足分别为M、N．求证：BM=CN【答案】见解析【分析】先由角平分线性质得到DM=DN，再证Rt△DMB≌Rt△DNC，根据全等三角形对应边相等即可得到答案.【详解】证明：∵AD平分∠BAC，DM⊥AB，DN⊥AC,∴DM=DN又∵点D是BC的中点∴BD=CD ,∴Rt △DMB ≌Rt △DNC(HL)∴BM=CN.【点睛】本题主要考查角平分线的性质、三角形全等的判定（AAS 、ASA 、SSS 、SAS 、HL ），熟练掌握全等三角形的判定是解题的关键.22．瑞士著名数学家欧拉是18世纪数学界最杰出的人物之一，我们现在可以见到很多以欧拉来命名的常数、公式、定理，在分式中，就有这样一个欧拉公式：若a ，b ，c 是两两不同的数，称()()()()()()111P a b a c b a b c c a c b =++------为欧拉分式， （1）请代入合适的值，并猜想：若a ，b ，c 是两两不同的数，则P =______；（2）证明你的猜想；（3）若a ，b ，c 是两两不同的数，试求()()()()()()bc ac ab a b a c b a b c c a c b ++------的值．【答案】（1）0；（2）见解析；（3）1【分析】利用分式的基本性质进行通分化简运算.【详解】(1)当a=1,b=2,c=3时 ()()()()()()()11112132123313211 =+-1+=022P =++-⨯--⨯--⨯-， P=0（2）()()()()()()()()()b c c a a b P a b a c b c a b a c b c a b a c b c ---=++---------()()()0b c c a a b a b a c b c -+-+-==---． （3）原式()()()()()()()()bc a b c bc a c b bc a b a c b a b c c a c b +-+-=++------ ()()()()()()()()()()()()=0+1a b c a c b bc bc bc a b a c b a b c c a c b b a b c c a c b c b c b c bc b c b⎡⎤--=++++⎢⎥----------⎣⎦----=-=． 【点睛】本题主要考查分式的基本运算，熟练掌握分式的通分、约分、化简求值是解决该问题的关键.23．阅读下列解方程组的部分过程，回答下列问题解方程组25 323 x yx y-=⎧⎨-=⎩①②现有两位同学的解法如下：解法一；由①，得x＝2y+5，③把③代入②，得1(2y+5)﹣2y＝1．……解法二：①﹣②，得﹣2x＝2．……(1)解法一使用的具体方法是________，解法二使用的具体方法是______，以上两种方法的共同点是________．(2)请你任选一种解法，把完整的解题过程写出来【答案】 (1)代入消元法；加减消元法；基本思路都是消元；(2)13 xy=-⎧⎨=-⎩.【分析】（1）分析两种解法的具体方法，找出两种方法的共同点即可；（2）将两种方法补充完整即可．【详解】解：(1)解法一使用的具体方法是代入消元法，解法二使用的具体方法是加减消元法，以上两种方法的共同点是基本思路都是消元(或都设法消去了一个未知数，使二元问题转化为了一元问题)；故答案为代入消元法，加减消元法，基本思路都是消元(或都设法消去了一个未知数，使二元问题转化为了一元问题)；(2)方法一：由①得：x＝2y+5③，把③代入②得：1(2y+5)﹣2y＝1，整理得：4y＝﹣12，解得：y＝﹣1，把y＝﹣1代入③，得x＝﹣1，则方程组的解为13 xy=-⎧⎨=-⎩；方法二：①﹣②，得﹣2x＝2，解得：x＝﹣1，把x＝﹣1代入①，得﹣1﹣2y＝5，解得：y＝﹣1，则方程组的解为13 xy=-⎧⎨=-⎩．【点睛】本题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．24．在日历上，我们可以发现其中某些数满足一定的规律，如图是2020年1月份的日历．如图所选择的两组四个数，分别将每组数中相对的两数相乘，再相减，例如：9×11﹣3×17= ，12×14﹣6×20= ，不难发现，结果都是 ．（1）请将上面三个空补充完整；（2）请你利用整式的运算对以上规律进行证明．【答案】（1）1，1，1；（2）证明见解析．【分析】（1）直接利用已知数据计算求出即可；（2）设四个数围起来的中间的数为x ，则四个数依次为x ﹣7，x ﹣1，x+1，x+7，列式计算即可得出结论．【详解】（1）9×11﹣3×17=1，12×14﹣6×20=1，不难发现，结果都是：1．故答案为：1，1，1．（2）设四个数围起来的中间的数为x ，则四个数依次为x ﹣7，x ﹣1，x+1，x+7则(x ﹣1)·(x+1)﹣(x ﹣7)·(x+7) =22(1)(49)x x ---=22149x x --+=1．【点睛】本题考查了整式的混合运算，正确发现数字之间的变化规律是解答本题的关键．25．计算：（1）534153a b c a b -÷；（2）()()()2212y y y --+-.【答案】（1）25ab c -；（2）36y -+.【分析】（1）根据单项式除以单项式的法则计算，把系数、相同底数的幂分别相除作为商的因式，对于只在被除数里含有的字母，连同他的指数作为商的一个因式；（2）完全平方公式的应用，多项式乘以多项式的应用，合并同类项的化简.【详解】（1）原式5431(153)a b c --=-÷25ab c =-；（2）原式2244(22)y y y y y =-+--+- 22442y y y y =-+-++36y =-+，故答案为：（1）25ab c -；（2）36y -+.【点睛】（1）利用单项式除以单项式法则计算，要注意系数的符号问题，同底数幂相除，底数不变，指数相减； （2）完全平方公式的应用，多项式乘以多项式的法则，以及合并同类项，注意括号前面是负号时，去括号变符号的问题.八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．由四舍五入得到的近似数48.0110⨯，精确到（ ）A ．万位B ．百位C ．百分位D ．个位【答案】B【分析】由于48.0110⨯=80100，观察数字1所在的数位即可求得答案.【详解】解：∵48.0110⨯=80100，数字1在百位上，∴ 近似数48.0110⨯精确到百位，故选 B.【点睛】此题主要考查了近似数和有效数字，熟记概念是解题的关键.2．如图，△ABC ≌△ADE ，点D 落在BC 上，且∠EDC ＝70°，则∠B 的度数等于（ ）A ．50°B ．55°C ．60°D ．65°【答案】B 【分析】直接利用全等三角形的性质得出AB ＝AD ，∠B ＝∠ADE ，进而利用已知得出答案．【详解】解：∵△ABC ≌△ADE ，∴AB ＝AD ，∠B ＝∠ADE ，∴∠B ＝∠ADB ，∴∠BDA ＝∠ADE ，∵∠EDC ＝70°，∴∠BDA ＝∠ADE ＝12×（180°﹣70°）＝55°． 故选：B ．【点睛】考核知识点：全等三角形性质.理解性质是关键.3．下列全国志愿者服务标识的设计图中，是轴对称图形的是（ ）A ．B ．C ．D ．【答案】C【分析】根据轴对称图形的概念判断即可．【详解】解：A 、B 、D 中的图形不是轴对称图形，C 中的图形是轴对称图形，故选：C ．【点睛】本题考查了轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合． 4．如图:ACD ∠是ABC ∆的外角,CE 平分ACD ∠,若60A ∠=︒,40B ∠=︒,则ECD ∠等于（ ）A ．30B ．40︒C ．45︒D ．50︒【答案】D 【分析】根据三角形外角性质求出ACD ∠，根据角平分线定义求出即可．【详解】∵6040A B ∠∠=︒=︒，，∴100ACD A B ∠=∠+∠=︒，∵CE 平分ACD ∠， ∴111005022ECD ACD ∠=∠=⨯︒=︒， 故选：D ．【点睛】本题考查了角平分线定义和三角形外角性质，能熟记三角形外角性质的内容是解此题的关键． 5．如图，AD 是ABC ∆的中线，E ，F 分别是AD 和AD 延长线上的点，连接BF ，CE ，且CE AD ⊥.BF AD ⊥.有下列说法：①CE BF =；②ABD ∆和ACD ∆的面积相等；③BAD CAD ∠=∠；④BDF CDE ∆∆≌.其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C 【分析】先利用AAS 证明△BDF ≌△CDE ，则即可判断①④正确；由于AD 是△ABC 的中线，由于等底同高，那么两个三角形的面积相等，可判断②正确；不能判断BAD CAD ∠=∠，则③错误；即可得到答案.【详解】解：∵CE AD ⊥，BF AD ⊥，∴∠F=∠CED=90°，∵AD 是ABC ∆的中线，∴BD=CD ，∵∠BDF=∠CDE ，∴△BDF ≌△CDE （AAS ），故④正确；∴BF=CE ，故①正确；∵BD=CD ，∴ABD ∆和ACD ∆的面积相等；故②正确；不能证明BAD CAD ∠=∠，故③错误；∴正确的结论有3个，故选：C.【点睛】本题考查了全等三角形判定和性质，以及三角形中线的性质，解题的关键是证明△BDF ≌△CDE ． 6．如图，直线y mx n =+与y kx b =+的图像交于点（3，-1），则不等式组,0mx n kx b mx n +≥+⎧⎨+≤⎩的解集是（）A ．3x ≤B ．n x m ≥-C ．3n x m -≤≤D ．以上都不对【答案】C 【分析】首先根据交点得出3b n m k-=-，判定0,0m k ＜＞，然后即可解不等式组. 【详解】∵直线y mx n =+与y kx b =+的图像交于点（3，-1）∴31,31m n k b +=-+=-∴33m n k b +=+，即3b n m k-=- 由图象，得0,0m k ＜＞∴mx n kx b +≥+，解得3x ≤0mx n +≤，解得n x m≥-∴不等式组的解集为：3n x m -≤≤ 故选：C.【点睛】此题主要考查根据函数图象求不等式组的解集，利用交点是解题关键.7．等腰三角形的一个角是80°，则它的顶角的度数是（ ）A ．80°B ．80°或20°C ．80°或50°D ．20°【答案】B【解析】试题分析：分80°角是顶角与底角两种情况讨论求解． ①80°角是顶角时，三角形的顶角为80°，②80°角是底角时，顶角为180°﹣80°×2=20°， 综上所述，该等腰三角形顶角的度数为80°或20°． 考点：等腰三角形的性质．8．如图，ABCD 是正方形场地，点E 在DC 的延长线上，AE 与BC 相交于点F ，有甲、乙、丙三名同学同时从点A 出发，甲沿着A ﹣B ﹣F ﹣C 的路径行走至C ，乙沿着A ﹣F ﹣E ﹣C ﹣D 的路径行走至D ，丙沿着A ﹣F ﹣C ﹣D 的路径行走至D ，若三名同学行走的速度都相同，则他们到达各自的目的地的先后顺序（由先至后）是（ ）A ．甲乙丙B ．甲丙乙C ．乙丙甲D ．丙甲乙【答案】B【分析】本题考查了正方形的性质，直角三角形的性质的应用，题目比较典型，难度适中．根据正方形的性质得出AB=BC=CD=AD，∠B=∠ECF，根据直角三角形得出AF＞AB，EF＞CF，分别求出甲、乙、丙行走的距离，再比较即可．【详解】解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=90°，甲行走的距离是AB+BF+CF=AB+BC=2AB；乙行走的距离是AF+EF+EC+CD；丙行走的距离是AF+FC+CD，∵∠B=∠ECF=90°，∴AF＞AB，EF＞CF，∴AF+FC+CD＞2AB，AF+FC+CD＜AF+EF+EC+CD，∴甲比丙先到，丙比乙先到，即顺序是甲丙乙，故选B．【点睛】本题考查1.正方形的性质；2.线段的性质：两点之间线段最短；3.比较线段的长短．9．下列命题中，是假命题的是（）A．同旁内角互补B．对顶角相等C．两点确定一条直线D．全等三角形的面积相等【答案】A【分析】逐一对选项进行分析即可.【详解】A选项，两直线平行，同旁内角互补，故该命题是假命题；B选项，对顶角相等，故该命题是真命题；C选项，两点确定一条直线，故该命题是真命题；D选项，全等三角形的面积相等，故该命题是真命题.故选：A.【点睛】本题主要考查真假命题，会判断命题的真假是解题的关键.10．计算23a a 的结果是（）A．5a B．6a C．6a D．5a【答案】A【解析】根据同底数幂的乘法公式进行计算即可得解.【详解】根据同底数幂的乘法公式m nm n a a a +⋅=（m ，n 都是正整数）可知23235a a a a +⋅==，故选：A.【点睛】 本题主要考查了整式的乘法，熟练掌握同底数幂的乘法公式是解决本题的关键.二、填空题11．平面上有三条直线两两相交且不共点，那么平面上到此三条直线距离相等的点的个数是_____．【答案】1【分析】根据角平分线性质的逆定理，结合三角形内角平分线和外角平分线作出图形即可解答．【详解】解：到三条直线的距离相等的点应该有A 、B 、C 、D 共1个，故答案为：1．【点睛】本题考查了角平分线性质的逆定理，掌握角平分线性质的逆定理是解题的关键．12．如图，(0,1.7)A ，(0.6,0)C ，BC AC ⊥，BC AC =，则点B 的坐标为____．【答案】()2.30.6，【分析】如图，作BM ⊥x 轴于M ，由△AOC ≌△CMB ，推出CM=OA ，BM=OC ，由此即可解决问题．【详解】如图，作BM ⊥x 轴于M ，∵()01.7A ，，() 0.60C ，， ∴ 1.7OA =，0.6OC =，∵∠ACB=90°，∴∠ACO+∠BCM=90°，∠OAC+∠ACO=90°，∴∠OAC=∠BCM ，在△AOC 和△CMB 中，90AOC CMB OAC MCB AC CB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≌△CMB ，∴ 1.7CM OA ==， 0.6BM OC ==，∴0.6 1.7 2.3OM OC CM =+=+=，∴点B 坐标为()2.30.6，， 故答案为：()2.30.6，． 【点睛】本题考查坐标与图形的性质、全等三角形的判定和性质、等腰直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．13．比较大小：321-__________5【答案】＜【分析】先确定32的大小，再计算321-的大小，即可与5比较.【详解】∵5<32<6,∴4<321-<5,∴321-<5,故答案为：＜.【点睛】此题考查实数的大小比较，确定无理数的大小是解题的关键.14．如图，∠AOB ＝30°，OP 平分∠AOB ，PC ∥OB 交OA 于C ，PD ⊥OB 于D ．如果PC ＝8，那么PD 等于____________ ．【答案】1【分析】根据角平分线的性质，角平分线上的点到两角的距离相等，因而过P 作PE ⊥OA 于点E ，则PD=PE ，因为PC ∥OB ，根据三角形的外角的性质得到：∠ECP=∠COP+∠OPC=30°，在直角△ECP 中求得PD 的长．【详解】解：过P 作PE ⊥OA 于点E ，∵OP 平分∠AOB ，PD ⊥OB 于D∴PD=PE ，∵PC ∥OB ∴∠OPC=∠POD ，又∵OP 平分∠AOB ，∠AOB=30°，∴∠OPC=∠COP=15°，∠ECP=∠COP+∠OPC=30°，在直角△ECP 中，142PE PC == 则PD=PE=1．故答案为：1．【点睛】本题主要考查了角平分线的性质和含有30°角的直角三角形的性质，正确作出辅助线是解决本题的关键．15．若211m m --的值为零，则15m +-的值是____． 【答案】-1【分析】根据分式的值为零的条件：分子＝0且分母≠0即可求出m ，然后代入求值即可． 【详解】解：∵211m m --的值为零 ∴21010m m ⎧-=⎨-≠⎩解得：m=-1∴111551m +-+=-=--故答案为：-1．【点睛】此题考查的是分式的值为零的条件和零指数幂的性质，掌握分式的值为零的条件：分子＝0且分母≠0和零指数幂的性质是解决此题的关键．16510x <<的整数x 的值 __________．【答案】3x 的范围.【详解】∵，<4，∴x 是大于2小于3的整数，故答案为：3.【点睛】.17．分解因式：29a -=__________．【答案】()()33a a +-【解析】试题分析：本题考查实数范围内的因式分解，因式分解的步骤为：一提公因式；二看公式．在实数范围内进行因式分解的式子的结果一般要分到出现无理数为止．先把式子写成a 2-32，符合平方差公式的特点，再利用平方差公式分解因式．a 2-9=a 2-32=（a+3）（a-3）．故答案为（a+3）（a-3）．考点：因式分解-运用公式法．三、解答题18．某商场计划购进A 、B 两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：（1）若商场预计进货款为3500元，则这两种台灯各购进多少盏？（2）若商场规定B 型台灯的进货数量不超过A 型台灯进货数量的4倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？【答案】（1）75盏；25盏 （2）购进A 型台灯20盏，B 型台灯80盏；1元【分析】（1）设商场应购进A 型台灯x 盏，表示出B 型台灯为（100﹣x ）盏，然后根据进货款＝A 型台灯的进货款+B 型台灯的进货款列出方程求解即可；（2）设商场销售完这批台灯可获利y 元，根据获利等于两种台灯的获利总和列式整理，再求出x 的取值范围，然后根据一次函数的增减性求出获利的最大值．【详解】解：（1）设购进A 型台灯x 盏，则购进B 型台灯（100﹣x ）盏，由题意可得：30x +50（100﹣x ）＝3500∴x ＝75∴100﹣x ＝25答：购进A 型台灯75盏，购进B 型台灯25盏；（2）设商场销售完这批台灯可获利y 元，y ＝15x +20（100﹣x ）＝﹣5x +2000又∵100﹣x ≤4x ，∴x ≥20∵k ＝﹣5＜0，∴y 随x 的增大而减小∴当x ＝20时，y 取得最大值，最大值是1．答：购进A 型台灯20盏，购进B 型台灯80盏时获利最多，此时利润为1元．【点睛】本题考查了一次函数的应用，主要利用了一次函数的增减性，（2）题中理清题目数量关系并列式求出x 的取值范围是解题的关键．19．如图，在平面直角坐标系中，ABC ∆三个顶点的坐标分别是()()()2,1,1,3,4,4A B C .（1）在图中画出ABC ∆关于y 轴对称的图形111A B C ∆，并写出点C 的对应点1C 的坐标；（2）在图中x 轴上作出一点P ，使得1PB PC +的值最小（保留作图痕迹，不写作法）【答案】（1）见解析；（2）见解析【分析】（1）利用轴对称的性质找出A 1、B 1、C 1关于y 轴对称点，再依次连接即可；（2）作点C 关于x 轴的对称点C 2，连接B 1C 2，与x 轴交点即为P .【详解】解：（1）如图，△A 1B 1C 1即为所作图形，其中C 1的坐标为（-4，4）；（2）如图点P 即为所作点.【点睛】本题考查了作图—轴对称，最短路径问题，解题的关键在于利用轴对称的性质作出最短路径.20．解方程组：3224x yx y=⎧⎨-=-⎩①②．【答案】23 xy⎧⎨⎩＝＝【分析】方程组利用代入消元法求出解即可．【详解】3224x yx y=⎧⎨-=-⎩①②，把①代入②得：x−3x＝−4，即x＝2，把x＝2代入①得：y＝3，∴方程组的解为23 xy⎧⎨⎩＝＝．【点睛】此题考查了解二元一次方程组，熟练掌握代入消元法是解本题的关键．21．知识背景我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在十三章《轴对称》中学习了等腰三角形的性质和判定．在一些探究题中经常用以上知识转化角和边，进而解决问题。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．已知,,a b c 为ABC ∆的内角,,A B C 所对应的边，满足下列条件的三角形不是直角三角形的是（ ）A ．4,5AB BC AC === B ．::2a b c =C ．::5:4:3A B C ∠∠∠=D ．34,55a cbc == 【答案】C 【分析】运用直角三角形的判定方法：当一个角是直角时，或两边的平方和等于第三条边的平方，也可得出它是直角三角形．分别判定即可．【详解】A 、∵4,5AB BC AC ===，∴22245162541+=+==，即222BC AC AB +=,∴△ABC 是直角三角形，故本选项符合题意；B 、∵::1:2a b c =，∴222142+==∴a 2+b 2=c 2，∴△ABC 是直角三角形，故本选项不符合题意；C 、∵∠A ：∠B ：∠C=5：4：3，又∵∠A+∠B+∠C=180°，∴最大角∠A=75°，∴△ABC 不是直角三角形，故本选项符合题意；D 、∵a=35c ，b=45c ， （35c ）2+（45c ）2=c 2， ∴a 2+b 2=c 2，∴△ABC 是直角三角形，故本选项不符合题意．故选：C ．【点睛】此题主要考查了勾股定理的逆定理、直角三角形的判定方法，灵活的应用此定理是解决问题的关键． 2．平面直角坐标系中，点P 的坐标是（2，-1），则直线OP 经过下列哪个点（ ）A ．()1,2-B ．()2,1-C ．()1,2-D ．14,2⎛⎫- ⎪⎝⎭【答案】B【解析】先求出直线OP 的表达式，再把四个选项带人公式即可.【详解】∵点P 的坐标是（2，-1），∴设直线OP 的表达式为：y=kx ，把（2，-1）代入，解得k=-12，y=-12x ． 把（-1，2），（-2，1），（1，-2），（4，-12）代入y=﹣12x ，（-2，1）满足条件． 故选：B ．【点睛】本题考查的是平面直角坐标系，熟练掌握一次函数是解题的关键.3．若2x y -=，3xy =，则22x y xy -的值为（ ）A ．1B ．1-C ．6D ．6-【答案】C【分析】原式首先提公因式xy ，分解后，再代入求值即可．【详解】∵2x y -=，3xy =，∴22()326xy x x x y y y =-=⨯=-．故选：C ．【点睛】本题主要考查了提公因式分解因式，关键是正确确定公因式．4．下列命题是真命题的有（ ）①若a 2=b 2，则a=b ；②内错角相等，两直线平行．③若a ，b 是有理数，则|a+b|=|a|+|b|；④如果∠A=∠B ，那么∠A 与∠B 是对顶角．A ．1个B ．2个C ．3个D ．4个 【答案】D【解析】试题解析：①若a 2=b 2，则a=b ；是假命题；②内错角相等，两直线平行．是真命题；③若a ，b 是有理数，则|a+b|=|a|+|b|；是假命题；④如果∠A=∠B ，那么∠A 与∠B 是对顶角．是假命题；故选A ．5．如图，已知ABC ∆，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF CA =；连接DE 、EF 、FD ，得DEF ∆.若ABC ∆的面积为k ，则DEF ∆的面积为( )A．10k B．15k C．18k D．20k【答案】C【分析】如图所示：连接AE、CD,要求△DEF的面积，可以分三部分来计算，利用高一定时，三角形的面积与高对应的底成正比的关系进行计算；利用已知△ABC的面积k计算与它同高的三角形的面积，然后把所求各个面积相加即可得出答案．【详解】如图所示：连接AE、CD∵BD＝AB∴S△ABC＝S△BCD＝k则S△ACD＝2 k∵AF＝3AC∴FC＝4AC∴S△FCD＝4S△ACD＝4×2k＝8k同理求得：S△ACE＝2S△ABC＝2kS△FCE＝4S△ACE＝4×2k＝8kS△DCE＝2S△BCD＝2×k＝2k∴S△DEF＝S△FCD＋S△FCE＋S△DCE＝8k＋8k＋2k＝18 k故选：C【点睛】本题主要考查三角形的面积与底的正比关系的知识点：当高相同时，三角形的面积与高对应的底成正比的关系，掌握这一知识点是解题的关键．6．眉山市某初级中学连续多年开设第二兴趣班．经测算，前年参加的学生中，参加艺术类兴趣班的学生占48%，参加体育类的学生占29%，参加益智类的学生占23%；去年参加的学生中，参加艺术类兴趣班的学生占36%，参加体育类的学生占33%，参加益智类的学生占31%（如图）．下列说法正确的是（ ）A ．前年参加艺术类的学生比去年的多B ．去年参加体育类的学生比前年的多C ．去年参加益智类的学生比前年的多D ．不能确定参加艺术类的学生哪年多【答案】D 【分析】在比较各部分的大小时，必须在总体相同的情况下才能比较，所以无法确定参加艺术类的学生哪年多．【详解】解：眉山市某初级中学参加前年和去年的兴趣班的学生总人数不一定相同，所以无法确定参加各类活动的学生哪年多．故选D ．【点睛】本题考查了扇形统计图．扇形统计图直接反映部分占总体的百分比大小，但是在比较各部分的大小时，必须在总体相同的情况下才能比较．7．下列各式：3x y -，43x π-，21x x -，2xy ，2x y +其中分式共有几个（ ）． A ．1B ．2C ．3D ．4 【答案】B【分析】根据分式的定义，即可完成求解．【详解】3x y -、43x π-、2xy 的分母不含未知数，故不是分式； 21x x -、2x y +符合分式定义，故为分式； 故选：B ．【点睛】本题考查了分式的知识；解题的关键是熟练掌握分式的定义，即可得到答案．8．下列图案中不是轴对称图形的是（ ）A ．B ．C ．D ．【答案】D【分析】根据轴对称图形的概念对各选项分析判断即可得解．【详解】A．是轴对称图形，故本选项不合题意；B．是轴对称图形，故本选项不合题意；C．是轴对称图形，故本选项不合题意；D．不是轴对称图形，故本选项正确．故选：D．【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．9．已知三角形两边长分别为7、11，那么第三边的长可以是( )A．2 B．3 C．4 D．5【答案】D【解析】设第三边长为x，由题意得：11﹣7＜x＜11+7，解得：4＜x＜18，故选D．点睛:此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边，三角形的两边差小于第三边．10．下列图形是轴对称图形的是( )A．B． C． D．【答案】B【解析】根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．据此对图中的图形进行判断．解：A、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，故本选项错误；B、有六条对称轴，是轴对称图形，故本选项正确；C、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，故本选项错误；D、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，故本选项错误．故选B．二、填空题11．如图，△ABC是等腰直角三角形，AB=BC，已知点A的坐标为（﹣2，0），点B的坐标为（0，1），则点C 的坐标为__．【答案】【解析】试题分析：作轴于，根据条件可证得≌，故，，所以，所以. 考点：1.辅助线的添加；2.三角形全等.12．如图，在平面直角坐标系中，边长为1的正方形OA 1B 1C 1的两边在坐标轴上，以它的对角线OB 1为边作正方形OB 1B2C 2，再以正方形OB 1B 2C 2的对角线OB 2为边作正方形OB 2B 3C 3，以此类推……则正方形OB 2019B 2020C 2020的顶点B 2020的坐标是 _____.【答案】1010(2,0)【分析】首先先求出B 1、B 2、B 3、B 4、B 5、B 6、B 7、B 8、B 9、B 10的坐标，找出这些坐标之间的规律，然后根据规律计算出点B 2020的坐标．【详解】∵正方形OA 1B 1C 1的边长为1，∴OB 12∴OB 2=2∴B 2（0，2），同理可知B 3（-2，2），B 4（-4，0），B 5（-4，-4），B 6（0，-8），B 7（8，-8），B 9（16，16），B 10（0，32）．由规律可以发现，每经过8次作图后，点的坐标符号与第一次坐标的符号相同，每次正方形的边长变为原2∵2020÷8=252⋯⋯4，∴B 8n+4（-24k+2，0），∴B 2020（-21010，0）．故答案为（-21010，0）．【点睛】此题考查的是一个循环规律归纳的题目，解答此题的关键是确定几个点坐标为一个循环，再确定规律即可． 13．如图，扶梯AB 的坡比为4:3，滑梯CD 的坡比为1:2，若30AE BC ==米，一男孩经扶梯AB 走到滑梯的顶部BC ，然后从滑梯CD 滑下，共经过了_____米．【答案】(80405)+ 【分析】根据两个坡度比求出BE 和DF ，再利用勾股定理求出AB 和CD ，最后加上BC 就是经过的路程长． 【详解】解：∵AB 的坡度是4:3，∴43BE AE =， ∵30AE =，则4303BE =， ∴40BE =， ∵CD 的坡度是1:2，∴12CF DF =， ∵40CF BE ==，则4012DF =， ∴80DF =，根据勾股定理，2222304050AB AE BE =+=+=，22224080405CD CF DF =+=+=，503040580405AB BC CD ++=++=+．故答案是：80405+．【点睛】本题考查解直角三角形的实际应用，解题的关键是抓住坡度的比，利用这个关系去解直角三角形． 14．如图，上海实行垃圾分类政策后，各街道、各小区都在积极改造垃圾房，在工地一边的靠墙处，用12米长的栏围一个占面积为20平方米的长方形临时垃圾堆放点，栅栏只围三边，并且开一个2米的小门，方便垃圾桶的搬运.设垂直于墙的一边长为x 米．根据题意，建立关于x 的方程是____．【答案】(142)20x x -=【分析】设垃圾房的宽为x 米，由栅栏的长度结合图形，可求出垃圾房的长为（14-2x ）米，再根据矩形的面积公式即可列出关于x 的一元二次方程，此题得解．【详解】设垃圾房的宽为x米，则垃圾房的长为（14-2x）米，根据题意得：x（14-2x）=1．故答案为：x（14-2x）=1．【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．15．如图所示的数轴上，点B与点C关于点A对称，A、B两点对应的实数是3和1-，则线段BC的长为_____________．【答案】23+2【分析】根据对称的性质，即对称点到对称中心的距离相等，即可列式计算.【详解】解：∵点B和点C关于点A对称∴BC=2AB--=3+1∵AB=3(1)∴BC=2⨯(3+1)=23+2故答案为23+2.【点睛】本题考查了对称的性质以及数轴上两点间距离的计算.-.数轴上两点间距离：AB=a b16．如图，五边形ABCDE的外角中，∠1＝∠2＝∠3＝∠4＝75°，则∠A的度数是_____．【答案】120°．【分析】根据多边形的外角和求出与∠A相邻的外角的度数，然后根据邻补角的和等于180°列式求解即可．【详解】∵∠1＝∠2＝∠3＝∠4＝75°，∴与∠A相邻的外角＝360°﹣75°×4＝360°﹣300°＝60°，∴∠A＝180°﹣60°＝120°．故答案为120°．【点睛】本题主要考查了多边形外角和定理，熟练掌握相关概念是解题关键.17．已知111y x =-，且2111y y =-，3211y y =-，4311y y =-，…，111n n y y -=-，请计算2019y =__________（用含x 在代数式表示）．【答案】2x -【分析】首先将1y 代入2y ，用x 表示出2y ，以此类推，进一步表示出3y 、4y ，最后根据计算结果得出循环规律，据此进一步求解即可.【详解】∵111y x =-， ∴2111111211x y y x x -===----，3211=21112y x x y x ==-----， 43111=11(2)1y y x x ==----， 由此可得，n y 是以11x -、12x x --、2x -依次循环， ∵20193673÷=，∴20193=2y y x =-，故答案为：2x -.【点睛】本题主要考查了分式的运算，准确找出循环规律是解题关键.三、解答题18．如图，CD ⊥AB ，BE ⊥AC ，垂足分别为点D ，E ，其中BE ，CD 相交于点O ，∠BAO =∠CAO ．求证：OB =OC ．【答案】见解析【分析】根据垂直的定义和角平分线的性质可得∠BDO =∠CEO =90°、OD =OE ，然后利用ASA 即可证出△ODB ≌△OEC ，从而证出结论．【详解】解：∵CD ⊥AB ，BE ⊥AC ，∴∠BDO =∠CEO =90°．∵∠BAO =∠CAO ，∴OD =OE ．在△ODB 和△OEC 中BDO CEO OD OEBOD COE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ODB ≌△OEC （ASA ）．∴OB =OC ．【点睛】此题考查的是角平分线的性质、全等三角形的判定及性质，掌握角平分线的性质、全等三角形的判定及性质是解决此题的关键．19．再读教材：宽与长的比是51-（约为0.618）的矩形叫做黄金矩形，黄金矩形给我们以协调、匀称的美感．世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计，下面我们用宽为2的矩形纸片折叠黄金矩形（提示：2MN =）第一步：在矩形纸片一端利用图①的方法折出一个正方形，然后把纸片展平．第二步：如图②，把这个正方形折成两个相等的矩形，再把纸片展平．第三步：折出内侧矩形的对角线AB ，并把AB 折到图③中所示的AD 处．第四步：展平纸片，按照所得的点D 折出,DE 使,DE ND ⊥则图④中就会出现黄金矩形．问题解决：（1）图③中AB =_ （保留根号）；（2）如图③，判断四边形BADQ 的形状，并说明理由；（3）请写出图④中所有的黄金矩形，并选择其中一个说明理由．【答案】（15（2）菱形，见解析；（3）黄金矩形有矩形BCDE ，矩形MNDE ，见解析【分析】（1）由题意可知：NC=BC=2，∠BCN=90°，点A 为NC 的中点，从而求出AC ，然后利用勾股定理即可求出结论；（2）根据矩形的性质和平行线的性质可得∠=∠BQA QAD ,然后根据折叠的性质可得BAQ QAD AB AD ∠=∠=,，从而证出BQ AD =，即可证出四边形BADQ 是平行四边形，再根据菱形的判定定理即可证出结论；（3）根据黄金矩形即可证出结论．【详解】解：()1由题意可知：NC=BC=2，∠BCN=90°，点A 为NC 的中点∴AC=12NC=1 ∴22AC BC +55()2四边形BADQ 是菱形如图③，四边形ACBF 是矩形，//∴BQ ADBQA QAD ∴∠=∠由折叠得：BAQ QAD AB AD ∠=∠=,BQA BAQ ∴∠=∠BQ AB ∴=BQ AD ∴=//BQ AD ，∴四边形BADQ 是平行四边形AB AD =∴四边形BADQ 是菱形()3下图中的黄金矩形有矩形BCDE ，矩形MNDE以矩形BCDE 为例，理由如下: 5,1AD AN AC ===，51CD AD AC ∴=-=．又2,BC =51CD BC -∴= ∴矩形BCDE 是黄金矩形．以矩形MNDE 为例，理由如下:5,1AD AN AC ===，AM=21∴=+=+ND AD AN ．∴==MN ND ∴矩形MNDE 是黄金矩形．【点睛】此题考查的是勾股定理、矩形的判定及性质、菱形的判定及性质和折叠的性质，掌握勾股定理、矩形的判定及性质、菱形的判定及性质、折叠的性质和黄金矩形的定义是解决此题的关键．20．计算：（1（2）-1）0﹣|1【答案】（1）0；（2）5【分析】（1）先求算术平方根与立方根，再进行减法运算，即可；（2）先求零次幂，绝对值和算术平方根，再进行加减法运算，即可求解．【详解】（1）原式＝2﹣2＝0；（2）原式＝1+（1+3＝5【点睛】 本题主要考查实数的混合运算，掌握求算术平方根，立方根，零次幂是解题的关键．21．已知：如图1，在平面直角坐标系中，一次函数y ＝34x+3交x 轴于点A ，交y 轴于点B ，点C 是点A 关于y 轴对称的点，过点C 作y 轴平行的射线CD ，交直线AB 与点D ，点P 是射线CD 上的一个动点．(1)求点A ，B 的坐标．(2)如图2，将△ACP 沿着AP 翻折，当点C 的对应点C ′落在直线AB 上时，求点P 的坐标．(3)若直线OP 与直线AD 有交点，不妨设交点为Q(不与点D 重合)，连接CQ ，是否存在点P ，使得S △CPQ ＝2S △DPQ ，若存在，请求出对应的点Q 坐标；若不存在，请说明理由．【答案】（1）A（﹣4，0），B（0，3）；（2）P（4，83）；（3）满足条件的点Q（12，12）或（43，4）．【分析】令x=0，y=0即可求出A，B坐标.因为点C是点A关于y轴对称的点，求得C坐标，因为CD⊥x轴，所以求得D坐标，由折叠知，AC'=AC，所以C'D=AD﹣AC'，设PC=a，在Rt△DC'P中通过勾股定理求得a值，即可求得P点坐标.在S△CPQ=2S△DPQ情况下分类讨论P点坐标即可求解.【详解】解：（1）令x=0，则y=3，∴B（0，3），令y=0，则x+3=0，∴x=﹣4，∴A（﹣4，0）；（2）∵点C是点A关于y轴对称的点，∴C（4，0），∵CD⊥x轴，∴x=4时，y=6，∴D（4，6），∴AC=8，CD=6，AD=10，由折叠知，AC'=AC=8，∴C'D=AD﹣AC'=2，设PC=a，∴PC'=a，DP=6﹣a，在Rt△DC'P中，a2+4=（6﹣a）2，∴a=，∴P（4，）；（3）设P（4，m），∴CP=m，DP=|m﹣6|，∵S△CPQ=2S△DPQ，∴CP=2PD，∴2|m﹣6|=m，∴m=4或m=12，∴P（4，4）或P（4，12），∵直线AB的解析式为y=x+3①，当P（4，4）时，直线OP的解析式为y=x②，联立①②解得，x=12，y=12，∴Q（12，12），当P（4，12）时，直线OP解析式为y=3x③，联立①③解得，x=，y=4，∴Q（，4），即：满足条件的点Q（12，12）或（，4）．【点睛】本题主要考查了一元一次方程，二元一次方程，对称，折叠的综合应用，灵活运用是关键.22．如图，∠ABC=60°，∠1=∠1．（1）求∠3的度数；（1）若AD⊥BC，AF=6,求DF的长．【答案】（1）60°；（1）3【分析】（1）由三角形的外角性质，得到∠3=∠1+∠ABF，由∠1=∠1，得到∠3=∠ABC，即可得到答案；（1）由（1）∠3=∠ABC=60°，由AD⊥BC，则∠1=∠1=30°，则∠ABF=30°=∠1，则BF=AF=6，即可求出DF的长度．【详解】解：（1）根据题意，由三角形的外角性质，得∠3=∠1+∠ABF，∵∠1=∠1，∴∠3=∠1+∠ABF，∵∠ABC=∠ABF+∠1=60°，∴∠3=60°；（1）由（1）可知，∠3=60°，∵AD⊥BC，∴∠ADB=90°，∴∠1=30°， ∴12DF BF =， ∵∠3=∠1+∠ABF ，∴∠ABF=30°，∵∠1=∠1=30°，∴∠ABF=∠1=30°，∴BF=AF=6，∴1632DF =⨯=． 【点睛】本题考查了30°直角三角形的性质，三角形的外角性质，以及等角对等边，解题的关键是熟练掌握所学的性质进行求解．23．（模型建立）（1）如图1，等腰直角三角形ABC 中，90ACB ∠=，CB CA =，直线ED 经过点C ，过A 作AD ED ⊥于点D ，过B 作BE ED ⊥于点E .求证：BEC CDA ∆≅∆；（模型应用）（2）已知直线1l ：443y x =+与坐标轴交于点A 、B ，将直线1l 绕点A 逆时针旋转45至直线2l ，如图2，求直线2l 的函数表达式；（3）如图3，长方形ABCO ，O 为坐标原点，点B 的坐标为()8,6-，点A 、C 分别在坐标轴上，点P 是线段BC 上的动点，点D 是直线26y x =-+上的动点且在第四象限.若APD ∆是以点D 为直角顶点的等腰直角三角形，请直接．．写出点D 的坐标.【答案】（1）见解析；（2）y ＝−7x−21；（3）D （4，−2）或（203，223-）. 【分析】（1）根据△ABC 为等腰直角三角形，AD ⊥ED ，BE ⊥ED ，可判定BEC CDA ∆≅∆；（2）①过点B 作BC ⊥AB ，交l 2于C ，过C 作CD ⊥y 轴于D ，根据△CBD ≌△BAO ，得出BD ＝AO ＝3，CD ＝OB ＝4，求得C （−4，7），最后运用待定系数法求直线l 2的函数表达式；（3）根据△APD是以点D为直角顶点的等腰直角三角形，当点D是直线y＝−2x＋6上的动点且在第四象限时，分两种情况：当点D在矩形AOCB的内部时，当点D在矩形AOCB的外部时，设D（x，−2x＋6），分别根据△ADE≌△DPF，得出AE＝DF，据此列出方程进行求解即可．【详解】解：（1）证明：∵△ABC为等腰直角三角形，∴CB＝CA，∠ACD＋∠BCE＝90°，又∵AD⊥ED，BE⊥ED，∴∠D＝∠E＝90°，∠EBC＋∠BCE＝90°，∴∠ACD＝∠EBC，在△ACD与△CBE中，D EACD EBC CA CB∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴BEC CDA∆≅∆（AAS）；（2）①如图2，过点B作BC⊥AB，交l2于C，过C作CD⊥y轴于D，∵∠BAC＝45°，∴△ABC为等腰直角三角形，由（1）可知：△CBD≌△BAO，∴BD＝AO，CD＝OB，∵直线l1：y＝43x＋4中，若y＝0，则x＝−3；若x＝0，则y＝4，∴A（−3，0），B（0，4），∴BD＝AO＝3，CD＝OB＝4，∴OD＝4＋3＝7，∴C（−4，7），设l2的解析式为y＝kx＋b，则7403k bk b=-+⎧⎨=-+⎩，解得：721 kb=-⎧⎨=-⎩，∴l2的解析式为：y＝−7x−21；（3）D（4，−2）或（203，223-）．理由：当点D是直线y＝−2x＋6上的动点且在第四象限时，分两种情况：当点D在矩形AOCB的内部时，如图，过D作x轴的平行线EF，交直线OA于E，交BC于F，设D（x，−2x＋6），则OE＝2x−6，AE＝6−（2x−6）＝12−2x，DF＝EF−DE＝8−x，由（1）可得，△ADE≌△DPF，则DF＝AE，即：12−2x＝8−x，解得x＝4，∴−2x＋6＝−2，∴D（4，−2），此时，PF＝ED＝4，CP＝6＝CB，符合题意；当点D在矩形AOCB的外部时，如图，过D作x轴的平行线EF，交直线OA于E，交直线BC于F，设D（x，−2x＋6），则OE＝2x−6，AE＝OE−OA＝2x−6−6＝2x−12，DF＝EF−DE＝8−x，同理可得：△ADE≌△DPF，则AE＝DF，即：2x−12＝8−x，解得x＝203，∴−2x＋6＝223 -，∴D（203，223-），此时，ED＝PF＝203，AE＝BF＝43，BP＝PF−BF＝163＜6，符合题意，综上所述，D点坐标为：（4，−2）或（203，223-）【点睛】本题属于一次函数综合题，主要考查了点的坐标、矩形的性质、待定系数法、等腰直角三角形的性质以及全等三角形等相关知识的综合应用，解决问题的关键是作辅助线构造全等三角形，运用全等三角形的性质进行计算，解题时注意分类思想的运用．24．2019年，在新泰市美丽乡村建设中，甲、乙两个工程队分别承担某处村级道路硬化和道路拓宽改造工程．己知道路硬化和道路拓宽改造工程的总里程数是1．6千米，其中道路硬化的里程数是道路拓宽里程数的2倍少1千米．（1）求道路硬化和道路拓宽里程数分别是多少千米；（2）甲、乙两个工程队同时开始施工，甲工程队比乙工程队平均每天多施工10米．由于工期需要，甲工程队在完成所承担的13施工任务后，通过技术改进使工作效率比原来提高了15．设乙工程队平均每天施工a 米，若甲、乙两队同时完成施工任务，求乙工程队平均每天施工的米数a 和施工的天数．【答案】（1）道路硬化里程数为5.4千米，道路拓宽里程数为3.2千米；（2）乙工程队平均每天施工20米，施工的天数为160天【分析】（1）设道路拓宽里程数为x 千米，则道路硬化里程数为（2x-1）千米，根据道路硬化和道路拓宽改造工程的总里程数是1.6千米，即可得出关于x 的一元一次方程，解之即可得出结论；（2）设乙工程队平均每天施工a 米，则甲工程队技术改进前每天施工（a+10）米，技术改进后每天施工65（a+10）米，由甲、乙两队同时完成施工任务，即可得出关于a 的分式方程，解之经检验后即可得出a 值，再将其代入3200a中可求出施工天数． 【详解】解：（1）设道路拓宽里程数为x 千米，则道路硬化里程数为(21)x -千米，依题意，得：(21)8.6x x +-=，解得： 3.2x =，21 5.4x -=∴．答：道路硬化里程数为5.4千米，道路拓宽里程数为3.2千米．（2）设乙工程队平均每天施工a 米，则甲工程队技术改进前每天施工(10)a +米，技术改进后每天施工点6(10)5a +米， 依题意，得：乙工程队施工天数为3200a天， 甲工程队技术改造前施工天数为：15400180031010a a ⨯=++天， 技术改造后施工天数为：15400(1)30003610(10)5a a ⨯-=++天． 依题意，得：3200180030001010a a a =+++， 解得：20a =，经检验，20a =是原方程的解，且符合题意， 3200a ∴160=． 答：乙工程队平均每天施工20米，施工的天数为160天．【点睛】本题考查了一元一次方程的应用、列代数式以及分式方程的应用，解题的关键是：（1）找准等量关系，正确列出一元一次方程；（2）根据各数量之间的关系，用含a 的代数式表示出施工天数；找准等量关系，正确列出分式方程．25．在一次夏令营活动中，老师将一份行动计划藏在没有任何标记的点C 处，只告诉大家两个标志点A ，B 的坐标分别为（﹣3，1）、（﹣2，﹣3），以及点C 的坐标为（3，2）（单位：km ）．（1）请在图中建立直角坐标系并确定点C 的位置；（2）若同学们打算从点B 处直接赶往C 处，请用方位角和距离描述点C 相对于点B 的位置．【答案】（1）作图见解析；（2）52km.【分析】(1)、利用点A 和点B 的坐标得出原点所在的位置，建立平面直角坐标系，进而得出点C 的位置；(2)、利用所画的图形，根据勾股定理得出答案．【详解】解：（1）根据A （﹣3，1），B （﹣2，﹣3）画出直角坐标系，描出点C （3，2），如图所示；（2）2，所以点C 在点B 北偏东45°方向上，距离点B 的2 km 处．【点睛】本题主要考查的是平面直角坐标系的基础知识以及直角三角形的勾股定理，属于基础题型．根据点A 和点B 的坐标得出坐标原点的位置是解题的关键．八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．下列各数中为无理数的是（）A．18B．0.8C．8D．38【答案】C【分析】无理数就是无限循环小数，依据定义即可作出判断．【详解】A．18是有理数，不符合题意；B．0.8是有理数，不符合题意；C．8是无限不循环小数，是无理数，正确；D．38=2是整数，不符合题意；故选：C．【点睛】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，6，0.8080080008…（每两个8之间依次多1个0）等形式．2．4的平方根是（）A．±16 B．2±C．±2 D．2【答案】B【分析】先计算42=，再根据平方根的定义即可得到结论．【详解】解：∵42=，∴2的平方根是2±，故选：B．【点睛】本题考查平方根的定义，注意本题求的是4的平方根，即2的平方根．3．如图是人字型金属屋架的示意图，该屋架由BC、AC、BA、AD四段金属材料焊接而成，其中A、B、C、D四点均为焊接点，且AB=AC，D为BC的中点，假设焊接所需的四段金属材料已截好，并已标出BC段的中点D，那么，如果焊接工身边只有可检验直角的角尺，而又为了准确快速地焊接，他应该首先选取的两段金属材料及焊接点是（）A．AB和AD，点A B．AB和AC，点BC ．AC 和BC, 点CD ．AD 和BC ，点D【答案】D 【分析】根据全等三角形的判定定理SSS 推知△ABD ≌△ACD ，则∠ADB=∠ADC=90°．【详解】解：根据题意知，∵在△ABD 与△ACD 中，AB AC AD AD BD CD ⎧⎪⎨⎪⎩＝＝＝ ， ∴△ABD ≌△ACD （SSS ），∴∠ADB=∠ADC=90°，∴AD ⊥BC ，根据焊接工身边的工具，显然是AD 和BC 焊接点D ．故选：D ．【点睛】本题考查了全等三角形的应用．巧妙地借助两个三角形全等，寻找角与角间是数量关系．4．对于函数y=-3x+1，下列说法不正确的是（ ）A ．它的图象必经过点(1，-2)B ．它的图象经过第一、二、四象限C ．当x>13时，y>0 D ．它的图象与直线y=-3x 平行 【答案】C【分析】根据一次函数图象上点的坐标特征对A 进行判断；根据一次函数的性质对B 、D 进行判断；令y ＞0，得到x ＜13，则可对C 进行判断． 【详解】解：A.当x=1时，y=-2，正确；B.函数经过一、二、四象限，正确；C.令y ＞0，即-3x+1＞0，解得x ＜13， 错误； D.∵两个直线的斜率相等，∴图象与直线平行，正确．故答案为：C.【点睛】此题考查一次函数的性质，解题关键在于掌握k ＞0，y 随x 的增大而增大，函数从左到右上升；k ＜0，y 随x 的增大而减小，函数从左到右下降．由于y=kx+b 与y 轴交于（0，b ），当b ＞0时，（0，b ）在y 轴的正半轴上，直线与y 轴交于正半轴；当b ＜0时，（0，b ）在y 轴的负半轴，直线与y 轴交于负半轴． 5．直线y ＝k 1x+b 1（k 1＞0）与y ＝k 2x+b 2（k 2＜0）相交于点（﹣3，0），且两直线与y 轴围成的三角形面积为12那么b 2﹣b 1的值为（ ）A ．3B ．8C ．﹣6D ．﹣8【答案】D【分析】直线y＝k1x+b1与y轴交于B点，则B（0，b1），直线y＝k2x+b2与y轴交于C点，则C（0，b2），根据三角形面积公式即可得出结果．【详解】解：如图，直线y＝k1x+b1与y轴交于B点，则B（0，b1），直线y＝k2x+b2与y轴交于C点，则C（0，b2），∵△ABC的面积为12，∴12OA·（OB+OC）＝12，即12×3×（b1﹣b2）＝12，∴b1﹣b2＝8，∴b2﹣b1＝﹣8，故选：D．【点睛】本题考查了一次函数的应用，正确理解题意，能够画出简图是解题的关键．6124336）A．5到6之间B．6到7之间C．7到8之间D．8到9之间【答案】C33124336433=233．∵5336，∴7＜233+81243367和8之间．故选：C．【点睛】本题考查了估算无理数的大小，其常见的思维方法：用有理数逼近无理数，求无理数的近似值．7．如果分式33x-有意义，则x的取值范围是（）A．x＞3 B．x≠3C．x＜3 D．x＞0 【答案】B【分析】分式有意义的条件是分母不等于零，从而得到x﹣2≠1．【详解】∵分式33x-有意义，∴x﹣2≠1．解得：x≠2．故选：B【点睛】本题主要考查的是分式有意义的条件，掌握分式有意义时，分式的分母不为零是解题的关键．8．甲，乙两班举行电脑汉字输入速度比赛，参赛学生每分钟输入汉字的个数经统计计算后，结果如下。

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．已知正多边形的一个外角为36°，则该正多边形的边数为( ).A ．12B ．10C ．8D ．6【答案】B【分析】利用多边形的外角和是360°，正多边形的每个外角都是36°，即可求出答案．【详解】解：360°÷36°＝10，所以这个正多边形是正十边形．故选B ．【点睛】本题主要考查了多边形的外角和定理．是需要识记的内容．2．在△ABC 中，若∠A ＝80°，∠B ＝30°，则∠C 的度数是（ ）A ．70°B ．60°C ．80°D ．50° 【答案】A【分析】根据三角形的内角和定理，即可求出答案．【详解】解：∵∠A ＝80°，∠B ＝30°，∴180803070C ∠=︒-︒-︒=︒，故选：A ．【点睛】本题考查了三角形的内角和定理，解题的关键是掌握三角形的内角和等于180°． 3．在代数式2222123252,,,,,33423x x xy x x x x +-+中，分式共有( )． A ．2个B ．3个C ．4个D ．5个 【答案】B【分析】根据分式定义：如果A ，B 表示两个整式，并且B 中含有字母，那么式子A B叫做分式进行分析即可． 【详解】解：代数式21325,,42x x x x++是分式，共3个， 故选：B ．【点睛】此题主要考查了分式定义，关键是掌握分式的分母必须含有字母，而分子可以字母，也可以不含字母，亦即从形式上看是A B的形式，从本质上看分母必须含有字母． 4．如图，ABC ∆是直角三角形，90BAC ∠=︒，点D 、E 分别在BC 、AC 上，且AB AD AE ==．下列结论：①45EDC ∠=︒，②12EBD EAD ∠=∠， ③当DA DC =时，ABD ∆是等边三角形，④当22.5C ∠=︒时，BD DE =，其中正确结论的个数有（ ）A ．1个B ．2个C ．3个D ．4个【答案】D 【分析】①②构造辅助圆，利用圆周角定理解决问题即可；③想办法证明BD ＝AD 即可；④想办法证明∠BAD ＝45°即可解决问题．【详解】解：如图，由题意：AB AD AE ==，以A 为圆心AB 为半径，作⊙A ．∵1122EBD EAD BED BAD ∠=∠∠=∠，， ∴()11904522EDC EBD BED EAD BAD ∠=∠+∠=∠∠=⨯︒=︒＋ ，故①②正确， 当DA DC =时，∠DAC ＝∠C ，∵∠BAD ＋∠DAC ＝90°，∠ABD ＋∠C ＝90°，∴∠BAD ＝∠ABD ，∴BD ＝AD ，∵AB ＝AD ，∴AB ＝AD ＝BD ，∴△ABD 是等边三角形，故③正确，当22.5C ∠=︒时，∠ABD ＝∠ADB ＝67.5°，∴∠BAD ＝180°−2×67.5°＝45°，∴∠DAE ＝∠BAD ＝45°，∵AB ＝AE ，AD ＝AD ，∴△BAD ≌△EAD （SAS ），∴BD DE =，故④正确．故选：D ．【点睛】本题考查全等三角形的判定和性质，圆周角定理，等腰三角形的性质，等边三角形的判定和性质等知识，解题的关键是熟练掌握基本知识．5．已知：△ABC ≌△DCB ，若BC=10cm ，AB=6cm ，AC=7cm ，则CD 为（ ）A ．10cmB ．7cmC ．6cmD ．6cm 或7cm【答案】C【分析】全等图形中的对应边相等.【详解】根据△ABC ≌△DCB ，所以AB=CD,所以CD=6，所以答案选择C 项.【点睛】本题考查了全等，了解全等图形中对应边相等是解决本题的关键.6．立方根等于本身的数是（ ）A ．-1B ．0C ．±1D ．±1或0 【答案】D【分析】根据立方根的定义得到立方根等于本身的数．【详解】解：∵立方根是它本身有3个，分别是±1，1．故选：D ．【点睛】本题主要考查了立方根的性质．对于特殊的数字要记住，立方根是它本身有3个，分别是±1，1．立方根的性质：（1）正数的立方根是正数． （2）负数的立方根是负数．（3）1的立方根是1．7．如图，已知点A 的坐标为()2,2，点B 的坐标为()0,1-，点C 在直线y x =-上运动，当CA CB +最小时，点C 的坐标为（ ）A ．22,55⎛⎫- ⎪⎝⎭B ．()1,1-C ．22,55⎛⎫- ⎪⎝⎭D ．()1,1-【分析】连接AB ，与直线y x =-的交点就是点C ，此时CA CB +最小，先求出直线AB 的解析式，然后求出点C 的坐标即可【详解】解：根据题意，如图，连接AB ，与直线y x =-的交点就是点C ，则此时CA CB +最小，设点A 、B 所在的直线为y kx b =+，则221k b b +=⎧⎨=-⎩，解得：321k b ⎧=⎪⎨⎪=-⎩， ∴312y x =-， ∴312y x y x =-⎧⎪⎨=-⎪⎩，解得：2525x y ⎧=⎪⎪⎨⎪=-⎪⎩， ∴点C 的坐标为：22,55⎛⎫-⎪⎝⎭； 故选：A.【点睛】本题考查了一次函数的图形和性质，以及最短路径问题，解题的关键是正确确定点C 的位置，求出直线AB 的解析式，进而求出点C.8．若等腰三角形的顶角为80，则它的一个底角度数为( )A ．20B ．50C ．80D ．100 【答案】B【分析】由已知顶角为80°，根据等腰三角形的两底角相等的性质及三角形内角和定理，即可求出它的一个底角的值．【详解】解：∵等腰三角形的顶角为80°，∴它的一个底角为（180°-80°）÷2=50°．【点睛】本题主要考查了等腰三角形的性质及三角形内角和定理．通过三角形内角和，列出方程求解是正确解答本题的关键．9．若x= -1．则下列分式值为0的是（ ）A ．11x - B ．+1x x C ．21x x - D ．1x x- 【答案】C 【分析】将1x =-代入各项求值即可．【详解】A. 将1x =-代入原式，1111112x ==----，错误； B. 将1x =-代入原式，+1x x 无意义，错误； C. 将1x =-代入原式，()2211101x x ---==-，正确； D. 将1x =-代入原式，11121x x ---==-，错误； 故答案为：C ．【点睛】 本题考查了分式的运算，掌握分式的性质以及运算法则是解题的关键．10．满足下列条件的ABC ∆中，不是直角三角形的是( )A ．222b c a =-B ．::3:4:5a b c =C ．C A B ∠=∠-∠D ．::3:4:5A B C ∠∠∠=【答案】D【分析】根据勾股定理的逆定理可判断A 、B 两项，根据三角形的内角和定理可判断C 、D 两项，进而可得答案．【详解】解：A 、∵222b c a =-，∴222+=a b c ，∴∠C=90°，所以△ABC 是直角三角形，本选项不符合题意；B 、由::3:4:5a b c =可设3,4,5a k b k c k ===，∵()()()222222234255a b k k k k c +=+===，∴∠C=90°，所以△ABC 是直角三角形，本选项不符合题意；C 、∵C A B ∠=∠-∠，∴B C A ∠+∠=∠，∵∠A+∠B+∠C=180°，∴2∠A=180°，∴∠A=90°，所以△ABC 是直角三角形，本选项不符合题意；D 、由::3:4:5A B C ∠∠∠=可设3,4,5A k B k C k ∠=∠=∠=，∵∠A+∠B+∠C=180°，∴345k k k ++=180°，解得：15k =︒，∴45,60,75A B C ∠=︒∠=︒∠=︒，所以△ABC 不是直角三角形，本选项符合题意．故选：D ．【点睛】本题考查了勾股定理的逆定理和三角形的内角和定理，属于基础题型，熟练掌握勾股定理的逆定理是解题的关键．二、填空题11．点P 在第四象限内，点P 到x 轴的距离是1，到y 轴的距离是2，那么点P 的坐标为_______．【答案】 (2,−1).【解析】根据点P 在第四象限可知其横坐标为正，纵坐标为负即可确定P 点坐标．【详解】∵点P 在第四象限，∴其横、纵坐标分别为正数、负数，又∵点P 到x 轴的距离为1，到y 轴的距离为2，∴点P 的横坐标为2，纵坐标为−1.故点P 的坐标为(2,−1).故答案为：(2,−1).【点睛】此题考查点的坐标，解题关键在于掌握第四象限内点的坐标特征.12．如图，已知Rt ABC ∆的三边长分别为6、8、10，分别以它们的三边作为直径向外作三个半圆，则图中阴影部分的面积为_______．【答案】24 【分析】根据图形关系可得阴影部分面积为：22261811101682222222πππ⎛⎫⎛⎫⎛⎫⨯+⨯+⨯⨯-⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 【详解】因为已知Rt ABC ∆的三边长分别为6、8、10所以62+82=102由已知可得：图中阴影部分的面积为 22261811101682222222πππ⎛⎫⎛⎫⎛⎫⨯+⨯+⨯⨯-⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=24故答案为：24【点睛】考核知识点：直角三角形性质.弄清图形的面积和差关系是关键.13．甲乙两人进行飞镖比赛，每人各投5次，所得平均环数相等，其中甲所得环数的方差为15，乙所得环数如下：0，1，5，9，10，那么成绩较稳定的是_____(填“甲”或“乙”)．【答案】甲． 【解析】乙所得环数的平均数为：0159105++++=5， S 2=1n[21x x （－）+22x x （－）+23x x （－）+…+2n x x （－）] =15[205（－）+215（－）+255（－）+295（－）+2105（－）] =16.4，甲的方差＜乙的方差，所以甲较稳定.故答案为甲.点睛：要比较成绩稳定即比方差大小，方差越大，越不稳定；方差越小，越稳定.14．如图，△ABC ≌△ADE ，∠B=80°，∠C=30°，则∠E 的度数为________．【答案】30°【分析】根据△ABC ≌△ADE 得到∠E=∠C 即可.【详解】解：∵△ABC ≌△ADE ，∴∠C=∠E ，∵∠C=30°，∴∠E=30°. 故答案为：30°. 【点睛】本题考查了全等三角形的性质，全等三角形的对应角相等，对应边相等，难度不大.15．如图，已知//AE BD ，1130∠=︒，230∠=︒，则C ∠=__________．【答案】20°【分析】由//AE BD ，得∠AEC =230∠=︒，结合1130∠=︒，即可得到答案．【详解】∵//AE BD ，230∠=︒，∴∠AEC =230∠=︒，∵∠1+∠AEC+∠C=180°，∴∠C=180°-130°-30°=20°．故答案是：20°．【点睛】本题主要考查平行线的性质定理和三角形内角和定理，掌握平行线的性质定理和三角形内角和定理是解题的关键．16．一次函数1y kx b =+与2y x a =+的图象如图，则下列结论：①k 0<；②0a >；③当3x <时，12y y <，正确的是__________.【答案】①【分析】根据一次函数的图象和性质即可判断出k 和a 的取值范围，再根据图象的交点横坐标结合函数图象即可得到③的结论．【详解】解：①y 1=kx+b 的图象可知y 随x 的增大而减小，所以k ＜0，故此选项正确；②y 2=x+a 的图象与y 轴相交于负半轴，则a ＜0，故此选项错误；③由于两函数图象交点横坐标为3，则当x ＜3时，y 1＞y 2，故此选项错误．故答案为：①．【点睛】本题考查一次函数的图象和性质，一次函数与不等式的关系．对于一次函数y=kx+b ，k 决定函数的增减性，b 决定函数与y 轴的交点．两个函数比较大小，谁的图象在上面谁的值就大．17．中国高铁再创新高，2019年全国高铁总里程将突破35000公里，约占世界高铁总里程的23，稳居世界第一，将35000用科学计数法表示为__________．【答案】3.5×1． 【分析】科学记数法的表示形式为a ×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．【详解】35000＝3.5×1．故答案为：3.5×1．【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a ×10n 的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．三、解答题18．解不等式组：215(1)2723x x x x +≥-⎧⎪-⎨<-⎪⎩，并把解集表示在数轴上． 【答案】12x -<≤，数轴见解析【分析】根据不等式的性质求出各不等式的解集，根据找不等式组解集的规律找出即可．【详解】解：215(1)2723x x x x +≥-⎧⎪⎨-<-⎪⎩①② 解不等式①得：x ≤2，解不等式②得：x ＞-1，解集在数轴上表示为：∴原不等式组的解集为：-1＜x ≤2．【点睛】本题主要考查了解一元一次不等式组，在数轴上表示不等式的解集等知识点的理解和掌握，能根据不等式的解集找出不等式组的解集是解此题的关键．19．某超市用5000元购进某种干果后进行销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，购进干果的数量是第一次的1.5倍，但这次每干克的进价比第一次的进价提高了5元．（1）该种干果第一次的进价是每千克多少元？（2）如果超市按每千克40元的价格销售，当大部分干果售出后，余下的100千克按售价的6折售完，超市销售这种干果共盈利多少元？【答案】（1）25元；（2）超市销售这种干果共盈利4400元【分析】（1）分别设出该种干果第一次和第二次的进价，根据“第二次购进干果的数量是第一次的1.5倍”列出方程，解方程即可得出答案；（2）先求出两次购进干锅的数量，再根据利润公式计算利润即可得出答案.【详解】解：（1）设该种干果第一次的进价是每千克x 元，则第二次的进价是每千克(5)x +元. 根据题意得500090001.55x x ⨯=+， 解得25x =.经检验，25x =是所列方程的解.答：该种干果第一次的进价是每千克25元（2）第一次购进该种干果的数量是500025200÷=（千克），再次购进该干果的数量是200 1.5300⨯=（千克），获得的利润为(200300100)+-40100400.6⨯+⨯⨯500090004400--=（元）.答：超市销售这种干果共盈利4400元.【点睛】本题考查的是分式方程在实际生活中的应用，难度适中，需要熟练掌握销售利润相关的计算公式. 20．如图，在ABCD 中，对角线AC ，BD 交于点O ，E 是AD 上任意一点，连接EO 并延长，交BC 于点F ，连接AF ，CE ．（1）求证：四边形AFCE 是平行四边形；（2）若60DAC ∠=，15ADB ∠=，6AC =．求出ABCD 的边BC 上的高h 的值．【答案】 (1)详见解析;(2)33【分析】(1)根据平行四边形性质得BO=DO,AO=CO,AD ∥BC,构造条件证△AOE ≌△COF （ASA ）,证CF=AE,CF ∥AE,即可;(2)作AH ⊥BC,根据直角三角形性质得CH=116322AC =⨯=,再运用勾股定理可得. 【详解】证明:（1）∵在▱ABCD 中,AC,BD 交于点O,∴BO=DO,AO=CO,AD ∥BC,∴∠OAE=∠OCF,在△AOE 和△COF 中OAE OCF AO COAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AOE ≌△COF （ASA ）,∴CF=AE,∵CF ∥AE,∴四边形AFCE 是平行四边形.(2)作AH ⊥BC,因为四边形ABCD 是平行四边形,所以AD ∥BC,所以∠DAH=∠AHC=90°,因为60DAC ∠=,所以∠CAH=30°,所以CH=116322AC =⨯= 所以AH=22226333AC CH -=-=所以ABCD 的边BC 上的高h 的值是33.【点睛】考核知识点:勾股定理,平行四边形性质和判定.熟练运用平行四边形性质和勾股定理是关键.21．某城市为创建国家卫生城市，需要购买甲、乙两种类型的分类垃圾桶（如图所示），据调查该城市的A 、B 、C 三个社区积极响应号并购买，具体购买的数和总价如表所示． 社区甲型垃圾桶 乙型垃圾桶 总价 A10 8 3320 B5 9 2860 C a b 2820（1）运用本学期所学知识，列二元一次方程组求甲型垃圾桶、乙型垃圾桶的单价每套分别是多少元？ （2）按要求各个社区两种类型的垃圾桶都要有，则a ＝ ．【答案】（1）甲型垃圾桶的单价每套为140元，乙型垃圾桶的单价每套为240元；（2）3或1．【分析】（1）设甲型垃圾桶的单价为x 元，乙型垃圾桶的单价每套为y 元，根据图表中的甲型、乙型垃圾桶的数量和它们的总价列出方程组即可解答；（2）根据图表中的数据列出关于a\b 的二元一次方程，结合a 、b 的取值范围求整数解即可．【详解】（1）设甲型垃圾桶的单价每套为x 元，乙型垃圾桶的单价每套为y 元，根据题意，得 1083320592860x y x y +=⎧⎨+=⎩ 解得140240x y =⎧⎨=⎩答：甲型垃圾桶的单价每套为140元，乙型垃圾桶的单价每套为240元；（2）由题意，得140a+240b ＝2820整理得，7a+12b ＝141因为a 、b 都是整数，所以310a b =⎧⎨=⎩或153a b =⎧⎨=⎩答：a 的值为3或1．故答案为3或1．【点睛】本题考查了二元一次方程组的实际应用，掌握解二元一次方程组的方法是解题的关键．22．如图，AD 为ABC ∆的角平分线，DE AB ⊥于点E ，DF AC ⊥于点F ，连接EF 交AD 于点O ，=60BAC ∠︒．探究：判断AEF ∆的形状，并说明理由；发现：DO 与AD 之间有怎样的数量关系，请直接写出你的结论，不必说明理由．【答案】探究：△AEF是等边三角形，理由见解析；发现：DO=14 AD【分析】（1）根据角平分线的性质得到DE=DF，证明Rt△AED≌Rt△AFD，根据全等三角形的性质得到AE=AF，根据有一个角为60°的等腰三角形是等边三角形即可得出结论；（2）根据等边三角形的性质、30°角所对直角边等于斜边的一半计算即可．【详解】探究：△AEF是等边三角形．理由如下：∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，∴DE=DF，∠AED=∠AFD=90°．在Rt△AED和Rt△AFD中，∵DE DF AD AD=⎧⎨=⎩，∴Rt△AED≌Rt△AFD(HL)，∴AE=AF．∵∠BAC=60°，∴△AEF是等边三角形．发现：DO=14AD．理由如下：∵AD为△ABC的角平分线，∠BAC=60°，∴∠EAD=30°，∴DE=12 AD．∵△AEF是等边三角形，AD为△ABC的角平分线，∴∠AEF=60°，AD⊥EF．∵DE⊥AB，∴∠DEA=90°，∴∠DEO=30°，∴OD=12 DE，∴DO=14 AD．【点睛】本题考查了等边三角形的判定和性质、30°角所对直角边等于斜边的一半的性质，掌握30°角所对直角边等于斜边的一半是解答本题的关键．23．某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整.收集数据从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下：甲 78 86 74 81 75 76 87 70 75 9075 79 81 70 74 80 86 69 83 77乙 93 73 88 81 72 81 94 83 77 8380 81 70 81 73 78 82 80 70 40整理、描述数据按如下分数段整理、描述这两组样本数据：（说明：成绩80分及以上为生产技能优秀，70--79分为生产技能良好，60--69分为生产技能合格，60分以下为生产技能不合格）分析数据两组样本数据的平均数、中位数、众数如下表所示：得出结论： a .估计乙部门生产技能优秀的员工人数为____________；b .可以推断出_____________部门员工的生产技能水平较高，理由为_____________.（至少从两个不同的角度说明推断的合理性）【答案】a.240，b.乙；理由见解析.【解析】试题分析：（1）由表可知乙部门样本的优秀率为：12100%60%40⨯= ，则整个乙部门的优秀率也是60%，因此即可求解；（2）观察图表可得出结论.试题解析：如图：整理、描述数据按如下分数段整理 按如下分数段整理数据：成绩x 人数部门4049x≤≤5059x≤≤6069x≤≤7079x≤≤8089x≤≤90100x≤≤甲0 0 1 11 7 1乙 1 0 0 7 10 2a.估计乙部门生产技能优秀的员工人数为400×40=240（人）；b.答案不唯一，言之有理即可．可以推断出甲部门员工的生产技能水平较高，理由如下：①甲部门生产技能测试中，测试成绩的平均数较高，表示甲部门生产技能水平较高；②甲部门生产技能测试中，没有生产技能不合格的员工．可以推断出乙部门员工的生产技能水平较高，理由如下：①乙部门生产技能测试中，测试成绩的中位数较高，表示乙部门生产技能水平优秀的员工较多；②乙部门生产技能测试中，测试成绩的众数较高，表示乙部门生产技能水平较高．24．如图，已知点B在线段AE上，分别以AB，BE为边长在AE上方作正方形ABCD，BEFG，点P 为AB中点，连接CF，CP，FP，设AB a，BE b=．（1）若2a b=，请判断CPF的形状，并说明理由；（2）请用含a，b的式子表示CPF的面积；（3）若CPF的面积为6，6AE=，求AB的长．【答案】（1）等腰三角形，理由见解析；（2）21144a ab+；（3）4【分析】(1)利用题目所给条件，通过SAS证明EFP△≌BPC△，可得出结果；(2)根据图像可知，BCPF EFPABC CD ADCPFES S S S S=+--正方形梯形△△梯形，分别求出各部分面积可求出最终结果；(3) 若CPF 的面积为6，则211644a ab +=，因式分解后可解出最终结果． 【详解】（1）CPF 为等腰三角形．∵点P 为AB 的中点， ∴1122BP AB a ==， ∵BE EF b ==，2a b =， ∴BP EF =，12EP b a a BC =+==， ∵90E CBP ∠=∠=︒，∴EFP △≌BPC △，∴PF PC =， ∴CPF 为等腰三角形．（2）∵211112242EFP S b b a ab b ⎛⎫=+=+ ⎪⎝⎭△， 113224ADCP S a a a a 2⎛⎫=+= ⎪⎝⎭梯形， ()2111222BCFE S b a b ab b =+=+梯形， ∴B CPF EFP ABC C D ADCP FE S S S S S =+--正方形梯形△△梯形2222211113112242444a ab b ab b a a ab ⎛⎫=++-+-=+ ⎪⎝⎭． （3）∵6CPF S =△， ∴211644a ab +=， ∴()164a a b +=， ∵6a b AE +==， ∴1664a ⨯=， ∴4a =，即4AB =．【点睛】本题主要考查三角形综合问题，涉及证明三角形全等，三角形面积的求解，需要熟练掌握全等三角形以及多边形中三角形面积求解的方法，利用数形结合的思想是解题的关键．25．某校在八年级开展环保知识问卷调查活动，问卷一共10道题，每题10分，八年级（三）班的问卷得分情况统计图如下图所示：（1）扇形统计图中，a 的值为 ________．（2）根据以上统计图中的信息，求这问卷得分的众数和中位数分别是多少分？（3）已知该校八年级共有学生600人，请估计问卷得分在80分以上（含80分）的学生约有多少人？【答案】（1）14%；（2）90分，85分；（3）420【分析】（1）利用60分的百分比a 等于1减去其他部分的百分比即可得到；（2）先计算得出调查的总人数，找到这组数据从低到高排列的第25、26个得分，即可即可得到中位数； （3）用600乘以80分及以上的百分比即可得到答案.【详解】（1）120%30%20%16%14%a ＝﹣﹣﹣﹣＝；（2）①问卷得分的众数是90分，②问卷调查的总人数为： 714%50÷=（人），第25、26个人的得分分别为80分、90分， 问卷得分的中位数是8090852+=（分）； （3）600(20%30%20%)⨯++=6000.7420⨯=（人）答：估计问卷得分在80分以上（含80分）的学生约有420人.【点睛】此题考查数据的整理计算，能正确计算部分的百分比，求数据的总数，中位数，利用样本的数据计算总体的对应数据.八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，点A，B为定点，定直线l//AB，P是l上一动点．点M，N分别为PA，PB的中点，对于下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是（）A．②③B．②⑤C．①③④D．④⑤【答案】B【解析】试题分析：①、MN=12AB，所以MN的长度不变；②、周长C△PAB=12（AB+PA+PB），变化；③、面积S△PMN=14S△PAB=14×12AB·h，其中h为直线l与AB之间的距离，不变;④、直线NM与AB之间的距离等于直线l与AB之间的距离的一半，所以不变；⑤、画出几个具体位置，观察图形，可知∠APB的大小在变化．故选B考点：动点问题，平行线间的距离处处相等，三角形的中位线2．如图，足球图片正中的黑色正五边形的外角和是（）A．180B．360C．540D．720【答案】B【分析】根据多边形的外角和，求出答案即可．【详解】解：∵图形是五边形，∴外角和为：360°．故选：B．【点睛】本题考查了多边形的内角和外角，能熟记多边形的外角和公式是解此题的关键3．已知四边形ABCD中，AC与BD交于点O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下四种说法：①如果再加上条件“BC＝AD”，那么四边形ABCD一定是平行四边形；②如果再加上条件“∠BAD＝∠BCD”，那么四边形ABCD一定是平行四边形；③如果再加上条件“OA＝OC”，那么四边形ABCD一定是平行四边形；④如果再加上条件“∠DBA＝∠CAB”，那么四边形ABCD一定是平行四边形．其中正确的说法是（）A．①②B．①③④C．②③D．②③④【答案】C【解析】其中正确的说法是②、③．因为再加上条件“∠BAD=∠BCD”，即可求得另一组对角相等，那么四边形ABCD一定是平行四边形；如果再加上条件“AO=OC”，即可证明△AOB≌△COD，所以，AB=DC，那么四边形ABCD一定是平行四边形．故正确的说法②、③．故选C.4．如图，△ABC中，AB＝AC，∠A＝36°，BD是AC边上的高，则∠DBC的度数是（）A．18°B．24°C．30°D．36°【答案】A【解析】试题分析：先根据等腰三角形的性质求得∠C的度数，再根据三角形的内角和定理求解即可. ∵AB＝AC，∠A＝36°∴∠C＝72°∵BD是AC边上的高∴∠DBC＝180°-90°-72°＝18°故选A.考点：等腰三角形的性质，三角形的内角和定理点评：三角形的内角和定理是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.5．如图，Rt△ABC中，∠C＝90°，∠B＝30°，分别以点A和点B为圆心，大于12AB的长为半径作弧，两弧相交于M、N两点，作直线MN，交BC于点D，连接AD，若BD＝6，则CD的长为（）A．2 B．4 C．6 D．3【答案】D【分析】由作图过程可得DN是AB的垂直平分线，AD＝BD＝6，再根据直角三角形10度角所对直角边等于斜边一半即可求解．【详解】由作图过程可知：DN是AB的垂直平分线，∴AD＝BD＝6∵∠B＝10°∴∠DAB＝10°∴∠C＝90°，∴∠CAB＝60°∴∠CAD＝10°∴CD＝12AD＝1．故选：D．【点睛】本题考查了作图-基本作图、线段垂直平分线的性质、含10度角的直角三角形，解决本题的关键是掌握线段垂直平分线的性质．6．《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”．意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等．两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）．问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（）A．11910813x yy x x y=⎧⎨+-+=⎩（）（）B ．10891311y x x yx y+=+⎧⎨+=⎩C ．91181013x y x y y x （）（）=⎧⎨+-+=⎩D ．91110813x yy x x y =⎧⎨+-+=⎩（）（）【答案】D【分析】根据题意可得等量关系：①9枚黄金的重量=11枚白银的重量；②（10枚白银的重量+1枚黄金的重量）-（1枚白银的重量+8枚黄金的重量）=13两，根据等量关系列出方程组即可． 【详解】设每枚黄金重x 两，每枚白银重y 两， 由题意得：91110813x y y x x y =⎧⎨+-+=⎩（）（），故选D ． 【点睛】此题主要考查了由实际问题抽象出二元一次方程组，关键是正确理解题意，找出题目中的等量关系． 7．如果一个等腰三角形的两条边长分别为3和7，那么这个等腰三角形的周长为（ ） A ．13 B ．17 C ．13或17 D ．以上都不是【答案】B【解析】当3厘米是腰时，则3+3＜7，不能组成三角形，应舍去； 当7厘米是腰时，则三角形的周长是3+7×2=17（厘米）． 故选B ．8．下列从左边到右边的变形，属于因式分解的是（ ）． A ．()222a b a b -=- B ．()22121x x x x -+=-+C ．()22211x x x -+=- D ．()222x y x y -=-【答案】C【分析】根据因式分解的定义即可判断．【详解】因式分解是指把多项式化成几个单项式或多项式积的形式，A 、B 错误，C 正确． 而()()22:D x y x y x y -=+-，故D 不正确． 故选C ． 【点睛】此题主要考查因式分解的判断，解题的关键熟知因式分解的定义．9．顺次连接矩形各边中点得到的四边形是（ ） A ．平行四边形 B ．矩形C ．菱形D ．正方形【答案】C【分析】根据三角形的中位线定理，得新四边形各边都等于原四边形的对角线的一半，进而可得连接对角线相等的四边形各边中点得到的四边形是菱形． 【详解】解：如图，矩形ABCD 中，,AC BD ∴=,,,E F G H 分别为四边的中点，1//,,2EF BD EF BD ∴=1//,,2GH BD GH BD = 1,2FG AC = //,,EF GH EF GH ∴=∴ 四边形ABCD 是平行四边形，11,,,22AC BD EF BD FG AC === ,EF FG ∴=∴ 四边形EFGH 是菱形．故选C ． 【点睛】本题主要考查了矩形的性质、菱形的判定，以及三角形中位线定理，关键是掌握三角形的中位线定理及菱形的判定．10．等腰三角形的两边长为3，7，则其腰长为（ ） A ．6 B ．3或7C ．3D ．7【答案】D【分析】根据等腰三角形的定义、三角形的三边关系定理即可得． 【详解】由等腰三角形的定义得：其腰长为3或7， （1）当腰长为3时，这个等腰三角形的三边长为3,3,7，+<，不满足三角形的三边关系定理，此时337即其腰长不能为3；（2）当腰长为7时，这个等腰三角形的三边长为3,7,7，+>，满足三角形的三边关系定理；此时377综上，这个等腰三角形的腰长为7，故选：D．【点睛】本题考查了等腰三角形的定义、三角形的三边关系定理，熟练掌握等腰三角形的定义是解题关键．二、填空题11．市运会举行射击比赛，射击队从甲、乙、丙、丁四人中选拔一人参赛．在选拔赛中，每人射击10次，计算他们10次成绩（单位：环）的平均数及方差如下表．根据表中提供的信息，你认为最合适的人选是_____，理由是_________．【答案】丁；综合平均数和方差两个方面说明丁成绩既高又稳定【分析】根据甲，乙，丙，丁四个人中甲和丁的平均数最大且相等，甲，乙，丙，丁四个人中丁的方差最小，说明丁的成绩最稳定，得到丁是最佳人选．【详解】∵甲，乙，丙，丁四个人中甲和丁的平均数最大且相等，甲，乙，丙，丁四个人中丁的方差最小，说明丁的成绩最稳定，∴综合平均数和方差两个方面说明丁成绩既高又稳定，∴丁是最佳人选．故答案为：丁．【点睛】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．12．如果把人的头顶和脚底分别看作一个点，把地球赤道看作一个圆，那么身高2m的小赵沿着赤道环行一周，他的头顶比脚底多行_____m．【答案】4π．【分析】根据圆的周长公式，分别求出赤道的周长和人头沿着赤道环形一周的周长即可得到答案． 【详解】解：设地球的半径是R ，则人头沿着赤道环形时，人头经过的圆的半径是（R+2）m ， ∴赤道的周长是2πRm ，人头沿着赤道环形一周的周长是2π（R+2）m ， ∴他的头顶比脚底多行2π（R+2）﹣2πR ＝4πm ， 故答案为：4π. 【点睛】本题主要考查了圆的周长的计算方法，难度不大，理解题意是关键．13．用12根火柴棒（等长）拼成一个三角形，火柴棒不允许剩余、重叠和折断，则能摆出不同的三角形的个数是 _______个． 【答案】3【详解】设摆出的三角形的的三边有两边是x 根，y 根， 则第三边是12-x-y 根，根据三角形的三边关系定理得出：12,12,x y x y x y y +----所以6,6,6xy x y +又因为x ，y 是整数，所以同时满足以上三式的x ，y 的值的是;2,5;3,4;3,5;4,4;4,5;5,5. 则第三边对应的值是5,5,4,4,3,2；因而三边的值可能是：2,5,5或者3,4,5或者4,4,4共有三种情况， 则能摆出的不同三角形的个数是3 【点睛】本题属于对三角形三边关系的基本性质和大小的考查，需要考生对三角形三边关系熟练运用14．在某中学举行的演讲比赛中，八年级5名参赛选手的成绩如下表所示，你根据表中提供的数据，计算出这5名选手成绩的方差_______．【答案】6.8 ；【分析】首先根据五名选手的平均成绩求得3号选手的成绩，然后利用方差公式直接计算即可． 【详解】解：观察表格知道5名选手的平均成绩为91分， ∴3号选手的成绩为：91×5-90-95-89-88=93（分）， ∴方差为：15[（90-91）2+（95-91）2+（93-91）2+（89-91）2+（88-91）2]=6.8， 故答案为：6.8. 【点睛】。