六年级数学-人教版-分数乘法-培优-讲义

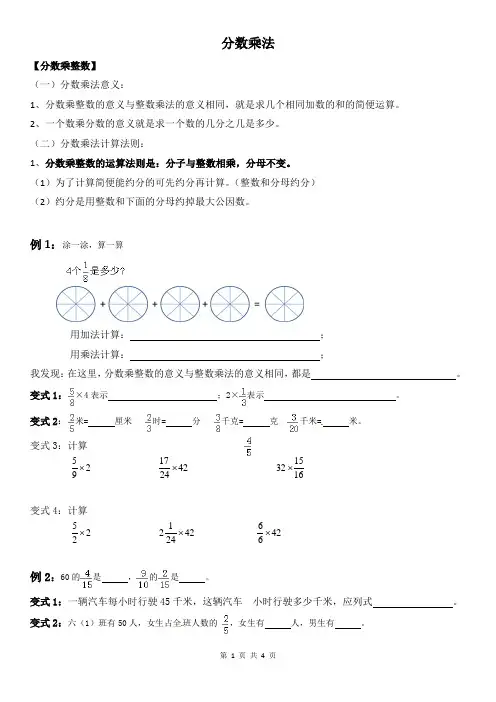
分数乘法【分数乘整数】（一）分数乘法意义：1、分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

2、一个数乘分数的意义就是求一个数的几分之几是多少。

（二）分数乘法计算法则：1、分数乘整数的运算法则是：分子与整数相乘，分母不变。

（1）为了计算简便能约分的可先约分再计算。

（整数和分母约分）（2）约分是用整数和下面的分母约掉最大公因数。

例1：涂一涂，算一算用加法计算： ；用乘法计算： ；我发现：在这里，分数乘整数的意义与整数乘法的意义相同，都是 。

变式1：×4表示 ；2×表示 。

变式2：米= 厘米 时= 分 千克= 克千米= 米。

变式3：计算295⨯ 422417⨯ 161532⨯变式4：计算225⨯ 422412⨯ 4266⨯例2：60的是 ，的是 。

变式1：一辆汽车每小时行驶45千米，这辆汽车 小时行驶多少千米，应列式 。

变式2：六（1）班有50人，女生占全班人数的 ，女生有 人，男生有 。

变式3：用5千克棉花的和1千克铁的相比较，结果是（ ）。

A.5千克棉花的重B.1千克铁的重C.一样重D.无法比较变式4：全世界有桦数40种，我国的桦树的种类占其中的，我国有多少种桦树？分数乘分数】1、分数乘分数的运算法则是：用分子相乘的积做分子，分母相乘的积做分母。

（分子乘分子，分母乘分母）（1）如果分数乘法算式中含有带分数，要先把带分数化成假分数再计算。

（2）分数化简的方法是：分子、分母同时除以它们的最大公因数。

（3）在乘的过程中约分，是把分子、分母中，两个可以约分的数先划去，再分别在它们的上、下方写出约分后的数。

（约分后分子和分母必须不再含有公因数，这样计算后的结果才是最简单分数）。

（4）分数的基本性质：分子、分母同时乘或者除以一个相同的数（0除外），分数的大小不变。

2、积与因数的关系：一个数（0除外）乘大于1的数，积大于这个数。

a ×b=c,当b >1时，c>a 。

第1讲分数乘法一，整数、小数乘分数【知识梳理】1.分数乘分数的计算方法：用分子相乘的积作分子，用分母相乘的积作分母。

用字母表示为：b d b da c a c⨯⨯=⨯()0,0a c≠≠【注意】计算分数乘分数时，为了简便，可以先约分，再计算。

2.分数乘整数：求几个相同加数和的运算；分数乘分数的计算方法同样适用于分数乘整数，即先把整数化为分母是1的分数，再计算。

3.小数乘分数的计算方法：（1）把小数化成分数计算；（2）如果所乘分数能化成有限小数，也可以把分数化成小数计算；（3）小数和分母能约分的，先约分再计算比较简便。

例1.计算：（1）7384⨯；（2）7489⨯；（3）3475⨯；（4）314×718；例2.计算：（1）126×213；（2）292314⨯；（3）211135⨯；（4）533174⨯.例3.计算：（1）71339⨯；（2）51012⨯. (3)133×9；（4）2897⨯.例4.计算：422417⨯ 321615⨯ 659⨯ 1430⨯例5：某食堂原有煤212吨，烧去了85，还剩几分之几？剩下多少吨？例6.一块冰，每小时失去其质量的一半，8小时后的质量为kg 165，一开始这块冰的质量是多少千克？ 例7. 1. 判断题．（1）小数乘分数，可以把小数化成分数计算，但不可以把分数化成小数计算 （ ） （2）小数乘分数的意义就是求这个小数的几分之几是多少 （ ）2.用三种方法计算2.4×433.计算下面各题：__________ ____________________ ____________________ __________试一试： 1、分数乘以整数112×11＝ 92×27＝ 6017×8＝ 509×8＝ 187×3＝ 9825×7＝52×2500＝ 3×97＝ 127×6＝ 174×5＝ 545×6＝ 5027×2＝2、分数乘以分数85×154＝ 209×215＝ 56×35＝ 257×1415＝ 113×21＝2811×338＝ 3920×1513＝ 187×143＝ 165×158＝ 3925×3013＝3. 分数乘以小数 （1）把小数画成分数0.6 1.8 0.45 0.125 2.5（2）把分数化成小数43 57 83 21 41 87 52（3）计算0.8×43 57×1.5 83×2.4 2.6×21 3.5×75 0.45×530.625×154 8.8×225 0.56×7552×0.15 87×0.24 2.6×1310达标检测一、计算(直接写出得数)73× 65 = 95 × 43 = 258 × 245 = 107 × 143=87 × 73= 2120 × 83 = 209 × 154 = 145 × 2521=二、填空1、看图列式计算（ ）×（ ）=（ ）（ ）×（ ）=（）2、先涂色表示计算结果，再填空。

分数乘法解决问题学生姓名年级学科授课教师日期时段教学核心分数乘法解决问题课型培训辅导/课堂讲解教学目标(1)、理解分数乘法的意义.使学生掌握分数乘法的计算方法.并能运用这个方法能熟练、灵活地进行相关计算；和计算法则.倒数的认识.(2)、使学生能分辨清楚先乘后加减的运算顺序.并能熟练地应用乘法运算定律进行简便计算.(3)、引导学生准确地找到单位“1”.并能熟练地解答一步和二步的乘法应用题.重点难点重点：回顾和整理本单元的知识.牢记知识点.熟练计算和应用.难点：找准单位“1”.正确分析应用题的数量关系.课前引导1.上次学习的分数乘法的应用题都掌握了吗？2.今天我们将复习一下分数乘法的有关内容.你准备好了吗？知识导图课前检测1. ×5表示：（）. ×表示：（）.2. kg的是（）kg. m的是（）m.3.计算.×100＝（）×＝（）×＝（）4. （判断）1吨的和3吨的一样重.（）5. （判断）×＝×＝（）6. 一种正方形方砖的边长是米.它的周长是多少？面积是多少？导学一：分数乘法重点讲解 1：分数乘整数1.分数乘整数的意义与整数乘法的意义（）.都是求（）；2.分数乘整数.用分数的（）乘整数的积作分子.（）不变.例 1. 小新、爸爸和妈妈一起吃一个蛋糕.每人吃个.3人一共吃多少个？列式：列式：课堂练习1. 看图写算式.）.4. 一根包装带长米.6根这样的包装带长多少米？5. 小时＝（ ）分； 千米＝（ ）米6. 口算下面各题. ×2＝2＝＝重点讲解 2：一个数乘分数一个数乘几分之几.表示求这个数的几分之几是多少.例 1. 1桶水有12升.算式：12×3想：求3个12L.就是求12L 的（ ）倍是多少.桶是多少升？求： （ ）＋（ ）＋（ ）＝（ ）（ 2.）×（ ）＝（ ×4表示（ ）3.算式：12×想：求12L的一半.就是求12L的是多少.桶是多少升？算式：想：求12L 的是多少.课堂练习米.2根长多少？ 根长多少？ 根长多少？ 算式：（）算式：（）算式：（）2. 列出乘法算式.（只列式.不计算） ①80厘米的 是多少？ ② 的 是多少？ 算式：（）算式：（）重点讲解 3：分数乘分数分数乘分数.用分子相乘的积作分子.分母相乘的积作分母.能约分的先约分.例 1.李伯伯家有一块 公顷的地.（1） 种土豆的面积是多少公顷？求： 1. 一根木棍长×× ＝ × ＝× ＝×× ＝公顷的 是多少公顷？（2） 种玉米的面积是多少公顷？课堂练习1.×3表示：（）× 表 示：（）.2. 先涂色表示计算结果.再填空.3. 口算 ＝ ＝4. 一辆汽车每小时行90千米.从甲地到乙地行了 小时.甲乙两地相距多少千米？从乙地到丙地行了40分钟.乙、丙两地相距多少千米？重点讲解 4：一个数（0除外）乘大于1或小于的数一个数（0除外）乘大于1的数.积比原来的数（）；一个数（0除外）乘小于1的数（0除外）.积比原来的数（ ）.例1.课堂练习1. 在○ 里填上“＞”“＜”或“＝”.导学二：分数乘法应用题重点讲解 1：确定单位“1”（1）“的”字前面是单位“1”；（2）“是”、“占”、“相当于”、“比”的后面是单位“1”.例 1. 女生人数是男生的.把（）看作单位“1”.例 2. 一袋大米.吃了.把（）看作单位“1”. 例 3. 甲比乙多.把（）看作单位“1”.课堂练习1.男生人数是女生的.把（）看作单位“1”.2.一条路.修完了.是把（）看作单位“1”.3.铅笔数量比圆珠笔多.把（）看作单位“1”.重点讲解 2：求一个数的的几分之几是多少的应用题1.找分率句.写数量关系式；2．根据题目中的数量关系.按照：单位“1”×分率＝分率对应量.列出算式求出所要求的对应量.例 1. 两班各收集多少个？例 2. 某班有男生20人.女生人数是男生的.求女生有多少人?列式：课堂练习1.甲乙两地相距420千米.一辆汽车行驶了全程的.行驶了多少千米？2.一个果园占地20公顷.其中的种苹果树. 种梨树.苹果树和梨树各种了多少公顷？重点讲解 3：比单位“1”多（或少）几分之几的应用题例 1. 学校春季给学生做体检.量得小东的体重是36千克.小远的体重比小东轻.小远的体重是多少千克？小东的体重比小远多多少千克？课堂练习1.一件西服原价180元.现在的价格比原来降低了 .现在的价格是多少元？2.希望小学三年级有学生216人.四年级的人数比三年级多 .四年级有学生多少人？重点讲解 4：连续求一个数的的几分之几是多少的应用题例 1.3个同学跳绳.小明跳了120下.小红跳了多少下？课堂练习1.小军的爷爷今年65岁.爸爸的年龄是爷爷的.小军的年龄是爸爸的.小军今年多少岁？2.公牛有30头.母牛的头数相当于公牛的.小牛的头数相当于母牛的.小牛有多少头？重点讲解 5：分数应用题综合运用例 1. 小明看一本书.共240页.第一天看了这本书的.第二天看了这本书的.小明这两天共看了多少页？还剩几页未看？第三天.他从第几页开始看起？例 2. 一袋大米20千克.第一次吃去它的.第二次吃去它的千克.还剩多少千克？课堂练习1.一堆煤重40吨.第一天运走这堆煤的.第二天运走吨.两天一共运了多少吨煤？2.果园里有梨树40棵.（1）如果桃树的棵数是梨树的.那么桃树有多少棵？（2）如果桃树的棵数比梨树多.那么桃树有多少棵？（3）如果桃树的棵数比梨树少 .那么桃树有多少棵？（4）如果桃树的棵数比梨树少.那么桃树比梨树少多少棵？限时考场模拟1.2. 两根都是2米长的绳子.第一根截去它的.第二根截去米.比较两根绳子余下的部分.则（）A. 一样长B. 第一根长C. 第二根长D. 不能确定3. 一根绳子截成两根.一段占全长的.一段长米.比较这两根绳子.则（）A. 一样长B. 第一根长C. 第二根长D. 不能确定4. 把5米长的绳子平均分成6段.每段长（）米.每段占全长的.5.一根铁丝长米.截去.还剩下；截去米.还剩下（）米.6.修一条路.原计划投资56万元.实际比原计划节约投资 .修这条路实际比原计划节约投资多少万元？7.一块平行四边形的木板.高是米.底比高长 .这块木板的面积是多少平方米？8.修一条长400米的环形跑道.已经铺好了150米.再铺多少米就正好铺完了全长的？课后作业1. ＋＋＋ =（）×（）=（）2. 12个是（）；24的是（）.3. 的倒数是（）；（）和互为倒数.4. ×（）= ×（）=0.5×（）5.在○里填上＞、＜或=6.边长分米的正方形的周长是（）分米.7.六（1）班有50人.女生占全班人数的.女生有（）人.男生有（）.8.（判断）60的相当于80的.（）9.（判断）冰箱的数量相当于电视机的,冰箱的数量比电视机少.（）10.看图列式计算.11.某鞋店进来皮鞋600双.第一周卖出总数的.第二周卖出总数的.⑴两周一共卖出总数的几分之几？⑵两周一共卖出多少双？⑶还剩多少双？12.六年级同学给灾区的小朋友捐款.六一班捐了500元.六二班捐的是六一班的.六三班捐的是六二班的 .六三班捐款多少元？13.甲乙两个仓库.甲仓存粮30吨.如果从甲仓中取出放入乙仓.则两仓存粮数相等.两仓一共存粮多少千克？1.上次的课后作业完成了吗？还有什么不懂得吗？2.今天学习的内容是复习分数的乘法.你掌握了吗？3.回去记得完成课后练习.做到温故而知新.课前检测1.5个的和是多少；的是多少.2. .3.40. .4.对5.错6. （米）；（平方米）导学一重点讲解 1：分数乘整数例题1.解析:；课堂练习1. . .. ；2.4个的和是多少3.1. .；3. .4. 米解析:求6根同样长的包装就是求6个是多少.用乘法计算. （米）5.24；700解析: 把小时转换分钟.用乘法.×60=24（分）把千米转换米.用乘法. ×1000=700（米） 6. ,, ,重点讲解 2：一个数乘分数1.. 2. .； 例题1.3； ； 12×.课堂练习重点讲解 3：分数乘分数例题1. 公顷； 公顷解析: （1）求 公顷的 .就是把 公顷平均分成5份.取其中的1份.也就是把1公顷平均分成（2×5）份.取其中的1 份.即. （2）（公顷）课堂练习1.3个 的和是多少；的 是多少.2. ；解析:＝ ； × = 3. .. .. .4.75千米；60千米解析: （千米）； . （千米） 重点讲解 4：一个数（0除外）乘大于1或小于的数例题1. ； . . .解析:在分数乘法的时候需要把结果约成最简分数.课堂练习1.＜.＞.＝.＜.＞.＜导学二重点讲解 1：确定单位“1”例题1.男生的人数解析: “是”、“占”、“相当于”、“比”的后面是单位“1”.所以单位“1”是男生的人数.需要具体.2.一袋大米3.乙课堂练习1.女生的人数2.一条路3.圆珠笔数量重点讲解 2：求一个数的的几分之几是多少的应用题例题1.一班：60个；二班：72个解析:一班：180×=60（个）；二班：180×=72（个）2.课堂练习1.420×=300（千米）2.8公顷； 5公顷解析:苹果树：20×=8（公顷）；梨树：20×=5（公顷）重点讲解 3：比单位“1”多（或少）几分之几的应用题例题1.小远体重： 30（千克）；相差重量： 6（千克）解析:小远体重：36×=30（千克）；相差重量：36－30=6（千克）或36×=6（千克）课堂练习1.144元解析:比单位“1”少.用1- 表示.180×（1- ）=144（元）2.264（人）解析:比单位“1”多.用1+ 表示.216×（1+ ）=264（人）重点讲解 4：连续求一个数的的几分之几是多少的应用题例题1.50（下）解析:先求120的是多少.再求“120的”的是多少.最后用连乘的方法.120××=50（下）课堂练习1.12岁解析:先求65的是多少.再求“65的”的是多少.最后用连乘的方法.65××=12（岁）2.16（头）解析:先求30的是多少.再求“30的”的是多少.最后用连乘的方法.30××=16（头）重点讲解 5：分数应用题综合运用例题1.140（页）；100（页）；141（页）解析:两天共看页数240×=140（页）；还剩页数240－140=100（页）；第3天.从第141页开始看起140＋1=141（页）2.（千克）解析:20×－= （千克）课堂练习1. （吨）解析:40×＋= （吨）2.（1）40×=24（棵）；（2）40×=64（棵）；（3）40×=16（棵）；（4）40×=24（棵）限时考场模拟；2；29；571.2.C解析: 第一根剩下的：2×（1-）= 米；第二根剩下的：2- = 米3.C解析: 因为第一段占全长的.所以第二段段占全长的.4. ；5. ；解析: 1- = ；- =6.49（万元）解析:56×（1- ）=49（万元）7. （平方米）解析:底：×（1+ ）= 米；面积：×= （平方米）8.90（米）解析:400×-150=90（米）课后作业1. ；3；2.10；163. ；44. ；；0.65.＞；=；＜6.2解析: ×4=2（分米） 7.女生20人；男生： 30人解析: 女生：50×=20（人）；男生：50-20=30（人）8.对解析: 60×=24；80×=249.对10.160（米）；306（吨）解析:400×（1- ）=160（米）；168×（1+ ）=306（吨）11.（1）；（2）345双；（3）255双解析:（1）+= ；（2）600×（+ ）=345（双）；（3）600-345=255（双）12.450元解析:500×× =450（元）13.一共有54000千克.解析:甲仓库现在的存粮=乙仓库现在的存粮：30×（1- ）=27(吨).两个仓库的总数没变.所以一共有27×2=54（吨）.54吨=54000千克.。

第二讲：分数乘法（下）应用题专讲：在解这类问题时，通常将标准量设为单位1，即 单位1对应的量，分析题中的数量关系，找出“量”与“率”之间的对应关系。

通过找“关键句”，找单位“l ”，画线段图，列出相应的数量关系分析推理，使隐蔽的事件件明朗化，复杂的关系简单化，充分进行思维的发散，不局限于1某一种解题方法。

一、“量”与“率”的混淆校有杉树多少棵？练习1.六年级同学给灾区捐款。

六(1)班捐了500元，六(2)班捐的是六(1)班的54,六(3)班捐的是六(2)班的89，六( 3)班捐款多少元？练习2.学校举行跳绳比赛，李红每分钟跳168下，是陈亮的87。

王伟跳的是陈亮的32。

王伟每分钟跳了多少下？练习3.某家电商城运来1000台冰箱，第一天卖出41，第二天比第一天多卖出了51，两天一共卖出冰箱多少台？四、巧妙的统一单位:“1”【例4-1】.一条路长1200米，第一天修了全长的31：第二天修了第一天的43。

第一天修了多少米？第二天修了全长的几分之几？ 第二天修了多少米？51第二天看了余下的25 ，练习5.甲、乙、丙三辆卡车一起运一批肥料，要求一次运走。

甲车运了全部的31，乙车运了余下的85。

丙车运的占这批肥料的几分之几？五、常考易错题【例5-1】一辆自行车原价380元。

商场搞活动降价51，这辆自行车现价多少元？练习1：一件衣服原价是250元，搞活动便宜了41，这件衣服现价多少元？8151洒练习2.六(4)班有48人，预订《少年报》和《语文报》这两种刊物，每个人都至少订了其中的一种，已知有32的同学订了《少年报》，有43的同学订了《语文报》，两种刊物都订的同学有多少人？过关练习1. 丁丁的体重比豆豆轻83，豆豆的体重是42千克，丁丁的体重是多少千克？2.玉兔号月球车的长是150 cm ，宽是长的32，高是宽的1011。

玉兔号月球车的高是多少厘米？3.一本书共120页，天天第一天看了1，第二天看了总页数的1，第三天从哪一页看起？4. 5.了6.8.有419.某家电商城运来1000台冰箱，第一天卖出41，第二天比第一天多卖出了51，两天一共卖出冰箱多少台？附加题：甲、乙两车从A 、B 两地同时相对开出，经过8小时相遇。

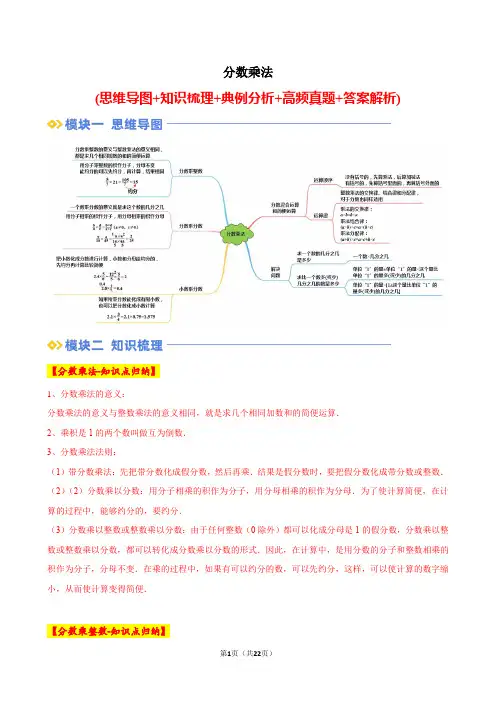
分数乘法(思维导图+知识梳理+典例分析+高频真题+答案解析)【分数乘法-知识点归纳】1、分数乘法的意义：分数乘法的意义与整数乘法的意义相同，就是求几个相同加数和的简便运算．2、乘积是1的两个数叫做互为倒数．3、分数乘法法则：（1）带分数乘法：先把带分数化成假分数，然后再乘．结果是假分数时，要把假分数化成带分数或整数．（2）（2）分数乘以分数：用分子相乘的积作为分子，用分母相乘的积作为分母．为了使计算简便，在计算的过程中，能够约分的，要约分．（3）分数乘以整数或整数乘以分数：由于任何整数（0除外）都可以化成分母是1的假分数，分数乘以整数或整数乘以分数，都可以转化成分数乘以分数的形式．因此，在计算中，是用分数的分子和整数相乘的积作为分子，分母不变．在乘的过程中，如果有可以约分的数，可以先约分，这样，可以使计算的数字缩小，从而使计算变得简便．【分数乘整数-知识点归纳】1、分子乘整数，可以求出一共有多少个这样的分数单位，而分数单位的个数其实就是分子乘整数的积，因此整数乘分子作分子。

求几个分数单位的和，分数单位不变，也就是分母不变。

2、分数乘整数的意义：分数乘整数，也是表示几个相同加数相加，与整数乘法的意义相同。

3、分数乘整数的计算方法：分数乘整数，用分子乘整数的积作分子，分母不变。

其实就是计算分数单位的个数。

【整数乘分数-知识点归纳】1、一个数乘分数的意义就是求一个数的几分之几是多少。

2、“一个数乘分数”指的是第二个因数必须是分数，不能是整数。

（第一个因数是什么都可以）3、方法总结；（1）、整数与分数相乘，用分数的分子与整数相乘，分母不变；（2）、计算时能约分的可以先约分再计算出结果。

【分数乘分数-知识点归纳】分数乘法的计算法则1、整数和分数相乘：整数和分子相乘的积作分子，分母不变。

2、分数和分数相乘：分子相乘的积作分子，分母相乘的积作分母。

【典例1】在“世界无烟日”健康知识竞赛中，小星答对了50道题，小铭答对的题数比小星少15。

第一单元：分数乘法一、分数乘法的概念分数乘法是指在乘法运算中，其中有一个或两个乘数是分数，通过乘法运算规则，计算出分数的乘积。

分数乘法涉及到分数的乘法运算法则，要求掌握分数相乘的方法和技巧。

二、分数乘法的基本原理1. 分数乘法的定义分数乘法是指两个分数相乘的运算。

示例：1/2 × 3/4 = 3/82. 分数乘法的规则分数相乘时，先将两个分数的分子和分母分别相乘，得到的结果即为分数的乘积。

示例：1/3 × 2/5 = (1×2) / (3×5) = 2/153. 分数乘法的方法分数相乘时，可以先化简分数，然后再进行乘法运算得到最简分数，也可以先进行分子相乘和分母相乘，再进行化简得到最简分数。

示例：4/6 × 5/3 = 20/18 = 10/9三、分数乘法的实际应用1. 分数乘法在日常生活中的运用分数乘法在日常生活中有着广泛的应用，比如在烹饪中需要按照食谱中的比例计算食材的用量，就需要进行分数乘法的运算来得到准确的结果。

示例：如果食谱中需要用1/2杯的面粉，而需要一倍的食谱，则需要1/2 × 1 = 1/2杯的面粉。

2. 分数乘法在数学问题中的应用在解决数学问题中，也会遇到分数相乘的情况，需要根据题目要求进行分数乘法的运算。

示例：假设一个长方形的长为2/3米，宽为1/4米，求其面积。

解：长方形的面积为长乘以宽，即(2/3) × (1/4) = 2/12 = 1/6平方米。

四、分数乘法中的注意事项1. 分数乘法的注意事项在进行分数乘法运算时，需要注意分子相乘、分母相乘的顺序，并且最终的结果需要进行化简，得到最简分数形式。

示例：5/6 × 2/3 = (5×2) / (6×3) = 10/18 = 5/92. 分数乘法中的常见错误在分数乘法中，常见的错误包括忽略化简、分子错乘、分母错乘等，需要学生在练习分数乘法时要注意避免这些错误。

第一讲：分数乘法（上）【知识点一】分数的基本性质1、分数乘整数的意义：求几个相同加数和的简便运算例：512×6，表示（ ），还可以表示（ ）。

注意： 求几个相同分数的和是多少 或 求一个分数的几倍是多少 就用 这个分数ד几”。

例：求3个112是多少，即可以列式（ ）。

练习：1、685⨯的意义是（ ），或（ ），得（ ）。

2、计算下列各题并说出计算方法。

9×718 = 347 ×28= 130×12 = 注意：分数的结果必须是最简分数。

2、分数乘分数的意义：是求一个数的几分之几是多少。

例如： 27 ×512 ，表示：27 的512是多少。

例 题：（说说计算方法及意义和图） 79×32= 32×23= 47×47= 3、（1）分数乘分数的计算方法也适用于小数乘分数，先把小数化成分数，再根据分数成分数的计算方法，然后计算。

例如：1417121715.0=⨯=⨯。

（2）分数乘分数，这里的分数也可以是带分数，计算时先把带分数化成假分数，再根据分数成分数的计算方法，然后计算。

例如：157513751312=⨯=⨯。

分数乘分数的简便算法也适用于分数连乘法。

例如281578315327158332=⨯⨯⨯⨯=⨯⨯。

例 题 34 ×815 ×310= 判断：12×14 和14×12的结果相同，意义也相同。

（ ） 4、单位换算。

412吨=（ ）千克 65小时=（ ）分 43分=（ ）秒 257平方米=（ ）平方分米 总结：5.常考填空题比20米多43是（ ）米 100米增加52是（ ）米 【知识点二】因数与积的大小关系1、比较大小，并说说你发现了什么规律 3231⨯○31 2152⨯○52 32×1○32 5×45○5 0×31○31总结：当一个因数大于1时，积大于另一个因数（0除外）；当一个因数小于1时，积小于另一个因数（0除外）；当一个因数小于1时，积就等于另一个因数。

人教版六年级上数学分数与乘法讲义专题一 知识体系一、分数乘法（一）分数乘法的意义：1、分数乘整数与整数乘法的意义相同。

都是求几个相同加数的和的简便运算。

例如： 98×5表示求5个98的和是多少？ 2、分数乘分数是求一个数的几分之几是多少。

例如： 98×43表示求98的43是多少？ （二）分数乘法的计算法则：1、分数与整数相乘：分子与整数相乘的积做分子，分母不变。

（整数和分母约分）2、分数与分数相乘：用分子相乘的积做分子，分母相乘的积做分母。

3、为了计算简便，能约分的要先约分，再计算。

注意：当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

（三）规律：（乘法中比较大小时） 一个数（0除外）乘大于1的数，积大于这个数。

一个数（0除外）乘小于1的数（0除外），积小于这个数。

一个数（0除外）乘1，积等于这个数。

（四）分数混合运算的运算顺序和整数的运算顺序相同。

（五）整数乘法的交换律、结合律和分配律，对于分数乘法也同样适用。

乘法交换律： a × b = b × a乘法结合律：( a × b )×c = a × ( b × c )乘法分配律：（ a + b ）×c = a c + b c二、分数乘法的解决问题（已知单位“1”的量（用乘法），求单位“1”的几分之几是多少）1、画线段图：（1）两个量的关系：画两条线段图；（2）部分和整体的关系：画一条线段图。

2、找单位“1”：在句中几分之几的前面；或“占”、“是”、“比”的后面3、求一个数的几倍：一个数×几倍；求一个数的几分之几是多少：一个数×几几。

4、已知一个数比另一个数多（或少）几分之几，求这个数是多少？（1）单位“1”的量±单位“1”的量×另一个数比单位“1”的量多（或少）的几分之几=另一个数（2）单位“1”的量×（1±另一个数比单位“1”的量多（或少）的几分之几）=另一个数5、写数量关系式技巧：（1）“的”相当于“×”“占”、“是”、“比”相当于“÷”（2）几分之几前是“的”：单位“1”的量×几分之几=几分之几对应量（3）几分之几前是“多或少”的意思：单位“1”的量×（1±几分之几）=几分之几对应量练一、看图列式计算。

人教版六年级分数乘法培优讲义内容一、知识回顾知识点1、分数基本概念：分数的读法与写法？分数单位？分数的分类？知识点2、分数的应用（求一个数是另一个数的几分之几或者多(少)几分之几)例1、小新家养鹅7只，养鸭10只,养鹅的只数是鸭的几分之几？例2、甲是4，乙是5，则甲比乙少几分之几?乙比甲大几分之几？总结归纳:对应练习：1、错误!的分数单位是( ），它有（）个这样的分数单位。

2、六年级参加一次植树活动中，其中六（1）班植树50棵，六（2）班植80棵，求六（2）班比六（1）班多几分之几?六(1）班比六（2）班少几分之几？知识点3、找最大公因数和最小公倍数方法例3、找一下几组数的最大公因数和最小公倍数。

(1） 8和9 （2）4和12 （3）8和12 （4）24和36总结归纳：二、分数乘法及简便运算1、分数乘法的意义2、分数大小的比较：3、分数乘法的计算法则：4、分数乘法简便运算的公式定律和整数乘法的简便运算是一样的，基本上有以下三个：乘法交换律：________________________乘法结合律：________________________乘法分配律：________________________做题时，我们要善于观察，仔细审题,发现数字与数字之间的关系，根据题意来选择适当的公式或方法，进行简便运算。

对应练习：（1） 12。

8－5。

6－4。

4 （2) 1.25×2。

5×32 （3)0。

9999×0.7+0.1111×2。

7三、典例分析例1、连乘—-乘法交换律的应用1）1474135⨯⨯ 2）56153⨯⨯ 3）266831413⨯⨯对应练习：(1) 计算：31556⨯⨯ (2) 计算:5117()678⨯⨯ （3)计算： 3792425875⨯⨯⨯总结归纳：例2、乘法分配律的应用 1)27)27498(⨯+ 2）4)41101(⨯+ 3）16)2143(⨯+对应练习:（1）计算：61(79)718⨯+⨯ （1）计算:15118()396⨯+- (1)计算:2322177()114346⨯⨯-总结归纳:例3、乘法分配律的逆运算1）213115121⨯+⨯ 2）61959565⨯+⨯ 3）751754⨯+⨯对应练习:(1）计算：3515413413⨯+⨯ （2)计算:599717241724⨯+⨯ （3）计算：4636+713713⨯⨯例4、添加因数“1" 1)759575⨯- 2）9216792⨯- 3）23233117233114+⨯+⨯总结：涉及定律：乘法分配律逆向运算基本方法：添加因数“1”，将其中一个数n 转化为1×n 的形式,将原式转化为两两之积相加减的形式，再提取公有因数，按乘法分配律逆向定律运算.例5、数字化加式或减式 1)16317⨯2）19718⨯ 3）316967⨯能力提升:1、先计算,再观察每道算式的特点，你能发现什么规律？(1) 1134-= 1134⨯ (2）1156- 1156⨯ 你能根据发现的规律再写出几组这样的算式吗?2、计算100991431321211⨯+⨯+⨯+⨯3、一根绳子长355米，第一次用去了全长的51，第二用去了51米,两次一共用了多少米？。