华师在线概率统计课后复习

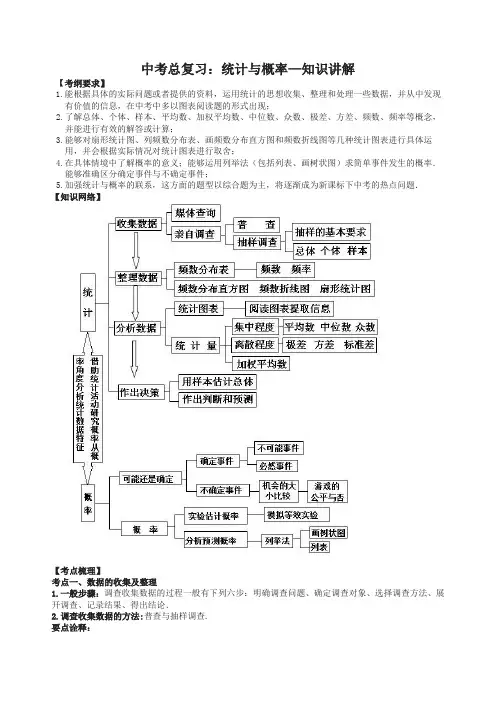
中考总复习：统计与概率—知识讲解【考纲要求】1.能根据具体的实际问题或者提供的资料，运用统计的思想收集、整理和处理一些数据，并从中发现有价值的信息，在中考中多以图表阅读题的形式出现；2.了解总体、个体、样本、平均数、加权平均数、中位数、众数、极差、方差、频数、频率等概念，并能进行有效的解答或计算；3.能够对扇形统计图、列频数分布表、画频数分布直方图和频数折线图等几种统计图表进行具体运用，并会根据实际情况对统计图表进行取舍；4.在具体情境中了解概率的意义；能够运用列举法（包括列表、画树状图）求简单事件发生的概率．能够准确区分确定事件与不确定事件；5.加强统计与概率的联系，这方面的题型以综合题为主，将逐渐成为新课标下中考的热点问题．【知识网络】【考点梳理】考点一、数据的收集及整理1.一般步骤：调查收集数据的过程一般有下列六步：明确调查问题、确定调查对象、选择调查方法、展开调查、记录结果、得出结论．2.调查收集数据的方法:普查与抽样调查.要点诠释：(1)通过调查总体的方式来收集数据的，抽样调查是通过调查样本方式来收集数据的．(2)一般地，当总体中个体数目较多，普查的工作量较大；受客观条件的限制，无法对所有个体进行普查；或调查具有破坏性时，不允许普查,这时我们往往会用抽样调查来体现估计总体的思想.(3)用抽签的办法决定哪些个体进入样本．统计学家们称这种理想的抽样方法为简单的随机抽样. 3.数据的统计:条形统计图、折线统计图、扇形统计图是三种最常用的统计图．要点诠释：这三种统计图各具特点：条形统计图可以直观地反映出数据的数量特征；折线统计图可以直观地反映出数据的数量变化规律；扇形统计图可以直观地反映出各部分数量在总量中所占的份额．考点二.数据的分析1.基本概念：总体：把所要考查的对象的全体叫做总体；个体：把组成总体的每一个考查对象叫做个体；样本：从总体中取出的一部分个体叫做总体的一个样本；样本容量：样本中包含的个体的个数叫做样本容量；频数：在记录实验数据时，每个对象出现的次数称为频数；频率：每个对象出现的次数与总次数的比值（或者百分比）称为频率；平均数：在一组数据中，用数据的总和除以数据的总个数就得到这组数据的平均数；中位数：将一组数据从小到大依次排列，位于正中间位置的数（或正中间两个数据的平均数）叫做这组数据的中位数；众数：在一组数据中，出现频数最多的数叫做这组数据的众数；极差：一组数据中的最大值减去最小值所得的差称为极差；方差：我们可以用“先平均，再求差，然后平方，最后再平均”得到的结果表示一组数据偏离平均值的情况，这个结果通常称为方差．计算方差的公式：设一组数据是，是这组数据的平均数。

单选题反映试题鉴别能力的指标是2.欲分析某高校男女毕业生对16 种职业的选择顺序是否存在显著关系，可采用的方法是A.和差相关法B.等级相关法C.点二列相关法D.x 2检验答案:B3.下列成绩中，那一项表明学生的成绩最好？A.Z=6. 7B.Z=-2C.Z=-9. 5D.Z:5答案:八4.分析测试內容与预测內容之间的一致性程度，这种测试效度的方法叫A.效标关联度B.内容效度C.结构效度D.预测效度答案:B5.欲抽样比较实验班与非实验班的考试成绩的差异性问题，应使用何种检验方法？A.t检验B.u检验C.x 2检验答案:A6.对数据资料计算综合指标，然后根裾综合指标值对教育客观事物给予评价。

这种方法称为A.描述性统计B.推断性统计C.定量统计D.相关统计答案:A7.某一学生在期末考试屮，语文成绩66,政治成绩74,语文的全班平均分和标准差分别为65和13;政泊的全班T 均分和标准差分别为75和10。

请问该生的语文与政治成绩哪一个好？A.语文B.政治D. 答度分度度度:A区信效难案C.一样好D.无法比较答案:A8.由于各种偶然W素的影响产生的，没宥固定倾向的误差称为A.系统误差B.抽样误差C.随机误差D.条件误差答案:C9.全卷的题目难度分配一般易：中：难之比为：A.4： 4： 2B.3： 6： 1C.5： 3： 2D.3： 5： 2答案:D10.欲分析外语成绩与学生的内外旳性格类型的关系，宜采用的方法是A.不只左相关法B.等级相关法C.点二列相关法D.x 2检验1.反映某一事物或现象水T的指标是A.绝对数B.相对数C.平均数D.标准差答案:C2.对信度的估计方法釆用A.T检验B.u检验C.相关法D.x 2检验答案:C3.教育统计学的研究对象为A.教育现象的本质与规律B.教育现象C.教育现象的数量方面D.教育评价的质暈方面答案:C4.反映试题鉴别能力的指标是A.区分度B.信度C.效度D.难度5.对同一对象不同时期的某项目的差异评价称为A.诊断评价B.横A评价C.安置评价D.纵向评价答案:D6.对提出问题事先安排好答案，让对方从中选择的问卷类型是A.限制式B.幵放式C.半限制式D.半开放式答案:A7.在已知芥个平均数的基础上再计算加权平均数的方法，称为A.等级平均数B.组距数列平均数C.总平均数D.评分平均数答案:C8.欲分析学生生源地类型与外语兴趣的关系，宜采用的方法是A.积差相关法B.等级相关法C.点二列相关法D.x 2检验答案:D9.随机抽取100名高一学生做两题奥数题，两题都通过的有55人，第一题通过而第二题为通过的有5人; 第二题通过而第一题为通过的有15 人：两题都未通过的有25人。

1.解 记A ={产品能通过检查}，B i ={产品中有i 个次品} (i =0,1,2)，则012()0.3,()0.4,()0.3P B P B P B ===，101099980121010100100(|)1,(|)0.9,(|)0.809C C P A B P A B P A B C C ====≈，由全概率公式，得所求概率为20()()(|)0.903i i i P A P B P A B ==≈∑。

我们要求的概率是332.0903.03.01)()()|()()()|(0000≈⨯===A PB P B A P A P AB P A B P2、4、0.02%95%0.21%0.02%95%(10.02%)(190%)⨯=≈⨯+-⨯-5、解 （1）244104(210)()(2)(2)3332(2)120.977210.9544X P X P -----<≤=<≤=Φ-Φ-=Φ-=⨯-= （2）由4444()()1()()0.9(1.28)3333X d d dP X d P ---->=>=-Φ=Φ≥=Φ 得4 1.283d-≥，故 0.16d ≤。

6、解（1）由概率密度的性质，有 2211()arctan 11A f x dx dx A dx A x A x x π∞∞∞∞-∞-∞-∞-∞=====++⎰⎰⎰，故 1A π=。

（2）由概率计算公式知，所求概率为11021111(01)arctan (1)44P X dx x x ππππ≤≤===⋅=+⎰； （3）随机变量函数X Y e =的分布函数为ln 20,0;()()1(ln ),0.(1)X yY y F y P e y P X y dx y x π-∞≤⎧⎪=<=⎨<=>⎪+⎩⎰ 故X Y e =的概率密度是20,0;()()1,0.(1(ln ))Y Y y f y F y y y y π≤⎧⎪'==⎨>⎪+⎩8、解 （1）由联合概率密度的性质，有(2)2001(,)2x y xy Cf x y dxdy Cedxdy C e dx e dy ∞∞∞∞∞∞-+---∞-∞====⎰⎰⎰⎰⎰⎰，故 2C =。

第六章 参数估计一、参数的点估计 1. 矩估计法矩估计法：用样本矩代替总体矩，从而得到未知参数的估计。

注： 1）总体均值()E X 的矩估计是样本均值X ；总体方差()D X 的矩估计是样本二阶中心矩211()ni i X X n =-∑；2）矩估计法简便；估计总体均值和总体方差时不必知道总体的分布. 3）矩估计法需要总体的原点矩存在. 2．最大似然估计法 （1）似然函数： 设12,,,n x x x 为取自含未知参数θ的总体X 的样本观测值.对离散随机变量总体X ，似然函数定义为1()(;)ni i i L P X x θθ===∏；这就是样本出现的（联合）概率.对密度为(;)f x θ的连续随机变量总体X ，似然函数定义为1()(;)ni i L f x θθ==∏。

（2）最大似然估计：选取参数θ的取值，使样本观测值12,,,n x x x 出现的概率最大,即使得似然函数()L θ达到最大值.求参数θ的最大似然估计值，就是求似然函数()L θ的最大值点。

在ln ()L θ可导时可以通过求解似然方程:ln ()0d L d θθ=得到. 3．衡量点估计量好坏的标准（1）无偏性称12ˆ(,,,)n X X X θθ=为未知参数θ的无偏估计，如果()E θθ=.注：1）用无偏估计12ˆ(,,,)n X X X θθ=代替未知参数θ不产生系统误差；2）样本均值11ni i X X n ==∑是总体均值()E X 的无偏估计；样本方差22211()1ni i S X nX n ==--∑是总体方差()D X 的无偏估计。

3）无偏估计不唯一，当然应选方差较小者为好. 2. 有效性设1112ˆ(,,,)n X X X θθ=与2212ˆ(,,,)n X X X θθ=都是未知参数θ的无偏估计，称1θ比2θ有效，如果12()()D D θθ<.如，2n ≥时，总体均值的无偏估计X 比1X 有效，因为1()()()D X D X D X n=<。

概率论与数理统计答案（华东师大魏宗舒版）第一章 事件与概率1.1 写出下列随机试验的样本空间及表示下列事件的样本点集合。

(1)10件产品中有1件是不合格品，从中任取2件得1件不合格品。

(2)一个口袋中有2个白球、3个黑球、4个红球，从中任取一球，(ⅰ)得白球，(ⅱ)得红球。

解 (1)记9个合格品分别为 921,正正正，， ，记不合格为次，则，，，，，，，，，)()()(){(1913121次正正正正正正正 =Ω，，，，，，，，，)()()()(2924232次正正正正正正正 ，，，，，，，)()()(39343次正正正正正 )}()()(9898次正次正正正，，，，，，=A ){(1次正，，，，)(2次正)}(9次正，，(2)记2个白球分别为1ω，2ω，3个黑球分别为1b ，2b ，3b ，4个红球分别为1r ，2r ，3r ，4r 。

则=Ω{1ω，2ω，1b ，2b ，3b ，1r ，2r ，3r ，4r }(ⅰ) =A {1ω，2ω} (ⅱ) =B {1r ，2r ，3r ，4r }1.2 在数学系的学生中任选一名学生，令事件A 表示被选学生是男生，事件B 表示被选学生是三年级学生，事件C 表示该生是运动员。

(1) 叙述C AB 的意义。

(2)在什么条件下C ABC =成立？ (3)什么时候关系式B C ⊂是正确的？ (4) 什么时候B A =成立？解 (1)事件C AB 表示该是三年级男生，但不是运动员。

(2) C ABC = 等价于AB C ⊂，表示全系运动员都有是三年级的男生。

(3)当全系运动员都是三年级学生时。

(4)当全系女生都在三年级并且三年级学生都是女生时`。

1.3 一个工人生产了n 个零件，以事件i A 表示他生产的第i 个零件是合格品（n i ≤≤1）。

用i A 表示下列事件：(1)没有一个零件是不合格品；(2)至少有一个零件是不合格品； (3)仅仅只有一个零件是不合格品； (4)至少有两个零件是不合格品。

华师《概率论与数理统计》在线作业
一、单选题（共15 道试题，共60 分。

）
1. 一部件包括10部分。

每部分的长度是一个随机变量，它们相互独立且具有同一分布。

其数学期望为2mm，均方差为0.05mm，规定总长度为20±0.1mm时产品合格，则产品合格的概率为（）。

A. 0.527
B. 0.364
C. 0.636
D. 0.473
正确答案：D
2. 一条自动生产线上产品的一级品率为0.6，现检查了10件，则至少有两件一级品的概率为（）。

A. 0.012
B. 0.494
C. 0.506
D. 0.988
正确答案：D
3. 每颗炮弹命中飞机的概率为0.01，则500发炮弹中命中5发的概率为（）。

A. 0.1755
B. 0.2344
C. 0.3167
D. 0.4128
正确答案：A
4. 工厂每天从产品中随机地抽查50件产品，已知这种产品的次品率为0.1%，，则在这一年内平均每天抽查到的次品数为（）。

A. 0.05
B. 5.01
C. 5
D. 0.5
正确答案：A
5. 炮战中，在距离目标250米，200米，150米处射击的概率分别为0.1, 0.7, 0.2, 而在各处射击时命中目标的概率分别为0.05, 0.1, 0.2。

若已知目标被击毁，则击毁目标的炮弹是由距目标250米处射出的概率为（）。

A. 交换行为
B. 投资行为
C. 协议行为。

作业1．第25题设标准正态分布N（0，1）的分布函数为，则（）（A）（B）-（C）1-（D）1+A.；B.；C.；D..标准答案：C您的答案：题目分数：1.0此题得分：0.02．第26题设P（B）>0，则在事件B已发生的条件下，事件A的条件概率定义为P(A│B)=( ) (A)(B)(C)P(A)P(B) (D)P(AB)P(B)A.；B.；C.；D..标准答案：B您的答案：题目分数：1.0此题得分：0.03．第27题设来自总体N（0，1）的简单随机样本，记，则=() （A）n（B）n-1（C）（D）A.见题B.见题C.见题D.见题标准答案：C您的答案：题目分数：1.0此题得分：0.04．第29题设样本X1,X2,...X n，来自正态总体X~N（）,其中未知，样本均值为，则下列随机变量不是统计量的为（）（A）（B）X1 （C）Min(X1,,...X n) (D)A.；B.；C.；D..标准答案：D您的答案：题目分数：1.0此题得分：0.05．第30题假设样本X1,X2,...X n来自总体X,则样本均值与样本方差S2=2独立的一个充分条件是总体X服从（）。

A.二项分布B.几何分布C.正态分布D.指数分布标准答案：A您的答案：题目分数：1.0此题得分：0.06．第31题设A,B是两个随机事件，且,,,则必有（）（A）（B）（C）（D）A.见题B.见题C.见题D.见题标准答案：C您的答案：题目分数：0.5此题得分：0.07．第32题设随机变量X~U（0，1），则它的方差为D(X)=（）A.1/2B.1/3C.1/4D.1/12标准答案：D您的答案：题目分数：0.5此题得分：0.08．第33题设正态分布X~N（2），则P（│X-│>3）=( ) (A)0.5 (B)0.1 (C)0.05 (D)0.0027A.；B.；C.；D..标准答案：D您的答案：题目分数：0.5此题得分：0.09．第34题设来自总体的简单随机样本，则（）（A）（B）（C）（D）A.见题B.见题C.见题D.见题标准答案：D您的答案：题目分数：0.5此题得分：0.010．第35题对于任意两事件A,B（）（A）若,则A,B一定独立（B）若,则A,B有可能独立（C）若,则A,B一定独立（D）若,则A,B一定不独立A.见题B.见题C.见题D.见题标准答案：B您的答案：题目分数：0.5此题得分：0.011．第36题如果P(A)=0.5,P(B)=0.4,P(B│A)=0.6,则P(AB)=( )A.0.1B.0.2C.0.24D.0.3标准答案：D您的答案：题目分数：0.5此题得分：0.012．第37题某人向同一目标独立重复射击，每次射击命中目标的概率为,则此人第4次射击恰好第2次命中的概率为（）(A)(B)(C)(D)A.见题B.见题C.见题D.见题标准答案：C您的答案：题目分数：0.5此题得分：0.013．第59题概率函数为P（X=k）=p K(1-p)1-K，k=0.1的分布称为( )（A）“0-1”分布（B）几何分布（C）超几何分布（D）泊松分布A.；B.；C.；D.。

期中期末串讲--概率课后练习主讲教师：黄老师题一：下列关于概率的叙述正确的是( )A．某运动员投篮5次，投中4次，投中的概率为0.4B．任意抛掷一枚硬币两次，两次都是正面的概率为1 3C．选择题的四个选项中有且只有一个正确，若从中任选一个，选对的概率为1 4D．飞机失事死亡的概率为0.000000000038，因此乘飞机失事而死亡是不可能事件题二：下列有关概率的叙述，何者正确( )A．投掷一枚图钉，针尖朝上、朝下的概率一样B．投掷一枚质地均匀的硬币，正面朝上的概率是1 2C．统一发票有“中奖”与“不中奖”二种情形，所以中奖概率是1 2D．在一副没有大小王的扑克牌中任意抽一张，抽到的牌是6的概率是2 27题三：甲袋中装有8只红球、2只黑球；乙袋中装有25只红球、5只黑球．这些球除了颜色以外没有其他区别．(1)从甲袋中随机取出一球，求取出黑球的概率；(2)如果从其中一个袋中随机取出一球，你想取出的是黑球，那么选哪个袋成功的机会更大？请说明理由．题四：一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同)，其中有白球4个，黄球2个，若从中任意摸出一个球，这个球是白球的概率为13．(1)求口袋中红球的个数；(2)小明说：“口袋中共有三种颜色的球，所以从袋中任意摸出一球，摸到红球、白球或黄球的概率都是13”．请你判断小明的说法正确吗？为什么？题五：某校组织的联欢会上有一个闯关游戏：将四张画有含30°的直角三角形、正方形、等腰三角形、平行四边形这四种图形的卡片任意摆放，将有图形的一面朝下，从中任意翻开一张，如果翻开的图形是轴对称图形就可以过关，那么翻一次就过关的概率是____．题六：如图，已知△ABC的两条中线AD，BE相交于点F，得到8个图形：△ABD，△ACD，△BAE，△BCE，△FAB，△FAE，△FBD，四边形CEFD，现从中任取两个图形，求取得的这两个图形面积相等的概率．题七：有下面四张数字卡片．如果从这四张卡片中任意抽取三张摆成一个三位数，那么摆成奇数的可能性是______．题八：如图，有五张点数分别为2，3，7，8，9的扑克牌，从中任意抽取两张，则其点数之积是偶数的概率为______．题九：从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如表：(1)请填空：根据以上数据可以估计：该玉米种子发芽的概率为_____；(精确到0.1)题十：下表是一名同学在罚球线上投篮的实验结果，根据表中数据，回答问题：(1)估计这名同学投篮一次，投中的概率是多少？(精确到0.1)(2)根据此概率，估计这名同学投篮622次，投中的次数约是多少？期中期末串讲--概率课后练习参考答案题一： C．详解：A．某运动员投篮5次，投中4次，投中的概率为0.8，错误；B．任意抛掷一枚硬币两次，两个都是正面的概率为14，错误；C．选择题的四个选项中有且只有一个正确，若从中任选一个，选对的概率为14，正确；D．飞机失事死亡的概率为0.000000000038，因此乘飞机失事而死亡是随机事件，错误．故选C．题二： B．详解：A．由于图钉质地不均匀，所以针尖朝上、朝下的概率不一样，错误；B．投掷一枚质地均匀的硬币，正面朝上和反面朝上的机会均等，都是12，正确；C．“中奖”与“不中奖”两种情形的机会不一定均等，错误；D．在一副没有大小王的扑克牌中任意抽一张，抽到的牌是6的概率是113，错误．故选B．题三：15；甲．详解：(1)因为甲袋中装有8只红球、2只黑球，共10只球，故P(甲袋取出黑球)=2÷10=15，答：取出黑球的概率为15；(2)因为乙袋中装有25只红球、5只黑球，共30只球，故P(乙袋取出黑球)=5÷30=16，因为15＞16，所以想取出的是黑球，那么选甲袋成功的机会更大．题四： 6个；不正确．详解：(1)口袋中乒乓球的总数为4÷13=12(个)，则红球的个数为12－4－2=6(个)，答：口袋中红球的个数是6个；(2)不正确．∵P(白球)=13，P(红球)=612=12，P(黄球)=212=16，∴小明的说法不正确．题五：12．详解：根据题意可得：有含30°的直角三角形、正方形、等腰三角形、平行四边形卡片共4张，正方形、等腰三角形的卡片是轴对称图形，有2张，任意翻开一张，翻开的图形是轴对称图形的概率是24=12．题六：27．详解：从8个图形中任取两个图形有(8×7)÷2=28种取法，其中面积相等的有三种情况：①面积为△ABC面积的12的三角形有4个(△ABD，△ACD，△BAE，△BCE)，则面积相等的图形有6对；②面积为△ABC面积的16的三角形有2个(△FAE，△FBD)，则面积相等的图形有1对；③面积为△ABC面积的13的图形有2个(△FAB，四边形CEFD)，则面积相等的图形有1对．综上所述，面积相等的图形共有8对，故取得两个图形面积相等的概率为828=27．题七：49．详解：把这4个数字，任意抽出三张摆成数的个数为：4×3×2=24；百位为0的个数，3×2=6，则摆成三位数的个数为24-6=18；奇数个数为：2×2×2=8，则奇数可能性为8÷18=49．题八：7 10．详解：根据题意，当不考虑抽牌顺序时，可以画出如下的树形图从上图可以看出，从五张牌中任意抽取两张，共有10种抽法，其中抽取的点数之积是偶数的有7种，所以点数之积是偶数的概率：P=7 10．题九： 0.8；6400．详解：(1)根据题干知：当种子粒数5000粒时，种子发芽的频率趋近于0.801，故可以估计种子发芽的概率为0.801，精确到0.1，即为0.8；(2)由(1)知：种子的发芽率是0.8，故估计8000粒种子能发芽的粒数为8000×0.8=6400(粒)．题十： 0.5；311次．详解：(1)估计这名球员投篮一次，投中的概率约是0.5；(2)622×0.5=311(次)．故估计这名同学投篮622次，投中的次数约是311次．。

华师《概率论与数理统计》在线作业-0004
如果随机变量X和Y满足D（X+Y）=D（X-Y），则下列式子正确的是（）。

A:X与Y相互独立
B:X与Y不相关
C:DY=0
D:DX*DY=0
参考选项：B
假设一个小孩是男是女是等可能的，若某家庭有三个孩子，在已知至少有一个
女孩的条件下，求这个家庭中至少有一个男孩的概率为（）。

A:3/4
B:7/8
C:6/7
D:4/5
参考选项：C
设随机变量X和Y独立同分布，记U=X-Y，V=X+Y，则随机变量U与V必然（）。

A:不独立
B:独立
C:相关系数不为零
D:相关系数为零
参考选项：D
甲、乙、丙3部机床独立工作，由一个工人照管，某段时间内它们不需要工作
照管的概率分别为0.9、0.8 及0.85。

则在这段时间内有机床需要工作照管的
概率为（）。

A:0.612
B:0.388
C:0.059
D:0.941
参考选项：B
设X,Y为两个随机变量，则下列等式中正确的是（）。

A:E(X+Y)=E(X)+E(Y)
B:D(X+Y)=D(X)+D(Y)
C:E(XY)=E(X)E(Y)
D:D(XY)=D(X)D(Y)
参考选项：A
袋中有5个白球，3个黑球。

从中任取两个球，则取出的两个球都是白球的概率
为（）。

A:5/14
1。

课 题： 概率与统计 一、教学内容与教学目标(1) 概率与统计（14课时）离散型随机变量的分布列。

离散型随机变量的期望值和方差。

抽样方法。

总体分布的估计。

正态分布。

线性回归。

(2) 教学目标（1）了解离散型随机变量的意义，会求出某些简单的离散型随机变量的分布列。

（2）了解离散型随机变量的期望值、方差的意义，会根据离散型随机变量的分布列求出期望值、方差。

（3）会用随机抽样、系统抽样、分层抽样等常用的抽样方法从总体中抽取样本。

（4）会用样本频率分布估计总体分布。

（5）了解正态分布的意义及主要性质。

（6）了解线性回归的方法和简单应用。

二、典例解析例1 在医学生物学试验中，经常以果蝇作为试验对象，一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到．．两只苍蝇都飞出，再关闭小孔.以ξ表示笼内还剩下的果蝇．．．．．的只数. （Ⅰ）写出ξ的分布列（不要求写出计算过程）； （Ⅱ）求数学期望Eξ；（Ⅲ）求概率P （ξ≥Eξ）. 解：（Ⅰ）ξ的分布列为：ξ0 1 2 3 4 5 6P728628528428328228128（Ⅱ）数学期望为2(162534)228E ξ=⨯+⨯+⨯=．（Ⅲ）所求的概率为5432115()(2)2828P E P ξξξ++++===≥≥．例2 某电脑游戏开发公司设计了一种新的“横拟世界杯——足球大赛”游戏，该游戏中的“罚点球” 确定的规则如下；玩家每一轮罚10个点球，每罚一个点球，玩家可选定球门已划定的9个区域中的某一个主罚，守门员则可守住9个区域中的3个区域.（Ⅰ）求玩家玩完一轮，10个点球罚中的ε个的概率)(k P =ε的表示式（k =0，1，2，…，10）； （Ⅱ）求玩家玩完一轮，至少罚中2个点球的概率。

（结果保留小数点后4位即可，近似计算参考数据0000169.0)31(10≈）. 解：（Ⅰ）玩家罚中一个点球的概率为32，罚不中的概率为.31且每次罚球的结果是相互独立的，故).32,10(~B ξ ∴ξ的分布列为10,,2,1,0,)31()32()(1010 =⋅==-k C k P kkkξ（Ⅱ）9996.0)31(20)31(1)1()0(1)2(1010≈⋅--==-=-=≥ξξξP P P 。

概率论_华东师范大学中国大学mooc课后章节答案期末考试题库2023年1.设F(x,y)是随机变量(X,Y)的分布函数, 则P(X>2,Y>3)=1-F(2,3).参考答案:错误2.设F(x,y)是随机变量(X,Y)的分布函数, 则P(X>2,Y>3)=1+F(2,3).参考答案:错误3.随机事件A与B相互独立当且仅当随机事件类【图片】与【图片】相互独立.参考答案:正确4.若随机变量X的特征函数为【图片】,则VarX=_____参考答案:15.随机变量X与Y相互独立, Y与Z相互独立, 则Y与乘积XZ独立.参考答案:错误6.若【图片】, 则当【图片】时有【图片】成立.参考答案:正确7.二维正态分布的边际分布为一维正态分布.参考答案:正确8.联合分布可以确定边际分布;反之,边际分布也可以确定联合分布.参考答案:错误9.设【图片】的联合概率密度函数为【图片】则条件概率【图片】=______________.(保留至小数点后三位)参考答案:0.13510.只要样本空间所含样本点的个数是有限个,就一定可以用古典方法来计算事件发生的概率.参考答案:错误11.从整数1-200中随机地取一个数, 求取到的整数既不能被2整除又不能被3整除的概率为_____.（答案保留至小数点后三位）参考答案:0.33512.随机变量X服从正态分布N(0,4), 则随机变量X^2(即X的平方)服从Gamma分布Ga(1/2,1/8).参考答案:正确13.设随机变量X与Y相互独立且都服从指数分布Exp(1), 则max(X,Y)也服从指数分布.参考答案:错误14.一段时间内进入某便利店的顾客数X服从泊松分布P(2), 每个顾客购买某品牌奶茶的概率为0.2, 且每个顾客是否购买该品牌奶茶相互独立. 设Y表示进入该便利店购买这种奶茶的人数, 则P(Y=0)=____(保留至小数点后两位).参考答案:0.6715.设随机变量Y服从标准正态分布N(0,1), 定义随机变量【图片】则概率【图片】参考答案:正确16.射击训练中射击者对同一目标进行射击,且互不影响. 如果每位射击手击中目标的概率为0.6. 两位射击手同时进行射击, 则目标被击中的概率为_____.(答案保留至小数点后2位)参考答案:0.8417.随机变量X与Y都服从正态分布, X与Y不相关, 则X与Y一定相互独立.参考答案:错误18.随机变量X服从正态分布N(0,4), 则随机变量【图片】服从Gamma分布.参考答案:正确19.设随机变量Y服从标准正态分布N(0,1), 定义随机变量【图片】则概率【图片】_____.(保留至小数点后3位)参考答案:0.34120.设随机变量(X,Y)服从均匀分布U(D), 其中D={(x,y): 0参考答案:正确21.设F(x,y)是随机变量(X,Y)的分布函数, 则【图片】参考答案:错误22.设随机变量【图片】与随机变量【图片】相互独立, 则随机变量X与随机变量Y 也相互独立.参考答案:错误23.二维均匀分布的边际分布仍为均匀分布.参考答案:错误24.设【图片】是任意给定的非空样本空间, 则【图片】上至少有2个不同的事件域.参考答案:错误25.设随机变量X与Y同分布, 且P(X=0)=1/2, P(X=-1)=P(X=1)=1/4. 又已知P(XY=0)=1, 则概率P(X=Y)=________.参考答案:26.用频率方法确定事件发生的概率, 实际上是以频率的极限来代替事件发生的概率.参考答案:错误27.若随机变量X的特征函数为【图片】,则数学期望EX=____.参考答案:228.设某个随机试验的样本空间【图片】中含有5个样本点, 则【图片】上的事件域最多可以含有多少个随机事件?参考答案:3229.设随机变量X与Y相互独立, Y与Z相互独立, X与Z相互独立, 则随机变量X, Y, Z相互独立.参考答案:错误30.任何一个概率分布,其特征函数都存在.参考答案:正确31.随机变量X与Y相互独立, 则随机变量【图片】与随机变量【图片】也相互独立.参考答案:正确32.设随机变量(X,Y)服从二维正态分布【图片】, 则E(X|Y)的数学期望为【图片】.参考答案:错误33.设【图片】是n维随机向量, 且诸【图片】的二阶矩存在, 则【图片】参考答案:正确34.若【图片】是独立同分布的随机变量序列, k阶矩存在, 那么【图片】.参考答案:正确35.设随机变量X, Y, Z相互独立,则X与Y+Z相互独立.参考答案:正确36.射击训练中射击者对同一目标进行射击,且互不影响. 如果每位射击手击中目标的概率为0.6. 三位射击手同时进行射击, 则目标被击中的概率为_____.(答案保留至小数点后3位)参考答案:0.93637.若对任意的n, 【图片】与【图片】独立, 且【图片】, 【图片】, 那么【图片】.参考答案:错误38.若【图片】的特征函数【图片】点点收敛到某个函数f(t), 那么【图片】依分布收敛.参考答案:错误39.若【图片】,【图片】, 则【图片】参考答案:正确40.若【图片】, 【图片】, 那么【图片】.参考答案:错误41.若对任意【图片】, 有【图片】 ,则【图片】.参考答案:正确42.随机事件A,B和C相互独立, 则一定三三独立.参考答案:正确43.随机事件A,B和C相互独立, 则一定两两独立.参考答案:正确44.设随机变量X与Y相互独立, 且X服从正态分布N(1,4), Y服从Gamma分布Ga(1,2), 则随机变量X^2-2X+16Y+1服从Gamma分布Ga(3/2, 1/8).参考答案:正确45.设随机变量(X,Y)服从均匀分布U(D), 其中D={(x,y): 0参考答案:0.057146.设随机变量(X,Y)的概率密度函数为【图片】则概率【图片】______ (保留至小数点后3位)参考答案:0.33347.随机事件A和B相互独立当且仅当A和B互不相容.参考答案:错误48.10只产品中有3件是次品, 现依次从中不返回地取出2件, A表示事件"第一件是次品", B表示事件"第二件是次品", 则A和B相互独立.参考答案:错误49.10只产品中有3件是次品, 现依次从中有返回地取出2件, A表示事件"第一件是次品", B表示事件"第二件是次品", 则A和B相互独立.参考答案:正确50.抛掷一枚骰子, 首次出现点数4的平均抛掷次数为___次.参考答案:651.设随机变量X的概率密度函数p(x)满足p(1+x)=p(1-x), 且【图片】,则概率P(X<0)=__________.参考答案:0.252.设随机变量X与-X有相同的概率密度函数p(x), 则p(x)-p(-x)=_______参考答案:53.离散型随机变量的分布函数一定不是连续函数.参考答案:正确54.分布函数连续的随机变量是连续型随机变量.参考答案:错误55.设随机变量(X,Y)的概率密度函数为【图片】则常数c=__________.(保留至小数点后3位)参考答案:0.12556.若【图片】,【图片】,则【图片】.参考答案:正确57.依概率收敛的随机变量序列中一定存在几乎处处收敛的子列.参考答案:正确58.设随机变量(X,Y)服从均匀分布U(D), 其中D={(x,y): 0参考答案:0.284759.设随机变量(X,Y)服从均匀分布U(D), 其中D为矩形(0,2)×(2,3). 设p(x)为X的概率密度函数, 则p(1)=__________.参考答案:0.560.已知X的概率密度函数为【图片】, 则数学期望EX=____参考答案:61.已知X的概率密度函数为【图片】, 则概率P(X>0)=____.(用小数表示)参考答案:0.562.设F(x,y)是随机变量(X,Y)的分布函数, 则【图片】参考答案:正确63.已知随机变量X的分布列为【图片】其中c为未知常数, 则概率P(X>1)=____.(保留至小数点后二位)参考答案:0.5064.具有无记忆性的分布只有指数分布和几何分布.参考答案:正确65.设随机变量X服从正态分布N(1,9), 则数学期望【图片】为( )参考答案:1066.相互独立的两个事件A和B都不发生的概率为0.25, 而且A发生同时B不发生的概率与A不发生B发生的概率相同, 则P(B)=____.参考答案:0.5##%_YZPRLFH_%##0.5067.设随机变量(X,Y)服从均匀分布U(D), 其中D={(x,y): 0参考答案:0.057168.设随机变量(X,Y)服从均匀分布U(D), 其中D={(x,y): 0参考答案:0.047169.设随机变量(X,Y)服从均匀分布U(D), 其中D={(x,y): 0参考答案:0.824370.设随机变量X和Y都服从标准正态分布, 则商X/Y服从柯西分布.参考答案:错误71.设随机变量(X,Y)服从均匀分布U(D), 其中D={(x,y): 0参考答案:正确72.随机变量X服从正态分布N(0,4), 则随机变量X^2(即X的平方)服从Gamma分布.参考答案:正确73.设随机变量(X,Y)服从二维正态分布【图片】, 则E(X|Y)的分布为正态分布.参考答案:正确74.设随机变量(X,Y)服从二维正态分布【图片】, 则协方差Cov(X+Y,X-Y)=【图片】.参考答案:错误75.设随机变量X,Y,Z两两之间的相关系数皆为ρ, 则ρ≥-0.5.参考答案:正确76.射击训练中射击者对同一目标进行射击,且互不影响. 如果每位射击手击中目标的概率为0.6. 至少需要____位射击手同时进行射击, 才能以至少99%的概率击中目标.参考答案:677.随机事件A和B相互独立当且仅当P(A|B)=P(A).参考答案:错误78.随机事件A,B和C三三独立, 则一定两两独立.参考答案:错误79.设随机变量X服从正态分布N(1,9), 则方差VarX=_____.参考答案:980.设随机变量X服从N(0,1), 则概率P(X<-1.96)=___.(保留至小数点后四位)参考答案:0.025081.设随机变量(X,Y)的联合概率密度函数为【图片】, 则概率P(X<1/2)=____参考答案:1/482.多项分布的边际分布是二项分布.参考答案:正确83.某工厂共有3条生产线生产同一种产品, 各条生产线的产量分别占总产量的25%, 35%和40%. 各生产线的不合格品率依次为4%, 3%和2%. 现从该厂生产的这种产品中任取一件发现是不合格品, 则是第1条生产线生产的概率为____(保留至小数点后2位)参考答案:0.3584.随机事件A, B和C两两独立, 则一定三三独立.参考答案:错误85.设随机变量(X,Y)服从正态分布N(0,1;1,4;ρ), 且X与Y相互独立, 则ρ=_________.参考答案:86.设随机变量【图片】服从均匀分布【图片】, 当【图片】时, 随机变量【图片】服从均匀分布【图片】则数学期望【图片】_______.(保留至小数点后2位)参考答案:0.2587.设随机变量X与Y相互独立, 且X服从指数分布Exp(1), Y服从Gamma分布Ga(2,1). 设p(x,y)是(X,Y)的联合概率密度函数, 则p(1,1)=____.(保留至小数点后三位.)参考答案:0.13588.某保险公司制定理赔方案,如果一年内一个顾客的投保事件A发生了, 则需要赔偿该顾客10000元. 若已知一年内投保事件A发生的概率是0.001, 为使保险公司的期望收益是理赔金额的5%, 则应该收该顾客______元保费.参考答案:51089.设随机变量X服从正态分布N(1,4), F(x)为X的分布函数, 则F(X)服从均匀分布U(0,1).参考答案:正确90.某工厂共有3条生产线生产同一种产品, 各条生产线的产量分别占总产量的25%, 35%和40%. 各生产线的不合格品率依次为4%, 3%和2%. 现从该厂生产的这种产品中任取一件, 则抽到不合格品的概率为____(答案保留至小数点后4位)参考答案:0.028591.随机变量X服从指数分布Exp(2), Y服从指数分布Exp(3), 且X与Y相互独立, 则X+Y服从指数分布Exp(5).参考答案:错误92.随机变量X服从泊松分布P(2), Y服从泊松分布P(3), 则X+Y服从泊松分布P(5).参考答案:错误93.同时抛掷两枚骰子, 至少有一颗骰子的点数小于3的概率为________（答案保留至小数点后三位）参考答案:0.55694.已知随机事件A和B互不相容, 【图片】, 【图片】, 则【图片】=______参考答案:0.195.盒子里装有3 个黑球、2 个红球、2 个白球，从中任取4 个, 用X表示取到的黑球数, Y表示取到的红球数, 则P(X=Y)=______.(结果保留至小数点后3位) 参考答案:0.25796.卡方分布【图片】的方差为____参考答案:1097.Gamma分布Ga(2,2)的峰度系数为____.参考答案:398.设随机变量X服从均匀分布U(0,1), 则【图片】____.(保留至小数点后二位)参考答案:0.2599.设随机变量(X,Y)的概率密度函数为【图片】则概率【图片】_____.(保留至小数点后3位)参考答案:0.375100.不可能事件【图片】是任何事件的子事件.参考答案:正确101.已知【图片】与【图片】是随机事件,则【图片】.参考答案:错误102.现要从有9个男生5个女生的社团中选出3位学生代表, 则这3位被选中的代表中至少有1位是女生的概率为_____（答案保留至小数点后三位）参考答案:0.769103.设X为连续型随机变量,则函数f(X)也是连续型随机变量.参考答案:错误104.设随机变量X服从二项分布b(n,p), Y服从二项分布b(m,p), 则X+Y服从二项分布b(n+m,p).参考答案:错误105.设随机变量(X,Y)服从均匀分布U(D), 其中【图片】, 则概率【图片】_____.(保留至小数点后3位)参考答案:0.785106.设随机变量(X,Y)服从均匀分布U(D), 其中D为以0为中心, 2为半径的圆盘.设p(x)为X的概率密度函数, 则π与p(0)的积为__________.参考答案:1。

统计与概率——概率1一．选择题（共8小题）1．掷一枚质地均匀的硬币10次，下列说法正确的是（）A．可能有5次正面朝上B．必有5次正面朝上C．掷2次必有1次正面朝上D．不可能10次正面朝上2．下列事件是必然事件的是（）A．如果|a|=|b|，那么a=bB．平分弦的直径垂直于弦，并且平分弦所对的两条弧C．半径分别为3和5的两圆相外切，则两圆的圆心距为8D．三角形的内角和是360°3．下列说法正确的是（）A．“打开电视机，它正在播广告”是必然事件B．“一个不透明的袋中装有8个红球，从中摸出一个球是红球”是随机事件C．为了了解我市今年夏季家电市场中空调的质量，不宜采用普查的调查方式进行D．销售某种品牌的凉鞋，销售商最感兴趣的是该品牌凉鞋的尺码的平均数4．下列事件是必然事件的是（）A．某射击运动员射击一次，命中靶心B．单项式加上单项式，和为多项式C．打开电视机，正在播广告D．13名同学中至少有两名同学的出生月份相同5．下列说法正确的是（）A．必然事件发生的概率为0B．一组数据1，6，3，9，8的极差为7C．“面积相等的两个三角形全等”这一事件是必然事件D．“任意一个三角形的外角和等于180°”这一事件是不可能事件6．下列事件是随机事件的是（）A．通常情况温度降到0℃以下，纯净的水结冰B．随意翻到一本书的某页，这页的页码是偶数C．度量三角形的内角和，结果是360°D．测量某天的最低气温，结果为﹣180℃7．下列事件中属于不可能事件的是（）A．某投篮高手投篮一次就进球B．打开电视机，正在播放世界杯足球比赛C．掷一次骰子，向上的一面出现的点数不大于6D．在1个标准大气压下，90℃的水会沸腾8．一个不透明的袋子中装有5个黑球和3个白球，这些球的大小、质地完全相同，随机从袋子中摸出4个球，则下列事件是必然事件的是（）A．摸出的四个球中至少有一个球是白球B．摸出的四个球中至少有一个球是黑球C．摸出的四个球中至少有两个球是黑球D．摸出的四个球中至少有两个球是白球二．填空题（共8小题）9．同时掷两枚硬币，两枚硬币全部正面朝上的概率为_________．10．布袋中装有3个红球和6个白球，它们除颜色外其他都相同，如果从布袋里随机摸出一个球，那么所摸到的球恰好为红球的概率是_________．11．在一个不透明的袋子中装有若干个除颜色外形状大小完全相同的球，如果其中有3个白球，且摸出白球的概率是，那么袋子中共有球_________个．12．在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球，如果口袋中装有3个红球且摸到红球的概率为，那么口袋中球的总个数为_________．13．任意抛掷一枚均匀的骰子一次，朝上的点数大于4的概率等于_________．14．五张分别写有﹣1，2，0，﹣4，5的卡片（除数字不同以外，其余都相同），现从中任意取出一张卡片，则该卡片上的数字是负数的概率是_________．15．如果从初三（1）、（2）、（3）班中随机抽取一个班与初三（4）班进行一场拔河比赛，那么恰好抽到初三（1）班的概率是_________．16．100件外观相同的产品中有5件不合格，现从中任意抽取1件进行检测，抽到不合格产品的概率是_________．三．解答题（共8小题）17．一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球．（1）求从袋中摸出一个球是黄球的概率；（2）现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是，求从袋中取出黑球的个数．18．某商场为了吸引顾客，设立了可以自由转动的转盘（如图，转盘被均匀分为20份），并规定：顾客每购买200元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得200元、100元、50元的购物券，凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可以直接获得购物券30元．（1）求转动一次转盘获得购物券的概率；（2）转转盘和直接获得购物券，你认为哪种方式对顾客更合算？19．红花中学现要从甲、乙两位男生和丙、丁两位女生中，选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛．（1）请用树状图或列表法列举出各种可能选派的结果；（2）求恰好选派一男一女两位同学参赛的概率．20．某同学报名参加校运动会，有以下5个项目可供选择：径赛项目：100m，200m，400m（分别用A1、A2、A3表示）；田赛项目：跳远，跳高（分别用B1、B2表示）．（1）该同学从5个项目中任选一个，恰好是田赛项目的概率为_________；（2）该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率．21．在一个口袋里有四个完全相同的小球，把它们分别标号为1，2，3，4，小明和小强采取的摸取方法分别是：小明：随机摸取一个小球记下标号，然后放回，再随机摸取一个小球，记下标号；小强：随机摸取一个小球记下标号，不放回，再随机摸取一个小球，记下标号．（1）用画树状图（或列表法）分别表示小明和小强摸球的所有可能出现的结果；（2）分别求出小明和小强两次摸球的标号之和等于5的概率．22．一个口袋中有3个大小相同的小球，球面上分别写有数字1、2、3，从袋中随机地摸出一个小球，记录下数字后放回，再随机地摸出一个小球．（1）请用树形图或列表法中的一种，列举出两次摸出的球上数字的所有可能结果；（2）求两次摸出的球上的数字和为偶数的概率．23．甲、乙两人用如图的两个分格均匀的转盘A、B做游戏，游戏规则如下：分别转动两个转盘，转盘停止后，指针分别指向一个数字（若指针停止在等份线上，那么重转一次，直到指针指向某一数字为止）．用所指的两个数字相乘，如果积是奇数，则甲获胜；如果积是偶数，则乙获胜．请你解决下列问题：（1）用列表格或画树状图的方法表示游戏所有可能出现的结果．（2）求甲、乙两人获胜的概率．24．在一个不透明的袋子里装有3个乒乓球，分别标有数字1，2，3，这些乒乓球除所标数字不同外其余均相同．先从袋子里随机摸出1个乒乓球，记下标号后放回，再从袋子里随机摸出1个乒乓球记下标号，请用画树状图（或列表）的方法，求两次摸出的乒乓球标号乘积是偶数的概率．统计与概率——概率1参考答案与试题解析一．选择题（共8小题）1．（掷一枚质地均匀的硬币10次，下列说法正确的是（）A．可能有5次正面朝上B．必有5次正面朝上C．掷2次必有1次正面朝上 D．不可能10次正面朝上考点：随机事件．分析：根据随机事件是指在一定条件下，可能发生也可能不发生的事件，可得答案．解答：解：A、是随机事件，故A正确；B、不是必然事件，故B错误；C、不是必然事件，故C错误；D、是随机事件，故D错误；故选：A．点评：解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．2．下列事件是必然事件的是（）A．如果|a|=|b|，那么a=bB．平分弦的直径垂直于弦，并且平分弦所对的两条弧C．半径分别为3和5的两圆相外切，则两圆的圆心距为8D．三角形的内角和是360°考点：随机事件．专题：常规题型．分析：必然事件就是一定发生的事件，即发生的概率是1的事件．解答：解：A、如果|a|=|b|，那么a=b或a=﹣b，故A选项错误；B、平分弦的直径垂直于弦，并且平分弦所对的两条弧，此时被平分的弦不是直径，故B选项错误；C、半径分别为3和5的两圆相外切，则两圆的圆心距为8，故C选项正确；D、三角形的内角和是180°，故D选项错误，故选：C．点评：考查了随机事件，解决本题要正确理解必然事件、不可能事件、随机事件的概念，理解概念是解决基础题的主要方法．用到的知识点为：必然事件指在一定条件下一定发生的事件；不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．3．下列说法正确的是（）A．“打开电视机，它正在播广告”是必然事件B．“一个不透明的袋中装有8个红球，从中摸出一个球是红球”是随机事件C．为了了解我市今年夏季家电市场中空调的质量，不宜采用普查的调查方式进行D．销售某种品牌的凉鞋，销售商最感兴趣的是该品牌凉鞋的尺码的平均数考点：随机事件；全面调查与抽样调查；统计量的选择．分析：根据随机事件、必然事件的定义，可判断A、B，根据不同调查方式的特点，可判断C，根据数据的集中趋势，可判断D．解答：解：A、是随机事件，故A错误；B、是必然事件，故B错误；C、调查对象大，适宜用抽查的方式，不宜用普查，故C正确；D、销售商最感兴趣的是众数，故D错误；故选：C．点评：本题考查了随机事件，全面调查与抽样调查以及统计量的选择．解决本题需要正确理解必然事件、不可能事件、随机事件的概念．用到的知识点为：确定事件包括必然事件和不可能事件．必然事件指在一定条件下一定发生的事件；不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．4．下列事件是必然事件的是（）A．某射击运动员射击一次，命中靶心B．单项式加上单项式，和为多项式C．打开电视机，正在播广告D．13名同学中至少有两名同学的出生月份相同考点：随机事件．分析：必然事件就是一定发生的事件，根据定义即可作出判断．解答：解：A、某射击运动员射击一次，命中靶心是随机事件；B、单项式加上单项式，和为多项式是随机事件；C、打开电视机，正在播广告是随机事件；D、13名同学中至少有两名同学的出生月份相同，因为一年又12个月，所以是必然事件，故选：D．点评：本题考查了必然事件以及随机事件的定义．解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．5．下列说法正确的是（）A．必然事件发生的概率为0B．一组数据1，6，3，9，8的极差为7C．“面积相等的两个三角形全等”这一事件是必然事件D．“任意一个三角形的外角和等于180°”这一事件是不可能事件考点：随机事件；方差；概率的意义．专题：常规题型．分析：根据必然事件、不可能事件、随机事件的概念可区别各类事件，可得答案．解答：解：A、必然事件发生的概率为1，故A错误；B、一组数据1，6，3，9，8的极差为8，故B错误；C、面积相等两个三角形全等，是随机事件，故C错误；D、“任意一个三角形的外角和等于180°”是不可能事件，故D正确；故选：D．点评：本题考查了随机事件，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事．6．下列事件是随机事件的是（）A．通常情况温度降到0℃以下，纯净的水结冰B．随意翻到一本书的某页，这页的页码是偶数C．度量三角形的内角和，结果是360°D．测量某天的最低气温，结果为﹣180℃考点：随机事件．专题：常规题型．分析：一个概率事件分为：确定事件（包括：必然事件与不可能事件）和随机事件．必然事件发生的可能性是“1”，不可能事件发生的可能性是“0”，随机事件发生的可能性为“0～1”之间．据此可以判断答案B是正确的．解答：解：A．通常情况温度降到0℃以下，纯净的水结冰，这是一个必然事件，发生的可能性是“1”；B．随意翻到一本书的某页，这页的页码是偶数，这是一个不确定事件，发生的可能性是“0.5”；这页的页码也可能是奇数；C．度量三角形的内角和，结果是360°，这是一个不可能事件，发生的可能性是“0”；三角形内角和为180°；D．测量某天的最低气温，结果为﹣180°，这是一个不可能事件，发生的可能性是“0”．故选B．点评：此题考查是概率统计中一个事件发生的可能性大小．需要了解一个概率事件分为：确定事件（包括：必然事件与不可能事件）和随机事件．必然事件发生的可能性是“1”，不可能事件发生的可能性是“0”，随机事件发生的可能性为“0～1”之间．7．下列事件中属于不可能事件的是（）A．某投篮高手投篮一次就进球B．打开电视机，正在播放世界杯足球比赛C．掷一次骰子，向上的一面出现的点数不大于6D．在1个标准大气压下，90℃的水会沸腾考点：随机事件．专题：常规题型．分析：不可能事件就是一定不会发生的事件，依据定义即可判断．解答：解：A、是随机事件，故A选项错误；B、是随机事件，故B选项错误；C、是必然事件，故C选项错误；D、是不可能事件，故D选项正确．故选：D．点评：本题考查了不可能事件的定义，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．8．一个不透明的袋子中装有5个黑球和3个白球，这些球的大小、质地完全相同，随机从袋子中摸出4个球，则下列事件是必然事件的是（）A．摸出的四个球中至少有一个球是白球B．摸出的四个球中至少有一个球是黑球C．摸出的四个球中至少有两个球是黑球D．摸出的四个球中至少有两个球是白球考点：随机事件．分析：必然事件就是一定发生的事件，依据定义即可作出判断．解答：解：A、是随机事件，故A选项错误；B、是必然事件，故B选项正确；C、是随机事件，故C选项错误；D、是随机事件，故D选项错误．故选：B．点评：本题考查了必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．二．填空题（共8小题）9．同时掷两枚硬币，两枚硬币全部正面朝上的概率为．考点：概率公式．分析：列举出所有情况，看所求的情况占总情况的多少即可．解答：解：可能出现的情况有：正正，正反，反正，反反，所以全部正面朝上的概率为．点评：此题考查了列举法求概率，解题的关键是找到所有的情况．10．布袋中装有3个红球和6个白球，它们除颜色外其他都相同，如果从布袋里随机摸出一个球，那么所摸到的球恰好为红球的概率是．考点：概率公式．专题：常规题型．分析：根据概率公式，求摸到红球的概率，即用红球除以小球总个数即可得出得到红球的概率．解答：解：∵一个布袋里装有3个红球和6个白球，∴摸出一个球摸到红球的概率为：=．故答案为：．点评：此题主要考查了概率公式的应用，由已知求出小球总个数再利用概率公式求出是解决问题的关键．11．在一个不透明的袋子中装有若干个除颜色外形状大小完全相同的球，如果其中有3个白球，且摸出白球的概率是，那么袋子中共有球12个．考点：概率公式．分析：设袋中共有球x个，根据概率公式列出等式解答．解答：解：设袋中共有球x个，∵有3个白球，且摸出白球的概率是，∴=，解得x=12（个）．故答案为：12．点评：本题考查了概率公式，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m 种结果，那么事件A的概率P（A）=．12．在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球，如果口袋中装有3个红球且摸到红球的概率为，那么口袋中球的总个数为15．考点：概率公式．分析：由在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球，如果口袋中装有3个红球且摸到红球的概率为，利用概率公式求解即可求得答案．解答：解：∵在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球，如果口袋中装有3个红球且摸到红球的概率为，∴口袋中球的总个数为：3÷=15．故答案为：15．点评：此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总情况数之比．13．任意抛掷一枚均匀的骰子一次，朝上的点数大于4的概率等于．考点：概率公式．分析：由任意抛掷一枚均匀的骰子一次，朝上的点数大于4的有2种情况，直接利用概率公式求解即可求得答案．解答：解：∵任意抛掷一枚均匀的骰子一次，朝上的点数大于4的有2种情况，∴任意抛掷一枚均匀的骰子一次，朝上的点数大于4的概率等于：=．故答案为：．点评：此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总情况数之比．14．五张分别写有﹣1，2，0，﹣4，5的卡片（除数字不同以外，其余都相同），现从中任意取出一张卡片，则该卡片上的数字是负数的概率是．考点：概率公式．分析：由五张分别写有﹣1，2，0，﹣4，5的卡片（除数字不同以外，其余都相同），直接利用概率公式求解即可求得答案．解答：解：∵五张分别写有﹣1，2，0，﹣4，5的卡片（除数字不同以外，其余都相同），∴该卡片上的数字是负数的概率是：．故答案为：．点评：此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总情况数之比．15．如果从初三（1）、（2）、（3）班中随机抽取一个班与初三（4）班进行一场拔河比赛，那么恰好抽到初三（1）班的概率是．考点：概率公式．分析：由从初三（1）、（2）、（3）班中随机抽取一个班与初三（4）班进行一场拔河比赛，直接利用概率公式求解即可求得答案．解答：解：∵从初三（1）、（2）、（3）班中随机抽取一个班与初三（4）班进行一场拔河比赛，∴恰好抽到初三（1）班的概率是：．故答案为：．点评：此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总情况数之比．16．100件外观相同的产品中有5件不合格，现从中任意抽取1件进行检测，抽到不合格产品的概率是．考点：概率公式．分析：由100件外观相同的产品中有5件不合格，直接利用概率公式求解即可求得答案．解答：解：∵100件外观相同的产品中有5件不合格，∴从中任意抽取1件进行检测，抽到不合格产品的概率是：=．故答案为：．点评：此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．三．解答题（共8小题）17．一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球．（1）求从袋中摸出一个球是黄球的概率；（2）现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是，求从袋中取出黑球的个数．考点：概率公式；分式方程的应用．分析：（1）由一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球，直接利用概率公式求解即可求得答案；（2）首先设从袋中取出x个黑球，根据题意得：=，继而求得答案．解答：解：（1）∵一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球，∴从袋中摸出一个球是黄球的概率为：=；（2）设从袋中取出x个黑球，根据题意得：=，解得：x=2，经检验，x=2是原分式方程的解，所以从袋中取出黑球的个数为2个．点评：此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．18．某商场为了吸引顾客，设立了可以自由转动的转盘（如图，转盘被均匀分为20份），并规定：顾客每购买200元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得200元、100元、50元的购物券，凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可以直接获得购物券30元．（1）求转动一次转盘获得购物券的概率；（2）转转盘和直接获得购物券，你认为哪种方式对顾客更合算？考点：概率公式．专题：图表型．分析：（1）由转盘被均匀分为20份，转动一次转盘获得购物券的有10种情况，直接利用概率公式即可求得答案；（2）首先求得指针正好对准红色、黄色、绿色区域的概率，继而可求得转转盘的情况，继而求得答案．解答：解：（1）∵转盘被均匀分为20份，转动一次转盘获得购物券的有10种情况，∴P（转动一次转盘获得购物券）==．（2）∵P（红色）=，P（黄色）=，P（绿色）==，∴（元）∵40元＞30元，∴选择转转盘对顾客更合算．点评：此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总情况数之比．19．红花中学现要从甲、乙两位男生和丙、丁两位女生中，选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛．（1）请用树状图或列表法列举出各种可能选派的结果；（2）求恰好选派一男一女两位同学参赛的概率．考点：列表法与树状图法．专题：常规题型．分析：（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果；（2）由（1）可求得恰好选派一男一女两位同学参赛的有8种情况，然后利用概率公式求解即可求得答案．解答：解：（1）画树状图得：则共有12种等可能的结果；（2）∵恰好选派一男一女两位同学参赛的有8种情况，∴恰好选派一男一女两位同学参赛的概率为：=．点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．20．某同学报名参加校运动会，有以下5个项目可供选择：径赛项目：100m，200m，400m（分别用A1、A2、A3表示）；田赛项目：跳远，跳高（分别用B1、B2表示）．（1）该同学从5个项目中任选一个，恰好是田赛项目的概率为；（2）该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率．考点：列表法与树状图法．分析：（1）由5个项目中田赛项目有2个，直接利用概率公式求解即可求得答案；（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好是一个田赛项目和一个径赛项目的情况，再利用概率公式即可求得答案．解答：解：（1）∵5个项目中田赛项目有2个，∴该同学从5个项目中任选一个，恰好是田赛项目的概率为：；故答案为：；（2）画树状图得：∵共有20种等可能的结果，恰好是一个田赛项目和一个径赛项目的12种情况，∴恰好是一个田赛项目和一个径赛项目的概率为：=．点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．21．在一个口袋里有四个完全相同的小球，把它们分别标号为1，2，3，4，小明和小强采取的摸取方法分别是：小明：随机摸取一个小球记下标号，然后放回，再随机摸取一个小球，记下标号；小强：随机摸取一个小球记下标号，不放回，再随机摸取一个小球，记下标号．（1）用画树状图（或列表法）分别表示小明和小强摸球的所有可能出现的结果；（2）分别求出小明和小强两次摸球的标号之和等于5的概率．考点：列表法与树状图法．分析：（1）首先根据题意画出树状图，然后由树状图得出所有可能的结果，注意是放回实验还是不放回实验；（2）根据（1）可求得小明两次摸球的标号之和等于5的有4种可能，小强两次摸球的标号之和等于5的有4种可能，然后利用概率公式求解即可求得答案．。

第1章 随机事件与概率 一、 基本概念概率论研究随机现象的统计规律性。

1．事件的运算及关系 ● 事件的并A ∪B =“两事件A 与B 中至少有一件发生”。

● 事件的交A ∩B =AB =“两事件A 与B 都发生”。

1ni i A == “n 个事件12,,,n A A A 中至少有一件发生”；1ni i A == “n 个事件12,,,n A A A 都发生”。

● 事件的运算规律（1）交换律：A B B A =，AB BA =；（2）结合律：()()A B C A B C =，()()AB C A BC =；（3）分配律：()A B C AB AC =，()()()A BC A B A C =；（4）对偶律：AB AB =，AB A B =。

11nni i i i A A ===；11nni i i i A A ===.● 包含若事件A 的发生必然导致事件B 的发生，则称事件B 包含事件A ，记为B A ⊂。

● 相等当事件B 包含事件A 且事件A 也包含事件B 时，则称事件A 与B 相等,记为A =B 。

● 互不相容（互斥）若两事件A 与B 不可能同时发生，即AB =φ，则称事件A 与B 互不相容。

● 对立若两事件A 与B 互不相容，且它们的并是必然事件，即A ∪B =Ω，AB =φ，则称A 与B 互为对立事件，记为A B =或B A =。

● 独立称A 与B 相互独立，如果 P (AB )=P (A )P (B )。

注意两事件互不相容、对立与独立之间的关系。

2．概率与条件概率随机事件发生的可能性大小称为随机事件的概率.条件概率是指事件B 已经发生的条件下，事件A 发生的概率，记作(|)P A B 。

定义 设()0P B >，则在事件B 已发生的条件下, 事件A 的条件概率定义为()(|)()P AB P A B P B =。

二、基本方法1．频率方法（统计方法）独立重复试验n 次，当n 充分大时，可把事件A 出现的频率nA A f n n )()(μ=作为A 的概率P (A )的近似值。