下载文档原格式
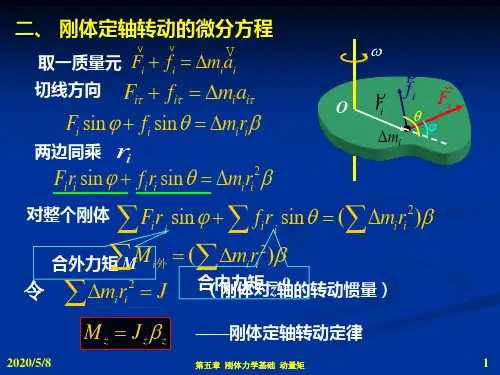
刚体定轴转动知识点总结1. 刚体的转动定轴刚体的转动定轴是指固定不动的直线，沿其进行转动的刚体的每一个质点所受的力矩的代数和等于零。
在实际中，通常通过支点来实现转动定轴，比如钟摆、摇摆、旋转的转轴等。
2. 刚体的角位移、角速度和角加速度在刚体定轴转动中，刚体围绕定轴线进行旋转，其角位移、角速度和角加速度是非常重要的物理量。
角位移表示刚体在围绕定轴线旋转的过程中所经过的角度变化量，通常用θ表示；角速度表示刚体围绕定轴线旋转的速度，通常用ω表示；角加速度表示刚体围绕定轴线旋转的加速度，通常用α表示。
3. 牛顿第二定律在刚体定轴转动中的应用牛顿第二定律也适用于刚体定轴转动的情况。
在刚体定轴转动中，外力会给刚体带来转动运动，根据牛顿第二定律，刚体的角加速度与作用在其上的外力矩成正比。
因此，可以根据力矩的大小和方向来分析刚体的转动运动。
4. 转动惯量和转动动能在刚体定轴转动中，转动惯量是一个非常重要的物理量。
转动惯量描述了刚体围绕定轴线旋转的难易程度，其大小与刚体的质量分布和轴线的位置有关。
转动动能是刚体围绕定轴线旋转的能量，其大小取决于刚体的转动惯量和角速度。
5. 转动定律和角动量守恒定律在刚体定轴转动中，转动定律和角动量守恒定律是非常重要的定律。
转动定律描述了刚体受力矩产生的角加速度与所受力矩的关系，角动量守恒定律描述了刚体转动过程中角动量的守恒规律。
6. 平衡条件和稳定性分析在刚体定轴转动中，平衡条件和稳定性分析是非常重要的内容。
通过平衡条件，可以分析刚体围绕定轴线旋转的平衡状态。
稳定性分析则是分析刚体在平衡状态下的稳定性，通常通过刚体的势能函数和平衡位置的稳定性来进行分析。
7. 应用领域刚体定轴转动的理论和方法在工程技术、航空航天、机械制造、物理学等领域都有重要的应用价值。
比如在机械制造中，可以通过分析刚体的定轴转动来设计机械装置；在航空航天中，可以通过分析刚体的定轴转动来设计飞行器的运动控制系统。
转动动能守恒定律
一、转动动能的概念
1. 对于一个绕固定轴转动的刚体，转动动能的表达式为E_{k}=(1)/(2)Iω^2，其中I是刚体对给定轴的转动惯量，ω是刚体转动的角速度。
- 转动惯量I取决于刚体的质量分布和转轴的位置。
对于一些简单形状的刚体，有特定的转动惯量计算公式。
例如，对于质量为m、半径为r的均匀圆盘，绕通过圆心垂直于盘面的轴转动时，转动惯量I = (1)/(2)mr^2；对于质量为m、长度为L的细棒，绕通过棒中心垂直于棒的轴转动时，转动惯量I=(1)/(12)mL^2。
2. 与平动动能类似，转动动能是描述刚体转动状态下具有的能量。
平动动能是(1)/(2)mv^2，这里的v是平动速度，而转动动能中的ω是角速度，反映了刚体转动的快慢。
1. 定律内容
- 如果一个刚体所受的合外力矩为零，即M = 0时，刚体的转动动能守恒，也就是(1)/(2)I_{1}ω_{1}^2=(1)/(2)I_{2}ω_{2}^2。
这意味着在转动过程中，虽然刚体的转动惯量I和角速度ω可能会发生变化，但它们的乘积Iω^2保持不变。
2. 适用条件
- 系统（刚体）所受的合外力矩为零。
这一条件类似于平动中的动量守恒定律（合外力为零）。
例如，在光滑的水平面上，一个圆盘绕中心轴转动，如果没有摩擦力矩等外力矩的作用，圆盘的转动动能守恒。
- 在一些实际问题中，需要准确分析系统的受力情况，判断是否满足合外力矩为零的条件。
例如，对于一个由多个刚体组成的系统，如果它们之间的内力矩不影响系统的总角动量（满足角动量守恒的条件下），并且系统没有受到外力矩作用，那么系统的转动动能也守恒。
3. 应用实例。
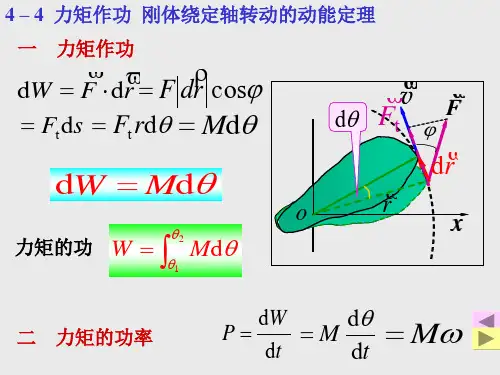
谁能讲解一下关于扭矩、转动惯量、载荷、能量等相关姿势啊！问题回答时间：2009-09-12 08:14:31扭矩在物理学中就是力矩的大小，等于力和力臂的乘积，国际单位是牛米Nm，此外我们还可以看见kgm、lb-ft这样的扭矩单位，由于G=mg，当g=9.8的时候，1kg的重量为9.8N，所以1kgm＝9.8Nm，而磅尺lb-ft 则是英制的扭矩单位，1lb=0.4536kg;1ft=0.3048m，可以算出1lb-ft＝0.13826kgm。
在人们日常表达里，扭矩常常被称为扭力（在物理学中这是2个不同的概念）。
现在我们举个例子：8代Civic 1.8的扭矩为173.5Nm@4300rpm，表示引擎在4300转/分时的输出扭矩为173.5Nm，那173.5N的力量怎么能使1吨多的汽车跑起来呢？其实引擎发出的扭矩要经过放大（代价就是同时将转速降低）这就要靠变速箱、终传和轮胎了。
引擎释放出的扭力先经过变速箱作“可调”的扭矩放大（或在超比挡时缩小）再传到终传（尾牙）里作进一步的放大（同时转速进一步降低），最后通过轮胎将驱动力释放出来。
如某车的1挡齿比（齿轮的齿数比，本质就是齿轮的半径比）是3，尾牙为4，轮胎半径为0.3米，原扭矩是200Nm的话，最后在轮轴的扭力就变成200×3×4＝2400Nm（设传动效率为100%）在除以轮胎半径0.3米后，轮胎与地面摩擦的部分就有2400Nm/0.3m＝8000N的驱动力，这就足以驱动汽车了。
若论及机械效率，每经过一个齿轮传输，都会产生一次动力损耗，手动变速箱的机械效率约在95%左右，自排变速箱较惨，约剩88%左右，而传动轴的万向节效率约为98%。
整体而言，汽车的驱动力可由下列公式计算：补充一点：为什么引擎的功率能由扭矩计算出来呢？我们知道，功率P＝功W÷时间t 功W＝力F×距离s 所以，P＝F×s/t＝F×速度v这里的v是线速度，而在引擎里，曲轴的线速度＝曲轴的角速度ω×曲轴半径r，代入上式得：功率P＝力F×半径r×角速度ω；而力F×半径r＝扭矩得出：功率P＝扭矩×角速度ω所以引擎的功率能从扭矩和转速中算出来角速度的单位是弧度/秒，在弧度制中一个派代表180度扭矩的计算方法扭矩=9550×电机功率÷电机功率输入转数×速比×使用系数刚体绕轴转动惯性的度量。
转动动能定理转动动能定理引言：在物理学中，旋转运动是一种非常重要的运动形式。
它广泛应用于机械、电子、化学等领域。
而转动动能定理则是研究旋转运动的重要定理之一。
一、定义1.1 转动惯量在物理学中，物体的转动惯量是描述物体对于旋转运动的惯性大小的物理量。
它表示了一个物体对于绕某个轴旋转时所表现出来的抵抗力大小。
1.2 角速度角速度是指一个物体绕某个轴线旋转时单位时间内所经过的角度。
它通常用符号ω表示，单位是弧度每秒（rad/s）。
1.3 转动角加速度转动角加速度是指一个物体绕某个轴线旋转时单位时间内角速度变化量，通常用符号α表示，单位是弧度每秒平方（rad/s²）。
二、公式推导2.1 转动运动定律在刚体绕固定轴线做匀加速直线运动时，其加速度a与作用力F之间有如下关系：F=ma同样，在刚体绕固定轴线做匀加速圆周运动时，其加速度a与作用力F 之间也有如下关系：F=ma但是，由于旋转运动涉及到角度的概念，因此在刚体绕固定轴线做匀加速圆周运动时，我们需要引入一个新的物理量——转动惯量。
2.2 转动惯量的定义当一个物体绕某个轴线旋转时，它所表现出来的抵抗力大小与以下三个因素有关：1）物体质量的大小；2）轴线距离物体质心的远近；3）物体形状和密度分布情况。
因此，我们可以定义一个新的物理量——转动惯量I来描述这种抵抗力大小。
具体而言，当一个质量为m、距离轴线为r、转动惯量为I的物体绕某个轴线旋转时，它所表现出来的抵抗力大小可以表示为：τ=Iα其中τ表示物体所受到的扭矩（或者说力矩），α表示物体绕轴线旋转时所表现出来的角加速度。
2.3 转动动能定理在刚体绕固定轴线做匀加速圆周运动时，其机械能守恒，即E=K+U=常数其中E表示机械能，K表示动能，U表示势能。
我们可以将刚体的机械能分解为平动动能和转动动能两部分：E=Kp+Kr+U其中Kp表示平动动能，Kr表示转动动能。
根据定义可知，Kp=½mv²Kr=½Iω²因此，E=½mv²+½Iω²+U我们将上式两边同时对时间求导数，得到：dE/dt=mvdv/dt+Iωdω/dt+dU/dt由于匀加速圆周运动中v、ω和r之间有如下关系：v=rω因此，dv/dt=r dω/dt代入上式可得：dE/dt=mvr dω/dt+I dω/dt+dU/dt根据牛顿第二定律可以得到：F=mvr dω/dt=τ因此，dE/dt=τdθ/dt+dU/dθ dθ/dt=d(τθ)/dt+dU/dθ dθ/dt=d(τθ)/dt+dU/dt=dWext/dt其中Wext表示外力所做的功。
高一物理同轴转动知识点同轴转动是物理学中一种重要的运动形式，也是力学和电磁学的基本概念之一。
同轴转动涉及到刚体和转动轴线的运动，能帮助我们更好地理解物体的旋转和旋转力学。
1. 同轴转动的定义和特点同轴转动是指物体围绕一个固定的轴线旋转的运动形式。
在同轴转动中，物体的所有点都绕着同一个轴线旋转，且每个点的转动速度相同。
这是因为同轴转动中，转动轴线是固定的，整个物体保持稳定的旋转。
2. 转动惯量和转动定律转动惯量是同轴转动中一个重要的物理量，它表示物体对转动的惯性大小。
转动惯量的大小与物体的质量分布和旋转轴线的位置有关。
对于同轴转动，我们可以通过以下公式计算转动惯量：I = Σmiri²其中，I表示转动惯量，m表示质点的质量，ri表示质点距离转轴的距离，Σ表示对所有质点进行求和。
转动定律也是同轴转动中一个重要的定律，它描述了物体在外力作用下的转动行为。
根据转动定律，物体的转动角加速度与外力矩成正比，与物体的转动惯量成反比。
转动定律可以用以下公式表示：τ = Iα其中，τ表示外力矩，I表示转动惯量，α表示转动角加速度。
3. 转动动能和动能定理同轴转动中，物体具有转动动能，它表示物体旋转时的能量。
转动动能的大小与物体的转动惯量和角速度有关。
对于同轴转动，我们可以用以下公式计算转动动能：K = 1/2Iω²其中，K表示转动动能，I表示转动惯量，ω表示角速度。
动能定理可以将力学中的力和物体的加速度联系起来。
同样，转动动能定理将力矩和物体的转动角加速度联系起来。
根据转动动能定理，物体的转动动能的增量等于外力矩对物体所做的功。
转动动能定理的公式为：ΔK = τΔθ其中，ΔK表示转动动能的增量，τ表示外力矩，Δθ表示转动的角位移。
4. 滑轮和转动惯量在同轴转动中，滑轮是一种常见的应用。
滑轮是由一个或多个连续转动的轮子组成的装置，可以改变力的方向和大小。
在滑轮中，我们需要计算物体的转动惯量，以确定力的作用对物体运动的影响。
