第十二章4波的衍射和干涉

波的衍射与干涉的计算波的衍射与干涉是物理学中重要的现象和计算方法。

它们描述了波动现象在传播过程中的特性和影响。

在本文中，我们将介绍一些和波的衍射与干涉相关的计算方法，并探讨它们的应用。

波的衍射是指波在遇到障碍物或通过缝隙时发生弯曲和扩散的现象。

当波传播到障碍物或缝隙时，它们会发生折射、散射和干涉，从而形成衍射效应。

衍射现象的计算可以通过洛伦兹-费涅尔衍射公式进行。

这个公式是根据赫尔姆霍兹方程和亥姆霍兹方程推导出来的，它可以描述波在衍射过程中的传播和干涉特性。

为了更好地理解波的衍射与干涉的计算过程，我们可以以光波为例。

当光波通过一个狭缝时，它会发生衍射现象。

通过公式计算，我们可以得到波的幅度和相位分布，从而进一步分析其衍射图样。

干涉是指两个或多个波相遇时相互叠加形成新的波形的现象。

其中，干涉可以分为相干干涉和非相干干涉。

相干干涉一般指的是相干光通过分束器或其他装置分为两束，并在某一点上相遇形成干涉条纹。

这种情况下，我们可以使用杨氏干涉实验来计算干涉条纹的宽度和间距。

波的相位是波动现象中的一个重要概念，它描述了波的振动状态。

在衍射和干涉的计算中，相位是一个关键的参数。

相位的计算可以通过波的传播速度、波长、振荡周期等指标来确定。

除了理论计算，实验也是研究波的衍射与干涉的重要途径。

在实验中，我们可以利用干涉仪、衍射光栅等装置来观察和测量衍射与干涉现象。

这些实验可以帮助我们验证理论模型，并进一步理解波的行为。

波的衍射与干涉在不同领域具有广泛的应用。

在光学领域，干涉和衍射技术被广泛应用于激光干涉测量、光学薄膜研究等领域。

在声学领域，波的干涉和衍射技术被应用于无损检测、声学成像等领域。

此外，衍射和干涉还在电子学、无线通信等领域中起着重要作用。

综上所述，波的衍射与干涉是物理学中的重要现象和计算方法。

通过对波动方程和干涉公式的理解和运用，我们可以计算出波的衍射和干涉的特性，进一步理解波的行为和物理规律。

在实际应用中，波的衍射与干涉技术具有广泛的应用前景，为各个领域的研究和应用提供了重要的理论基础。

《波的干涉与衍射》讲义一、波的基本概念在我们探讨波的干涉与衍射现象之前，先来了解一下波的一些基本概念。

波是一种能量传递的方式，它可以在介质中传播。

常见的波有机械波和电磁波。

机械波需要介质来传播，比如水波、声波；电磁波则不需要介质，比如光波、无线电波。

波具有一些重要的特性，如波长、频率、波速等。

波长是指相邻两个波峰或波谷之间的距离；频率是指单位时间内波振动的次数；波速则是波在介质中传播的速度，它等于波长与频率的乘积。

二、波的干涉当两列或两列以上的波在空间相遇时，就会发生波的干涉现象。

波的干涉条件有两个：一是两列波的频率必须相同；二是两列波的振动方向必须相同，并且具有固定的相位差。

我们来想象一下这样的场景：有两个相同的波源，它们同时向外发出频率相同的波。

当这些波在空间中传播并相遇时，在某些区域，两列波的振动总是相互加强，形成振动加强区；而在另一些区域，两列波的振动总是相互削弱，形成振动减弱区。

振动加强区的特点是振幅增大，能量增强；振动减弱区的特点则是振幅减小，能量减弱。

那么，如何确定哪些地方是振动加强区，哪些地方是振动减弱区呢？这就要用到干涉的条件和波的叠加原理。

假设两列波的波程差为Δr，波长为λ，当Δr 等于波长的整数倍时，两列波在该点振动加强；当Δr 等于半波长的奇数倍时，两列波在该点振动减弱。

波的干涉在生活中有很多实际应用。

比如，在光学中，利用干涉可以制作出高精度的测量仪器，如迈克尔逊干涉仪；在无线电技术中，干涉可以用于提高信号的接收质量。

三、波的衍射接下来，我们再来看波的衍射现象。

波在传播过程中遇到障碍物或小孔时，会偏离原来的直线传播路径，绕过障碍物或从小孔中“钻”过去，这种现象就是波的衍射。

衍射现象是否明显，与障碍物或小孔的尺寸以及波长有关。

当障碍物或小孔的尺寸比波长小得多时，衍射现象非常明显；当障碍物或小孔的尺寸与波长相差不多时，衍射现象也比较明显；当障碍物或小孔的尺寸比波长大得多时，衍射现象就不太明显了。

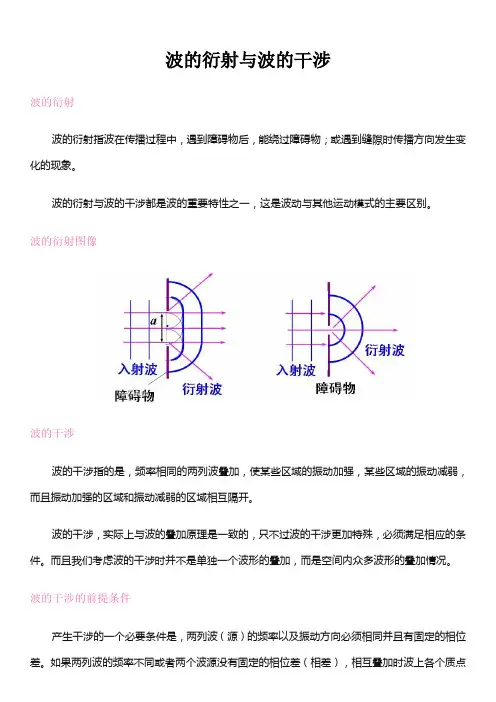
波的衍射与波的干涉波的衍射波的衍射指波在传播过程中，遇到障碍物后，能绕过障碍物；或遇到缝隙时传播方向发生变化的现象。

波的衍射与波的干涉都是波的重要特性之一，这是波动与其他运动模式的主要区别。

波的衍射图像波的干涉波的干涉指的是，频率相同的两列波叠加，使某些区域的振动加强，某些区域的振动减弱，而且振动加强的区域和振动减弱的区域相互隔开。

波的干涉，实际上与波的叠加原理是一致的，只不过波的干涉更加特殊，必须满足相应的条件。

而且我们考虑波的干涉时并不是单独一个波形的叠加，而是空间内众多波形的叠加情况。

波的干涉的前提条件产生干涉的一个必要条件是，两列波（源）的频率以及振动方向必须相同并且有固定的相位差。

如果两列波的频率不同或者两个波源没有固定的相位差（相差），相互叠加时波上各个质点的振幅是随时间而变化的，没有振动总是加强或减弱的区域，因而不能产生稳定的干涉现象，不能形成干涉图样。

波的干涉图样波的干涉所形成的图样叫做干涉图样，是非常好的理解波的干涉的工具。

下面我们通过波的干涉图样来进一步理解波的干涉。

如下图所示，为两个完全相同的波（S1与S2）在平面内的传播。

如果用实线来描述波峰，虚线表示波谷。

根据波的叠加原理，在平面内图像中的波峰与波峰（以及波谷与波谷）的交汇处，为振动加强点。

与之对应的是，波峰与波谷的交汇处，振动削弱。

这样，就犹如波的干涉的定义描述的那样：波的干涉指的是，频率相同的两列波叠加，使某些区域的振动加强，某些区域的振动减弱，而且振动加强的区域和振动减弱的区域相互隔开。

可能上面的图像太复杂了，不好辨识出来。

那么接下来我们通过一部分干涉图像来分析。

如下图所示，同样为两个完全相同的波（S1与S2）在平面内的传播。

实线来描述波峰的，显然波谷就是相邻的两条实线中间的位置（没有画出来）。

比较容易看出来，a点是振动削弱的（波峰与波谷交汇处），b点是振动加强的（波谷与波谷交汇处）。

波的衍射与波的干涉区别从定义上来找两者的区别：波的衍射定义：波的衍射指波在传播过程中，遇到障碍物后，能绕过障碍物；或遇到缝隙时传播方向发生变化的现象。

波的干涉和衍射现象波的干涉和衍射是波动现象中非常重要且有趣的现象。

它们具有深刻的物理意义，不仅可以解释光的行为，还可以应用于各个领域。

本文将介绍波的干涉和衍射现象，并探讨它们在光学和其他领域中的应用。

波的干涉是指两个或多个波相互叠加时产生的干涉现象。

当两个波波峰或波谷相遇时，它们会相互增强，形成明亮的干涉条纹；而当波峰与波谷相遇时，则会相互抵消，形成暗条纹。

这种干涉现象可以用叠加原理解释。

波动理论认为，波既具有粒子特性，也具有波动特性，而干涉现象正是波动特性的体现。

波的干涉现象最早被英国物理学家托马斯·杨发现并解释为光的干涉。

杨实验通过将光线分成两道光，然后让它们通过两个微细的狭缝，之后让它们重新重合。

当光线重合时，就会观察到明暗相间的干涉条纹。

这一实验验证了光是一种波动现象，并奠定了光的波动理论的基础。

波的干涉除了可以发生在光波上，还可以发生在其他类型的波上，比如水波、声波等。

比如，当水波通过两个狭缝时，也会出现干涉现象，形成明暗相间的水波纹。

这种水波干涉现象在海洋学研究中被广泛应用，可以用来研究海浪的传播和波动特性。

波的衍射是指波通过障碍物或孔径时发生的偏斜现象。

当波通过一个小孔时，会呈现出一种扩散的现象，形成从中心向外辐射的光圈。

波的衍射现象可以解释为波通过障碍物或孔径时，波的传播方向发生了改变。

波的衍射现象对于光学的发展起到了重要作用。

它帮助人们理解了光是如何传播的，并为光的波动理论提供了重要的支持。

在现代光学中，衍射也被广泛应用于衍射光栅、衍射仪器等方面。

光栅是光的波长级衍射光栅，它可以分解复杂的光谱，对于光谱分析具有重要意义。

许多重要的科学实验，如迈克尔逊干涉仪的工作原理也依赖于衍射现象。

除了光学，波的干涉和衍射现象在其他学科中也有着广泛的应用。

比如，在声学中，波的干涉和衍射现象可以用来制作音乐乐器或调音。

在地质学中，地震波的干涉和衍射现象可以用来研究地壳的结构和地震活动。

第十二章机械波第4节波的衍射和干涉课时分层训练「基础达标练」1．一块小石子投入河水中激起一列水波，遇到障碍物后能发生明显衍射现象，障碍物是()A．静止在河面的渔船B．静止在河面的货船C．竖立在河中的竹竿D．竖立在河中的桥墩解析：选C河水中激起一列水波，遇到障碍物后能发生明显衍射现象，依据发生明显的衍射现象的条件是障碍物的尺寸与波长相差不大或者比波长小，故该障碍物的尺寸较小，故C正确，A、B、D错误．2．(多选)当两列水波发生干涉时，如果两列波的波峰在P点相遇，则() A．质点P的振动始终是加强的B．质点P的振幅最大C．质点P的位移始终最大D．质点P的周期最大解析：选AB P点为波峰与波峰叠加，为振动加强点，振动始终加强，振幅最大．位移在变化，有时为零，有时最大，故A、B正确，C错误；质点P的周期不变，选项D错误．3．(2019·山西怀仁八中高二月考)已知空气中的声速为340 m/s.现有几种声波：①周期为120s，②频率为104Hz，③波长为10 m，它们传播时若遇到宽约为13 m的障碍物，能产生显著的衍射现象的是() A．①和②B．②和③C．①和③D．都可以解析：选C由波速公式v＝λf得：波长λ＝vf＝v T，则①②③三种声波的波长分别为λ1＝340×120 m ＝17 m ，λ2＝340104 m ＝0.034 m ，λ3＝10 m ，根据发生明显衍射现象的条件可知，①③两声波的波长与障碍物的尺寸差不多，能产生明显的衍射现象，故C 正确．4．(多选)某同学注意到手机摄像头附近有一个小孔，查阅手机说明后知道手机内部小孔位置处安装了降噪麦克风．进一步翻阅技术资料得知：降噪麦克风通过降噪系统产生与外界噪音相位相反的声波，与噪音叠加从而实现降噪的效果．如图是理想情况下的降噪过程，实线对应环境噪声，虚线对应降噪系统产生的等幅反相声波．则( )A ．降噪过程实际上是声波发生了干涉B ．降噪过程可以消除通话时的所有背景杂音C ．降噪声波与环境噪声的传播速度相等D ．P 点经过一个周期传播的距离为一个波长解析：选AC 分析题意可知，降噪过程实际上是声波发生了干涉，降噪声波与环境声波波长相等，波速相等，频率相同，由于两列声波等幅反相，使噪声振动减弱，A 选项正确；降噪过程不能消除通话时的所有背景杂音，只能消除与降噪声波频率相同的杂音，B 选项错误；机械波传播的速度由介质决定，所以降噪声波与环境噪声的传播速度相等，C 选项正确；机械波在传播过程中，介质中的质点不会随波移动，D 选项错误．5．(多选)两列完全相同的机械波于某时刻的叠加情况如图所示，图中的实线和虚线分别表示波峰和波谷，此时( )A ．a 、b 连线中点振动加强B．a、b连线中点速度为零C．a、b、c、d四点速度均为零D．再经过12周期c、d两点振动仍然减弱解析：选ACD题图是两列频率相同的相干水波于某时刻的叠加情况，实线和虚线分别表示波峰和波谷，则a点是波谷与波谷相遇点，b是波峰与波峰相遇点，c、d两点是波峰与波谷相遇点．则a、b两点是振动加强的，且ab连线上也是振动加强的，c、d两点是振动减弱的，故A正确，B错误；a、b分别处于波谷、波峰位置，此时它们的速度为零，c、d是波峰、波谷相遇点，为减弱点，其振幅为零，则c、d的速度也为零，因此它们的速度均为零，故C正确；c、d两点处于波谷与波峰相遇处，再经过12周期，c、d两点振动仍然减弱，故D正确．6．(多选)(2019·福建师大附中高二期中)如图所示，两列简谐横波分别沿x 轴正方向和负方向传播，两波源分别位于x＝－1.0 m和x＝5.0 m处，两列波的速率均为v＝2 m/s，两波源的振幅均为A＝2 cm.图示为t＝0时刻两列波的图象(传播方向如图所示)，此刻平衡位置处于x＝1.0 m和x＝3.0 m的M、N两质点刚开始振动．质点P、Q的平衡位置分别处于x＝2.0 m和x＝2.5 m处，关于各质点运动情况判断正确的是()A．质点Q的起振方向沿y轴正方向B．t＝1.25 s时刻，质点M的位移为－4 cmC．两列波能发生干涉，发生干涉后质点P为振动减弱点D．两列波能发生干涉，发生干涉后质点Q为振动加强点解析：选ACD M、N点刚起振，由同侧法可知，M点向下振动，N点向上振动，即两列波的起振方向相反．由两列波的传播速度相等，Q距N点近，故N点的振动形式先传播到Q点，故Q点的起振方向与N点的起振方向相同，起振时沿y轴向上，A对；M点距两波源的距离差值为一个波长，因两列波的起振方向相反，故M点为振动减弱点，两列波的振幅相同，故M点的位移始终为零，B错；同理可判断P为振动减弱点，Q为振动加强点，C、D对．7．如图是水面上两列频率相同的波在某时刻的叠加情况，以波源S1、S2为圆心的两组同心圆弧分别表示同一时刻两列波的波峰(实线)和波谷(虚线)，S1的振幅A1＝4 cm，S2的振幅A2＝3 cm，则下列说法正确的是()A．质点D是振动减弱点B．质点A、D在该时刻的高度差为14 cmC．再过半个周期，质点B、C是振动加强点D．质点C的振幅为7 cm解析：选B题图是两列频率相同的相干水波于某时刻的叠加情况，实线和虚线分别表示波峰和波谷，则D点是波谷与波谷相遇点，A点是波峰与波峰相遇点，B、C两点是波峰与波谷相遇点．则A、D两点是振动加强的，且B、C两点是振动减弱的．质点D是振动加强点，故A错误；S1的振幅A1＝4 cm，S2的振幅A2＝3 cm，质点A是处于波峰叠加位置，相对平衡位置高度为7 cm，而质点D处于波谷叠加位置，相对平衡位置为－7 cm，因此质点A、D在该时刻的高度差为14 cm，故B正确；B、C两点是振动减弱点，再过半个周期，质点B、C 仍是振动减弱点，故C错误；质点C是波峰与波谷的叠加点，则其合振幅为1 cm，故D错误．8．甲、乙两人分乘两只小船在湖中钓鱼，两船相距24 m．有一列水波在湖面上传播，使每只船每分钟上下浮动20次，当甲船位于波峰时，乙船位于波谷，这时两船之间还有5个波峰．(1)此水波的波长为多少？波速为多少？(2)若此波在传播过程中遇到一根竖立的电线杆，是否会发生明显的衍射现象？(3)若该波经过一跨度为30 m的桥洞，桥墩直径为3 m，桥墩处能否看到明显衍射？(4)若该桥为一3 m宽的涵洞，洞后能否发生明显衍射？解析：(1)由题意知：周期T＝6020s＝3 s.设波长为λ，则5λ＋λ2＝24 m，λ＝4811m.由v＝λT 得，v＝4811×3m/s＝1611m/s.(2)由于λ＝4811m，大于竖立电线杆的直径，所以此波通过竖立的电线杆时会发生明显的衍射现象．(3)(4)由于λ＝4811m>3 m，所以此波无论是通过直径为3 m的桥墩，还是通过宽为3 m的涵洞，都能发生明显衍射现象．答案：(1)4811m1611m/s(2)会(3)能(4)能「能力提升练」9．(多选)甲、乙两列简谐横波在同一均匀介质中相向传播并相遇，在t＝0时刻两列波的位置如图所示．若两列波的周期分别为T甲和T乙，则()A．这两列波相遇时能产生干涉现象B．这两列波将同时到达坐标原点C．在t＝34T乙时刻，x＝0.1 m处质点受到的回复力为零D．在t＝2T甲时刻，x＝0.1 m处质点的位移为零解析：选BD两列简谐横波在同一均匀介质内传播，可知波速相等，由题图可知两列波的波长不相等，由v＝λf可知，频率不相等，不能产生干涉现象，故A错误；两列简谐横波在同一均匀介质内传播，可知波速相等，此时两列波到原点的距离相等，根据t＝x v可知这两列波将同时到达坐标原点，故B正确；时刻，乙波刚好传播到原点处，此时x＝0.1 m处质点位于波峰，受到在t＝34T乙的回复力不为零，故C错误；根据图象可知T甲＝0.2v，T乙＝0.4v，即T乙＝2T甲，在t＝2T甲时刻，甲波刚好传播到x＝0.1 m处，乙波波形中点平衡位置传到x＝0.1 m处，此时x＝0.1 m 处质点的位移为零，故D正确．10．(多选)如图甲所示，在水平面内的三个质点分别位于直角三角形ABC的顶点上，已知AB＝6 m，AC＝8 m．t0＝0时刻A、B开始振动，波动图象均如图乙所示，所形成的机械波在水平面内传播，在t＝4 s时C点开始振动．则()A．该机械波的传播速度大小为4 m/sB．两列波相遇后，C点振动加强C．两列波相遇后，C点振动减弱D．该列波的波长是2 mE．该列波的周期T＝1 s解析：选BDE分析图乙可知，波长为2 m，D选项正确；介质决定波速，两波源在同一介质中传播，故两列波的波速相同，根据几何关系可知，A处振动＝2 m/s，A选项错误；两波源振动情况相同，两波源先到达C点，波速v＝ACt到介质中某质点的波程差为整数个波长时，该质点为振动加强点．C点到A、B两点的路程差为Δs＝BC－AC＝λ，故C点为振动加强点，B选项正确，C选项错误；根据波长、周期和波速的关系可知，T＝λv＝1 s，E选项正确．11．(多选)(2019·全国卷Ⅲ)水槽中，与水面接触的两根相同细杆固定在同一个振动片上．振动片做简谐振动时，两根细杆周期性触动水面形成两个波源．两波源发出的波在水面上相遇，在重叠区域发生干涉并形成了干涉图样．关于两列波重叠区域内水面上振动的质点，下列说法正确的是()A．不同质点的振幅都相同B．不同质点振动的频率都相同C．不同质点振动的相位都相同D．不同质点振动的周期都与振动片的周期相同E．同一质点处，两列波的相位差不随时间变化解析：选BDE在波的干涉实验中，质点在振动加强区的振幅是两列波振幅之和，质点在振动减弱区的振幅是两列波振幅之差，A项错误；沿波的传播方向上，波不停地向外传播，故各质点的相位不都相同，C项错误；两波源振动频率相同，其他各质点均做受迫振动，故频率均与振源频率相同，周期均与振动片的周期相同，B、D项正确；同一质点到两波源的距离确定，故波程差恒定，即相位差保持不变，E项正确．12．(多选)如图所示，在x轴上有两个沿竖直方向振动的波源S1、S2(图中未画出)在两波源之间有a、b两个点，二者间距为2 m．已知a点振动始终减弱且振幅为2 cm，b点振动始终加强且振幅为8 cm，观察发现b点连续出现两次波峰间隔时间为2 s，假设a、b之间没有振动加强点和减弱点．则下列判断正确的是()A．两波源S1、S2振动周期一定相同，且周期为2 sB．两波源S1、S2在介质中产生的机械波的波长为4 mC．波源S1振幅可能是5 cmD．两波源S1、S2在介质中产生的机械波的波速为4 m/s解析：选ACD 两列波发生干涉，它们的频率、周期一定是相等的，b 点连续出现两次波峰间隔时间为2 s ，可知两波源的周期都是2 s ，故A 正确；由题假设a 、b 之间没有振动加强点和减弱点，a 点振动始终减弱，b 点振动始终加强；设a 到左右两个波源的距离分别为x a 1和x a 2，则：|x a 1－x a 2|＝⎝ ⎛⎭⎪⎫n ＋12λ；① 设b 到左右两个波源的距离分别为x b 1和x b 2，则：|x b 1－x b 2|＝nλ②a 、b 之间的距离：L ＝|x a 1－x b 1|＝|x b 2－x a 2|＝2 m ③联立①②③式可得λ＝8 m ，故B 错误；由于a 点振动始终减弱且振幅为2 cm ，b 点振动始终加强且振幅为8 cm ，设A 的振幅为A 1，B 的振幅为A 2，则：A 1＋A 2＝8 cm ；|A 1－A 2|＝2 cm可得A 1＝3 cm 或A 1＝5 cm ，故C 正确；两列波的波速：v ＝λT ＝82＝4 m/s ，故D 正确．13．如图是两个波源振动频率相同、振动方向相同的两列波在空间传播的情景，实线表示波峰，虚线表示波谷．a 为虚线交点，b 为实线交点，c 为a 与b 连线的中点．(1)从图示时刻开始，经过12周期，a 、b 、c 各点分别处于什么位置？ (2)从图示时刻开始，经过34周期，a 、b 、c 各点又分别处于什么位置？解析：(1)由题图可知，此刻a 、b 点分别是两列波的波谷相遇点和波峰相遇点，都是振动加强点；而c 点处于加强区域，所以c 点也是加强点，a 、b 、c 三点的振幅为两列波的振幅之和．此刻a 点在波谷，b 点在波峰，c 点在平衡位置，经12周期后，a点在波峰，b点在波谷，c点仍在平衡位置．(2)经过34周期，a点在平衡位置，将向波谷振动；b点在平衡位置，将向波峰振动；c点为a、b的中点，所以此刻c点在波峰位置．答案：(1)a在波峰，b在波谷，c在平衡位置(2)a在平衡位置，b在平衡位置，c在波峰14.有频率相同、振动方向相同的两个声源S1和S2，如图所示．一人站在声源北方的A点，此人此时听到的声音很响，这个人向东慢慢移动，声音逐渐减弱，到B点时几乎听不到声音，测得A、B间距离为1.5 m．则：(1)S1、S2声波的波长λ为多少？(2)若此人由B点再向正南方向移动，声音逐渐变响，那么，此人沿正南方向至少走多远，声音又变得很响？解析：(1)依题意，A在S1S2的中垂线上，S1A＝S2A，此点为声波叠加振动加强处，走到B点几乎听不到声音，B点是声波叠加振动减弱处，则S1B－S2B＝λ2由几何关系S1B＝5 m，λ＝2 m.(2)设此人沿BS2走到C点，振动又一次加强．S1C－S2C＝2 m，S2C2＝(S2C＋2)2－S1S22得S2C＝1.25 m，BC＝BS2－S2C＝(4－1.25)m＝2.75 m.答案：(1)2 m(2)2.75 m。

4、波的衍射和干涉一、波的衍射1.波的衍射：波绕过障碍物的现象。

如声音传播中的“隔墙有耳”现象。

2.发生明显衍射的条件是：只有缝、孔的宽度或障碍物的尺寸跟波长相差不多，或比波长更小时，才能观察到明显的衍射现象。

3.波的衍射现象是波所特有的现象。

二、波叠加原理和独立传播原理1.~2.几列波相遇时能够保持各自的运动状态，继续传播，在它们重叠的区域里，介质的质点同时参与这几列波引起的振动，质点的位移等于这几列波单独传播时引起的位移的矢量和。

三、波的干涉1.波的干涉：频率相同的两列波叠加，使某些区域的振动加强，某些区域的振动减弱，而且振动加强和振动减弱的区域相互隔开的现象叫做波的干涉。

注意：（1）振动加强的区域振动始终加强，振动减弱的区域振动始终减弱；（2）振动加强（减弱）的区域是指质点的振幅大（小），而不是指振动的位移大（小），因为位移是在时刻变化的。

2.产生干涉的条件：两列波的频率必须相同。

3.干涉是波特殊的叠加：频率不同的两列波相遇，叠加区各点的合振动的振幅，有时是两个振动的振幅之和，有时是两个振动的振幅之差，没有振动总是得到加强或总是减弱的区域，这样的两列波叠加，是波普通的叠加，而不是干涉。

因此，干涉是波特殊的叠加。

4.干涉也是波特有的现象。

由波的干涉所形成的图样叫做干涉图样。

{5.当两相干波源振动步调相同时，到两波源的路程差△s是波长整数倍处是加强区；而路程差是半波长奇数倍处是减弱区。

振动加强位置公式：d1=s1-s2 =±nλ (n=0、1、2、3……)振动减弱位置公式：d2=s1-s2 =±（2n+1）λ/2 (n=0、1、2、3……):1．一列水波穿过小孔产生衍射现象，衍射后水波的强度减弱是因为（ ） A 、水波的波长增大 B 、水波的周期增大 C 、水波的频率减小 D 、水波的振幅减小2．如图所示，S 为波源，M 、N 为两块挡板，其中M 板固定，N 板可上下移动，两板中间有狭缝。

第4节波的衍射和干涉一、波的衍射1．定义：波绕过障碍物继续传播的现象。

2．两种衍射现象(1)在水波槽中，在波源的前方放一个障碍物，使波源振动产生水波。

当障碍物较大时波被阻挡，在靠近障碍物后面没有波，只是在障碍物较远处，波才稍微有些绕到“影子”区域里，如图12-4-1甲所示，虽然发生衍射现象，但不明显。

图12-4-1当障碍物较小时发现波能绕过障碍物继续前进，如同障碍物不存在一样，如图乙所示，衍射现象明显。

(2)在水波槽中，在波源前方放一个有孔的屏，使波源振动产生水波。

当孔较大时发现水波经过孔后在连接波源与孔的两边的两条直线所限制的区域里传播，如图丙所示。

当孔较小时发现孔后的整个区域里传播着以孔为中心的圆形波，如图丁所示，衍射现象明显。

3．发生明显衍射现象的条件只有当缝、孔的宽度或障碍物的尺寸跟波长相差不多，或者比波长更小时，才能观察到明显的衍射现象。

二、波的叠加1．波的叠加原理1.波绕过障碍物继续传播的现象叫做波的衍射。

2．发生明显衍射的条件：缝孔的宽度或障碍物的尺寸跟波长差不多，或者比波长小。

3．波的干涉是指频率相同的两列波叠加，使某些区域的振幅加大，某些区域的振幅减小。

几列波相遇时能够保持各自的运动状态，继续传播，在它们重叠的区域里，介质中的质点同时参与这几列波引起的振动，质点的位移等于这几列波单独传播时引起的位移的矢量和。

图12-4-2表示了分别向右、向左传播的两列波1和2在相遇区域内的叠加过程。

2．波的叠加原理是波具有独立传播性的必然结果，由于总位移是两个位移的矢量和，所以叠加区域的质点的位移可能增大，也可能减小。

两列同相波的叠加，振动加强，振幅增大。

(如图12-4-2所示)两列反相波的叠加，振动减弱，振幅减小。

(如图12-4-3所示)图12-4-2 图12-4-3三、波的干涉1．定义频率相同的两列波叠加时，某些区域的振幅加大、某些区域的振幅减小的现象。

2．稳定干涉条件(1)两列波的频率必须相同。

物理原理波的干涉与衍射物理原理：波的干涉与衍射一、引言波动理论是物理学中重要的研究领域，涉及各种波的行为和性质。

其中，波的干涉和衍射是波动理论中的两个重要现象。

本文将着重介绍波的干涉和衍射的基本原理及其应用。

二、波的干涉1. 干涉现象的定义干涉是指两个或多个波在特定条件下相遇时发生相互作用的现象。

干涉的结果取决于波的干涉相位差。

2. 干涉的分类干涉分为等厚干涉和等倾干涉两种类型。

等厚干涉是指波通过等厚介质产生的干涉现象，如牛顿环。

等倾干涉是指波通过等倾介质产生的干涉现象，如双缝干涉。

3. 干涉的原理干涉原理基于波的叠加原理，即波的合成等于各个波的矢量和。

干涉现象的出现是因为波的相位差引起的干涉条件改变。

4. 干涉的应用（1）干涉仪：干涉仪是利用波的干涉现象测量光的性质和物体的参数的仪器。

常见的干涉仪有迈克尔逊干涉仪和杨氏双缝干涉仪。

（2）涂膜技术：干涉技术可以应用于薄膜的制备和检测，用于提高光学元件的性能。

（3）干涉图案：干涉现象产生的干涉图案可以用于制作光栅、干涉滤波器等。

三、波的衍射1. 衍射现象的定义衍射是指波通过障碍物边缘或在有限孔径中传播时，波的传播方向和波前面发生弯曲和变形的现象。

2. 衍射的原理衍射原理基于海耶-菲涅尔原理，即波传播时，每个波前上的每个点都可以看作是波源，它们产生的次波相互叠加形成新的波前。

3. 衍射的特点（1）衍射现象的出现与波的波长和传播环境有关，有利于波的传播方向的弯曲。

（2）衍射现象在光学中明显，但也存在于其他波动现象中，如声波和水波。

4. 衍射的应用（1）光学衍射：衍射可以用于测量光的波长、制备光栅、研究光学仪器的分辨率等。

（2）声学衍射：衍射可以用于声学测量、超声波成像、喇叭和扩音器的设计等。

（3）电磁波衍射：衍射在天线设计、射频识别技术等方面有重要应用。

四、干涉与衍射的区别干涉和衍射是波的两种重要现象，它们之间存在一些区别：（1）干涉是在波的传播方向上相交的两个或多个波相互作用，衍射是波通过障碍物边缘或有限孔径时发生的波的弯曲与变形。

第4课时 波的衍射和干涉[研究选考·把握考情]知识点一 波的衍射[基 础 梳 理]1.定义：波可以绕过障碍物继续传播，这种现象叫做波的衍射。

2.发生明显衍射的条件：缝、孔的宽度或障碍物的尺寸跟波长相差不多，或者比波长更小。

3.一切波都能发生衍射，衍射是波特有的现象。

[要 点 精 讲]1.衍射是波特有的现象，一切波都可以发生衍射。

2.波的衍射总是存在的，只有“明显”与“不明显”的差异，“障碍物或孔的尺寸比波长小或跟波长差不多”只是发生明显衍射的条件。

3.波传到小孔(障碍物)时，小孔(障碍物)仿佛一个新波源，由它发出与原来同频率的波在孔(障碍物)后传播，就偏离了直线方向。

因此，波的直线传播只是在衍射不明显时的近似情况。

【例1】 如图1所示是利用发波水槽观察到的水波衍射图象，从图象可知( )图1A.B侧波是衍射波B.A侧波速与B侧波速相等C.减小挡板间距离，衍射波的波长将减小D.增大挡板间距离，衍射现象将更明显解析小孔是衍射波的波源，A侧是衍射波，A错误；在同一种介质中，波速相等，故B正确；根据波速、波长和频率的关系式v＝λf，由于波速和频率不变，故波长不变，故C错误；波长越长越容易发生衍射现象，与波的频率和振幅没有关系，在波长无法改变的情况下可以减小挡板间距，故D错误。

答案 B知识点二波的叠加[基础梳理]1.波的独立传播特性：几列波相遇时各自的波长、频率等运动特征，不受其他波的影响。

2.波的叠加原理：在几列波重叠的区域里，介质的质点同时参与这几列波引起的振动，质点的位移等于这几列波单独传播时引起的位移的矢量和。

[即学即练]波源在绳的左端发出半个波①，频率为f1，振幅为A1；同时另一波源在绳右端发出半个波②，频率为f2(f2＞f1)，振幅为A2，P为绳的中点，如图2所示，下列说法正确的是( )图2A.两列波同时到达P点B.两列波相遇时P点波峰值可达到A1＋A2C.两列波相遇再分开后，各自保持原波形传播D.因频率不同，这两列波相遇不能叠加解析因P为绳的中点，故两列波同时到达P点，A正确；因f2＞f1，故λ2＜λ1，当①的波峰传至P点时，②的波峰已过了P点，即两波峰在P点不会相遇，根据波的叠加原理，P点的波峰值不会达到A1＋A2，选项B错误，选项C正确；因波的叠加没有条件，故选项D错误。