初中数学知识提纲

初中数学几何知识点提纲_中考数学几何复习提纲1.基本概念-点、线、面的定义与性质-角的定义与性质-直线、射线、线段的性质2.角的分类-钝角、直角、锐角的定义与判断-平角与周角的定义与判断-对顶角、同位角的概念与性质3.图形的分类-三角形的分类与性质-四边形的分类与性质-多边形的分类与性质4.三角形的性质-三角形内角和定理-三角形外角和定理-同旁内角相等定理5.三角形的相似性-相似三角形的定义与判断-相似三角形的性质与判定方法-相似三角形中的比例关系6.三角形的面积-三角形面积计算公式-直角三角形的特殊性质-任意三角形的面积计算方法7.四边形的性质-平行四边形的性质与判定方法-矩形、正方形、菱形、长方形的性质与判定方法-梯形、平行四边形、矩形面积的计算方法8.圆的性质-圆的定义与性质-圆的直径、半径、弧长的计算方法-圆的面积的计算方法9.垂直与平行-垂直与平行线的判定方法-垂线的性质与判定方法-平行线的性质与判定方法10.空间几何-空间几何图形的投影与视图-空间几何图形的旋转、平移、镜面对称性质-空间几何图形的切割与拼接1.平面几何-点、线、面的定义与性质-基本图形（三角形、四边形、多边形）的分类与性质-三角形的内角和定理、外角和定理、中位线定理、高的性质与应用2.类似与全等-相似三角形的定义与性质-相似三角形的判定方法-相似三角形中的比例关系与应用3.角的平分线与垂直平分线-角的平分线的性质与判定方法-垂直平分线的性质与判定方法-相关题目的解题技巧与方法4.平行线与四边形-平行线的性质与判定方法-平行线与四边形内角和的关系-各种四边形的性质与判定方法5.圆-圆的定义与性质-弧长、弦长、扇形面积的计算方法-圆锥与球的性质与计算方法6.空间几何-空间几何图形的投影与视图-空间几何图形的旋转、平移、镜面对称性质。

初中数学几何知识点提纲初中数学几何知识点提纲1、过两点有且只有一条直线2、两点之间线段最短3、同角或等角的补角相等4、同角或等角的余角相等5、过一点有且只有一条直线和已知直线垂直6、直线外一点与直线上各点连接的所有线段中，垂线段最短7、平行公理经过直线外一点，有且只有一条直线与这条直线平行8、如果两条直线都和第三条直线平行，这两条直线也互相平行9、同位角相等，两直线平行10、内错角相等，两直线平行11、同旁内角互补，两直线平行12、两直线平行，同位角相等13、两直线平行，内错角相等14、两直线平行，同旁内角互补15、定理三角形两边的和大于第三边16、推论三角形两边的差小于第三边17、三角形内角和定理三角形三个内角的和等于180°18、推论1直角三角形的两个锐角互余19、推论2三角形的一个外角等于和它不相邻的两个内角的和20、推论3三角形的一个外角大于任何一个和它不相邻的内角21、全等三角形的对应边、对应角相等22、边角边公理(SAS)有两边和它们的夹角对应相等的两个三角形全等23、角边角公理(ASA)有两角和它们的夹边对应相等的两个三角形全等24、推论(AAS)有两角和其中一角的对边对应相等的两个三角形全等25、边边边公理(SSS)有三边对应相等的两个三角形全等26、斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角三角形全等27、定理1在角的平分线上的点到这个角的两边的距离相等28、定理2到一个角的两边的距离相同的点，在这个角的平分线上29、角的平分线是到角的两边距离相等的所有点的集合30、等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31、推论1等腰三角形顶角的平分线平分底边并且垂直于底边32、等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33、推论3等边三角形的各角都相等，并且每一个角都等于60°34、等腰三角形的判定定理如果一个三角形有两个角相等，那么这两个角所对的边也相等(等角对等边)35、推论1三个角都相等的三角形是等边三角形36、推论2有一个角等于60°的等腰三角形是等边三角形37、在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半38、直角三角形斜边上的中线等于斜边上的一半39、定理线段垂直平分线上的点和这条线段两个端点的距离相等40、逆定理和一条线段两个端点距离相等的点，在这条线段的垂直平分线上41、线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42、定理1关于某条直线对称的两个图形是全等形43、定理2如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线44、定理3两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上45、逆定理如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称46、勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方，即a^2+b^2=c^247、勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2，那么这个三角形是直角三角形48、定理四边形的内角和等于360°49、四边形的外角和等于360°50、多边形内角和定理n边形的内角的和等于(n-2)×180°51、推论任意多边的外角和等于360°52、平行四边形性质定理1平行四边形的对角相等54、推论夹在两条平行线间的平行线段相等55、平行四边形性质定理3平行四边形的对角线互相平分56、平行四边形判定定理1两组对角分别相等的四边形是平行四边形57、平行四边形判定定理2两组对边分别相等的四边形是平行四边形58、平行四边形判定定理3对角线互相平分的四边形是平行四边形59、平行四边形判定定理4一组对边平行相等的四边形是平行四边形60、矩形性质定理1矩形的四个角都是直角61、矩形性质定理2矩形的对角线相等62、矩形判定定理1有三个角是直角的四边形是矩形63、矩形判定定理2对角线相等的平行四边形是矩形64、菱形性质定理1菱形的四条边都相等65、菱形性质定理2菱形的对角线互相垂直，并且每一条对角线平分一组对角66、菱形面积=对角线乘积的一半，即S=(a×b)÷267、菱形判定定理1四边都相等的四边形是菱形68、菱形判定定理2对角线互相垂直的平行四边形是菱形69、正方形性质定理1正方形的四个角都是直角，四条边都相等70、正方形性质定理2正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角71、定理1关于中心对称的两个图形是全等的72、定理2关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分73、逆定理如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称74、等腰梯形性质定理等腰梯形在同一底上的两个角相等75、等腰梯形的两条对角线相等76、等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77、对角线相等的梯形是等腰梯形78、平行线等分线段定理如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等79、推论1经过梯形一腰的中点与底平行的直线，必平分另一腰80、推论2经过三角形一边的中点与另一边平行的直线，必平分第三边81、三角形中位线定理三角形的中位线平行于第三边，并且等于它的一半82、梯形中位线定理梯形的中位线平行于两底，并且等于两底和的一半L=(a+b)÷2 S=L×h83、(1)比例的基本性质如果a:b=c:d,那么ad=bc;如果ad=bc,那么a:b=c:d84、(2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85、(3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86、平行线分线段成比例定理三条平行线截两条直线，所得的对应线段成比例87、推论平行于三角形一边的直线截其他两边(或两边的延长线)，所得的对应线段成比例88、定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例，那么这条直线平行于三角形的第三边89、平行于三角形的一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例90、定理平行于三角形一边的直线和其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似91、相似三角形判定定理1两角对应相等，两三角形相似(ASA)92、直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93、判定定理2两边对应成比例且夹角相等，两三角形相似(SAS)94、判定定理3三边对应成比例，两三角形相似(SSS)95、定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似96、性质定理1相似三角形对应高的比，对应中线的比与对应角平分线的比都等于相似比97、性质定理2相似三角形周长的比等于相似比98、性质定理3相似三角形面积的比等于相似比的平方99、任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值100、任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值101、圆是定点的距离等于定长的点的集合102、圆的内部可以看作是圆心的距离小于半径的点的集合103、圆的外部可以看作是圆心的距离大于半径的点的集合104、同圆或等圆的半径相等105、到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的圆106、和已知线段两个端点的距离相等的点的轨迹，是着条线段的垂直平分线107、到已知角的两边距离相等的点的轨迹，是这个角的平分线108、到两条平行线距离相等的点的轨迹，是和这两条平行线平行且距离相等的一条直线109、定理不在同一直线上的三个点确定一条直线110、垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111、推论1①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心，并且平分弦所对的两条弧③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧112、推论2圆的两条平行弦所夹的弧相等113、圆是以圆心为对称中心的中心对称图形114、定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等115、推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116、定理一条弧所对的圆周角等于它所对的圆心角的一半117、推论1同弧或等弧所对的圆周角相等;同圆或等圆中，相等的圆周角所对的弧也相等118、推论2半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径119、推论3如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形120、定理圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角121、①直线L和⊙O相交d﹤r②直线L和⊙O相切d=r③直线L和⊙O相离d﹥r122、切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123、切线的性质定理圆的切线垂直于经过切点的半径124、推论1经过圆心且垂直于切线的直线必经过切点125、推论2经过切点且垂直于切线的直线必经过圆心126、切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角127、圆的外切四边形的两组对边的和相等128、弦切角定理弦切角等于它所夹的弧对的圆周角129、推论如果两个弦切角所夹的弧相等，那么这两个弦切角也相等130、相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等131、推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项132、切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项133、推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等134、如果两个圆相切，那么切点一定在连心线上135、①两圆外离d﹥R+r②两圆外切d=R+r③两圆相交R-r﹤d﹤R+r(R﹥r)④两圆内切d=R-r(R﹥r)⑤两圆内含d﹤R-r(R﹥r)136、定理相交两圆的连心线垂直平分两圆的公共弦137、定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138、定理任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆139、正n边形的每个内角都等于(n-2)×180°/n140、定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141、正n边形的面积Sn=pnrn/2 p表示正n边形的周长142、正三角形面积√3a/4 a表示边长143、如果在一个顶点周围有k个正n边形的角，由于这些角的和应为360°，因此k×(n-2)180°/n=360°化为(n-2)(k-2)=4144、弧长计算公式：L=n∏R/180145、扇形面积公式：S扇形=n∏R/360=LR/2146、内公切线长=d-(R-r)外公切线长=d-(R+r)初中数学几何知识点图形认识初步1、(1)几何图形：我们把从实物中抽象出的各种图形称为几何图形。

2024初中数学知识点复习提纲一、代数与函数1.一元一次方程与一元一次不等式•含有绝对值的一元一次不等式的解法•解一元一次方程和不等式时的变形方法•应用一元一次方程和不等式解决实际问题2.一次函数与一次函数图像•一次函数的定义、性质和图像表示•利用一次函数解决实际问题•一次函数和一元一次方程、不等式的关系3.二次根式•关于二次根式的定义、性质和化简方法•二次根式的运算和求值•应用二次根式解决实际问题4.整式的定义、性质和运算•多项式的基本概念、性质和表示方法•多项式的加、减、乘和整式除法运算•利用整式解决实际问题二、几何与测量1.平面几何初步•直线、线段、射线、角的基本概念及刻画方法•同位角、对顶角、内错角等角度关系•垂直、平行、相交、交错等线段关系•用角度关系和线段关系解决几何问题2.平面图形初步•三角形的基本性质、分类和判定方法•四边形、多边形、圆的定义和性质•识别和绘制各种平面图形•应用平面图形解决实际问题3.直线、角、面积测量•直线的测量方法和误差控制•利用角度测量解决几何问题•平面图形的面积计算及其应用4.立体几何•空间图形的基本概念、分类以及基本变换方法•立体图形的体积和表面积计算•应用立体几何解决实际问题三、数据与概率1.统计基础知识•数据和变量的定义、分类及其表示方法•统计描述性分析方法（频数、频率、中位数、平均数等）•数据图表的绘制和分析2.概率初步•随机事件和样本空间的定义、性质及表示方法•概率的定义、性质和计算方法•统计与概率的关系及其应用3.统计与概率的实际应用•利用统计和概率解决实际问题•假设检验及其应用以上是2024初中数学知识点复习提纲，希望对广大中学生有所帮助。

最新沪教版初中数学知识点汇总教学提纲一、整数1.整数的概念和性质-整数的定义-整数的比较和排序-整数的加法、减法、乘法和除法-整数的混合运算2.整数的应用-整数的应用实例（温度计、海拔、负号的应用等）-整数的实际问题解决二、有理数1.有理数的概念和性质-有理数的定义-有理数的比较和排序-有理数的加法、减法、乘法和除法-有理数的混合运算2.有理数的应用-有理数的应用实例（比例、百分数、利润等）-有理数的实际问题解决三、代数式与初等代数1.代数式的概念和基本运算-代数式的定义-代数式的加法、减法、乘法和除法-代数式的合并同类项和分解因式2.一元一次方程与一元一次不等式-一元一次方程的概念和性质-一元一次不等式的概念和性质-一元一次方程与不等式的解-实际问题转化为一元一次方程和不等式3.一元二次方程与一元二次不等式-一元二次方程的概念和性质-一元二次不等式的概念和性质-一元二次方程与不等式的解-实际问题转化为一元二次方程和不等式四、平面图形1.正方形、长方形、菱形、梯形、平行四边形的性质-图形的定义和性质-图形的含义和要素-同种图形的性质和区别2.三角形的性质-三角形的定义和分类-三角形的角度和边长关系-三角形的高、中线和中心3.直角三角形和勾股定理-直角三角形的定义和性质-勾股定理的概念和应用-直角三角形和勾股定理的实际问题解决五、空间几何与立体几何1.空间几何的基本概念-立体图形的分类和要素-圆柱、圆锥、球体的性质-空间几何问题的解决方法2.体积的计算-立体图形的体积概念和计算方法-直方体、正方体和圆柱的体积计算-实际问题中的体积应用3.平行四边形面积的计算-平行四边形面积的概念和计算方法-三角形面积和平行四边形面积的关系-实际问题中的面积应用六、统计与概率1.统计的基本概念和数据的收集整理-统计的定义和目的-数据的收集和整理方法-数据的图表表示和分析2.概率的基本概念和计算方法-概率的定义和性质-概率的计算方法和运用以上是最新沪教版初中数学知识点汇总的教学提纲，内容详实且全面，旨在帮助学生全面掌握初中数学的基本概念、性质和运算方法，并能应用于实际问题的解决。

七年级上册数学知识点提纲初一数学上册知识点提纲七年级上册数学知识点提纲一、整式的加减1.单项式：表示数字或字母乘积的式子，单独的一个数字或字母也叫单项式。

2.单项式的系数与次数：单项式中的数字因数，称单项式的系数;单项式中所有字母指数的和，叫单项式的次数。

3.多项式：几个单项式的和叫多项式。

4.多项式的项数与次数：多项式中所含单项式的个数就是多项式的项数，每个单项式叫多项式的项;多项式里，次数最高项的次数叫多项式的次数。

5.整式：①单项式②多项式。

6.同类项：所含字母相同，并且相同字母的指数也相同的单项式是同类项。

7.合并同类项法则：系数相加，字母与字母的指数不变。

8.去(添)括号法则：去(添)括号时，若括号前边是“+”号，括号里的各项都不变号;若括号前边是“-”号，括号里的各项都要变号。

9.整式的加减：一找：(划线);二“+”：(务必用+号开始合并);三合：(合并)。

10.多项式的升幂和降幂排列：把一个多项式的各项按某个字母的指数从小到大(或从大到小)排列起来，叫做按这个字母的升幂排列(或降幂排列)。

二、一元一次方程1.等式：用“=”号连接而成的式子叫等式。

2.等式的性质：等式性质1：等式两边都加上(或减去)同一个数或同一个整式，所得结果仍是等式;等式性质2：等式两边都乘以(或除以)同一个不为零的数，所得结果仍是等式。

3.方程：含未知数的等式，叫方程。

4.方程的解：使等式左右两边相等的未知数的值叫方程的解;注意：“方程的解就能代入”。

5.移项：改变符号后，把方程的项从一边移到另一边叫移项.移项的依据是等式性质1。

6.一元一次方程：只含有一个未知数，并且未知数的次数是1，并且含未知数项的系数不是零的整式方程是一元一次方程。

7.一元一次方程的标准形式：ax+b=0(x是未知数，a、b是已知数，且a≠0)。

8.一元一次方程解法的一般步骤：化简方程__分数基本性质。

去分母__同乘(不漏乘)最简公分母。

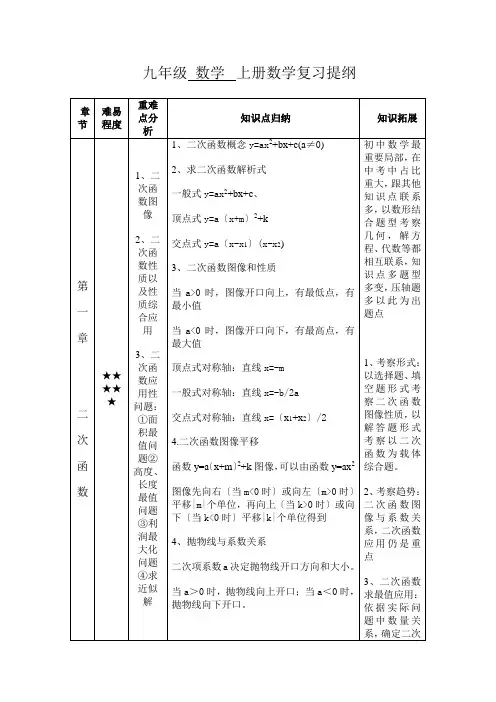
章节难易程度重难点分析知识点归纳知识拓展第一章二次函数★★★★★1、二次函数图像2、二次函数性质以及性质综合应用3、二次函数应用性问题：①面积最值问题②高度、长度最值问题③利润最大化问题④求近似解1、二次函数概念y=ax2+bx+c(a≠0)2、求二次函数解析式一般式y=ax2+bx+c、顶点式y=a〔x+m〕2+k交点式y=a〔x-x1〕(x-x2)3、二次函数图像和性质当a>0时，图像开口向上，有最低点，有最小值当a<0时，图像开口向下，有最高点，有最大值顶点式对称轴：直线x=-m一般式对称轴：直线x=-b/2a交点式对称轴：直线x=〔x1+x2〕/24.二次函数图像平移函数y=a〔x+m〕2+k图像，可以由函数y=ax2图像先向右〔当m<0时〕或向左〔m>0时〕平移|m|个单位，再向上〔当k>0时〕或向下〔当k<0时〕平移|k|个单位得到4、抛物线与系数关系二次项系数a决定抛物线开口方向和大小。

当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口。

初中数学最重要局部，在中考中占比重大，跟其他知识点联系多，以数形结合题型考察几何，解方程、代数等都相互联系，知识点多题型多变，压轴题多以此为出题点1、考察形式：以选择题、填空题形式考察二次函数图像性质，以解答题形式考察以二次函数为载体综合题。

2、考察趋势：二次函数图像与系数关系，二次函数应用仍是重点3、二次函数求最值应用：依据实际问题中数量关系，确定二次|a|越大，则抛物线开口越小。

一次项系数b和二次项系数a共同决定对称轴位置。

当a与b同号时〔即ab＞0〕，对称轴在y 轴左；当a与b异号时〔即ab＜0〕，对称轴在y 轴右。

常数项c决定抛物线与y轴交点抛物线与y轴交于〔0，c〕抛物线与x轴交点个数Δ= b2-4ac＞0时，抛物线与x轴有2个交点。

Δ= b2-4ac=0时，抛物线与x轴有1个交点。

Δ= b2-4ac＜0时，抛物线与x轴没有交点5、二次函数应用函数解析式，结合方程、一次函数等知识解决实际问题〔对于二次函数最大〔小〕值确定，一定要注意二次函数自变量取值范围，同时兼顾实际问题中对自变量特殊约定，结合图像进展理解〕第二章简单事件概率★★★☆☆1、简单事件概率2、用频率估计概率3、概率简单应用1、确定事件〔必然事件和不可能事件〕和不确定事件2、用列举法〔列表法和树状图法〕计算简单事件发生概率P〔A〕= m / n3、事件发生概率是有大小，必然事件发生概率是1，不可能事件发生概率是0，不确定事件发生概率在0与1之间4、知道大量试验时频率可作为事件发生概率估计值\5、概率实际应用掌握对事件解及分类，学会画树状图或列表方法解题，在中考中通常以选择题考察概念，以填空题、简答题考察概率计算1.考察形式：简单事件概率计算，利用列表法或树状图法求解简单事件概率2、考察趋向：用列举法〔列表法和树状图法〕计算简单事件发生概率，概率在实际问题〔判别“划算〞、“公平〞〕中应用第三章圆根本性质★★★★☆1、图形旋转2、垂径定理3、弧、弦与圆心角关系4、圆心角与圆周角关系，直径所对圆周角特征5、圆内接四边1、圆有关概念，点与圆位置关系，确定圆条件〔不在同一条直线上三点确定一个圆〕2、图形旋转：旋转特征和旋转性质3、垂径定理：垂直于弦直径平分这条弦，并且平分弦所对弧推论1：平分弦直径垂直于弦，并且平分弦所对弧推论2：平分弧直径垂直平分弧所对弦4、弧、弦与圆心角关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等，则其余各组量都相等5、一条弧所对圆周角等于它所对圆心角一半，直径所对圆周角等于90°6、圆内接四边形对角互补，正多边形内角和为〔n-2〕*180°正多边形中心角为n/360°7、弧长L=nπr/180扇形面积S= nπr2/360初三数学难点，知识点多，涉及定理多，题型多变，几何题通常与三角形结合，角与边关系需要灵活运用，需要牢记特殊角所对应边比值关系，添关键辅助线帮助解题是考试中一大难点1、考察形式：以选择题、填空题形式考察有关性质和计算，把简单几何体通过几何变换求某阴影局部面积形和正多边形6、弧长及扇形面积2、考察趋向：与圆有关计算与证明第四章相似三角形★★★★★重点1、比例线段2、由平行线截得比例线段3、相似三角形性质与判定4、相似三角形应用难点：1、相似三角形判定题型与圆1、比例根本形式；2、公式拓展：〔1〕更比性质(交换比例内项或外项)：〔2〕反比性质(把比前项、后项交换)：．〔3〕合、分比性质：．3、三角形中平行线分线段成比例定理:平行于三角形一边直线截其它两边(或两边延长线)所得对应线段成比例4、对应角相等，对应边成比例三角形，叫通常与二次函数结合来考察，在动点问题时学会分类讨论，通过相似来得到角度、边大小，证明两个三角形相似是考试中难点，要学会添辅助线，必要时需要设x列方程得到需要解1、考察形式：相似三角形简单计算、识别与作图以选择题、填空题形式出现，相似三角形性质与其他知识综合以解答题形式出现2、考察趋向：形结合2、利用相似三角形性质来解决实际问题做相似三角形．相似用符号“∽〞表示5、三角形相似判定方法〔1〕、定义法：三个对应角相等，三条对应边成比例两个三角形相似．〔2〕、平行法：平行于三角形一边直线和其它两边(或两边延长线)相交，所构成三角形与原三角形相似．〔3〕、判定定理1：如果一个三角形两个角与另一个三角形两个角对应相等，则这两个三角形相似．简述为：两角对应相等，两三角形相似．〔4〕、判定定理2：如果一个三角形两条边与另一个三角形两条边对应成比例，并且夹角相等，则这两个三角形相似．简述为：两边对应成比例且夹角相等，两三角形相似．〔5〕、判定定理3：如果一个三角形三条边与另一个三角形三条边对应成比例，则这两个三角形相似．简述为：三边对应成比例，两三角形相似．6、(1)相似三角形对应高比，对应中线比和对应角平分线比都等于相似比．(2)相似三角形周长比等于相似比．(3)相似三角形面积比等于相似比平方．相似三角形判定，利用相似证明线段成比例、乘积问题；相似三角形与全等三角形、四边形、圆知识综合探索；相似三角形在函数背景下坐标相应计算，在动态问题中特征作用等。

初中数学总复习提纲一、数的性质和运算1.自然数、整数、有理数、实数和虚数的含义及其性质2.整数的运算规则：加法、减法、乘法、除法、绝对值运算3.有理数的运算规则：加法、减法、乘法、除法、混合运算4.指数与指数运算5.逻辑与集合二、代数式与方程式1.代数式的定义及其性质2.平方、完全平方、立方和完全立方的求解3.一元一次方程的解法4.一元一次方程组的解法5.一元二次方程的解法及其应用6.用方程表示实际问题并解决实际问题7.勾股定理及其应用三、数与图形1.二维图形的边、角、面及其性质2.三角形、四边形和多边形的性质及其关系3.三角形的线段、角、面积公式及应用4.三角形的相似性质及其应用5.圆的定义、性质及公式6.圆的面积和周长的计算7.空间几何体的计算四、函数与应用1.函数的概念和性质2.函数图像的平移、伸缩和反射3.一次函数、二次函数、三次函数及其图像4.绝对值函数、分段函数及其图像5.函数的复合、反函数和逆函数6.数据的收集、整理、统计和分析7.概率与统计五、单位换算与计算检验1.长度、面积、体积和质量的单位换算2.时间、速度、密度、温度、角度的单位换算3.百分数和比例的计算4.计算结果的检验5.合理估算的方法与应用六、解题方法与思维培养1.数学解题的基本方法2.算术平均数、几何平均数和均值不等式的应用3.推理与证明4.逻辑思维与数学思维的培养5.综合应用题的解决方法以上是初中数学总复习的提纲，根据这个提纲进行复习，可以全面复习初中数学知识，有助于提高数学应试能力。

每个模块都要结合习题进行巩固，多做一些实际应用题，提高解决问题的能力。

同时，要注重思维培养和解题方法的掌握，通过多思考、多讨论、多练习，培养学生的数学思维能力。

2022-2023初一数学上册人教版提纲数学是三大主科之一，同时也是必考科目。

很多人都说数学最难学，数学也是非常拉分的科目，下面小编给大家分享一些初一数学上册人教版提纲，希望能够帮助大家，欢迎阅读初一数学上册人教版提纲(一)正负数1.正数：大于0的数。

2.负数：小于0的数。

3.0即不是正数也不是负数。

4.正数大于0，负数小于0，正数大于负数。

(二)有理数1.有理数：由整数和分数组成的数。

包括：正整数、0、负整数，正分数、负分数。

可以写成两个整之比的形式。

(无理数是不能写成两个整数之比的形式，它写成小数形式，小数点后的数字是无限不循环的。

如：π)2.整数：正整数、0、负整数，统称整数。

3.分数：正分数、负分数。

(三)数轴1.数轴：用直线上的点表示数，这条直线叫做数轴。

(画一条直线，在直线上任取一点表示数0，这个零点叫做原点，规定直线上从原点向右或向上为正方向;选取适当的长度为单位长度，以便在数轴上取点。

)2.数轴的三要素：原点、正方向、单位长度。

3.相反数：只有符号不同的两个数叫做互为相反数。

0的相反数还是0。

4.绝对值：正数的绝对值是它本身，负数的绝对值是它的相反数;0的绝对值是0，两个负数，绝对值大的反而小。

(四)有理数的加减法1.先定符号，再算绝对值。

2.加法运算法则：同号相加，到相同符号，并把绝对值相加。

异号相加，取绝对值大的加数的符号，并用较大的绝对值减去较小的绝对值。

互为相反数的两个数相加得0。

一个数同0相加减，仍得这个数。

3.加法交换律：a+b=b+a两个数相加，交换加数的位置，和不变。

4.加法结合律：(a+b)+c=a+(b+c)三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

5.a?b=a+(?b)减去一个数，等于加这个数的相反数。

(五)有理数乘法(先定积的符号，再定积的大小)1.同号得正，异号得负，并把绝对值相乘。

任何数同0相乘，都得0。

2.乘积是1的两个数互为倒数。

初中数学复习提纲一、有理数1.有理数的概念及性质：a.有理数的定义；b.有理数的比较大小；c.有理数的加法、减法、乘法、除法运算；d.有理数的化简及约分；e.有理数的负数及绝对值；f.有理数的十分制及百分制换算。

二、代数式1.代数式的基本概念：a.代数式的定义及元素的分类；b.代数式的值及求值；c.代数式的化简；d.代数式的展开与合并；e.代数式的因式分解；f.代数式的公式变形。

三、方程与不等式1.一元一次方程：a.一元一次方程的概念及解法；b.一元一次方程的应用。

2.一元一次不等式：a.一元一次不等式的概念及解法；b.一元一次不等式的应用。

3.二元一次方程组：a.二元一次方程组的概念及解法；b.二元一次方程组的应用。

四、几何1.直线、角、面的概念及性质：a.直线及直线的分类；b.角的概念及角的分类；c.角的性质；d.面的概念及面的分类；e.面的性质。

2.图形的周长与面积：a.三角形、矩形、正方形的周长与面积；b.圆的周长与面积；c.梯形、平行四边形的周长与面积；d.圆环的周长与面积。

3.合作与相似：a.合作的概念及性质；b.相似的概念及性质；c.相似三角形的应用。

五、统计与概率1.统计的基本概念及方法：a.数据的搜集、整理、分析；b.频数表、频率表与频率多角形；c.平均数、中位数与众数；d.极差与四分位数。

2.概率的基本概念及计算：a.随机事件与样本空间；b.事件的概率与计算；c.事件的互斥与相互独立；d.古典概型与加法定理；e.条件概率与乘法定理。

六、函数1.函数的概念及表示法：a.函数的定义及特点；b.函数的表示与自变量与因变量的关系。

2.一次函数与二次函数：a.一次函数的概念、性质与图像；b.一次函数的斜率与截距；c.二次函数的概念、性质与图像；d.二次函数的顶点与对称轴。

以上为初中数学复习提纲，涵盖了有理数、代数式、方程与不等式、几何、统计与概率、函数等重要知识点，每个知识点包括了基本概念、性质与解题方法，并且列举了一些常用的应用题目。

2024初中数学七年级下册知识点提纲一、有理数1. 有理数的定义和表示方法•有理数定义：是可以表示成两个整数比值的数，包括正整数、负整数、0以及带分数。

•有理数表示方法：分数表示、小数表示、整数表示。

2. 有理数的大小比较和绝对值•有理数大小比较：同号比大小，异号比绝对值大小。

•有理数绝对值：正数和0的绝对值等于它本身，负数的绝对值等于它相反数。

3. 有理数的加减法运算•加法运算：同号数相加，异号数作差；分数相加需要通分。

•减法运算：转化为加法运算；分数相减需要通分。

4. 有理数的乘除法运算•乘法运算：同号相乘得正，异号相乘得负；分数相乘需要约分。

•除法运算：除以非0有理数相当于乘以它的倒数；分数除法相当于乘以倒数。

二、比例与比例分配1. 比例及其性质•比例：等比关系的比较方法，分为同比和异比。

•比例性质：比例中两对相邻项的乘积相等；比例可逆。

2. 比例分配•同比例分配：依照比例将一定数额的量分成若干份；分配量的和等于总量。

•异比例分配：依照比例将一定数额的量分给若干个对象。

3. 常见应用•速度、距离、时间的比例关系求解。

•面积、体积的比例关系求解。

•商品的比价问题求解。

三、平面图形的认识1. 基本概念•点、线、面的概念与特点。

•角度的概念与度量。

•平行线的定义和判定方法。

2. 三角形•三角形的定义、性质及分类。

•根据边、角的关系求解三角形基本量。

•利用勾股定理求解直角三角形基本量。

3. 四边形•四边形的定义、性质及分类。

•矩形、正方形、菱形、平行四边形等四边形的性质及应用。

4. 圆的认识•圆的基本概念及性质。

•利用圆的周长公式和面积公式求解基本量。

四、代数式的应用1. 代数式•代数式的概念和含义。

•代数式加减的基本性质。

2. 解一元一次方程•一元一次方程的定义和性质。

•利用等式的性质解一元一次方程。

•应用题：车站问题、饮料配方问题等。

3. 解一元二次方程•一元二次方程的定义和性质。

•利用配方法或公式法解一元二次方程。

初中数学内容提纲代数部分（一)有理数1．有理数的概念有理数。

数轴。

相反数。

数的绝对值。

有理数大小的比较.（1）有理数的意义,用正数与负数表示相反意义的量，把给出的有理数归类。

（2）数轴、相反数、绝对值等概念和数轴的画法,用数轴上的点表示整数或分数（以刻度尺为工具），求有理数的相反数与绝对值（绝对值符号内不含字母）。

(3）有理数大小比较的法则，用不等号连接两个或两个以上不同的有理数。

2．有理数的运算有理数的加法与减法。

代数和.加法运算律。

有理数的乘法与除法。

倒数。

乘法运算律。

有理数的乘方。

有理数的混的运算。

科学记数法。

近似数与有效数字。

(1）有理数的加、减、乘、除、乘方的意义，有理数的运算法则、运算律、运算顺序以及有理数的混合运算（不超过6个数），运用运算律简化运算。

（2）倒数概念，求有理数的倒数。

（3）大于10的有理数的科学记数法。

（4）近似数与有效数字的概念，根据指定的精确度或有效数字的个数，用四舍五入法求有理数的近似数；用计算器求一个数的平方与立方（尚无条件的学校可使用算表）。

（5）有理数的加法与减法、乘法与除法可以相互转化。

（二）整式的加减代数式。

代数式的值.整式。

单项式。

多项式。

合并同类项. 去括号与添括号。

数与整式相乘。

整式的加减法.(1）用字母表示有理数.（2）代数式、代数式的值的概念，列出代数式表示简单的数量关系,求代数式的值。

(3）整式、单项式及其系数与次数、多项式次数、项与项数的概念，把一个多项式按某个字母降幂排列或升幂排列.（4）合并同类项的方法，去括号、添括号的法则，数与整式相乘的运算以及整式的加减运算。

（5）用字母表示数、列代数式和求代数式的值、整式的加减，抽象概括的思维方法和特殊与一般的辩证关系。

(三）一元一次方程等式。

等式的基本性质.方程和方程的解.解方程. 一元一次方程及其解法. 一元一次方程的应用.（1）等式和方程的有关概念，等式的基本性质，检验一个数是不是某个一元方程的解。

初中数学总复习提纲第一章 实数★重点★ 实数的有关概念及性质，实数的运算 ☆内容提要☆一、重要概念1．数的分类及概念 数系表：说明：“分类”的原则：1）相称（不重、不漏）2）有标准2．非负数：正实数与零的统称。

（表为：x ≥0） 常见的非负数有：性质：若干个非负数的和为0，则每个非负担数均为0。

3．倒数： ①定义及表示法②性质：A.a ≠1/a （a ≠±1）;B.1/a 中，a ≠0;C.0＜a ＜1时1/a ＞1;a＞1时，1/a ＜1;D.积为1。

4．相反数： ①定义及表示法②性质：A.a ≠0时，a ≠-a;B.a 与-a 在数轴上的位置;C.和为0,商实数无理数(无限不循环小数)0 (有限或无限循环性数) 整数分数 正无理数 负无理数 0 实数 负数 整数 分数 无理数有理数正数整数 分数 无理数有理数│a │2a a (a ≥0)(a 为一切实数)为-1。

5．数轴：①定义（“三要素”）②作用：A.直观地比较实数的大小;B.明确体现绝对值意义;C.建立点与实数的一一对应关系。

6．奇数、偶数、质数、合数（正整数—自然数）定义及表示：奇数：2n-1偶数：2n （n 为自然数）7．绝对值：①定义（两种）：代数定义：几何定义：数a 的绝对值顶的几何意义是实数a 在数轴上所对应的点到原点的距离。

②│a │≥0,符号“││”是“非负数”的标志;③数a 的绝对值只有一个;④处理任何类型的题目，只要其中有“││”出现，其关键一步是去掉“││”符号。

二、实数的运算1． 运算法则（加、减、乘、除、乘方、开方）2． 运算定律（五个—加法[乘法]交换律、结合律;[乘法对加法的] 分配律）3． 运算顺序：A.高级运算到低级运算;B.（同级运算）从“左” 到“右”（如5÷51³5）;C.(有括号时)由“小”到“中”到“大”。

三、应用举例（略）附：典型例题1． 已知：a 、b 、x 在数轴上的位置如下图，求证：│x-a │+│x-b │ =b-a.2.已知：a-b=-2且ab<0，（a ≠0，b ≠0），判断a 、b 的符号。

第七章一元一次方程7.1 一元一次方程重点：一元一次方程的基本概念难点：一元一次方程的意义考点：方法：课时：特殊教法：7.2 解一元一次方程重点：解一元一次方程难点：考点：方法：课时：特殊教法：7.3 用一元一次方程解决实际问题重点：难点：考点：方法：课时：特殊教法：第八章相交线与平行线8.1 相交线重点：难点：考点：方法：课时：特殊教法：8.2 两条直线平行的条件重点：难点：考点：方法：课时：特殊教法：8.3 平行线的特征重点：难点：考点：方法：课时：特殊教法：第九章二元一次方程组9.1 二元一次方程组重点：难点：考点：方法：课时：特殊教法：9.2 二元一次方程组的解法重点：难点：考点：方法：课时：特殊教法：9.3 二元一次方程组的应用重点：难点：考点：方法：课时：特殊教法：第十章整式乘法与因式分解10.1 同底数幂的乘法难点：考点：方法：课时：特殊教法：10.2 幂的乘方与积的乘方重点：难点：考点：方法：课时：特殊教法：10.3 同底数幂的除法重点：难点：考点：方法：课时：特殊教法：10.4 整式的乘法重点：难点：方法：课时：特殊教法：10.5 乘法公式重点：难点：考点：方法：课时：特殊教法：10.6 因式分解重点：难点：考点：方法：课时：特殊教法：10.7 提公因式法重点：难点：考点：方法：课时：特殊教法：10.8 公式法重点：难点：考点：方法：课时：特殊教法：第十一章三角形11.1 三角形的再认识重点：难点：考点：方法：课时：特殊教法：11.2 三角形的内角与外角重点：难点：考点：方法：课时：特殊教法：11.3 三角形的角平分线、中线和高重点：难点：考点：方法：课时：特殊教法：11.4全等图形重点：难点：考点：方法：课时：特殊教法：11.5两个三角形全等的条件重点：难点：考点：方法：课时：特殊教法：11.6直角三角形全等的条件重点：难点：考点：方法：课时：特殊教法：11.7 用尺规作三角形重点：难点：考点：方法：课时：特殊教法：第十二章统计的初步认识12.1 数据的收集重点：难点：考点：方法：课时：特殊教法：12.2 数据的整理重点：难点：考点：方法：课时：特殊教法：12.3 统计图重点：难点：考点：方法：课时：特殊教法：八年级（下）第二十章平移与旋转20.1 平移教学目标知识与技能目标：1、结合生活中的具体实例认识图形的平移，探索它的性质.2、经历观察、思考、概括、抽象等过程，进一步发展学生的空间观念.过程与方法目标：通过观察生活中的各种丰富的实例，让学生体会平移现象，让学生通过各种图形的平移，体验感受图形平移主要是移动的方向和距离，并探索它的基本性质.情感态度与价值观目标认识和欣赏这些图形在现实生活中的应用，体会到数学与实际生活的密切联系，认识数学价值.并体验数学活动充满探索与创造，培养学生勇于探索，敢于创新的精神.20.2 旋转20.3 中心对称与中心对称图形20.4 图案的设计与欣赏第二十一章函数21.1 变量与函数【学习目标】1．认识变量、常量2．学会用含一个变量的代数式表示另一个变量【重难点】理解常量和变量的概念；理解常量和变量的相对性21.2 函数关系的表示法21.3 函数的应用第二十二章四边形22.1 平行四边形的性质教学目标：1.知识与技能：掌握平行四边形的定义及对边相等、对角相等、对角线互相平分的性质，并能用它们解决简单的问题．通过旋转等操作活动体会平行四边形的中心对称性．在操作、探究等数学活动中提高学生的探究能力，进一步提高学生的说理和初步的推理能力.2.过程与方法：经历平行四边形有关概念的形成过程和性质的探究过程；采用多种方法（观察、作图、实验、变换、推理等）探索平行四边形性质，体验解决问题策略的多样性；体会平移、旋转等图形变换在研究平行四边形及其性质中的应用．将探究过程与说理紧密结合．渗透"类比"、"转化"的数学思想．3.情感、态度、价值观：在探究活动与性质应用中，有意识地培养学生独立思考的习惯和积极的情感态度，促进良好数学观的形成，同时增强交流与合作意识.教学重点：平行四边形性质的探究与性质的应用．教学难点：平行四边形对角线互相平分、中心对称性的探究．运用平移、旋转的图形变换思想探究平行四边形的性质．教法：启导探究法.学法：自主探究、合作交流.22.2 平行四边形的识别教学目标：22.3 三角形的中位线1、掌握三角形中位线的概念。

初中数学知识点复习提纲新一轮中考复习备考周期正式开始，你是不是还在为了数学怎么复习而苦恼呢?你知道初中数学的知识点有哪些吗?以下是小编精心收集整理的初中数学知识点复习提纲，肯定会对你有所帮助的，来阅读一下吧!初中数学知识点复习提纲1.有理数的加法运算：同号相加一边倒;异号相加“大”减“小”，符号跟着大的跑;绝对值相等“零”正好.2.合并同类项：合并同类项，法则不能忘，只求系数和，字母、指数不变样.3.去、添括号法则：去括号、添括号，关键看符号，括号前面是正号，去、添括号不变号，括号前面是负号，去、添括号都变号.4.一元一次方程：已知未知要分离，分离方法就是移，加减移项要变号，乘除移了要颠倒.5.平方差公式：平方差公式有两项，符号相反切记牢，首加尾乘首减尾，莫与完全公式相混淆.5.1完全平方公式：完全平方有三项，首尾符号是同乡，首平方、尾平方，首尾二倍放中央;首±尾括号带平方，尾项符号随中央.5.2因式分解：一提(公因式)二套(公式)三分组，细看几项不离谱，两项只用平方差，三项十字相乘法，阵法熟练不马虎，四项仔细看清楚，若有三个平方数(项)，就用一三来分组，否则二二去分组，五项、六项更多项，二三、三三试分组，以上若都行不通，拆项、添项看清楚.5.3单项式运算：加、减、乘、除、乘(开)方，三级运算分得清，系数进行同级(运)算，指数运算降级(进)行.5.4一元一次不等式解题的一般步骤：去分母、去括号，移项时候要变号，同类项合并好，再把系数来除掉，两边除(以)负数时，不等号改向别忘了.5.5一元一次不等式组的解集：大大取较大，小小取较小，小大、大小取中间，大小、小大无处找.一元二次不等式、一元一次绝对值不等式的解集：大(鱼)于(吃)取两边，小(鱼)于(吃)取中间.6.1分式混合运算法则：分式四则运算，顺序乘除加减，乘除同级运算，除法符号须变(乘);乘法进行化简，因式分解在先，分子分母相约，然后再行运算;加减分母需同，分母化积关键;找出最简公分母，通分不是很难;变号必须两处，结果要求最简.6.2分式方程的解法步骤：同乘最简公分母，化成整式写清楚，求得解后须验根，原(根)留、增(根)舍，别含糊.6.3最简根式的条件：最简根式三条件，号内不把分母含，幂指数(根指数)要互质、幂指比根指小一点.6.4特殊点的坐标特征：坐标平面点(x，y)，横在前来纵在后;(+，+)，(-，+)，(-，-)和(+，-)，四个象限分前后;x轴上y为0，x为0在y轴.象限角的平分线：象限角的平分线，坐标特征有特点，一、三横纵都相等，二、四横纵却相反.平行某轴的直线：平行某轴的直线，点的坐标有讲究，直线平行x轴，纵坐标相等横不同;直线平行于y轴，点的横坐标仍照旧.6.5对称点的坐标：对称点坐标要记牢，相反数位置莫混淆，x轴对称y相反，y轴对称x相反;原点对称记，横纵坐标全变号.7.1自变量的取值范围：分式分母不为零，偶次根下负不行;零次幂底数不为零，整式、奇次根全能行.7.2函数图象的移动规律：若把一次函数的解析式写成y=k(x+0)+b，二次函数的解析式写成y=a(x+h)2+k的形式，则可用下面的口诀“左右平移在括号，上下平移在末稍，左正右负须牢记，上正下负错不了”.7.3一次函数的图象与性质的口诀：一次函数是直线，图象经过三象限;正比例函数更简单，经过原点一直线;两个系数k与b，作用之大莫小看，k是斜率定夹角，b与y轴来相见，k为正来右上斜，x增减y增减;k为负来左下展，变化规律正相反;k的绝对值越大，线离横轴就越远.7.4二次函数的图象与性质的口诀：二次函数抛物线，图象对称是关键;开口、顶点和交点，它们确定图象现;开口、大小由a断，c与y轴来相见;b的符号较特别，符号与a相关联;顶点位置先找见，y轴作为参考线;左同右异中为0，牢记心中莫混乱;顶点坐标最重要，一般式配方它就现;横标即为对称轴，纵标函数最值见.若求对称轴位置，符号反，一般、顶点、交点式，不同表达能互换.7.5反比例函数的图象与性质的口诀：反比例函数有特点，双曲线相背离得远;k为正，图在一、三(象)限，k为负，图在二、四(象)限;图在一、三函数减，两个分支分别减.图在二、四正相反，两个分支分别增;线越长越近轴，永远与轴不沾边.8.1特殊三角函数值记忆：首先记住30度、45度、60度的正弦值、余弦值的分母都是2，正切、余切的分母都是3，分子记口诀“123，321，三九二十七”既可.三角函数的增减性：正增余减8.2平行四边形的判定：要证平行四边形，两个条件才能行，一证对边都相等，或证对边都平行，一组对边也可以，必须相等且平行.对角线，是个宝，互相平分“跑不了”，对角相等也有用，“两组对角”才能成.8.3梯形问题的辅助线：移动梯形对角线，两腰之和成一线;平行移动一条腰，两腰同在“△”现;延长两腰交一点，“△”中有平行线;作出梯形两高线，矩形显示在眼前;已知腰上一中线，莫忘作出中位线. 8.4添加辅助线歌：辅助线，怎么添?找出规律是关键.题中若有角(平)分线，可向两边作垂线; 线段垂直平分线，引向两端把线连;三角形边两中点，连接则成中位线;。

第一章 实数1．1实数的有关概念及实数的分类一、规定了原点．．、正方向．．．和单位长度．．．．的直线叫做数轴。

数轴上所有的点与全体实数是一一对应关系。

二、⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧无限不循环小数负无理数正无理数无理数数有限小数或无限循环小负分数正分数分数负整数零正整数整数有理数实数三、在数轴上，原点两旁且与原点距离相等的两个点所表示的数是互为相反数。

四、两个互为相反数的和等于零；互为倒数的两个数的积等于1；零没有倒数。

五、偶数一般用n 2（n 为整数）来表示，奇数一般用12+n 来表示。

六、有理数都可以表示为nm （m ，n 为整数且m ，n 互质）的形式；任何一个分数都可以化成有限小数或无限循环小数的形式。

七、绝对值⎩⎨⎧<-≥==)0()0(2a a a a a a八、非负数 像a ，2a ，)0(≥a a 形式的数都表示非负数。

非负数性质①最小的非负数是0；②若几个非负数的和是0，则每个非负数都是0。

九、近似数与有效数字 一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位，这时，从左边第一个不是0的数字起到精确的数位止，所有的数字都叫这个数的有效数字。

十．科学记数法 把一个数记成n a 10⨯的形式叫做科学记数法，其中101<≤a ，n 为整数。

第二章 代数式2．1整式一、 代数式的分类⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧无理式分式多项式单项式整式有理式代数式 二、同类项 所含的字母相同并且相同字母的指数也相同的项叫做同类项，合并同类项时，只把系数相加，所含字母和字母的指数不变。

三、整式的运算（1）整式的加减 先去括号或添括号，再合并同类项。

（2）整式的乘除 幂的运算性质①n m n m a a a +=⋅（m ，n 为整数，0≠a ）；②mn n m a a =)(（m ，n 为整数，0≠a ）；③n n n b a ab ⋅=)(（n 为整数且0≠a ）；④n m n m a a a -=÷（m ，n 为整数，0≠a ）。

初中数学总复习提纲第一章 实数★重点★ 实数的有关概念及性质，实数的运算 ☆内容提要☆一、重要概念1．数的分类及概念 数系表：说明：“分类”的原则：1）相称（不重、不漏）2）有标准2．非负数：正实数与零的统称。

（表为：x ≥0） 常见的非负数有： 性质：若干个非负数的和为0，则每个非负担数均为0。

3．倒数： ①定义及表示法②性质： A.a ≠1/a （a ≠±1）;B.1/a 中，a ≠0;C.0＜a ＜1时1/a ＞1;a ＞1时，1/a ＜1;D.积为1。

4．相反数： ①定义及表示法②性质：A.a ≠0时，a ≠-a;B.a 与-a 在数轴上的位置;C.和为0,商为-1。

5．数轴：①定义（“三要素”）②作用：A.直观地比较实数的大小;B.明确体现绝对值意义;C.建立点与实数的一一对应关系。

6．奇数、偶数、质数、合数（正整数—自然数）定义及表示：奇数：2n-1偶数：2n （n 为自然数）7．绝对值：①定义（两种）：代数定义： 几何定义：数a 的绝对值顶的几何意义是实数a 在数轴上所对应的点到原点的距离。

②│a │≥0,符号“││”是“非负数”的标志;③数a 的绝对值只有一个;④处理任何类型的题目，只要其中有“││”出现，其关键一步是去掉“││”符号。

二、实数的运算1． 运算法则（加、减、乘、除、乘方、开方）2． 运算定律（五个—加法[乘法]交换律、结合律;[乘法对加法的] 分配律）3． 运算顺序：A.高级运算到低级运算;B.（同级运算）从“左” 到“右”（如5÷51×5）;C.(有括号时)由“小”到“中”到“大”。

三、应用举例（略）附：典型例题1． 已知：a 、b 、x 在数轴上的位置如下图，求证：│x-a │+│x-b │ =b-a.实数无理数(无限不循环小数)正分数 负分数 正整数 0 负整数 (有限或无限循环性整数分数0 实数 负数 整数 分数无理数有理数 正数整数分数无理数有理数 │a │ a (a ≥0)(a 为一切实数) a(a≥-a(a<0) │a │=2.已知：a-b=-2且ab<0，（a ≠0，b ≠0），判断a 、b 的符号。

重庆初中数学知识要点一、基本知识㈠、数与代数 、数与式：1、有理数 顺序：先算乘方，再算乘除，最后算加减，有括号要先算括号里的。

2、实数 数：①实数分有理数和无理数。

②在实数范围内，相反数，倒数，绝对值的意义和有理数范围内的相反数，倒数，绝对值的意义完全一样。

③每一个实数都可以在数轴上的一个点来表示。

3、代数式 数式：单独一个数或者一个字母也是代数式。

合并同类项：①所含字母相同，并且相同字母的指数也相同的项，叫做同类项。

②把同类项合并成一项就叫做合并同类项。

③在合并同类项时，我们把同类项的系数相加，字母和字母的指数不变。

4、整式与分式 式运算：加减运算时，如果遇到括号先去括号，再合并同类项。

幂的运算：m n m n a a a +=g ，()m n mn a a = m n m n a a a -÷=方法：提公因式法、运用公式法、分组分解法、十字相乘法。

分式的运算：分式方程： B 、方程与不等式1、方程与方程组 一元一次方程的步骤：二元一次方程：二元一次方程组：解二元一次方程组的方法：代入消元法/加减消元法。

1）一元二次方程的二次函数的关系 二次方程的解法 函数有顶点（-b/2a,4ac-b 2/4a ）(1）配方法： (2)分解因式法：提取公因式，套用公式法，和十字相乘法。

(3)公式法：这方法也可以是在解一元二次方程的万能方法了，方程的根X 1={-b+√[b 2-4ac)]}/2a ，X 2={-b-√[b 2-4ac)]}/2a3）解一元二次方程的步骤： 4）韦达定理=-b/a ，二根之积=c/a ，也可以表示为x 1+x 2=-b/a,x 1.x 2=c/a 。

一元一次方程根的情况△=b 2-4ac ，这里可以分为3种情况： I 当△>0时，一元二次方程有2个不相等的实数根； II 当△=0时，一元二次方程有2个相同的实数根； III 当△<0时，一元二次方程没有实数根2、不等式与不等式组 式的解集：一元一次不等式组：3、函数 ：因变量，自变量。