1996年考研数学二试题及答案

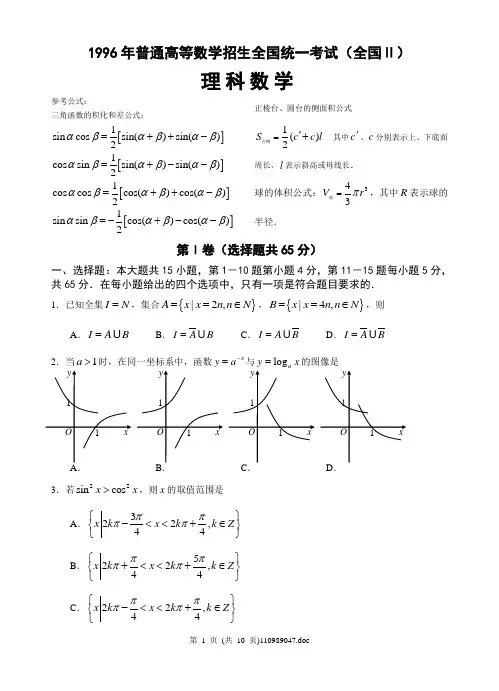
1996年普通高等数学招生全国统一考试（全国Ⅱ）理科数学参考公式：三角函数的积化和差公式：[]1sin cos sin()sin()2αβαβαβ=++- []1cos sin sin()sin()2αβαβαβ=+--[]1cos cos cos()cos()2αβαβαβ=++-[]1sin sin cos()cos()2αβαβαβ=-+--正棱台、圆台的侧面积公式1()2S c c l ='+台侧 其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长．球的体积公式：343V r π=球，其中R 表示球的半径．第Ⅰ卷（选择题共65分）一、选择题：本大题共15小题，第1－10题第小题4分，第11－15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集I N =，集合{}|2,A x x n n N ==∈，{}|4,B x x n n N ==∈，则A ．I AB =B ．I A B =C ．I A B =D ．I A B =2．当1a >时，在同一坐标系中，函数x y a -=与logy x =的图像是3．若22sin cos x x >，则x 的取值范围是A ．322,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭B ．522,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭C ．22,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭D ．322,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭4．复数4A．1+ B．1-+ C．1- D．1--5．如果直线,l m 与平面,,αβγ满足：l βγ= ，l ∥α，m α⊂和m γ⊥，那么必有A ．a γ⊥且l m ⊥B ．αγ⊥且m ∥βC ．m ∥β且l m ⊥D ．α∥β且αγ⊥ 6．当22x ππ-≤≤时，函数()sin f x x x =+的A ．最大值是1，最小值是－1B ．最大值是1，最小值是12-C ．最大值是2，最小值是－2D ．最大值是2，最小值是－17．椭圆33cos ,15sin ,x y ϕϕ=+⎧⎨=-+⎩的两个焦点的坐标是A ．(3,5)-，(3,3)--B ．(3,3)，(3,5)-C ．(1,1)，(7,1)-D ．(7,1)-，(1,1)--8．若02πα<<，则arcsin[cos()]arccos[sin()]2παπα+++等于A ．2πB ．2π-C ．22πα- D ．22πα--9．将边长为a 的正方形A B C D 沿对角线A C 折起，使得B D a =，则三棱锥D A B C -的体积为A ．36aB ．312aC12D．31210．等比数列{}n a 的首项11a =-，前n 项和为n S ，若1053132S S =，则lim n n S →∞等于A ．23B ．23-C ．2D ．2-11．椭圆的极坐标方程为32cos ρθ=-，则它的短轴上的两个顶点的极坐标是A ．(3,0)，(1,)πB．)2π，3)2πC ．(2,)3π，5(2,)3π D．arctan2，2arctan2π-12．等差数列{}n a 的前m 项和为30，前2m 项和为100，则它的前3m 项和为A ．130B ．170C ．210D ．26013．设双曲线22221(0)x y a b ab-=<<的半焦距为c ，直线l 过(,0)a ，(0,)b 两点，已知原点到直线l4，则双曲线的离心率为A ．2 B． CD．314．母线长为1，的圆锥体积最大时，其侧面展开图圆心角ϕ等于A．3B．3C． D315．设()f x 是(,)-∞+∞上的奇函数，(2)()f x f x +=-，当01x ≤≤时，()f x x =，则(7.5)f 等于A ．0.5B ．0.5-C ．1.5D ． 1.5-第Ⅱ卷（非选择题共85分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上．16．已知圆22670x y x +-+=与抛物线22(0)y px p =>的准线相切，则p ＝ ． 17．正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有 个（用数字作答）．18．tan 20tan 4020tan 40++的值是 ．19．如图，正方形A B C D 所在平面与正方形ABEF 所在平面成60°的二面角，则异面直线A D 与B F 所成角的余弦值是 ．ABDCFE三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．20．（本小题满分10分）解不等式1log (1)1a x ->．21．（本小题满分11分）已知△ABC 的三个内角A 、B 、C 满足：2A C B +=，11cos cos cos ACB+=-，求cos2A C -的值．22．（本小题满分12分）如图，在正三棱柱111ABC A B C -中，1E BB ∈，截面1A EC ⊥侧面1AC ． （1）求证：1BE EB =；（2）若111AA A B =，求平面1A EC 与平面111A B C 所成二面角（锐角）的度数．注意：在下面横线上填写适当内容，使之成为（1）的完整证明，交解答（2）．（右下图）（1）证明：在截面1A EC 内，过E 作1EG A C ⊥，G 是垂足． ①∵∴E G ⊥侧面1AC ，取A C 的中点F ，连结B F ，F G ，由A B B C =得BF AC ⊥， ②∵∴B F ⊥侧面1AC ，得B F ∥F G ，B F 、F G 确定一个平面，交侧面1AC 于F G ． ③∵ ∴B E ∥F G ，四边形B E G F 是平行四边形，B E F G =， ④∵ ∴F G ∥1A A ，△1AA C ∽△F G C ，⑤∵ ∴111122F G A A B B ==，即112B E B B =，故1BE EB =23．（本小题满分12分）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22％，人A 1ACB1C 1EA 1 A CB B 1C 1EF G均粮食占有量比现在提高10％．如果人口年增长率为1％，那么耕地平均每年至多只能减少多少公顷（精确到1公顷）？ （粮食单产＝总产量耕地面积，人均粮食占有量＝总产量总人口数24．（本小题满分12分）已知1l 、2l 是过点(0)P 的两条互相垂直的直线，且1l 、2l 与双曲线221y x -=各有两个交点，分别为1A 、1B 和2A 、2B ． （1）求1l 的斜率1k 的取值范围；（2）若1122|||A B A B =，求1l 、2l 的方程．25．（本小题满分12分）已知a 、b 、c 是实数，函数2()f x ax bx c =++，()g x ax b =+，当11x -≤≤时，|()|1f x ≤．（1）证明：||1c ≤；（2）证明：当11x -≤≤时，|()|2g x ≤；（3）设0a >，当11x -≤≤时，()g x 的最大值为2，求()f x ．数学试题参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力13．14．15．16．三、解答题 17．1996年普通高等学校招生全国统一考试数学试题(理工农医类)参考解答及评分标准说明：一．本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误，就不再给分．三．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 四．只给整数分数．选择题和填空题不给中间分．一．选择题：本题考查基本知识和基本运算．第(1)－(10)题每小题4分，第(11)－(15)题每小题5分．满分65分．(1)C (2)A (3)D (4)B (5)A (6)D (7)B (8)A (9)D (10)B (11)C (12)C (13)A (14)D (15)B二．填空题：本题考查基本知识和基本运算．每小题4分，满分16分．（16）2 （17）32（18）3（19）42三．解答题(20)本小题考查对数函数性质，对数不等式的解法，分类讨论的方法和运算能力．满分11分．解：(Ⅰ)当a ＞1时，原不等式等价于不等式组：⎪⎪⎩⎪⎪⎨⎧>->-.11,011a x x——2分由此得xa 11>-．因为1－a <0，所以x <0，∴.011<<-x a——5分 (Ⅱ)当0<a <1⎪⎪⎩⎪⎪⎨⎧<->-.11,011a x x由①得，x >1或x <0，由②得，,110a x -<<∴ax -<<111 ——10分 综上，当1>a 时，不等式的解集为⎭⎬⎫⎩⎨⎧<<-011x a x；当10<<a 时，不等式的解集为⎭⎬⎫⎩⎨⎧-<<a x x 111 ——11分(21)本小题考查三角函数基础知识，利用三角公式进行恒等变形和运算的能力．满分12分． 解法一：由题设条件知B =60°，A +C =120°． ——2分 ∵,2260cos 2-=-∴22cos 1cos 1-=+CA将上式化为C A C A cos cos 22cos cos -=+ 利用和差化积及积化和差公式，上式可化为)]cos()[cos(22cos2cos2C A C A C A C A -++-=-+ ——6分将21)cos(,2160cos 2cos-=+==+C A C A代入上式得)cos(222)2cos(C A C A --=- 将1)2(cos 2)cos(2--=-C A C A 代入上式并整理得 023)2cos(2)2(cos 242=--+-CA C A ——9分,0)32cos22)(22cos2(=+---C A C A∵,032cos22≠+-C A ∴.022cos2=--C A 从而得.222cos=-C A ——12分解法二：由题设条件知B =60°，A +C =120°． 设αα2,2=--=C A C A 则，可得α+= 60A ，α-=60C——3分所以)60cos(1)60cos(1cos 1cos 1αα-++=+CAααααs23c211s23c211++-=ααα22sin 43cos 41cos -=43cos cos 2-=αα ——7分依题设条件有Bcos 243cos cos 2-=-αα，∵21cos =B ∴2243cos cos 2-=-αα整理得,023cos 2cos 242=-+αα——9分,0)3cos 22)(2cos 2(=+-αα∵03cos 22≠+α，∴02cos 2=-α．从而得222cos=-C A ． ——12分(22)本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力及运算能力．满分12分．(Ⅰ) ①∵面A 1EC ⊥侧面AC 1， ——2分②∵面ABC ⊥侧面AC 1， ——3分 ③∵BE ∥侧面AC 1， ——4分 ④∵BE ∥AA 1， ——5分 ⑤∵AF =FC ， ——6分(Ⅱ)解：分别延长CE 、C 1B 1交于点D ，连结A 1D ．∵1EB ∥11112121,CC BB EB CC ==，∴,21111111B A C B DC DB ===∵∠B 1A 1C 1=∠B 1 C 1A 1=60°，∠DA 1B 1=∠A 1DB 1=21（180°－∠D B 1A 1）=30°，∴∠DA 1C 1=∠DA 1B 1+∠B 1A 1C 1=90°，即1DA ⊥11C A ——9分∵CC 1⊥面A 1C 1B 1，即A 1C 1是A 1C 在平面A 1C 1D 上的射影，根据三垂线定理得DA 1⊥A 1C ， 所以∠CA 1C 1是所求二面角的平面角． ——11分∵CC 1=AA 1=A 1B 1=A 1C 1，∠A 1C 1C =90°，∴∠CA 1C 1=45°，即所求二面角为45° ——12分 (23)本小题主要考查运用数学知识和方法解决实际问题的能力，指数函数和二项式定理的应用，近似计算的方法和能力．满分10分．解：设耕地平均每年至多只能减少x 公顷，又设该地区现有人口为P 人，粮食单产为M 吨/公顷．依题意得不等式%)101(10%)11()1010(%)221(4104+⨯⨯≥+⨯-⨯+⨯PM P x M ——5分 化简得]22.1)01.01(1.11[10103+⨯-⨯≤x——7分∵]22.1)01.01(1.11[10103+⨯-⨯)]01.001.01(22.11.11[1022101103+⨯+⨯+⨯-⨯=C C]1045.122.11.11[103⨯-⨯≈1.4≈ —— 9分∴x ≤4（公顷）．答：按规划该地区耕地平均每年至多只能减少4公顷． ——10分 (24)本小题主要考查直线与双曲线的性质，解析几何的基本思想，以及综合运用知识的能力．满分12分．解：（I ）依题设，l 1、l 2的斜率都存在，因为l 1过点P )0,2(-且与双曲线有两个交点，故方程组⎪⎩⎪⎨⎧=-≠+=1)0)(2(2211x y k x k y ① ——1分有两个不同的解．在方程组①中消去y ，整理得01222)1(2121221=-++-k x k x k ②若0121=-k ，则方程组①只有一个解，即l 1与双曲线只有一个交点，与题设矛盾，故0121≠-k ，即11≠k ，方程②的判别式为).13(4)12)(1(4)22(2121212211-=---=∆k k k k设2l 的斜率为2k ，因为2l 过点)0,2(-P 且与双曲线有两个交点，故方程组⎪⎩⎪⎨⎧=-≠+=.1),0)(2(2222x y k x k y ③ 有两个不同的解．在方程组③中消去y ，整理得01222)1(2222222=-++-k x k x k ④ 同理有)13(4,0122222-=∆≠-k k又因为l 1⊥l 2，所以有k 1·k 2=－1．——4分于是，l 1、l 2与双曲线各有两个交点，等价于⎪⎪⎩⎪⎪⎨⎧≠-=⋅>->-.1,1,013,0131212221k k k k k 解得⎪⎩⎪⎨⎧≠<<.1,33311k k ——6分∴)3,1()1,33()33,1()1,3(1 ----∈k ——7分(Ⅱ)设),(),,(221111y x B y x A 由方程②知112,122212121212121--=⋅--=+k k x x k k x x∴│A 1B 1│2=(x 1－x 2)2+(y 1－y 2)222121))(1(x x k -+=2212121)1()13)(1(4--+=kk k ⑤ ——9分同理，由方程④可求得222B A ，整理得2212121222)1()3)(1(4k k k B A --+=⑥由22115B A B A =，得2222115B A B A =将⑤、⑥代入上式得22121212212121)1()3)(1(45)1()13)(1(4k k k kk k --+⨯=--+解得21±=k取21=k 时，)2(22:),2(2:21+-=+=x y l x y l ； 取21-=k 时，)2(22:),2(2:21+=+-=x y l x y l ．——12分(25)本小题主要考查函数的性质、含有绝对值的不等式的性质，以及综合运用数学知识分析问题与解决问题的能力．满分12分．(Ⅰ)证明：由条件当－1≤x ≤1时，│f (x )│≤1，取x =0得│c │=│f (0)│≤1，即│c │≤1． ——2分(Ⅱ)证法一：当a >0时，g (x )=ax +b 在[－1，1]上是增函数，∴g (－1)≤g (x )≤g (1)， ∵│f (x )│≤1 (－1≤x ≤1)，│c │≤1，∴g (1)=a +b =f (1)－c ≤│f (1)│+│c │≤2， g (－1)=－a +b =－f (－1)+c ≥－(│f (－1)│+│c │)≥－2， 由此得│g (x )│≤2; ——5分 当a <0时，g (x )=ax +b 在[－1，1]上是减函数，∴g (－1)≥g (x )≥g (1)， ∵│f (x )│≤1 (－1≤x ≤1)，│c │≤1，∴g (－1)=－a +b =－f (－1)+c ≤│f (－1)│+│c │≤2， g (1)=a +b =f (1)－c ≥－(│f (1)│+│c │)≥－2，由此得│g (x )│≤2; ——7分 当a =0时，g (x )=b ，f (x )=bx +c ．∵－1≤x ≤1，∴│g (x )│=│f (1)－c │≤│f (1)│+│c │≤2．综上得│g (x )│≤2． ——8分证法二：由4)1()1(22--+=x x x ，可得b ax x g +=)()2121(])21()21[(22--++--+=x x b x x a])21()21([])21()21([22c x b x a c x b x a +-+--++++=),21()21(--+=x f x f ——6分当－1≤x ≤1时，有,0211,1210≤-≤-≤+≤x x根据含绝对值的不等式的性质，得2)21()21()21()21(≤-++≤--+x f x f x f x f即│g (x )│≤2． ——8分(Ⅲ)因为a >0，g (x )在[－1，1]上是增函数，当x =1时取得最大值2，即g (1)=a +b =f (1)－f (0)=2． ①∵－1≤f (0)=f (1)－2≤1－2=－1，∴c =f (0)=－1． ——10分 因为当－1≤x ≤1时，f (x )≥－1，即f (x )≥f (0)，根据二次函数的性质，直线x =0为f (x )的图像的对称轴，由此得0,02==-b ab 即由① 得a =2．所以 f (x )=2x 2－1． ——12分。

1996数学二考研真题及答案理工数学二试题详解及评析一、填空题（1）设y=某+e某2'，则y|某=0=.23【答】1.3某223某1【详解】y=某+e1+e2，21'所以y|=.某=03（2）∫(某d某=.【答】2.【详解】∫(某d某=∫11(某+22'1某2d某11)=∫2+∫d某=0+2=2(3)微分方程y+2y+5y=0的通解为.【答】y=e某''(C1co2某+C2in2某).2【详解】特征方程λ+2λ+5=0的解为λ=1±2i，所以通解为y=e 某(C1co2某+C2in2某)31inln1+=.某某（4）lim某inln1+某→∞【答】2.【详解】方法一：令=t,则由洛必达法则知某原式＝liminln(1+3t)inln(1+t)t→0t=lim31t→0coln(1+3t)1+3tcoln(1+t)1+t=lim31t→01+3t1+t=2方法二：直接利用三角函数和差化积公式.原式＝1+3ln1+ln1+113lim某→∞2某in+某2co某2ln+2=lim某1某→∞2某in+12=lim某→∞2某in某+1 =2（5）由曲线y=某+1某,某=2及y=2所围图形的面积S=【答】ln212.【详解】S=∫2某+11某2d某=122某+ln某2某2|11=ln22二、选择题（1）设当某→0时，e某(a某2+b某+1)是比某2高阶的无穷小，则（A）a=2,b=1.（B）a=1,b=1（C）a=12,b=1（D）a=1,b=1【答】应选（A）【详解】方法一：由于某→0时，e某=1+某+1某2+o(某22)】【则由lim某→0e(a某+b某+1)某22某→0某=0=lim(1b)某+a某2+o(某2)22某必有1b=0,解得a=方法二：因lim某→0a=02,b=1.2e某2a某b,=lim某→02某e某(a某2+b某+1)某2某→0某→0又lim2某=0,lime2a某b=1b必有b=1,从而(某)e某2a某be某2a原式＝lim=lim=12a=0,某→0某→02某2所以a=1.22（2）设函数f(某)在区间(δ,δ)内有定义，若当某∈(δ,δ)时，恒有f(某)≤某，则某=0必是f(某)（A）间断点.（B）连续而不可导的点(C)可导的点，且f'(0)=0（D）可导的点，f'(0)≠0【】【答】应选（C）.【详解】由定义lim某→0f(某)f(0)f(某)f(某)=lim=lim2某=0，某→0某→0某某某由题设必有f(0)=0因此f'(0)=0（3）设f(某)处处可导，则（A）当limf(某)=∞,必有limf某→∞'(某)=∞,（B）当limf某→∞'f(某)=∞,(某)=∞,，必有某lim→∞'某→+∞（C）当limf(某)=+∞,必有limf某→+∞(某)=+∞,（D）当limf某→+∞'f(某)=+∞,(某)=+∞,，必有某lim→+∞【】【答】应选（D）.【详解】方法一：利用举反例排除不正确选项.令f(某)=某,则limf'、（C）均不正确.(某)=±∞,但f'(某)=1，可见（A）因而只有（D）是正确选项.方法二：若limf某→+∞'(某)=+∞,则存在M>0及某0>0，当某>某0时，f'(某)>M于是当某>某0时，有f(某)f(某0)=f从而有'(ξ)(某某0)>M(某某0)f(某)>f(某0)+M(某某0)→+∞(某→+∞)（4）在区间(∞,+∞)内，方程某+某co某=0（A）无实根.（B）有且仅有一个实根（C）有且仅有两个实根（D）有无穷多个实根【】【答】应选（C）【详解】令f(某)=某+某co某,由于f(某)=f(某)，故f(某)为偶函数，因此只需考虑f(某)=0在(0,+∞)内的实根情况.当某≥0时，f(某)=某+某co某,4121412141213114f(某)=某+某2+in某42'可见，当某∈0,ππ'时，在f某>0,f某()()0,内单调增加，且f(0)=1，f22π>1，2因此f(某)=0在0,当某≥π上有唯一实根；2π2时，f(某)>0，故在(0,+∞)上f(某)仅存在唯一实根根据f(某)关于y轴对称的性质，f(某)=0在(∞,+∞)上有且仅有两个实根.（5）设f(某),g(某)在区间[a,b]上连续，且g(某)<f(某)<m,（m 为常数），由曲线y=g(某),y=f(某),某=a及某=b所围成平面图形绕直线y=m旋转而成的旋转体积为（A）（B）（C）（D）∫∫∫babπ2mf(某)+g(某)f(某)g(某)d某,π2mf(某)g(某)f(某)g(某)d某,πmf(某)+g(某)f(某)g(某)d某,πmf(某)g(某)f(某)g(某)d某,【】abab∫a【答】应选（B）【详解】因为dV=πmg(某)()22π(mf(某))d某V=∫πmg(某)d某∫aπmf(某)d某a=∫π2mf(某)g(某)f(某)g(某)d 某a所以正确选项应为（B）三、计算bb2b2∫ln0.【详解】方法一：原式＝∫ln2e=+∫ln2ln2某0=+lne某+2=+ln22((|ln20方法二：令e某=int,则d某=cotdt,intπππcot1dt=π2dtπ2intdtint6int6π原式＝π62=ln(cct+cott)π6=ln2+22(方法三：原式＝=t,则t21=+=1dt2201t1t=（2）求+ln2+2(d某∫1+in某【详解】方法一：原式＝1in某1某tan=+C∫co2tco某某d某=∫原式＝∫22某某某co+in1+tanec2某d1+tan22=2∫=+C2某某1+tan1tan+22方法二：某=tf(u2)du∫d2y0(3)设，其中f(u)具有二阶导数，且f(u)≠0，求2.22d某y=f(t)【详阶】因为d某=f(t2)dtdy=4tf(t2)f'(t2),dt所以dydy==4tf'(t2),d某dtdyddy1==2d某dtd某dt(4)求函数f(某)=2'22''2+fttft42()()ft21某在某=0点处带拉格朗日型余项的n阶泰勒展开式.1+某【详解】f(某)在在某=0点处带拉格朗日型余项的n阶泰勒展开式为：f(某)=f(0)+f'(0)某+1''1n1n+1f(0)某2+"+f()(0)某n+f()(θ某)某n+1n!2!n+1!其中0<θ<1.可见，关键是求出f(某)在在某=0点的k阶导数f(k)(0),k=0,1,2,",n+1由于f(某)=21,1+某(1)2k!k=1,2,",n+1kf()(某)=)k+1((1+某)所以f(某)=12某+2某+"+(1)2某+(1)2nnn+12某n+1(1+θ某)n+2(0<θ<1)（5）求微分方程y+y=某的通解.【详解】对应的齐次方程的特征方程为：λ+λ=0解得λ=0,λ=1故齐次方程的通解为y=C1+C2e设非齐次方程的特解为：某a某+b某+c,代入原方程，得a=某''22(2),b=1,c=2,3因此，原方程得通解为y=某3某2+2某+C1+C2e某3（6）设有一正椭圆柱体，其底面得长、短分别为2a,2b,用过此柱体底面得短轴与底面成α角π<<0α，求此楔形体的体积V.的平面截此柱体，得一楔形体（如图）2【详解】方法一：底面椭圆的方程为：某2y2+=1,以垂直于y轴的平行平面截此楔形体所得的截面为直角三角形，其一直角边为a2b2令一直角边长为α,故截面面积为a2y2S(y)=12tanα2b楔形体积为V=2∫方法二：ba2y22a2btanα12tanαdy=2b3某2y2底面椭圆的方程为2+2=1,以垂直于某轴平行平面截此楔形体所得的截面为矩形，ab其一边长为2y=2令一边长为某tanα，故截面面积S(某)=2α楔形体的体积V=∫a2a2b2αd某=tanα3四、计算不定积分【详解】方法一：arctan某∫某21+某2arctan某arctan某arctan某=∫某21+某2∫某2∫1+某2==arctan某112+∫某arctan()某某1+某22arctan某111212 +∫2d某某arctan()某2某1+某22arctan某11某22(arctan某)+ln=+C某221+某2方法二：令某=tant,则原式＝2cctt1)dt=(∫=2arctan某)+C=12某2,某<13五、设函数f(某)=某,1≤某≤212某16,某>2（1）写出f(某)的反函数g(某)的表达式；（2）g(某)是否有间断点、不可导点，若有，指出这些点.【详解】（1）由题设，f(某)的反函数为某<1g(某)=1≤某≤8某+16,某>812（2）由于函数f(某)在(∞,+∞)内单调增加且连续，故反函数g(某)在在(∞,+∞)内单调增加且连续，没有间断点.由于f'(0)=0，且f(0)=0，故某=0是g(某)的不可导点，f(1)=1和f(2)=8是g(某)的两个可能的不可导点，由于f'(10)=4,f'(1+0)=3,所以某=1是f(某)的不可导点，因此g(某)在f(1)=1处不可导；又f2(1+0)=f'(20)=12,故f(某)在某=2处可导，因此g(某)在某=f(2)=8处可导.六、设函数y=y(某)由方程2y2y+2某y某=1所确定，试求y=y(某)的驻点，并判别322它是否为极值点.【详解】对原方程两边求导，得3y2y'2yy'+某y'+y某=0,令y=0，得y=某，代入原方程，有2某某1=0从而解得唯一的驻点某=1.在（某）式两边对某求导得3y2y+某y+2(3y1)y+2y1=0,2'''2'32()因此y''|(1,1)=>02故驻点某=1是y=y(某)的极小点.七、设f(某)在区间[a,b]上具有二阶导数，且f(a)=f(b)=0,f存在ξ∈(a,b)和η∈(a,b)，使f【详解】方法一（用反证法）若不存在ξ∈(a,b)，使f'(a)f'(b)>0，证明：(ξ)=0及f''(η)=0.(ξ)=0，则在区间(a,b)内恒有f(某)>0或f(某)<0，不妨设f(某)>0（对f(某)<0，类似可证），则f(某)f(b)f(b)=lim=lim某→b某→b某bf(某)f(a)f'(a)=lim+=lim+某→a某→a某a'f(某)≤0,某bf(某)≥0某a从而f'(a)f'(b)≤0，这与已知条件矛盾，即在(a,b)内至少存在一点ξ,使f(ξ)=0(ξ)=f(b)及罗尔定理，知存在η1∈(a,ξ)和η2∈(ξ,b)，使再由f(a)=ff'(η1)=f'(η2)=0.'又在区间[η1,η2]上，对f方法二：不妨设f'(某)应用罗尔定理，知存在η∈(η1,η2)(a,b)，使f''(η)=0.，即(a)>0,f'(b)>0（对f'(a)<0,f'(b)<0时类似可证）lim+某→af(某)f(某)>0,lim>0,某→b某b某a由极限的保号性，存在某1∈(a,a+δ1)和某2∈(bδ2,b)使得f(某1)>0及f(某2)<0，其中δ1,δ2为充分小的正数，显然某1<某2在区间[某1,某2]上应用介值定理知，存在ξ∈(某1,某2)(a,b)使f以下证明类似方法一.八、设f(某)为连续函数，'y+ay=f(某)的解f(某)，其中a是正常数；（1）求初值问题=0y|某=0ka某（2）若f(某)≤k（k为常数），证明：当某≥0时，有y(某)≤(1e).a(ξ)=0【详解】（1）原方程的通解为y(某)=ea某f(某)ea某d某+C=ea某F(某)+C,∫其中F(某)是f(某)e的任一原函数a某由y(0)=0,得C=F(0)故y(某)=ea某a某atF某F0=eftedt,()()()∫0at某或者在原方程的两端同乘以e，得y'ea某+ayea某=f(某)ea某从而ye所以ye(a某')=f(某)e某0a某a某=∫f(t)eatdt,a某或y(某)=e（2）∫f(t)e某atdt,f(某)≤ea某∫f(t)eatdt≤kea某∫eatdt 某某ka某a某e(e1)ak=(1ea某)(某≥0)a≤。

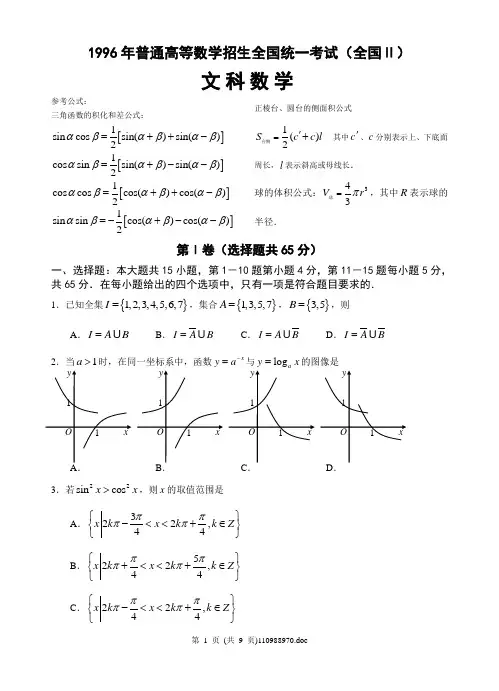
1996年普通高等数学招生全国统一考试（全国Ⅱ）文科数学参考公式：三角函数的积化和差公式：[]1sin cos sin()sin()2αβαβαβ=++- []1cos sin sin()sin()2αβαβαβ=+--[]1cos cos cos()cos()2αβαβαβ=++-[]1sin sin cos()cos()2αβαβαβ=-+--正棱台、圆台的侧面积公式1()2S c c l ='+台侧 其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长．球的体积公式：343V r π=球，其中R 表示球的半径．第Ⅰ卷（选择题共65分）一、选择题：本大题共15小题，第1－10题第小题4分，第11－15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集{}1,2,3,4,5,6,7I =，集合{}1,3,5,7A =，{}3,5B =，则A ．I AB =B ．I A B =C ．I A B =D ．I A B =2．当1a >时，在同一坐标系中，函数xy a -=与logy x =的图像是3．若22sin cos x x >，则x 的取值范围是A ．322,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭B ．522,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭C ．22,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭D ．322,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭44等于A ．1B ．1-C ．1D ．1-5．6名同学排成一排，其中甲、乙两必须排在一起的不同排法有A ．720种B ．360种C ．240种D ．120种6．已知α是第三象限角，24sin 25α=-，则tan 2α＝ A ．43B ．34 C ．34- D ．43-7．如果直线,l m 与平面,,αβγ满足：l βγ= ，l ∥α，m α⊂和m γ⊥，那么必有A ．a γ⊥且l m ⊥B ．αγ⊥且m ∥βC ．m ∥β且l m ⊥D ．α∥β且αγ⊥8．当22x ππ-≤≤时，函数()sin f x x x =的A ．最大值是1，最小值是－1B ．最大值是1，最小值是12-C ．最大值是2，最小值是－2D ．最大值是2，最小值是－18．若02πα<<，则arcsin[cos()]arccos[sin()]2παπα+++等于A ．2π B ．2π-C ．22πα- D ．22πα--9．中心在原点，准线方程为4x =±，离心率为12的椭圆方程是 A ．22143x y += B ．22134x y += C ．2214x y += D ．2214y x += 10．圆锥母线长为1，侧面展开图圆心角为240°，该圆锥的体积A B ．881π C D ．1081π11．椭圆222515091890x x y y -+++=的两个焦点坐标是A ．(3,5)-，(3,3)--B ．(3,3)，(3,5)-C ．(1,1)，(7,1)-D ．(7,1)-，(1,1)--12．将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD a =，则三棱锥D ABC -的体积为A ．36aB ．312aCD13．等差数列{}n a 的前m 项和为30，前2m 项和为100，则它的前3m 项和为A ．130B ．170C ．210D ．26014．设双曲线22221(0)x y a b a b-=<<的半焦距为c ，直线l 过(,0)a ，(0,)b 两点，已知原点到直线l，则双曲线的离心率为 A ．2BCD15．设()f x 是(,)-∞+∞上的奇函数，(2)()f x f x +=-，当01x ≤≤时，()f x x =，则(7.5)f 等于A ．0.5B ．0.5-C ．1.5D ． 1.5-第Ⅱ卷（非选择题共85分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上．16．已知点(2,3)-与抛物线22(0)y px p =>的焦点的距离是5，则p ＝ ．17．正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有 个（用数字作答）．18．tan 20tan 4020tan 40+的值是 ． 19．如图，正方形ABCD 所在平面与正方形ABEF 所在平面成60°的二面角，则异面直线AD 与BF 所成角的余弦值是 ．三、解答题：本大题共6小题，共69分，解答应写出文字说明，证明过程或演算步骤．ABDCF EA 1AC BB 1C 1E F20．（本小题满分11分）解不等式log (1)1a x a +->．21．（本小题满分12分）设等比数列{}n a 的前n 项和为n S ．若3692S S S +=，求数列的公比q ． 22．（本小题满分11分）已知△ABC 的三个内角A、B 、C 满足：2A C B +=，11cos cos cos A C B+=-，求cos 2A C -的值． 23．（本小题满分12分）【注意：本题的要求是，参照标①的写法，在标号②、③、④、⑤的横线上填写适当步骤，完成（1）证明的全过程，并解答（2）．】如图，在正三棱柱111ABC A B C -中，13AA AB a ==，E ，F 分别是1BB ，1CC 上的点，且BE a =，2CF a =．（1）求证：面AEF ⊥面ACF ； （2）求三棱锥1A AEF -的体积．（1）证明：在截面1A EC 内，过E 作1EG AC ⊥，G 是垂足．①∵BE a =，2CF a =，BE ∥CF ，延长FE 与CB 延长线交于D ，连结AD ．∴△DBE ∽△DCF ∴DB BEDE CF= ② ∴DB AB =．③ ∴DA AC ⊥④ ∴FA AD ⊥⑤ ∴面AEF ⊥面ACF ．24．（本小题满分12分）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22％，人均粮食占有量比现在提高10％．如果人口年增长率为1％，那么耕地平均每年至多只能减少多少公顷（精确到1公顷）？A 1AC BB 1C 1E FD（粮食单产＝总产量耕地面积，人均粮食占有量＝总产量总人口数25．（本小题满分12分）已知1l 、2l 是过点(P 的两条互相垂直的直线，且1l 、2l 与双曲线221y x -=各有两个交点，分别为1A 、1B 和2A 、2B ． （1）求1l 的斜率1k 的取值范围；（2）若1A 恰 是双曲线的一个顶点，求22||A B 的值．数学试题参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力二、填空题．本题考查基础知识,基本概念和基本运算技巧 13． 14． 15． 16．三、解答题 17．1996年普通高等学校招生全国统一考试数学试题(文史类)参考解答及评分标准说明：一．答指出了每题要考查主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准相应的评分细则．二．对计算题，当考生的解答某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答较错误，就不再给分．三．解答右端所注分数，表示考生正确做到这一步应得累加数． 四．只给整数分数，选择题和填空题不给中间分．一．选择题：本题考查基本知识和基本运算，第(1)－(10)题每小题4分，第(11)－(15)题每小题5分．满分65分．(1)C (2)A (3)D (4)B (5)C (6)D (7)A (8)D (9)A (10)C (11)B (12)D (13)C (14)A (15)B二．填空题：本题考查基本知识和基本运算．每小题4分，满分16分．(16)4 (17)32 (18)3 (19)42 三．解答题(20)本小题考查对数函数性质，对数不等式的解法，分类讨论的方法和运算能力，满分11分． 解：（Ⅰ）当a >1时，原不等式等价于不等式组：⎩⎨⎧>-+>-+.1,01a a x a x 解得 x >2a －1． (Ⅱ)当0<a <1时，原不等式等价于不等式组：⎩⎨⎧<-+>-+.101a a x a x 解得 a －1<x <2a －1综上，当a >1时，不等式的解集为{x |x >2a －1};当0<a <1时，不等式的解集为{x |a －1<x <2a －1}．(21)本小题主要考查等比数列的基础知识，逻辑推理能力和运算能力．满分12分．解：若q =1，则有S 3=3a 1，S 6=6a 1，S 9=9a 1．但a 1≠0，即得S 3＋S 6≠2S 9，与题设矛盾，q ≠1．又依题意S 3＋S 6=2S 9可得qq a q q a q q a --=--+--1)1(21)1(1)1(916131整理得q 3(2q 6－q 3－1)=0． 由q ≠0得方程 2q 6－q 3－1=0．(2q 3＋1)(q 3－1)=0， ∵ q ≠1，q 3－1≠0，∴ 2q 3＋1=0∴ q =－243(22)本小题考查三角函数基础知识，利用三角公式进行恒等变形和运算能力．满分12分． 解法一：由题设条件知B =60º，A ＋C =120º．∵ －︒60cos 2=－22∴ C A cos 1cos 1+=－22 将上式化为 cos A ＋cos C =－22 cos A cos C利用和差化积及积化和差公式，上式可化为2cos2C A +cos 2CA -=－2[cos(A ＋C)＋cos(A －C)] 将cos 2)(C A +=cos60º=21，cos(A +C )= 21代入上式得cos 2)(C A -=22－2cos(A －C)cos(A －C)=2cos 22)(C A -－1代入上式并整理得42cos 22)(C A -＋2cos 2)(C A -－32=0，(2cos2C A -－2)(22cos 2CA -＋3)=0． ∵ 22cos 2C A -＋3≠0，∴ 2cos 2C A -－2=0，∴ cos 2C A -=22．解法二：由题设条件知 B=60º，A ＋C =120º．设α=2C A - 则2C A -=2α，可得A=60º＋α，C=60º－α 所以)60cos(1)60cos(1cos 1cos 1o o αα-++=+C A =ααsin 23cos 211-＋ααsin 23cos 211+=ααα22sin 43cos 41cos -=43cos cos 2-αα依题得B cos 243cos cos 2-=-α，∵ cos B =21，∴ 2243cos cos 2-=-αα． 整理得42cos 2α＋2cos α－32=0， (2cos α－2)(22cos α＋3)=0，∵ 22cos α＋3≠0，∴ 2cos α－2=0从而得cos 222=-C A ． (23)本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力运算能力．满分12分．(Ⅰ)②∵BE :CF =1:2 ∴ DC =2BD ，∴ DB =BC ，③∵△ABD 是等腰三角形，且∠ABD =120º，∴∠BAD =30º，∴∠CAD =90º， ④∵FC ⊥面ACD ， ∴CA 是F A 在面ACD 上射影，且CA ⊥AD ， ⑤∵F A ∩AC =A ，DA ⊥面ACF ，DA ⊂面ADF ⑥∴面ADF ⊥面ACF ． (Ⅱ)解： ∵ F AA E AEF A V V 11--=．在面A 1B 1C 1内作B 1G ⊥A 1C 1，垂足为G ．B 1G=23a 面A 1B 1C 1⊥面A 1 C ∵ B 1G ⊥面A 1 C ，∵ E ∈B B 1，而B B 1∥面A 1 C ，∴ 三棱柱E －AA 1F 的高为23a F AA S 1∆=AA 1·2AC =232a ∴43311a V V F AA E AEF A ==-- (24)本小题主要考查运用数学知识和方法解决实际问题的能力，指数函数和二项式定理的应用，近似计算的方法和能力．满分10分．解：设耕地平均每年至多只能减少x 公项，又设该地区现有人口为p 人，粮食单产为M 吨/公顷．依题意得不等式()()()()%10110%111010%2214104+⨯⨯≥+⨯-⨯+⨯PM P xM化简得x ≤103×[1－22.1)01.01(1.110+⨯]．∵ ()⎥⎦⎤⎢⎣⎡+⨯-⨯22.101.011.1110103=103×[1－22.11.1×(1＋110C ×0.01＋210C ×0.012＋…)] ≈103×[1－22.11.1×1.1045]≈4.1 9分∴ x ≤4(公顷)答：按规则该地区耕地平均每年至多只能减少4公顷．(25)本小题主要考查直线与双曲线的性质，解析几何的基本思想，以及综合运用知识的能力．满分12分．解：依题设：l 1、l 2都存在，因为l 1过点P ()02，-且与双曲线有两个交点，故方程组 y =k 1(x ＋2)(k 1≠0)，y 2－x 2=1 ①有两个不同的解，在方程组①中消去y ，整理得(21k －1)x 2＋2221k x ＋221k －1=0 ② 若(21k －1)=0，则方程①只有一个解，则l 1与以曲线只有一个交点，与题设矛盾． 故(21k －1) ≠0，即|k 1|≠1．方程②的判别式为 △ 1=(2221k )2－4(21k －1)(221k －1)=4(321k －1)设l 2的斜率k 2，因为l 2过点P ()02，-且与双曲线有两个交点，故方程组 y =k 2(x ＋2)(k 2≠0)，y 2－x 2=1 ③有两个不同的解，在方程组③中消去y ，整理得(22k －1)x 2＋2222k x ＋222k －1=0 ④ 同理有(22k －1) ≠0，△2=4(322k －1) 又因为l 1⊥l 2，所以有k 1·k 2=－1 于是，l 1、l 2与双曲线各有两个交点，等价于 321k －1>0， 322k －1>0， k 1·k 2=－1， |k 1|≠1． 解得3||331<<k ， |k 1| ≠1．∴ k 1∈(－3，－1) ∪(－1，－33)∪(33，1)∪(1，3) (Ⅱ)双曲线y 2－x 2=1的顶点(0，1)、(0，－1)．取A 1(0，1)时，有 k 1(0＋2)=1，解得k 1=22．从而k 2=11k -=－2． 将k 2=－2代入方程④得 x 2＋42x ＋3=0 ⑤记l 2与双曲线的两交点为A 2(x 1，y 1)、B 2(x 2，y 2)，则|A2B2|2=(x1－x2)2+(y1－y2)2=3(x1－x2)2=3[(x1＋x2)2－4x1x2]．由⑤知x1＋x2=－42x1x2=3∴| A2 B2|2=60，| A2 B2|=215当取A1(0，－1)时，由双曲线y2－x2=1关于x轴的对称性，知| A2 B2|=215所以l1过双曲线的一个顶点时，|A2 B2|=215。

1996年全国硕士研究生入学统一考试数学试题参考解答及评分标准数 学（试卷一）一、填空题：(本题共5小题，每小题3分，满分15分)(1) 设2lim()8xx x a x a→∞+=-，则a = ln2 .(2) 设一平面经过原点及点)2,3,6(-，且与平面824=+-z y x 垂直，则此平面方程为2x +2y –3z = 0 ．(3) 微分方程''2'2xy y y e -+=的通解为)1sin cos (21++=x c x c e y x(4) 函数)ln(2２ ＋ｚy x u +=)在A (1，0，1)处沿点A 指向点B (3，-2，2)方向的方向导数为12.(5) 设A 是4 ⨯3矩阵，且A 的秩r(A)=2,而B = ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-301020201，则r(AB) = 2 .二、选择题：(本题共5小题，每小题3分，满分15分) (1) 已知2)()(y x ydydx ay x +++ 为某函数的全微分，则a 等于 (D)(A) –1. (B) 0 . (C) 1 . (D) 2.(2) 设()x f 有二阶连续导数, 且(0)0f '=,0()lim 1x f x x→''=,则 (B)(A) )0(f 是()x f 的极大值 (B) )0(f 是()x f 的极小值(C) (0,(0))f 是曲线()y f x =的拐点(D) )0(f 不是()x f 的极值, (0,(0))f 也不是曲线y =()x f 的拐点.(3) 设0n a >(1,2,)n = ，且∑∞=1n n a 收敛,常数(0,)2πλ∈,则级数21(1)(tan )n n n n a n λ∞=-∑ (A)(A) 绝对收敛 (B) 条件收敛 （C ） 发散 (D) 敛散性与λ有关.(4) 设()x f 有连续的导数，(0)0f =，)0('f ≠0，F ()x =,)()(202dt t f t x x-⎰且当0→x 时，)('x F 与k x 同阶无穷小，则k 等于 (C)(A) 1. （B ）2. (C) 3. (D) 4.(5) 四阶行列式 4433221100000000a b a b b a b a 的值等于 (D)(A) 4321a a a a -4321b b b b (B) 4321a a a a +4321b b b b (C)（2121b b a a -）（4343b b a a -） (D) （3232b b a a -）（4141b b a a -） 三、(本题共2小题，每小题5分，满分10分) (1) 求心形线)cos 1(θ+=a r 的全长,其中0>a .解：()sin r a θθ'=-，……2分22()ds r r d θ'=+22(1cos )(sin )2|cos |2a d a d θθθθθ=++-=……3分 利用对称性，所求心形线的全长0022cos 8sin822s a d a a ππθθθ===⎰. ……5分(2) 设101=x ,n n x x +=+61(n=1,2,…)，试证数列{}n x 极限存在，并求此极限.证：由110x =及216164x x =+==，知12x x >.假设对某正整数k 有1k k x x +>，则有11266k k k k x x x x +++=+>+=，故由归纳法知，对一切正整数n ，都有1n n x x +>.即{}n x 为单调减少数列. ……3分又由16n n x x +=+，显见0(1,2,)n x n >= ，即{}n x 有下界. 根据极限存在准则，知lim n n x →∞存在.……4分令lim n n x a →∞=，对16n n x x +=+两边取极限，得6a a =+从而260a a --=.因此32a a ==-或.因为0(1,2,)n x n >= ,所以0a ≥.舍去2a =-，故极限值3a =. ……5分四、(本题共2小题，每小题6分，满分12分)(1) 计算曲面积分⎰⎰++Szdxdy dydz z x ）（2,其中S 为有向曲面22y x z +=，(10≤≤z )，其法向量与z 轴正向的夹角为锐角.解一： 以1S 表示法向量指向z 轴负向的有向平面221(1)z x y =+≤，D 为1S 在XOY平面上的投影区域，则1(2)()S Dx z dxdy zdxdy dxdy π++=-=-⎰⎰⎰⎰.……2分记Ω表示由S 和1S 所围的空间区域，则由高斯公式知1(2)(21)S S x z dxdy zdxdy dv +Ω++=-+⎰⎰⎰⎰⎰212421113000336()6242r r r d rdr dz r r dr ππθππ⎡⎤=-=--=--=-⎢⎥⎣⎦⎰⎰⎰⎰. ……5分 因此13(2)()22S x z dxdy zdxdy πππ++=---=-⎰⎰. ……6分解二： 以,yz xy D D 表示S 在,YOZ XOY 平面平面上的投影区域，则(2)Sx z dxdy zdxdy ++⎰⎰2222(2)()(2)()yzyzxyD D D z y z dydz z y z dydz x y dxdy =--+--++⎰⎰⎰⎰⎰⎰2224()yzxyD D z y dydz x y dxdy =--++⎰⎰⎰⎰……2分其中3111222214(1)3yzyD z y dydz dy z y dz y dy--=-=-⎰⎰⎰4204431sin cos 334224y t tdt πππ==⋅⋅⋅=⎰；21222()2xyD x y dxdy d r rdr ππθ+=⋅=⎰⎰⎰⎰，……5分所以1(2) 4.222S x z dxdy zdxdy πππ++=-+=-⎰⎰. ……6分(2) 设变换⎩⎨⎧+=-=ay x v y x u 2 可把方程0622222=∂∂-∂∂∂+∂∂y z y x z x x 简化为02=∂∂∂v u z，求常数a .解：,2z z z z z z a x u v y u v∂∂∂∂∂∂=+=-+∂∂∂∂∂∂.……1分 22222222z z z z x u u v v ∂∂∂∂=++∂∂∂∂∂,2222222(-2)zz z z a a x yu u v v ∂∂∂∂=-++∂∂∂∂∂∂, 2222222244z z z z a a y u u v v ∂∂∂∂=-+∂∂∂∂∂. ……4分将上述结果代入原方程，经整理后得2222(105)(6)0z z a a a u v v∂∂+++-=∂∂∂. 依题意知a 应满足260,1050a a a +-=+≠且，解之得3a =.……6分五、(本题满分7分) 求级数∑∞=-222)1(1n nn 的和.解：设22()(||1)1nn x S x x n ∞==<-∑，……1分则2111()()211n n S x x n n ∞==--+∑，其中122111111n n n n n n x x x x x n n n ∞∞∞-=====--∑∑∑. 23111(0)1n nn n x x x n x n ∞∞===≠+∑∑.……3分设11()n n g x x n∞==∑，则11111()(||1)1n n n n g x x x x n x ∞∞-=='⎛⎫'===< ⎪-⎝⎭∑∑. 于是00()()(0)()ln(1)(||1)1x x dtg x g x g g t dt x x t'=-===--<-⎰⎰.从而21()[ln(1)][ln(1)]222x x S x x x x x =-------221ln(1)(||10)42x x x x x x+-=+-<≠且.……5分 因此221153ln 2(1)2284nn s n ∞=⎛⎫==- ⎪-⎝⎭∑. ……7分六、(本题满分7分)设对任意0>x ,曲线)(x f y =上点))(,(x f x 处的切线在y 轴上的截距等于⎰xdt t f x0)(1,求)(x f 的一般表达式. 解：曲线()y f x =上点(,())x f x 处的切线方程为()()()Y f x f x X x '-=-. ……1分 令0X =，得截距()()Y f x xf x '=-.……3分由题意，知01()()()xf t dt f x xf x x '=-⎰. 即0()[()()]x f t dt x f x xf x '=-⎰.上式对x 求导，化简得()()0xf x f x ''+=， ……5分即('())0d xf x dx=，积分得1'()x f x C =. 因此12()ln f x C x C =+（其中12,C C 为任意常数）.……7分七、(本题满分8分)设)(x f 在[]1,0上具有二阶导数，且满足条件a x f ≤)(，b x f ≤)(''，其中b a ,都是非负常数，c 是()0,1内的任意一点.证明22)('b a c f +≤.证：2()()()()()(),(*)2!f x c f x f c f c x c ξ''-'=+-+其中(),01c x c ξθθ=+-<<. ……2分在(＊)式中令0x =，则有211()(0)(0)()()(0),01;2!f c f f c f c c c ξξ''-'=+-+<<<在(＊)式中令1x =，则有222()(1)(1)()()(1),01;2!f c f f c f c c c ξξ''-'=+-+<<<上述两式相减得22211(1)(0)()()(1)()2!f f f c f c f c ξξ'''''⎡⎤-=+--⎣⎦. ……5分 于是22211|()|(1)(0)()(1)()2!f c f f f c f c ξξ'''''⎡⎤=----⎣⎦ 222111(1)|(0)||()|(1)|()|2!2!f f f c f c ξξ''''≤++-+22[(1)]2ba a c c ≤++-+. ……7分又因22(0,1),(1)1c c c ∈-+≤，故|()|22bf c a '≤+. ……8分八、(本题满分6分)设T A I ξξ=-,其中I 是n 阶单位矩阵,ξ是n 维非零列向量,Tξ是ξ的转置.证明： (1) A A =2的充要条件是1=ξξT ；(2) 当1=ξξT 时,A 是不可逆矩阵. 证：(1) 2()()2T T T T T A I I I ξξξξξξξξξξ=--=-+(2)(2)T T T T I I ξξξξξξξξ=--=--.A A =2即(2)T T T I I ξξξξξξ--=-，亦即()T T I ξξξξ-=O ，因为ξ是非零列向量，0T ξξ≠，故A A =2的充要条件是10T ξξ-=，即1T ξξ=.……3分 (2) 用反证法：当1T ξξ=时A A =2.若A 可逆，则有121A A A A --=，从而A I =.这与T A I I ξξ=-≠矛盾，故A 是不可逆矩阵.……6分九、(本题满分8分)已知二次型32312132132166255),,(x x x x x x cx x x x x x f -+-++=的秩为2. (1) 求参数c 及此二次型对应矩阵的特征值； (2) 指出方程123(,)4f x x x =表示何种二次曲面.解：(1) 此二次型对应矩阵为A =51315333c -⎛⎫ ⎪-- ⎪ ⎪-⎝⎭， ……1分因()2r A =，故513||153033A c-=--=-，解得3c =.容易验证此时A 的秩的确是2. ……3分这时，||(4)(9)I A λλλλ-=--，故所求特征值为0,4,9λλλ===.……6分 (2) 由上述特征值可知，123(,,)1f x x x =表示椭圆柱面. ……8分十、填空题 (本题共2小题，每小题3分，满分6分)(1) 设工厂A 和工厂B 的产品的次品率分别为1%和2%，现从A 和B 的产品分别占60%和40%的一批产品中随机抽取一件，发现是次品，则该次品属A 生产的概率是37.(2) 设,ξη是两个相互独立且均服从正态分布2))2N 的随机变量，则随机变量||ξη- 的数学期望(||)E ξη-＝2π.十一、(本题满分6分)设,ξη是相互独立且服从同一分布的随机变量，已知ξ的分布律为1(),1,2,33P i i ξ===. 又设max{,},min{,}X Y ξηξη==.(1) 写出二维随机变量(,)X Y 发分布律；(2) 求随机变量X 的数学期望.解：(1)Y X1 2 3 11 / 9 0 02 2 / 9 1 / 9 032 / 92 / 91 / 9……4分(2) 13522()1239999E X =⋅+⋅+⋅=……6分 注：写对分布律中的1个数得1分，2～4个得2分，5～7个得3分，8～9个得4分.数 学（试卷二）一、填空题【 同数学一 第一题 】 二、选择题【 同数学一 第二题 】三、(本题共2小题，每小题5分，满分10分) (1) 计算积分dxdy y x D⎰⎰+22，其中D=(){}x y x x y y x 2,0,22≤+≤≤ .解：原式2cos 40d r rdr πθθ=⋅⎰⎰3408cos 3d πθθ=⎰……3分 42340088110(1sin )sin sin sin 23339d ππθθθθ⎡⎤=-=-=⎢⎥⎣⎦⎰……5分(2) 【 同数学一 第三、（1）题 】 (3) 【 同数学一 第三、（2）题 】四 ~ 七、【 同数学一 第四 ~ 七题 】 八、(本题共2小题，每小题6分，满分12分)(1) 求齐次线性方程组⎪⎩⎪⎨⎧=++=-+=++000543321521x x x x x x x x x 的基础解系.解：110011100111100001010011100010⎛⎫⎛⎫⎪ ⎪-→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭……3分解得基础解系为12(1,0,1,0,1),(1,1,0,0,0)ξξ=--=-. ……6分(2) 【 同数学一 第八题 】九、(本题满分8分)【 同数学一 第九题 】数 学（试卷三）一、填空题：(本题共5小题，每小题3分，满分15分) (1) 设322)(x e x y -+=, 则==|'x y 1/3.(2)=-+⎰-1122)1(dx x x 2 .(3) 052=+'+''y y y 的通解为)2sin 2cos (21x c x c e y x +=-. (4) =+-+∞→)]11ln(sin )31ln([sin lim xx x x 2 .(5) 由曲线1y x x =+,2x =及2y =所围图形的面积S =1ln 22-. 二、选择题：(本题共5小题，每小题3分，满分15分)(1) 设当0→x 时，)1(2++-bx ax e x 是比2x 高阶的无穷小，则 （A ）(A) 121==b a ， (B) 11==b a ， (C) 121=-=b a ， (D) 11=-=b a ，. (2) 设函数()f x 在区间),(δδ-内有定义，若当),(δδ-∈x 时，恒有2()f x x ≤，则0x = 必是()f x 的 （C ）(A) 间断点(B) 连续而不可导的点 (C) 可导的点，且(0)0f '=.(D) 可导的点，且(0)0f '≠(3) 设()f x 处处可导，则 （D ）(A) 当lim ()x f x →-∞=-∞时，必有lim ()x f x →-∞'=-∞．(B) 当lim ()x f x →-∞'=-∞时，必有lim ()x f x →-∞=-∞．(C) 当lim ()x f x →+∞=+∞时，必有lim ()x f x →+∞'=+∞．(D) 当lim ()x f x →+∞'=+∞时，必有lim ()x f x →+∞=+∞．(4) 在区间),(∞-∞内，方程 0cos 2141=-+x x x（C ）(A) 无实根 (B) 有且仅有一个实根 (C) 有且仅有二个实根 (D) 有无穷多个实根 (5) 设()()f x g x 、在区间[,]a b 上连续，且()()g x f x m <<（m 为常数），则曲线()y g x =，()y f x =，x a =及x b =所围成图形绕直线y m =旋转而成的旋转体体积为 （B ）(A)⎰-+-badx x g x f x g x f m .)]()()][()(2[π(B)⎰---ba dx x g x f x g x f m .)]()()][()(2[π (C)⎰-+-b adx x g x f x g x f m .)]()()][()([π (D)⎰---badx x g x f x g x f m .)]()()][()([π三、(本题共6小题，每小题5分，满分30分) (1) 计算⎰--2ln 021dx e x解一：原式2ln 2ln 22220111x x xxee dx ee e --=-=--+-⎰⎰……3分 ln 22033ln(1)ln(23)x x e e --=-=++.……5分解二：令sin xet -=，则cos sin tdx dt t-=， 原式2222666cos 1sin sin sin t dt dt tdt t t ππππππ==-⎰⎰⎰……3分 2633ln(csc cot )ln(23)t t ππ=-+=+-. ……5分(2) 求⎰+x dxsin 1解一：原式21sin cos x dx x-=⎛⎜⎠ ……2分 1tan cos x C x=-+.……5分解二：原式222sec 2(cos sin )(1tan )222x dxdx x x x ==++⎛⎛⎜⎜⎜⎜⎜⎠⎠ ……3分2(1tan )222(1tan )1tan 22x d C x x+-==+++⎛⎜⎜⎜⎠.……5分(3) 设2022()[()]tx f u duy f t ⎧=⎪⎨⎪=⎩⎰,其中()f u 具有二阶导数，且()0f u ≠，求22d y dx .解：222(),4()(),dx dy f t tf t f t dt dt'==所以22224()()4()()dydy tf t f t dt tf t dx dx f t dt''===. ……2分 22222214[()2()]()d y d dy f t t f t dx dx dt dx f t dt '''+⎛⎫== ⎪⎝⎭. ……5分 (4) 求函数()f x =xx+-11在0x =点处带拉格朗日型余项的n 阶泰勒展开式.解：2()11f x x=-+，()1(1)2!()(1,2,,1)(1)k k k k f x k n x +-⋅==++ . ……3分 所以12122()122(1)2(1)(1)n n n n n x f x x x x ξ+++=-+++-+-+ (ξ在0与x 之间).……5分 (5) 求微分方程2'''x y y =+的通解.解一：对应的齐次方程的特征方程为20λλ+=，解之得0,1λλ==-，故齐次方程的通解为12xy C C e -=+.……2分设非齐次方程的特解为2()x ax bx C ++，代入原方程得1,1,23a b c ==-=. 因此，原方程的通解为3212123x y x x x C C e -=-+++. ……5分 解二：令p y '=，代入原方程得2p p x '+=，……2分故()()220022xxxxx x p ex e dx C e x exe e C --=+=-++⎰.再积分得到20(22)xy x x c e dx -=-++⎰3212123x x x x C C e -=-+++. ……5分 解三：原方程为2()y y x ''+=，两边积分得3013y y x C '+=+. ……3分30213x x y e x C e dx C -⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦⎛⎜⎠()320213663x x x x x x e x e x e xe e C e C -⎡⎤=-+-++⎢⎥⎣⎦3212123x x x x C C e -=-+++. ……5分 (6) 设有一正椭圆柱体，其底面的长、短轴分别为22a b 、，用过此柱体底面的短轴且与底面成α解（20πα<<）的平面截此柱体，得一楔形体（如图），求此楔形体的体积V.解一：底面椭圆的方程为22221x y a +=，以垂直于y 轴的平行平面截此楔形体所得的截面为直角三角形，其一直角边长为221y a b -，另一直角边长为221y a bα-，故截面面积222()1tan 2a y S y b α⎛⎫=- ⎪⎝⎭，……3分 楔形体的体积为22220221tan tan 23ba y a bV dy b αα⎛⎫=-=⎪⎝⎭⎰. ……5分解二：底面椭圆的方程为22221x y +=，以垂直于x 轴的平行平面截此楔形体所得的截面为矩形，其一边长为22221x y b a=-tan x α，故截面面积22()21x S x bx aα=-，……3分楔形体的体积为32222222002221tan 1tan 33ab x a x a b V dx b a a ααα⎡⎤⎛⎫-⎢⎥=-=-= ⎪⎢⎥⎝⎭⎢⎥⎣⎦⎰. ……5分 四、(本题满分8分) 计算不定积分⎰+.)1(22dx x x arctgx解一：原式22arctan arctan 1x x dx dx x x =-+⎛⎛⎜⎜⎠⎠……2分 22arctan 1(arctan )(1)2x dx x x x x =-+-+⎛⎜⎠ ……4分 2222arctan 1111()(arctan )212x d x x x x x ⎛⎫=-+-- ⎪+⎝⎭⎛⎜⎠ ……6分 222arctan 11(arctan )ln 221x x x C x x=--+++. ……8分解二：令tan x t =，则原式2(csc 1)t t dt -⎰=……2分 2cos 1cot sin 2t t t dt t t =-+-⎰……4分21cot ln |sin |2t t t t C =-+-+……6分 22arctan 1(arctan )21x x C x x =-+++.……8分五、(本题满分8分)设函数⎪⎩⎪⎨⎧>-≤≤--<-=.2,1612,21,,1,21)(32x x x x x x x f(1) 写出()f x 的反函数()g x 的表达式；(2) 问()g x 是否有间断点与不可导点，若有，指出这些点.解：(1) 由题设，()f x 的反函数为3112()1816812x x g x x x x x ⎧--<-⎪⎪⎪=-≤≤⎨⎪+⎪>⎪⎩. ……4分(2) ()g x 在(,)-∞+∞内处处连续，没有间断点.……5分 ()g x 的不可导点是01x x ==-及.……8分 （注：多写一个不可导点8x =扣1分）六、(本题满分8分)设函数()y y x =由方程1222223=-+-x xy y y 所确定. 试求()y y x =的驻点，并判 别它们是否为极值点.解：对原方程两边求导可得2320()y y yy xy y x '''-++-=*……2分令0y '=，得y x =.将此代入原方程有32210x x --=.从而解得唯一的驻点1x =. ……5分()*式两边求导，得22(32)2(31)210y y x y y y y ''''-++-+-=.因此(1,1)1|02y ''=>，故驻点1x =是()y y x =的极小值点. ……8分七、(本题满分8分)设()f x 在区间[,]a b 上具有二阶导数，且()()0f a f b ==，'()'()0.f a f b >证明存在(,)a b ξ∈和),(b a ∈η，使()0f ξ=及0)(''=ηf .证一：先用反证法证明存在(,)a b ξ∈，使()0f ξ=. 若不存在(,)a b ξ∈，使()0f ξ=，则在区间(,)a b 内恒有()0f x >或()0f x <. 不妨设()0f x >（对()0f x <，类似可证），则()()()()lim lim 0x b x b f x f b f x f b x b x b--→→-'==≤--， ……3分 ()()()()lim lim 0x a x a f x f a f x f a x ax a ++→→-'==≥--.从而()()0f a f b ''≤，这与已知条件矛盾. 这即证得存在(,)a b ξ∈,使得()0f ξ=. ……5分再由()()()f a f f b ξ==及罗尔定理，知存在12(,)(,)a b ηξηξ∈∈和，使得12()()0f f ηη''==. 又在区间12[,]ηη上对()f x '应用罗尔定理知，存在12(,)(,)a b ηηη∈⊂，使()0f η''=.……8分证二：不妨设()0,()0f a f b ''>>（对()0,()0f a f b ''<<类似可证），即()lim 0x a f x x b +→>-，()lim 0x b f x x b-→>-. 故存在11(,)x a a δ∈+和22(,)x b b δ∈-，使1()0f x >及2()0f x <，其中12,δδ为充分小的正数. 显然12x x <，在区间12[,]x x 上应用介值定理知，存在一点12(,)(,)x x a b ξ∈⊂，使得()0f ξ=. ……5分 以下同证一. 八、(本题满分8分) 设()f x 为连续函数.(1) 求初值问题0'()0|x y ay f x y -+=⎧⎪⎨=⎪⎩的解()y y x =，其中a 是正常数； (2) 若()f x k ≤(k 为常数)，证明：当0≥x 时，有()(1).ax k y x e a-≤-证一：(1) 原方程的通解为()[()][()]axax ax y x ef x e dx C e F x C --=+=+⎰， ……2分其中()F x 是()axf x e 的任一原函数.由(0)0y =得(0)C F =-，故()[()(0)]()xax ax at y x e F x F e f t e dt --=-=⎰.……4分 (2) 0()()xaxat y x ef t e dt -≤⎰……6分 0xaxat kee dt -≤⎰(1)(1),0ax ax ax k k e e e x a a--≤-=-≥. ……8分证二：在原方程的两端同乘以ax e ，得()ax ax ax y e aye f x e '+=.从而()()ax axye f x e '=，……2分 所以0()xaxat yef t e dt =⎰或0()xaxat y ef t e dt -=⎰.……4分（2）同证一数 学（试卷四）一、填空题：(本题共5小题，每小题3分，满分15分)(1) 设方程yy x =确定y 是x 的函数，则dy =(1ln )dxx y +.(2) 设⎰+=c x dx x xf arcsin )(，则=⎰)(x f dx 231(1)3x C -. (3) 设（00,y x ）是抛物线c bx ax y ++=2上的一点，若在该点的切线过原点，则系数,,a b c应满足的关系是200(),c a ax c b ≥=或任意.(4) 设 123222212311111231111n n n n n n n a a a a A a a a a a a a a ----⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦，123n x x X x x ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦，1111B ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ ，其中(;,1,2,,)i j a a i j i j n ≠≠= ，则线性方程组B X A T=的解是(1,0,,0)T X =(5) 设由来自正态总体X ～)9.0,(2μN 容量为9的简单随机样本，得样本均值5=X ，则未知参数μ的置信度为0.95的置信区间是 ( 4.412 , 5.588 ) 二、选择题：(本题共5小题，每小题3分，满分15分)(1) 累次积分dr r r r f d ⎰⎰20cos 0)sin ,cos (πθθθθ可以写成 (D)(A) dx y x f dy y y ⎰⎰-102),(. (B)dx y x f dy y ⎰⎰-1102),(. (C)dy y x f dx ⎰⎰101),(. (D)dy y x f dx x x ⎰⎰-12),(.(2) 下述各选项正确的是 (A)(A) 若21nn u∞=∑和21nn v∞=∑都收敛，则21()nn n uv ∞=+∑收敛(B) 若1n nn u v∞=∑收敛，则21nn u∞=∑和21nn v∞=∑都收敛(C) 若级数1n n u ∞=∑发散，则1n u n≥ (D) 若级数1nn u∞=∑收敛，且n n u v ≥(1,2,)n = ，则级数1nn v∞=∑也收敛(3) 设n 阶矩阵A 非奇异),2(≥n A *是矩阵A 的伴随矩阵，则 (C)(A) (A *)*=A A n 1- (B) (A *)*=A A n 1+(C) (A *)*=A An 2-(D) (A *)*=A An 2+(4) 设有任意两个n 维向量组12,,,m ααα 和12,,,m βββ ，若存在两组不全为零的12,,,mλλλ 和12,,,m k k k ,使111111()()()()0m m m m m m k k k k λαλαλβλβ+++++-++-= ,则 (D)(A) 12,,,m ααα 和 12,,,m βββ 都线性相关 (B) 12,,,m ααα 和 12,,,m βββ 都线性无关 (C) 11221122,,,,,,,m m m m αβαβαβαβαβαβ+++--- 线性无关 (D)11221122,,,,,,,m m m m αβαβαβαβαβαβ+++--- 线性相关(5) 已知0<P (B )<1,且P )()(])[(2121B A P B A P B A A +=+,则下列选项成立的是 (B)(A) )()(])[(2121B A P B A P B A A P +=+ (B) )()()(2121B A P B A P B A B A P +=+ (C) 1212()()()P A A P A B P A B +=+ (D) )()()()()(2211A B P A P A B P A P B P += 三、(本题满分6分)设()f x =()00,0xg x e x x x -⎧-≠⎪⎪⎨⎪⎪=⎩若若，其中()g x 有二阶连续导数，且(0)1g =, (0)1g '=-. (1) 求()f x '； (2) 讨论()f x '-∞+∞在（，）上的连续性.解：(1) 当0x ≠时，有22[()]()()()(1)()x x xx g x e g x e xg x g x x e f x x x---''+-+-++'==. ……1分 当0x =时,有20()(0)lim xx g x e f x-→-'= ……2分 00()()(0)1lim lim 222x x x x g x e g x e g x --→→'''''+--===. ……3分所以2()()(1)0()(0)102x xg x g x x e x x f x g x -'⎧-++≠⎪⎪'=⎨''-⎪=⎪⎩若若.……4分(2) 因为在0x =处，有0lim ()x f x →'00()()()(1)()lim lim22x x xx x g x xg x g x e x e g x e x ---→→''''''+-+-+-== (0)1(0)2g f ''-'==.……5分 从而()f x '在0x ≠处连续，所以()f x '在(,)-∞+∞上为连续函数.……6分四、(本题满分6分)设函数()z f u =，方程()()xyu u p t dt ϕ=+⎰确定u 是x 、y 的函数，其中()f u 、()u ϕ可微；(),()p t u ϕ' 连续，且()1u ϕ'≠. 求 ()()z zp y p x x y∂∂+∂∂. 解：由()z f u =可得();();z u z uf u f u x x y y∂∂∂∂''==∂∂∂∂ ……1分在方程()()x yu u p t dt ϕ=+⎰两边分别对,x y 求偏导数，得()()u uu p x x x ϕ∂∂'=+∂∂, ……2分 ()()u uu p y y yϕ∂∂'=-∂∂. ……3分 所以()(),1()1()u p x u p y x u y u ϕϕ∂∂-==''∂-∂-； ……5分 于是()()()()()()()01()1()z z p x p y p x p y p y p x f u x y u u φφ⎡⎤∂∂'+=-=⎢⎥''∂∂--⎣⎦. ……6分五、(本题满分6分) 计算2(1)xx xe dx e -+∞-+⎰. 解一： 2200(1)(1)x x x x xe xe dx dx e e +∞+∞--=++⎛⎛⎜⎜⎠⎠011xxd e +∞-⎛⎫= ⎪+⎝⎭⎛⎜⎠ ……1分00111xxx dx e e ∞+∞=-+++⎛⎜⎠ ……2分 011x dx e+∞=+⎛⎜⎠. ……3分令x e t =，则1dx dt t=.于是2101(1)(1)x x xe dx dt e t t +∞+∞--=++⎛⎛⎜⎜⎠⎠ ……4分 1111ln 11t dt t t t +∞+∞⎛⎫=-= ⎪++⎝⎭⎛⎜⎠ ……5分 ln 2=.……6分解二：21(1)1x x xxe dx xd e e ---⎛⎫= ⎪++⎝⎭⎛⎛⎜⎜⎠⎠111x xx dx ee --=-++⎛⎜⎠ 11x x x x e dx e e-=-++⎛⎜⎠ln(1)1x x xxe e C e =-+++. ……3分 所以20lim ln(1)ln 2(1)1x x x x x x xe xe dx e e e +∞--→+∞⎡⎤=-++⎢⎥++⎣⎦⎛⎜⎠. ……4分其中lim ln(1)lim ln(1)11x x x x xxx x xe xe e x x e e e →+∞→+∞⎡⎤⎡⎤-+=-+-+⎢⎥⎢⎥++⎣⎦⎣⎦ lim ln 00011x x x x x e e e →+∞⎡⎤=-+=+=⎢⎥++⎣⎦ ……5分 因此20ln 2ln 2(1)x x xe dx e +∞--=+=+⎛⎜⎠. ……6分六、(本题满分5分)设)(x f 在区间[0,1]上可微，且满足条件120(1)2()f xf x dx =⎰，求证：存在ξ)1,0(∈，使0)()(='+ξξξf f .证：设()()F x xf x =. 由积分中值定理，可见存在1(0,)2η∈.使112201()()()2xf x dx F x dx F η==⎰⎰. ……2分由已知条件，有1201(1)2()2()()2f xf x dx F F ηη==⋅=⎰.……3分 由于(1)(1)()F f F η==，……4分并且()F x 在[,1]η上连续，在(,1)η上可导.故由罗尔定理知：存在(,1)(0,1)ξη∈⊂，使得()0F ξ'=，即()()0f f ξξξ'+=.……5分七、(本题满分6分)设某种商品的单价为p 时，售出的商品数量Q 可以表示成c bp aQ -+=，其中,,a b c 均为正数，且a bc >.(1) 求p 在何范围变化时，使相应销售额增加或减少；(2) 要使销售额最大，商品单价p 应取何值？最大销售额是多少？ 解：(1) 设售出商品的销售额为R ，则a R PQ P c a b ⎛⎫==-⎪+⎝⎭，令22()0()ab c P b R p b -+'==+. 得00ab bp b a bc c c ==>. ……2分 当0bp a bc c <<时，有0R '>.所以随p 的增加，相应的销售额也增加. ……4分当bp a bc c>时，有0R '<.所以随p 的增加，相应的销售额将减少.……5分 (2) 由(1)知，当bp a bc c=时，销售额R 取得最大值，最大销售额为2max (/)()/R ab c b c a bc ab c==. ……6分八、(本题满分6分)求微分方程x y x y dx dy 22+-=的通解. 解：令y z x =，则dy dzz x dx dx=+. ……1分 当0x >时，原方程化为21dz z x z z dx +=+21dx x z =-+， ……3分 其通解为221ln(1)ln 1C z z x C z z x+=-++或＝,……5分代回原变量，得通解22(0)y x y C x +>＝.……6分当0x <时，原方程的解与0x >时相同.九、(本题满分8分)设矩阵A= 010010000010012y ⎫⎛⎪ ⎪⎪⎪⎝⎭(1) 已知A 的一个特征值为3，试求y ； (2) 求矩阵P ，使(AP)T(AP)为对角矩阵.解：(1) 因为22||(1)[(2)21]0I A y y λλλλ-=--++-=. 当3λ=时，代入上式解得2y =.……3分于是0100100000210012A ⎛⎫⎪⎪= ⎪ ⎪⎝⎭. (2) 由T A A =，得2()()T T AP AP P A P =.而矩阵21000010000540045A ⎛⎫⎪⎪= ⎪ ⎪⎝⎭， ……4分 考虑二次型22222222212343412344495585()55T X A X x x x x x x x x x x x =++++=++++， ……6分 令1122334444,,,5y x y x y x x y x ===+=，即11223344100001000014/50001x y x y x y x y ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎪= ⎪ ⎪ ⎪- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 取10000100400150001P ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎭-⎪⎪⎝，则有100001000050()(900)05TAP AP ⎛⎫ ⎪ ⎪= ⎪ ⎪⎪ ⎪⎝⎭.……8分(2) 另解：2A 的特征值为11λ=（三重），29λ=.……5分对应于11λ=的特征向量为123(1,0,0,0),(0,1,0,0),(0,0,1,1),T T T ααα===-经正交标准化后，得向量组123(1,0,0,0),(0,1,0,0),)22T T Tβββ===；……6分 对应于29λ=的特征向量为4(0,0,1,1)T α=,经单位化后,得422Tβ=. ……7分令()123410000100,,,00220022P ββββ⎛⎫ ⎪ ⎪ ⎪== ⎝，则210000100001000()()09T T P A P AP AP ⎛⎫ ⎪⎪== ⎪ ⎪⎝⎭.……8分十、(本题满分8分)设向量12,,,t ααα 是齐次线性方程组AX = 0的一个基础解系，向量β不是方程组 AX= 0的解，即A β≠0. 试证明向量组β，β+1α，β+2α，…，β+t α线性无关. 解：设有一组数12,,,,t k k k k ，使得1()0tiii k k ββα=++=∑，……1分 即11()()t tiiii i k k k βα==+=-∑∑ （1）……2分上式两边同时左乘矩阵A ，有11()()0t tiiii i k k A k A βα==+=-=∑∑.因为0A β≠，故10tii k k=+=∑ （2）……4分从而，由（1）式得1()0tiii k α=-=∑.由于向量组1,.......,t αα是基础解系，所以120t k k k ==== .……6分 因而由（2）式得0k =.因此向量组β，β+1α，……，β+t α线性无关.……8分十一、(本题满分7分)假设一部机器在一天内发生故障的概率为0.2，机器发生故障时全天停止工作，若一周5个工作日里无故障，可获得利润10万元；发生一次故障仍可获得利润5万元；发生二次故障多获得利润0元；发生三次或三次以上故障就要亏损2万元.求一周内期望利润是多少？解：以X 表示一周五天内机器发生故障的天数，则X 服从参数为(5,0.2)的二项分布.即55{}0.20.8(0,1,2,3,4,5)kk kP X k C k -==⋅⋅=……2分 于是5{0}0.80.328P X ===, 145{1}0.20.80.410P X C ==⋅⋅=;……3分2235{2}0.20.80.205P X C ==⋅⋅=;{3}1{0}{1}{2}0.057P X P x P x P x ≥=-=-=-==. ……4分以Y 表示所获利润，则()Y f X ==10,05,10,22,3X X X X =⎧⎪=⎪⎨=⎪⎪≥⎩若若若－若，……5分所以100.32850.41000.20520.057 5.216EY =⨯+⨯+⨯-⨯=（万元）.……7分十二、(本题满分6分)考虑一元二次方程x 2+ Bx + C = 0，其中B,C 分别是将一枚骰子接连掷两次先后出现的 点数.求方程有实根的概率p 和有重根的概率q .解：一枚色子（骰子）掷两次，其基本事件总数为36. 方程组有实根的充分必要条件是224,4B BC C ≥≤. ……2分B1 2 3 4 5 6 使2/4C B ≤的基本事件个数 0 1 2 4 6 6 使2/4C B =的基本事件个数11……4分因此，使方程组有实根的基本事件个数为1246619++++=.于是1936p =. ……5分 同理，使方程组有重根的基本事件个数为112+=，于是213618q ==. ……6分十三 (本题满分6分)设12,,,n X X X 独立且与X 同分布，k k EX α=(1,2,3,4)k =.求证：当n 充分大时，∑==n i i n X n z 121近似服从正态分布，并求出其分布参数. 解：依题意，12,,,n X X X 独立同分布，于是22212,,,n X X X 也独立同分布.由(1,2,3,4)k k EX k α==，有……1分 22i EX α=，2422242()i i i DX EX EX αα=-=-； ……2分 2211nn i i EZ EX n α===∑，……3分 22422111()n n i i DZ DX n nαα===-∑……4分根据中心极限定理2242()/n n U n αα=-即当n 充分大时，n Z 近似服从参数为2422(,)a a a n-的正态分布.……6分数 学（试卷五）一、填空题：(本题共5小题，每小题3分，满分15分) (1) 【 同数学四 第一、(1) 题 】 (2) 【 同数学四 第一、(2) 题 】 (3) 设)1ln(2x x y ++=，则3x y '''=532(4) 五阶行列式aa a a a a a a a---------11110001100011000123451a a a a a =-+-+-.(5) 一实习生用同一台机器接连独立地制造3个同种零件，第i 个零件是不合格品的概率1(1,2,3)1i p i i ==+,以X 表示3个零件中合格品的个数，则P (X=2)=1124. 二、选择题：(本题共5小题，每小题3分，满分15分)(1) 设0)()(00=''='x f x f ,0)(0>'''x f , 则下列选项正确的是 (D)(A) )(0x f '是)(x f '的极大值 (B) )(0x f 是)(x f 的极大值(C) )(0x f 是)(x f 的极小值 (D) ))(,(00x f x 是曲线)(x f y =的拐点 (2) 【 同数学三 第二、(3) 题 】 (3) 【 同数学四 第二、(3) 题 】 (4) 【 同数学四 第二、(4) 题 】(5) 设A ，B 为任意两个事件，且A ⊂B , P (B )>0，则下列选项必然成立的是 (B)(A) ()()P A P A B < (B) ()()P A P A B ≤ (C) ()()P A P A B > (D) ()()P A P A B ≥ 三、(本题满分6分)【 同数学四 第三题 】 四、(本题满分7分) 设2(,)xyt f x y e dt -=⎰，求222222yfx y y x f x f y x ∂∂+∂∂∂-∂∂解：22x y fye x-∂=∂， ……2分 22x y f xey-∂=∂，222322x y f xy e x -∂=-∂， ……4分 222322x y f x ye y -∂=-∂，22222(12)x y f x y ex y-∂=-∂∂. ……6分 于是222222222x y x f f y f ey x x y x y -∂∂∂-+=-∂∂∂∂. ……7分五、(本题满分6分)【 同数学四 第五题 】六、(本题满分7分)【 同数学四 第七题 分值不同 】 七、(本题满分9分)已知一抛物线通过x 轴上的两点A ( 1, 0 )，B ( 3, 0 ).(1) 求证：两坐标轴与该抛物线所围图形的面积等于x 轴与该抛物线所围图形的面积； (2) 计算上述两个平面图形绕x 轴旋转一周所产生的两个旋转体体积之比. 解：(1) 设过,A B 两点的抛物线方程为(1)(3)y a x x =--， 则抛物线与两坐标轴所围图形的面积为110|(1)(3)|S a x x dx =--⎰……1分1204||(43)||3a x x dx a =-+=⎰. ……2分 抛物线与x 轴所围图形的面积为321|(1)(3)|S a x x dx =--⎰……3分 3214||(43)||3a x x dx a =-+=⎰.……4分所以12S S =.(2) 抛物线与两坐标轴所围图形绕x 轴旋转所得旋转体的体积为12210[(1)(3)]V a x x dx π=--⎰……5分124320[(1)4(1)4(1)]a x x x dxπ=---+-⎰5324120(1)4(1)38[(1)].5315x x a x a ππ--=--+=……6分抛物线与x 轴所围图形绕x 轴旋转所得旋转体的体积为32221[(1)(3)]V a x x dx π=--⎰353241(1)4(1)(1)53x x a x π⎡⎤--=--+⎢⎥⎣⎦ ……7分216.15a π=……8分 所以12198V V =.……9分八、(本题满分5分)设)(x f 在[,]a b 上连续，在(,)a b 内可导，且1()()ba f x dx fb b a=-⎰ 求证：在(,)a b 内至少存在一点ξ, 使 )(ξf ' = 0.证：因为()f x 在[,]a b 上连续，由积分中值定理可知，在(,)a b 内存在一点c ，使得()()()baf x dx f c b a =-⎰. ……2分 即()()()baf x dxf c f b b a==-⎰.……3分因为()f x 在[,]c b 上连续，在(,)c b 内可导，故由罗尔定理，在(,)c b 内至少存在一点出ξ，使得()0f ξ'=，其中(,)(,)c b a b ξ∈⊂.……5分九、(本题满分9分)已知线性方程组 ⎪⎪⎩⎪⎪⎨⎧+t= x - 6x - x - x -1=7x +px + x 2+3x -1= 4x + 6x - x + 2x 0= x 3+2x -x x 4321432143214321，讨论参数p, t 取何值时，方程组有解? 无 解? 当有解时, 试用其导出组的基础解系表示通解.解：方程组系数矩阵A 的增广矩阵为11230104112164101221327100800116100002A p p t t ---⎛⎫⎛⎫⎪ ⎪-- ⎪ ⎪=→⎪ ⎪-+ ⎪ ⎪---+⎝⎭⎝⎭……3分(1) 当2t ≠-时，()()A A ≠秩秩，方程组无解. ……4分 (2) 当2t =-时，()()A A =秩秩，方程组有解.……5分(a) 若8p =-,得通解1212141122(,010001x c c c c --⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-- ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭为任意常数）.……7分(b) 若8p ≠-得通解1112(0001x c c --⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭为任意常数）.……9分十、(本题满分7分)设有4阶方阵A 满足条件30I A +=，I A A T2=，0A <，其中I 是4阶单位阵，求方阵A 的伴随阵*A 的一个特征值.解：由3|(3)|0I A A I +=--=，得A 的一个特征值3λ=-. ……1分 又4|||2|2||16T AA I I ===，2||||||16T A A A ==.于是||4A =-.……3分由于||0A <，知A 可逆.设A 的对应于特征值3λ=-的特征向量为α，则3A αα=-，由此得11(3)A A A αα--=-.即113A αα-=-，知13-是1A -的特征值. ……5分 由于*114||(4)()33A A A αααα-==--=，所以*A 有特征值43.……7分十一、(本题满分7分)【 同数学四 第十一题 】 十二、(本题满分6分)某电路装有三个同种电气元件，其工作状态相互独立，且无故障工作时间都服从参数为λ> 0的指数分布.当三个元件都无故障时，电路正常工作，否则整个电路不能正常工作，试求电路正常工作的时间T 的概率分布.解：以(1,2,3)i X i =表示第i 个电气元件无故障工作的时间，则123,,X X X 相互独立且同分布，其分布函数为1,0()00x e x F x x λ-⎧->=⎨≤⎩若，若，……1分设()G t 是T 的分布函数.当0t ≤时，()0G t =.当0t >时，有(){}1{}G t P T t P T t =≤=->……3分 1231{,,}P X t X t X t =->>>……4分 1231{}{}{}P X t P X t P X t =->⋅>⋅> ……5分 31[1()]F t =-- ……6分 31t e λ-=-.……7分总之，31,0()00t e t G t t λ-⎧->=⎨≤⎩若，若，于是T 服从参数为3λ的指数分布.。

1996年考研数学二试卷及答案一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.) (1) 设232()x y x e -=+,则0x y ='=＿＿＿＿＿＿.(2)121(x dx -+=⎰＿＿＿＿＿＿.(3) 微分方程250y y y '''++=的通解为＿＿＿＿＿＿.(4) 31lim sin ln(1)sin ln(1)x x x x →∞⎡⎤+-+=⎢⎥⎣⎦＿＿＿＿＿＿.(5) 由曲线1,2y x x x=+=及2y =所围图形的面积S =＿＿＿＿＿＿.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1) 设当0x →时,2(1)xe ax bx -++是比2x 高阶的无穷小,则 ( )(A) 1,12a b == (B) 1,1a b == (C) 1,12a b =-=- (D) 1,1a b =-=(2) 设函数()f x 在区间(,)δδ-内有定义,若当(,)x δδ∈-时,恒有2|()|f x x ≤,则0x =必是()f x 的 ( ) (A) 间断点 (B) 连续而不可导的点 (C) 可导的点,且(0)0f '= (D) 可导的点,且(0)0f '≠(3) 设()f x 处处可导,则 ( )(A) 当lim ()x f x →-∞=-∞,必有lim ()x f x →-∞'=-∞(B) 当lim ()x f x →-∞'=-∞,必有lim ()x f x →-∞=-∞(C) 当lim ()x f x →+∞=+∞,必有lim ()x f x →+∞'=+∞(D) 当lim ()x f x →+∞'=+∞,必有lim ()x f x →+∞=+∞(4) 在区间(,)-∞+∞内,方程1142||||cos 0x x x +-= ( )(A) 无实根 (B) 有且仅有一个实根 (C) 有且仅有两个实根 (D) 有无穷多个实根(5) 设(),()f x g x 在区间[,]a b 上连续,且()()g x f x m <<(m 为常数),由曲线(),y g x =(),y f x x a ==及x b =所围平面图形绕直线y m =旋转而成的旋转体体积为 ( )(A) [][]2()()()()bam f x g x f x g x dx π-+-⎰(B) [][]2()()()()bam f x g x f x g x dx π---⎰(C) [][]()()()()bam f x g x f x g x dx π-+-⎰(D)[][]()()()()bam f x g x f x g x dx π---⎰三、(本题共6小题,每小题5分,满分30分.) (1)计算ln 0⎰.(2) 求1sin dxx +⎰.(3) 设2022(),[()],t x f u du y f t ⎧=⎪⎨⎪=⎩⎰其中()f u 具有二阶导数,且()0f u ≠,求22d y dx .(4) 求函数1()1xf x x-=+在0x =点处带拉格朗日型余项的n 阶泰勒展开式. (5) 求微分方程2y y x '''+=的通解.(6) 设有一正椭圆柱体,其底面的长、短轴分别为22a b 、,用过此柱体底面的短轴与底面成α角(02πα<<)的平面截此柱体,得一锲形体(如图),求此锲形体的体积V .四、(本题满分8分)计算不定积分22arctan (1)xdx x x +⎰.α五、(本题满分8分)设函数2312,1,(),12,1216, 2.x x f x x x x x ⎧-<-⎪=-≤≤⎨⎪->⎩(1) 写出()f x 的反函数()g x 的表达式；(2) ()g x 是否有间断点、不可导点,若有,指出这些点.六、(本题满分8分)设函数()y y x =由方程3222221y y xy x -+-=所确定,试求()y y x =的驻点,并判别它是否为极值点.七、(本题满分8分)设()f x 在区间[,]a b 上具有二阶导数,且()()0f a f b ==,()()0f a f b ''>,试证明：存在(,)a b ξ∈和(,)a b η∈,使()0f ξ=及()0f η''=.八、(本题满分8分)设()f x 为连续函数,(1) 求初值问题0(),0x y ay f x y ='+=⎧⎪⎨=⎪⎩的解()y x ,其中a 为正的常数；(2) 若|()|f x k ≤(k 为常数),证明：当0x ≥时,有|()|(1)ax ky x e a-≤-.答案一、填空题(本题共5小题,每小题3分,满分15分.) (1)【答案】13132221132x xy x e e ,---⎛⎫⎛⎫'=+⋅- ⎪ ⎪⎝⎭⎝⎭02111323x y =⎛⎫'=-= ⎪⎝⎭.(2)【答案】2注意到对称区间上奇偶函数的积分性质,有原式()1122112121022x x dx dx --⎡⎤⎡⎤=+-==+=⎣⎦⎣⎦⎰⎰. (3)【答案】()12cos2sin 2xy ec x c x -=+因为250y y y '''++=是常系数的线性齐次方程,其特征方程2250r r ++=有一对共轭复根1212r ,r i.=-±故通解为()12cos2sin 2xy e c x c x -=+.(4)【答案】2因为x →∞时,sin ln 1ln 1k k kx x x⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭(k 为常数),所以, 原式3131lim sin ln 1lim sin ln 1lim lim 312x x x x x x x x x x x x →∞→∞→∞→∞⎛⎫⎛⎫⎛⎫⎛⎫=+-+=⋅-⋅=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. (5)【答案】1ln 22-曲线1y x ,x =+2y =的交点是()12,,2211,x y x x x '-⎛⎫'=+= ⎪⎝⎭当1x >时 1y x x=+(单调上升)在2y =上方,于是212211211ln 2ln 2.22S x dxx x x x ⎛⎫=+- ⎪⎝⎭⎛⎫=+-=- ⎪⎝⎭⎰二、选择题(本题共5小题,每小题3分,满分15分.) (1)【答案】(A)方法1：用带皮亚诺余项泰勒公式.由()21x e ax bx -++()()222112!x x x ax bx ο⎛⎫=+++-++ ⎪⎝⎭()()()222112b x a x x x οο⎛⎫=-+-+ ⎪⎝⎭令,可得 10111202b ,a ,b .a ,-=⎧⎪⇒==⎨-=⎪⎩应选(A). 方法2：用洛必达法则.由2200(1)2lim lim 0,2x x x x e ax bx e ax bx x→→-++--=洛 有 ()lim 210 1.xx e ax b b b →--=-=⇒=又由 0022121limlim 02222x x x x e ax b e a a a x →→----===⇒=. 应选(A).(2)【答案】(C)方法一：首先,当0x =时,|(0)|0(0)0f f ≤⇒=. 而按照可导定义我们考察2()(0)()00(0)f x f f x x x x x x x-≤=≤=→→,由夹逼准则, 0()(0)(0)lim0x f x f f x→-'==,故应选(C).方法二：显然,(0)0f =,由2|()|f x x ≤,(,)x δδ∈-,得2()1(,0)(0,)f x x xδδ≤∈-,,即2()f x x 有界,且 200()(0)()(0)limlim 0x x f x f f x f x x x →→-⎛⎫'==⋅= ⎪⎝⎭. 故应选(C).方法三：排除法.令3(),(0)0,f x x f '==故(A)、(B)、(D)均不对,应选(C). (3)【答案】(D)方法一：排除法.例如()f x x =,则(A),(C)不对；又令()xf x e -=,则(B)不对.故应选择(D).方法二：由lim ()x f x →+∞'=+∞,对于0M >,存在0x ,使得当0x x >时,()f x M '>.由此,当0x x >时,由拉格朗日中值定理,0000()()()()()()()f x f x f x x f x M x x x ξ'=+->+-→+∞→+∞,从而有lim ()x f x →+∞=+∞,故应选择(D).(4)【答案】(C)令1142()||||cos f x x x x =+-,则()()f x f x -=,故()f x 是偶函数,考察()f x 在(0,)+∞内的实数个数：1142()cos f x x x x =+-(0x >).首先注意到(0)10f =-<,1142()()()10,222f πππ=+>>当02x π<<时,由零值定理,函数()f x 必有零点,且由314211()sin 042f x x x x --'=++>,()f x 在(0,)2π单调递增,故()f x 有唯一零点.当2x π≥时,11114242()cos ()()10,22f x x x x ππ=+-≥+->没有零点； 因此,()f x 在(0,)+∞有一个零点.又由于()f x 是偶函数,()f x 在(,)-∞+∞有两个零点.故应选(C). (5)【答案】(B)见上图,作垂直分割,相应于[],x x dx +的小竖条的体积微元22(())(())dV m g x dx m f x dx ππ=---[][](())(())(())(())m g x m f x m g x m f x dx π=-+-⋅--- [][]2()()()()m g x f x f x g x dx π=--⋅-,于是 [][]2()()()()baV m g x f x f x g x dx π=--⋅-⎰,故选择(B).三、(本题共6小题,每小题5分,满分30分.) (1)方法一：换元法.u =,则221ln(1),21u x u dx du u=--=-, 所以2ln 2200011111)2)11211u du du du u u u u==-=+----+⎰1ln(22==. 方法二：换元法.令sin xe t -=,则cos ln sin ,sin t x t dx dt t =-=-,:0ln 2:26x t ππ→⇒→,ln 62026cos 1cos sin sin sin t t dt t dt t tππππ⎛⎫⎛⎫=⋅-=- ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰2266ln(csc cot )cos ln(22t t t ππππ=--=-. 方法三：分部积分法和换元法结合.原式ln 2ln 0()x e e --==-⎰⎰22ln 2x xee--=-+⎰令xe t =,则:0ln 2:12x t →⇒→,原式2211ln(t =+=+⎰ln(22=-+.(3)这是由参数方程所确定的函数,其导数为22222()()24()()dydy f t f t t dt tf t dx dx f t dt'⋅⋅'===, 所以 2222221()(4())4()4()2()d y d dy dt d dt tf t f t tf t t dx dt dx dx dt dx f t ''''⎡⎤=⋅=⋅=+⋅⋅⎣⎦ 22224()2()()f t t f t f t '''⎡⎤=+⎣⎦. (4)函数()f x 在0x =处带拉格朗日余项的泰勒展开式为()(1)1(0)()()(0)(0),(01)!(1)!n n n n f f x f x f f x x x n n θθ++'=++++<<+.对于函数1()1xf x x -=+,有 12()12(1)1,1f x x x-=-=+-+2()2(1)(1),f x x -'=⋅-+ 3()2(1)(2)(1),f x x -''=⋅-⋅-+,,()(1)()2(1)!(1)n n n f x n x -+=-⋅+所以 ()(0)2(1)!,(1,2,3),n n fn n =-⋅ =故 121112()122(1)2(1)(01)1(1)n n n n n xx f x x x x xx θθ+++-==-+++-+- <<++. (5)方法一：微分方程2y y x ''+=对应的齐次方程0y y '''+=的特征方程为20r r +=,两个根为120,1r r ==-,故齐次方程的通解为12x y c c e -=+.设非齐次方程的特解2()Y x ax bx c =⋅++,代入方程可以得到1,1,23a b c ==-=, 因此方程通解为3212123xy c c ex x x -=++-+. 方法二：方程可以写成2()y y x ''+=,积分得303x y y c '+=+,这是一阶线性非齐次微分方程,可直接利用通解公式求解.通解为30(())3dxdx xy e c e dx C -⎰⎰=++⎰33001(())()33xx x x xx e c e dx C e x de c e C --=++=++⎰⎰320(3)3x xx x e x e e x dx c Ce --=-++⎰ 332200(2)33x x xx x x x x x e e x dx c Ce e e x e xdx c Ce ----=-++=--++⎰⎰ 3202()3x x x x x x e e x e c Ce --=-+-++ 32123x x x x c Ce -=-+++. 方法三：作为可降阶的二阶方程,令y P '=,则y P '''=,方程化为2P P x '+=,这是一阶线性非齐次微分方程,可直接利用通解公式求解.通解为220020()(22)2 2.x x x x x x xP e c x e dx e c x e xe e c e x x ---=+=+-+=+-+⎰再积分得 321223xx y c c e x x -=++-+. (6)建立坐标系,底面椭圆方程为22221x y a b+=.方法一：以垂直于y 轴的平面截此楔形体所得的截面为直角三角形, 其中一条直角边长为22a x b y b=-22tan a b y bα-, 故截面面积为22221()()tan 2a S y b y bα=-⋅. 楔形体的体积为222220022()tan ()tan 3bb a V S y dy b y dy a b b αα==-=⎰⎰.方法二：以垂直于x 轴的平面截此楔形体所得的截面为矩形,其中一条边长为222b y a x a=-另一条边长为tan x α⋅, 故截面面积为22()2tan bS x x a x aα=-,楔形体的体积为22200222()tan tan 3aa b V S x dx x a x dx a b a αα==-=⎰⎰.四、(本题满分8分) 方法一：分部积分法.2222arctan arctan arctan (1)1x x xdx dx dx x x x x =-++⎰⎰⎰1arctan ()arctan (arctan )xd xd x x=--⎰⎰2211arctan arctan (1)2dx x x x x x -+-+⎰分部 22111arctan ()arctan 12x x dx x x x x =-+--+⎰ 22111arctan ln ln(1)arctan 22x x x x C x =-+-+-+.方法二：换元法与分部积分法结合.令arctan x t =,则2tan ,sec x t dx tdt ==,2222222arctan sec cot (1)tan (1tan )tan x t t t dx dt dt t tdt x x t t t ===++⎰⎰⎰⎰2(csc 1)(cot )t t dt td t tdt =-=--⎰⎰⎰21cot cot 2t t dt t -+-⎰分部 2cos 1cot sin 2x t t dt t x =-+-⎰211cot sin sin 2t t d t t t =-+-⎰21cot ln sin 2t t t t C =-+-+.五、(本题满分8分)【解析】为了正确写出函数()f x 的反函数()g x ,并快捷地判断出函数()g x 的连续性、可导性,须知道如下关于反函数的有关性质.(1) 由题设,函数()f x的反函数为1,()18,16,8.12xg x xxx⎧<-⎪⎪⎪=-≤≤⎨⎪+⎪>⎪⎩(2) 方法一：考察()f x的连续性与导函数.注意2312,1,(),12,1216,2x xf x x xx x⎧-<-⎪=-≤≤⎨⎪->⎩在(,1),(1,2),(2,)-∞--+∞区间上()f x分别与初等函数相同,故连续.在1,2x x=-=处分别左、右连续,故连续.易求得24,1,()3,12,(1)4,(1)3,12,2(2)12,(2)12(2)12.x xf x x x f fxf f f-+-+-<-⎧⎪'''=-<<-=-=⎨⎪>⎩'''==⇒=由于函数()f x在(,)-∞+∞内单调上升且连续,故函数()g x在(,)-∞+∞上单调且连续,没有间断点.由于仅有0x=时()0f x'=且(0)0f=,故0x=是()g x的不可导点；仅有1x=-是()f x的不可导点(左、右导数∃,但不相等),因此()g x在(1)1f-=-处不可导.方法二：直接考察()g x的连续性与可导性.注意1,()18,16,8,12xg x xxx⎧<-⎪⎪⎪=-≤≤⎨⎪+⎪>⎪⎩在(,1),(1,8),(8,)-∞--+∞区间上()g x分别与初等函数相同,故连续.在1,8x x=-=处分别左、右连续,故连续,即()g x在(,)-∞+∞连续,没有间断点.()g x 在(,1),(1,8),(8,)-∞--+∞内分别与初等函数相同,在0x =不可导,其余均可导.在1x =-处,1111(1),(1),43x x g g -++=--=-'⎛'''-==-== ⎝ (1)g '⇒-不∃.在8x =处,881161(8),(8),121212x x x g g -+-+=='+'⎛⎫''====⎪⎝⎭ (8)g '⇒∃.因此,()g x 在(,)-∞+∞内仅有0x =与1x =-两个不可导点.六、(本题满分8分) 方程两边对x 求导,得22320,(32)0.y y yy xy y x y y x y y x ''''-++-=-++-= ①令0,y '=得y x =,代入原方程得32210x x --=,解之得唯一驻点1x =；对①两边再求导又得22(32)(32)10x y y x y y y x y y '''''-++-++-=. ②以1,0x y y '===代入②得11210,0,2x y y =''''-==> 1x =是极小点.定理：设函数()f x 在0x 处具有二阶导数且00()0,()0f x f x '''=≠,那么 (1) 当0()0f x ''<时,函数()f x 在0x 处取得极大值； (2) 当0()0f x ''>时,函数()f x 在0x 处取得极小值.七、(本题满分8分)首先证明(,)a b ξ∃∈,使()0f ξ=：方法一：用零点定理.主要是要证明()f x 在(,)a b 有正值点与负值点.不妨设()0,f a '>()0f b '>.由()()lim ()()0x a f x f a f a f a x a ++→-''==>-与极限局部保号性,知在x a =的某右邻域,()()0f x f a x a->-,从而()0f x >,因而111,,()0x b x a f x ∃>>>；类似地,由()0f b '>可证 2122,,()0x x x b f x ∃<<<.由零点定理,12(,)(,)x x a b ξ∃∈⊂,使()0f ξ=.方法二：反证法.假设在(,)a b 内()0f x ≠,则由()f x 的连续性可得()0f x >,或()0f x <,不妨设()0f x >.由导数定义与极限局部保号性,()()()()()lim lim 0x a x a f x f a f x f a f a x ax a +++→→-''===≥--,()()()()()lim lim 0x b x b f x f b f x f b f b x b x b ---→→-''===≤--,从而()()0f a f b ''≤,与()()0f a f b ''>矛盾.其次,证明(,)a b η∃∈,()0f η''=：由于()()()0f a f f b ξ===,根据罗尔定理,12(,),(,)a b ηξηξ∃∈∈,使12()()0f f ηη''==；又由罗尔定理, 12(,)(,),()0a b f ηηηη''∃∈⊂=.注：由0()0f x '>可得：在000(,),()()x x f x f x δ-<；在000(,),()()x x f x f x δ+>.注意由0()0f x '>得不到()f x 在00(,)x x δδ-+单调增的结果！ 4.罗尔定理：如果函数()f x 满足(1) 在闭区间[,]a b 上连续； (2) 在开区间(,)a b 内可导；(3) 在区间端点处的函数值相等,即()()f a f b =, 那么在(,)a b 内至少有一点ξ(a b ξ<<),使得()0f ξ'=.八、(本题满分8分)(1) ()y ay f x '+=为一阶线性非齐次微分方程,可直接利用通解公式求解.通解为[]()()()ax ax ax y x e f x e dx C e F x C --⎡⎤=+=+⎣⎦⎰,其中()F x 是()axf x e 的任一原函数,由(0)0y =得(0)C F =-,故[]0()()(0)()xax ax at y x e F x F e e f t dt --=-=⎰.(2) 当0x ≥时,0()()()xxaxat axat y x ee f t dt ee f t dt --=⋅≤⎰⎰001(1)x x ax at ax at ax k ke e dt ke e e a a---⎛⎫≤⋅=⋅=- ⎪⎝⎭⎰.。

1996年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页．第Ⅱ卷3至8页．共150分．考试时间120分钟．第Ⅰ卷(选择题共65分)注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．3．考试结束，监考人将本试卷和答题卡一并收回．一．选择题：本大题共15小题，第1—10题每小题4分，第11—15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的(1) 已知全集I =N ，集合A ={x │x =2n ，n ∈N }，B ={x │x =4n ，n ∈N }，则 ( )(A) B A I =(B)B A I =(C) B A I =(D) B A I =(2) 当a >1时，在同一坐标系中，函数y =a －x 与y =log a x 的图像( )(3) 若sin 2x >cos 2x ，则x 的取值范围是 ( )(A) ⎭⎬⎫⎩⎨⎧∈+<<-Z k k x k x ,412432ππππ (B) ⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,452412ππππ (C) ⎭⎬⎫⎩⎨⎧∈+<<-Z k k x k x ,4141ππππ (D) ⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,4341ππππ(4) 复数54)31()22(i i -+等于( )(A) i 31+(B) i 31+-(C) i 31-(D) i 31--(5) 如果直线l 、m 与平面α、β、γ满足：l l ,γβ =∥m m 和αα⊂,,⊥γ，那么必有( )(A)α⊥γ且l ⊥m (B)α⊥γ且m ∥β (C)m ∥β且l ⊥m(D)α∥β且α⊥γ(6) 当x x x f x cos 3sin )(,22+=≤≤-函数时ππ的( ) (A) 最大值是1，最小值是－1 (B) 最大值是1，最小值是－21 (C) 最大值是2，最小值是－2 (D) 最大值是2，最小值是－1(7) 椭圆⎩⎨⎧+-=+=ϕϕsin 51,cos 33y x 的两个焦点坐标是( )(A) (－3，5)，(－3，－3) (B) (3，3)，(3，－5) (C) (1，1)，(－7，1)(D) (7，－1)，(－1，－1))](arccos[sin )]2(arcsin[cos ,20)8(απαππα+++<<则若等于( )(A)2π (B) －2π (C)2π－2α (D) －2π－2α (9) 将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD =a ，则三棱锥D －ABC 的体积为( )(A) 63a(B) 123a(C)3123a (D)3122a (10) 等比数列{}n a 的首项a 1=－1，前n 项和为S n ，若3231510=S S 则n n S ∞→lim 等于( )(A)32(B) －32 (C) 2 (D) －2(11) 椭圆的极坐标方程为θρcos 23-=，则它在短轴上的两个顶点的极坐标是( )(A) (3，0)，(1，π)(B) (3，2π)，(3，23π)(C) (2，3π)，(2，35π)(D) (7，23arctg)，(7，23arctg -2π) (12) 等差数列{}n a 的前m 项和为30，前2m 项和为100，则它的前3m 项和为( )(A) 130(B) 170(C) 210(D) 260(13) 设双曲线)0(12222b a by a x <<=-的半焦距为c ,直线l 过),0)(0,(b a 两点，已知原点到直线l 的距离为c 43，则双曲线的离心率为 ( )(A) 2(B)3(C)2 (D)332 (14) 母线长为1的圆锥体积最大时，其侧面展开图圆心角ϕ等于 ( )(A)π322 (B)π332 (C)π2(D)π362 (15) 设f (x )是(－∞，+∞)上的奇函数，f (x +2)=－f (x )，当0≤x ≤1时，f (x )=x ，则f (7.5) 等于( )(A) 0.5 (B) －0.5(C) 1.5(D) －1.5第Ⅱ卷(非选择题共85分)二．填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．(16)已知圆07622=--+x y x 与抛物线)0(22>=p px y 的准线相切，则P=(17)正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有 个（用数字作答）(18)40tg 20tg 340tg 20tg ++的值是(19)如图，正方形ABCD 所在平面与正方形ABEF 所在平面成60°的二面角，则异面直线AD 与BF 所成角的余弦值是三．解答题：本大题共6小题;共69分．解答应写出文字说明、证明过程或演算步骤．(20)解不等式1)11(log >-xa ．(21)已知△ABC 的三个内角A ，B ，C 满足：BC A B C A cos 2cos 1cos 1,2-=+=+，求2cosCA -的值． 22．如图，在正三棱柱ABC －A 1B 1C 1中，E ∈BB 1，截面A 1EC ⊥侧面AC 1．(Ⅰ)求证：BE =EB 1;(Ⅱ)若AA 1=A 1B 1;求平面A 1EC 与平面A 1B 1C 1所成二面角(锐角)的度数．注意：在下面横线上填写适当内容，使之成为(Ⅰ)的完整证明，并解答(Ⅱ)．(右下图)(Ⅰ)证明：在截面A 1EC 内，过E 作EG ⊥A 1C ，G 是垂足． ① ∵∴EG ⊥侧面AC 1;取AC 的中点F ，连结BF ，FG ，由AB =BC 得BF ⊥AC ，② ∵∴BF ⊥侧面AC 1;得BF ∥EG ，BF 、EG 确定一个平面，交侧面AC 1于FG ． ③ ∵∴BE ∥FG ，四边形BEGF 是平行四边形，BE =FG ， ④ ∵ ∴FG ∥AA 1，△AA 1C ∽△FGC ， ⑤ ∵ ∴112121BB AA FG ==，即11,21EB BE BB BE ==故 23．某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%，人均粮食占有量比现在提高10%．如果人口年增长率为1%，那么耕地平均每年至多只能减少多少公顷（精确到1公顷）?（粮食单产=耕地面积总产量，人均粮食占有量=总人口数总产量）24．已知l 1、l 2是过点)0,2(-P 的两条互相垂直的直线，且l 1、l 2与双曲线122=-x y 各有两个交点，分别为A 1、B 1和A 2、B 2．(Ⅰ)求l 1的斜率k 1的取值范围；(Ⅱ)若12211,5l B A B A 求 、l 2的方程25．已知a 、b 、c 是实数，函数f (x )=ax 2+bx +c ，g (x )=ax +b ，当－1≤x ≤1时，│f (x )│≤1．(Ⅰ)证明：│c │≤1；(Ⅱ)证明：当－1≤x ≤1时，│g (x )│≤2；(Ⅲ)设a >0，当－1≤x ≤1时，g (x )的最大值为2，求f (x )．1996年普通高等学校招生全国统一考试数学试题(理工农医类)参考解答及评分标准说明：一．本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误，就不再给分．三．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 四．只给整数分数．选择题和填空题不给中间分．一．选择题：本题考查基本知识和基本运算．第(1)－(10)题每小题4分，第(11)－(15)题每小题5分．满分65分．(1)C (2)A (3)D (4)B(5)A(6)D(7)B(8)A(9)D(10)B (11)C (12)C (13)A (14)D (15)B二．填空题：本题考查基本知识和基本运算．每小题4分，满分16分．（16）2 （17）32 （18）3（19）42三．解答题(20)本小题考查对数函数性质，对数不等式的解法，分类讨论的方法和运算能力．满分11分．解：(Ⅰ)当a ＞1时，原不等式等价于不等式组：⎪⎪⎩⎪⎪⎨⎧>->-.11,011a xx——2分由此得xa 11>-． 因为1－a <0，所以x <0， ∴.011<<-x a——5分(Ⅱ)当0<a <1时，原不等式等价于不等式组：⎪⎪⎩⎪⎪⎨⎧<->-.11,011a xx由①得，x >1或x <0， 由②得，,110ax -<< ∴ax -<<111 ——10分综上，当1>a 时，不等式的解集为⎭⎬⎫⎩⎨⎧<<-011x a x；当10<<a 时，不等式的解集为⎭⎬⎫⎩⎨⎧-<<a x x 111 ——11分(21)本小题考查三角函数基础知识，利用三角公式进行恒等变形和运算的能力．满分12分．解法一：由题设条件知B =60°，A +C =120°． ——2分∵,2260cos 2-=-∴22cos 1cos 1-=+CA 将上式化为C A C A cos cos 22cos cos -=+ 利用和差化积及积化和差公式，上式可化为)]cos()[cos(22cos 2cos2C A C A CA C A -++-=-+ ——6分将21)cos(,2160cos 2cos-=+==+C A C A 代入上式得)cos(222)2cos(C A C A --=- 将1)2(cos 2)cos(2--=-CA C A 代入上式并整理得 023)2cos(2)2(cos 242=--+-CA C A ——9分,0)32cos 22)(22cos2(=+---C A C A ∵,032cos 22≠+-CA ∴.022cos2=--CA 从而得.222cos=-C A ——12分解法二：由题设条件知B =60°，A +C =120°． 设αα2,2=--=C A CA 则，可得α+= 60A ，α-= 60C ——3分所以)60cos(1)60cos(1cos 1cos 1αα-++=+C A ααααsin 23cos 211sin 23cos 211++-=ααα22sin 43cos 41cos -=43cos cos 2-=αα——7分依题设条件有Bcos 243cos cos 2-=-αα， ∵21cos =B ∴2243cos cos 2-=-αα整理得,023cos 2cos 242=-+αα——9分,0)3cos 22)(2cos 2(=+-αα∵03cos 22≠+α， ∴02cos 2=-α． 从而得222cos =-C A ． ——12分(22)本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力及运算能力．满分12分．(Ⅰ) ①∵面A 1EC ⊥侧面AC 1，——2分 ②∵面ABC ⊥侧面AC 1， ——3分 ③∵BE ∥侧面AC 1， ——4分 ④∵BE ∥AA 1， ——5分 ⑤∵AF =FC ，——6分(Ⅱ)解：分别延长CE 、C 1B 1交于点D ，连结A 1D ． ∵1EB ∥11112121,CC BB EB CC ==， ∴,21111111B A C B DC DB ===∵∠B 1A 1C 1=∠B 1 C 1A 1=60°， ∠DA 1B 1=∠A 1DB 1=21（180°－∠D B 1A 1）=30°， ∴∠DA 1C 1=∠DA 1B 1+∠B 1A 1C 1=90°，即1DA ⊥11C A——9分∵CC 1⊥面A 1C 1B 1，即A 1C 1是A 1C 在平面A 1C 1D 上的射影，根据三垂线定理得DA 1⊥A 1C ， 所以∠CA 1C 1是所求二面角的平面角． ——11分∵CC 1=AA 1=A 1B 1=A 1C 1，∠A 1C 1C =90°， ∴∠CA 1C 1=45°，即所求二面角为45°——12分 (23)本小题主要考查运用数学知识和方法解决实际问题的能力，指数函数和二项式定理的应用，近似计算的方法和能力．满分10分．解：设耕地平均每年至多只能减少x 公顷，又设该地区现有人口为P 人，粮食单产为M 吨/公顷．依题意得不等式%)101(10%)11()1010(%)221(4104+⨯⨯≥+⨯-⨯+⨯P M P x M ——5分化简得]22.1)01.01(1.11[10103+⨯-⨯≤x ——7分 ∵]22.1)01.01(1.11[10103+⨯-⨯ )]01.001.01(22.11.11[1022101103 +⨯+⨯+⨯-⨯=C C ]1045.122.11.11[103⨯-⨯≈ 1.4≈—— 9分∴x ≤4（公顷）．答：按规划该地区耕地平均每年至多只能减少4公顷．——10分(24)本小题主要考查直线与双曲线的性质，解析几何的基本思想，以及综合运用知识的能力．满分12分．解：（I ）依题设，l 1、l 2的斜率都存在，因为l 1过点P )0,2(-且与双曲线有两个交点，故方程组⎪⎩⎪⎨⎧=-≠+=1)0)(2(2211x y k x k y ① ——1分有两个不同的解．在方程组①中消去y ，整理得01222)1(2121221=-++-k x k x k ②若0121=-k ，则方程组①只有一个解，即l 1与双曲线只有一个交点，与题设矛盾，故0121≠-k ，即11≠k ，方程②的判别式为).13(4)12)(1(4)22(2121212211-=---=∆k k k k设2l 的斜率为2k ，因为2l 过点)0,2(-P 且与双曲线有两个交点，故方程组⎪⎩⎪⎨⎧=-≠+=.1),0)(2(2222x y k x k y ③ 有两个不同的解．在方程组③中消去y ，整理得01222)1(2222222=-++-k x k x k ④同理有)13(4,0122222-=∆≠-k k 又因为l 1⊥l 2，所以有k 1·k 2=－1．——4分于是，l 1、l 2与双曲线各有两个交点，等价于⎪⎪⎩⎪⎪⎨⎧≠-=⋅>->-.1,1,013,0131212221k k k k k 解得⎪⎩⎪⎨⎧≠<<.1,33311k k——6分∴)3,1()1,33()33,1()1,3(1 ----∈k ——7分(Ⅱ)设),(),,(221111y x B y x A 由方程②知112,122212121212121--=⋅--=+k k x x k k x x ∴│A 1B 1│2=(x 1－x 2)2+(y 1－y 2)222121))(1(x x k -+=2212121)1()13)(1(4--+=k k k ⑤ ——9分同理，由方程④可求得222B A ，整理得2212121222)1()3)(1(4k k k B A --+=⑥ 由22115B A B A =，得2222115B A B A =将⑤、⑥代入上式得22121212212121)1()3)(1(45)1()13)(1(4k k k k k k --+⨯=--+ 解得21±=k 取21=k 时，)2(22:),2(2:21+-=+=x y l x y l ； 取21-=k 时，)2(22:),2(2:21+=+-=x y l x y l ． ——12分(25)本小题主要考查函数的性质、含有绝对值的不等式的性质，以及综合运用数学知识分析问题与解决问题的能力．满分12分．(Ⅰ)证明：由条件当－1≤x ≤1时，│f (x )│≤1，取x =0得 │c │=│f (0)│≤1， 即│c │≤1．——2分(Ⅱ)证法一：当a >0时，g (x )=ax +b 在[－1，1]上是增函数， ∴g (－1)≤g (x )≤g (1)，∵│f (x )│≤1 (－1≤x ≤1)，│c │≤1， ∴g (1)=a +b =f (1)－c ≤│f (1)│+│c │≤2，g (－1)=－a +b =－f (－1)+c ≥－(│f (－1)│+│c │)≥－2， 由此得│g (x )│≤2;——5分当a <0时，g (x )=ax +b 在[－1，1]上是减函数， ∴g (－1)≥g (x )≥g (1)，∵│f (x )│≤1 (－1≤x ≤1)，│c │≤1，∴g (－1)=－a +b =－f (－1)+c ≤│f (－1)│+│c │≤2， g (1)=a +b =f (1)－c ≥－(│f (1)│+│c │)≥－2， 由此得│g (x )│≤2;——7分 当a =0时，g (x )=b ，f (x )=bx +c ． ∵－1≤x ≤1，∴│g (x )│=│f (1)－c │≤│f (1)│+│c │≤2． 综上得│g (x )│≤2． ——8分证法二：由4)1()1(22--+=x x x ，可得b ax x g +=)()2121(])21()21[(22--++--+=x x b x x a ])21()21([])21()21([22c x b x a c x b x a +-+--++++= ),21()21(--+=x f x f ——6分当－1≤x ≤1时，有,0211,1210≤-≤-≤+≤x x 根据含绝对值的不等式的性质，得2)21()21()21()21(≤-++≤--+x f x f x f x f 即│g (x )│≤2．——8分(Ⅲ)因为a >0，g (x )在[－1，1]上是增函数，当x =1时取得最大值2， 即g (1)=a +b =f (1)－f (0)=2． ①∵－1≤f (0)=f (1)－2≤1－2=－1， ∴c =f (0)=－1．——10分因为当－1≤x ≤1时，f (x )≥－1，即f (x )≥f (0)，根据二次函数的性质，直线x =0为f (x )的图像的对称轴，由此得0,02==-b ab即 由① 得a =2． 所以 f (x )=2x 2－1． ——12分。

考研数学二（常微分方程）历年真题试卷汇编1(题后含答案及解析) 题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．(1989年)微分方程y〞－y＝eχ＋1的一个特解应具有形式(式中a，b 为常数) 【】A．aeχ＋bB．aχeχ＋bC．aeχ＋bχD．aχeχ＋bχ正确答案：B解析：y〞－y＝eχ＋1的特解应为方程y〞－y＝eχ和y〞－y＝1的特解之和，而特征方程为r2－1＝0，解得r＝±1 因此y－y＝eχ的特解应为y1*＝aχeχ，y〞－y＝1的特解应为y2*＝b 则原方程特解应具有形式y＝aχeχ＋b 知识模块：常微分方程2．(1998年)已知函数y＝f(χ)在任意点χ处的增量△y＝＋α，其中α是比△χ(△χ→0)的高阶无穷小，且y(0)＝π，则y(1)＝【】A．B．2πC．πD．正确答案：A解析：由于△y与△χ＋α，其α是比△χ(△χ→0)高阶的无穷小，则解此变量可分离方程得y＝Cearctanχ，再由y(0)＝π得C＝π故y＝兀earctanχ，y(1)＝π知识模块：常微分方程3．(2000年)具有特解y1＝e－χ，y2＝2χe－χ，y3＝3eχ的三阶常系数齐次线性微分方程是【】A．y〞′－y〞－y′＋y＝0B．y〞′＋y〞－y′－y＝0C．y〞′－6y〞＋11y′－6y＝0D．y〞′－2y〞－y′＋2y＝0正确答案：B解析：由本题所给三个特解可知，所求方程的特征方程的根为λ1＝1，λ2＝－1(二重)，故特征方程是(λ－1)(λ＋1)2＝0，展开得λ3＋λ2－λ－1＝0 从而，微分方程应为y′〞＋y′－y＝0，则应选B．知识模块：常微分方程4．(2002年)设y＝y(χ)是二阶常系数微分方程y〞＋py′＋qy＝e3χ满足初始条件y(0)＝y′(0)＝0的特解，则当χ→0时，函数的极限．【】A．不存在B．等于1C．等于2D．等于3正确答案：C解析：由于y(χ)是方程y〞＋py′＋qy＝e3χ满足初始条件y(0)＝y′(0)＝0的特解，在方程y〞＋py′＋qy＝e3χ中，令χ＝0 得y〞(0)＋Py′(0)＋qy(0)＝e0＝1 即y〞(0)＝1 所以应选C．知识模块：常微分方程5．(2003年)已知y＝是微分方程y′＝的解，则φ()的表达式为【】A．B．C．D．正确答案：A解析：将y＝代入方程y′＝得故应选A．知识模块：常微分方程填空题6．(1994年)微分方程ydχ＋(χ2－4χ)dy＝0的通解为_______．正确答案：(χ－4)y4＝Cχ．解析：该方程是一个变量可分离方程，即(χ－4)y4＝Cχ知识模块：常微分方程7．(1995年)微分方程y〞＋y＝－2χ的通解为_______．正确答案：y＝－2χ＋C1cosχ＋C2sinχ．解析：特征方程为r2＋1＝0，解得r1＝i，r2＝－I 齐次通解为＝C1cos χ＋C2sinχ易观察出非齐次一个特解为y*＝－2χ则原方程通解为y＝C1>cosχ＋C2sinχ－2χ知识模块：常微分方程8．(1996年)微分方程y〞＋2y′＋5y＝0的通解为_______．正确答案：y＝e－χ(C1cos2χ＋C2sin2χ)．解析：特征方程为r2＋2r＋5＝0，r1，2＝－1±2i 故通解为y＝C1e－χcos2χ＋C2e－χsin2χ．知识模块：常微分方程9．(1999年)微分方程y〞－4y＝e2χ的通解为________．正确答案：y＝C1e－2χ＋(C2＋χ)e2χ(C1，C2为任意常数)．解析：特征方程为r2－4＝0，r1，2＝±2 齐次通解为＝1e－2χ＋C2e2χ设非齐次方程特解为y*Aχe2χ代入原方程得A＝，故原方程通解为知识模块：常微分方程10．(2001年)过点(，0)且满足关系式y′arcsinχ＋＝1的曲线方程为_______·正确答案：yarcsinχ＝χ－．解析：由y′arcsinχ＋＝1 知(yarcsinχ)′＝1 则yarcsinχ＝χ＋C 由因此yarcsinχ＝χ－知识模块：常微分方程11．(2002年)微分方程yy〞＋y′2＝0满足初始条件的特解是_______．正确答案：y2＝χ＋1或y＝解析：令y′＝P，则，y〞＝，代入原方程得则所求的特解为y2＝χ＋1．知识模块：常微分方程12．(2004年)微分方程(y＋χ3)dχ－2χdy＝0满足的特解为_______．正确答案：解析：方程(y＋χ3)dχ－2χdy＝0可改写为设方程为一阶线性方程，则其通解为由知C＝1，则所求特解为y＝知识模块：常微分方程13．(2005年)微分方程χy′＋2y＝χlnχ满足y(1)＝－的解为_______．正确答案：解析：方程χy＋2y＝χlnχ是一阶线性方程，方程两端同除以χ得：y′＋＝lnχ，则通解为由y(1)＝－得，C＝0，则知识模块：常微分方程解答题解答应写出文字说明、证明过程或演算步骤。