计算物理基础
- 格式:doc
- 大小:43.00 KB
- 文档页数:3


物理基础公式总结归纳物理是一门研究自然界各种物质运动和相互作用规律的学科。
在物理学的学习过程中,公式是我们重要的工具之一,能够帮助我们理解各种现象,并且进行计算预测。
本文将对一些常见的物理基础公式进行总结归纳,以供参考。
1. 力学1.1 平均速度(v)= 路程(s)/ 时间(t)1.2 加速度(a)= 速度变化(Δv)/ 时间(t)1.3 牛顿第二定律(F)= 质量(m) ×加速度(a)1.4 动能(E_kin)= 1/2 ×质量(m) ×速度²(v²)1.5 动量(p)= 质量(m) ×速度(v)1.6 动量守恒定律:在一个封闭系统内,系统的总动量在没有外力作用时保持不变1.7 引力(F)= 万有引力常量(G) × (质量1 ×质量2) / 距离²2. 热学2.1 热传导定律: 热传导速率(Q)= 热导率(k) ×横截面积(A)×温度差(ΔT) / 物体厚度(d)2.2 热膨胀定律: 线膨胀量(ΔL)= 原长(L)×线膨胀系数(α)×温度变化(ΔT)2.3 热平衡定律: 热量的净传递总是从高温物体向低温物体传递,直到达到热平衡状态3. 电学3.1 电流(I)= 电量(Q)/ 时间(t)3.2 电阻(R)= 电压(V)/ 电流(I)3.3 电流强度(I)= 电压(V)/ 电阻(R)3.4 电阻与电流、电压的关系: 电阻(R)= 电压(V)/ 电流强度(I)= V/I3.5 库仑定律:两个电荷之间的作用力与它们之间的距离成正比,与电荷的大小成反比3.6 电功(W)= 电压(V) ×电量(Q)4. 光学4.1 光速(c)= 299792458 m/s4.2 光的折射定律: 折射率(n1/n2)= 入射角(θ1)/ 折射角(θ2)4.3 焦距(f)= 透镜与物体的距离(d1) ×透镜与像的距离(d2)/(透镜与物体的距离(d1) + 透镜与像的距离(d2))4.4 倍率(M)= 图像高度(h2)/ 物体高度(h1)5. 波动5.1 波长(λ)= 光速(c)/ 频率(f)5.2 波速(v)= 波长(λ) ×频率(f)5.3 声音速度(v)= 频率(f) ×波长(λ)通过以上的公式总结归纳,我们可以看到物理学中的公式丰富多样,每个公式都可以帮助我们解决不同的问题。


学习指导计算物理课程的学习内容包括计算工具、算法、作图、编程、物理应用等不同的组成部分,对这些不同的内容要针对其特点采用不同学习方法才能有效地提高学习效率。
MATLAB是本课程采用计算工具,它包含指令与语法两大内容。
作为一种商业化的用途广泛的计算软件,其指令多达数千条。
而我们所使用的不过是几百条,其中需要的熟练掌握并记忆的不过一百多条。
学习MATLAB不是要求精通MATLAB,而是会将MATLAB为我所用。
所以教材中采用的教学方法是边学边用,要用才学,学了就用,不用不学。
对于一些不常用的指令不必专门学习与记忆,而是在用到时,通过help系统查询其用法后直接使用。
对于需要重点掌握的指令都在技能点给以说明。
数值算法是数值计算的理论指导,但是计算物理课程学习数值算法是重在实际应用而不是研究算法理论。
从这一点出发,再考虑到MATLAB的指令实际上已经将几乎所有的基本算法都编成了指令,这些算法已经远远超过教科书所能讲授的内容。
所以课程中采用的教学方法是,示范性地介绍一些最基本的算法理论,尽量详细介绍MATLAB的指令,以便学生既能理解指令是如何进行数值计算,又能在计算与编程中充分运用指令完成各种复杂计算。
事实上,掌握了指令相当于掌握了基本算法并完成了用基本算法编程的双重任务,是一箭双雕的学习方法。
将作图或者说“科学计算可视化”列入学习内容,是本课程独有的做法,是“计算机图形学”在计算物理教学中的创新性应用的结果。
图形学丰富的技术手段和丰硕的研究成果使得可视化在数值研究中越来越重要,图形不仅成为理解数据内涵的重要手段,而且成为数值计算之后,研究数据结果最有效的后续方法。
这些方法包括图形和图像、动画、虚拟现实与仿真等等。
本课程能够完成这个学习目标是由于MATLAB已经达到作图软件的图形功能,完成作图以及制作图形界面几乎是举手之劳。
这也是选择MATLAB的又一个优势。
MATLAB的编程语句、语法与文件种类十分简单,应该牢记并熟练掌握。

计算物理基础
计算物理基础是物理学中一个重要的分支,它借助计算机和数值方法来研究物理现象。
通过数值模拟和计算,我们可以更深入地理解和预测物理系统的行为。
本文将介绍计算物理的基础知识,包括数值方法、模拟技术和应用领域。
数值方法是计算物理的核心,它涉及将物理问题转化为数学问题,并利用计算机进行求解。
常见的数值方法包括有限差分法、有限元法和蒙特卡洛方法等。
这些方法可以用来求解微分方程、积分方程和优化问题等。
通过数值方法,我们可以模拟物理现象,如流体力学、固体力学和量子力学等。
模拟技术是计算物理中的另一个重要概念,它通过构建数学模型来描述物理系统,并利用计算机进行仿真。
模拟技术可以帮助我们研究复杂的物理现象,如天体物理、等离子体物理和原子物理等。
通过模拟技术,我们可以模拟宇宙的演化、核聚变反应和材料的特性等。
计算物理的应用领域非常广泛,涵盖了自然科学、工程技术和医学健康等多个领域。
在物理学中,计算物理可以用来研究粒子物理、宇宙学和凝聚态物理等。
在工程技术中,计算物理可以用来优化设计、模拟流体动力学和分析结构力学等。
在医学健康中,计算物理可以用来模拟生物系统、优化医疗设备和研究生物分子等。
总的来说,计算物理是一门强调理论与实践结合的学科,它通过数值方法和模拟技术来研究物理现象,为解决实际问题提供了重要的工具和方法。
希望本文可以帮助读者更好地了解计算物理的基础知识,激发对物理学的兴趣和热爱。

计算物理基础试题及答案一、选择题(每题2分,共10分)1. 在经典力学中,牛顿第二定律的表达式是什么?A. F = maB. F = mvC. F = m/aD. F = a/m答案:A2. 根据能量守恒定律,一个物体的动能和势能之和在没有外力作用下是:A. 增加的B. 减少的C. 不变的D. 无法确定答案:C3. 以下哪个选项是波动方程的基本特征?A. 波速B. 波长C. 频率D. 所有选项都是答案:D4. 在量子力学中,海森堡不确定性原理表明了什么?A. 粒子的位置和动量可以同时准确测量B. 粒子的位置和动量不能同时准确测量C. 粒子的能量和时间可以同时准确测量D. 粒子的能量和时间不能同时准确测量答案:B5. 根据麦克斯韦方程组,电磁波在真空中的传播速度是多少?A. cB. 2cC. c/2D. 10c答案:A二、填空题(每题2分,共10分)6. 一个物体在水平面上做匀速直线运动,其动力学方程为 F =__________。
答案:07. 根据热力学第一定律,系统吸收的热量Q与对外做功W之间的关系为ΔU = __________ + W。
答案:Q8. 一个波包的波函数可以表示为Ψ(x,t) = A * e^(i(kx - wt)),其中A是__________,k是__________,w是__________。
答案:振幅;波数;角频率9. 量子力学中的泡利不相容原理指出,一个原子中的两个电子不能具有完全相同的一组量子数,这些量子数包括:__________、__________、__________和__________。
答案:主量子数、角量子数、磁量子数、自旋量子数10. 根据狭义相对论,长度的洛伦兹收缩公式为 L = L0 *__________。
答案:√(1 - v^2/c^2)三、简答题(每题10分,共30分)11. 简述牛顿运动定律的三个定律。
答案:牛顿第一定律(惯性定律)指出,一个物体若没有受到外力,将保持静止或匀速直线运动的状态。


计算物理知识点总结一、计算方法1.1 数值积分数值积分是计算物理中常用的一种方法,它用于求解复杂的积分运算。
数值积分的基本原理是将积分区间分割成若干小区间,然后对每个小区间进行近似计算,最后将这些结果累加起来,得到整个积分的近似值。
1.2 微分方程数值解微分方程在物理学中广泛应用,而一般情况下微分方程是无法直接求解的,因此需要利用数值方法来求解。
微分方程数值解的基本原理是将微分方程离散化,然后用数值方法求解离散化后的方程,从而得到微分方程的近似解。
1.3 存储器和算法计算物理中使用的数学模型往往需要大量的内存和计算时间,因此如何有效地利用存储器和设计算法变得尤为重要。
在实际应用中,通常需要根据具体问题的特点来选择合适的存储器和算法,以提高计算效率和准确性。
1.4 随机数生成在模拟技术中,常常需要使用随机数来模拟物理过程中的随机性。
因此如何生成高质量的随机数成为一个重要的问题。
现代的计算机通常能够生成高质量的随机数序列,但需要注意的是,随机数的生成方法和质量直接影响了模拟结果的准确性。
二、模拟技术2.1 蒙特卡洛方法蒙特卡洛方法是一种常用的模拟技术,它通过使用随机数来模拟物理系统的行为。
蒙特卡洛方法广泛应用于统计物理、量子力学等领域,具有很高的准确性和灵活性。
2.2 分子动力学模拟分子动力学模拟是一种用于研究原子和分子在时间和空间上的运动规律的方法。
通过对分子之间的相互作用力进行近似计算,然后用数值积分方法求解微分方程,得到了分子的运动轨迹和能量变化。
2.3 能带结构计算能带结构是固体物理和半导体物理中的一个重要概念,它描述了材料中电子的能量分布情况。
计算物理可以通过模拟方法来计算材料的能带结构,从而帮助研究者理解材料的电子性质和相应的物理特性。
2.4 流体动力学模拟流体动力学模拟是一种用于研究流体运动规律的方法,它广泛应用于气体、液体和等离子体等领域。
通过对流体的运动和相互作用进行模拟,可以帮助研究者理解流体的物理特性,并且为相关工程应用提供参考。
《计算物理基础》教学大纲二、教学目标本课程是为物理学专业和应用物理学专业的本科生开设的专业核心课程之一,是用数值方法求解典型物理问题的一门实用性专业课程。
本课程使学生掌握线性代数、常微分方程、逼近与插值、和非线性方程组等常见计算问题的通用数值解法和编程技巧。
本课程结合典型物理问题,有选择地介绍若干主要数值方法(如元胞自动机方法、蒙特卡罗模拟方法、密度泛函方法、分子动力学方法等)和软件应用,并结合计算机技术适当介绍计算科学的进展,为学生进一步从事有关的科学和技术研究,以及数值计算方法和软件研发打下基础。
本课程教学目标:通过课堂教学和课后实践练习,使学生掌握科学计算的基本方法,掌握典型物理问题的数值解法及计算结果的可视化。
三、教学内容及基本要求第一章绪论(2/1)(一)教学目标1.理解科学计算在科学研究中的意义,了解计算物理在物理学研究中的地位,了解MATLAB软件的发展历史和MATLAB应用于科学计算的基本情况。
2. 熟练掌握启动和退出MATLAB的方法;了解MATLAB的主要功能;熟练掌握命令窗口的使用;熟练掌握MATLAB的帮助的使用方法。
(二)重点、难点重点:MATLAB命令窗口的使用;难点:初接触MATLAB时,不熟悉可执行哪些命令。
(三)教学方法通过演示执行几个简单的常用命令,讲清重点;结合帮助系统和DEMO,剖析几个常用命令的使用方法,突破难点;结合多媒体命令的使用,提高学生学习计算物理基础课程的兴趣。
(四)教学内容1. 学习科学计算的意义(1)科学研究方法的演化(2)MATLAB软件的发展历史(3)MATLAB应用于科学计算的基本情况(4)实验物理、理论物理、计算物理三种研究物理学手段的特点(5)串行计算概念和并行计算概念2. MATLAB软件的基本功能(1)MATLAB启动和退出(2)了解MATLAB的主要功能(3)命令窗口的使用(4)MATLAB的帮助系统的使用3.MATLAB趣味例程(1)MATLAB的DEMO(2)MATLAB趣味例程演示(3)用拍现象和调制技术举例介绍用MATLAB模拟物理现象和物理过程(五)作业及要求描绘拍现象和调制现象。

计算物理基础试题及答案一、选择题1. 在计算物理中,下列哪个选项是用于描述量子态的?A. 波函数B. 概率密度C. 动量D. 能量答案:A2. 根据薛定谔方程,下列哪项是正确的?A. 时间依赖的薛定谔方程是量子力学的基本方程B. 薛定谔方程只适用于非相对论量子力学C. 薛定谔方程描述的是粒子的波动性质D. 所有选项都是正确的答案:D二、填空题3. 计算物理中,______是描述粒子在空间中分布的概率密度函数。
答案:波函数4. 在量子力学中,粒子的波函数通常用希腊字母______表示。
答案:ψ(psi)三、简答题5. 简述计算物理中蒙特卡洛方法的基本原理。
答案:蒙特卡洛方法是一种基于随机抽样的数值计算方法,它通过生成随机数来模拟物理系统的行为,从而获得系统的统计性质。
这种方法特别适合于处理多维积分和复杂系统的随机过程。
四、计算题6. 假设一个粒子的波函数为ψ(x) = A * e^(-ax),其中A是归一化常数,a是正实数。
求粒子在位置x=0处的概率密度。
答案:概率密度ρ(x) = |ψ(x)|^2 = |A * e^(-ax)|^2。
由于波函数需要归一化,即∫|ψ(x)|^2 dx = 1,我们可以通过计算积分来确定A 的值。
对于x=0,概率密度ρ(0) = |A|^2。
7. 给定一个一维量子势阱,其势能V(x)在区间[0, L]内为0,在区间外为无穷大。
求该势阱中粒子的基态能量。
答案:对于一个一维无限深势阱,基态能量可以通过求解薛定谔方程得到。
基态波函数是正弦函数,其能量为E_0 = (n^2 * π^2 * ħ^2) / (2 * m * L^2),其中n=1,m是粒子质量,ħ是约化普朗克常数。
因此,基态能量E_0 = (π^2 * ħ^2) / (2 * m * L^2)。
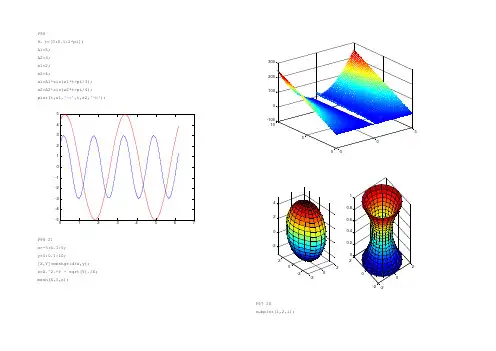
P968、t=[0:0.1:2*pi]; A1=5; A2=3; w1=2; w2=4;x1=A1*sin(w1*t+pi/3); x2=A2*sin(w2*t+pi/4); plot(t,x1,'-r',t,x2,'-b');1234567-5-4-3-2-1012345P98 21 x=-5:0.1:5; y=0:0.1:10;[X,Y]=meshgrid(x,y); z=X.^2.*Y + sqrt(Y)./X; mesh(X,Y,z);-2024-22P97 20subplot(1,2,1);[X0,Y0,Z0]=sphere(20);X=2*X0;Y=3*Y0;Z=4*Z0+1;surf(X,Y,Z);axis equalsubplot(1,2,2)t=-1:0.1:1;[X,Y,Z]=cylinder(1+t.^2,20);%形成旋转曲面surf(X,Y,Z);P195 1x=[-1.0 -0.75 -0.50 -0.25 0 0.25 0.50 0.75 1.00];y=[-0.2209 0.3295 0.8826 1.4392 2.0003 2.5645 3.1334 3.7061 4.2836]; a=polyfit(x,y,1);P151 3syms vvp=1578;f=int(4/pi^(1/2)*v^2/vp^3*exp(-v^2/vp^2),v,0,Inf);VF=vpa(f);1. 解:依题,取 a 5,c 1,m 16, x0 1xn 1 (5xn 1)(mod16),x0 1,x伪随机数:n n162. 解:依题,取 a 137,c 187,m 256,x0 1xn 1 (137xn 187)(mod 256),x0 1,xn 2 (137xn 1 187)(mod 256),x x x伪随机数:n n ,n 1 n 1 ,n 2 n 2256 256 2563. 解:引入二维随机均匀分布向量(x,) 表示针在桌上的位置,s 1 1x [0, ], f (x ) ;[0, ], f () .1 22 s / 2 0 2 / 2 0其中,s 为线间的距离,l 为针长度,x 为线中点到最近平行线的距离,为针与线平行线间的夹角。
物理基础分析公式归纳总结物理学作为一门自然科学,通过对物质和能量的运动规律的研究,以数学模型和分析方法为基础,形成了许多重要的物理基础公式。
本文将对其中一些常见的物理基础公式进行归纳总结,并解释其应用。
一、力学公式1. 牛顿第二定律F = m*a力(F)等于物体的质量(m)乘以加速度(a)。
这个公式表明了力和运动之间的关系,可以用来计算物体所受的力和加速度。
2. 万有引力定律F = G*(m1*m2)/r^2两个物体之间的引力(F)等于它们质量的乘积(m1*m2)乘以万有引力常数(G),除以距离的平方(r^2)。
这个公式描述了物体之间的引力,广泛应用于天体力学研究。
3. 动能公式K = 1/2*m*v^2物体的动能(K)等于其质量(m)乘以速度(v)的平方的一半。
这个公式用来计算物体的动能,而动能则可以用来描述物体的运动状态。
4. 等速直线运动公式v = v0 + a*t相对于初速度(v0),物体在恒定加速度(a)作用下,经过时间(t)后的速度(v)。
这个公式适用于等速直线运动的情况,可以用来计算物体的速度。
二、热学公式1. 热传导公式Q = k*A*(ΔT/l)物体的热传导热流(Q)等于热导率(k)乘以物体的横截面积(A)乘以温度差(ΔT),再除以物体的厚度(l)。
这个公式描述了热传导现象,用来计算热传导的热流。
2. 热容公式Q = m*C*ΔT物体吸收或释放的热量(Q)等于其质量(m)乘以比热容(C)乘以温度差(ΔT)。
这个公式用来计算物体吸收或释放的热量。
3. 热辐射公式P = ε*σ*A*T^4热辐射功率(P)等于物体表面的发射率(ε)乘以斯特藩-玻尔兹曼常数(σ)乘以物体表面的面积(A)乘以温度的四次方(T^4)。
这个公式用来描述物体通过热辐射释放的能量。
三、电磁学公式1. 电容公式C = Q/V电容(C)等于电荷(Q)除以电压(V)。
这个公式描述了电容器的电容量,用来计算电荷和电压的关系。
计算物理学基础李华
计算物理学基础是计算物理学的入门课程之一。
它涵盖了数值计算方法、数值分析、数据结构、算法设计等内容。
以下是一些参考内容:
1. 数值计算方法:二分法、牛顿法、割线法、拉格朗日插值法、牛顿插值法、梯形法、辛普森法、龙格-库塔法、欧拉法等。
2. 数值分析:数值误差、截断误差、舍入误差、数值稳定性、数值收敛性、误差估计等。
3. 数据结构:数组、链表、栈、队列、堆、树、图等。
4. 算法设计:分治法、动态规划、贪心算法、回溯算法、随机算法等。
5. 计算物理应用:求解微分方程、积分方程、偏微分方程,模拟物理过程,计算相互作用等。
需要注意的是,以上只是计算物理学基础的部分内容,学习计算物理还需要对具体应用领域有一定的了解和掌握。
计算物理基础学习心得体会学习物理基础课程是我大学生活中一段重要的经历,通过这门课程的学习,我深刻体会到物理的深奥和实用性,同时也收获了一系列宝贵的学习心得和体会。
首先,学习物理基础课程让我更全面地了解了自然界的基本规律和运动规律。
通过学习力学、热学、电磁学等内容,我对自然界的各种现象有了更深刻的认识。
比如,学习力学让我了解了物体运动的规律,了解了力、加速度和质量之间的关系。
学习热学让我理解了温度、热力学参数和传热原理等概念,这对我们理解和解释热现象具有重要意义。
学习电磁学让我了解了带电粒子的运动规律、电场和磁场的概念以及电磁波的传播特性,这对我们理解电磁现象和电子设备的原理有着重要作用。
其次,学习物理基础课程增强了我解决问题和分析问题的能力。
物理是一门探究自然规律的科学,它注重实验和观察,逻辑严密且精确。
在学习过程中,我们经常需要通过观察实验现象、分析实验数据和运用物理公式来解决问题。
这培养了我锐利的观察力、辨析问题的能力以及理论联系实际问题的能力。
通过大量练习和实践,我能够更快地理解和解决物理问题,也学会了运用物理知识解释和分析我们日常生活中遇到的问题。
另外,学习物理基础课程让我更加注重实验和动手能力的培养。
在物理课堂上,我们不仅进行了许多理论知识的学习,还有很多实验和操作的训练。
通过亲自操作仪器和观测实验现象,我更好地理解了物理理论,并培养了实际操作的能力。
物理实验一方面培养了我对实验条件和实验数据的观察和分析能力,另一方面也增加了我对物理实验装置和仪器设备的了解和熟悉程度。
这不仅提高了我的实验能力,还为我今后从事相关实验工作提供了基础。
最后,学习物理基础课程让我深刻体会到物理学科的广泛应用和重要性。
物理学是一门应用广泛的学科,它不仅在日常生活中起着重要作用,还在各个领域发挥着重要的作用。
无论是工程学、医学、天文学还是生物学,都离不开物理学的原理和方法。
通过学习物理基础课程,我更加明确了物理学科的重要性以及其对其他学科的支持作用。
《计算物理基础》教学大纲一、课程基本信息中文名称计算物理基础英文名称Computational Physics适用专业物理学应用物理学先修课程高等数学、计算机基础、程序设计、大学物理课程类别专业核心课程修读性质必修学分/学时2学分/46学时(12)考核方式考查二、教学目标本课程是为物理学专业和应用物理学专业的本科生开设的专业核心课程之一,是用数值方法求解典型物理问题的一门实用性专业课程。
本课程使学生掌握线性代数、常微分方程、逼近与插值、和非线性方程组等常见计算问题的通用数值解法和编程技巧。
本课程结合典型物理问题,有选择地介绍若干主要数值方法(如元胞自动机方法、蒙特卡罗模拟方法、密度泛函方法、分子动力学方法等)和软件应用,并结合计算机技术适当介绍计算科学的进展,为学生进一步从事有关的科学和技术研究,以及数值计算方法和软件研发打下基础。
本课程教学目标:通过课堂教学和课后实践练习,使学生掌握科学计算的基本方法,掌握典型物理问题的数值解法及计算结果的可视化。
三、教学内容及基本要求第一章绪论(2/1)(一)教学目标1.理解科学计算在科学研究中的意义,了解计算物理在物理学研究中的地位,了解MATLAB软件的发展历史和MATLAB应用于科学计算的基本情况。
2. 熟练掌握启动和退出MATLAB的方法;了解MATLAB的主要功能;熟练掌握命令窗口的使用;熟练掌握MATLAB的帮助的使用方法。
(二)重点、难点重点:MATLAB命令窗口的使用;难点:初接触MATLAB时,不熟悉可执行哪些命令。
(三)教学方法通过演示执行几个简单的常用命令,讲清重点;结合帮助系统和DEMO,剖析几个常用命令的使用方法,突破难点;结合多媒体命令的使用,提高学生学习计算物理基础课程的兴趣。
(四)教学内容1. 学习科学计算的意义(1)科学研究方法的演化(2)MATLAB软件的发展历史(3)MATLAB应用于科学计算的基本情况(4)实验物理、理论物理、计算物理三种研究物理学手段的特点(5)串行计算概念和并行计算概念2. MATLAB软件的基本功能(1)MATLAB启动和退出(2)了解MATLAB的主要功能(3)命令窗口的使用(4)MATLAB的帮助系统的使用3.MATLAB趣味例程(1)MATLAB的DEMO(2)MATLAB趣味例程演示(3)用拍现象和调制技术举例介绍用MATLAB模拟物理现象和物理过程(五)作业及要求描绘拍现象和调制现象。
高中物理基础公式高中物理基础公式是学习物理的基础,掌握了这些公式,才能更好地理解和解决物理问题。
以下是一些高中物理基础公式的正文和拓展:1. 质点公式质点公式是指一个质点的质量可以用其体积和密度计算的公式。
具体来说,质量m=密度×体积,其中密度是质点的常数,通常用g/cm3表示。
例如,一个质量为1千克的质点,其体积为1立方厘米,则其密度为1000千克/立方米。
2. 动量公式动量公式是指一个物体在任意时刻的动量等于其质量与速度的乘积。
具体来说,动量p=m×v,其中m是物体的质量,v是物体的速度。
动量公式在物理学中应用广泛,可以用来计算物体的速度、加速度等。
3. 能量公式能量公式是指一个物体的能量等于其质量与速度的乘积,也可以等于其动量与时间的乘积。
具体来说,能量E=m×v×a,其中m是物体的质量,v是物体的速度,a是物体的加速度。
这个公式在物理学中应用广泛,可以用来计算物体的能量、功率、功等。
4. 功和功率公式功和功率公式是指一个物体的功等于其速度与时间的乘积,而功率等于功与时间的乘积。
具体来说,功W=m×v×t,功率P=W/t,其中m 是物体的质量,v是物体的速度,t是物体的时间。
这两个公式在物理学中应用广泛,可以用来计算物体的功率、速度、加速度等。
5. 力和速度公式力和速度公式是指一个物体受到的力等于其质量与加速度的乘积,而速度等于物体所受的加速度与时间的乘积。
具体来说,F=m×a,v=at,其中m是物体的质量,a是物体的加速度,t是物体的时间。
这两个公式在物理学中应用广泛,可以用来计算物体受到的力、速度等。
装订线
北京师范大学2007 ~2008 学年第二学期期末考试试卷(A卷)
课程名称计算物理基础任课教师姓名:彭芳麟
卷面总分: 100 分考试时长: 100 分钟考试类别:闭卷□√开卷□其他□院(系):物理专业:物理年级: 06
姓名:学号:
阅卷教师(签字):
一.选择题(10分) (对下面语句加以判断)
1. W = [ ]; ( 对)
2. a=5, A=7, Aa=9; ( 对)
3. x=0:0.1:6; A=[x; 4*x]; B=sin(A); plot(x,B) ( 对)
4. u = 1E-4 ( 对 )
5. syms x, y, z, a, b ( 错 )
二.填空题(10分)
列举冒号:的各种功能.
表示取从x到y的数值,如
x = 1:5; % x = 1 2 3 4 5
还可以设置步进
x = 1:2:10; % x = 1 3 5 7 9
表示取全部行/列及其它维数
A为矩阵,
则B=A(:,2:3)表示截取A矩阵中“所有行”的“2~3”列的元素,并组成数组B。
2.程序中将长的语句分行书写时应该在分行处加上的符号是:。
3.在语句后面加上分号;的作用是:结束语句
4.方括号[ ]的功能有:矩阵运算
5.花括号{ }功能:用于单元阵列的赋值、定义字符串数组、引用结构数组元素
三.说明下列指令的用法与功能(10分)
1.pause :停顿:例如:pause (0.5);
2.sphere 画三维球体:例如sphere(0.5);
3.polar 极坐标画图:th=0:0.01:pi; polar (th,sin(th*pi).*cos(th))
4.demo 查看示例
5.format 改变显示方式
四.简答题(20分)
1. 叙述调试程序的方法
对于很简单的程序,直接运行皆可,MATLAB 会自动检测有错误的语句。
对于和复杂的程序,可以逐句运行,看看每句执行的情况,如果有错,随时修正。
更复杂的程序,可以分块设置间断点,然后分块调试,调试一部分程序在调试下一部分程序。
2.实时动画有两种,简单叙述它们的画法.
MATLAB 用图像句柄来控制图形对象。
通过查看图形句柄的所包含的图形属性,并通过改变其中的函数值及线形来改变图形。
五.程序题(20分)
1. 已知 24210.2;( 1.6 1.6)2y x x x +-=-≤≤,这是一个隐函数,
a) 用隐函数作图指令可以直接画它图形,请写出相应的语句。
ezplot('y^2+0.5*x^4-x^2=0.2',[-1.6,1.6])
b) 如果不用这种指令作图,则很烦琐,为了对比,请再编一个程序画图,不得用隐函数作图的指令。
y=solve('y^2+0.5*x^4-x^2-0.2','y');
解出y 关于x 的函数在用x=-1.6:0.1:1.6;
在求出y ;plot (x ,y );
2. 高斯—勒让德积分公式是
11
1()()N n n n f x dx w f x =-=∑⎰,取N=3, 1321321/20.774597;00.555556;0.88888935()2
2x x x w w w f x x =-=====⎛⎫=+ ⎪⎝⎭ 编出计算程序,要求不得用for 循环语句 。
f=@(x)(1.5*x+2.5).^0.5;
w1=0.555556;w3=w1;w2=0.888889;
x1=0.774597;x3=-x1;
x2=0;
W=f(x1)*w1;
W=W+f(x2)*w2;
W=W+f(x3)*w3;
disp(W);
六.问答题 (20分)
1.本学期学过的内容从知识结构上可以分为几个部分?
大括号用于单元阵列的赋值
中括号用于形成一个向量或矩阵
小括号通常用于一般的算术表达式,指示优先运算,还用于表示函数变量、向量下标和矩阵下标等到
2.你觉得需要增加什么内容或者删除什么内容?
3.那些内容你在本科学习中可以用到或者将会用到?
4.那些内容对你比较难学,你认为可以如何改进?。