考研数学 D讲义8考研基础班

2012年考研数学基础班讲义（高等数学）第一章 函数 极限 连续一、函数1 函数的概念：2 函数的性态：单调性 奇偶性 周期性 有界性 有界性 ：定义：;)(,,0M x f I x M ≤∈∀>∃ 3 复合函数与反函数 (函数的复合,求反函数) 4 基本的初等函数与初等函数 1）基本初等函数:将幂函数 ,指数,对数,三角,反三角统称为基本初等函数。

了解它们定义域,性质,图形. 2）初等函数：由基本初等函数经过有限次的加、减、乘、除和复合所得到且能用一个解析式表示的函数. 常考题型：1。

函数有界性、单调性、周期性及奇偶性的判定； 2。

复合函数；例1 是)(e |sin |)(cos +∞<<−∞=x x x x f x （A）有界函数. （B）单调函数. （C）周期函数 （D）偶函数. 例2 已知[],1)(,sin )(2x x f x x f −==ϕ则______)(=x ϕ的定义域为._______解：； )1arcsin(2x −].2,2[−例3 设则⎩⎨⎧≥−<=⎩⎨⎧>+≤−=0,,0,)(,0,2,0,2)(2x x x x x f x x x x x g [].________)(=x f g解=)]([x f g ⎩⎨⎧≥+<+.0,2,0,22x x x x 二、极限 1 极限概念1) 数列极限: A a n n =∞→lim ：0 ,0>∃>∀N ε,当时，恒有N n >ε<−||A a n .2）函数极限: ： A x f x =∞→)(lim 0 ,0>∃>∀X ε,当时，恒有X x >||ε<−|)(|A x f .类似的定义 A x f x =+∞→)(lim ，A x f x =−∞→)(lim 。

A x f x =∞→)(lim ⇔ =+∞→)(lim x f x A x f x =−∞→)(limA x f x x =→)(lim 0：0 ,0>∃>∀δε,当δ<−<||00x x 时，恒有ε<−|)(|A x f 。

一元函数积分学 考纲要求：（1）理解原函数的概念，理解不定积分和定积分的概念（2）掌握不定积分的基本公式，掌握不定积分和定积分的性质及定积分中值定 理，掌握换元积分法与分部积分法（3）会求有理函数 三角函数有理式和简单的无理函数的积分（数一数二要求 数三参考）（4）理解积分上限函数，会求它的导数，掌握牛顿-莱布尼茨公式 （5）了解反函数的概念，会计算反常积分（6）掌握用定积分表达和计算一些几何量和物理量（平面图形的面积，平面曲 线的弧长， 旋转体的体积及侧面积，平行截面面积为已知的立体体积，功， 引力，压力，质心，形心等）及函数的平均值（数一，数二），会利用定积 分计算平面图形的面积，旋转体的体积和函数的平均值。

会利用定积分求 解简单的经济应用问题。

（数三）知识结构框架：⎪⎪⎩⎪⎪⎨⎧反常积分变限积分定积分原函数与不定积分概念⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧华里士公式周期性化简计算几何意义计算；分部积分积分表：凑；第二换元定积分的计算简单无理式积分数有理式积分有理函数积分；三角函部积分法第二类换元积分法；分基本积分表：凑微分法不定积分的计算计算⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧经济应用（数三）物理应用（数一数二）二）弧长，侧面积（数一数体体积平面图形的面积和旋转几何应用应用一元函数积分学的概念1.原函数：如果在区间I 上，可导函数函数为的)(导x F ()x f ，即I x ∈∀，都有)()(x f x F ='成立，则称)(x F 是)(x f 在区间I 上的一个 原函数.注：原函数必须指明是函数在哪个区间上的原函数。

定理：若()()()必有无穷多个原函数则上有一个原函数x f x F x f ,在区间 定理：()()的全体原函数函数族包括了x f C x F +对任意常数C，形如 2.不定积分：函数)(x f 在区间I 上的所有原函数称为)(x f 的不定积分，记为⎰dx x f )(，即C x F dx x f +=⎰)()(.例1：设函数()x f 在()∞+∞，-上连续，则()=⎰dx x f d ()()x f A :()dx x f B ）（ ()()C x f C + ()()dx x f D '答案：B例2：若()()有一个原函数是（）则的导函数是x f x x f ,sec 2 ()x A cos ln 1- ()x B sin ln 1- ()x C sin 1+ ()x D cos 1-答案：A2：定积分定义：设函数()x f 在区间[]b a ,上有界，将[]b a ,任意分成n 个子区间[]i i x x ,1-， 分点为11210,---=∆=<<<=i i i n n x x x b x x x x x a 为该小区间的长度， 在每个小区间[]i i x x ,1-上任意取一点i ξ，对()()()i ni i i i x f n i x f ∆=∆∑=13,2,1ξξ求和 ，记{}i ni x ∆=≤≤1max λ，若对[]b a ,的 任意分法，()i ni i x f ∆∑=→1lim ξλ极限存在，则称此极限为()x f 在区间[]b a ,上的定积分，记为()dx x f b a⎰，即定积分()()i ni i bax f dx x f ∆=∑⎰=→1lim ξλ可积的条件：例3 ⎪⎭⎫ ⎝⎛+++++++++∞→n n n n n n n n n 2224211lim答案：dx x x⎰++10211例4：∑∑==∞→ni nj n n ij 114lim答案：41例5：()()=++∑∑==∞→ni nj n j n i n n1122lim答案：()()dy y dx x ⎰⎰++102101111定积分的几何意义若0)(≥x f ，则dx x f ba ⎰)(表示以曲线)(x f y =、两直线b x a x ==,与x 轴所围成的曲边梯形的面积. 若0)(≤x f ，则dx x f ba ⎰)(表示以曲线)(x f y =、两直线b x a x ==,与x 所围成的曲边梯形的面积的负值 若)(x f 在[]b a ,上有正有负，则dx x f ba ⎰)(表示曲边梯形的面积的代数和，在0)(≥x f 部分，取“+”，在0)(≤x f 部分，取“-”定积分的性质：当()()()0.==-=<⎰⎰⎰bababadx x f b a dx x f dx x f a b 时，特别的，时，约定（1）⎰-=baa b dx 1（2）[]⎰⎰⎰±=±b ab abadx x g k dx x f k dx x g k x f k )()()()(2121（3）⎰⎰⎰∀+=b aabc dx x f dx x f dx x f c c,)()()(（4）在[]b a ,上，)()(x g x f ≤，则⎰⎰≤b abadx x g dx x f )()(特别地⎰⎰≤babadx x f dx x f )()(（5）Mm ,是)(x f 在[]b a ,上的最小值与最大值，则⎰-≤≤-b aa b M dx x f a b m )()()(（6）积分中值定理：设函数()x f 在区间[]b a ,上连续，则存在[]b a ,∈ξ，使得()()()a b f dx x f ba -=⎰ξ3：变限积分：设函数()x f 在区间[]b a ,上连续，并且设x 为[]b a ,上的一点，考察()x f 在部分区间[]x a ,上的定积分()dx x f xa ⎰首先，由于()x f 在区间[]x a ,上仍旧连续，因此这个定积分存在。

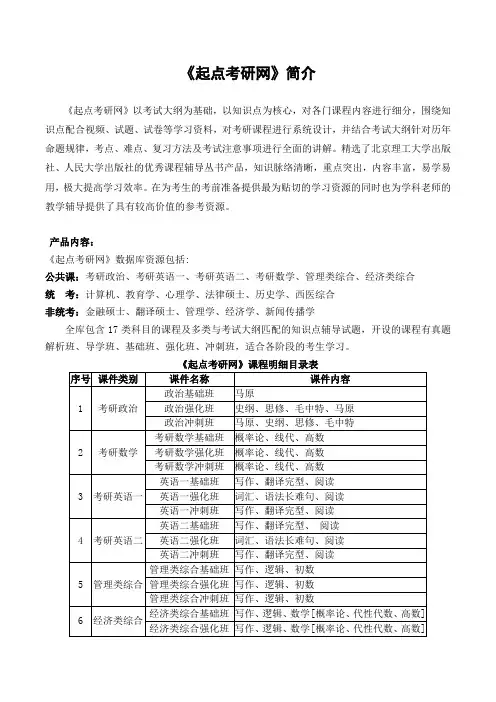
《起点考研网》简介
《起点考研网》以考试大纲为基础，以知识点为核心，对各门课程内容进行细分，围绕知识点配合视频、试题、试卷等学习资料，对考研课程进行系统设计，并结合考试大纲针对历年命题规律，考点、难点、复习方法及考试注意事项进行全面的讲解。

精选了北京理工大学出版社、人民大学出版社的优秀课程辅导丛书产品，知识脉络清晰，重点突出，内容丰富，易学易用，极大提高学习效率。

在为考生的考前准备提供最为贴切的学习资源的同时也为学科老师的教学辅导提供了具有较高价值的参考资源。

产品内容：
《起点考研网》数据库资源包括:
公共课：考研政治、考研英语一、考研英语二、考研数学、管理类综合、经济类综合
统考：计算机、教育学、心理学、法律硕士、历史学、西医综合
非统考：金融硕士、翻译硕士、管理学、经济学、新闻传播学
全库包含17类科目的课程及多类与考试大纲匹配的知识点辅导试题，开设的课程有真题解析班、导学班、基础班、强化班、冲刺班，适合各阶段的考生学习。

产品特点：
知识碎片化：知识点，以考试大纲为基础，将各门课程按知识点划分
多方位解读：知识点、视频、试题、试卷
内容权威：优秀师资，专家讲授，精选课程
功能强大：章节练习，在线考试，在线听讲，模拟自考
操作简便：操作简便，个性化设计知名机构授权，资源体系完善
售后服务
公司建立了一整套规范的运作体系和流程，为广大用户提供故障诊断、故障排除、技术咨询等全方位的技术支持。

技术支持
公司对所售软件产品均提供24小时技术支持，常规问题电话指导和远程协助，电话指导和远程协助不能解决的，必要时48小时内到现场解决。

考研数学讲义 D9考研基础班哎呀，说起考研数学，那可真是让不少小伙伴们又爱又恨啊！今天咱们就来聊聊这个考研数学讲义 D9 考研基础班。

就拿我之前遇到的一个学生小李来说吧。

他呀，一开始对考研数学那叫一个头疼，看着那些公式定理，就像看天书似的。

后来他参加了这个 D9 考研基础班，仿佛找到了救命稻草。

在这个基础班里，讲义的编排那是相当贴心。

它不是一股脑地把所有知识点堆给你，而是循序渐进，就像爬楼梯一样，一步一步来。

比如说，在讲解函数极限这一块，先从最基本的概念入手，什么是极限，极限的定义是啥，讲得明明白白。

然后通过一些简单易懂的例子，像计算一个简单函数在某一点的极限，让你一下子就明白了其中的门道。

而且啊，这讲义里的例题可不是随便选的。

那都是老师们精心挑选出来的，具有代表性的题目。

就像有一道关于数列极限的例题，从最初的分析题目条件，到一步步的解题思路，再到最后的答案，整个过程清晰明了。

小李跟我说，他以前看到这种题就发懵，但是通过这个例题，他突然就开窍了，知道该从哪里下手了。

还有哦，这个讲义对于一些容易混淆的知识点，也做了特别的处理。

比如说，无穷小和无穷大的关系，很多同学总是搞不清楚。

讲义里就专门用一个板块，对比着讲解它们的区别和联系，还配上了生动的图表，让你一眼就能看明白。

另外，每一章后面还有配套的练习题。

这些练习题的难度也是逐步增加的，刚开始是一些基础的巩固练习，让你把刚学的知识点掌握扎实。

然后就是一些稍微有点难度的提升题，考验你对知识点的灵活运用能力。

小李一开始做这些练习题的时候，错误百出，但是他没有放弃，对照着讲义上的讲解，一道题一道题地琢磨，慢慢地，错误越来越少，解题的速度也越来越快。

再说说这讲义的排版吧，字体大小适中，行间距也很舒服，不会让你看着觉得密密麻麻，心里发慌。

重点的知识点还用不同的颜色标出来，一目了然。

总之啊，这个考研数学讲义 D9 考研基础班，真的是为考研的同学们打下了坚实的基础。

第一章 函数、极限、连续第二章§1.1 函数（甲）内容要点 一、函数的概念1.函数的定义设D 是一个非空的实数集，如果有一个对应规划f ，对每一个x D ∈，都能对应惟一的一个实数y ，则这个对应规划f 称为定义在D 上的一个函数，记以y =f (x )，称x 为函数的自变量，y 为函数的因变量或函数值，D 称为函数的定义域，并把实数集{}|(),Z y y f x x D ==∈称为函数的值域。

2.分段函数如果自变量在定义域内不同的值，函数不能用同一个表达式表示，而要用两上或两个以上的表达式来表示。

这类函数称为分段函数。

例如21<1() -115 >1x x y f x x x x x +-⎧⎪==≤≤⎨⎪⎩是一个分段函数，它有两个分段点，x ＝－1和x ＝1，它们两侧的函数表达式不同，因此讨论函数y =f (x )在分段点处的极限、连续、导数等问题时，必须分别先讨论左、右极限，左、右连续性和左、右导数。

需要强调：分段函数一般不是初等函数，不能用初等函数在定义域内皆连续这个定理。

3.隐函数形如y =f (x )有函数称为显函数，由方程F （x ，y ）=0确定的y ＝y (x )称为隐函数，有些隐函数可以化为显函数（不一定是一个单值函数），而有些隐函数则不能化为显函数。

4.反函数如果y =f (x )可以解出()x y ϕ=是一个函数（单值），则称它为f (x )的反函数，记以1()xfy -=。

有时也用1()y fx -=表示。

二、基本初等函数1.常值函数 y ＝C （常数）2.幂函数y xα=（α常数）3.指数函数xy a =（a ＞0，a ≠1常数）xy e=（e ＝2.7182…，无理数）4.对数函数 log a y x=（a ＞0，a ≠1常数）常用对数 10log lg y x x == 自然对数 log ln e y x x ==5.三角函数sin ;cos ;tan .y x y x y x ===cot ;sec ;csc .y x y x y x ===6.反三角函数 arcsin ;cos ;y x y arc x ==arctan ;cot .y x y arc x ==基本初等函数的概念、性质及其图像非常重要，影响深远。

经验贴：上岸前辈分享考研数学复习规划、名师推荐、辅导用书摘要：上岸前辈分享考研数学复习规划、名师推荐、辅导用书，我们一起来看看他的数学是如何复习？考研数学的复习，选对老师，后期跟到这位老师学至关重要！一、那我们就先来聊聊老师选谁好！1、汤家凤汤老师的基础班我觉得讲得是所有老师里最负责最踏实的！因为绝大部分老师都是一个样，收着讲，而不是全局概括，往往基础班讲高数上册的前三四章就匆匆了事，汤老师是比较务实的人，他的基础班除了比较偏的几个知识点（三重积分、第二型曲线曲面积分等），从数一到数三的内容都会讲完，你要是看完高数课本，再把老汤的基础班看完，是极好的，你定会打一个不错的基础，但是（重点）！但是如果你不听他的基础课就直接奔着强化课去听，那么就会感觉比较吃力，因为老汤的强化班是建立在基础班上的，算是对基础班的一个延伸概括，当然，他老人家讲课有两个不足之处：（1）重视题量，对概念的讲解却不是特别深入！（这点和张宇正好相反）所以他的课适合基础差的同学打基础的，通过做题来深化对知识点的认识（2）口音问题，这是老汤被黑的重要原因，老汤的江苏南京人，讲话口音有点怪怪的，普通话讲得并不是太好，但是多听几节课，这也不是什么大问题。

概括：所以考研的同学可以打基础的时候看完课本直接上手老汤的基础班！权当练习！2、张宇名师简介：张宇，江湖人称宇哥，他独树一帜，是考研老师新生派的代表人物，其微博名字也为宇哥考研，为人风趣幽默，讲课就像讲故事，听起来毫不费力，如果你对数学没兴趣，听宇哥的课会激发你对数学的热情，听宇哥的课就是一个感觉，上瘾！好听！有意思！相信绝大部分同学都听过他的sin狗（广义化）的公式，宇哥的一大能力就是他能将数学抽象问题形象化，复杂问题简单化例如，二重积分大面包切切切切切、狗减sin狗等于六分之一狗三、夹逼准则哪里跑、格林闭关七天研究出格林公式、欠阿贝尔两块钱以及普京题抓住重点、毛主席题举重若轻等等，这些本来在高数课本中枯燥繁琐的东西在张宇口中变得呼之欲出、极为生动，这都能反应宇哥的特色，我有时候时常思考一个问题，如果中国的老师，都能像宇哥这样循循善诱，讲起课来娓娓动听，那么大部分人都会爱上学习这件事情。

考研数学高分导学班讲义汤家凤课程配套讲义说明1、配套课程名称2013年考研数学高分导学（汤家凤，16课时）2、课程内容此课件为汤家凤老师主讲的2013考研数学高分导学班课程。

此课程包含线代和高数，请各位学员注意查看。

3、主讲师资汤家凤——文都独家授课师资，数学博士，教授，全国著名考研数学辅导专家，全国唯一一个能脱稿全程主讲的数学辅导老师，全国大学生数学竞赛优秀指导老师。

汤老师对数学有着极其精深的研究，方法独到。

汤老师正是凭借多年从事考研阅卷工作的经验，通过自己的归纳总结，在课堂上为学生列举大量以往考过的经典例子。

深入浅出，融会贯通，让学生真正掌握正确的解题方法。

严谨的思维、激情的课堂，轻松的学习，这是汤老师课堂的特色！主讲：高等数学、线性代数。

4、讲义20页（电子版）文都网校2011年9月15日2013考研数学高分导学班讲义线性代数部分—矩阵理论一、矩阵基本概念1、矩阵的定义—形如??mn m m n n a a a a a a a a a 212222111211，称为矩阵n m ?，记为n m ij a A ?=)(。

特殊矩阵有（1）零矩阵—所有元素皆为零的矩阵称为零矩阵。

（2）方阵—行数和列数都相等的矩阵称为方阵。

（3）单位矩阵—主对角线上元素皆为1其余元素皆为零的矩阵称为单位矩阵。

（4）对称矩阵—元素关于主对角线成轴对称的矩阵称为对称矩阵。

2、同型矩阵—行数和列数相同的矩阵称为同型矩阵。

若两个矩阵同型且对应元素相同，称两个矩阵相等。

3、矩阵运算（1）矩阵加、减法：=??????? ??=mn m m n n mn m m n n b b b b b b b b b B a a a a a a a a a A 212222111211212222111211,，则±±±±±±±±±=±mn mn m m m m n n n n b a b a ba b a b a b a b a b a b a B A221122222221211112121111。

2023考研数学武忠祥高等数学0基础讲义
对于2023年考研数学武忠祥老师的高等数学零基础讲义，这里可以为你提供一些相关信息。

武忠祥老师的高等数学零基础讲义是针对那些数学基础薄弱的考生而设计的。

这个讲义旨在帮助考生建立数学基础，理解数学概念，掌握数学方法，从而更好地应对考研数学的挑战。

讲义的内容涵盖了高等数学的主要知识点，包括极限、导数、积分、级数等。

同时，讲义还注重解题方法的讲解，帮助考生提高解题能力。

此外，这个讲义还有以下特点：
1. 结构清晰：讲义的章节安排合理，知识点层次分明，易于考生理解。

2. 解析详尽：对于每个知识点和题目，讲义都提供了详细的解析过程，帮助考生深入理解。

3. 习题丰富：讲义包含了大量的习题，供考生巩固所学知识，提高解题能力。

4. 实用性强：讲义不仅注重理论知识的讲解，还注重实际应用，帮助考生解决实际问题。

总的来说，武忠祥老师的高等数学零基础讲义对于那些希望在考研数学中取得好成绩的考生来说是一个非常实用的学习资料。

如果你需要更深入的学习高等数学，建议你可以购买正版讲义进行学习。

同时，也可以在评论区与其他考生交流学习心得，共同进步。

考研数学的命题特点1. 基础性【例一】极限定义1、lim x →∙是什么？（lim n →∞是什么？）①lim x →∙1）“x →∙”存在六种情形 （1）0x x →00,0,x x εδ∃><-< （2）0x x +→00,0,x x εδ∃><-<（3）0x x -→00,0,x x εδ∃><-<(4) x →∞0,,X x X ∃>> (5) x →+∞0,,X x X ∃>> (6) x →-∞0,,X x X ∃><-2极限趋向的“过程性”——若lim x →∙f(x)∃，则f(x)在x →∙时处处有定义（命题A ⇒B ，则B ⇒A ）故有：若f(x)在x →∙时至少一点无定义，⇒lim x →∙f(x)不存在。

（2016）求0lim x →1sin sin()1sin()x x x x⎛⎫ ⎪⎝⎭【分析】x →∙，xsin(1x)→0x ~0, sinx ~x. 狗~0，sin 狗~狗xsin(1x )→0, xsin(1x )~sin(xsin(1x))故原式=1知道为什么这么做不对吗？来看看正解吧!【正解】当x=π1k ，|k|充分大，xsin(1x )=0。

还记得极限的定义吗？0x →时可以取到0嘛？答案当然是不可以！但是却可以取到除零外任意小的点，例如取x=π1k ，此时xsin(1x )的极限=0。

所以xsin(1x)在时0x →不能叫0→，而叫做无穷小量。

故f(x)= 1sin(sin())1sin()x x x x在x=π1k 处无定义，⇒原极限不∃ ②lim n →∞n →∞只有一种情形，专指n →+∞∃N>0, n>N（注意n 是自然数，没有负的，而且都是整数，所以是离散的） 2、极限定义 ①函数极限的定义 若0lim x x →f(x)=A ⇔∀ε>0, ∃δ>0,当0<|x-x0|<δ时，|f(x)-A|<ε②数列极限的定义。

预备知识轻松学一、函数基础知识1.函数的概念设数集R D ⊂，则称映射R D f →:为定义在D 上的函数，通常简记为D x x f y ∈=),(，其中x 称为自变量，y 称为因变量，D 称为定义域，{}D x x f y y D f ∈==),(|)(称为值域，f 称为对应法则。

2.函数的性质（1）单调性任取21x x <，有)()(21x f x f <，则函数)(x f 单调递增；任取21x x <，有)()(21x f x f >，则函数)(x f 单调递减。

（2）周期性若)()(x f T x f =+，则()f x 是以T 为周期的周期函数。

（3）奇偶性设函数()f x 的定义域D 关于原点对称.如果对其定义域D 内的任意一点x ，都有()()f x f x -=（或()()f x f x -=-），则称()f x 是一个偶函数（或奇函数）。

（4）有界性若M x f ≤)(，则函数有上界；若m x f ≥)(，则函数有下界；若0>M，对于I x ∈∀，有⇒≤M x f )(函数有界。

3.复合函数和反函数（1）复合函数设函数)(u f y =的定义域为f D ，函数)(x g u =的定义域为g D ，且其值域f g D D g ⊂)(，则由下式确定的函数[]g D x x g f y ∈=,)(称由函数)(x g u =与函数)(u f y =构成的复合函数，它的定义域为g D ，变量u 称为中间变量。

（2）反函数设函数)(:D f D f →是单射，则它存在逆映射D D f f →-)(:1，称此映射1-f 为函数f 的反函数，即：对每个)(D f y ∈，有唯一的D x ∈，使得y x f =)(，于是有)(1y f x -=.由于习惯上自变量用x 表示，因变量用y 表示，所以D x x f y ∈=),(的反函数也常记为)(),(1D f x x f y ∈=-.二、常用函数1．基本初等函数幂函数，指数函数，对数函数，三角函数与反三角函数称为基本初等函数.以下为几个常见的基本初等函数的图像及性质：名称及表达式定义域图形（举例）特性幂函数y x α=随α而不同，但在(0,)+∞中都有意义经过点(1,1)；在第一象限内当0>α时，为增函数；当0<α时，为减函数指数函数xy a =(0,1)a a >≠(,)-∞+∞图象在x 轴上方，过点(0,1)．当01a <<时，为减函数；当1a >时，为增函数对数函数log a y x=(0,1)a a >≠(0,)+∞图像在y 轴的右侧；过点(1,0)；当01a <<时，为减函数；当1a >时为增函数三角函数正弦函数sin y x=(,)-∞+∞以2π为周期；奇函数，图形关于原点对称；在两直线1y =与1y =-之间，即1sin 1x -≤≤余弦函数cos y x=(,)-∞+∞以2π为周期；偶函数，图形关于y 轴对称；在两直线1y =与1y =-之间，即1cos 1x -≤≤正切函数tan y x=(21)2x k π≠+(0,1,2,)k =±±⋅⋅⋅以π为周期；奇函数；在区间,22ππ⎡⎤-⎢⎥⎣⎦上是增函数；值域为R反三角函数反正弦函数arcsin y x=[1,1]-单调增加；奇函数；值域：,22ππ⎡⎤-⎢⎥⎣⎦反余弦函数arccos y x=[1,1]-单调减少；值域：[0,]π反正切函数arctan y x=(,)-∞+∞单调增加；奇函数；值域：,22ππ⎛⎫-⎪⎝⎭2．初等函数由常数和基本初等函数经过有限次的四则运算以及有限次的复合步骤所构成并可用一个式子表示的函数，称为初等函数.3．分段函数12(),()(),g x x I f x h x x I ∈⎧=⎨∈⎩；(1)符号函数：1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩；(2)绝对值函数：(),()0()(),()0f x f x f x f x f x ≥⎧=⎨-<⎩；(3)取整函数：[()]f x ：不超过()f x 的最大整数值；(4)最值函数：{}(),()()max (),()(),()()f x f x g x f x g x g x f x g x ≥⎧=⎨<⎩；{}(),()()min (),()(),()()g x f x g x f x g x f x f x g x ≥⎧=⎨<⎩.三、常用公式1．代数（1）幂函数公式1(0)aa x x x-=≠，a b a bx x x +⋅=，()a k ak x x =，a b a b x x =.（2）对数公式ln ln ln (0),(0)x x v v u e e x x u e u ==>=>ln ln ln()a b ab +=，ln ln lnaa b b-=,ln ln k a k a =，其中0,0a b >>.（3）一元二次方程（2(0)y ax bx c a =++≠）图像：若0a >，开口向上；若0a <，开口向下；对称轴为2bx a-=。

2024考研数学李林高等数学辅导讲义解析一、概述2024年考研数学高等数学一直是考研学子备战考试的焦点。

为帮助考生更好地掌握数学知识，提高解题能力，李林老师精心编写了高等数学辅导讲义。

本文将对李林老师的辅导讲义进行解析，帮助考生更好地理解和应用这些知识。

二、讲义内容概述李林老师的高等数学辅导讲义分为多个章节，涵盖了高等数学的各个知识点，包括微积分、多元函数、级数、常微分方程等内容。

讲义内容扎实，逻辑严谨，既包括基础知识的讲解，也包括典型例题的分析和解答，适合考生系统复习和巩固知识点。

三、微积分部分1.极限与连续讲义对极限与连续的概念进行了详细介绍，从基本概念到极限存在的条件，再到连续性的定义和性质，帮助考生理解和掌握这一重要知识点。

讲义中还包括了大量例题分析，帮助考生加深对极限与连续的理解，提高解题能力。

2.微分与微分中值定理针对微分的定义和微分中值定理等内容，讲义中提供了详细的公式推导和典型例题讲解，帮助考生掌握微分的概念和性质，熟练运用微分中值定理解决实际问题。

3.不定积分与定积分在不定积分与定积分部分，讲义重点讲解了换元积分法、分部积分法等解题技巧，并结合典型例题进行深入分析，帮助考生掌握积分的计算方法和技巧，提高解题效率。

四、多元函数部分1.多元函数的概念与性质讲义对多元函数的概念、多元函数的极限、连续性、偏导数等内容进行了系统介绍，并结合实际问题进行讲解，帮助考生理解多元函数的重要性及其在实际问题中的应用。

2.方向导数与梯度在方向导数与梯度的部分，讲义对方向导数的定义、计算方法和梯度的概念进行了详细讲解，并提供了大量例题进行分析，帮助考生掌握这一知识点的计算方法和应用技巧。

五、级数部分1.数项级数的收敛性与敛散性讲义对数项级数的收敛性与敛散性进行了全面介绍，包括正项级数的收敛判别法、一般项级数的审敛法等内容，帮助考生系统掌握级数收敛性的判别方法，提高解题能力。

2.幂级数与傅立叶级数在幂级数与傅立叶级数部分，讲义介绍了幂级数的收敛半径、函数展开成幂级数的方法，以及傅立叶级数的基本概念和性质，帮助考生理解级数在实际问题中的应用。

考研数学高等数学基础讲义目录第一讲极限 (1)第二讲高等数学的基本概念串讲 (9)第三讲高等数学的基本计算串讲 (13)第四讲高等数学的基本定理串讲 (24)第五讲微分方程 (27)第六讲多元函数微积分初步 (29)1 第一讲 极限核心考点概述1.极限的定义2.极限的性质3.极限的计算4.连续与间断内容展开 一、极限的定义1. lim 是什么？ lim 是什么？x →∙n →∞（1）lim 的情况：x →∙①“ x → ∙ ”代表六种情形： x → x , x → x +, x → x -, x → ∞, x → +∞, x → -∞②函数极限运算的过程性——必须保证在作极限运算的过程中函数处处有定义，否则极限过程便无从谈起，于是极限就不会存在了。

比如下面这个例子：sinx sin 1 x【例】计算lim x →0. x sin 1x事实上，在 x = 0 点的任一小的去心邻域内，总有点 x = → 0（| k | 为充分大的正整数），k πsin x s in 1 sin x s in 1 x x 使 在该点没有定义，故lim不存在. x sin 1 x x →0x sin 1x（2）lim 是什么？n →∞2.极限的定义（1）函数极限的定义：lim f (x ) = A ⇔ ∀ε > 0, ∃δ > 0, 当0 < x →x 0x - x 0< δ 时，恒有f (x ) - A < ε1n n12注：趋向方式六种（2）数列极限定义：lim x = a ⇔ ∀ε > 0, ∃N > 0, 当n > N 时，恒有 x - a < ε n →∞注：趋向方式只有一种【例】以下三个说法，（1）“ ∀ε > 0 ，∃X > 0 ，当 x > X 时，恒有件；εf (x ) - A < e 10”是“ lim x →+∞f (x ) = A ”的充要条（ 2 ）“ ∀ 正整数 N ， ∃ 正整数 K ，当 0 <“ lim f (x ) = A ”的充要条件；x →x 0x - x 0 ≤ K时，恒有 f (x ) - A ≤ 1 ” 是 2N（3）“ ∀ε ∈ (0,1) ， ∃ 正整数 N ，当n ≥ N 时，恒有| x n - a |≤ 2ε ”是“数列{x n } 收敛于a ” 的充要条件；正确的个数为（）（A ）0 （B ）1（C ）2（D ）3二、极限的性质1.唯一性（1） lim e x= ∞, lim e x= 0 ，（2）limsin x 不存在（3）lim arctan x 不存在（4）lim [x ]x →+∞x →-∞x →0xx →∞x →0不存在1- π e x 1【例】设k 为常数，且 I = lim x →0+k ⋅ arctan 存在，求 k 的值，并计算极限 I 。