动力学的两大基本问题

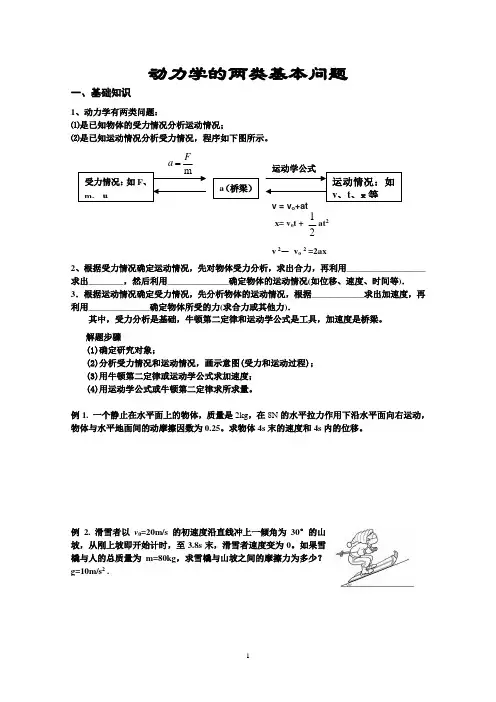
动力学的两类基本问题一、基础知识1、动力学有两类问题：⑴是已知物体的受力情况分析运动情况；⑵是已知运动情况分析受力情况，程序如下图所示。

2、根据受力情况确定运动情况，先对物体受力分析，求出合力，再利用__________________求出________，然后利用______________确定物体的运动情况(如位移、速度、时间等)．3．根据运动情况确定受力情况，先分析物体的运动情况，根据____________求出加速度，再利用______________确定物体所受的力(求合力或其他力)．其中，受力分析是基础，牛顿第二定律和运动学公式是工具，加速度是桥梁。

解题步骤(1)确定研究对象；(2)分析受力情况和运动情况，画示意图(受力和运动过程)；(3)用牛顿第二定律或运动学公式求加速度；(4)用运动学公式或牛顿第二定律求所求量。

例1. 一个静止在水平面上的物体，质量是2kg ，在8N 的水平拉力作用下沿水平面向右运动，物体与水平地面间的动摩擦因数为0.25。

求物体4s 末的速度和4s 内的位移。

例2. 滑雪者以v 0=20m/s 的初速度沿直线冲上一倾角为30°的山坡，从刚上坡即开始计时，至3.8s 末，滑雪者速度变为0。

如果雪橇与人的总质量为m=80kg ，求雪橇与山坡之间的摩擦力为多少？g=10m/s 2 .运动学公式 a （桥梁） 运动情况：如v 、t 、x 等 受力情况：如F 、m 、μ m F a v = v o +atx= v o t + at 2 21v 2－ v o 2 =2ax二、练习1、如图所示，木块的质量m＝2 kg，与地面间的动摩擦因数μ＝0.2，木块在拉力F＝10 N作用下，在水平地面上从静止开始向右运动，运动5.2 m后撤去外力F.已知力F与水平方向的夹角θ＝37°(sin 37°＝0.6，cos 37°＝0.8，g取10 m/s2)．求：(1)撤去外力前，木块受到的摩擦力大小；(2)刚撤去外力时，木块运动的速度；(3)撤去外力后，木块还能滑行的距离为多少？（1）2.8N（2）5.2m/s （3）6.76m2、如图所示，一个放置在水平台面上的木块，其质量为2 kg，受到一个斜向下的、与水平方向成37°角的推力F＝10 N 的作用，使木块从静止开始运动，4 s 后撤去推力，若木块与水平面间的动摩擦因数为 0.1.(取g＝10 m/s2)求：(1)撤去推力时木块的速度为多大？(2)撤去推力到停止运动过程中木块的加速度为多大？(3)木块在水平面上运动的总位移为多少？3、如图5所示，在倾角θ＝37°的足够长的固定的斜面上，有一质量为m＝1 kg的物体，物体与斜面间动摩擦因数μ＝0.2，物体受到沿平行于斜面向上的轻细绳的拉力F＝9.6 N的作用，从静止开始运动，经2 s绳子突然断了，求绳断后多长时间物体速度大小达到22 m/s？(sin 37°＝0.6，g取10 m/s2)4、如图所示，有一足够长的斜面，倾角α＝37°，一小物块从斜面顶端A处由静止下滑，到B 处后，受一与小物块重力大小相等的水平向右的恒力作用，小物块最终停在C点(C点未画出)．若AB长为2.25 m，小物块与斜面间动摩擦因数μ＝0.5，sin 37°＝0.6，cos 37°＝0.8，g ＝10 m/s2.求：(1)小物块到达B点的速度多大？(2)B、C距离多大？5、如图所示，在倾角θ=30°的固定斜面的底端有一静止的滑块，滑块可视为质点，滑块的质量m=1kg，滑块与斜面间的动摩擦因数μ＝36，斜面足够长．某时刻起，在滑块上作用一平行于斜面向上的恒力F=10N，恒力作用时间t1=3s后撤去．求：从力F开始作用时起至滑块返冋斜面底端所经历的总时间t及滑块返回底端时速度v的大小（g=10m/s2）6、(2013山东)如图所示，一质量m＝0.4 kg的小物块，以v0＝2 m/s的初速度，在与斜面成某一夹角的拉力F作用下，沿斜面向上做匀加速运动，经t＝2 s的时间物块由A点运动到B点，A、B之间的距离L＝10 m．已知斜面倾角θ＝30°，物块与斜面之间的动摩擦因数μ＝33.重力加速度g取10 m/s2.(1)求物块加速度的大小及到达B点时速度的大小；(2)拉力F与斜面夹角多大时，拉力F最小？拉力F的最小值是多少？7、如图所示，AB和CD为两条光滑斜槽，它们各自的两个端点均分别位于半径为R和r的两个相切的圆上，且斜槽都通过切点P.设有一重物先后沿两个斜槽，从静止出发，由A滑到B和由C滑到D，所用的时间分别为t1和t2，则t1与t2之比为()A．2∶1 B．1∶1 C.∶1 D．1∶8、如下图所示，光滑水平面上放置质量分别为m、2m的A、B两个物体，A、B间的最大静摩擦力为μmg，现用水平拉力F拉B，使A、B以同一加速度运动，则拉力F的最大值为( )A．μmg B．2μmg C．3μmg D．4μmg9、物体A放在物体B上，物体B放在光滑的水平面上，已知m A=6kg，m B=2kg，A、B间动摩擦因数μ=0.2，如图所示．现用一水平向右的拉力F作用于物体A上，则下列说法中正确的是（g=10m/s2）（）A．当拉力F＜12N时，A相对B静止不动B．当拉力F＞12N时，A一定相对B滑动C．无论拉力F多大，A相对B始终静止D．当拉力F=24N时，A对B的摩擦力等于6N10、物体A的质量m1＝1kg，静止在光滑水平面上的木板B的质量为m2＝0.5kg、长L＝1m，某时刻A以v0＝4m/s的初速度滑上木板B的上表面，为使A不致于从B上滑落，在A滑上B的同时，给B施加一个水平向右的拉力F，若A与B之间的动摩擦因数μ＝0.2，试求拉力F大小应满足的条件。

动力学的两类基本问题、连接体模型特训目标特训内容目标1已知受力情况求运动情况(1T-4T)目标2已知运动情况求受力情况(5T-8T)目标3加速度相同的连接体问题(9T-12T)目标4加速度不同的连接体问题(13T-16T)【特训典例】一、已知受力情况求运动情况1图为鲁能巴蜀中学“水火箭”比赛现场，假设水火箭从地面以初速度10m/s竖直向上飞出，在空中只受重力与空气阻力，水火箭质量为1kg，空气阻力方向始终与运动方向相反，大小恒为2.5N，g取10m/s2，则下列说法正确的是()A.水火箭运动过程中，经过同一高度时(除最高点外)，上升时的速率大于其下落时的速率B.水火箭所能上升的最大高度为2003mC.水火箭从离开地面到再次回到地面的总时间为1.6sD.当水火箭竖直向下运动且位于地面上方1m时，速度大小为35m/s【答案】AD【详解】A．由于空气阻力，运动过程中一直做负功，使得物体机械能减小，则同一高度处下落时动能较小，故速度较小，故A正确；B．水火箭向上运动时，空气阻力向下，加速度a1=g+fm=12.5m/s2则上升的最大高度为h m=v202a1=4m故B错误；C．从地面到最高点时间为t=v0a1=0.8s水火箭下落时空气阻力向上，加速度a2=g-fm=7.5m/s2所以下落时间大于上升时间，运动总时间大于1.6s，故C错误；D．水火箭位于地面上方1m，即下落h=3m故v=2a2h=35m/s故D正确。

故选AD。

2如图，水平直杆AB与光滑圆弧杆BC在B点平滑连接，固定在竖直平面内，一直径略大于杆的圆环穿在水平直杆上的A点。

现让圆环以v0=4m/s的初速度由A向B运动，同时在竖直面内对圆环施加一垂直于杆向上的恒力F，运动到B点时撤去恒力F，之后圆环沿圆弧杆BC上滑。

已知AB长度L=6m，BC 半径R=64m，圆环质量m=0.2kg，圆环与直杆AB间动摩擦因数μ=0.2，恒力F=3N，重力加速度g= 10m/s2，π2≈10，下列说法正确的是()A.圆环到达B点时的速度为2m/sB.圆环能够到达的最大高度为0.2mC.圆环在BC上运动的时间约为8sD.圆环能返回A点【答案】ABC【详解】A．直杆对圆环的弹力大小为N=F-mg=1N方向竖直向下，对圆环分析有μN=ma解得a=1m/s2根据速度与位移关系有v2-v20=-2aL解得v=2m/s，A正确；mv2解得h=0.2m，B正确；B．圆环能够到达的最大高度的过程有mgh=12C．根据上述可知h=0.2m≪R=64m则圆环在圆弧上的运动可以等效为单摆，则T=2πR g圆环在BC上运动的时间约为t=1T解得t=8s，C正确；2D．圆环返回B点至停止过程有-μmgx=0-1mv2解得x=1m<L=6m可知，圆环不能返回A点，D2错误。

牛顿运动定律的应用—动力学两类基本问题1.动力学两类基本问题是指已知物体的受力情况求其运动情况和已知物体的运动情况求其受力情况，解决这两类基本问题的思路方法示意图如下：其中受力分析是基础，牛顿第二定律和运动学公式是工具，加速度是连接力和运动的桥梁．2.解题关键(1)两类分析——物体的受力分析和物体的运动过程分析；(2)两个桥梁——加速度是联系运动和力的桥梁；速度是各物理过程间相互联系的桥梁．3.两类动力学问题的解题步骤类型1已知物体受力情况，分析物体运动情况【题型1】如图所示滑沙游戏中，做如下简化：游客从顶端A点由静止滑下8s后，操纵刹车手柄使滑沙车匀速下滑至底端B点，在水平滑道上继续滑行直至停止.已知游客和滑沙车的总质量m＝70kg，倾斜滑道AB长l AB＝128m，倾角θ＝37°，滑沙车底部与沙面间的动摩擦因数μ＝0.5.滑沙车经过B点前后的速度大小不变，重力加速度g取10m/s2，sin37°＝0.6，cos37°＝0.8，不计空气阻力.(1)求游客匀速下滑时的速度大小；(2)求游客匀速下滑的时间；(3)若游客在水平滑道BC段的最大滑行距离为16m，则他在此处滑行时，需对滑沙车施加多大的水平制动力？【题型2】如图所示为四旋翼无人机，它是一种能够垂直起降的小型遥控飞行器，目前正得到越来越广泛的应用．一架质量为m＝2 kg的无人机，其动力系统所能提供的最大升力F＝36 N，运动过程中所受空气阻力大小恒定，无人机在地面上从静止开始，以最大升力竖直向上起飞，在t＝5 s时离地面的高度为75 m(g取10 m/s2)．(1)求运动过程中所受空气阻力大小；(2)假设由于动力系统故障，悬停的无人机突然失去升力而坠落．无人机坠落地面时的速度为40 m/s，求无人机悬停时距地面高度；(3)假设在第(2)问中的无人机坠落过程中，在遥控设备的干预下，动力系统重新启动提供向上最大升力．为保证安全着地，求无人机从开始下落到恢复升力的最长时间．类型2已知物体运动情况，分析物体受力情况【题型3】如图甲所示，一质量m＝0.4 kg的小物块，以v0＝2 m/s的初速度，在与斜面平行的拉力F作用下，沿斜面向上做匀加速运动，经t＝2 s的时间物块由A点运动到B点，A、B之间的距离L＝10 m．已知斜面倾角θ＝30°，物块与斜面之间的动摩擦因数μ＝33.重力加速度g取10 m/s2.求：(1)物块到达B点时速度和加速度的大小；(2)拉力F的大小；(3)若拉力F与斜面夹角为α，如图乙所示，试写出拉力F的表达式(用题目所给物理量的字母表示)．【题型4】如图甲所示，质量m＝1kg的物块在平行斜面向上的拉力F作用下从静止开始沿斜面向上运动，t＝0.5s时撤去拉力，利用速度传感器得到其速度随时间的变化关系图象(v －t图象)如图乙所示，g取10m/s2，求：(1)2s内物块的位移大小x和通过的路程L；(2)沿斜面向上运动的两个阶段加速度大小a1、a2和拉力大小F.针对训练1.如图所示，某次滑雪训练，运动员站在水平雪道上第一次利用滑雪杖对雪面的作用获得水平推力F ＝100 N 而由静止向前滑行，其作用时间为t 1＝10 s ，撤除水平推力F 后经过t 2＝15 s ，他第二次利用滑雪杖对雪面的作用获得同样的水平推力，第二次利用滑雪杖对雪面的作用距离与第一次相同．已知该运动员连同装备的总质量为m ＝75 kg ，在整个运动过程中受到的滑动摩擦力大小恒为f ＝25 N ，求：(1)第一次利用滑雪杖对雪面作用获得的速度大小及这段时间内的位移大小；(2)该运动员(可视为质点)第二次撤除水平推力后滑行的最大距离．2.如图所示，质量M ＝10 kg 的木楔ABC 静置于粗糙水平地面上，木楔与地面间的动摩擦因数μ＝0.2.在木楔的倾角θ为37°的斜面上，有一质量m ＝1.0 kg 的物块由静止开始从A 点沿斜面下滑，当它在斜面上滑行距离s ＝1 m 时，其速度v ＝2 m/s ，在这过程中木楔没有动．(sin 37°＝0.6，cos 37°＝0.8，重力加速度g ＝10 m/s 2)求：(1)物块与木楔间的动摩擦因数μ1；(2)地面对木楔的摩擦力的大小和方向；(3)在物块沿斜面下滑时，如果对物块施加一平行于斜面向下的推力F ＝5 N ，则地面对木楔的摩擦力如何变化？(不要求写出分析、计算的过程)3.在水平地面上有一质量为10 kg 的物体，在水平拉力F 的作用下由静止开始运动，10 s 后拉力大小减为F 4，方向不变，再经过20 s 停止运动．该物体的速度与时间的关系如图所示(g ＝10 m/s 2)．求：(1)整个过程中物体的位移大小；(2)物体与地面的动摩擦因数．4.如图甲所示，光滑平台右侧与一长为L ＝2.5 m 的水平木板相接，木板固定在地面上，现有一小滑块以初速度v 0＝5 m/s 滑上木板，恰好滑到木板右端静止。

动力学两类基本问题的分析上海师范大学附属中学 李树祥一、根据运动情况确定物体的受力1、解题步骤：（1）确定研究对象，并将研究对象从周围环境中隔离出来。

分析研究对象的受力，并画出受力图（注意：研究对象有时也可以选几个物体组成的整体，但上海市高中物理学科教学基本要求中，对用牛顿第二定律的计算，仅限于受到恒力作用的单个物体，且质量不变）。

（2）受力较为复杂时，要建立坐标系。

物体做变速直线运动时：建立的坐标系以保证列式、计算方便。

一般以运动方向为一个坐标轴，以垂直运动方向为另一个轴。

物体做曲线运动时：一般沿半径和切线方向建立坐标系。

（3）考察物体的运动情况。

若题中没有明确给出加速度，则要根据运动学公式求出加速度（如是匀变速直线运动，则要使用匀变速公式；如是匀速圆周运动，则要利用向心加速度公式求加速度）。

（4）列牛顿第二定律方程，求出某个力。

2、运用牛顿定律解题的常规做法：⑴物体只受一个力作用时，物体所受合外力就是此力，则此力就等于ma 。

⑵物体受两个力时，通常用作图法。

即物体受这两个力的合力必与加速度a 同方向，据此推知合力的方向，并作出力合成的平行四边形，利用三角形知识求解有关量。

⑶物体受三个力或超过三个力时，通常建立坐标系，应用正交分解法列出牛顿定律的分量表达式：∑F x =ma x∑F y =ma y应用正交分解法要注意：①坐标系的选取以计算方便为原则，一般选定加速度方向为坐标轴方向（有时也以少分解矢量为原则）。

②加速度的分解仅限于在两个正交方向上分解，不要在任意方向上分解。

③列分量表达式时，代入公式的合外力、加速度都必须是该方向上的分量，不要张冠李戴。

④运用牛顿第二定律进行计算时，各物理量单位都必须取国际制单位。

3、充分发挥数学公式的三个作用：⑴确定各个物理量之间的数值关系； ⑵确定各个物理量之间的单位关系；⑶若公式是矢量表达式，则可以确定矢量的方向。

例如，需要求某物理量的大小和方向时，可事先假定该物理量沿某方向，然后列出数学矢量式，若求出的结果。

动力学两类基本问题1．由受力情况判断物体的运动状态，处理这类问题的基本思路是：先求出几个力的合力，由牛顿第二定律(F合＝ma)求出加速度，再应用运动学公式求出速度或位移．2．由物体的运动情况判断受力情况，处理这类问题的基本思路是：已知加速度或根据运动规律求出加速度，再由牛顿第二定律求出合力，从而确定未知力，至于牛顿第二定律中合力的求法可用力的合成和分解法(平行四边形定则)或正交分解法．3．求解上述两类问题的思路，可用如图所示的框图来表示：解决两类动力学基本问题应把握的关键(1)做好两个分析——物体的受力分析和物体的运动过程分析；根据物体做各种性质运动的条件即可判定物体的运动情况、加速度变化情况及速度变化情况．(2)抓住一个“桥梁”——物体运动的加速度是联系运动和力的桥梁．【典例1】(2013·江南十校联考，22)如图3－3－2所示，倾角为30°的光滑斜面与粗糙平面的平滑连接．现将一滑块(可视为质点)从斜面上的A点由静止释放，最终停在水平面上的C点．已知A点距水平面的高度h＝0.8 m，B点距C点的距离L ＝2.0 m．(滑块经过B点时没有能量损失，g＝10 m/s2)，求：(1)滑块在运动过程中的最大速度；(2)滑块与水平面间的动摩擦因数μ；(3)滑块从A点释放后，经过时间t＝1.0 s时速度的大小．图3－3－2教你审题关键词获取信息①光滑斜面与粗糙的水平面滑块在斜面上不受摩擦力，水平面受摩擦力②从斜面上的A点由静止释放滑块的初速度v0＝0③最终停在水平面上的C点滑块的末速度为零④滑块经过B点时没有能量损失斜面上的末速度和水平面上的初速度大小相等第二步：分析理清思路→抓突破口做好两分析→受力分析、运动分析①滑块在斜面上：滑块做初速度为零的匀加速直线运动．②滑块在水平面上：滑块做匀减速运动．第三步：选择合适的方法及公式→利用正交分解法、牛顿运动定律及运动学公式列式求解．解析(1)滑块先在斜面上做匀加速运动，然后在水平面上做匀减速运动，故滑块运动到B点时速度最大为v m，设滑块在斜面上运动的加速度大小为a1，则有mg sin 30°＝ma1，v2m＝2a1hsin 30°，解得：v m＝4 m/s(2)滑块在水平面上运动的加速度大小为a2，μmg＝ma2v2m＝2a2L，解得：μ＝0.4(3)滑块在斜面上运动的时间为t1，v m＝a1t1得t1＝0.8 s由于t>t1，滑块已经经过B点，做匀减速运动的时间为t－t1＝0.2 s设t＝1.0 s时速度大小为v＝v m－a2(t－t1)解得：v＝3.2 m/s答案(1)4 m/s(2)0.4(3)3.2 m/s1．解决两类动力学基本问题应把握的关键(1)两类分析——物体的受力分析和物体的运动过程分析；(2)一个桥梁——物体运动的加速度是联系运动和力的桥梁．2．解决动力学基本问题时对力的处理方法(1)合成法：在物体受力个数较少(2个或3个)时一般采用“合成法”．(2)正交分解法：若物体的受力个数较多(3个或3个以上)，则采用“正交分解法”．3．解答动力学两类问题的基本程序(1)明确题目中给出的物理现象和物理过程的特点．(2)根据问题的要求和计算方法，确定研究对象，进行分析，并画出示意图．(3)应用牛顿运动定律和运动学公式求解．突破训练3如图5所示，在倾角θ＝37°的足够长的固定的斜面上，有一质量为m＝1 kg的物体，物体与斜面间动摩擦因数μ＝0.2，物体受到沿平行于斜面向上的轻细绳的拉力F＝9.6 N的作用，从静止开始运动，经2 s绳子突然断了，求绳断后多长时间物体速度大小达到22 m/s？(sin 37°＝0.6，g取10 m/s2)图5答案 5.53 s解析此题可以分为三个运动阶段：力F存在的阶段物体沿斜面向上加速，受力分析如图所示，由牛顿第二定律和运动学公式得：F－F f－mg sin θ＝ma1F f＝μF N＝μmg cos θv1＝a1t1解得：a1＝2 m/s2v1＝4 m/s第二阶段为从撤去力F到物体沿斜面向上的速度减为零，受力分析如图所示由牛顿第二定律和运动学公式mg sin θ＋μmg cos θ＝ma20－v1＝－a2t2解得：a2＝7.6 m/s2t2＝0.53 s第三阶段物体反向匀加速运动(因为mg sin θ>μmg cos θ)mg sin θ－μmg cos θ＝ma3v2＝a3t3解得：a3＝4.4 m/s2t3＝5 st＝t2＋t3＝5.53 s题组一动力学两类基本问题1．如图3-2-5所示，水平桌面由粗糙程度不同的AB、BC两部分组成，且AB＝BC，小物块P(可视为质点)以某一初速度从A点滑上桌面，最后恰好停在C点，已知物块经过AB与BC两部分的时间之比为1∶4，则物块P与桌面上AB、BC部分之间的动摩擦因数μ1、μ2之比为(P物块在AB、BC上所做的运动均可看作匀变速直线运动)()图3-2-5A．1∶1B．1∶4C．4∶1 D．8∶1解析：选D由牛顿第二定律可知，小物块P在AB段减速的加速度a1＝μ1g，在BC段减速的加速度a2＝μ2g，设小物块在AB段运动时间为t，则可得：v B＝μ2g·4t，v0＝μ1gt＋μ2g·4t，由x AB＝v0＋v B2·t，x BC＝v B2·4t，x AB＝x BC可求得：μ1＝8μ2，故D正确。

第三章牛顿运动定律专题强化三动力学两类基本问题和临界极值问题专题解读1.本专题是动力学方法处理动力学两类基本问题、多过程问题和临界极值问题，高考在选择题和计算题中命题频率都很高．2．学好本专题可以培养同学们的分析推理能力，应用数学知识和方法解决物理问题的能力．3．本专题用到的规律和方法有：整体法和隔离法、牛顿运动定律和运动学公式、临界条件和相关的数学知识．过好双基关————回扣基础知识训练基础题目一、动力学的两类基本问题1．由物体的受力情况求解运动情况的基本思路：先求出几个力的合力，由牛顿第二定律(F合＝ma)求出加速度，再由运动学的有关公式求出速度或位移．2．由物体的运动情况求解受力情况的基本思路：已知加速度或根据运动规律求出加速度，再由牛顿第二定律求出合力，从而确定未知力．3．应用牛顿第二定律解决动力学问题，受力分析和运动分析是关键，加速度是解决此类问题的纽带，分析流程如下：受力情况二、动力学中的临界与极值问题1．临界或极值条件的标志(1)题目中“刚好”“恰好”“正好”等关键词句，明显表明题述的过程存在着临界点．(2)题目中“取值范围”“多长时间”“多大距离”等词句，表明题述过程存在着“起止点”，而这些“起止点”一般对应着临界状态．(3)题目中“最大”“最小”“至多”“至少”等词句，表明题述的过程存在着极值，这个极值点往往是临界点．2．常见临界问题的条件(1)接触与脱离的临界条件：两物体相接触或脱离，临界条件是弹力F N＝0.(2)相对滑动的临界条件：静摩擦力达到最大值．(3)绳子断裂与松弛的临界条件：绳子断裂的临界条件是绳中张力等于它所能承受的最大张力；绳子松弛的临界条件是F T＝0.(4)最终速度(收尾速度)的临界条件：物体所受合外力为零．研透命题点————细研考纲和真题分析突破命题点1．解题关键(1)两类分析——物体的受力分析和物体的运动过程分析；(2)两个桥梁——加速度是联系运动和力的桥梁；速度是各物理过程间相互联系的桥梁．2．常用方法(1)合成法(2)正交分解法◆类型1已知物体受力情况，分析物体运动情况【例1】(2021·河北卷)如图，一滑雪道由AB 和BC 两段滑道组成，其中AB 段倾角为θ，BC 段水平，AB 段和BC 段由一小段光滑圆弧连接，一个质量为2kg 的背包在滑道顶端A 处由静止滑下，若1s 后质量为48kg 的滑雪者从顶端以1.5m/s 的初速度、3m/s 2的加速度匀加速追赶，恰好在坡底光滑圆弧的水平处追上背包并立即将其拎起，背包与滑道的动摩擦因数为μ＝112，重力加速度取g ＝10m/s 2，sin θ＝725，cos θ＝2425，忽略空气阻力及拎包过程中滑雪者与背包的重心变化，求：(1)滑道AB段的长度；(2)滑雪者拎起背包时这一瞬间的速度．答案(1)9m(2)7.44m/s解析(1)A→B过程对背包(m1)：受力分析，由牛顿第二定律得m1g sinθ－μm1g cosθ＝m1a1解得a1＝2m/s2①由运动分析得：l＝1a1t2②，v1＝a1t③2对滑雪者(m2)：由运动分析得l＝v0(t－t0)＋1a2(t－t0)2④2v2＝v0＋a2(t－t0)，其中t0＝1s⑤联立①②③④⑤得t＝3s，v1＝6m/s，v2＝7.5m/s，l＝9m(2)滑雪者拎起背包过程水平方向动量守恒，有m1v1＋m2v2＝(m1＋m2)v解得v＝7.44m/s滑雪者拎起背包时的速度为7.44m/s【变式1】(多选)如图甲所示，质量为m的小球(可视为质点)放在光滑水平面上，在竖直线MN的左侧受到水平恒力F1作用，在MN的右侧除受F1外还受到与F1在同一直线上的水平恒力F2作用，现小球从A点由静止开始运动，小球运动的v－t图像如图乙所示，下列说法中正确的是()A．小球在MN右侧运动的时间为t1－t2B．F2的大小为m v1t1＋2mv1 t3－t1C．小球在MN右侧运动的加速度大小为2v1 t3－t1D．小球在0～t4时间内运动的最大位移为v1t2答案BC解析小球在MN右侧运动的时间为t3～t1，故A错误；小球在MN右侧的加速度大小a2＝2v1t3－t1，在MN的左侧，由牛顿第二定律可知F1＝ma1＝mv1t1，在MN的右侧，由牛顿第二定律可知F2－F1＝ma2得F2＝2mv1t3－t1＋mv1t1，故B、C正确；t2时刻后小球反向运动，所以小球在0～t4时间内运动的最大位移是v1t22，故D错误．◆类型2已知物体运动情况，分析物体受力情况【例2】如图甲所示，一质量m＝0.4kg的小物块，以v0＝2m/s的初速度，在与斜面平行的拉力F作用下，沿斜面向上做匀加速运动，经t＝2s的时间物块由A点运动到B点，A、B之间的距离L＝10m．已知斜面倾角θ＝30°，物块与斜面之间的动摩擦因数μ＝33.重力加速度g取10m/s2.求：(1)物块到达B点时速度和加速度的大小；(2)拉力F的大小；(3)若拉力F与斜面夹角为α，如图乙所示，试写出拉力F的表达式(用题目所给物理量的字母表示)．答案(1)8m/s3m/s2(2)5.2N(3)F＝mg sinθ＋μcosθ＋ma cosα＋μsinα解析(1)物块做匀加速直线运动，根据运动学公式，有L＝v0t＋12at2，v＝v0＋at，联立解得a＝3m/s2，v＝8m/s(2)对物块受力分析可得，平行斜面方向F cosα－mg sinθ－F f＝ma，垂直斜面方向F N＝mg cosθ其中F f＝μF N解得F＝mg(sinθ＋μcosθ)＋ma＝5.2N(3)拉力F与斜面夹角为α时，物块受力如图所示根据牛顿第二定律有F cosα－mg sinθ－F f＝ma F N＋F sinα－mg cosθ＝0其中F f＝μF NF＝mg sinθ＋μcosθ＋macosα＋μsinα.【变式2】如图所示，粗糙的地面上放着一个质量M＝1.5kg的斜面体，斜面部分光滑，底面与地面的动摩擦因数μ＝0.2，倾角θ＝37°，在固定在斜面的挡板上用轻质弹簧连接一质量m＝0.5kg的小球，弹簧劲度系数k＝200 N/m，现给斜面施加一水平向右的恒力F，使整体向右以a＝1m/s2的加速度匀加速运动(已知sin37°＝0.6，cos37°＝0.8，g取10m/s2)．求：(1)F的大小；(2)弹簧的形变量及斜面对小球的支持力大小．答案(1)6N(2)0.017m 3.7N解析(1)对整体应用牛顿第二定律：F－μ(M＋m)g＝(M＋m)a，解得F＝6N.(2)设弹簧的形变量为x，斜面对小球的支持力为F N对小球受力分析：在水平方向：kx cosθ－F N sinθ＝ma在竖直方向：kx sinθ＋F N cosθ＝mg解得x＝0.017m，F N＝3.7N.多过程问题分析步骤1．将“多过程”分解为许多“子过程”，各“子过程”间由“衔接点”连接．2．对各“衔接点”进行受力分析和运动分析，必要时画出受力图和过程示意图．3．根据“子过程”“衔接点”的模型特点选择合理的物理规律列方程．4．分析“衔接点”速度、加速度等的关联，确定各段间的时间关联，并列出相关的辅助方程．5．联立方程组，分析求解，对结果进行必要的验证或讨论．【例3】如图所示，两滑块A、B用细线跨过定滑轮相连，B距地面一定高度，A可在细线牵引下沿足够长的粗糙斜面向上滑动．已知m A＝2kg，m B ＝4kg，斜面倾角θ＝37°.某时刻由静止释放A，测得A沿斜面向上运动的v －t图像如图所示．已知g＝10m/s2，sin37°＝0.6，cos37°＝0.8.求：(1)A与斜面间的动摩擦因数；(2)A沿斜面向上滑动的最大位移；(3)滑动过程中细线对A拉力所做的功．答案(1)0.25(2)0.75m(3)12J解析(1)在0～0.5s内，根据图像，A、B系统的加速度为a1＝vt ＝20.5m/s2＝4m/s2对A、B系统受力分析，由牛顿第二定律有m B g－m A g sinθ－μm A g cosθ＝(m A＋m B)a1得：μ＝0.25(2)B落地后，A减速上滑．由牛顿第二定律有m A g sinθ＋μm A g cosθ＝m A a2将已知量代入，可得a2＝8m/s2故A减速向上滑动的位移为x2＝v22a2＝0.25m0～0.5s内A加速向上滑动的位移x1＝v22a1＝0.5m所以，A上滑的最大位移为x＝x1＋x2＝0.75m(3)A加速上滑过程中，由动能定理：W－m A gx1sinθ－μm A gx1cosθ＝12m A v2－0得W＝12J.【变式3】如图所示，一足够长斜面上铺有动物毛皮，毛皮表面具有一定的特殊性，物体上滑时顺着毛的生长方向，毛皮此时的阻力可以忽略；下滑时逆着毛的生长方向，会受到来自毛皮的滑动摩擦力，现有一物体自斜面底端以初速度v0＝6m/s冲上斜面，斜面的倾角θ＝37°，经过2.5s物体刚好回到出发点，(g＝10m/s2，sin37°＝0.6，cos37°＝0.8)．求：(1)物体上滑的最大位移；(2)若物体下滑时，物体与毛皮间的动摩擦因数μ为定值，试计算μ的数值．(结果保留两位有效数字)答案(1)3m(2)0.42解析(1)物体向上滑时不受摩擦力作用，设最大位移为x.由牛顿第二定律可得：mg sin37°＝ma1代入数据得：a1＝6m/s2由运动学公式有：v20＝2a1x联立解得物体上滑的最大位移为：x＝3m(2)物体沿斜面上滑的时间为：t1＝v0a1＝66s＝1s物体沿斜面下滑的时间为：t2＝t－t1＝1.5s下滑过程中，由运动学公式有：x＝12a2t22由牛顿第二定律可得：mg sin37°－μmg cos37°＝ma2联立解得：μ≈0.421．基本思路(1)认真审题，详尽分析问题中变化的过程(包括分析整体过程中有几个阶段)；(2)寻找过程中变化的物理量；(3)探索物理量的变化规律；(4)确定临界状态，分析临界条件，找出临界关系．2．思维方法极限法把物理问题(或过程)推向极端，从而使临界现象(或状态)暴露出来，以达到正确解决问题的目的假设法临界问题存在多种可能，特别是非此即彼两种可能时，或变化过程中可能出现临界条件，也可能不出现临界条件时，往往用假设法解决问题数学法将物理过程转化为数学表达式，根据数学表达式解出临界条件【例4】如图所示，一弹簧一端固定在倾角为θ＝37°的光滑固定斜面的底端，另一端拴住质量为m1＝6kg的物体P，Q为一质量为m2＝10kg的物体，弹簧的质量不计，劲度系数k＝600N/m，系统处于静止状态．现给物体Q施加一个方向沿斜面向上的力F ，使它从静止开始沿斜面向上做匀加速运动，已知在前0.2s 时间内，F 为变力，0.2s 以后F 为恒力，sin 37°＝0.6，cos 37°＝0.8，g 取10m/s 2.求：(1)系统处于静止状态时，弹簧的压缩量x 0；(2)物体Q 从静止开始沿斜面向上做匀加速运动的加速度大小a ；(3)力F 的最大值与最小值．答案(1)0.16m (2)103m/s 2(3)2803N 1603N 解析(1)设开始时弹簧的压缩量为x 0对整体受力分析，平行斜面方向有(m 1＋m 2)g sin θ＝kx 0解得x 0＝0.16m(2)前0.2s 时间内F 为变力，之后为恒力，则0.2s 时刻两物体分离，此时P 、Q 之间的弹力为零且加速度大小相等，设此时弹簧的压缩量为x 1对物体P ，由牛顿第二定律得kx 1－m 1g sin θ＝m 1a前0.2s 时间内两物体的位移x 0－x 1＝12at 2联立解得a ＝103m/s 2(3)对两物体受力分析知，开始运动时拉力最小，分离时拉力最大NF min＝(m1＋m2)a＝1603对Q应用牛顿第二定律得F max－m2g sinθ＝m2aN.解得F max＝m2(g sinθ＋a)＝2803【变式4】两物体A、B并排放在水平地面上，且两物体接触面为竖直面，现用一水平推力F作用在物体A上，使A、B由静止开始一起向右做匀加速运动，如图a所示，在A、B的速度达到6m/s时，撤去推力F.已知A、B 质量分别为m A＝1kg、m B＝3kg，A与地面间的动摩擦因数μ＝0.3，B与地面间没有摩擦，B物体运动的v－t图像如图b所示．g取10m/s2，求：(1)推力F的大小；(2)A刚停止运动时，物体A、B之间的距离．答案(1)15N(2)6m解析(1)在水平推力F作用下，设物体A、B一起做匀加速运动的加速度为a，由B的v－t图象得：a＝3m/s2对于A、B组成的整体，由牛顿第二定律得：F－μm A g＝(m A＋m B)a代入数据解得：F＝15N.(2)撤去推力F后，A、B两物体分离．A在摩擦力作用下做匀减速直线运动，B做匀速运动，设A匀减速运动的时间为t，对于A有：μm A g＝m A a A解得：a A＝μg＝3m/s2根据匀变速直线运动规律有：0＝v0－a A t解得：t＝2s撤去力F后，A的位移为x A＝v0t－1a A t2＝6m2B的位移为x B＝v0t＝12m所以，A刚停止运动时，物体A、B之间的距离为Δx＝x B－x A＝6m.。

3.2牛二应用一：动力学的两类基本问题一、学习目标会用牛顿第二定律分析和解决两类基本问题：已知受力情况求解运动情况，已知运动情况求解受力情况。

二、知识梳理1.已知力求运动：知道物体受到的作用力，应用牛顿第二定律求加速度，如果再知道物体的初始运动状态，应用运动学公式就可以求出物体的运动情况——任意时刻的位置和速度，以及运动轨迹。

2.已知运动求力：知道物体的运动情况，应用运动学公式求出物体的加速度，再应用牛顿第二定律，推断或者求出物体的受力情况。

3.两类基本问题的解题步骤：（1）确定研究对象，明确物理过程；（2）分析研究对象的受力情况和运动情况，必要时画好受力图和运动过程示意图；（3）根据牛顿第二定律和运动学公式列方程；合力的求解常用合成法或正交分解法；要特别注意公式中各矢量的方向及正负号的选择，最好在受力图上标出研究对象的加速度的方向；（4）求解、检验，必要时需要讨论。

三、典型例题1.有三个光滑斜轨道1、2、3，它们的倾角依次是60°，45°，30°，这些轨道交于O点．现有位于同一竖直线上的三个小物体甲、乙、丙分别沿这三个轨道同时从静止自由下滑，如图所示，物体滑到O点的先后顺序是（）A．甲最先，乙稍后，丙最后B．乙最先，然后甲和丙同时到达C．甲、乙、丙同时到达D．乙最先，甲稍后，丙最后2.如图甲所示，为测定物体冲上粗糙斜面能达到的最大位移x与斜面倾角θ的关系，将某一物体每次以不变的初速率v0沿足够长的斜面向上推出，调节斜面与水平方向的夹角θ，实验测得x与斜面倾角θ的关系如图乙所示，g取10 m/s2，根据图象可求出()A．物体的初速率v0＝3 m/sB．物体与斜面间的动摩擦因数μ＝0.75C．取不同的倾角θ，物体在斜面上能达到的位移x的最小值x min＝1.44 mD．当θ＝45°时，物体达到最大位移后将停在斜面上3.我国歼-15舰载战斗机首次在“辽宁舰”上成功降落，有关资料表明，该战斗机的质量m=2.0v=80 m/s减小到零所用时间t=2.5 ×104 kg，降落时在水平甲板上受阻拦索的拦阻，速度从s．若将上述运动视为匀减速直线运动，求：该战斗机在此过程中(1)加速度的大小a；(2)滑行的距离x；(3)所受合力的大小F．4.如图所示，一质量为m =2kg 的物体静止在水平地面上，物体与水平地面间的动摩擦因数μ=0.2，现对物体施加一水平向右的恒定拉力F =12N ，取g =10m/s 2。

动力学的两类基本问题一、 已知物体的受力情况，求解物体的运动情况 【例1】质量m =1.5kg 的物体，在水平恒力F =15N 的作用下，从静止开始运动0.5s 后撤去该力，物体继续滑行一段时间后停下来。

已知物体与水平面的动摩擦因数为μ=0.2，g 取10m/s 2，求：（1）恒力作用于物体时的加速度大小；（2）撤去恒力后物体继续滑行的时间；（3）物体从开始运动到停下来的总位移大小。

【变式拓展1】质量m ＝4kg 的物块，在一个平行于斜面向上的拉力F ＝40N 作用下，从静止开始沿斜面向上运动，如图所示，已知斜面足够长，倾角θ＝37°，物块与斜面间的动摩擦因数µ＝0.2，力F 作用了5s ，求物块在5s 内的位移及它在5s 末的速度。

（g ＝10m/s 2，sin37°＝0.6，cos37°＝0.8）【变式拓展2】如图所示，质量m =2kg 的物体与水平地面间的动摩擦因数为μ=0.5，在与水平成θ=37°，大小F =10N 的恒力作用下，从静止开始向右运动，经过t 1=4.0s 时撤去恒力F ，求物体在地面上滑行的总位移s ．(g =10m/s 2，sin37°=0.6，cos37°=0.8)【变式拓展3】如图所示，放在水平面上质量为G=10N 的物体受到一个斜向下方的10N 的推力F 作用，这个力与水平方向成θ=37°角，在此恒力的作用下，物体匀速滑动．（g=10m/s 2，要求保留两位有效数字，sin37°=0.6 cos37°=0.8）求：（1）物体与水平面间的滑动摩擦因数？（2）若将此力改为水平向右，从静止开始求10s 末物体速度和10s 内物体的位移？【变式拓展4】如图所示，质量m=2kg 的物体静止于水平地面的A 处，A 、B 间距L=20m．用大小为30N，沿水平方向的外力拉此物体，经t 0=2s 拉至B 处．（取g=10m/s 2）（1）求物体与地面间的动摩擦因数μ；（2）该外力作用一段时间后撤去，使物体从A 处由静止开始运动并能到达B 处，求该力作用的最短时间t ．【变式拓展6】质量为10kg的物体在F=200N的水平推力作用下，从粗糙斜面的底端由静止开始沿斜面运动，斜面固定不动，与水平地面的夹角θ=37°．力F作用2秒钟后撤去，物体在斜面上继续上滑了1.25秒钟后，速度减为零．求：物体与斜面间的动摩擦因数μ和物体的总位移s．(已知sin37°=0.6，cos37°=0.8．g=10m/s2)二、已知运动情况求物体的受力情况【例1】质量m=1.5kg的物块(可视为质点)在水平恒力F作用下，从水平面上A点由静止开始运动，运动一段距离撤去该力，物块继续滑行t=2.0s停在B点．已知A、B两点间的距离s=5.0m，物块与水平面间的动摩擦因数μ=0.20，取重力加速度g=10m/s2，求恒力F【变式拓展1】如图所示，质量为0.5kg的物体在与水平面成300角的拉力F作用下，沿水平桌面向右做直线运动，经过0.5m的距离速度由0.6m/s变为0.4m/s，已知物体与桌面间的动摩擦因数μ＝0.1，求作用力F的大小。

物理总复习：牛顿第二定律及其应用编稿：李传安 审稿：【考纲要求】1、理解牛顿第二定律，掌握解决动力学两大基本问题的基本方法；2、了解力学单位制；3、掌握验证牛顿第二定律的基本方法，掌握实验中图像法的处理方法。

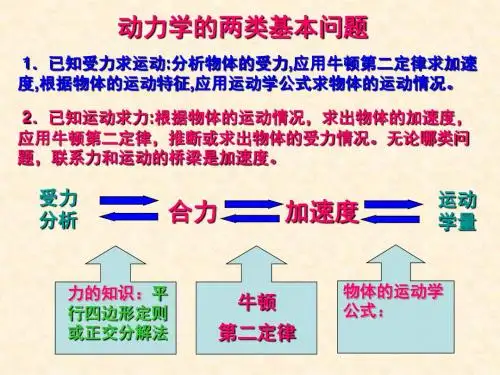
【知识网络】牛顿第二定律内容：物体运动的加速度与所受的合外力成正比，与物体的质量成反比，加速度的方向与合外力相同。

解决动力学两大基本问题（1）已知受力情况求运动情况。

（2）已知物体的运动情况，求物体的受力情况。

运动=F ma−−−→←−−−合力 加速度是运动和力之间联系的纽带和桥梁【考点梳理】要点一、牛顿第二定律1、牛顿第二定律牛顿第二定律内容：物体运动的加速度与所受的合外力成正比，与物体的质量成反比，加速度的方向与合外力相同。

要点诠释：牛顿第二定律的比例式为F ma ∝；表达式为F ma =。

1 N 力的物理意义是使质量为m=1kg 的物体产生21/a m s =的加速度的力。

几点特性：（1）瞬时性：牛顿第二定律是力的瞬时作用规律，力是加速度产生的根本原因，加速度与力同时存在、同时变化、同时消失。

（2）矢量性： F ma =是一个矢量方程，加速度a 与力F 方向相同。

（3）独立性：物体受到几个力的作用，一个力产生的加速度只与此力有关，与其他力无关。

（4）同体性：指作用于物体上的力使该物体产生加速度。

要点二、力学单位制1、基本物理量与基本单位力学中的基本物理量共有三个，分别是质量、时间、长度；其单位分别是千克、秒、米；其表示的符号分别是kg 、s 、m 。

在物理学中，以质量、长度、时间、电流、热力学温度、发光强度、物质的量共七个物理量 作为基本物理量。

以它们的单位千克（kg ）、米（m ）、秒（s ）、安培（A ）、开尔文（K ）、坎 德拉（cd ）、摩尔（mol ）为基本单位。

2、 基本单位的选定原则（1）基本单位必须具有较高的精确度，并且具有长期的稳定性与重复性。

（2）必须满足由最少的基本单位构成最多的导出单位。

2023届高三物理一轮复习重点热点难点专题特训专题16 动力学的两类基本问题、连接体模型特训目标 特训内容目标1 已知受力情况求运动情况（1T —4T ） 目标2 已知运动情况求受力情况（5T —8T ） 目标3 加速度相同的连接体问题（9T —12T ） 目标4加速度不同的连接体问题（13T —16T ）一、已知受力情况求运动情况1．如图所示，一小球塞在一个竖直圆管中，让圆管由距地面为5m h =处静止自由下落，与地面发生多次弹性碰撞，运动过程中，圆管始终保持竖直。

已知圆管的质量为4kg M =，小球的质量为1kg m =，小球与圆管之间的滑动摩擦力大小为40N f =，210m/s g =，不计空气阻力。

下列说法中正确的是（ ）A ．圆管第一次与地面碰撞后，与球在空中相对静止之前，圆管的加速度大小为230m/sB ．圆管第一次与地面碰撞后，与球在空中相对静止之前，小球的加速度大小为250m/sC ．圆管与地面第一次碰撞后到第二次碰撞前，圆管与小球获得的共同速度为0.6m/sD ．圆管从释放到第二次触地的过程中，小球相对圆管下降的高度为4m 【答案】D【详解】AB ．圆管第一次与地面碰撞后，圆管与球在空中相对静止之前，对圆管和球受力分析，以向下为正方向，由牛顿第二定律1+Mg f Ma =；2f mg ma -=可得2120m/s a =；2230m/s a =-故AB 错误；C ．圆管和球一起下落h ，设第一次与地相撞前瞬间速度为v 0：202v gh =第一次反弹后至第二次相撞前，设经过t 两者共速，速度为v ，以向下为正方向，则0102v v a t v a t =-+=+解得2m/s v =-，C 错误；D ．设管在t 内的位移为x 1：012v v x t +=设小球在t 内的位移为x 2：022v vx t -+= 小球相对管道下降的高度12h x x =-；h =4m ，D 正确。

高一必修一物理笔记整理（实用版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的教育资料，如幼儿教案、音乐教案、语文教案、知识梳理、英语教案、物理教案、化学教案、政治教案、历史教案、其他范文等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, this store provides various types of educational materials for everyone, such as preschool lesson plans, music lesson plans, Chinese lesson plans, knowledge review, English lesson plans, physics lesson plans, chemistry lesson plans, political lesson plans, history lesson plans, and other sample texts. If you want to learn about different data formats and writing methods, please stay tuned!高一必修一物理笔记整理本店铺整理的《高一必修一物理笔记整理》希望能够帮助到大家。

动力学的两类基本问题
例1
水平面上有相距15 m 的A 、B 两点，一质
量为2 kg 的物体在大小为16 N 、方向斜向上的力F 作用下，从A 点由静止开始做直线运动．某
时刻撤去F ，物体到达B 点时速度为0.若物体与水平面间的动摩擦因数μ＝34
，重力加速度g 取10 m/s 2.求物体从A 运动到B 的最短时间．
①由静止开始做直线运动；②某时刻撤去F ，
物体到达B 点时速度为0.
答案 4 s
解析 撤去F 前对物体受力分析如图所示，根据牛顿第二定律有
F cos α－F f ＝ma 1①
F f ＝μF N ②
F N ＝mg －F sin α③
x 1＝12
a 1t 12④ 撤去F 后物体只受重力、弹力和摩擦力，利用牛顿第二定律有
μmg ＝ma 2⑤
x 2＝12
a 2t 22⑥ x 1＋x 2＝s ⑦
a 1t 1＝a 2t 2⑧
根据v －t 图象中速度与时间轴所围面积代表位移，由于减速过程物体的加速度不变，在总位移不变的情况下只有增大加速过程的加速度才能让时间变短．由①②③联立可得F cos α
－μ(mg －F sin α)＝ma 1利用数学知识可得最大加速度a 1＝F 1＋μ2
m
－μg ＝2.5 m/s 2，联立④⑤⑥⑦⑧可求得t 1＝3 s ，t 2＝1 s ，则总时间t ＝t 1＋t 2＝4 s.。