离散数学结构 习题5

离散数学试题第一部分选择题一、单项选择题1．下列是两个命题变元p，q的小项是（ C ）A．p∧┐p∧q B．┐p∨qC．┐p∧q D．┐p∨p∨q2．令p：今天下雪了，q：路滑，则命题“虽然今天下雪了，但是路不滑”可符号化为（ D ）A．p→┐q B．p∨┐qC．p∧q D．p∧┐q3．下列语句中是命题的只有（ A ）A．1+1=10 B．x+y=10C．sinx+siny<0 D．x mod 3=24．下列等值式不正确的是（ C ）A．┐(∀x)A⇔(∃x)┐AB．(∀x)(B→A(x))⇔B→(∀x)A(x)C．(∃x)(A(x)∧B(x))⇔(∃x)A(x)∧(∃x)B(x)D．(∀x)(∀y)(A(x)→B(y))⇔(∃x)A(x)→(∀y)B(y)5．谓词公式(∃x)P(x,y)∧(∀x)(Q(x,z)→(∃x)(∀y)R(x,y,z)中量词∀x的辖域是（ C ）A．(∀x)Q(x,z)→(∃x)(∀y)R(x,y,z))B．Q(x,z)→(∀y)R(x,y,z)C．Q(x,z)→(∃x)(∀y)R(x,y,z)D．Q(x,z)6．设A={a,b,c,d}，A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪I A，则对应于R的A的划分是（ D ）A．{{a},{b,c},{d}} B．{{a,b},{c},{d}}C．{{a},{b},{c},{d}} D．{{a,b},{c,d}}7．设A={Ø}，B=P(P(A))，以下正确的式子是（ A ）A．{Ø,{Ø}}∈B B．{{Ø,Ø}}∈BC．{{Ø},{{Ø}}}∈B D．{Ø,{{Ø}}}∈B8．设X，Y，Z是集合，一是集合相对补运算，下列等式不正确的是（ A ）A．(X-Y)-Z=X-(Y∩Z)B．(X-Y)-Z=(X-Z)-YC．(X-Y)-Z=(X-Z)-(Y-Z)D．(X-Y)-Z=X-(Y∪Z)9．在自然数集N上，下列定义的运算中不可结合的只有（ D ）A．a*b=min(a,b)B．a*b=a+bC．a*b=GCD(a,b)(a,b的最大公约数)02324# 离散数学试题第1 页共4页02324# 离散数学试题 第 2 页 共4页D ．a*b=a(mod b)10.设R 和S 是集合A 上的关系,R ∩S 必为反对称关系的是( A ) A ．当R 是偏序关系,S 是等价关系; B ．当R 和S 都是自反关系; C ．当R 和S 都是等价关系; D ．当R 和S 都是传递关系11.设R 是A 上的二元关系,且R ·R ⊆R,可以肯定R 应是( D ) A ．对称关系; B ．全序关系; C ．自反关系; D ．传递关系第二部分 非选择题二、填空题1．设论域是{a,b,c}，则(∀x)S(x)等价于命题公式 S(a)∧S(b)∧S(c) ；(x ∃)S(x)等价于命题公式 S(a)∨S(b) ∨S(c) 。

离散数学（1-4-5章）自测题《离散数学1-4-5章》练习题第1章集合1、在0（）Φ之间写上正确的符号。

(1) = (2) ?(3) ∈(4) ?2、若集合S的基数|S|=5，则S的幂集的基数|P(S)|=（）。

3、设P={x|(x+1)2≤4且x∈R},Q={x|5≤x2+16且x∈R},则下列命题哪个正确（） (1) Q?P (2) Q?P (3) P?Q (4) P=Q4、若A-B=Ф，则下列哪个结论不可能正确？( )(1) A=Ф (2) B=Ф(3) A?B (4) B?A5、判断下列命题哪几个为正确？( )(1) {Ф}∈{Ф,{{Ф}}} (2) {Ф}?{Ф,{{Ф}}} (3) Ф∈{{Ф}}(4) Ф?{Ф} (5) {a,b}∈{a,b,{a},{b}}6、设Ａ，Ｂ，Ｃ是三个集合，证明：a、A? (B－C)＝(A?B)－(A?C)b、(A－B)?(A－C)=A－(B?C)第4章关系1、设Ａ＝｛1,2,3,4,5,6｝，B={1,2,3}，从Ａ到B的关系Ｒ＝｛〈x,y〉|x=y2｝，求R 和R-1的集合表示和关系矩阵表示。

2、设S={１,２,３,４}，Ａ上的关系Ｒ＝｛〈1,2〉，〈2,1〉，〈2,3〉，〈3,4〉｝求(1)R R (2) R-1。

3、设Ａ＝｛1，2，3，4，5，6｝，Ｒ是A上的整除关系，求R= {( )}。

4、设A={1,2,3},写出下列图示关系的关系矩阵，并讨论它们的性质：5、R是A={1,2,3,4,5,6}上的等价关系，R=I{<1,5>,<5,1>,<2,4>,<4,2>,<3,6>,<6,3>}A求R诱导的划分。

6．画出下列集合关于整除关系的哈斯图.(1){1, 2, 3, 4, 6, 8, 12, 24}.(2){1,2,…..,9}.并指出它的极小元，最小元，极大元，最大元。

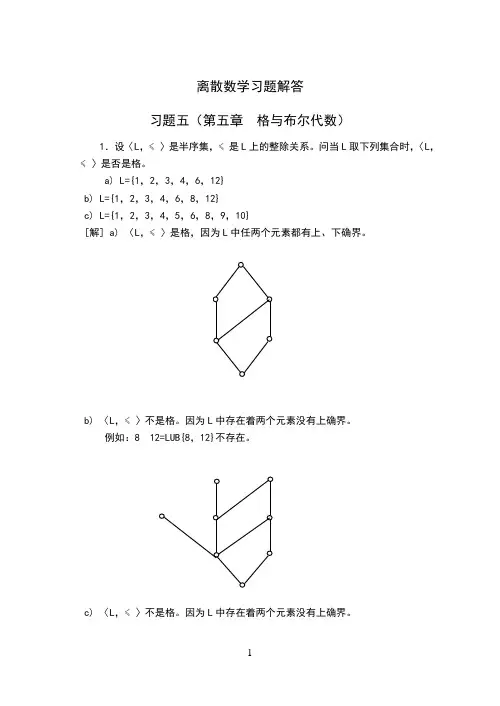
离散数学习题解答习题五（第五章 格与布尔代数）1．设〈L ，≼〉是半序集，≼是L 上的整除关系。

问当L 取下列集合时，〈L ，≼〉是否是格。

a) L={1，2，3，4，6，12} b) L={1，2，3，4，6，8，12} c) L={1，2，3，4，5，6，8，9，10}[解] a) 〈L ，≼〉是格，因为L 中任两个元素都有上、下确界。

b) 〈L ，≼〉不是格。

因为L 中存在着两个元素没有上确界。

例如：812=LUB{8，12}不存在。

c) 〈L ，≼〉不是格。

因为L 中存在着两个元素没有上确界。

16312486312411倒例如：46=LUB{4，6}不存在。

2．设A ，B 是两个集合，f 是从A 到B 的映射。

证明：〈S ，⊆〉是〈2B，⊆〉的子格。

其中S={y|y=f (x)，x ∈2A}[证] 对于任何B 1∈S ，存在着A 1∈2A，使B 1=f （A 1），由于f(A 1)={y|y ∈B ∧(x)(x ∈A 1∧f (x)=y)}⊆B 所以B 1∈2B，故此S ⊆2B；又B 0=f (A)∈S (因为A ∈2A)，所以S 非空；对于任何B 1，B 2∈S ，存在着A 1，A 2∈2A，使得B 1=f (A 1)，B 2=f (A 2)，从而 L ∪B{B 1，B 2}=B 1∪B 2=f (A 1)f (A 2)=f (A 1∪A 2) （习题三的8的1）） 由于A 1∪A 2⊆A ，即A 1∪A 2∈2A，因此f (A 1∪A 2)∈S ，即上确界L ∪B{B 1，B 2}存在。

对于任何B 1，B 2∈S ，定义A 1=f –1(B 1)={x|x ∈A ∧f (x)∈B 1}，A 2=f -1(B 2)={x|x ∈A ∧f (x)∈B 2}，则A 1，A 2∈2A，且显然B 1=f (A 1)，B 2=f (A 2)，于是GLB{B 1，B 2}=B 1∩B 2=f (A 1)∩f (A 2) ⊇f (A 1∩A 2) （习题三的8的2））又若y ∈B 1∩B 2，则y ∈B ，且y ∈B 2。

离散数学辅助教材概念分析结构思想与推理证明第一部分集合论刘国荣交大电信学院计算机系离散数学习题解答习题一（第一章集合）1. 列出下述集合的全部元素：1）A={x | x ∈N∧x是偶数∧x＜15}2）B={x|x∈N∧4+x=3}3）C={x|x是十进制的数字}[解] 1）A={2，4，6，8，10，12，14}2）B=∅3）C={0，1，2，3，4，5，6，7，8，9}2. 用谓词法表示下列集合：1）{奇整数集合}2）{小于7的非负整数集合}3）{3，5，7，11，13，17，19，23，29}[解] 1）{n n∈I∧(∃m∈I)(n=2m+1)}；2）{n n∈I∧n≥0∧n<7}；3）{p p∈N∧p>2∧p<30∧⌝(∃d∈N)(d≠1∧d≠p∧(∃k∈N)(p=k⋅d))}。

3. 确定下列各命题的真假性：1）∅⊆∅2）∅∈∅3）∅⊆{∅}4）∅∈{∅}5）{a，b}⊆{a，b，c，{a，b，c}}6）{a,b}∈(a，b，c，{a，b，c})7）{a，b}⊆{a，b，{{a，b，}}}8）{a，b}∈{a，b，{{a，b，}}}[解]1）真。

因为空集是任意集合的子集；2）假。

因为空集不含任何元素；3）真。

因为空集是任意集合的子集；4）真。

因为∅是集合{∅}的元素；5）真。

因为{a，b}是集合{a，b，c，{a，b，c}}的子集；6）假。

因为{a,b}不是集合{a，b，c，{a，b，c}}的元素；7）真。

因为{a，b}是集合{a，b，{{a，b}}}的子集；8）假。

因为{a,b}不是集合{a，b，{{a，b}}}的元素。

4. 对任意集合A，B，C，确定下列命题的真假性：1）如果A∈B∧B∈C，则A∈C。

2）如果A∈B∧B∈C，则A∈C。

3）如果A⊂B∧B∈C，则A∈C。

[解] 1）假。

例如A={a}，B={a，b}，C={{a}，{b}}，从而A∈B∧B∈C但A∈C。

第十四章部分课后习题参考答案5、设无向图G有10条边，3度与4度顶点各2个，其余顶点的度数均小于3,问G至少有多少个顶点？在最少顶点的情况下，写出度数列、厶(G)、.(G)。

解：由握手定理图G的度数之和为：2 10=203度与4度顶点各2个，这4个顶点的度数之和为14度。

其余顶点的度数共有6度。

其余顶点的度数均小于3,欲使G的顶点最少，其余顶点的度数应都取2,所以，G至少有7个顶点,出度数列为3,3,4,4,2,22 .1(G) = 4「(G) = 2 .7、设有向图D的度数列为2, 3, 2, 3,出度列为1, 2，1，1，求D的入度列，并求厶(D),、：(D)，：(D)「.(D),.厂(D),解：D的度数列为2, 3, 2, 3,出度列为1, 2, 1, 1, D的入度列为1,1,1,2..：(D) =3,、(D) =2, ：(D) =2,、• (D) = 1,.厂(D) = 2,、_(D) = 18设无向图中有6条边，3度与5度顶点各1个，其余顶点都是2度点，问该图有多少个顶点？解：由握手定理图G的度数之和为：2 6=12设2度点x个，则3 1 5 1 2x =12 , x=2，该图有4个顶点.14、下面给出的两个正整数数列中哪个是可图化的？对可图化的数列，试给出3种非同构的无向图，其中至少有两个时简单图。

(1) 2,2,3,3,4,4,5 (2) 2,2,2,2,3,3,4,4解：(1) 2+2+3+3+4+4+5=23 是奇数，不可图化；⑵2 + 2+2+2+3+3+4+4=16,是偶数，可图化；18、设有3个4阶4条边的无向简单图G1、G2、G3,证明它们至少有两个是同构的。

证明：4阶4条边的无向简单图的顶点的最大度数为3,度数之和为8,因而度数列为2, 2, 2, 2;3, 2, 2, 1; 3, 3, 1, 1。

但3, 3, 1, 1对应的图不是简单图。

所以从同构的观点看，4阶4条边的无向简单图只有两个：所以，G i 、G 2、G 3至少有两个是同构的。

习题答案（P151~P153）1．用枚举法给出下列集合解：（2）{-3，2}（4）{5，6，7，8，9，10，11，12，13，14，15}2．用抽象法说明下列集合解：（2）{x|x为素数，10<x<20}（4）{x|x为中国的省会}（6）{x|x=2k+1，k∈I}3．判断下列哪些∈关系成立，为什麽？解：根据只有集合中的元素才与该集合有∈关系，故（1）、（4）、（6）、（7）成立，（2）、（3）、（5）、（8）不成立。

4．判断下列哪些集合相等（全集是整数集合I）解：A=G，B=E，C=F6．写出下列集合的幂集解：（2）ρ（{1，∅}）={∅，{1}，{∅}，{1，∅}}（4）ρ（{∅，{a}，{∅}}）={∅，{∅}，{{a}}，{{∅}}，{∅，{a}}，{∅，{∅}}，{{a}，{∅}}，{∅，{a}，{∅}}}7．当把“⊆”插入空位时哪一个为真？解：（1）、（2）、（3）、（6）为真，（4）、（5）为假。

8．设A、B、C分别是集合，若A∈B，B∈C，哪麽A∈C一定成立吗？解：不一定，例如，A={a}，B={{a}}，C={{{a}}}，虽然A∈B，B∈C，但A∈C不成立。

10．设U={1，2，3，4，5}，A={1，4}，B={1，2，5}和C={2，4}试写出下列集合（8）ρ（A）-ρ（C）解：ρ（A）-ρ（C）={∅，{1}，{4}，{1，4}}-{∅，{2}，{4}，{2，4}}={{1}，{1，4}}11．证明下列恒等式（1）A-（B⋂C）=（A-B）⋃（A-C）（2）（A-B）⋂B=∅解：（1）A-（B⋂C）= A⋂~（B⋂C）= A⋂（~B⋃~C）=（A⋂~B）⋃（A⋂~C）=（A-B）⋃（A-C）（2）（A-B）⋂B=（A⋂~B）⋂B= A⋂（~B⋂B）= ∅12．设A、B、C是集合，下列等式成立的条件是什么？（1）（A-B）⋃（A-C）=A（2）（A-B）⋃（A-C）= ∅解：（1）因为（A-B）⋃（A-C）= （A⋂~B）⋃（A⋂~C）= A⋂（~B⋃~C）= A⋂~（B⋂C）= A-（B⋂C）所以（A-B）⋃（A-C）=A 当且仅当A-（B⋂C）=A 由-的定义可知A⋂（B⋂C）=∅（2）由（1）可知，（A-B）⋃（A-C）=A-（B⋂C）所以（A-B）⋃（A-C）=∅当且仅当A-（B⋂C）=∅由定理5.11可知A⊆（B⋂C）13. 设A，B是集合（1）A-B=B，问A和B有何关系？（2）A-B=B-A, 问A和B有何关系？解：（1）A=B=φ。

第5章一.填空题1. 群中有唯一的（）。

2. 如果群运算是可交换的，则群为（）。

3. 设*是定义在集合A上的二元运算，如果对于A中任意的两个元素x,y，都有x*y∈A，则称二元运算*在A上是（）。

4. 设*是定义在集合A上的二元运算，如果对于A中任意的两个元素x,y，都有x*y=y*x，则称二元运算*在A上是（）。

5. 设★是定义在有理数集合Q上的二元运算，如果对于Q中任意的两个元素x,y，都有x★y=x+y-x*y，其中*表示普通乘法元算，则二元运算★在Q上是（）。

（填写可交互/不可交换）6. 设*是定义在集合A上的二元运算，如果对于A中任意的元素x,y,z，都有(x*y)*z=x*(y*z) ，则称二元运算*在A上是（）。

7. 设★是定义在非空集合A上的二元运算，如果对于A中任意的两个元素x,y，都有x*y=y，则二元运算★在A上是（）。

（填写可结合/不可结合）8. 设*，★是定义在集合A上的两个二元运算，如果对于A中任意的元素x,y,z，都有(x*y) ★z=（x★z）*(y★z)，z★(x*y)=(z★x)*(z★y),则称二元运算★对于*在A上是（）。

9. 设*，★是定义在集合A上的两个可交换的二元运算，如果对于A中任意的元素x,y，都有x*(x★y)=x, x★(x*y)=x,则称二元运算*对于★在A上满足（）。

10. 设*是定义在集合A上的二元运算，如果对于A中任意的元素x，都有x*x=x，则称二元运算*是（）。

11. 设*是定义在集合A上的二元运算，如果在A中存在元素el，对于A中任意的元素x，都有el*x=x，则称el为A中关于运算*的（）。

12. 设*是定义在集合A上的二元运算，如果在A中存在元素ol，对于A中任意的元素x，都有ol*x=x，则称ol为A中关于运算*的（）。

13. 设*是定义在集合A上的二元运算，如果在A中存在元素er，对于A中任意的元素x，都有x*erl =x，则称er为A中关于运算*的（）。

《离散数学》第三部分----代数结构一、选择或填空1、设A={2,4,6}，A上的二元运算*定义为：a*b=max{a,b}，则在独异点<A,*>中，单位元是( )，零元是( )。

答：2，62、设A={3,6,9}，A上的二元运算*定义为：a*b=min{a,b}，则在独异点<A,*>中，单位元是( )，零元是( )；答：9，33、设〈G,*〉是一个群，则(1) 若a,b,x∈G，a*x=b，则x=( )；(2) 若a,b,x∈G，a*x=a*b，则x=( )。

答：（1）a*-1 b （2）b4、设a是12阶群的生成元，则a2是( )阶元素，a3是( )阶元素。

答：6,45、代数系统<G,*>是一个群，则G的等幂元是( )。

答：单位元6、设a是10阶群的生成元，则a4是( )阶元素，a3是( )阶元素。

答：5，107、群<G,*>的等幂元是( )，有( )个。

答：单位元，18、素数阶群一定是( )群, 它的生成元是( )。

答：循环群，任一非单位元9、设〈G,*〉是一个群，a,b,c∈G，则(1) 若c*a=b，则c=( )；(2) 若c*a=b*a，则c=( )。

答：（1）b1-*a(2) b10、<H,,*>是<G,,*>的子群的充分必要条件是( )。

答：<H,,*>是群或∀ a，b ∈G，a*b∈H，a-1∈H 或∀ a,b ∈G，a*b-1∈H 11、群＜A,*＞的等幂元有( )个，是( )，零元有( )个。

答：1，单位元，012、在一个群〈G,*〉中，若G中的元素a的阶是k，则a-1的阶是( )。

答：k13、在自然数集N上，下列哪种运算是可结合的？（）(1) a*b=a-b (2) a*b=max{a,b} (3) a*b=a+2b (4) a*b=|a-b| 答：(2)14、任意一个具有2个或以上元的半群，它（）。

习题五1.设个体域D={a,b,c}，在D 中消去公式(()())x F x yG y ∀∧∃的量词。

甲乙用了不同的演算过程：甲的演算过程如下：(()())(()(()()()))(()(()()()))(()(()()()))(()(()()()))(()()())(()()())x F x yG y x F x G a G b G c F a G a G b G c F b G a G b G c F c G a G b G c F a F b F c G a G b G c ∀∧∃⇔∀∧∨∨⇔∧∨∨∧∧∨∨∧∧∨∨⇔∧∧∧∨∨乙的演算过程如下：(()())()()(()()())(()()())x F x yG y xF x yG y F a F b F c G a G b G c ∀∧∃⇔∀∧∃⇔∧∧∧∨∨ 显然，乙的演算过程简单，试指出乙在演算过程中的关键步骤。

解：乙在演算中的关键步骤是，在演算开始就利用量词辖域收缩与扩张等值式，将量词的辖域缩小，因而演算简单。

2. 设个体域D={a,b,c}，消去下列各式的量词：(1)(()())(2)(()())(3)()()(4)(,)())x y F x G y x y F x G y xF x yG y x F x y yG y ∀∃∧∀∃∨∀→∀∀→∃（解：（1）))()()(())()()((c G b G a G c F b F a F ∨∨∧∧∧ （2）))()()(())()()((c G b G a G c F b F a F ∧∧∨∧∧ （3）))()()(())()()((c G b G a G c F b F a F ∧∧→∧∧ （4）))()()(()),(),(),((c G b G a G y c F y b F y a F ∨∨→∨∨在（1）（2）（4）中均将量词的辖域缩小，所以演算结果都比较简单3. 设个体域D={1,2}，请给出两种不同的解释1I 和2I ，使得下面公式在1I 下都是真命题，而在2I 下都是假命题。

离散数学习题答案解析(总16页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--离散数学习题答案习题一及答案：（P14-15）14、将下列命题符号化：（5）李辛与李末是兄弟解：设p：李辛与李末是兄弟，则命题符号化的结果是p（6）王强与刘威都学过法语∧解：设p：王强学过法语；q：刘威学过法语；则命题符号化的结果是p q（9）只有天下大雨，他才乘班车上班→解：设p：天下大雨；q：他乘班车上班；则命题符号化的结果是q p （11）下雪路滑，他迟到了解：设p：下雪；q：路滑；r：他迟到了；则命题符号化的结果是()∧→p q r 15、设p：2+3=5.q：大熊猫产在中国.r：太阳从西方升起.求下列复合命题的真值：（4）()(())∧∧⌝↔⌝∨⌝→p q r p q r解：p=1，q=1，r=0，∧∧⌝⇔∧∧⌝⇔，p q r()(110)1p q r⌝∨⌝→⇔⌝∨⌝→⇔→⇔(())((11)0)(00)1∴∧∧⌝↔⌝∨⌝→⇔↔⇔()(())111p q r p q r19、用真值表判断下列公式的类型：（2）()→⌝→⌝p p q解：列出公式的真值表，如下所示：由真值表可以看出公式有3个成真赋值，故公式是非重言式的可满足式。

20、求下列公式的成真赋值： （4）()p q q ⌝∨→解：因为该公式是一个蕴含式，所以首先分析它的成假赋值，成假赋值的条件是：()10p q q ⌝∨⇔⎧⎨⇔⎩⇒0p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有：01，10，11。

习题二及答案：（P38）5、求下列公式的主析取范式，并求成真赋值： （2）()()p q q r ⌝→∧∧解：原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨，此即公式的主析取范式， 所以成真赋值为011，111。

*6、求下列公式的主合取范式，并求成假赋值： （2）()()p q p r ∧∨⌝∨解：原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔，此即公式的主合取范式， 所以成假赋值为100。

1-1，1-2（1）解：a)是命题，真值为T。

b)不是命题。

c)是命题，真值要根据具体情况确定。

d)不是命题。

e)是命题，真值为T。

f)是命题，真值为T。

g)是命题，真值为F。

h)不是命题。

i)不是命题。

（2）解：原子命题：我爱北京天安门。

复合命题：如果不是练健美操，我就出外旅游拉。

（3）解：a)(┓P ∧R)→Qb)Q→Rc)┓Pd)P→┓Q（4）解：a)设Q:我将去参加舞会。

R:我有时间。

P:天下雨。

Q (R∧┓P):我将去参加舞会当且仅当我有时间和天不下雨。

b)设R:我在看电视。

Q:我在吃苹果。

R∧Q:我在看电视边吃苹果。

c) 设Q:一个数是奇数。

R:一个数不能被2除。

（Q→R）∧(R→Q):一个数是奇数，则它不能被2整除并且一个数不能被2整除，则它是奇数。

(5) 解：a)设P：王强身体很好。

Q：王强成绩很好。

P∧Qb)设P：小李看书。

Q：小李听音乐。

P∧Qc)设P：气候很好。

Q：气候很热。

P∨Qd)设P： a和b是偶数。

Q：a+b是偶数。

P→Qe)设P：四边形ABCD是平行四边形。

Q ：四边形ABCD的对边平行。

P Qf)设P：语法错误。

Q：程序错误。

R：停机。

（P∨ Q）→ R(6) 解：a)P:天气炎热。

Q:正在下雨。

P∧Qb)P:天气炎热。

R:湿度较低。

P∧Rc)R:天正在下雨。

S:湿度很高。

R∨Sd)A:刘英上山。

B:李进上山。

A∧Be)M:老王是革新者。

N:小李是革新者。

M∨Nf)L:你看电影。

M:我看电影。

┓L→┓Mg)P:我不看电视。

Q:我不外出。

R:我在睡觉。

P∧Q∧Rh)P:控制台打字机作输入设备。

Q:控制台打字机作输出设备。

P∧Q1-3（1）解：a)不是合式公式，没有规定运算符次序（若规定运算符次序后亦可作为合式公式）b)是合式公式c)不是合式公式（括弧不配对）d)不是合式公式（R和S之间缺少联结词）e)是合式公式。

（2）解：a）A是合式公式，(A∨B)是合式公式，(A→(A∨B))是合式公式。

第4章:代数结构§4.1 代数运算习题4.11. 判断下列集合对所给地二元运算是否封闭。

（1）集合}|{Z Z ∈⨯=z z n n 关于普通加法与普通乘法运算,其n 是正整数。

（2）集合}12|{+∈-==Z n n x x S ，关于普通加法与普通乘法运算。

（3）集合}10{，=S 关于普通加法与普通乘法运算。

（4）集合}2|{+∈==Z n x x S n ，关于普通加法与普通乘法运算。

（5）n 阶)2(≥n 实可逆矩阵集合)(ˆR n M 关于矩阵加法与矩阵乘法运算。

对于封闭地二元运算,判断它们是否满足交换律,结合律与分配律,并在存在地情况下求出它们地单位元,零元与所有可逆元素地逆元。

解（1）封闭。

满足交换律,结合律与分配律,普通加法单位元0,没有零元,每个元素地逆元是其相反数。

普通乘法零元是0,如果n =1时有单位元1,只有1有逆元1自已,其它元素没有逆元。

如果n >1时,没有单位元。

（2）对普通加法不满足封闭。

对普通乘法满足封闭性,满足交换律,结合律。

没有零元,单位元是1,只有1有逆元1自已,其它元素没有逆元。

（3）对普通加法不满足封闭。

对普通乘法满足封闭性,满足交换律,结合律。

零元是0,单位元是1,只有1有逆元1自已,0没有逆元。

（4）对普通加法不满足封闭。

对普通乘法满足封闭性,满足交换律,结合律。

没有零元与单位元。

（5）封闭。

矩阵加法运算满足交换律,结合律,矩阵乘法满足结合律,不满足交换律。

矩阵加法与矩阵乘法满足分配律。

矩阵加法有单位元n 阶零矩阵,没有零元,每个矩阵地逆元是其相反矩阵。

矩阵乘法零元是n 阶零矩阵,单位元是n 阶单位矩阵,奇异矩阵没有逆元,非奇异矩阵有逆元,即其逆矩阵。

2. 判断下列集合对所给地二元运算是否封闭。

（1）正实数集合+R 与*运算,其*运算定义为: b a b a b a b a --⋅=*∈∀+，，R（2）2}{21≥=n a a a A n ，，，， 。

§4.6 环与域习题4.61．设。

证明关于复数地加法与乘法构成环,称为高斯整数环。

证明:（1） A 任意二个元素a+bi 与 c+di,都有（a+bi ）+（c+di ）=a+c +(b+d ) i 仍属于A,满足封闭性要求。

（2）+满足结合律。

（3）有单位元0。

（4）每个元素a+bi 都有逆元-a-bi（5）+满足交换律。

所以<A,+>是交换群。

（6）（a+bi ）×（c+di ）=ac-bd +(ad+bc ) i 仍属于A（（a+bi ）×（c+di ））×（w+ti ）=( ac-bd )w-(ad+bc )t+(( ac-bd )t+(ad+bc )w) i= acw -bdw -adt-bc t+(act-bd t+adw+bc w) i而（a+bi ）×（（c+di ））×（w+ti ）=（a+bi ）×（cw-dt+(ct+dw)i ）= acw -bdw -adt-bc t+(act-bd t+adw+bc w) i所以<A, ×>是半群。

（7）二个运算满足分配律。

综上所述,关于复数地加法与乘法构成环。

2．设为实数,称为实数域上地次多项式,令。

证明关于多项式地加法与乘法构成环,称为实数域上地多项式环。

证明:（1） 任意地二个多项式（a 0+a 1x+a 2x 2+….+a n x n ）+（b 0+b 1x+b 2x 2+….+b n x n ） = a 0+ b 0+( a 1+ b 1)x+….+ ( a m + b m )x m +….+ a n x n 仍然属于A,满足封闭性要求。

（2） 加法满足结合律与交换律。

（3） 有单位无0。

}1|{2-=∈+=i Z b a bi a A ，，A A n n n a a a x a x a x a a x f ，，，， 212210)(++++=)(x f n })(|)({N n x f x f A n ∈=，次多项式为实数域上的A（4） 每个多顶式a 0+a 1x+a 2x 2+….+a n x n 都有逆元-a 0-a 1x-a 2x 2-….-a n x n 所以关于多项式地加法是交换群。

第1章一.填空题1.2. 公式P→(Q→R)在联结词全功能集{﹁,∨}中等值形式为___________________。

3.4.5.6.7. 全体小项的析取式必为____________________式。

8. P,Q为两个命题，则德摩根律可表示为7. 全体小项的析取式必为_________式。

9. P,Q为两个命题，则吸收律可表示为____________________ 。

10. 设P：我有钱，Q：我去看电影。

命题“虽然我有钱，但是我不去看电影”符号化为_____ _______________。

11. 设P：我生病，Q：我去学校。

命题“如果我生病，那么我不去学校”符号化为_________ ___________。

12.13.14.15. 设P、Q为两个命题，交换律可表示为____________________。

16.17. 命题“如果你不看电影，那么我也不看电影”（P：你看电影，Q：我看电影）的符号化为____________________ 。

18.19.20.21. P：你努力，Q：你失败。

命题“除非你努力，否则你将失败”的翻译为_______________ _____。

22.23.24. 一个重言式和一个矛盾式的合取是____________________。

25. 全体小项的析取式为____________________ 。

26. 命题“如果你不看电影，那么我也不看电影”（P：你看电影，Q：我看电影）的符号化为____________________。

27.28. 设P：它占据空间，Q：它有质量，R：它不断运动，S：它叫做物质。

命题“占据空间的，有质量的而且不断运动的叫做物质”的符号化为____________________。

29.30.二.选择题1.2.3. 在除﹁之外的四大联结词中，满足结合律的有几个( )。

A. 2B.3C. 4D. 14. 判断下列语句哪个是命题( )。

习题 51. 设A={(a,b)|a,b∈N}.定义A上的一个二元关系R={（（a,b ）,(c,d)）|ad=bc},证明:R 是A 上的等价关系. 证：(){}+∈=N b a b a A ,|, ，R={（（a,b ）,(c,d)）|ad=bc} ①自反性：由A 的定义，N b a baab ∈=,()()()R b a b a ∈∴,,,②对称性 设()()()R d c b a ∈,,,，则bc ad = 即 ()()()R b a d c dacb ∈∴=,,,③传递性 设()()()R d c b a ∈1111,,，则1111c b d a =()()()R d c d c ∈2211,,，则2121c d d c =2121211211211c b d a c d b d c b d d a =⇒==⇒()()()R d c b a ∈∴2211,,,2. 定义复数集合的子集合C 1={a+bi|i 2=-1,a 、b ∈R,a ≠0}，在C 1上定义关系S 为：(a+bi)S(c+di)⇔ac>0。

证明：S 是C 1上的一个等价关系，并给出S 的等价类的几何说明。

证明:因为(a+b i )S(c+d i )⇔ac>0(a,b ∈R,a ≠0,c ≠0)r:∀a ≠0,a2>0⇔(a+b i )S(a+b i )s:(a+b i )S(c+d i )⇔ac>0⇔ca>0⇔(c+d i )S(a+b i ) t:(a+b i )S(c+d i )∧(c+d i )S(u+v i )⇔ac>0∧cu>0⇔ au>0⇔(a+b i )S(u+v i ) 综上，S 是C 1上的一个等价关系。

由于ac>0，必须a ≠0,c ≠0且a 和c 同号，故S 只有2个等价类，其一是[1]={a+bi|a>0}，另一个是[-1]={a+bi|a<0}，它们分别对应于复平面上右半部和左半部。

离散数学习题习题⼀⼀、将下列命题符号化：1、蓝⾊和黄⾊可以调配成绿⾊。

2、蓝⾊和黄⾊都是常⽤的颜⾊。

3、52和之和是⽆理数。

4、52和都是有理数。

5、⼩丽⼀边吃苹果，⼀边看电视。

6、王⼤⼒不仅是百⽶冠军，⽽且是500⽶冠军。

7、李冰只能选学英语或只能选学法语。

8、种⽠得⽠，种⾖得⾖。

9、经⼀事，长⼀智，并且不经⼀事，不长⼀智。

10、经⼀事，长⼀智，并且不长⼀智，不经⼀事。

11、李和平是⼭西⼈或陕西⼈。

12、王⼩红虽然没上过⼤学，但她⾃学成才。

⼆、求复合命题的真值：设p ：4是素数，q ：南京在北京的北边，r ：苹果树是落叶乔⽊。

1、()r q p ?∧∧?2、()()r p q p ?→∧?3、()()q p q p ∨?三、求下列公式的成真赋值和成假赋值： 1、)r q p ?∧∧? 2、()()r p q p ?→∧? 3、()()q p q p ∧?∨?∧四、判断公式的类型：1、()p q r p →?∧∧2、()()()r p q q p ∨?→?→→3、()()r p q p →?→4、()()()()()r q p q p q p ∨∧?∨?∧→??5、()()r q r p ?→??6、()()()q r p q p ∧∧→?∧五、将下列复合命题符号化，并求真值：1、若π是⽆理数，⾃然对数的底e 也是⽆理数。

只有3是偶数，4才是素数。

2是⽆理数，仅当5不是⽆理数。

5是⽆理数。

2、若2和3都是素数，则5是奇数。

2是素数，3也是素数，所以5或6是奇数。

3、设x y 2=，x 为实数。

推理如下：若y 在x=0可导，则y 在x=0连续。

y 在x=0连续，所以y 在x=0可导。

六、⽤等值演算法证明： 1、()1?∨?∨→r q p p2、()()()()1?∧?∨?∧q p q p q p3、()()0?→?∧∨?q p q p4、()()()q p q p q p ∧?∧∨5、()()r q p r p q →∧?→→6、()()()()()()r p q r q p r q p q p ∧?∨∧∧∨?∧∧?∨∧七、求主析取范式和主合取范式，成真赋值和成假赋值：()()()()()()()()()()()()()p p q q p q p p q q p r q p r q p q r q p r p q r q p ?→?→∧∨?→?∨→∧?∨∧∧→→?∧∨?∧?∨∧∧∨、、、、、、654321 ⼋、将已知的命题公式等值地化成给定的联结词完备集中的公式：(){}()}{()}{()}{}{(){}中的公式。