课程名称(中文)偏微分方程数值解专题

《偏微分方程》课程教学大纲一、课程基本信息课程代码：16002102课程名称：偏微分方程英文名称：Partial Differential Equations课程类别：专业课学时：32学分： 2适用对象: 数学与应用数学、信息与计算科学考核方式：考查先修课程：数学分析、常微分方程、高等代数二、课程简介偏微分方程是以建立数学模型、进行理论分析和解释客观现象并进而解决实际问题为内容的一门数学分支学科，是现代数学的一个重要分支。

它在微分几何、物理学、计算数学和计算机图形学、金融数学等学科中都有许多重要应用。

本课程主要内容包括：偏微分方程的基本概念，二阶方程的特征理论和分类，分离变量法，双曲型、抛物型及椭圆型方程的求解方法及基本理论。

通过本课程的学习使学生初步认识如何从实际问题出发建立微分方程模型，培养学生分析问题和解决某些实际问题的能力，为日后的学习和工作打下坚实的基础，提供强有力的工具。

Partial differential equation is a branch of mathematics that establishes mathematical models, analyzes and interprets objective phenomena and then solves practical problems, is an important branch of modern mathematics. It also has many important applications in differential geometry, physics, computational mathematics and computer graphics, financial mathematics and other disciplines. The main contents of this course include: the basic concept of partial differential equation, the characteristic theory and classification of the second order equations, the method of separation of variables, the methods of solving hyperbolic，parabolic and elliptic equations and the basic theory of them. Through learning of this course makes students to know how to establish a differential equation model starting from the practical problems, to cultivate students' ability to analyze problems and solve some practical problems, lay a solid foundation for future study and work and provide a powerful tool.三、课程性质与教学目的课程性质：专业选修教学目的：偏微分方程是数学专业的一门重要专业课程。

偏微分方程的数值解法偏微分方程（Partial Differential Equation，PDE）是描述物理、化学、工程学等许多科学领域中变化的方程。

由于PDE的求解通常是困难的，因此需要使用数值方法。

本文将介绍偏微分方程的数值解法。

一般来说，求解PDE需要求得其解析解。

然而，对于复杂的PDE，往往不存在解析解，因此需要使用数值解法求解。

数值解法可以分为两类：有限差分法和有限元法。

有限差分法是将计算区域分成网格，利用差分公式将PDE转化为离散方程组，然后使用解线性方程组的方法求解。

有限元法则是将计算区域分成有限数量的单元，每个单元内使用多项式函数逼近PDE的解，在单元之间匹配边界条件，得到整个区域上的逼近解。

首先讨论有限差分法。

常见的差分公式包括前向差分、后向差分、中心差分等。

以一维热传导方程为例，其偏微分方程形式为：$$ \frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial x^2} $$其中，$u(x,t)$表示物理量在时刻$t$和位置$x$处的值。

将其离散化，可得到：$$ \frac{u(x_i,t_{j+1})-u(x_i,t_j)}{\Delta t}=\frac{u(x_{i+1},t_j)-2u(x_i,t_j)+u(x_{i-1},t_j)}{\Delta x^2} $$其中，$x_i=i\Delta x$，$t_j=j\Delta t$，$\Delta x$和$\Delta t$分别表示$x$和$t$上的网格大小。

该差分方程可以通过简单的代数操作化为：$$ u_{i,j+1}=u_{i,j}+\frac{\Delta t}{\Delta x^2}(u_{i+1,j}-2u_{i,j}+u_{i-1,j}) $$其中，$u_{i,j}$表示在网格点$(x_i,t_j)$处的数值解。

由于差分方程中一阶导数的差分公式只具有一阶精度，因此需要使用两个网格点来逼近一阶导数。

算法大全第20章偏微分方程的数值解偏微分方程（Partial Differential Equations，简称PDE）是描述自然界中各种物理现象的数学方程。

这些方程中的未知函数是多变量函数，而不是常微分方程中的单变量函数。

求解PDE是科学与工程中的重要问题，尤其在现代科学中，PDE的求解对于理解和预测自然现象具有重要的意义。

偏微分方程的数值解是指通过数值计算方法来求解PDE的近似解。

由于大多数情况下，PDE的解析解很难获得，因此数值解方法成为研究这些方程的重要工具之一、对于偏微分方程的数值解的研究主要集中在以下几个方面：1. 有限差分法（Finite Difference Method）：这是求解PDE最常用的方法之一、该方法通过将微分方程在空间和时间上进行离散化，转化为差分方程或代数方程组，然后通过求解这些方程组来得到数值解。

有限差分法的基本思想是将空间和时间进行网格划分，将未知函数的值在网格点上进行逼近，并用差分格式代替微分运算。

2. 有限元法（Finite Element Method）：该方法通过将求解域划分为若干个较小的单元，然后在每个单元中构建适当的数学模型，求解局部的代数问题，最终得到整个求解域的逼近解。

有限元法的优点是能够处理比较复杂的几何形状，适用于非结构网格，但需要更多的计算资源。

3. 边界元法（Boundary Element Method）：该方法主要用于求解边界值问题，将求解域划分为边界和内部两个部分。

边界元法通过在边界上离散化未知函数，并构建适当的积分方程来求解问题。

边界元法常用于求解椭圆型PDE，计算效率较高。

4. 特征线法（Characteristics Method）：该方法通过在方程中寻找适当的特征曲线，将PDE转化为一维常微分方程，然后求解这个常微分方程。

特征线法对于具有特殊类型边界条件的问题有很好的适用性，但在处理高维问题时存在困难。

以上只是偏微分方程数值解研究的一些常见方法，根据具体问题的特点和要求，还可以选择其他数值方法。

中国海洋大学本科生课程大纲课程属性：公共基础/通识教育/学科基础/专业知识/工作技能，课程性质：必修、选修一、课程介绍1.课程描述：本课程介绍数值求解偏微分方程的基本方法及相关的理论基础。

本课程针对数学类专业高年级（三年级）本科生开设。

课程基本内容包括：有限差分方法、差分格式的稳定性、收敛性分析；变分原理，Galerkin有限元方法等。

通过对模型问题的基本数值方法进行分析，阐明构造数值方法的基本思想和技巧。

通过本课程学习，使学生了解并掌握数值求解偏微分方程的基本思想、基本概念和基本理论（数值格式的相容性、稳定性、收敛性及误差估计等），能够运用算法语言对所学数值方法编制程序在计算机上运行实施并对数值结果进行分析。

培养学生理论联系实际，解决实际问题的能力和兴趣。

2.设计思路：偏微分方程是应用数学的核心内容，在其他科学、技术领域具有广泛深入的应用。

掌握偏微分方程的基础理论及求解方法是数学类专业本科生培养的基本要求。

本课程是在数学物理方程课程基础上开设的延展应用型课程，是一门数值分析理论与实践应用高度融合的专业课。

课程引导学生通过数值方法探讨和理解应用数学工具解决实际- 6 -问题的途径及理论分析框架。

学习本课程需要学生掌握了“数学分析”、“数学物理方程”、“数值分析”及“泛函分析”的核心基本内容。

课程内容安排分为有限差分方法和有限元方法两个单元模块，这是目前应用最广泛、理论发展最完善的两类数值方法，两者既有关联又有本质区别，能够体现偏微分方程数值解法的基本特征。

首先介绍有限差分方法。

有限差分方法是近似求解偏微分方程的应用最广泛的数值方法，以对连续的“导数（微分）”进行离散的“差分”近似为基本出发点，利用Fourier 分析及数值分析的基本理论，讨论椭圆、抛物、双曲等三类典型偏微分方程近似求解方法及近似方法的数学理论分析。

有限元方法是20世纪中期发展起来的基于变分原理的数值方法，具有更直接的物理背景含义，因而受到力学、工程等应用领域广泛的关注和应用。

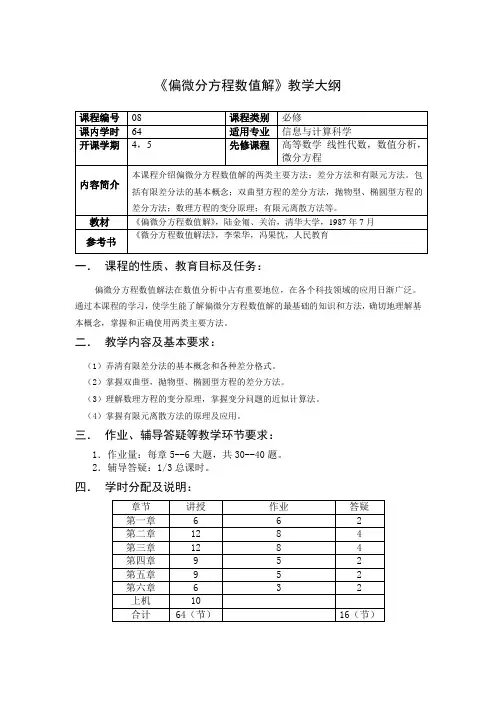
《偏微分方程数值解》教学大纲
一．课程的性质、教育目标及任务：
偏微分方程数值解法在数值分析中占有重要地位，在各个科技领域的应用日渐广泛。

通过本课程的学习，使学生能了解偏微分方程数值解的最基础的知识和方法，确切地理解基本概念，掌握和正确使用两类主要方法。

二．教学内容及基本要求：
（1）弄清有限差分法的基本概念和各种差分格式。

（2）掌握双曲型，抛物型、椭圆型方程的差分方法。

（3）理解数理方程的变分原理，掌握变分问题的近似计算法。

（4）掌握有限元离散方法的原理及应用。

三．作业、辅导答疑等教学环节要求：
1．作业量：每章5--6大题，共30--40题。

2．辅导答疑：1/3总课时。

四．学时分配及说明：。

偏微分方程:《偏微分方程》共分八章：第一章为绪论；第二、三章分别介绍了一阶方程、具有两个自变量的二阶方程的基本知识；第四、五、六章分别介绍了三类基本方程：波动方程、热传导方程和Laplace方程的定解问题的适定性、求解方法及解的性质；第七章主要介绍了一阶拟线性双曲守恒律方程组的一些基本知识；第八章介绍了Cauehy-Kovalevskaya定理。

另有两个附录：Fourier反演公式；Li-Yau估计。

《偏微分方程》不仅把注意力集中在传统的偏微分方程基础知识上，而且还有目的地介绍一些当代数学知识，譬如在几何分析中具有重要作用的Li-Yau估计和Hamack不等式等。

《偏微分方程》的另一特点是，除在每节后面为读者准备了一些习题之外，还在一些章节后面为读者准备了一些思考题和“开放问题（open problem）”。

这些问题具有一定的启发性，对提高学生对本门课程的学习兴趣有很大帮助。

偏微分方程数值解：通过数值计算方法，在计算机上对偏微分方程的近似求解。

科学和工程中的大多数实际问题都归结为偏微分方程的定解问题，由于很难求得这些定解问题的解析解（在经典意义下甚至没有解），人们转向求解它们的数值近似解。

简介：通过数值计算方法，在计算机上对偏微分方程的近似求解。

科学和工程中的大多数实际问题都归结为偏微分方程的定解问题，由于很难求得这些定解问题的解析解（在经典意义下甚至没有解），人们转向求解它们的数值近似解。

通常先对问题的求解区域进行网格剖分，然后基于有限元法、有限差分法和有限体积法等数值方法，对原定解问题或其等价形式离散，并归结为一个线性代数方程组，最终在计算机上求得精确解在离散网格点上的近似值。

求解涉及数值方法及其理论分析（稳定性、收敛性、误差估计）、计算机上的实现等一系列问题。

求解效率：求解的效率，一方面依赖计算机运行的速度，另一方面也依赖数值方法或算法，而且这方而更为重要。

自从1946年第一台电子计算问世（运行速度每秒500次乘法），到目前的千万亿次的超级计算机，计算速度得到了飞速发展。

偏微分方程数值解讲义教学设计1. 课程简介本课程是针对大学数学及计算机专业的高年级本科生或研究生开设的，旨在介绍偏微分方程数值解方法，包括有限差分法、有限元法和谱方法等。

本课程的学习目标是掌握偏微分方程数值解的基础理论和常用方法，以及了解数值解的数学原理和应用场景，并能够扩展应用所学知识解决相关实际问题。

2. 教学内容2.1 引言•偏微分方程的概念、分类和基本理论；•数值解的概念和分类，数值解的误差理论。

2.2 有限差分法•一维抛物方程、波动方程、椭圆方程的有限差分格式；•非线性偏微分方程的数值求解；•高维问题的数值求解。

2.3 有限元法•一维线性抛物方程、波动方程、椭圆方程的有限元求解方法；•二维和三维问题的有限元求解方法；•有限元法的加权残差方法和变分原理。

2.4 谱方法•调和方程的分离变量方法和Fourier级数解法；•Laplace方程的Fourier级数解法和离散正交函数解法；•泊松方程的Fourier级数解法和离散正交函数解法。

3. 教学手段3.1 讲课本课程采用讲课和练习相结合的方式，通过讲解理论知识和数值计算实例，并基于MATLAB或Python等数值计算软件进行演示。

3.2 练习结合课程中的实例，进行数值计算作业和课程项目的设计，以提高学生的理论知识和计算能力。

4. 教材教材推荐：•Numerical Solution of Partial Differential Equations: Finite Difference Methods by G. D. Smith •Finite Element Method: A Practical Course by C. S.Chen5. 教学评估学生的教学成绩考核由以下三部分组成：•期中考试（占成绩的30%）；•期末考试（占成绩的50%）；•课程设计作业（占成绩的20%）。

6. 教学进度内容讲课时间引言2课时有限差分法（一）6课时有限差分法（二）6课时有限差分法（三）4课时有限元法（一）6课时有限元法（二）6课时有限元法（三）4课时谱方法6课时课程设计作业4课时或更多7. 总结本文介绍了一个偏微分方程数值解讲义的教学设计，包括课程简介、教学内容、教学手段、教材、教学评估和教学进度等方面的内容。

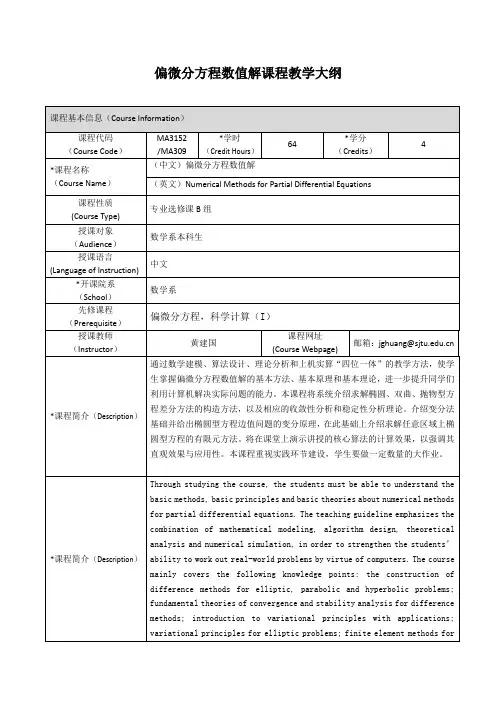
《偏微分方程数值解》课程教学大纲Numerical Solution of Partial Differential Equation课程代码： 课程性质：专业基础理论课/选修适用专业：信息计算开课学期：7总学时数：48总学分数：3编写年月：2003年3月修订年月：2007年7月执笔：王琦一、课程的性质和目的《偏微分方程数值解法》是计算数学专业的一门重要专业基础课。

它不仅对学生今后从事科研具有居高临下的指导作用，而且对于学习其它后继课程和解决一些实际问题都是一门重要的工具，同时对于训练思维能力起着很大作用。

本大纲是根据教育改革发展和面向二十一世纪高等数学专业课程设置和教学内容改革的要求，针对培养目标的需要进行设计的。

二、课程教学内容及学时分配第一章常微分方程初值问题10学时第二章变分原理8学时第三章椭圆型方程----有限差分法和有限元法10学时第四章离散方程的解法8学时第五章抛物型方程和双曲型方程12学时第一章常微分方程初值问题1.1 引论1.2 Euler方法和线形多步方法1.3 稳定性，收敛性和误差估计1.4 预估—校正算法1.5 Runge—Kutta方法第二章常微分方程初值问题2.1 二次函数的极值2.2 二阶椭圆边值问题2.3 Ritz方法第三章椭圆型方程----有限差分法和有限元法3.1 差分逼近的基本概念3.2 一维差分格式，矩形网和三角网差分格式3.3 极值定理3.4 解一维问题的线形元及误差估计3.5 解二维问题的矩形元和三角形元3.6 有限元方程3.7 收敛阶的估计第四章离散方程的解法4.1 离散方程的基本特征4.2 追赶法与迭代法4.3 超松弛法4.4 共轭斜量法第五章抛物型方程和双曲型方程5.1 稳定性与收敛性5.2 分离变量法5.3 差分格式的应用5.4 交替方向隐格式5.5 线形双曲型方程的差分逼近5.6 拟线形双曲型方程组5.7 基本定解问题和特征线法5.8 特征差分格式四、本课程与其它课程的联系与分工先修课程：数学分析，高等代数，常微分方程。

偏微分方程数值解讲义
《偏微分方程数值解讲义》是为高等院校计算数学专业高年级本科生和研究生偏微分方程数值解法课程编写的教材。

全书分为差分方法和有限元方法两个相互独立的部分。

差分方法部分的先修课程是数值分析、数值代数；有限元部分则同时要求学生对实变函数与泛函分析有初步的了解。

掌握一定的数学物理方程的理论和方法无疑有助于本课程的深入学习。

《偏微分方程数值解讲义》在选材上注重充分反映偏微分方程数值解法中的核心内容，力图展现算法构造与分析的基本思想；在内容的处理上，体现了由浅入深、循序渐进的原则；在叙述表达上，严谨精练、清晰易读，便于教学与自学。

为便于读者复习、巩固、理解和拓广所学的知识，每章之后配置了相当数量的习题，并在书后附上了大部分习题的答案或提示。

《偏微分方程数值解讲义》可作为综合大学、理工科大学、高等师范院校计算数学以及相关学科的本科生和研究生的教材或教学参考书，也可供从事计算数学、应用数学和科学工程计算研究的科技人员参考。

《偏微分方程数值解法》课程简介
课程名称：偏微分方程数值解法
英文名称：Numerical Solutions of Partial Differential Equations
课程编号：00907722
课程学时：32
课程学分：2
课程性质：学位课
适用专业：应用数学
预修课程：数学分析、高等代数、微分方程、数值代数、数值逼近等课程
大纲执笔人：张继红
主要教学内容：
本课程主要介绍边值问题的变分形式；椭圆和抛物型方程的有限元法；椭圆型方程的有限差分法；抛物型方程的有限差分法；双曲型方程的有限差分法等。

本课程通过对基本的典型算法进行仔细剖析，使学生循序渐进地掌握算法设计的基本思路和技巧，为今后解决实际问题或进入深层次地研究奠定良好的基础。

了解偏微分方程数值解产生的实际和历史背景，加深学生对微分方程数值解的重要性和必要性地认识，为以后的研究与实际应用打下扎实的基础。

教材及主要参考书：
1、李荣华，《偏微分方程数值解法》，高等教育出版社，2005.
2、李荣华、冯果忱编，《微分方程数值解法》（第三版），高等教育出版社，1996.
3、余德浩，汤华中，《微分方程数值解法》，科学出版社，2002.
4、李庆扬，王能超，易大义编，《数值分析》清华大学出版社，2001.
1。