《计算机仿真技术》试题(含完整答案)

中南大学考试试卷2009 -- 2010 学年 1 学期期末考试试题 时间110分钟计算机仿真技术 课程 32 学时 2 学分 考试形式： 开 卷 专业年级： 自动化06级 总分100分，占总评成绩70% 注：请将答案写在答卷上一 填写下列运算结果（本题12分，每空2分）已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=542031321i A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=581051301i B ,则 (1) A (1:3,3)＝ 305⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(2) B (2:3 ) ＝ []11(3) A ’＝112234305i ⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦(4) B.’＝ 111058305i ⎡⎤⎢⎥⎢⎥⎢⎣⎦+⎥ (5) A.*B ＝ 10931155023225i i +⎡⎤⎢⎥+⎢⎥⎢⎥⎣⎦(6) A*B ＝ 63418415531160312i i i i i +⎡⎤⎢⎥+++⎢⎥⎢⎥+⎣⎦二 判断正误（本题20分，每小题2分）(1) 计算机仿真的三要素为系统、模型和计算机。

（ √ ）(2) 在MATLAB 中，变量名区分字母的大小写，但是MATLAB 提供的标准函数名以及命令名必须用小写字母。

（ × ）(3) MATLAB 中运算符号前带有小点表示执行元素对元素的运算。

（ √ ）(4) 在MATLAB 中，2ⅹ2的矩阵A=[1 2，3 4]是一种正确的输入方式。

（ × ）(5) clc 命令不仅用于清除命令窗口显示的内容同时也删除MATLAB 工作空间中的变量。

（ × ）(6) MATLAB 提供了3种逻辑操作符，其中~表示非。

（ √ ）(7) subplot(211)把屏幕分成两个部分，并把曲线放在左半部分。

（ × ）(8) 数值积分法中，计算步长越小，总误差越小。

（ × ）(9) tf2ss 函数只能将传递函数模型转换成为可控标准型状态方程。

（ √ ）(10) 函数文件中函数名称和文件名可以不同。

控制系统计算机辅助设计综合实验指导实验名称：连续与离散系统校正实验，系统可控性与可观性实验，系统的simulink仿真实验陈茜编实验人：苏建聪学号：200830810122班级：08电气工程及其自动化1班信息工程系实验任务书1. 有一个单位负反馈控制系统，如果控制对象的传递函数为设计要求：① 相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

2. 有一个单位负反馈控制系统，如果控制对象的传递函数为：试设计一个串联滞后校正装置。

设计要求：①相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

3. 有一个单位负反馈控制系统，如果控制对象的传递函数为 ()()4+=s s k s G p试设计一个串联超前滞后校正装置，设计要求： ①相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

4. 系统结构图如图所示，其中，采样周期Ts=0.01s ，被控对象()()110+=s s s G ，()s G h 为零阶保持器。

用W 变换法设计一超前校正装置D(z)，使系统相位裕度γ≥50°，校验设计后系统的性能指标。

5. 系统结构图如图所示，其中，采样周期Ts=0.01s ，被控对象1)s(0.2s k )(+=s G ο，()s G h 为零阶保持器。

用对数频率法设计D(z)，使系统开环增益k ≥30(1/s)，截止频率ωc ≥15(1/s),相位裕度γ≥50 °1使 s 11se -1(s)-Tsh T G +≈=，求出未校正系统的开环系统的开环传递函数(s)(s)G G (s)0s =G ,的传递函数模型参数。

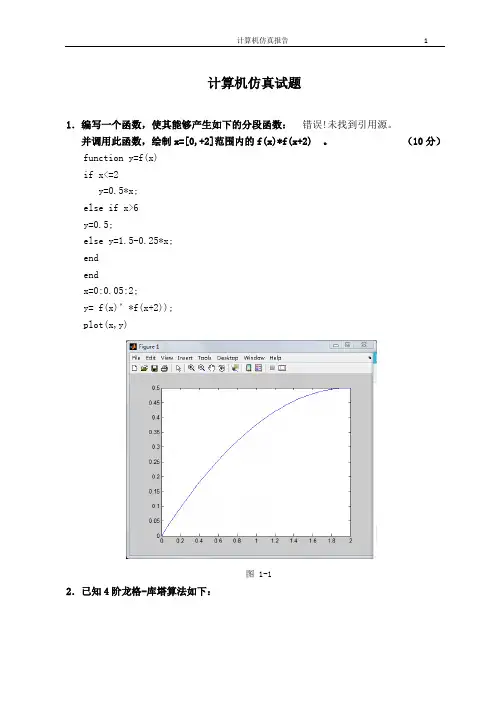
计算机仿真试题1．编写一个函数，使其能够产生如下的分段函数：错误！未找到引用源。

并调用此函数，绘制x=[0,+2]范围内的f(x)*f(x+2) 。

（10分）function y=f(x)if x<=2y=0.5*x;else if x>6y=0.5;else y=1.5-0.25*x;endendx=0:0.05:2;y= f(x)’*f(x+2));plot(x,y)图 1-12．已知4阶龙格-库塔算法如下：试利用该算法求解以下微分方程：（15分）本题可以调用MATLAB函数中龙格-库塔算法函数ode45，首先编写m文件：function dy=func(x,y)dy=-y+1;end再在主窗口调用此文件：[x,y]=ode45('func',[0,5],0)%这里的[0,5]为任取区间，表示方程在此范围的解。

运行结果如下:x =0.00010.00010.00020.00020.00050.00070.00100.00120.00250.00370.00500.00620.01250.01880.02510.0313 0.06270.09410.12550.15690.28190.40690.53190.65690.78190.90691.03191.15691.28191.40691.53191.65691.78191.90692.03192.15692.28192.40692.53192.65692.78192.90693.03193.15693.28193.40693.53193.65693.78193.90694.03194.15694.28194.40694.53194.65694.74274.82854.91425.0000y =0.00010.00010.00020.00020.00050.00070.00100.00120.0025 0.0037 0.0050 0.0062 0.0124 0.0186 0.0248 0.0309 0.0608 0.0898 0.1180 0.1452 0.2457 0.33430.41250.48160.54250.59630.64370.68550.72250.75510.78390.80930.83170.85150.86890.88430.89790.90990.92050.92980.93810.94540.95180.95740.96240.96690.97080.97420.97720.97990.98230.98430.98620.98780.98920.99050.99130.99200.99270.9933为只管起见，我们使用函数命令画出x-y（plot(x,y)）的关系如下图：图1-23．用matlab语言求下列系统的状态方程、传递函数、零极点增益、和部分分式形式的模型参数，并分别写出其相应的数学模型表达式：（15分）（1）G（s）=324327242410355024s s ss s s s+++++++（2）.X=2.25 -5 -1.25 -0.542.25 -4.25 -1.25 -0.2520.25 -0.5 -1.25 -121.25 -1.75 -0.25 -0.75 0X⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦uy= [0 2 0 2] X解：（1）a)求对应状态方程参数：num=[1 07 24 24]; den=[1 10 35 50 24]; [A,B,C,D]=tf2ss(num,den) 运行结果：A =-10 -35 -50 -241 0 0 00 1 0 00 0 1 0B =1C =1 7 24 24D =故，状态方程为：.X = x+ uY=[1 7 24 24]xb)求对应零极点增益模型参数：num=[1 07 24 24]; den=[1 10 35 50 24]; [Z,P,K]=tf2zp(num,den) 运行结果如下： Z =-2.7306 + 2.8531i -2.7306 - 2.8531i -1.5388P = -4.0000 -3.0000 -2.0000 -1.0000K = 1故变换后的零极点模型为： G(s)=c)求对应部分分式型：num=[1 07 24 24]; den=[1 10 35 50 24]; [R,P,H]=residue(num,den) 运行结果如下： R =4.0000 -6.0000 2.0000 1.0000P =-4.0000 -3.0000 -2.0000 -1.0000H = []故变换后的部分分式模型为：11223644)(+++++-+=s s s s s G（2）由题给条件，知：A=[2.25 -5 -1.25 -0.5; 2.25 -4.25 -1.25 -0.25;0.25 -0.5 -1.25 -1;1.25 -1.75-10 -35 -50 -24 1 0 0 0 0 1 0 0 0 0 1 010 0 0-0.25 -0.75] B=[4;2;2;0] C=[0 2 0 2],D=0 a)求传递函数矩阵： [num,den]=ss2tf(A,B,C,D) 运行结果为： num =0 4.0000 14.0000 22.0000 15.0000 den =1.0000 4.0000 6.2500 5.25002.2500 故，所对应传递函数模型为：25.225.525.641522144)(23423+++++++=s s s s s s s s Gb)求零极点模型：num=[0 4 14 22 15];en=[1 4 6.25 5.25 2.25]; [Z,P,K]=tf2zp(num,den) 运行结果为： Z =-1.0000 + 1.2247i -1.0000 - 1.2247i -1.5000 P =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iK =4.0000故，零极点模型为：)866.05.0()5.1()2247.11)(5.1(4)(2i s s i s s s G ±++±++=c)求对应部分分式模型： [R,P,H]=residue(num,den) 运行结果为： R =4.0000 -0.0000-0.0000 - 2.3094i -0.0000 + 2.3094iP =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iH = []故变换后的部分分式模型为：i s ii s i s s G 866.05.03094.2866.05.03094.25.14)(+++-+-++=4．已知一单位反馈系统开环传递函数为：，试绘制系统Nyquist图，判断闭环系统的稳定性，并求其单位阶跃响应。

一、数值计算，编程完成以下各题〔共20分，每题5分〕1、脉冲宽度为d ，周期为T 的矩形脉冲的傅里叶级数如下式描述：)2cos(/)/sin(21[)(1τπππτn T d n T d n T d f n ∑∞=+=当150=n ，41=T d ，2/12/1<<-τ，绘制出函数)(τf 的图形。

解： syms n t;f=((sin(n*pi/4))/(n*pi/4))*cos(2*pi*n*t); s=symsum(f,n,1,150); y=(1+2*s)/4; x=-0.5:0.01:0.5; Y=subs(y,'t',x); plot(x,Y)2、画出函数5505.025.55.15.1cos 5)5(sin )(2x x x x ex x f x +++-=在区间[3,5]的图形，求出该函数在区间[3, 5]中的最小值点m in x 和函数的最小值m in f .解：程序如下 x=3:0.05:5;y=(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5; mix_where=find(y==min(y)); xmin=x(mix_where); hold on; plot(x,y);plot(xmin,min(y),'go','linewidth',5);str=strcat('(',num2str(xmin),',',num2str(min(y)),')'); text(xmin,min(y),str); Xlabel('x')Ylabel('f(x)')经过运行后得到的图像截图如下：运行后的最小值点m in x =4.6，m in f = -8337.86253、画出函数xe x xf x 5.2cos )(3.02-⋅=-在[1，3]区间的图形，并用编程求解该非线性方程0)(=x f 的一个根，设初始点为20=x .解： x=1:0.02:3; x0=2;y=@(x)(cos(x).^2).*exp(-0.3*x)-2.5*abs(x); fplot(y,[1,3]); Xlabel('x') Ylabel('f(x)')X1=fzero('(cos(x).^2).*exp(-0.3*x)-2.5*abs(x)',x0)运行后求得该方程的一个根为z=0.3256。

《计算机仿真技术》考试试卷(B 卷)班级 姓名 学号一．填空题。

(每空1分，共20分)1、计算机仿真技术三要素是_______________、_________________、________________。

2、计算机仿真中模型能够代表系统来进行研究，模型主要有________________、________________、________________、________________等几类模型。

3、叙述simulink 中常见的固定步长的仿真算法有：________________、________________、________________、________________。

(任举四种)4、MATALB 主要相似性主要包含以下几种相似_________________、________________、___________________。

5、Simulink 中主要包含_________________、________________、_______________等几种模块。

6、符号运算中，泰勒级数计算的函数是________________，拉普拉斯变换的函数________________，傅里叶级数的计算函数是________________。

二．简答题。

(本题5小题，每题8分，共40分)1、简述根据信号类型分类，计算机仿真主要包含哪几种类型。

2、简述蒙特卡洛法建模的步骤。

3、m 函数文件和m 文本文件之间的区别。

4、叙述三维立体绘图常用的几个绘图指令及其功能。

5、简述matlab 软件的基本组成三．编程题 (本题6小题、共40分)根据下面要求，只需写出程序代码，不需计算结果和图形。

1、(5分)写出右面的矩阵D ，求出其大于4的元素有几个，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=059123107D并通过变量列出其在矩阵的位置和序号2、(5分)求解下面矩阵A 的行列式和逆矩阵，并利用命令取出系数矩阵的逆矩阵的第二行的数据，以小数点后面两位数值的形式显示出来。

系统仿真技术阶段练习⼀及答案系统仿真技术阶段练习⼀第⼀章：计算机仿真技术概述1．系统的概念，系统的边界。

2．模型的定义。

3．简述模型型谱。

4．仿真的定义。

5. 仿真三要素及三项基本活动之间的关系。

6．按照状态变量的特点，系统怎么分类？第⼆章数学建模⽅法1．什么是机理建模，对典型的RLC 电路进⾏建模。

2．什么叫做数据建模？数据建模的前提及主要⽅法。

3. 什么叫系统辨识，常见的系统辨识⽅法。

⿊箱⽩箱经济⽣理经济过程控制动⼒学电⼦电路集中参数常微分⽅程分布参数偏微分⽅程离散时间差分⽅程4．最⼩⼆乘的定义，公式？5．简述模糊建模、神经⽹络建模、模糊神经⽹络建模的定义，特点。

第⼀章：计算机仿真技术概述1.系统的概念，系统的边界。

答：A system can be defined as a set of component which are related by some forms of interaction ,and which act together to achieve some objective or purpose.在定义⼀个系统时，⾸先要确定系统的边界。

尽管世界上的事物是相互联系的，但当我们研究某⼀对象时，总是要将该对象与其环境(environment)区别开来。

边界确定了系统的范围。

边界以外对系统的作⽤称为系统的输⼊，系统对边界以外的环境的作⽤称为系统的输出。

2.模型的定义。

答：是对真实系统中那些有⽤的和令⼈感兴趣的特性的抽象化。

模型并不是对真实系统的完全复现。

如果M 能够⽤来回答关于系统（S)的问题，并且在精度范围A 之内，那末M 就是系统S 的模型。

3.简述模型型谱。

答：⽩箱：运⾏机理了解⽐较深⼊，基本上可以通过演绎的⽅法来建⽴模型；灰箱：对系统不太了解，要通过演绎和归纳相结合的⽅法来建⽴模型；⿊箱：对系统了解不太清楚，主要通过系统辨识的⽅法或数据收集和统计归纳的⽅法来建⽴模型，由于数据掌握得不够多，模型精度⼀般⽐较差。

题号 一 二 三 四 总分 得分一、填空（共15分，每空1分）１．机械系统的分类是 、 。

２．仿真系统模型的应用分别是 、 、 。

３．空间状态模型主要包括 、 。

４．机械工程领域常见的数字仿真算法是； 、 。

５．功率键合图主要组成部分是 、 、 、 、 。

二、根据系统模型编写C 程序求曲柄滑块机构的位移、速度、加速度（共15分）弹簧质量系统如下图，相关参数为k1=1.2，k2=1.5，k3=1.6。

三、建立空间状态方程（共20分，每题10分）1、 分析质量弹簧系统，列出该系统的微分方程然后根据微分方程写出其状态方程2、将传递函数转化为空间状态方程写出计算步骤得分阅卷人 得分阅卷人 得分阅卷人2四、画出下列系统的功率键合图并写出绘图步骤（共30分，每题10分）１． 绘出右图的键合图并写出步骤２. 绘出右图小车系统键合图并写出绘图步骤3. 一个生长在罐中的细菌的简单模型。

假定细菌的出生率和当前细菌的总数成正比，死亡率和当前的总数的平方成正比，试建立仿真模型，画出键合图。

五、列出系统的状态方程和simulink 模型（共20分）列出右图蹦极系统的状态方程并写出其状态方程。

桥梁距地面的距离是h2=50m ，人距桥梁的距离是h1=30m 。

系统参数为k=20，a1=a2=1，m=70，g=10系统数学模型是2009～2010学年第二学期《计算机仿真技术》期终试卷（B卷）…………………………………装…………订………线…………………………………专业级班姓名学号得分…………………………………密…………封…………线………………………………第3 页共3 页。

一、数值计算，编程完成以下各题（共20分，每小题5分） 1、脉冲宽度为d ，周期为T 的矩形脉冲的傅里叶级数如下式描述：)2cos(/)/sin(21[)(1τπππτn T d n T d n T d f n ∑∞=+=当150=n ，41=T d ，2/12/1<<-τ，绘制出函数)(τf 的图形。

解： syms n t;f=((sin(n*pi/4))/(n*pi/4))*cos(2*pi*n*t); s=symsum(f,n,1,150); y=(1+2*s)/4; x=-0.5:0.01:0.5; Y=subs(y,'t',x); plot(x,Y)2、画出函数5505.025.55.15.1cos 5)5(sin )(2x x x x ex x f x +++-=在区间[3,5]的图形，求出该函数在区间[3, 5]中的最小值点m in x 和函数的最小值m in f .解：程序如下 x=3:0.05:5;y=(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5; mix_where=find(y==min(y)); xmin=x(mix_where); hold on; plot(x,y);plot(xmin,min(y),'go','linewidth',5);str=strcat('(',num2str(xmin),',',num2str(min(y)),')'); text(xmin,min(y),str); Xlabel('x')Ylabel('f(x)')经过运行后得到的图像截图如下：运行后的最小值点m in x =4.6，m in f = -8337.86253、画出函数xe x xf x 5.2cos )(3.02-⋅=-在[1，3]区间的图形，并用编程求解该非线性方程0)(=x f 的一个根，设初始点为20=x .解： x=1:0.02:3; x0=2;y=@(x)(cos(x).^2).*exp(-0.3*x)-2.5*abs(x); fplot(y,[1,3]); Xlabel('x') Ylabel('f(x)')X1=fzero('(cos(x).^2).*exp(-0.3*x)-2.5*abs(x)',x0)运行后求得该方程的一个根为z=0.3256。

1、 控制系统的分析与设计方法可以分为 时域法 、 频域法 。

2、 根据仿真时间与系统实际时钟的关系，控制系统仿真可以分为 实时仿真 、 亚实时仿真 、 超实时仿真 。

3、 判断系统稳定性的方法主要有 利用极点判断稳定性 、 利用特征值判断系统稳定性 、利用李雅普洛夫第二法判断系统稳定性 。

4、 常用的离散化方法主要有 简单替换法 、 双线性变换法 、 零阶或一阶保持器法 。

5、 根据采样周期的选择不同，采样控制系统仿真可以分为 同步采样 、 异步采样 。

6、 增量式PID 控制器的表达式为()())2()1(2)()()1()()1()(-+--++--+-=k e k e k e k k e k k e k e k k u k u d i p 。

7、 已知系统脉冲传递函数为2121425)()()(----+-+==zz z z z z U z Y s G ，则该系统的差分方程为)3()2(5)3(4)2(2)(-+-+---=k u k u k y k y k y 。

8、 已知系统的状态方程为X X ⎥⎦⎤⎢⎣⎡--=2221&，则该系统是否稳定 是 （填是或否），其特征值为 2712,1j s ±-=。

1、简述计算机仿真的基本步骤。

答：（1）根据仿真目的确定仿真方案；（2）建立系统的数学模型；（3）选择合适仿真方法，建立仿真模型；（4）编写仿真程序并进行程序调试；（5）进行仿真实验；（6）仿真结果分析。

2、试比较数值积分法与离散相似法的区别。

答：数值积分法：比较成熟，精度较高，计算公式复杂，计算量大，适合离线仿真；离散相似法：计算公式简单，计算量小，速度快，精度较数值积分法低，适合在线仿真。

3、已知系统结构图如下图所示，1、2、3、4、5为典型环节，a 为常数，试写出其连接矩阵W 、W0、Wc （10分）解：由图可知⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+===-=415314231241x x u xx u x u xu ax r u ， 从而：r x x x x x a u u u u u U ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=000010100100101000100000100005432154321 []⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡==54321510000x x x x x x y所以：⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=01001010*******000010000a W ， ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=000010W ， []10000=c W4、已知系统状态空间表达式为[]⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=Xt y t u X X 01)()(012101&，⎥⎦⎤⎢⎣⎡=11)0(X ，计算步长1.0=h ，输入信号1=u （0≥t ）试采用欧拉法，四阶龙格－库塔法计算h t =时对应的y 值。

第0章绪论0-1 什么是仿真？它所遵循的基本原则是什么？答：仿真是建立在控制理论、相似理论、信息处理技术和计算机技术等理论基础之上的，以计算机和其他专用物理效应设备为工具，利用系统模型对真实或假想的系统进行试验，并借助专家经验知识、统计数据和信息资料对试验结果进行分析和研究，进而做出决策的一门综合性的试验性科学。

它所遵循的基本原则是相似原理。

0-2 仿真的分类有几种？为什么？答：依据相似原理来分：物理仿真、数学仿真和混合仿真。

物理仿真：就是应用几何相似原理，制作一个与实际系统相似但几何尺寸较小或较大的物理模型（例如飞机模型放在气流场相似的风洞中）进行实验研究。

数学仿真：就是应用数学相似原理，构成数学模型在计算机上进行研究。

它由软硬件仿真环境、动画、图形显示、输出打印设备等组成。

混合仿真又称数学物理仿真，它是为了提高仿真的可信度或者针对一些难以建模的实体，在系统研究中往往把数学仿真、物理仿真和实体结合起来组成一个复杂的仿真系统，这种在仿真环节中有部分实物介入的混合仿真也称为半实物仿真或者半物理仿真。

0-3 比较物理仿真和数学仿真的优缺点。

答：在仿真研究中，数学仿真只要有一台数学仿真设备（如计算机等），就可以对不同的控制系统进行仿真实验和研究，而且，进行一次仿真实验研究的准备工作也比较简单，主要是受控系统的建模、控制方式的确立和计算机编程。

数学仿真实验所需的时间比物理仿真大大缩短，实验数据的处理也比物理仿真简单的多。

与数学仿真相比，物理仿真总是有实物介入，效果直观逼真，精度高，可信度高，具有实时性与在线性的特点；但其需要进行大量的设备制造、安装、接线及调试工作，结构复杂，造价较高，耗时过长，灵活性差，改变参数困难，模型难以重用，通用性不强。

0-4 简述计算机仿真的过程。

答：第一步：根据仿真目的确定仿真方案根据仿真目的确定相应的仿真结构和方法，规定仿真的边界条件与约束条件。

第二步：建立系统的数学模型对于简单的系统，可以通过某些基本定律来建立数学模型。

第0章绪论0-1 什么是仿真？它所遵循的基本原则是什么？答：仿真是建立在控制理论、相似理论、信息处理技术和计算机技术等理论基础之上的，以计算机和其他专用物理效应设备为工具，利用系统模型对真实或假想的系统进行试验，并借助专家经验知识、统计数据和信息资料对试验结果进行分析和研究，进而做出决策的一门综合性的试验性科学。

它所遵循的基本原则是相似原理。

0-2 仿真的分类有几种？为什么？答：依据相似原理来分：物理仿真、数学仿真和混合仿真。

物理仿真：就是应用几何相似原理，制作一个与实际系统相似但几何尺寸较小或较大的物理模型（例如飞机模型放在气流场相似的风洞中）进行实验研究。

数学仿真：就是应用数学相似原理，构成数学模型在计算机上进行研究。

它由软硬件仿真环境、动画、图形显示、输出打印设备等组成。

混合仿真又称数学物理仿真，它是为了提高仿真的可信度或者针对一些难以建模的实体，在系统研究中往往把数学仿真、物理仿真和实体结合起来组成一个复杂的仿真系统，这种在仿真环节中有部分实物介入的混合仿真也称为半实物仿真或者半物理仿真。

0-3 比较物理仿真和数学仿真的优缺点。

答：在仿真研究中，数学仿真只要有一台数学仿真设备（如计算机等），就可以对不同的控制系统进行仿真实验和研究，而且，进行一次仿真实验研究的准备工作也比较简单，主要是受控系统的建模、控制方式的确立和计算机编程。

数学仿真实验所需的时间比物理仿真大大缩短，实验数据的处理也比物理仿真简单的多。

与数学仿真相比，物理仿真总是有实物介入，效果直观逼真，精度高，可信度高，具有实时性与在线性的特点；但其需要进行大量的设备制造、安装、接线及调试工作，结构复杂，造价较高，耗时过长，灵活性差，改变参数困难，模型难以重用，通用性不强。

0-4 简述计算机仿真的过程。

答：第一步：根据仿真目的确定仿真方案根据仿真目的确定相应的仿真结构和方法，规定仿真的边界条件与约束条件。

第二步：建立系统的数学模型对于简单的系统，可以通过某些基本定律来建立数学模型。

《计算机仿真技术》考试试卷(A卷)班级姓名学号一．填空题。

(每空1分，共20分)1、计算机仿真中系统由_________________、_________________、________________等三个要素组成。

2、常见的系统实验建模法有________________、________________、________________、________________等几种方法。

3、叙述simulink中常见的可变步长的仿真算法有：________________、________________、________________、________________。

(任举四种)4、MA TALB的Comand windows窗口中可以显示workspace中的全部变量的命令是_________________、_________________。

5、计算机仿真算法的算法引起的误差是________________、________________。

6、三维立体绘图中，________________ 是三维曲线绘图命令，________________是三维网格线绘图命令，________________着色表面图绘图命令。

7、符号运算中，泰勒级数计算的函数是________________傅里叶变换的函数________________二．简答题。

(本题5小题，每题8分，共40分)1、计算机仿真的目的和作用2、列举几种计算机仿真软件，并简要介绍一下（要求4种以上）3、matlab主界面主要包括那些窗口，分别有什么样的功能4、局部变量和全局变量之间的区别5、计算机仿真技术中相似性主要包含那几个方面三．编程题 (本题6小题、共40分)根据下面要求，写出程序代码。

1、(5分)设(2E －C -1B)A T =C -1，其中E 是4阶单位矩阵，A T 是4阶矩阵A 的转置。

求矩阵A2、(5分)输入下面的矩阵，求出特征多项式和特征根，并求出特征多项式的微分。

习题3
1、已知系统响应函数为)sin(11)(θ+-=-bt e b
t y bt ，其中21l b -=，)1arctan(2
l
l -=θ，要求用不同的线型或颜色，在同一张图上绘制l 取值为0.2,、0.4、0.6、0.8时，系统在[]18,0∈t 区间内的响应曲线，并要求用2.0=l 和8.0=l 对它们相应的两条曲线进行文字标志。

答：刚开始因为没有考虑到相乘或相除矩阵的维度而总出错，后来理解清楚之后就简单多了。

编写程序如下：
得到结果：
2、用plot
3、mesh 、surf 指令，绘制2222)1()1(1y x y x z ++++-=
三维图（x 、y 范围自定）。

答：用plot3时，我定义]100,0[∈x ，]100,0[∈y ；并分别令22)1(y x a +-=，22)1(y x b ++=。

同时需注意将1变换成与a 、b 同维的矩阵。

得到结果：
在利用mesh、surf绘图时，为了图形美观取]
x，x=y.
[-
∈
100
,
100
程序如下：
得到结果：
3、对向量t进行以下运算可以构成3个坐标的值向量：)
y=，
cos(t
x=，)
sin(t
z=。

利用plot3指令，并选用绿色的实线绘制相应的三维曲线。

t
答：取pi
:0(
:1.0
=。

注意绿色是‘g’。

编写程序如下：
t*
)
10
得到结果：。

计算机仿真技术与CAD第三版课后练习题含答案前言计算机仿真技术与CAD第三版是近年来广受欢迎的CAD教材。

本书涵盖了CAD 的基础知识、CAD的应用、计算机仿真技术等内容，适合CAD初学者和高级用户使用。

本文主要介绍本书的课后练习题及答案，希望对大家有所帮助。

第一章课后练习题及答案1.1 选择题1.以下哪项不是CAD应用的领域？A. 工程学B. 数学C. 植物学D. 医学答案：C2.CAD是什么的缩写？A. Computer-ded Design（计算机辅助设计）B. Computer-ded Distance（计算机辅助距离）C. Capsule-med Destruction（胶囊定向破坏）D. Capability-Assisted Driving（能力协助驾驶）答案：A1.2 填空题1.CAD软件主要分为三种类型，分别是2D __________ 、3D__________ 、仿真软件。

答案：制图软件、制造软件2.AutoCAD是一款 __________ 系统。

答案：二维制图3.CAD软件通常可以完成______________ 、___________ 、____________ 等操作。

答案：制图、设计、分析1.3 综合应用题设计一件简单的图形，包括设备名称、设备布局图、视图图和详细图。

并在AutoCAD中实现。

答：见图。

简单图形简单图形图中的简单图形包括了设备名称、设备布局图、视图图和详细图。

其中，设备名称为“简单图形”，设备布局图包含了该设备的位置、大小和方向信息，视图图包含了设备的3D视角，详细图则针对设备内部的结构进行了细节描绘。

使用AutoCAD可以方便地实现这件图形的设计和制图。

第二章课后练习题及答案……第三章课后练习题及答案……第四章课后练习题及答案……结语以上是《计算机仿真技术与CAD第三版》的部分课后练习题及答案，希望对大家有所帮助。

本书内容丰富、简明易懂，是一本非常优秀的CAD教材。