第一章 部分习题参考答案-高建强

一轮复习必修1 第1章第1、2节一、选择题1．下面关于绿藻和蓝藻的叙述不正确的是()A．绿藻和蓝藻都能进行光合作用，这与它们含有叶绿体有关B．绿藻和蓝藻合成蛋白质的场所都是核糖体C．绿藻有核膜、核仁，而蓝藻没有D．绿藻和蓝藻的大爆发与水体富营养化有关2．(2011·蚌埠模拟)下列有关生命系统结构层次的叙述不正确的是()A．细胞是地球上最基本的生命系统B．“三倍体”是从个体层次对体细胞染色体数量特征的描述C．“太湖中所有鱼”属于生命系统研究的一个结构层次D．物质循环是指组成生物体的元素在生命系统的最高层次内所进行的循环运动3．(2011·银川调研)下图是高中生物有关实验的操作和叙述：图甲是用低倍显微镜观察洋葱根尖细胞时某视野中的图像，如要看清有丝分裂期的细胞，应将装片适当向____移动；图乙是在高倍显微镜下观察到的黑藻叶细胞的细胞质处于不断流动的状态，图中所标记的那一个叶绿体实际流动所处的位置是位于____角，____时针方向流动()A．右、右下、逆B．右、右下、顺C．左、左下、逆D．左、左下、顺4．(2011·临沂模拟)在使用高倍镜观察酵母菌和大肠杆菌时()A．都可以观察到细胞壁、细胞核B．都可以观察到核糖体C．若发现视野上方较暗下方较亮，应调节反光镜D．在换用高倍镜之后，只能用粗准焦螺旋调焦5．(2010·南京质检)图a、b、c分别是三种生物细胞的结构模式图。

下列叙述正确的是()A．以上三种细胞内遗传物质的载体是染色体B．a细胞有细胞壁，而b、c细胞没有该结构C．三种细胞中共同具有的细胞器只有核糖体D．a、b细胞内具膜结构的细胞器构成了生物膜系统6．(2011·哈尔滨质检)下面甲图示洋葱根尖分生区连续分裂的细胞在各个时期细胞核内DNA含量的测定结果，乙图是一组目镜标有×5和×15字样、物镜标有×10和×40字样的镜头，丙图是某同学在乙图中选用的一组能放大50倍的镜头组合所观察到的图像。

高等数学加强版教材答案第一章表达式、方程、不等式1.1 表达式与算式1.1.1 表达式的概念与性质1.1.2 整式、分式及其化简1.1.3 多项式及其运算1.2 多项式的因式分解与整除式1.2.1 因式分解的基本思想1.2.2 因式分解的常用方法1.2.3 整式的除法运算1.3 一次不等式与一元一次方程1.3.1 一次不等式的基本性质1.3.2 一元一次方程的梯形图解法1.4 绝对值方程和绝对值不等式1.4.1 绝对值方程的解法1.4.2 绝对值不等式的解集求法第二章数列与数列极限2.1 通项与前n项和2.1.1 等差数列与等差数列的前n项和2.1.2 等比数列与等比数列的前n项和2.2 数列极限的概念及性质2.2.1 数列极限的定义与基本性质2.2.2 数列极限计算与判断2.3 数列极限的运算与不等式2.3.1 数列极限的运算法则2.3.2 数列极限与数列不等式的应用2.4 递推数列的极限2.4.1 递推数列的定义与性质2.4.2 递推数列的极限计算第三章函数与极限3.1 实数与函数3.1.1 实数的有理数和无理数3.1.2 函数的概念与性质3.2 函数的极限3.2.1 函数极限的定义与基本性质3.2.2 函数极限的计算与判断3.3 函数的连续性3.3.1 函数连续的定义与性质3.3.2 闭区间上连续函数的性质3.4 函数的导数3.4.1 导数的概念与基本性质3.4.2 常用函数的导数计算3.5 函数的应用3.5.1 极限在函数性质研究中的应用3.5.2 导数在函数性质研究中的应用第四章极限与微分4.1 函数极限的运算法则4.1.1 函数极限的四则运算4.1.2 复合函数的极限4.2 反函数与反函数的极限4.2.1 反函数的概念与性质4.2.2 反函数的极限计算4.3 微分与导数的基本性质4.3.1 微分的概念与性质4.3.2 导数的定义与求导法则4.4 高阶导数与隐函数微分4.4.1 高阶导数的定义与求法4.4.2 隐函数微分的基本公式4.5 导数的应用4.5.1 函数的单调性与极值问题4.5.2 用导数研究函数的图象和函数的应用第五章微分中值定理与高等数学基本技巧5.1 高阶导数与泰勒公式5.1.1 高阶导数的性质与求导法则5.1.2 函数的泰勒展开与泰勒公式5.2 微分中值定理及其应用5.2.1 罗尔定理与拉格朗日中值定理5.2.2 导数的应用：误差估计与函数图象5.3 函数的凸性与拐点5.3.1 函数的凸性及判定5.3.2 函数的拐点及其求法5.4 不定积分与定积分5.4.1 不定积分的定义与基本性质5.4.2 定积分的定义与性质5.5 微分方程5.5.1 微分方程的基本概念5.5.2 一阶微分方程的解法与应用。

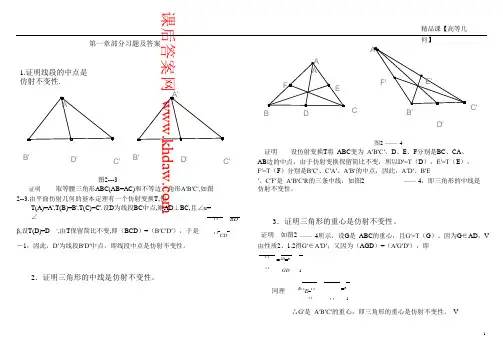
课后答案网1.证明线段的中点是仿射不变性.第一章部分习题及答案B DC B'精品课【高等几何】D'C'B' D'C'图2---3B' D'C'图2 ——4证明设仿射变换T将ABC变为A′B′C′，D、E、F分别是BC、CA、AB边的中点，由于仿射变换保留简比不变，所以D′=T（D），E′=T（E），F′=T（F）分别是B′C′、C′A′、A′B′的中点，因此，A′D′、B′E′、C′F′是A′B′C′R的三条中线，如图2 ——4，即三角形的中线是证明取等腰三角形ABC(AB=AC)和不等边三角形A′B′C′,如图仿射不变性。

2--3.由平面仿射几何的基本定理有一个仿射变换T,使T(A)=A',T(B)=B',T(C)=C'.设D为线段BC中点,则AD⊥BC,且∠α=∠' ' BD3．证明三角形的重心是仿射不变性。

β,设T(D)=D ’,由T保留简比不变,即（BCD）=（B′C′D′），于是' '=CD=证明如图2 ——4所示，设G是ABC的重心，且G′=T（G）。

因为G∈AD，V －1，因此，D′为线段B′D′中点，即线段中点是仿射不变性。

由性质2、1.2得G′∈A′D′；又因为（AGD）=（A′G′D′），即' ' =AD=32．证明三角形的中线是仿射不变性。

' ' GD 1同理B' 'E=' '' ' ' '=31∴G′是A′B′C′的重心，即三角形的重心是仿射不变性。

V1课后答案网4．角的平分线是不是仿射不变量？答：不是。

如图2 ——6所示。

DBC D'精品课【高等几何】C'B DC B' D' C'如图2 ——7设在仿射对应下，梯形ABCD（AB∥CD，AD‖BC）功能四边形A′B′C′D′相对应，由于仿射对应保持平性不变，所以A′B′∥C′D′,A′D′‖B′C′,故A′B′C′D′为梯形，即梯形在仿射对应下仍为梯形。

第一节质点参考系和坐标系【三维目标】知识与技能１．认识建立质点模型的意义和方法能根据具体情况将物体简化为质点，知道它是一种科学的抽象，知道科学抽象是一种普遍的研究方法。

２．理解参考系的选取在物理中的作用，会根据实际情况选定参考系。

３．认识一维直线坐标系，掌握坐标系的简单应用。

过程与方法１．体会物理模型在探索自然规律中的作用，初步掌握科学抽象理想化模型的方法。

２．通过参考系的学习，知道从不同角度研究问题的方法。

３．体会用坐标方法描述物体位置的优越性。

情感态度与价值观１．认识运动是宇宙中的普遍现象，运动和静止的相对性，培养学生热爱自然、勇于探索的精神。

２．渗透抓住主要因素，忽略次要因素的哲学思想。

３．渗透具体问题具体分析的辩证唯物主义思想。

教学重点１．理解质点概念以及初步建立质点要点所采用的抽象思维方法。

２．在研究具体问题时，如何选取参考系。

３．如何用数学上的坐标轴与实际的物理情景结合起来建立坐标系。

教学难点在什么情况下可以把物体看作质点。

课时安排１课时教学过程导入我们知道宇宙中的一切物体都在不停地运动着，机械运动是最基本、最普遍的运动形式，那么什么是机械运动呢？请列举几个运动物体的例子。

机械运动简称运动，指物体与物体间或物体的一部分和另一部分间相对位置随时间发生改变的过程。

新课教学一、物体和质点问题：选择以上一个较复杂的运动（例如鸟的飞行），我们如何描述它？引导学生分析：１．描述起来有什么困难？２．我们能不能把它当作一个点来处理？３．在什么条件下可以把物体当作质点来处理？小结１．只有质量，没有形状和大小的点叫做质点。

２．质点是一种科学抽象，一一种理想化的模型，这种忽略次要因素、突出主要因素（质量）的处理方法是一种非常重要的科学研究方法。

３．一个物体能否看成质点，取决于它的形状和大小在所研究问题中是否可以忽略不计，而跟自身体积的大小、质量的多少和运动速度的大小无关。

４．一个物体能否被看成质点，取决于所研究的问题的性质，同一个物体在不同的问题中，有的能被看作质点，有的却不能被看成质点。

新课程标准数学必修1第一章课后习题解答第一章 集合与函数概念1．1集合练习（P5）1.(1)中国∈A ，美国∉A ，印度∈A ，英国∉A.(2)∵A={x |x 2=x }={0，1}，∴-1∉A. (3)∵B={x |x 2+x -6=0}={-3，2}，∴3∉A.(4)∵C={x ∈N|1≤x ≤10}={1，2，3，4，5，6，7，8，9，10}，∴8∈C ，9.1∉C.2.(1){x |x 2=9}或{-3，3}; (2){2，3，5，7};(3){(x ，y )|⎩⎨⎧+=+=6-2x y 3x y }或{(1，4)};(4){x ∈R |4x -5<3}或{x |x <2}. 练习（P7）1.∅，{a }，{b }，{c }，{a ，b }，{a ，c }，{b ，c }，{a ，b ，c }.2.(1)a ∈{a ，b ，c }. (2)∵x 2=0，∴x =0.∴{x |x 2=0}={0}.∴0∈{0}.(3)∵x 2+1=0，∴x 2=-1.又∵x ∈R ，∴方程x 2=-1无解.∴{x ∈R |x 2+1=0}=∅.∴∅=∅. (4). (5)∵x 2=x ，∴x =0或x =1.∴{x |x 2=x }={0，1}.∴{0}{0，1}.(6)∵x 2-3x +2=0，∴x =1或x =2.∴{x |x 2-3x +2=0}={1，2}.∴{2，1}={1，2}.3.(1)由于1是任何正整数的公约数，任何正整数都是自身的公约数，所以8的公约数是1，2，4，8，即B={1，2，4，8}.∴AB.(2)显然B ⊆A ，又∵3∈A ，且3∉B ，∴B A. (3)4与10的最小公倍数是20，4与10的公倍数应是20的倍数，显然A=B.练习（P11）1.A∩B={5，8}，A ∪B={3，5，6，7，8}.2.∵x 2-4x -5=0，∴x =-1或x =5.∴A={x |x 2-4x -5=0}={-1，5}，同理，B={-1，1}.∴A ∪B={-1，5}∪{-1，1}={-1，1，5}，A∩B={-1，5}∩{-1，1}={-1}.3.A∩B={x |x 是等腰直角三角形}，A ∪B={x |x 是等腰三角形或直角三角形}.4.∵B={2，4，6}，A={1，3，6，7}，∴A∩(B)={2，4，5}∩{2，4，6}={2，4}， (A)∩(B)={1，3，6，7}∩{2，4，6}={6}.习题1.1 A 组（P11）1.(1)∈ (2)∈ (3)∉ (4)∈ (5)∈ (6)∈2.(1)∈ (2)∉ (3)∈3.(1){2，3，4，5}; (2){-2，1};(3){0，1，2}.(3)∵-3<2x -1≤3，∴-2<2x ≤4.∴-1<x ≤2.又∵x ∈Z ，∴x =0，1，2.∴B={x ∈Z |-3<2x -1≤3}={0，1，2}.4.(1){y |y ≥-4}; (2){x |x ≠0}; (3){x |x ≥54}. 5.(1)∵A={x |2x -3<3x }={x |x >-3}，B={x |x ≥2}，∴-4∉B ，-3∉A ，{2}B ，B A.(2)∵A={x |x 2-1=0}={-1，1}，∴1∈A ，{-1}A ，∅A ，{1，-1}=A. (3);. 6.∵B={x |3x -7≥8-2x }={x |x ≥3}，∴A ∪B={x |2≤x <4}∪{x |x ≥3}={x |x ≥2}，A∩B={x |2≤x <4}∩{x |x ≥3}={x |3≤x <4}.7.依题意，可知A={1，2，3，4，5，6，7，8}，所以A∩B={1，2，3，4，5，6，7，8}∩{1，2，3}={1，2，3}=B ，A∩C={1，2，3，4，5，6，7，8}∩{3，4，5，6}={3，4，5，6}=C.又∵B ∪C={1，2，3}∪{3，4，5，6}={1，2，3，4，5，6}.∴A∩(B ∪C)={1，2，3，4，5，6，7，8}∩{1，2，3，4，5，6}={1，2，3，4，5，6}.又∵B∩C={1，2，3}∩{3，4，5，6}={3}，∴A ∪(B∩C)={1，2，3，4，5，6，7，8}∪{3}={1，2，3，4，5，6，7，8}=A.8.(1)A ∪B={x |x 是参加一百米跑的同学或参加二百米跑的同学}.(2)A∩C={x |x 是既参加一百米跑又参加四百米跑的同学}.9.B∩C={x |x 是正方形}， B={x |x 是邻边不相等的平行四边形}，A={x |x 是梯形}.10.∵A ∪B={x |3≤x <7}∪{x |2<x <10}={x |2<x <10}，∴(A ∪B)={x |x ≤2或x ≥10}.又∵A∩B={x |3≤x <7}∩{x |2<x <10}={x |3≤x <7}，∴(A∩B)={x |x <3或x ≥7}. (A)∩B={x |x <3或x ≥7}∩{x |2<x <10}={x |2<x <3或7≤x <10}，A ∪(B)={x |3≤x <7}∪{x |x ≤2或x ≥10}={x |x ≤2或3≤x <7或x ≥10}.习题1.2 A 组（P24）1.∵A={1，2}，A ∪B={1，2}，∴B ⊆A ，∴B=∅，{1}，{2}，{1，2}.2.集合D={(x ，y )|2x -y =1}∩{(x ，y )|x +4y =5}表示直线2x -y =1与直线x +4y =5的交点坐标;由于D={(x ，y )|⎩⎨⎧=+=54y x 1y -2x }={(1，1)}，所以点(1，1)在直线y =x 上，即D C. 3.B={1，4}，当a =3时，A={3}，则A ∪B={1，3，4}，A∩B=∅;当a ≠3时，A={3，a }，若a =1，则A ∪B={1，3，4}，A∩B={1};若a =4，则A ∪B={1，3，4}，A∩B={4};若a ≠1且a ≠4，则A ∪B={1，a ，3，4}，A∩B=∅.综上所得，当a =3时，A ∪B={1，3，4}，A∩B=∅;当a =1，则A ∪B={1，3，4}，A∩B={1};当a =4，则A ∪B={1，3，4}，A∩B={4};当a ≠3且a ≠1且a ≠4时，A ∪B={1，a ，3，4}，A∩B=∅.4.作出韦恩图，如图1-1-3-16所示，图1-1-3-16由U=A ∪B={x ∈N|0≤x ≤10}，A∩(B)={1，3，5，7}，可知B={0，2，4，6，8，9，10}.1．2函数及其表示练习（P19）1.(1)要使分式741+x 有意义，需4x+7≠0，即x≠47-. 所以这个函数的定义域是(-∞，47-)∪(47-，+∞); (2)要使根式有意义，需1-x≥0，且x+3≥0，即-3≤x≤1.所以这个函数的定义域是［-3，1］.2.(1)f(2)=28，f(-2)=-28，f(2)+f(-2)=0;(2)f(a)=3a 3+2a ，f(-a)=-3a 3-2a ，f(a)+f(-a)=0.3.(1)两个函数的对应法则相同，而表示导弹飞行高度与时间关系的函数y=500x-5x 2是有实际背景的，这里x≥0;函数y=500x-5x 2，x ∈R ，这两个函数的定义域不同，故这两个函数不相等.(2)函数g(x)=x 0=1(x≠0)与函数f(x)=1，x ∈R 的对应法则相同，但定义域不同，所以不是相等的函数.已知函数解析式求函数值及不同变量的函数值的关系.练习（P23）1.设矩形一边长为xcm ，则另一边长为22x -50=22500x -.由题意，得y=x 22500x -，x ∈(0，50).2.图(A)与事件(2).图(B)与事件(3).图(D)与事件(1)吻合得最好.图(C)可叙述为:我出发后,为了赶时间,加速行驶,走了一段后,发现时间还早,于是放慢了速度.3.解析:由绝对值的知识，有f(x)=⎩⎨⎧<+-≥-.2,2,2,2x x x x 所以，f(x)=|x-2|的图象如下图所示.图1-2-2-234.与A 中元素60°对应的B 中的元素是23;与B 中元素22相对应的A 中的元素是45°. 习题1.2 A 组（P24）1.(1)(-∞，4)∪(4，+∞). (2)R .(3)要使分式有意义，只需x 2-3x+2≠0，即x≠1，且x≠2，所以这个函数的定义域是(-∞，1)∪(1，2)∪(2，+∞).(4)要使函数有意义，只需⎩⎨⎧≠≤⇒⎩⎨⎧≠-≥-,1,40104x x x x 即x≤4，且x≠1. 所以这个函数的定义域是(-∞，1)∪(1，4］. 2.(1)g(x)=xx 2-1=x-1，x≠0，该函数虽然与f(x)的对应关系相同，但是定义域不同， 所以f(x)与g(x)不相等. (2)g(x)=(x )4=x 2，x≥0，该函数虽然与f(x)的对应关系相同，但是定义域不同，所以f(x)与g(x)不相等. (3)g(x)=36x =x 2，x ∈R ，该函数与f(x)的对应关系相同，定义域相同，所以f(x)与g(x)相等.3. (1) (2)x ∈R ，y ∈R . x ∈(-∞，0)∪(0，+∞)，y ∈(-∞，0)∪(0，+∞).图1-2-2-24 图1-2-2-25(3) (4)x ∈R ，y ∈R . x ∈R ，y ∈［-2，+∞).图1-2-2-26 图1-2-2-27 4.f(2-)=8+52，f(-a)=3a 2+5a+2，f(a+3)=3a 2+13a+14; f(a)+f(3)=3a 2-5a+16.5.(1)点(3，14)不在f(x)的图象上;(2)f(4)=-3;(3)x=14.6.解析:由韦达定理知1+3=-b ，1×3=c ，∴b=-4，c=3.∴f(x)=x 2-4x+3.∴f(-1)=(-1)2-4×(-1)+3=8. 答案：f(-1)=8.7. (1) (2)图1-2-2-28 图1-2-2-29 8.y=x 10 x ∈(0，+∞)，y=21l-x x ∈(0，21l)， y=22x d - x ∈(0，d)，l=2x+x 20(x>0)，l=2202+d . 9.由题意，可知容器内溶液高度为x 的体积等于注入的溶液的体积，即π(2d )2·x=vt ，整理得x=24d v π·t. 当容器注满时有π(2d )2h=vt ，得t=vh d 42π. 所以该函数的定义域是t ∈［0，v h d 42π］，值域是x ∈［0，h ］. 10.共8个映射.图1-2-2-30B 组1.(1)［-5，0］∪［2，6);(2)［0，+∞);(3)［0，2)∪(5，+∞).2.图1-2-2-31(1)点(x ，0)和(5，y)，即纵坐标为0或横坐标为5的点不能在图象上. (2)略.3.略.4.(1)t=512342x x -++，x ∈［0，12］;(2)t=58320+≈3小时. 1．3 函数的基本性质练习（P32）1.从生产效率与生产线上工人数量的关系看，在生产劳动力较少的情况下，随人数的增加效率随着增大，但是到了一定数量后，人数再增多效率反而降低了.这说明劳动力可能过剩，出现了怠工等现象.2.图象如图1-3-2-2所示，图1-3-2-2函数的单调增区间为［8,12)，［13,18)；函数的单调减区间为［12,13)，［18,20］.3.函数的单调区间是［-1,0),［0,2),［2,4),［4,5］.在区间［-1,0),［2,4)上是减函数；在区间［0,2),［4,5］上是增函数.4.证明：设x 1、x 2∈R ，且x 1<x 2，则f (x 1)-f (x 2)=(-2x 1+1)-(-2x 2+1)=2(x 2-x 1).∵x 1<x 2，∴x 2-x 1>0.∴f (x 1)>f (x 2).∴函数f (x )=-2x +1在R 上是减函数.5.如图1-3-2-3所示，图1-3-2-3从图象上可以发现f （－2）是函数的一个最小值.练习（P36）1.（1）对于函数f （x ）=2x 4+3x 2，其定义域为（－∞,+∞）.因为对定义域内的每一个x ，都有f （－x ）=2（－x ）4+3（－x ）2=2x 4+3x 2=f （x ）,所以函数f （x ）=2x 4+3x 2为偶函数.（2）对于函数f （x ）=x 3－2x ，其定义域为（－∞，+∞）.因为对定义域内的每一个x ，都有f （－x ）=（－x ）3－2（－x ）=－x 3+2x =－（x 3－2x ）=－f （x ）,所以函数f （x ）=x 3－2x 为奇函数.（3）对于函数f (x )=xx 12+，其定义域为（－∞，0）∪（0，+∞）. 因为对定义域内的每一个x ，都有f （－x ）=x x -+-1)(2=xx 12+-=－f （x ）, 所以函数f (x )=xx 12+-为奇函数. （4）对于函数f (x )=x 2+1，其定义域为（－∞，+∞）.因为对定义域内的每一个x ，都有f （－x ）=(-x )2+1=x 2+1=f （x ）,所以函数f (x )=x 2+1为偶函数.2.f (x )的图象如图1-3-2-4所示，g (x )的图象如图1-3-2-5所示.图1-3-2-4 图1-3-2-5习题1.2 A 组（P39）1.（1）函数的单调区间是(-∞,25］,(25,+∞). 函数y =f (x )在区间(-∞,25］上是减函数，在区间(25,+∞)上是增函数. （2）函数的单调区间是(-∞,0］,(0,+∞).函数y =f (x )在区间(0,+∞)上是减函数，在区间(-∞,0］上是增函数. 图略.2.（1）设0<x 1<x 2，则有f (x 1)-f (x 2)=(x 12+1)-(x 22+1)=x 12-x 22=(x 1-x 2)(x 1+x 2).∵0<x 1<x 2，∴x 1-x 2<0，x 1+x 2<0. ∴f (x 1)>f (x 2). ∴函数f (x )在(-∞,0)上是减函数.（2）设0<x 1<x 2，则有f (x 1)-f (x 2)=(111x -)-(121x -)=21x 11x -=2121x x x x -. ∵0<x 1<x 2,∴x 1-x 2<0,x 1x 2>0. ∴f (x 1)<f (x 2). ∴函数f (x )在(-∞,0)上是增函数.3.设x 1、x 2是（－∞，+∞）上任意两个实数，且x 1＜x 2.则y 1－y 2=（mx 1+b ）－（mx 2+b ）=m （x 1－x 2）.∵x 1＜x 2，∴x 1－x 2＜0.当m ＜0时，∴y 1－y 2＞0，即y 1＞y 2.∴此时一次函数y =mx +b （m ＜0）在（－∞，+∞）上是减函数.同理可证一次函数y =mx +b （m ＞0）在（－∞,+∞）上是增函数.综上所得，当m ＜0时，一次函数y =mx +b 是减函数；当m ＞0时，一次函数y =mx +b 是增函数.4.心率关于时间的一个可能的图象，如图1-3-2-6所示，图1-3-2-65.y =502x -+162x -2100=501-(x 2-8100x )-2100=501-(x -4050)2+307 050. 由二次函数的知识,可得当月租金为4 050元时，租赁公司的月收入最大，最大收益为307 050元.6.图略，函数f (x )的解析式为⎩⎨⎧<-≥+.0),1(,0),1(x x x x x x B 组1.（1）函数f (x )在(-∞,1)上为减函数，在［1,+∞)上为增函数；函数g (x )在［2,4］上为增函数.（2）函数f (x )的最小值为－1，函数g (x )的最小值为0.2.设矩形熊猫居室的宽为x m ，面积为y m 2，则长为2330x -m ， 那么y =x 2330x -=21(30x -3x 2)=23-(x -5)2+275.所以当x =5时，y 有最大值275, 即宽x 为5 m 时才能使所建造的每间熊猫居室面积最大，最大面积是275m 2. 3.函数f (x )在(-∞,0)上是增函数.证明：设x 1<x 2<0，则-x 1>-x 2>0.∵函数f (x )在(0,+∞)上是减函数，∴f (-x 1)<f (-x 2).∵函数f (x )是偶函数，∴f (-x )=f (x ).∴f (x 1)<f (x 2).∴函数f (x )在(-∞,0)上是增函数.第一章 复习参考题A 组（P44）1.（1）A={－3，3}；（2）B={1，2}；（3）C={1，2}.2.（1）线段AB 的垂直平分线；（2）以定点O 为原心，以3 cm 为半径的圆.3.属于集合的点是△ABC 的外接圆圆心.4.A={－1,1}，（1）若a =0，则B=∅，满足B ⊆A ；（2）若a =－1，则B={－1}，满足B ⊆A ；（3）若a =1，则B={1}，满足B ⊆A.综上所述，实数a 的值为0,-1,1.5.A∩B={（x ,y ）｜⎩⎨⎧=+=0y 3x 0y -2x }={（x ,y ）|⎩⎨⎧==0y 0x }={（0,0）}; A∩C={（x ,y ）|⎩⎨⎧==3y -2x 0y -2x }=∅； B∩C={（x ,y ）｜⎩⎨⎧==+3y -2x 0y 3x }={（x ,y ）｜⎪⎪⎩⎪⎪⎨⎧-==5953y x }={（53,59-）}; （A∩B ）∪（B∩C ）={(0,0),(53,59-)}. 6.(1)要使函数有意义,必须|x |-2≥0,即x ≤-2或x ≥2,所以函数的定义域为{x |x ≤-2或x ≥2};（2）要使函数有意义，必须⎩⎨⎧≥+≥-,05,02x x 即⎩⎨⎧-≥≥,5,2x x 得x ≥2.所以函数的定义域为{x ｜x ≥2}；（3）要使函数有意义，必须⎩⎨⎧≠-≥-,05||,04x x 即x ≥4，且x ≠5. 所以函数的定义域为{x ｜x ≥4，且x ≠5}.7.（1）f （a ）+1=111++-a a =12+a ; （2）f （a +1）=)1(1)1(1+++-a a =a a +-2. 8.（1）∵f （－x ）=22)(1)(1x x ---+=2211xx -+，∴f （－x ）=f （x ）. （2）∵f （x 1）=22)1(1)1(1x x -+=221111x x -+=222211x x x x -+=1122-+x x =2211x x -+-,∴f （x 1）=－f （x ）. 9.二次函数f (x )的对称轴是直线x =8k ，则有8k ≤5或8k ≥20.解得k ≤40或k ≥160，即实数k 的取值范围是(-∞,40］∪［160,+∞).10.（1）函数y =x -2是偶函数； （2）它的图象关于y 轴对称；（3）函数在（0，+∞）上是减函数；（4）函数在（－∞，0）上是增函数.B 组 1.同时参加田径和球类比赛的有3人，只参加游泳一项比赛的有9人.提示：由题意知有15人参加游泳比赛，有8人参加田径比赛，有14人参加球类比赛，所以15+8+14=37，知共有37人次参加比赛.由已知共有28名同学参赛，且没有人同时参加三项，而37－28=9，知共有9名同学参加两项比赛.已知同时参加游泳和田径的有3人，同时参加游泳和球类的有3人，因此同时参加田径和球类的有3人；又已知有15人参加游泳比赛，因此只参加游泳一项的有9人.2.实数a 的取值范围为{a ｜a ≥0}.3.∵（A ∪B ）=（A ）∩（B ）={1，3}，A∩（B ）={2，4}，∴B={1,2,3,4}.∴B={5,6,7,8,9}.4.f （1）=1×（1+4）=5; f （－3）=－3×（－3－4）=21; f （a +1）=⎩⎨⎧-<++-≥++.1),3)(1(,1),5)(1(a a a a a a 5.证明：（1）f )2(21x x +=a ·221x x ++b =22221b ab b ax x +++=21（ax 1+b ）+21（ax 2+b ）=21［f （x 1）+f （x 2）］， ∴f （221x x +）=21［f （x 1）+f （x 2）］. （2）g （221x x +）=（221x x +）2+a ·221x x ++b =21（21x +ax 1+b ）+21（22x +ax 2+b ）－41（x 1－x 2）2 =21［g （x 1）+g （x 2）］－41（x 1－x 2）2, ∵－41（x 1－x 2）2≤0, ∴g （221x x +）≤21［g （x 1）+g （x 2）］. 6.（1）奇函数f （x ）在［－b ,－a ］上是减函数；（2）偶函数g （x ）在［－b ,－a ］上是减函数.7.若全月纳税所得额为500元，则应交纳税款为500×5%＝25（元）.此时月工资为800＋500＝1 300（元）；若全月纳税所得额为2000元，则应交纳税款为500×5%＋1500×10%＝175（元）.此时月工资为800＋500＋1500＝2800（元）.由于此人交纳税款为26.78元，则此人的工资在区间（1300，2800）内，所以他当月的工资、薪金所得是800＋500＋1.02578.26-≈1317.8（元）.奇、偶函数的性质(1)奇偶函数的定义域关于原点对称；奇函数的图象关于原点对称，偶函数的图象关于y 轴对称.(2)奇偶性是函数的整体性质，对定义域内任意一个x 都必须成立.(3)f (-x )=f (x )⇔f (x )是偶函数，f (-x )=-f (x )⇔f (x )是奇函数.(4)f (-x )=f (x )⇔f (x )-f (-x )=0,f (-x )=-f (x )⇔f (x )+f (-x )=0.(5)两个奇函数的和(差)仍是奇函数，两个偶函数的和(差)仍是偶函数.奇偶性相同的两个函数的积(商、分母不为零)为偶函数，奇偶性相反的两个函数的积(商、分母不为零)为奇函数；如果函数y =f (x )和y =g (x )的奇偶性相同，那么复合函数y =f ［g (x )］是偶函数，如果函数y =f (x )和y =g (x )的奇偶性相反，那么复合函数y =f ［g (x )］是奇函数，简称为“同偶异奇”.(6)如果函数y =f (x )是奇函数，那么f (x )在区间(a ,b )和(-b ,-a )上具有相同的单调性；如果函数y =f (x )是偶函数，那么f (x )在区间(a ,b )和(-b ,-a )上具有相反的单调性.(7)定义域关于原点对称的任意函数f (x )可以表示成一个奇函数与一个偶函数的和，即f (x )=2)()(2)()(x f x f x f x f -++--.(8)若f (x )是(-a ,a )(a ＞0)上的奇函数，则f (0)＝0；若函数f (x )是偶函数，则f (x )=f (-x )=f (|x |)=f (-|x |).若函数y =f (x )既是奇函数又是偶函数，则有f (x )=0。

第一章习题参考答案与提示第一章随机事件与概率习题参考答案与提示1．设为三个事件，试用表示下列事件，并指出其中哪两个事件是互逆事件：CBA、、CBA、、（1）仅有一个事件发生；（2）至少有两个事件发生；（3）三个事件都发生；（4）至多有两个事件发生；（5）三个事件都不发生；（6）恰好两个事件发生。

分析：依题意，即利用事件之间的运算关系，将所给事件通过事件表示出来。

CBA、、解：（1）仅有一个事件发生相当于事件CBACBACBA、、有一个发生，即可表示成CBACBACBA∪∪；类似地其余事件可分别表为（2）或ACBCAB∪∪ABCCBABCACAB∪∪∪；（3）；（4）ABCABC或CBA∪∪；（5）CBA；（6）CBABCACAB∪∪或。

ABCACBCAB−∪∪—由上讨论知，（3）与（4）所表示的事件是互逆的。

2．如果表示一个沿着数轴随机运动的质点位置，试说明下列事件的包含、互不相容等关系：x{}20|≤=xxA {}3|>=xxB{}9|<=xxC{}5|−<=xxD {}9|≥=xxE解：（1）包含关系：、ACD⊂⊂BE⊂。

（2）互不相容关系：C与E（也互逆）、B与、DE与。

D3．写出下列随机事件的样本空间：（1）将一枚硬币掷三次，观察出现H（正面）和T（反面）的情况；（2）连续掷三颗骰子，直到6点出现时停止, 记录掷骰子的次数；（3）连续掷三颗骰子，记录三颗骰子点数之和；；（4）生产产品直到有10件正品时停止，记录生产产品的总数。

提示与答案：（1）；{}TTTTTHTHTHTTTHHHTHHHTHHH,,,,,,,=Ω（2）；{ ,2,1=Ω}（3）；{}18,,4,3 =Ω（4）。

{} ,11,10=Ω4．设对于事件有CBA、、=)(AP4/1)()(==CPBP, ，8/1)(=ACP1第一章习题参考答案与提示0)()(==BCPABP，求至少出现一个的概率。

CBA、、提示与答案：至少出现一个的概率即为求，可应用性质4及性质5得CBA、、)(CBAP∪∪()PABC 5 / 8 =∪∪—5．设A、B为随机事件，(=−=BAPAP，，求)(ABP。

高数第一册 第一章习题1.13.(1)(,1)(1,)(2){|1,}1(1,1)(1,)(3)(1,1)x x x R -∞-⋃-+∞≠±∈∞-⋃-⋃+∞-或（-，） （4）22903[3,1)(1,3]10x x x x x ⎧⎫-≥⇒-⎪⎪⇒--⋃⎨⎬-⇒⎪⎪⎩⎭≤ ≤3＞＞1或＜-1 2222(5)(,3)(6)sin 0,,()241(7)114(1),11(1)3x x k x k k z x x x x x x πππ-∞≠≠≠∈⎡⎤≤⇒≤⇒≤+⇒-⎢⎥++⎣⎦（8）0ln 0x x x x x ⎧⎫⇒⇒⎨⎬⇒⎩⎭＞ ＞0＞1＞＞1(9)[1,2]-（10）21()x x x f x x x x x x x x ⎧⎫⇒⎪⎪⎪⎪=⇒⇒≠⇒∴⎨⎬⎪⎪⎪⎪⇒⎩⎭-1 ＜00≤≤10即0＜＜1 ＜ 0和0＜≤2e 1≤≤27．(1)(2)(3)(4)(5)奇函数偶函数偶函数偶函数非奇非偶 （6）2()()f x f x -==偶函数 （7）11()lnln ()11x xf x f x x x+--==-=--+奇函数） （8）2112()()2112x xxxf x f x -----===-++奇函数 （9）()sin cos f x x x -=--非奇非偶 13．（1）22(())(2)24,(())2,xxxx f x f f x x R ϕϕ====∈（2）11(())(0,1)111x f f x x xx-==≠-- （3）32221,()(1)3(1)256()56(1)(1)5(1)6x t f t t t t t f x x x f x x x +==---+=-+∴=-++=+-++则x=t-1,或：14．[]22(1)(0)0.(2)0,111111(3)01(4)1lg ,lg 1,lg 1,.1(5)11()(6)1log (16)y x x y x y y x y x x y y y xx y x y y x xy xx x y x x x =≤≤+∞=≥=-++===≠-+==-=--=≠-+∞⎧=≤≤∞反函数反函数x=,x-1=,x=1+反函数y ，定义域反函数定义域x ＞0反函数,定义域（x ）－＜＜1反函数16)＜＜+⎫⎪⎬⎪⎩⎭习题1.22。

高中第一章测试题及答案一、选择题（每题3分，共30分）1. 以下哪项不是高中数学第一章的重点内容？A. 集合的概念B. 函数的定义C. 微积分的初步D. 集合的运算2. 高中数学第一章中，集合的表示方法不包括以下哪一项？A. 列举法B. 描述法C. 韦恩图D. 函数表达式3. 若集合A={1,2,3}，集合B={2,3,4}，则A∩B等于：A. {1}B. {2,3}C. {3,4}D. {1,2,3,4}4. 函数f(x)=2x+1的定义域是：A. RB. ZC. QD. N5. 函数f(x)=x^2的值域是：A. RC. QD. N6. 以下哪项不是函数的基本性质？A. 单调性B. 奇偶性C. 连续性D. 可导性7. 函数y=f(x)的图像是一条直线，那么f(x)是：A. 一次函数B. 二次函数C. 三次函数D. 指数函数8. 函数f(x)=x^3-3x+2的极值点是：A. x=1B. x=-1C. x=0D. x=29. 函数f(x)=|x|的图像是：A. 一条直线B. 一条抛物线C. 一条V形曲线D. 一条水平线10. 函数f(x)=sin(x)的周期是：A. 2πB. πD. 0二、填空题（每题3分，共30分）1. 集合{1,2,3}的补集在全集U={1,2,3,4,5}中表示为______。

2. 函数f(x)=x^2的反函数是______。

3. 若函数f(x)在x=a处可导，则f(x)在x=a处______。

4. 函数y=2x-3与x轴的交点坐标为______。

5. 函数f(x)=x/(x+1)的值域是______。

6. 函数f(x)=√x的定义域是______。

7. 若函数f(x)在区间(a,b)上单调递增，则f(x)在该区间上______。

8. 函数f(x)=ln(x)的图像在y轴右侧是______。

9. 函数f(x)=x^2-4x+3的最小值是______。

10. 函数f(x)=cos(x)的图像在每个周期内______。

浙科版高一上册生物第一章课后练习：有机
化合物及生物大分子
1.(2010年高考江苏卷)某种蛋白酶是由129个氨基酸脱水缩合形成的蛋白质，下列叙述正确的是( )
A.该蛋白酶分子结构中至少含有129个氨基和129个羧基
B.该蛋白酶溶液与双缩脲试剂发生作用，产生紫色反应
C.利用透析法纯化该蛋白酶时，应以蒸馏水作为透析液
D.用含该蛋白酶的洗衣粉去除油渍，效果比其他类型加酶洗衣粉好
2.(2010年高考海南卷)下列关于糖的叙述，正确的是( )
A.葡萄糖和果糖分子均有还原性
B.葡萄糖和麦芽糖均可被水解
C.构成纤维素的单体是葡萄糖和果糖
D.乳糖可以被小肠上皮细胞直接吸收
3.(2009年高考江苏卷)下列关于细胞内化合物的叙述，正确的是( )
A.ATP脱去2个磷酸基团后是RNA的基本组成单位之一
B.糖元代谢的最终产物是葡萄糖
C.蔗糖和乳糖水解的产物都是葡萄糖
D.脂肪和生长激素是生物体内的能源物质
4.(2010年高考江苏卷)下列关于核酸的叙述中，正确的是( )
A.DNA和RNA中的五碳糖相同
B.组成DNA与ATP的元素种类不同
C.T2噬菌体的遗传信息储存在RNA中
D.双链DNA分子中嘌呤数等于嘧啶数
现在是不是感觉为大家准备的高一上册生物第一章课后练习很关键呢?欢迎大家阅读与选择!
精编高一生物课后练习题：细胞中的原子和分子习题
人教版高一上册生物第一章课后练习（汇总）。

第一章课外练习参考答案第一章绪论一、单项选择题1、（D）2、（A）3、（C）4、（B）5、（A）6、（D）7、（B）二、多项选择题1、（ABCDE）2、（ABCE）3、（ACDE）4、（AC）三、辨析题1、对。

一切管理对象，对行政机关及其工作人员的管理行为都有服从的义务。

行政机关在执行任务时要做到依法行政。

有法可依，有法必依，执法必严，违法必究。

这种法制性集中体现了行政管理的权威性。

2、错。

前半句是对的。

行政管理活动是以国家名义进行的代表国家并以强制力为后盾的。

后半句不对，国家权力机关具有强烈的阶级性，行政机关也不例外，因此行政管理具有政治性。

四、简答题1、答：行政管理学主要包括以下内容：（1）总论。

包括第一、二、三章，主要是研究和了解：行政管理学是一门综合性、应用型的科学，行政环境和行政职能是行政活动的依据和基础。

（2）主体论。

包括第四、五、六、七章，主要是研究和了解：行政主体包括行政组织和机构、行政领导以及执行公务的工作人员。

（3）过程论。

包括第八、九、十、十一、十二章，主要研究和了解行政管理是一个由多个环节和有机部分组成及有效运作的过程。

它们主要有行政决策、行政执行、行政协调、行政信息、行政监督。

（4）保障论。

包括第十三、十四、十五、十六章，主要研究和了解行政管理过程能够运行顺利并达到预期效果，必须依据一系列保障手段。

它们主要有：财务行政、行政法治、行政方法、行政道德。

（5）目的论。

包括第十七、十八章，主要研究和了解提高行政效率是行政管理的出发点和归缩，而行政改革是提高行政效率的必由之路。

2、答：（1）是西方自由资本主义时期结束后，随着垄断资本主义的发展，政府职能发展的结果；（2）当时各国政府机构普遍存在办事效率低下、腐败现象严重、官僚主义盛行等弊端，这是行政管理学和政府改革产生的契机。

五、论述题答：科技和管理是人类社会发展的两大助推器，我国作为发展中国家，要想在政治、经济、综合国力等各方面取得比较优势，就必须充分发挥政府对社会、经济发展的主导作用。

2019学年高中数学 第一章 不等关系与基本不等式 1.4(1) 比较法综合法与分析法课后练习 北师大版选修4-5一、选择题1．设0<x <1，则a ＝2x ，b ＝1＋x ，c ＝11－x 中最大的一个是( ) A ．a B ．b C ．cD ．不能确定解析： ∵0<x <1，∴1＋x >2x ＝4x >2x ， ∴只需比较1＋x 与11－x 的大小．∵1＋x －11－x ＝1－x 2－11－x ＝－x21－x <0，∴1＋x <11－x .答案： C2．已知a ，b ，c ，d ∈{正实数}且a b <c d，则( ) A ．a b <a ＋cb ＋d <cd B ．a ＋cb ＋d <a b <cdC ．a b <c d <a ＋cb ＋dD ．以上均可能解析： ∵a 、b 、c 、d 为正数， ∴要比较a b 与a ＋cb ＋d的大小，只要比较a (b ＋d )与b (a ＋c )的大小， 即ab ＋ad 与ab ＋bc 的大小， 即：ad 与bc 的大小． 又∵a b <c d，∴ad <bc ， ∴a b <a ＋cb ＋d.同理可得a ＋cb ＋d <cd. 故选A ． 答案： A3．已知a >2，x ∈R ，P ＝a ＋1a －2，Q ＝⎝ ⎛⎭⎪⎫12x 2－2，则P 、Q 的大小关系为( ) A ．P ≥Q B ．P >Q C ．P <QD ．P ≤Q解析： ∵a >2，∴a －2>0，P ＝a ＋1a －2＝a －2＋1a －2＋2≥2＋2＝4. 又Q ＝⎝ ⎛⎭⎪⎫12x 2－2≤⎝ ⎛⎭⎪⎫12－2＝4.∴P ≥Q .答案： A4．已知a 、b ∈R ，则“a ＋b >2，ab >1”是“a >1，b >1”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析： ∵a >1，b >1⇒a ＋b >2，ab >1a ＋b >2，ab >1⇒/ a >1，b >1举例说明a ＝4，b ＝13.答案： B 二、填空题5．设a >b >0，x ＝a ＋b －a ，y ＝a －a －b ，则x 、y 的大小关系是x ________y . 解析： ∵a >b >0，∴x －y ＝a ＋b －a －(a －a －b ) ＝b a ＋b ＋a －ba ＋a －b＝ba －b －a ＋ba ＋b ＋a a ＋a －b <0.答案： <6．在△ABC 中，a ，b ，c 分别是∠A ，∠B ，∠C 的对边，若∠C ＝90°，则a ＋bc的取值范围是________．解析： 由题意知c 2＝a 2＋b 2≥2ab ，即ab c 2≤12. ∴a ＋b c＝a 2＋b 2＋2abc 2＝1＋2abc2＝ 2.(当且仅当a ＝b 时取等号)． 又三角形中a ＋b >c .∴1<a ＋bc≤ 2. 答案： (1，2] 三、解答题7．设a ≥b >0，求证：3a 3＋2b 3≥3a 2b ＋2ab 2.证明： 3a 3＋2b 3－(3a 2b ＋2ab 2)＝3a 2(a －b )＋2b 2(b －a )＝(3a 2－2b 2)(a －b )．因为a ≥b >0，所以a －b ≥0,3a 2－2b 2>0，从而(3a 2－2b 2)(a －b )≥0，即3a 3＋2b 3≥3a 2b ＋2ab 2.8．(选修4－5：不等式选讲)设a ，b ，c 为正实数， 求证：1a 3＋1b 3＋1c3＋abc ≥2 3.证明： 因为a ，b ，c 为正实数，由平均值不等式可得 1a3＋1b 3＋1c 3≥331a 3·1b 3·1c3，即1a 3＋1b 3＋1c 3≥3abc，当且仅当1a 3＝1b 3＝1c3即a ＝b ＝c 时，等号成立．所以1a 3＋1b 3＋1c 3＋abc ≥3abc＋abc .而3abc ＋abc ≥23abc·abc ＝23，当且仅当3abc＝abc ，即abc ＝3时，等号成立．所以1a3＋1b 3＋1c3＋abc ≥2 3.9．已知a ，b ，c ∈R ＋，且ab ＋bc ＋ca ＝1.求证： (1)a ＋b ＋c ≥3； (2)a bc ＋b ac ＋cab≥3(a ＋b ＋c )． 证明： (1)要证a ＋b ＋c ≥3，由于a ，b ，c ∈R ＋，因此只需证(a ＋b ＋c )2≥3，即证a 2＋b 2＋c 2＋2(ab ＋bc ＋ca )≥3，根据条件，只需证a 2＋b 2＋c 2≥1＝ab ＋bc ＋ca .而这是可以由ab ＋bc ＋ca ≥a 2＋b 22＋b 2＋c 22＋c 2＋a 22＝a 2＋b 2＋c 2(当且仅当a ＝b ＝c ＝33时取等号)证得的．∴原不等式成立．(2)∵a bc ＋b ac＋ c ab ＝a ＋b ＋c abc， 在(1)中已证a ＋b ＋c ≥3， ∴原不等式只需证1abc≥a ＋b ＋c ，也就是只要证a bc ＋b ac ＋c ab ≤ab ＋bc ＋ca . 而a bc ＝ab ·ac ≤ab ＋ac2，b ac ≤ab ＋bc2，c ab ≤ac ＋bc2，∴a bc ＋b ac ＋c ab ≤ab ＋bc ＋ca ⎝ ⎛⎭⎪⎫a ＝b ＝c ＝33时取等号成立．∴原不等式成立．。

1、加快度（ A ）（ 1 ）加快度的定义 :加快度是表示速度改变快慢的物理量,它等于速度的改变量跟发生这一改变量所用时间的比值,定义式： av tv 0 t（ 2 ）加快度是矢量 ,它的方向是速度变化的方向（ 3 ）在变速直线运动中 ,若加快度的方向与速度方向同样,则质点做加快运动 ; 若加快度的方向与速度方向相反 ,则则质点做减速运动 .◎ 知识梳理1． 加快度是描绘速度变化快慢的物理量。

2．速度的变化量与所需时间的比值叫加快度。

3．公式： a=v t v 0，单位： m/s 2 是速度的变化率。

由此推导出：v t v 0 att4．加快度是矢量，其方向与v 的方向同样。

5．注意 v, v,v的差别和联系。

v 大，而v不必定大，反之亦然。

tt2、用电火花计时器 ( 或电磁打点计时器 （每隔 0.02 秒打一个点，此中 T=0.02 S) 研究匀变速直线运动（ A ）1、实验步骤：（1）把附有滑轮的长木板平放在实验桌上，将打点计时器固定在平板上 ,并接好电路（2）把一条细绳拴在小车上,细绳越过定滑轮 ,下边吊侧重量适合的钩码.（3）将纸带固定在小车尾部，并穿过打点计时器的限位孔（4）拉住纸带 ,将小车挪动至凑近打点计时器处 ,先接通电源 ,后松开纸带 .（5）断开电源 ,取下纸带O ABCDE（6）换上新的纸带，再重复做三次? ? ????3.072、常有计算：12.38（1）AB BCBC CD27.87 B2T， C2TCD BC 49.62.（2） aCBTT 277.40图 2-5考点 1：速度、加快度与速度变化量的关系速度加快度速度变化量意义 描绘物体运动快慢和方向 描绘物体速度变化快 描绘物体速度变化大 的物理量慢和方向的物理量小程度的物理量，是一过程量定义式vx vtat单位 m/sm/s 2决定要素v 的大小由 v 0、 a 、 t a 不是由 v 、△ v 、△ t 决定决定的，而是由 F 和m 决定。

2021年国开电大《高层建筑施工》课后练习1-10章答案第1章绪论1.1 课后思考题目1《高层建筑混凝土结构技术规程》规定：适用于10 层及10 层以上的住宅建筑和房屋高度大于24m的其他民用高层建筑结构。

题目2《高层民用建筑设计防火规范》规定：10 层及10 层以上的住宅建筑和建筑高度超过24m的其他公共建筑为高层建筑。

题目3《民用建筑设计通则》将建筑耐久年限分为四，高层建筑的耐久年限为一级，耐久年限为100年以上。

题目4简述使用高层建筑的主要优势有哪些？答：①丰富城市面貌，改善城市环境和景观。

②有利于人们的使用和管理。

利用建筑内部的竖向和横向交通缩短部门之间的联系距离，从而提高效率。

③节约城市建设用地。

④有利于改善城市环境和居住条件。

⑤高层建筑的发展带动了相关行业的发展。

⑥高层建筑的发展促进了科技进步。

题目5简述高层建筑的特点。

答：①由于建筑高度增加，电梯已成为高层建筑内部主要的垂直交通工具，并利用它组织方便、安全、经济的公共交通系统，从而对高层建筑的平面布局和空间组合产生了重大影响。

②高层建筑需要在底层和不同的高度设置设备层，在楼层的顶部设电梯间和水箱间。

建筑平面、立面设计要满足高层防火规范要求。

③由于高层建筑地下埋深嵌固的要求，一般要有一层至数层的地下室，作为设备层及车库、人防、辅助用房等。

题目6简述高层建筑的施工特点。

答：（1）工程量大、工序多、配合复杂（2）施工周期长、工期紧（3）基础深、基坑支护和地基处理复杂（4）高处作业多，垂直运输量大（5）结构装修、防水质量要求高，技术复杂（6）平行流水、立体交叉作业多，机械化程度高1.3课后思考题目7高层建筑按照其结构体系，分为框架体系、剪力墙体系、框架-剪力墙体系、框架-筒体体系和筒体体系四类。

题目8高层建筑结构按使用材料划分，主要有钢筋混凝土结构、钢结构、钢-钢筋混凝土组合结构，以钢筋混凝土结构在高层建筑中的应用最为广泛。

题目9高层建筑的基础有哪几种类型？答：（1）条形基础；（2）柱下梁式基础；（3）钢筋混凝土柱基础；（4）片筏基础；（5）箱形基础；（6）桩基础等。

第一章 多项式1． 用)(x g 除)(x f ，求商)(x q 与余式)(x r ： 1）123)(,13)(223+-=---=x x x g x x x x f ； 2）2)(,52)(24+-=+-=x x x g x x x f 。

解 1）由带余除法，可得92926)(,9731)(--=-=x x r x x q ； 2）同理可得75)(,1)(2+-=-+=x x r x x x q 。

2．q p m ,,适合什么条件时，有 1）q px x mx x ++-+32|1， 2）q px x mx x ++++242|1。

解 1）由假设，所得余式为0，即0)()1(2=-+++m q x m p ，所以当⎩⎨⎧=-=++0012m q m p 时有q px x mx x ++-+32|1。

2）类似可得⎩⎨⎧=--+=--010)2(22m p q m p m ，于是当0=m 时，代入（2）可得1+=q p ；而当022=--m p 时，代入（2）可得1=q 。

综上所诉，当⎩⎨⎧+==10q p m 或⎩⎨⎧=+=212m p q 时，皆有q px x mx x ++++242|1。

3．求()g x 除()f x 的商()q x 与余式：1）53()258,()3f x x x x g x x =--=+； 2）32(),()12f x x x x g x x i =--=-+。

解 1）432()261339109()327q x x x x x r x =-+-+=-；2）2()2(52)()98q x x ix i r x i=--+=-+。

4．把()f x 表示成0x x -的方幂和，即表成2010200()()...()n n c c x x c x x c x x +-+-++-+的形式：1）50(),1f x x x ==；2）420()23,2f x x x x =-+=-；3）4320()2(1)37,f x x ix i x x i x i =+-+-++=-。

湘教版高一上册地理第一章课后练习地球
的结构
本文是为进入高中的同学们整理的“高一上册地理第一章课后练习”通过练习来巩固学习过的知识，大家不要偷懒哦!赶快来动动大脑吧~~
1.关于地震波的叙述,正确的是( )
A.横波传播速度快于纵波
B.纵波只能在固体中传播
C.横波能在固体、液体中传播
D.纵波、横波波速均随通过的介质不同而变化
2.根据纵波和横波的传播速度思考,当陆地上发生地震时,在震中的人们一般会感到( )
A.左右摇晃
B.先左右摇晃后上下颠簸
C.先上下颠簸后左右摇晃
D.只上下颠簸
3.到目前为止,对地球内部的了解主要是通过( )
A.电波测试
B.地震波研究
C.岩石分析方法
D.放射性同位素的测定
4.地球内部划分为地壳、地幔和地核三个主要圈层,其划分依据是( )
A.地震波传播速度的突然变化
B.各层组成物质的不同
C.各层比重的不同
D.各层厚度的不同
5.下列关于莫霍面的说法,正确的是( )
A.位于地面以下2900千米深处
B.是德国科学家发现的
C.纵波和横波的传播速度都突然增加
D.纵波速度下降,横波完全消失
小编为大家提供的高一上册地理第一章课后练习大家仔细阅读了吗?最后祝同学们学习进步。