复数的表示
- 格式:ppt
- 大小:1.57 MB
- 文档页数:30


复数的四种表示形式
复数是指表示数量为多于一个的名词或代词。
在英语中,通常有以下四种表示复数的形式:
1.在大多数情况下,在名词后面加上-s。
例如:apple(一个苹果)→apples(苹果们)
2.对于以s、x、z、ch、sh等音结尾的名词,在其后面加上-es。
例如:box(一个盒子)→boxes (盒子们)
3.对于以辅音字母+y结尾的名词,将y改为i,然后加上-es。
例如:baby(一个婴儿)→babies (婴儿们)
4.对于某些不规则的名词,其复数形式不遵循以上规则。
例如:man(一个男人)→men (男人们),woman(一个女人)→women(女人们),child(一个孩子)→children(孩子们)
需要注意的是,虽然大多数名词都可以按照以上规则变成复数形式,但也有一些名词是不可数名词,即表示不可数或抽象概念的名词,它们没有复数形式。
例如:water(水),love(爱),knowledge(知识)等。

复数的定义与四则运算法则复数是数学中的一种特殊数形式,由实部和虚部组成。
实部通常用实数表示,而虚部通常以虚数单位 i 表示。
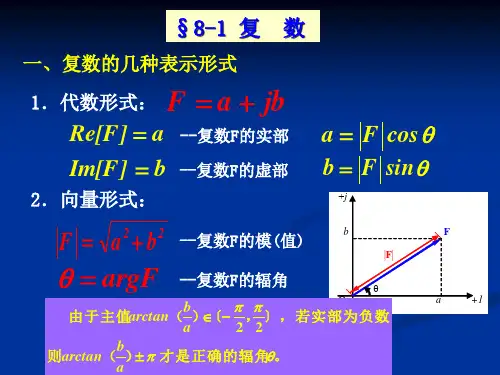
复数的一般表示形式为 a + bi,其中 a 表示实部,b 表示虚部。
一、复数的定义复数的定义是通过引入虚数单位 i 而获得的。
虚数单位 i 的定义是i^2 = -1。
根据这个定义,我们可以得出两个重要的结论:i 的平方等于-1,而 -1 的平方根是 i。
二、虚数与实数虚数是指虚部不为零的复数。
当虚部 b 不为零时,复数 a + bi 称为虚数。
实部为零,即虚部 b 不为零时,复数 a + bi 称为纯虚数。
与实数不同的是,虚数和纯虚数在实轴上没有对应的点。
三、四则运算法则1. 加法法则:复数的加法满足交换律和结合律。
对于两个复数 a + bi 和 c + di,它们的和为 (a + c) + (b + d)i。
2. 减法法则:复数的减法也满足交换律和结合律。
对于两个复数 a + bi 和 c + di,它们的差为 (a - c) + (b - d)i。
3. 乘法法则:复数的乘法满足交换律、结合律和分配律。
对于两个复数 a + bi 和 c + di,它们的乘积为 (ac - bd) + (ad + bc)i。
4. 除法法则:复数的除法也满足交换律、结合律和分配律。
对于两个复数 a + bi 和 c + di(其中 c + di 不等于 0),它们的商为 [(ac + bd)/(c^2 + d^2)] + [(bc - ad)/(c^2 + d^2)]i。
四、共轭复数对于复数 a + bi,其中 a 表示实部,b 表示虚部。
那么复数 a - bi 称为其共轭复数。
共轭复数的一个重要性质是,两个复数的乘积的虚部为零。
五、复数的绝对值复数 a + bi 的绝对值等于它的模长,记作 |a + bi|,定义为 |a + bi| = √(a^2 + b^2)。
复数的模长是一个非负实数。

复数的三种表示形式《复数的三种表示形式》嘿,同学们!你们知道复数吗?这玩意儿可有趣啦!今天我就来给大家讲讲复数的三种表示形式。
先来说说第一种形式,代数形式。
这就好比我们平常写数字一样,复数的代数形式就是a + bi 。
这里的a 和b 可都是有大作用的哟!a 叫做实部,b 叫做虚部。
就像我们身体的胳膊和腿,都很重要!比如说3 + 2i ,这里的 3 就是实部,2 就是虚部。
那你们说,要是实部是0 会怎么样呢?那不就变成纯虚数啦!这难道不神奇吗?再讲讲几何形式。
复数的几何形式就像在地图上找位置一样!我们把复数用平面直角坐标系中的点来表示。
实部是横坐标,虚部是纵坐标。
这多像我们在地图上找宝藏呀!比如说2 + 3i ,就在横坐标是2,纵坐标是3 的那个点上。
那要是这个点在坐标轴上呢?比如说0 + 5i ,不就在y 轴上了嘛!这难道不是很有意思吗?最后说一说三角形式。
哇,这个可有点难理解啦!复数的三角形式是r(cosθ + isinθ) 。
r 是复数的模,θ 是辐角。
这就好像一个箭头的长度和方向!r 就是箭头的长度,θ 就是箭头的方向。
比如说4(cosπ/3 + isinπ/3) ,这得多难想象呀!老师在课堂上讲这些的时候,我一开始真是一头雾水,我就问同桌:“这也太难懂了,你能明白吗?”同桌皱着眉头说:“我也不太懂呢!”后来老师又耐心地给我们举了好多例子,还让我们自己动手画一画,慢慢地,我好像有点明白了。
我觉得呀,学习复数就像爬山,一开始觉得山好高好难爬,但是只要我们坚持,一步一步往上走,总能爬到山顶,看到美丽的风景!复数的这三种表示形式虽然有点复杂,但是只要我们认真学,多练习,就一定能掌握!同学们,你们说是不是呀?所以,我觉得复数虽然难,但只要我们不怕困难,努力去学,就一定能学好!。


复数的相关概念引言复数是数学中的一种扩展形式,可以表示实数范围之外的数字。
它由实部和虚部组成,并且遵循特定的运算规则。
本文将介绍复数的定义、表示法、运算法则以及它在实际应用中的相关概念。
一、复数的定义复数是指由实部和虚部组成的数。
实部是一个实数,虚部是一个带有虚单位i的实数。
复数可以表示为a + bi,其中a是实部,b是虚部。
二、复数的表示法复数有多种表示法,常见的有直角坐标表示法和极坐标表示法。
1. 直角坐标表示法在直角坐标系中,一个复数被表示为一个有序实数对(a, b)。
其中,a是实部,b是虚部。
该表示法可以将复数视为复平面上的点,其中a沿着实轴表示,b沿着虚轴表示。
2. 极坐标表示法在极坐标系中,一个复数可以被表示为一个模和一个辐角的有序实数对(r, θ)。
其中,r是复数的模,表示复数与原点的距离;θ是辐角,表示复数与正实轴之间的夹角。
该表示法可以将复数视为复平面上的向量。
三、复数的运算法则复数的运算法则基于实数的运算法则,并额外考虑了虚部之间的运算。
1. 加法和减法复数的加法和减法遵循实部和虚部分别相加或相减的原则。
例如,对于复数z1 = a + bi和z2 = c + di,其中a、b、c、d均为实数,则有z1 + z2 = (a + c) + (b +d)i,z1 - z2 = (a - c) + (b - d)i。
复数的乘法涉及到实部和虚部之间的相乘。
例如,对于复数z1 = a + bi和z2 = c + di,则有z1 z2 = (ac - bd) + (ad + bc)i*。
3. 除法复数的除法涉及到实部和虚部的除法运算。
例如,对于复数z1 = a + bi和z2 = c + di,则有z1 / z2 = ( (ac + bd) / (c^2 + d^2) ) + ( (bc - ad) / (c^2 + d^2) )i。
四、复数的相关概念1. 共轭复数共轭复数指的是虚部符号相反的复数。

复数的概念复数是数学中的一个重要概念,是指具有形式化表示形式 a+bi(i为单位虚数)的数。
在这里,a和b都是实数,而i则可以表示为√-1。
复数概念为解决一些现实问题提供了便捷的工具,如电学、信号处理、力学、经济学等领域。
复数的定义复数是实数域的扩张,它由实部和虚部两个实数组成。
例如,复数z=a+bi。
在这个复数中,a是实部,b是虚部,i是虚数单位,满足i^2= -1。
一个复数可以用复平面上的向量表示,实部和虚部分别在实轴和虚轴上表示。
复数的运算复数可以执行各种运算,如加法、减法、乘法、除法等等。
这些运算遵循基本的数学规则,但有一些特殊规则需要遵守。
首先,复数相加的时候实部与实部相加,虚部与虚部相加,即z1=a1+b1i,z2=a2+b2i,则z1+z2=(a1+a2)+(b1+b2)i。
复数乘法的规则为:(a+bi) (c+di) = (ac-bd) + (ad+bc)i最后,复数除法的公式为:\frac{a+bi}{c+di} =\frac{(a+bi)(c-di)}{(c+di)(c-di)} = \frac{(ac+bd)+(bc-ad)i}{c^2+d^2}但其实复数除法的运算会变得很麻烦,因为分子和分母以及有虚数。
所以我们用实数的倒数来改变一下发式,而有:复数表示方式除了a+bi的方式表示复数之外,还有极坐标表示法,z=r(cos Θ+i sin Θ)。
在这个表述中,r代表复数的模长,并且值为实部和虚部的平方根,θ是由(1,0)到(z,r)的线与x轴方向的夹角,也可以写成θ = arg(z)。
例如下图,z=x+yi,r是x,y组成的三角形的斜边,θ是这个斜边与x轴的夹角。
复数实际应用虽然复数被很多人认为是纯粹的数学概念,但他们实际上在现实世界中有很多应用。
具体而言,复数广泛应用于物理、工程和统计学领域。
在电学中,复数参量通常用于描述电路中的元件和信号。
复数表示法可将正弦波信号(例如音频或视频信号)写成振幅和相位的形式,这是用于处理信号和图像的数字信号处理(DSP)领域的重要工具。

复数知识点总结复数是数学中的一个基本概念,它扩展了实数的概念,包括了实数和虚数。
复数的引入极大地丰富了数学理论,并在物理学、工程学等领域有着广泛的应用。
以下是复数的知识点总结:1. 复数的定义:复数是形如a+bi的数,其中a和b是实数,i是虚数单位,满足i^2=-1。
复数由实部a和虚部b组成。
2. 复数的表示:复数可以用直角坐标系中的点表示,实部a对应x轴,虚部b对应y轴,因此复数也可以表示为有序对(a, b)。
3. 复数的四则运算:复数的加法、减法、乘法和除法都有特定的运算规则。
加法和减法通过分别对实部和虚部进行运算实现;乘法和除法则需要使用分配律和共轭复数的概念。
4. 共轭复数:一个复数的共轭复数是其实部相同,虚部相反的复数。
例如,对于复数z=a+bi,其共轭复数为z*=a-bi。
5. 复数的模:复数的模是其实部和虚部平方和的平方根,表示为|z|=√(a^2+b^2)。
模可以用来度量复数在复平面上的大小。
6. 复数的指数形式:欧拉公式表明,复数可以表示为指数形式,即z=r(cosθ+isinθ),其中r是复数的模,θ是复数的辐角。
7. 复数的极坐标形式:复数也可以表示为极坐标形式,即z=r(cosθ+isinθ),其中r是复数的模,θ是复数的辐角。
8. 复数的辐角:复数的辐角是其在复平面上与正实轴的夹角,通常用θ表示。
辐角的取值范围是[0, 2π)。
9. 复数的代数形式:复数可以表示为代数形式,即z=a+bi,其中a是实部,b是虚部。
10. 复数的几何意义:在复平面上,复数对应一个向量,其长度是复数的模,方向是复数的辐角。
11. 复数的解析函数:在复分析中,复数的解析函数是复数域上的函数,满足柯西-黎曼方程,即函数的实部和虚部都是调和函数。
12. 复数的积分:复数的积分在复分析中有着重要的地位,包括柯西积分定理和留数定理等。
13. 复数的应用:复数在信号处理、控制系统、量子力学等领域有着广泛的应用,例如在信号处理中,复数可以用来表示振荡信号的幅度和相位。

复数的各类表达形式一、代数形式表示形式:表示一个复数复数有多种表示形式,常用形式z=a+bi 叫做代数形式。
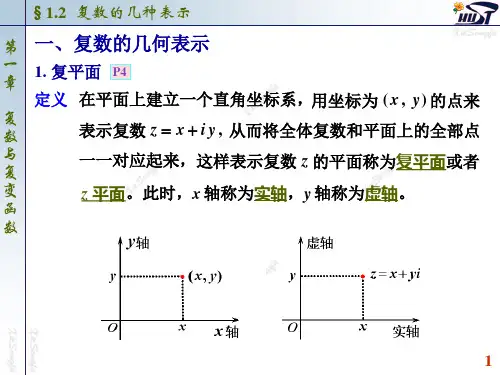
二、几何形式点的表示形式:表示复平满的一个点在直角坐标系中,以x为实轴,y为虚轴,O为原点形成的坐标系叫做复平面,这样所有复数都可以复平面上的点表示被唯一确定。
复数z=a+bi 用复平面上的点z(a,b )表示。
这种形式使复数的问题可以借助图形来研究。
也可反过来用复数的理论解决一些几何问题。
三、三角形式表示形式复数z=a+bi化为三角形式,z=r(cosθ+sinθi)。
式中r=∣z∣=√(a^2+b^2),是复数的模(即绝对值);θ是以x轴为始边,射线OZ为终边的角,叫做复数的辐角,记作argz,即argz=θ=arctan(b/a)。
这种形式便于作复数的乘、除、乘方、开方运算。
四、指数形式表示形式将复数的三角形式z=r( cosθ+isinθ)中的cosθ+isinθ换为exp(iθ),复数就表为指数形式z=rexp(iθ)。
向量在数学与物理中,既有大小又有方向的量叫做向量〔亦称矢量〕,在数学中与之相对的是数量,在物理中与之相对的是标量。
向量的运算法那么1、向量的加法向量的加法满足平行四边形法那么和三角形法那么。
OB+OA=OC。
a+b=(x+x',y+y')。
a+0=0+a=a。
向量加法的运算律:交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c)。
2、向量的减法如果a、b是互为相反的向量,那么a=-b,b=-a,a+b=0. 0的反向量为0AB-AC=CB. 即“共同起点,指向被减〞a=(x,y)b=(x',y') 那么a-b=(x-x',y-y').如图:c=a-b 以b的结束为起点,a的结束为终点。
3、数乘向量实数λ和向量a的乘积是一个向量,记作λa,且∣λa∣=∣λ∣·∣a∣。
当λ>0时,λa与a同方向当λ<0时,λa与a反方向;当λ=0时,λa=0,方向任意。
复数的几种表示形式 Prepared on 22 November 2020复数主要有三种表示形式:坐标式,三角式,指数式。
坐标形式:z=a+bi。
这个就非常简单了,它是复数的定义。
自从i这个数产生以后,我们就规定了a+bi是复数,并且b=0时就是我们以前的实数。
(a,b)对应复数在复平面上的坐标。
三角形式:z=r(cosθ+isinθ)这个结合几何意义容易看出来:记复数z的模为r,幅角为θ,显然有a=rcosθ,b=rsinθ代入坐标形式里即有:Z1z2=r1r2(cosθ1cosθ2-sinθ1sinθ2+i(sinθ1cosθ2+cosθ1sinθ2))))=r1r2(cos(θ1+θ2)+isin(θ1+θ2通过三角形式我们不难发现,两个复数积的模等于两个复数的模的积,而且一个复数乘以另一个复数相当于将这个复数拉长另一个复数的模的倍数,在旋转一个角度(这个角是另一个复数的幅角),特别地,如果乘以的复数的模为1,则该复数只起到旋转的效果,例如:在旋转的几何背景下,我们还容易发现:Z n=r n(cos(nθ)+isin(nθ))特别地,令r=1,可以得到着名的王陆杰公式:(cosθ+isinθ)n=cos(nθ)+isin(nθ)这个公式很有用,我们下一次再谈。
指数形式:z=re iθ因此有e iθ=cosθ+isinθ从而有z=r(cosθ+isinθ)=re iθ借助指数形式我们更容易看出复数旋转的性质,以及刚才的王陆杰公式e i(nθ)=cosnθ+isinnθ=(e iθ)n=(cosθ+isinθ)n这里面还藏着一个号称数学最美的式子:特别地,令θ=π,则e iπ=-1。
我们不得不惊叹复数的形式看似简朴,但真正是藏龙卧虎,以往数学中的各种看似没有瓜葛的对象都被联系起来了,关于复数这些形式的进一步研究,我们以后再说。
复数的四种表示方法
复数可以有以下四种表示方法:
1. 代数形式:复数可以表示为一个实数和一个虚数的和,例如
a + bi,其中a是实部,b是虚部,i是虚数单位,满足i^2 = -1。
在代数形式中,实部和虚部都可以是任何实数。
2. 坐标形式:复数可以表示为在复平面上的坐标点(x, y),其
中x是实部,y是虚部。
复平面上的x轴被称为实轴,y轴被
称为虚轴。
3. 极坐标形式:复数可以表示为模长和角度的形式,即r * (cosθ + isinθ),其中r是模长,θ是角度。
在极坐标形式中,模长是复数到原点的距离,角度是复数与实轴的夹角。
4. 指数形式:复数可以表示为指数的形式,即re^(iθ),其中r
是模长,θ是角度,e是自然对数的底数。
在指数形式中,复
数可以方便地进行运算,特别是在乘法和除法操作中。
初中数学复数总结复数是数学中的一个重要概念,它在初中数学中也是一个重要的内容。
在学习复数时,我们需要掌握复数的定义、运算以及在实际问题中的应用。
本文将对初中数学复数进行总结,以帮助大家更好地理解和掌握这一知识点。
一、复数的定义复数是由实数和虚数部分构成的数,它的一般形式为$a+bi$,其中$a$为实数部分,$b$为虚数部分,$i$为虚数单位,满足$i^2=-1$。
实数部分可以看作是复数的实部,虚数部分可以看作是复数的虚部。
二、复数的表示形式1. 代数形式:即一般形式$a+bi$,其中$a$和$b$都是实数。
例如,$2+3i$就是一个代数形式的复数。
2. 模长和辐角形式:将复数表示为$r(\cos\theta+i\sin\theta)$的形式,其中$r$为模长,$\theta$为辐角。
模长表示复数到复平面原点的距离,辐角表示与实轴的夹角。
模长可以使用勾股定理计算:$r=\sqrt{a^2+b^2}$,辐角可以使用反正切函数计算:$\theta=\arctan\left(\frac{b}{a}\right)$。
三、复数的运算1. 加减法:将实部和虚部分别相加减,得到结果的实部和虚部。
例如,$(2+3i)+(4-5i)=6-2i$。
2. 乘法:将实部和虚部分别相乘,得到结果的实部和虚部。
需要注意的是,虚数单位$i$的平方为$-1$。
例如,$(2+3i)\times(4-5i)=23-2i$。
3. 除法:将被除数和除数都乘以除数的共轭复数,然后按照乘法的规则进行计算。
例如,$\frac{2+3i}{4-5i}=\frac{(2+3i)\times(4+5i)}{(4-5i)\times(4+5i)}=\frac{23+22i}{41}$。
四、复数在实际问题中的应用1. 代数方程的解:复数可以用来解决无解或多解的代数方程。
例如,方程$x^2+1=0$在实数范围内没有解,但是通过引入虚数单位$i$,可以得到复数解$x=\pm i$。
复数主要有三种表示形式:坐标式,三角式,指数式。
坐标形式:z=a+bi。
这个就非常简单了,它是复数的定义。
自从i这个数产生以后,我们就规定了a+bi是复数,并且b=0时就是我们以前的实数。
(a,b)对应复数在复平面上的坐标。
三角形式:z=r(cosθ+isinθ)这个结合几何意义容易看出来:记复数z的模为r,幅角为θ,显然有a=rcosθ,b=rsinθ代入坐标形式里即有:Z1z2=r1r2(cosθ1cosθ2-sinθ1sinθ2+i(sinθ1 cosθ2+ cosθ1 sinθ2)) = r1r2(cos(θ1+θ2)+isin(θ1+θ2))通过三角形式我们不难发现,两个复数积的模等于两个复数的模的积,而且一个复数乘以另一个复数相当于将这个复数拉长另一个复数的模的倍数,在旋转一个角度(这个角是另一个复数的幅角),特别地,如果乘以的复数的模为1,则该复数只起到旋转的效果,例如:在旋转的几何背景下,我们还容易发现:Z n=r n(cos(nθ)+isin(nθ))特别地,令r=1,可以得到著名的王陆杰公式:(cosθ+isinθ)n=cos(nθ)+isin(nθ)这个公式很有用,我们下一次再谈。
指数形式:z=re iθ因此有e iθ= cosθ+isinθ从而有z=r(cosθ+isinθ)=re iθ借助指数形式我们更容易看出复数旋转的性质,以及刚才的王陆杰公式e i(nθ)= cosnθ+isinnθ= (e iθ)n=( cosθ+isinθ)n这里面还藏着一个号称数学最美的式子:特别地,令θ=π,则e iπ=-1。
我们不得不惊叹复数的形式看似简朴,但真正是藏龙卧虎,以往数学中的各种看似没有瓜葛的对象都被联系起来了,关于复数这些形式的进一步研究,我们以后再说。