正弦电磁场复数表示法解读
- 格式:doc
- 大小:1.68 MB
- 文档页数:8






复数三角公式是复数在三角函数中的应用,主要包括以下几种:
1. 欧拉公式:e^(ix) = cosx + isinx。
这个公式将复数、指数、三角函数联系在一起,是复数理论的基础。
2. 复数的正弦和余弦:sin(z) = (e^(iz) - e^(-iz)) / (2i),cos(z) = (e^(iz) + e^(-iz)) / 2。
这两个公式将复数与三角函数联系起来,使得复数可以表示为极坐标形式。
3. 复数的正切和余切:tan(z) = sin(z) / cos(z),cot(z) = 1 / tan(z)。
这两个公式将复数与三角函数的倒数联系起来。
4. 复数的正割和余割:sec(z) = 1 / cos(z),csc(z) = 1 / sin(z)。
这两个公式将复数与三角函数的倒数联系起来。
5. 复数的反正弦和反余弦:asin(z) = sin(z) / sqrt(1 - sin^2(z)),acos(z) = cos(z) / sqrt(1 - cos^2(z))。
这两个公式将复数与三角函数的反函数联系起来。
6. 复数的反余弦和反正弦:acosh(z) = (e^z + e^-z) / 2,acosh(z) = (e^z - e^-z) / 2。
这两个公式将复数与双曲三角函数的反函数联系起来。


电磁场复数-概述说明以及解释1.引言1.1 概述概述:电磁场是物质世界中广泛存在的一种物理场,它由电场和磁场共同组成。
电磁场在物质的运动、能量传递和信息传递等方面起着至关重要的作用。
复数是数学中一个重要的概念,它包含了实数和虚数,并能够用来描述具有振动、周期性等特征的物理量。
本文将探讨电磁场中复数的应用,分析复数在描述电磁场中的电场和磁场时的重要性,以及复数形式方程在电磁场中的实际应用。
通过深入研究电磁场和复数之间的关系,我们可以更好地理解电磁现象、提高相关技术的应用水平,并展望复数在电磁场领域未来的发展前景。
1.2文章结构1.2 文章结构:本文将首先介绍电磁场的基本概念,包括电场和磁场的产生、性质和相互作用,为读者提供对电磁场的整体认识。
接着,我们将重点关注复数在电磁场中的应用,探讨复数在描述电磁场中的振荡、波动和传播方面的重要性。
最后,我们将通过分析电磁场中的复数形式方程,展示复数在电磁场研究中的实际应用价值。
通过这些内容的阐述,读者将能够更全面地理解电磁场中复数的作用和重要性,以及未来应用的潜在前景。
1.3 目的通过本文的讨论和分析,旨在深入探讨电磁场中复数的重要性和应用。
我们将介绍电磁场的基本概念,以及复数在电磁场中的应用及其重要性。
同时,我们还将介绍电磁场中的复数形式方程,以便读者更好地理解和应用复数在电磁场中的作用。
通过本文的研究,希望读者能够对电磁场复数有更深刻的认识,并能够在实际应用中灵活运用复数的知识,为电磁场相关领域的发展贡献一份力量。
2.正文2.1 电磁场的基本概念电磁场是由电荷和电流所产生的物理场。
电荷是物质的一个基本属性,它可以是正电荷、负电荷或中性电荷。
电流则是电荷的移动,通常是通过导体中的电子流或电离液体中的离子流来实现的。
根据麦克斯韦方程组,电磁场可分为电场和磁场两部分。
电场是由电荷产生的,呈向外的径向分布,其作用可以通过库仑定律描述。
而磁场则是由电流产生的,呈环绕电流方向的环形分布,其作用可以通过安培定律描述。
复数电磁场分布
复数电磁场分布是电磁场理论中的一个重要概念,主要涉及到复数表示的电磁场量和复数形式的电磁场方程。
在处理一些具有波动性质的电磁场问题时,使用复数表示的电磁场量和电磁场方程可以使问题简化,方便分析。
复数电磁场分布主要应用于微波、光波等高频电磁波的传播、散射、辐射等问题。
在这些高频电磁波的传播过程中,由于波长相对较小,电磁波的波动性表现得更加明显,因此需要使用复数形式的电磁场量和电磁场方程来描述。
在复数电磁场分布中,电场强度E、磁场强度H等物理量都可以用复数表示。
复数形式的电磁场量和实数形式的量具有相同的物理意义,但是在计算和表达上更加方便。
复数形式的电磁场方程包括麦克斯韦方程组、波动方程等,这些方程可以方便地描述电磁波的传播、散射、辐射等过程。
通过求解复数形式的电磁场方程,可以得到电磁波的传播模式、相位、振幅等信息,这些信息对于微波、光波等高频电磁波的应用具有重要的意义。
例如,在通信、雷达、光学等领域中,需要利用复数电磁场分布来设计和优化器件的性能。
综上所述,复数电磁场分布在电磁场理论中具有重要的意义,它可以方便地描述具有波动性质的电磁波的传播、散射、辐射等过程,对于微波、光波等高频电磁波的应用具有重要的指导作用。
通过深入研究和应用复数电磁场分布,可以进一步推动电磁场理论的发展和应用。
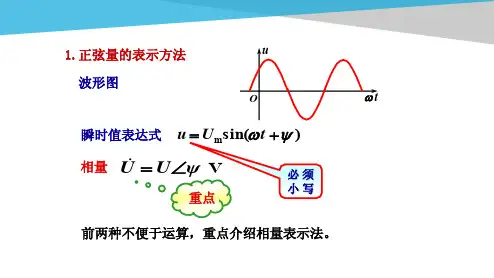
复数与正弦交流电教学内容及学时期分配:序号内容学时1 第一节复数的概念 12 第二节复数的四则运算 13 第三节正弦量的相量表示法 14 第四节相量形式的欧姆定律 25 第五节复阻抗的连接 26 本章小结与习题 17 本章总学时8教学目标:1.了解复数的各种表达式和相互转换关系,掌握复数的四则运算。
2.掌握正弦量的复数表示法,以及相量式的欧姆定律。
3.掌握运用相量法分析计算阻抗串、并联的正弦交流电路。
教学重点:1.掌握复数的四则运算以及各种表达式之间的相互转换。
2.掌握运用相量法分析计算正弦交流电路。
教学难点:理解相量法分析计算正弦交流电路。
教学学时:18学时,机动3学时。
1.复数的概念教学目标:知识:了解复数的各种表达式和相互转换关系。
技能:能熟练应用各种表达式相互转换解答有关问题。
教学重点:复数的各种表达式及相互转换。
教学难点:区别复数的各种表达式,理解相互转换关系。
教学学时:3学时,机动1学时。
教学过程:一、新课导入:应用复数分析正弦交流电路称为相量法,它在工程技术上有广泛的应用。
现在我们已对由R、L 、C 组成的电路,各部分的电流、电压都是与电源同频率的正弦量,现用复数来研究,引入新课。
二、进行新课:(一)、虚数单位参见图9-1给出的直角坐标系复数平面。
在这个复数平面上定义虚数单位为 1j -=即度 j 2 = -1,j 3 = - j ,j 4 = 1虚数单位j 又叫做90︒旋转因子。
(二)、复数的表达式一个复数Z 有以下四种表达式。
1.直角坐标式(代数式) Z = a + j b a 叫做复数Z 的实部,b 叫做复数Z 的虚部。
在直角坐标系中,以横坐标为实数轴,纵坐标为虚数轴,这样构成的平面叫做复平面。
任意一个复数都可以在复平面上表示出来。
例如复数A = 3 + j2在复平面上的表示如图9-1所示。
2.三角函数式在图9-1中,复数Z 与x 轴的夹角为 θ,因此可以写成Z = a + j b = |Z |(cos θ + jsin θ)式中|Z |叫做复数Z 的模,又称为Z 的绝对值,也可用r 表示,即22|Z | b a r +==θ 叫作复数Z 的辐角,从图9-1中可以看出⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧<<+π-><-π>=)0 0( arctan )0 0( arctan )0( arctan b a a b b a a b a a b ,,θ 复数Z 的实部a 、虚部b 与模|Z |构成一个直角三角形。