高中物理模型组合27讲(Word下载)爆炸反冲模型

爆炸、碰撞和反冲专题●1．碰撞过程是指：作用时间很短，作用力大．碰撞过程两物体产生的位移可忽略．●2．爆炸、碰撞和反冲动量近似守恒：有时尽管合外力不为零，但是内力都远大于外力，且作用时间又非常短，所以合外力产生的冲量跟内力产生冲量比较都可忽略，总动量近似守恒． ●3．三种碰撞的特点：(1)弹性碰撞——碰撞结束后，形变全部消失，末态动能没有损失．所以，不仅动量守恒，而且初、末动能相等，即 m 1v 1＋m 2v 2＝m 1v ＇1＋m 2v ＇222221122112211112222''+=+m v m v m v m v (2)一般碰撞——碰撞结束后，形变部分消失，动能有部分损失．所以，动量守恒，而初、末动能不相等，即 m 1v 1＋m 2v 2＝m 1v ＇1＋m 2v ＇2222211212211112222''+=+m v m v m v m v ＋ΔE K 减 (3)完全非弹性碰撞——碰撞结束后，两物体合二为一，以同一速度运动；形变完全保留，动能损失最大．所以，动量守恒，而初、末动能不相等，即 m 1v 1＋m 2v 2＝(m 1＋m 2)v222112212111()222+=m v m v m +m v ＋ΔE k max ●4．“一动一静”弹性正碰的基本规律如图5—32所示，一个动量为m 1v 1的小球，与一个静止的质量为m 2的小球发生弹性正碰，这种最典型的碰撞，具有一系列应用广泛的重要规律(1)动量守恒，初、末动能相等，即(2)根据①②式，碰撞结束时，主动球(m 1)与被动球(m 2)的速度分别为(3)判定碰撞后的速度方向当m 1＞m 2时；v ′1＞0，v ′2＞0——两球均沿初速v 1方向运动．当m 1＝m 2时；v ′1＝0，v ′2＝v 1——两球交换速度，主动球停下，被动球以v 1开始运动．当m 1＜m 2时；v ′1＜0，v ′2＞0——主动球反弹，被动球沿v 1方向运动． ●5．“一动一静”完全非弹性碰撞的基本计算关系如图5—33所示，在光滑水平面上，有一块静止的质量为M 的木块，一颗初动量为mv 0的子弹，水平射入木块，并深入木块d ，且冲击过程中阻力f 恒定．(1)碰撞后共同速度(v )根据动量守恒，共同速度为v ＝mv m+M……① (2)木块的冲击位移(s)设平均阻力为f ，分别以子弹，木块为研究对象，根据动能定理，有 fs ＝12Mv 2………②f (s ＋d )＝12m 20v -12mv 2……③ 由①、②和③式可得 s ＝+mm Md ＜d 在物体可视为质点时：d ＝0，s ＝0——这就是两质点碰撞瞬时，它们的位置变化不计的原因 (3)冲击时间(t )以子弹为研究对象，根据子弹相对木块作末速为零的匀减速直线运动，相对位移d ＝12v 0t ，所以冲击时间为 t ＝02d v (4)产生的热能Q在认为损失的动能全部转化为热能的条件下 Q ＝ΔE K ＝f ·s 相＝fd ＝12m 20v ()+MM m【例题1】质量相等的A 、B 两球在光滑水平面上沿同一直线、同一方向运动，A 球的动量是7kg ·m/s ，B 球的动量是5kg ·m/s ，当A 球追上B 球时发生碰撞，则碰撞后A 、B 两球的动量可能值是： A ．p A ＝6kg ·m/s ，p B ＝6kg ·m/s ； B ．p A ＝3kg ·m/s ，p B ＝9kg ·m/s ； C ．p A ＝-2kg ·m/s ，p B ＝14kg ·m/s ； D ．p A ＝-4kg ·m/s ，p B ＝17kg ·m/s ．【例题2】锤的质量是m 1，桩的质量为m 2，锤打桩的速率为一定值．为了使锤每一次打击后桩更多地进入土地，我们要求m 1m 2．假设锤打到桩上后，锤不反弹，试用力学规律分析说明为什么打桩时要求m 1m 2．训练题(1)甲、乙两个小球在同一光滑水平轨道上，质量分别是m 甲和m 乙．甲球以一定的初动能E k 0向右运动，乙球原来静止．某时刻两个球发生完全非弹性碰撞(即碰撞后两球粘合在一定)，下面说法中正确的是：A．m甲与m乙的比值越大，甲球和乙球组成的系统机械能的减少量就越小；B．m甲与m乙的比值越小，甲球和乙球组成的系统机械能的减少量就越小；C．m甲与m乙的值相等，甲球和乙球组成的系统机械能的减少量最小；D．m甲与m乙的值相等，甲球和乙球组成的系统机械能的减少量最大．(2)半径相等的两个小球甲和乙，在光滑水平面上沿同一直线相向运动．若甲球的质量大于乙球的质量，碰撞前两球的动能相等，则碰撞后两球的运动状态可能是：A．甲球的速度为零而乙球的速度不为零；B．乙球的速度为零而甲球的速度不为零；C．两球的速度均不为零；D．两球的速度方向均与原方向相反，两球的动能不变．(3)如图5—38所示，质量为m的子弹以速度v从正下方向上击穿一个质量为M的木球，击穿后木球上升高度为H，求击穿木球后子弹能上升多高？。

高中物理模型——爆炸反冲模型［模型概述］“爆炸反冲”模型是动量守恒的典型应用，其变迁形式也多种多样，如炮发炮弹中的化学能转化为机械能；弹簧两端将物块弹射将弹性势能转化为机械能；核衰变时将核能转化为动能等。

［模型讲解］例. 如图所示海岸炮将炮弹水平射出，炮身质量（不含炮弹）为M ，每颗炮弹质量为m ，当炮身固定时，炮弹水平射程为s ，那么当炮身不固定时，发射同样的炮弹，水平射程将是多少？解析：两次发射转化为动能的化学能E 是相同的。

第一次化学能全部转化为炮弹的动能；第二次化学能转化为炮弹和炮身的动能，而炮弹和炮身水平动量守恒，由动能和动量的关系式mp E k 22=知，在动量大小相同的情况下，物体的动能和质量成反比，炮弹的动能E mM M mv E E mv E +====2222112121，，由于平抛的射高相等，两次射程的比等于抛出时初速度之比，即：mM M v v s s +==122，所以m M M s s 2+=。

思考：有一辆炮车总质量为M ，静止在水平光滑地面上，当把质量为m 的炮弹沿着与水平面成θ角发射出去，炮弹对地速度为0v ，求炮车后退的速度。

提示：系统在水平面上不受外力，故水平方向动量守恒，炮弹对地的水平速度大小为θcos 0v ，设炮车后退方向为正方向，则mM mv v mv v m M -==--θθcos 0cos )(00， 评点：有时应用整体动量守恒，有时只应用某部分物体动量守恒，有时分过程多次应用动量守恒，有时抓住初、末状态动量即可，要善于选择系统，善于选择过程来研究。

［模型要点］内力远大于外力，故系统动量守恒21p p =，有其他形式的能单向转化为动能。

所以“爆炸”时，机械能增加，增加的机械能由化学能（其他形式的能）转化而来。

［误区点拨］忽视动量守恒定律的系统性、忽视动量守恒定律的相对性、同时性。

［模型演练］（2005年物理高考科研测试）在光滑地面上，有一辆装有平射炮的炮车，平射炮固定在炮车上，已知炮车及炮身的质量为M ，炮弹的质量为m ；发射炮弹时，炸药提供给炮身和炮弹的总机械能E 0是不变的。

第二十七讲 动量守恒定律一、动量守恒定律1.内容：如果一个系统不受外力，或者所受外力的________为0，这个系统的总动量保持不变。

2.表达式(1)p ＝p ′，系统相互作用前的总动量p 等于相互作用后的总动量p ′。

(2)m 1v 1＋m 2v 2＝____________，相互作用的两个物体组成的系统，作用前的动量和等于作用后的动量和。

(3)Δp 1＝_______，相互作用的两个物体动量的变化量等大反向。

(4)Δp ＝0，系统总动量的增量为零。

矢量和m 1v 1′＋m 2v 2′－Δp 23.适用条件(1)理想守恒：不受外力或所受外力的合力为____。

(2)近似守恒：系统内各物体间相互作用的内力________它所受到的外力。

(3)某一方向守恒：如果系统在某一方向上所受外力的合力为零，则系统在__________上动量守恒。

零远大于这一方向【典例1】(多选)如图所示，小车与木箱紧挨着静止放在光滑的水平冰面上，现有一男孩站在小车上用力向右迅速推出木箱。

关于上述过程，下列说法中正确的是( )A.男孩和木箱组成的系统动量守恒B.小车与木箱组成的系统动量守恒C.男孩、小车与木箱三者组成的系统动量守恒D.木箱的动量增量与男孩、小车的总动量增量大小相同解析　男孩和木箱组成的系统受小车的摩擦力，所以动量不守恒，A 错误；小车与木箱组成的系统受男孩的力为外力，所以动量不守恒，B 错误；男孩、小车与木箱三者组成的系统，所受合外力为0，所以动量守恒，C 正确；木箱的动量增量与男孩、小车的总动量增量大小相同，但方向相反，D 正确。

CD二、“三类”模型问题1.“子弹打木块”模型(1)“木块”放置在光滑的水平面上①运动性质：“子弹”对地在滑动摩擦力作用下做减速直线运动；“木块”在滑动摩擦力作用下做______直线运动。

②处理方法：通常由于“子弹”和“木块”的相互作用时间极短，内力远大于外力，可认为“子弹”与“木块”组成的系统在这一过程中动量守恒。

高三物理一轮复习——爆炸和反冲运动模型问题例5 (2019·全国卷Ⅲ·25)静止在水平地面上的两小物块A 、B ，质量分别为m A ＝1.0 kg ，m B ＝4.0 kg ；两者之间有一被压缩的微型弹簧，A 与其右侧的竖直墙壁距离l ＝1.0 m ，如图6所示．某时刻，将压缩的微型弹簧释放，使A 、B 瞬间分离，两物块获得的动能之和为E k ＝10.0 J ．释放后，A 沿着与墙壁垂直的方向向右运动．A 、B 与地面之间的动摩擦因数均为μ＝0.20.重力加速度取g ＝10 m/s 2.A 、B 运动过程中所涉及的碰撞均为弹性碰撞且碰撞时间极短．图6(1)求弹簧释放后瞬间A 、B 速度的大小；(2)物块A 、B 中的哪一个先停止？该物块刚停止时A 与B 之间的距离是多少？(3)A 和B 都停止后，A 与B 之间的距离是多少？答案 (1)4.0 m /s 1.0 m/s (2)物块B 先停止 0.50 m (3)0.91 m解析 (1)设弹簧释放瞬间A 和B 的速度大小分别为v A 、v B ，以向右为正方向，由动量守恒定律和题给条件有0＝m A v A －m B v B ①E k ＝12m A v A 2＋12m B v B 2② 联立①②式并代入题给数据得v A ＝4.0 m/s ，v B ＝1.0 m/s ③(2)A 、B 两物块与地面间的动摩擦因数相等，因而两者滑动时加速度大小相等，设为a .假设A 和B 发生碰撞前，已经有一个物块停止，此物块应为弹簧释放后速度较小的B .设从弹簧释放到B 停止所需时间为t ，B 向左运动的路程为s B ，则有m B a ＝μm B g ④s B ＝v B t －12at 2⑤ v B －at ＝0⑥在时间t 内，A 可能与墙发生弹性碰撞，碰撞后A 将向左运动，碰撞并不改变A 的速度大小，所以无论此碰撞是否发生，A 在时间t 内的路程s A 都可表示为s A ＝v A t －12at 2⑦联立③④⑤⑥⑦式并代入题给数据得s A ＝1.75 m ，s B ＝0.25 m ⑧这表明在时间t 内A 已与墙壁发生碰撞，但没有与B 发生碰撞，此时A 位于出发点右边0.25 m 处．B 位于出发点左边0.25 m 处，两物块之间的距离s 为s ＝0.25 m ＋0.25 m ＝0.50 m ⑨(3)t 时刻后A 将继续向左运动，假设它能与静止的B 碰撞，碰撞时速度的大小为v A ′，由动能定理有12m A v A ′2－12m A v A 2＝－μm A g ()2l ＋s B ⑩ 联立③⑧⑩式并代入题给数据得v A ′＝7 m/s ⑪故A 与B 将发生碰撞．设碰撞后A 、B 的速度分别为v A ″和v B ″，由动量守恒定律与机械能守恒定律有m A ()－v A ′＝m A v A ″＋m B v B ″⑫12m A v A ′2＝12m A v A ″2＋12m B v B ″2⑬ 联立⑪⑫⑬式并代入题给数据得v A ″＝375 m/s ，v B ″＝－275m/s ⑭ 这表明碰撞后A 将向右运动，B 继续向左运动．设碰撞后A 向右运动距离为s A ′时停止，B 向左运动距离为s B ′时停止，由运动学公式2as A ′＝v A ″2,2as B ′＝v B ″2⑮由④⑭⑮式及题给数据得s A ′＝0.63 m ，s B ′＝0.28 m ⑯s A ′小于碰撞处到墙壁的距离．由上式可得两物块停止后的距离s ′＝s A ′＋s B ′＝0.91 m拓展训练5 (2019·云南昆明市4月质检)科研人员乘热气球进行科学考察，气球、座舱、压舱物和科研人员的总质量为M ＝200 kg.热气球在空中以v 0＝0.1 m /s 的速度匀速下降，距。

爆炸 反冲 人船模型1．爆炸与反冲运动的特点：由于系统不受外力或内力远大于外力，所以动量守恒；由于系统内有其他形式的能量(如化学能)转化为动能，所以系统总动能增加．2．“人船模型”的特点(1)两物体满足动量守恒定律：m 1v 1－m 2v 2＝0.(2)运动特点：人动船动，人静船静，人快船快，人慢船慢，人左船右；人船位移比等于它们质量的反比；人船平均速度(瞬时速度)比等于它们质量的反比，即x 1x 2＝v 1v 2＝m 2m 1. (3)应用此关系时要注意一个问题：公式中v 1、v 2和x 一般都是相对地面而言的．1．(2019·安徽合肥市二模)如图1所示，某人站在一辆平板车的右端，车静止在光滑的水平地面上，现人用铁锤子连续敲击车的右端．下列对平板车的运动情况描述正确的是( )A ．锤子向右抡起的过程中，车向右运动B ．锤子下落的过程中车向左运动C ．锤子抡至最高点时，车速度为零D ．锤子敲击车瞬间，车向左运动2．将静置在地面上，质量为M (含燃料)的火箭模型点火升空，在极短时间内以相对地面的速度v 0竖直向下喷出质量为m 的炽热气体．忽略喷气过程重力和空气阻力的影响，则喷气结束时火箭模型获得的速度大小是( )A.m M v 0B.M m v 0C.M M －m v 0D.m M －m v 03．如图2所示，小车(包括固定在小车上的杆)的质量为M ，质量为m 的小球通过长度为L 的轻绳与杆的顶端连接，开始时小车静止在光滑的水平面上．现把小球从与O 点等高的地方释放(小球不会与杆相撞)，小车向左运动的最大位移是( )A.2LM M ＋mB.2Lm M ＋mC.ML M ＋mD.mL M ＋m4．(2019·湖北稳派教育上学期第二次联考)某同学为研究反冲运动，设计了如图3所示的装置，固定有挡光片的小车内表面水平，置于光滑水平面上，挡光片宽为d ，小车的左侧不远处有固定的光电门，用质量为m 的小球压缩车内弹簧，并锁定弹簧，整个装置处于静止，解除锁定，小球被弹射后小车做反冲运动并通过光电门，与光电门连接的计时器记录挡光片挡光时间为t ，小车、弹簧和挡光片的总质量为3m ，则小球被弹出小车的瞬间相对于地面的速度大小为( )A.d tB.2d tC.3d tD.4d t5．(多选)如图4所示，小车AB 放在光滑水平面上，A 端固定一个轻弹簧，B 端粘有油泥，AB 总质量为M ，质量为m 的木块C 放在小车上，用细绳连接于小车的A 端并使弹簧压缩，开始时AB 和C 都静止，当突然烧断细绳时，C 被释放，C 离开弹簧向B 端冲去，并跟B 端油泥粘在一起，忽略一切摩擦，下列说法正确的是()A．弹簧伸长过程中C向右运动，同时AB也向右运动B．C与B碰前，C与AB的速率之比为M∶mC．C与油泥粘在一起后，AB立即停止运动D．C与油泥粘在一起后，AB继续向右运动6．(2020·广东揭阳市模拟)如图5所示，水平地面上可视为质点的物体A和B紧靠在一起静止于b处，已知A的质量为3m，B的质量为m.两物体在足够大的内力作用下突然沿水平方向左右分离．B碰到c处的墙壁后等速率反弹，并追上已停在ab段的A，追上时B的速率等于两物体刚分离时B的速率的一半．A、B 与水平地面的动摩擦因数均为μ，b与c间的距离为d，重力加速度为g.求：(1)分离瞬间A、B的速率之比；(2)分离瞬间A获得的动能．答案精析1．C [锤子、人和车组成的系统在水平方向动量守恒，锤子向右抡起的过程中，车向左运动，故A 错误；锤子下落的过程中，有水平向左的速度，根据动量守恒定律，车向右运动，故B 错误；锤子抡至最高点时，速度为零，根据动量守恒定律，车的速度也为零，故C 正确；锤子向左敲击车瞬间，根据动量守恒定律，车向右运动，故D 错误．]2．D [取向下为正方向，由动量守恒定律可得：0＝m v 0－(M －m )v ′，故v ′＝m v 0M －m，选项D 正确．] 3．B [小球和小车组成的系统在水平方向上动量守恒，设小球和小车在水平方向上的速度大小分别为v 1、v 2，有m v 1＝M v 2，故mx 1＝Mx 2，x 1＋x 2＝2L ，其中x 1代表小球的水平位移大小，x 2代表小车的水平位移大小，因此x 2＝2Lm M ＋m，选项B 正确．] 4．C [解除锁定，小球被弹射后小车做反冲运动，经时间t 通过光电门，则小车匀速运动的速度大小为v 1＝d t，设小球的速度大小为v 2，根据反冲运动的特点可知，小车与小球总动量为零，根据动量守恒定律得：3m v 1＝m v 2，得小球的速度大小为v 2＝3d t，故选C.] 5．BC [AB 与C 组成的系统在水平方向上动量守恒，C 向右运动时，AB 应向左运动，故A 错误；设碰前C 的速率为v 1，AB 的速率为v 2，则0＝m v 1－M v 2，得v 1v 2＝M m，故B 正确；设C 与油泥粘在一起后，AB 、C 的共同速度为v 共，则0＝(M ＋m )v 共，得v 共＝0，故C 正确，D 错误．]6．(1)13 (2)2423μmgd 解析 (1)以水平向左为正方向，分离瞬间对A 、B 系统应用动量守恒定律有：3m v A －m v B ＝0解得：v A v B ＝13； (2)A 、B 分离后，A 物体向左匀减速滑行，对A 应用动能定理：－μ·3mgs A ＝0－12×3m v A 2 对B 从两物体分离后到追上A 的过程应用动能定理：－μmgs B ＝12m ⎝⎛⎭⎫v B 22－12m v B 2 两物体的路程关系是s B ＝s A ＋2d分离瞬间A 获得的动能E k A ＝12×3m v A 2 联立解得：E k A ＝2423μmgd .。

高中物理平射炮反冲模型
光滑的水平面上静止一辆质量为M的炮车，当炮车水平发射一枚质量为m的炮弹，炮弹出口时有的火药能量释放，其中有的能量转化为系统的内能，求炮弹和炮车的动能各为多少？
解析：炮弹和炮车组成的系统在水平方向上满足动量守恒，设炮弹和炮车的速度分别为，由动量守恒得，即动量大小关系
设炮弹和炮车的动能分别为，系统机械能的增加量为，则由能量守恒得
模型特征：
<1>在满足动量守恒的方向上，整个系统任意时刻的动量为零，即；
<2>炮车和炮弹获得动能为；
<3>让（1）式比上（2）式得，即炮弹和炮车获得动能与其质量成反比。

例1、如图所示，带有光滑的半径为R的圆弧轨道的滑块静止在光滑的水平面上，此滑块的质量为M，一个质量为m的小球静止从A点释放，当小球从滑块B处水平飞出时，求滑块的动能。

解析：当小球从B点飞出时，小球和滑块在水平方向上满足动量守恒，由上面的模型特点的滑块获得的动能为
例2、在光滑的水平面上放有质量分别为M、m的两小球，两球间放有一被压缩的轻质弹簧，其弹性势能为E，释放弹簧，两球被弹开，求小球m的最大速度。

解析：当弹簧完全弹开后，由上面的模型特征知，小球m的动能，由动能定理得小球的最大速度。

3>2>1>。

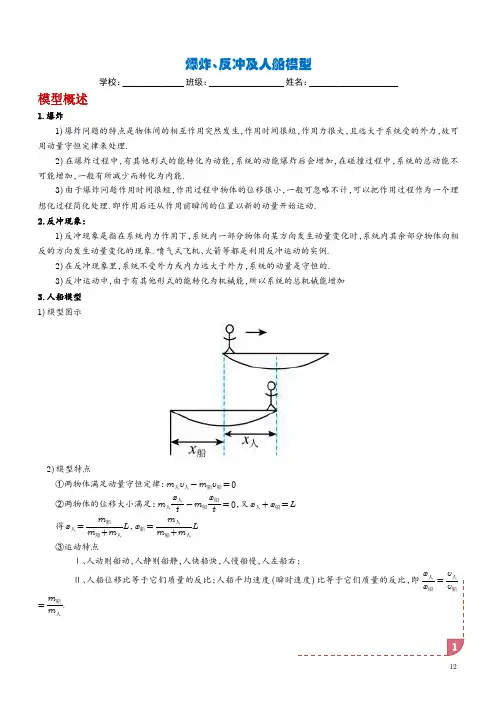
爆炸、反冲及人船模型学校：_________班级：___________姓名：_____________模型概述1.爆炸1)爆炸问题的特点是物体间的相互作用突然发生，作用时间很短，作用力很大，且远大于系统受的外力，故可用动量守恒定律来处理.2)在爆炸过程中，有其他形式的能转化为动能，系统的动能爆炸后会增加，在碰撞过程中，系统的总动能不可能增加，一般有所减少而转化为内能.3)由于爆炸问题作用时间很短，作用过程中物体的位移很小，一般可忽略不计，可以把作用过程作为一个理想化过程简化处理.即作用后还从作用前瞬间的位置以新的动量开始运动.2.反冲现象：1)反冲现象是指在系统内力作用下，系统内一部分物体向某方向发生动量变化时，系统内其余部分物体向相反的方向发生动量变化的现象.喷气式飞机、火箭等都是利用反冲运动的实例.2)在反冲现象里，系统不受外力或内力远大于外力，系统的动量是守恒的.3)反冲运动中，由于有其他形式的能转化为机械能，所以系统的总机械能增加3.人船模型1)模型图示2)模型特点①两物体满足动量守恒定律：m人v人-m船v船=0②两物体的位移大小满足：m人x人t-m船x船t=0，又x人+x船=L得x人=m船m船+m人L，x船=m人m船+m人L③运动特点Ⅰ、人动则船动，人静则船静，人快船快，人慢船慢，人左船右；Ⅱ、人船位移比等于它们质量的反比；人船平均速度(瞬时速度)比等于它们质量的反比，即x人x船=v人v船=m船m人.典题攻破1.爆炸1.(2024·青海海南·二模)斜向上发射的炮弹在最高点爆炸(爆炸时间极短)成质量均为m 的两块碎片，其中一块碎片沿原路返回。

已知炮弹爆炸时距地面的高度为H ，炮弹爆炸前的动能为E ，重力加速度大小为g ，不计空气阻力和火药的质量，则两块碎片落地点间的距离为()A.2EH mgB.22EH mgC.23EH mgD.42EH mg2.反冲2.(2024·山东潍坊·模拟预测)如图所示，返回舱接近地面时，相对地面竖直向下的速度为v ，此时反推发动机点火，在极短时间Δt 内，竖直向下喷出相对地面速度为u 、体积为V 的气体，辅助返回舱平稳落地。

高中物理模型汇总大全模型组合讲解——爆炸反冲模型［模型概述］“爆炸反冲”模型是动量守恒的典型应用，其变迁形式也多种多样，如炮发炮弹中的化学能转化为机械能；弹簧两端将物块弹射将弹性势能转化为机械能；核衰变时将核能转化为动能等。

［模型讲解］例. 如图所示海岸炮将炮弹水平射出，炮身质量（不含炮弹）为M ，每颗炮弹质量为m ，当炮身固定时，炮弹水平射程为s ，那么当炮身不固定时，发射同样的炮弹，水平射程将是多少？解析：两次发射转化为动能的化学能E 是相同的。

第一次化学能全部转化为炮弹的动能；第二次化学能转化为炮弹和炮身的动能，而炮弹和炮身水平动量守恒，由动能和动量的关系式mp E k 22=知，在动量大小相同的情况下，物体的动能和质量成反比，炮弹的动能E mM M mv E E mv E +====2222112121，，由于平抛的射高相等，两次射程的比等于抛出时初速度之比，即：mM M v v s s +==122，所以m M M s s 2+=。

思考：有一辆炮车总质量为M ，静止在水平光滑地面上，当把质量为m 的炮弹沿着与水平面成θ角发射出去，炮弹对地速度为0v ，求炮车后退的速度。

提示：系统在水平面上不受外力，故水平方向动量守恒，炮弹对地的水平速度大小为θcos 0v ，设炮车后退方向为正方向，则mM mv v mv v m M -==--θθcos 0cos )(00， 评点：有时应用整体动量守恒，有时只应用某部分物体动量守恒，有时分过程多次应用动量守恒，有时抓住初、末状态动量即可，要善于选择系统，善于选择过程来研究。

［模型要点］内力远大于外力，故系统动量守恒21p p =，有其他形式的能单向转化为动能。

所以“爆炸”时，机械能增加，增加的机械能由化学能（其他形式的能）转化而来。

［误区点拨］忽视动量守恒定律的系统性、忽视动量守恒定律的相对性、同时性。

［模型演练］（ 物理高考科研测试）在光滑地面上，有一辆装有平射炮的炮车，平射炮固定在炮车上，已知炮车及炮身的质量为M ，炮弹的质量为m ；发射炮弹时，炸药提供给炮身和炮弹的总机械能E 0是不变的。

模型组合讲解——爆炸反冲模型高志勇［模型概述］“爆炸反冲”模型是动量守恒的典型应用，其变迁形式也多种多样，如炮发炮弹中的化学能转化为机械能；弹簧两端将物块弹射将弹性势能转化为机械能；核衰变时将核能转化为动能等。

［模型讲解］例. 如图所示海岸炮将炮弹水平射出，炮身质量（不含炮弹）为M ，每颗炮弹质量为m ，当炮身固定时，炮弹水平射程为s ，那么当炮身不固定时，发射同样的炮弹，水平射程将是多少？解析：两次发射转化为动能的化学能E 是相同的。

第一次化学能全部转化为炮弹的动能；第二次化学能转化为炮弹和炮身的动能，而炮弹和炮身水平动量守恒，由动能和动量的关系式mp E k 22=知，在动量大小相同的情况下，物体的动能和质量成反比，炮弹的动能E mM M mv E E mv E +====2222112121，，由于平抛的射高相等，两次射程的比等于抛出时初速度之比，即：mM M v v s s +==122，所以m M M s s 2+=。

思考：有一辆炮车总质量为M ，静止在水平光滑地面上，当把质量为m 的炮弹沿着与水平面成θ角发射出去，炮弹对地速度为0v ，求炮车后退的速度。

提示：系统在水平面上不受外力，故水平方向动量守恒，炮弹对地的水平速度大小为θcos 0v ，设炮车后退方向为正方向，则mM mv v mv v m M -==--θθcos 0cos )(00， 评点：有时应用整体动量守恒，有时只应用某部分物体动量守恒，有时分过程多次应用动量守恒，有时抓住初、末状态动量即可，要善于选择系统，善于选择过程来研究。

［模型要点］内力远大于外力，故系统动量守恒21p p =，有其他形式的能单向转化为动能。

所以“爆炸”时，机械能增加，增加的机械能由化学能（其他形式的能）转化而来。

［误区点拨］忽视动量守恒定律的系统性、忽视动量守恒定律的相对性、同时性。

［模型演练］（2005年物理高考科研测试）在光滑地面上，有一辆装有平射炮的炮车，平射炮固定在炮车上，已知炮车及炮身的质量为M ，炮弹的质量为m ；发射炮弹时，炸药提供给炮身和炮弹的总机械能E 0是不变的。

高中物理模型组合２７讲（Word 下载）追碰模型 ［模型概述］追碰是物理上一个重要模型，它涉及到动量定理、动量守恒定律、能量守恒等诸多知识点。

从物理方法的角度看。

处理碰撞咨询题，通常使用整体法〔系统〕、能量方法，守恒方法及矢量运算。

〝追碰〞模型所设计的内容在每年的高考中能够以选择、运算题形式显现，因此该类试题综合性强，区分度大，分值权重高，因该部分内容恰是自然界最普遍的两个规律的联手演绎，是中学时期最重要的主干知识之一，因此相关内容就成为每年高考测试的热点内容。

［模型讲解］一、明白得动量守恒定律的矢量性例1. 如图1所示，光滑水平面上有大小相同的A 、B 两球在同一直线上运动，两球质量关系为A B m m 2=，规定向右为正方向，A 、B 两球的动量均为6kg ·m/s ，运动中两球发生碰撞，碰撞后A 球的动量增量为s m kg /4⋅-，那么：〔 〕图1A. 左方是A 球，碰撞后A 、B 两球速度大小之比为2:5B. 左方是A 球，碰撞后A 、B 两球速度大小之比为1:10C. 右方是A 球，碰撞后A 、B 两球速度大小之比为2:5D. 右方是A 球，碰撞后A 、B 两球速度大小之比为1:10解析：题中规定向右为正方向，而AB 球的动量均为正，因此AB 都向右运动，又A B m m 2=，因此B A v v 2=，能够判定A 球在左方，CD 错；碰撞后A 的动量变化s m kg p A /4⋅-=∆，依照动量守恒可知，B 球的动量变化s m kg p B /4⋅=∆，因此碰后AB 球的动量分不为s m kg s m kg p s m kg s m kg p B A /10/)46('/2/)46('⋅=⋅+=⋅=⋅-=，解得5:2':'=B A v v ，因此A 正确。

评点：动量守恒定律的矢量性即是重点又是难点，解题时要遵循以下原那么：先确定正方向，与正方向相同的矢量取正号，与正方向相反的矢量取负号，未知矢量当作正号代入式中，求出的结果假设大于零，那么与正方向相同，假设小于零那么与正方向相反，同时也要善于利用动量与动能的关系，但要注意它们的区不。

专题08 反冲爆炸模型及其拓展目录一．爆炸问题 (1)二．反冲运动 (1)三．人船模型问题 (1)一．爆炸问题1．（2023上·江苏扬州·高三扬州中学校考阶段练习）图所示，质量为m、带有光滑半圆形轨道的小车静止在光滑的水平地面上，其水平直径AB长度为2R。

现将质量也为m的小球从A点正上方R处由静止释放，然后由A点进入半圆形轨道后从B点冲出，已知重力加速度为g，不计空气阻力，下列说法正确的是（）2．（2023上·黑龙江哈尔滨·高三哈九中校考阶段练习）如图所示，质量分别为m、2m的两个小球A、B用长为L的轻质细绳连接，B球穿在光滑水平细杆上，初始时刻，细绳处于水平状态，将A、B由静止释放，空气阻力不计。

从释放到A球运动到最低点的过程中，下列说法正确的是（）3．（2024·全国·高三专题练习）如图所示，质量为3kg的光滑轨道静置于足够大的光滑水平地面上，光滑轨道的BC部分为半径为R的四分之一圆弧，CD部分水平。

质量为1kg的小球（可视为质点）从圆弧轨道顶端B正上方的A点由静止自由落下，与圆弧相切于B点并从B点进入圆弧。

已知AB=CD=R=0.3m，取重力加速度大小g =10m/s 2，下列说法正确的是（ ）A ．轨道对小球做正功B ．轨道的最大速度为3m/sC ．轨道对地面的最大压力为70ND ．两者分离时轨道移动了0.15m4．（2023·湖南·校联考模拟预测）如图，棱长为a 、大小形状相同的立方体木块和铁块，质量为m 的木块在上、质量为M 的铁块在下，正对用极短细绳连结悬浮在在平静的池中某处，木块上表面距离水面的竖直距离为h 。

当细绳断裂后，木块与铁块均在竖直方向上运动，木块刚浮出水面时，铁块恰好同时到达池底。

仅M m +M m +M m +M m +5．（2023·山东·济南一中统考二模）在空间技术发展过程中，喷气背包曾经作为宇航员舱外活动的主要动力装置，它能让宇航员保持较高的机动性。