下载文档原格式
现代控制理论基础实验一、 实验目的1. 熟悉MATLAB 的编程以及SIMULINK 仿真工具的使用。
2. 通过实验掌握极点配置及设计状态反馈控制器K 的方法。
3. 深入了解电动机速度控制系统的综合控制方法。
二、 实验内容电动机速度控制系统，设计状态反馈控制器K ，使得系统跟踪单位阶跃指令时无静态误差，超调量s t s 1%,5%<≤σ。
要求写出详细的设计步骤，给出仿真设计系统原理框图，给出仿真的输出波形图和误差波形图。
三、 实验原理控制系统最基本的结构形式是由受控系统和实现反馈控制规律的反馈环节所构成的反馈控制系统。
现代控制理论中，存在两种基本的反馈形式，即状态反馈和输出反馈。
实际情况中，状态反馈具有更好的特性和适应性。
系统动力学的各种特性或各种品质指标，在很大程度上是由系统的极点决定的。
所谓极点配置问题，就是通过状态反馈矩阵K 的选择，使闭环系统的极点，恰好处于所希望的位置。
从线性定常系统运动分析可知，如时域中超调量、过渡过程时间及频域中增益稳定裕度、相位稳定裕度，都被认为等价于系统极点位置，相应综合问题可视为极点配置问题。
四、系统设计1、根据图1计算出电机控制系统的传递函数，并化为状态空间模型图一 受控系统方块图（简化）)(1)10s(0.4s )(5.0]10.05s )(U 3.0)(U 4.0[s Y s Y s s =+-+-可求得受控系统的传递函数：5.2125.502^5.223^5.01.0)()()(++++==s s s s s U s Y s G 系统有一个零点z 1 = -5；用求根函数roots()计算函数极点 >> C=[1 22.5 50.125 2.5];>> roots(C) ans =-20.0000 -2.4490 -0.0510由题意设状态分别为：系统simulink 仿结构如下图二 受控系统simulink 仿真结构图⎪⎪⎪⎩⎪⎪⎪⎨⎧=+--=+=233121*10114.01*]*5.0)4.0[(1005.03.0x s x s x x u x u s x 化为标准形式可得：⎪⎪⎪⎭⎫ ⎝⎛'3'2'1x x x =⎪⎪⎪⎭⎫ ⎝⎛----01.0025.15.25.20020⎪⎪⎪⎭⎫ ⎝⎛321x x x +⎪⎪⎪⎭⎫ ⎝⎛016y=()100 x系统的性能指标：调节时间t s = 76.6s ，上升时间t r = 42.8s ，超调量0%=σ2、确定希望的极点希望的极点数为3，由系统要求超调量低于5%，ts 小于1秒选其中一对为主导极点1s 和2s ，另一个为远极点，并且认为系统的性能主要是由主导极点决定的，远极点所产生的影响很小，可以忽略不计。
一、前言随着科技的飞速发展，自动化、智能化已成为现代工业生产的重要特征。
为了更好地掌握现代控制理论，提高自己的实践能力，我参加了现代控制理论实训课程。
本次实训以状态空间法为基础，研究多输入-多输出、时变、非线性一类控制系统的分析与设计问题。
通过本次实训，我对现代控制理论有了更深入的了解，以下是对本次实训的总结。
二、实训目的1. 巩固现代控制理论基础知识，提高对控制系统的分析、设计和调试能力。
2. 熟悉现代控制理论在工程中的应用，培养解决实际问题的能力。
3. 提高团队合作意识，锻炼动手能力和沟通能力。
三、实训内容1. 状态空间法的基本概念：状态空间法是现代控制理论的核心内容，通过建立状态方程和输出方程，描述系统的动态特性。
2. 状态空间法的基本方法：包括状态空间方程的建立、状态转移矩阵的求解、可控性和可观测性分析、状态反馈和观测器设计等。
3. 控制系统的仿真与实现：利用MATLAB等仿真软件，对所设计的控制系统进行仿真，验证其性能。
4. 实际控制系统的分析：分析实际控制系统中的控制对象、控制器和被控量，设计合适的控制策略。
四、实训过程1. 理论学习：首先，我对现代控制理论的相关知识进行了复习，包括状态空间法、线性系统、非线性系统等。
2. 实验准备：根据实训要求，我选择了合适的实验设备和软件，包括MATLAB、控制系统实验箱等。
3. 实验操作：在实验过程中，我按照以下步骤进行操作：（1）根据实验要求，建立控制系统的状态空间方程。
（2）求解状态转移矩阵，并进行可控性和可观测性分析。
（3）设计状态反馈和观测器，优化控制系统性能。
（4）利用MATLAB进行仿真，观察控制系统动态特性。
（5）根据仿真结果，调整控制器参数，提高控制系统性能。
4. 结果分析：通过对仿真结果的分析，我对所设计的控制系统进行了评估，并总结经验教训。
五、实训成果1. 掌握了现代控制理论的基本概念和方法。
2. 提高了控制系统分析与设计能力，能够独立完成实际控制系统的设计。
实验三典型非线性环节一．实验要求1.了解和掌握典型非线性环节的原理。
2.用相平面法观察和分析典型非线性环节的输出特性。
二．实验原理及说明实验以运算放大器为基本元件，在输入端和反馈网络中设置相应元件（稳压管、二极管、电阻和电容）组成各种典型非线性的模拟电路。
三、实验内容3.1测量继电特性（1）将信号发生器（B1）的幅度控制电位器中心Y测孔，作为系统的-5V~+5V输入信号（Ui）：B1单元中的电位器左边K3开关拨上（-5V），右边K4开关也拨上（+5V）。
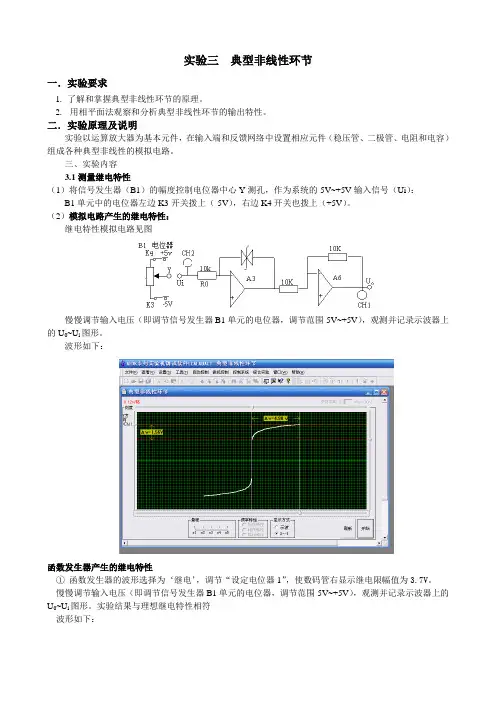
（2）模拟电路产生的继电特性：继电特性模拟电路见图慢慢调节输入电压（即调节信号发生器B1单元的电位器，调节范围-5V~+5V），观测并记录示波器上的U0~U i图形。
波形如下：函数发生器产生的继电特性①函数发生器的波形选择为‘继电’，调节“设定电位器1”，使数码管右显示继电限幅值为3.7V。
慢慢调节输入电压（即调节信号发生器B1单元的电位器，调节范围-5V~+5V），观测并记录示波器上的U0~U i图形。
实验结果与理想继电特性相符波形如下：3.2测量饱和特性将信号发生器（B1）的幅度控制电位器中心Y测孔，作为系统的-5V~+5V输入信号（Ui）：B1单元中的电位器左边K3开关拨上（-5V），右边K4开关也拨上（+5V）。
（2）模拟电路产生的饱和特性：饱和特性模拟电路见图3-4-6。
慢慢调节输入电压（即调节信号发生器B1单元的电位器，调节范围-5V~+5V），观测并记录示波器上的U0~U i图形。
如下所示：函数发生器产生的饱和特性①函数发生器的波形选择为‘饱和’特性；调节“设定电位器1”，使数码管左显示斜率为2；调节“设定电位器2”，使数码管右显示限幅值为3.7V。
慢慢调节输入电压（即调节信号发生器B1单元的电位器，调节范围-5V~+5V），观测并记录示波器上的U0~U i图形。
波形如下：。
3.3测量死区特性模拟电路产生的死区特性死区特性模拟电路见图3-4-7。
现代控制理论实验指导书实验一：线性系统状态空间分析1、模型转换图1、模型转换示意图及所用命令传递函数一般形式：)()(11101110n m a s a s a s a b s b s b s b s G n n n n m m m m ≤++++++++=----K KMATLAB 表示为：G=tf(num,den)，其中num,den 分别是上式中分子，分母系数矩阵。
零极点形式：∏∏==--=n i j mi i ps z s K s G 11)()()( MATLAB 表示为：G=zpk(Z,P ,K)，其中 Z ，P ，K 分别表示上式中的零点矩阵，极点矩阵和增益。
传递函数向状态空间转换：[A,B,C,D] = TF2SS(NUM,DEN)；状态空间转换向传递函数：[NUM,DEN] = SS2TF(A,B,C,D,iu)---iu表示对系统的第iu个输入量求传递函数；对单输入iu为1;验证教材P438页的例9-6。
求P512的9-6题的状态空间描述。
>> A=[0 1;0 -2];>> B=[1 0;0 1];>> C=[1 0;0 1];>> D=[0 0;0 0];>> [NUM,DEN] = ss2tf(A,B,C,D,1)NUM =0 1 20 0 0DEN =1 2 0>> [NUM,DEN] = ss2tf(A,B,C,D,2)NUM =0 0 10 1 0DEN =1 2 0给出的结果是正确的，是没有约分过的形式P512 9-6>> [A,B,C,D]=tf2ss([1 6 8],[1 4 3])A =-4 -31 0B =1C =2 5D =12、状态方程求解单位阶跃输入作用下的状态响应：G=ss(A,B,C,D);[y,t,x]=step(G);plot(t,x). 零输入响应[y,t,x]=initial(G,x0)其中，x0为状态初值。
现代控制理论实验引言现代控制理论是在工程控制领域中发展起来的一种理论体系，其应用范围非常广泛。
为了帮助学生更好地理解和掌握现代控制理论，学校开设了现代控制理论实验课程。
该实验课程旨在通过具体的实验操作，帮助学生巩固理论知识，培养实际操作能力，并能应用现代控制理论解决实际问题。
本文将介绍现代控制理论实验的内容、目的、实验装置和实验步骤。
实验内容现代控制理论实验主要包括以下内容： 1. PID控制器的设计与实现：通过调节比例、积分和微分参数，设计一个PID 控制器，并将其实现在实验装置上，观察控制效果。
2. 状态反馈控制器的设计与实现：利用状态观测器和状态反馈器，设计一个状态反馈控制器，并将其实现在实验装置上，观察控制效果。
3. 频域方法的应用：通过频域分析方法，设计一个控制器，使得实验装置的频率响应满足特定要求。
4. 鲁棒控制方法的应用：利用鲁棒控制方法设计一个控制器，能够在系统参数变化时保持系统的稳定性和性能。
实验目的现代控制理论实验的主要目的是培养学生的实践能力和问题解决能力。
具体目标包括： 1. 理解现代控制理论的基本原理与方法； 2. 掌握现代控制理论的实验操作技巧； 3. 理解研究现代控制理论的方法和途径； 4. 能够设计、实现和调试现代控制器，并分析控制效果； 5. 学会通过实验结果验证和改进控制算法。
实验装置现代控制理论实验装置主要包括：电机系统、传感器、数据采集卡、计算机控制软件和控制器实现装置。
电机系统是实验装置的核心部件，它模拟了真实的控制对象。
传感器用于感知电机系统的转速、位置或其他关键参数。
数据采集卡负责将传感器采集到的数据传输给计算机进行处理。
计算机控制软件包括了实验的开发工具和界面，可以实时控制电机系统并显示实验结果。
控制器实现装置是通过软件或硬件方式实现控制器，在实验中使用。
实验步骤本节将介绍现代控制理论实验的基本步骤。
具体步骤如下：步骤一：系统建模与参数辨识首先需要对实验装置进行数学建模，并通过实验数据对模型参数进行辨识。
现代控制理论实验一一、实验目的：1.熟悉MATLAB,掌握Simulink 工具的使用方法；2.根据传递函数设计出对应的能控、串联结构图；3.掌握极点配置状态反馈方法设计控制器技术；4.学会设计全维观测器。
二、实验内容： 已知系统传递函数)3)(2()1(6)(+++=s s s s s W 1. 用Simulink 对该系统进行实现（1）能控性实现（2）串联实现2. 以上述系统的串联实现为基础，实验研究：（1）系统在初始条件作用下的状态响应和输出响应（2）系统在阶跃输入信号作用下的状态响应和输出响应（3）分析系统在状态空间坐标原点的稳定性3. 以上述系统的能控实现为基础，设计状态反馈控制器要求：系统输出的最大超调量8.16%=δ，调节时间1=s t 秒仿真分析系统的实际工作效果，由系统输出的实际阶跃响应曲线计算最 大超调量、调节时间、稳态误差等系统的性能参数分析该系统在输出比例控制下是否会存在稳态误差？状态反馈控制下是否会存在稳态误差？分析出现这种差异的原因，讨论消除状态反馈稳态误差的方 法。
4. 以上述系统的串联实现为基础，设计系统的全维状态观测器，观测器极点全为-4。
仿真分析在原系统和观测器系统初始条件相同和不同时，观测状态与原状态变量的差值随时间变化的情况，例如改变观测器极点配置到-9，结果有何不同？5. 结合以上 3、4 的结果，应用观测状态实现状态反馈控制对比分析实际状态反馈与观测状态反馈系统控制效果的异同三、实验装置：1.微型计算机2.实验平台采用MATLAB 及Simulink 工具四、实验数据及分析1.（1）能控性实现根据状态空间表达式直接写出系统的能控标准I 型:[]066,100560100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=y u x x输出响应：（2）串联实现输出响应：2.（1）初始条件下的状态响应和输出响应：状态响应：输出响应：（2）阶跃信号作用下的状态响应和输出响应：状态响应：输出响应：分析系统在坐标原点的稳定性：在（1）中设置的初始值为1，1，1，由状态响应曲线可以看出X1并不能最终稳定在零点，其他两条输出曲线虽可稳定，但系统仍可认为在原点处是不稳定的。
现代控制理论在工程领域中扮演着至关重要的角色，通过实验可以帮助我们更好地理解和应用这些理论。
进行现代控制理论的实验可以让我们验证理论模型的准确性，调节控制器参数以实现系统稳定性和性能要求，并且深入理解各种控制策略的优缺点。
以下是一些可能的实验体会：
1. 系统响应特性：通过实验观察不同控制器对系统的响应特性的影响，包括超调量、调节时间、稳态误差等。
比较不同控制器（如P、PI、PD、PID控制器）的性能表现，理解各自的优劣。
2. 鲁棒性分析：实验中可以考虑引入干扰或参数变化，观察系统的鲁棒性能。
了解控制系统对外界干扰的抵抗能力，以及参数变化对系统性能的影响。
3. 系统优化：通过调节控制器参数，优化系统的性能指标。
比如，通过自整定控制器（Self-Tuning Controller）实现对系统动态性能的在线调节和优化。
4. 状态空间分析：利用状态空间方法建立系统模型，实现状态反馈控制。
通过实验验证状态反馈控制对系统性能的改善效果。
5. 非线性控制：尝试应用现代非线性控制理论，如模糊控制、神经
网络控制等，对非线性系统进行控制。
观察非线性控制方法相比传统控制方法的优势。
通过实验，可以更深入地理解现代控制理论的原理和方法，掌握控制系统设计和调试的技巧，提升工程实践能力。
同时，实验也有助于培养工程师的创新思维和问题解决能力。
中南大学现代控制实验报告指导老师设计者学号专业班级设计日期实验一 用MATLAB 分析状态空间模型1、实验设备PC 计算机1台，MATLAB 软件1套。
2、实验目的① 学习系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法；② 通过编程、上机调试，掌握系统状态空间表达式与传递函数相互转换方法。
3、实验原理说明线性系统数学模型的常见的形式有，输入输出模式数学模型（传递函数和微分方程）和状态空间模式数学模型（状态空间表达式或动态方程）。
传递函数模型一般可表示为：若上式中分子分母各项系数为常数，则系统称为线性定常系统(linear time invariant,LTI) 利用下列命令可轻易地将传递函数模型输入MATLAB 环境中。
>>num=[b0,b1,…,bn]; >>den=[1,a1,a2,…,an];而调用tf()函数可构造出对应传递函数对象。
调用格式为： >>G=tf(num,den);其中(num,den)分别为系统的分子和分母多项式系数的向量，返回变量G 为系统传递函数对象。
线性定常系统的状态空间模型可表示为表示状态空间模型的基本要素是状态向量和常数矩阵A ，B ，C ，D 。
用类似的方法可将其输入MA TLAB 环境，对单输入单输出系统，>>A=[a11,a12,…a1n;a21,a22,…a2n;…;an1,an2,…ann]; >>B=[b1;b2;…;bn]; >>C=[c1,c2,…cn]; >>D=d;调用ss()状态方程对象可构造状态方程模型，调用格式如下： >>ss(A,B,C,D)对于两种模型之间的转换，则可分别调用tf()和ss()完成，即： >>G1=tf(G) >>G2=ss(G ’)4、实验步骤① 根据所给系统的传递函数或A 、B 、C 矩阵，依据系统的传递函数阵和状态空间表达式之间的关系式，采用MATLAB 编程。
.现代控制理论实验报告组员：院系：信息工程学院专业：指导老师：年月日实验1 系统的传递函数阵和状态空间表达式的转换[实验要求]应用MATLAB 对系统仿照[例1.2]编程，求系统的A 、B 、C 、阵；然后再仿照[例1.3]进行验证。
并写出实验报告。
[实验目的]1、学习多变量系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法；2、通过编程、上机调试，掌握多变量系统状态空间表达式与传递函数相互转换方法。
[实验内容]1 设系统的模型如式(1.1)示。
p m n R y R u R x DCx y Bu Ax x ∈∈∈⎩⎨⎧+=+= (1.1)其中A 为n ×n 维系数矩阵、B 为n ×m 维输入矩阵 C 为p ×n 维输出矩阵，D 为传递阵，一般情况下为0，只有n 和m 维数相同时，D=1。
系统的传递函数阵和状态空间表达式之间的关系如式(1.2)示。
D B A SI C s den s num s G +-==-1)()()(()( (1.2)式(1.2)中，)(s num 表示传递函数阵的分子阵，其维数是p ×m ；)(s den 表示传递函数阵的按s 降幂排列的分母。
2 实验步骤① 根据所给系统的传递函数或（A 、B 、C 阵），依据系统的传递函数阵和状态空间表达式之间的关系如式(1.2)，采用MATLA 的file.m 编程。
注意：ss2tf 和tf2ss 是互为逆转换的指令；② 在MATLA 界面下调试程序，并检查是否运行正确。
③ [1.1] 已知SISO 系统的状态空间表达式为(1.3)，求系统的传递函数。
,2010050010000100001043214321u x x x x x x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=43210001x x x x y (1.3)程序:A=[0 1 0 0;0 0 -1 0;0 0 0 1;0 0 5 0]; B=[0;1;0;-2]; C=[1 0 0 0]; D=0;[num,den]=ss2tf(A,B,C,D,1)程序运行结果:num =0 -0.0000 1.0000 -0.0000 -3.0000 den =1.0000 0 -5.0000 0 0从程序运行结果得到:系统的传递函数为:24253)(ss s S G --= ④ [1.2] 从系统的传递函数式求状态空间表达式。
经典控制理论的研究对象主要是单输入单输出的系统，控制器设计时一般需要有关被控对象的较精确模型，现代控制理论主要是依据现代数学工具，将经典控制理论的概念扩展到多输入多输出系统。
极点配置问题就是通过选择反馈增益矩阵，将闭环系统的极点恰好配置在根平面上所期望的位置，以获得所希望的动态性能。
1、状态空间分析对于控制系统 X=AX+Bu 式中 X 为状态向量（n 维） u 控制向量（纯量） A n × n 维常数矩阵 B n ×1维常数矩阵 选择控制信号为： u = KX求解上式，得到 X(t )= (A +BK )x (t ) 方程的解为： x (t ) = e ( A +BK )t x (0)可以看出，如果系统状态完全可控，K 选择适当，对于任意的初始状态，当t 趋于无穷时，都可以使x (t )趋于0。
状态反馈闭环控制原理图如下所示：极点配置的设计步骤： （1）检验系统的可控性条件 （2）从矩阵 A 的特征多项式 αααn 1n 1n 1nS A sI s s ++++=---来确定ααn1的值。
（3）确定使状态方程变为可控标准型的变换矩阵 T T=WM 其中 =M []b b bAA2n 1n --W=⎥⎥⎥⎥⎥⎦⎢⎢⎢⎢⎢⎣---11n 2n 11n αααα （4）利用所期望的特征值，写出期望的多项式 ()()()=---μμμn21s s s αααn 1n 1n 1ns ss ++++--并确定αααn21，，的值。
（5）需要的状态反馈增益矩阵K 由以下方程确定2、极点配置及仿真直线一级倒立摆的状态空间模型，以小车加速度作为输入的系统状态方程为：μφφφφ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡X X ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡X X .820100.82800100000000010 μφφφ⎥⎦⎤⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡X X ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡X =Y 0001000001 则有：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=B ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=A 00D 01000001C .820100.82800100000000010 直线一级倒立摆的极点配置转化为：对于如上所述的系统，设计控制器，要求系统具有较短的调整时间（约3秒）和合适的阻尼（阻尼比ς = 0.5）。
