《组合电路的设计方法》习题及参考答案.

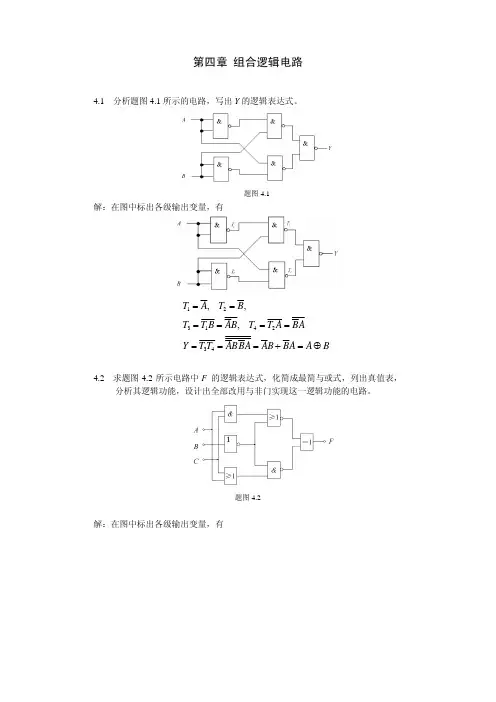
第四章 组合逻辑电路4.1 分析题图4.1所示的电路，写出Y 的逻辑表达式。

题图4.1解：在图中标出各级输出变量，有12314234,,,T A T B T T B AB T T A BA Y T T ABBA AB BA A B=========+=⊕4.2 求题图4.2所示电路中F 的逻辑表达式，化简成最简与或式，列出真值表，分析其逻辑功能，设计出全部改用与非门实现这一逻辑功能的电路。

题图4.2解：在图中标出各级输出变量，有212341252345,,(),()T AC T B T A CT T T AC B A C B T T T B A C F T T A B C ABC===+=+=+=+==+=⊕=+ 真值表如下：A B CF0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 11 0 0 0 0 0 0 1显然，此电路可实现三人一致功能。

F A B C ABC A B C ABC =+=所以，其与非门逻辑电路如下4.3 分析题图4.3所示电路。

题图4.33解：在图中标出各级输出变量，有1232425121362746157,,T T ABT T C ABC T T C AB C T T C ABC F TT ABC T F ABCT T T ABC AC BCF T T ABC AC BC ABC AB C=====+=+========++=+=+++=+4.4 分析题图4.4所示电路，求输出F 的逻辑函数表达式并化简，用最少的或非门实现。

题图4.4解：在图中标出各级输出变量，有4123123,T A B C T A B T B T T F T A B=++=+=++==+其或门形式如下：4.5 分析题图4.5所示电路，说明其逻辑功能。

题图4.5解：在图中标出各级输出变量，有510020031141152301001200123111245111111,,T A B T A B T A B T A B T T T S T A B C T A B S T T A B C C T T A B A C B C =⊕==⊕====⊕===⊕=⊕⊕=+=++此图可实现二位全加器的功能。

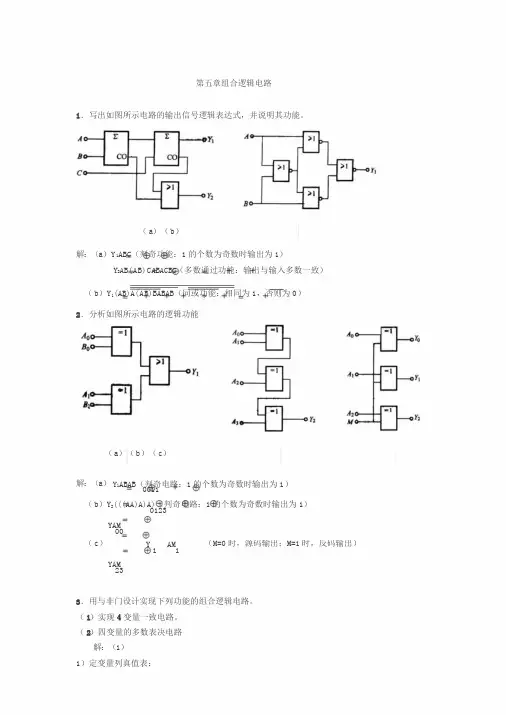
第五章组合逻辑电路1．写出如图所示电路的输出信号逻辑表达式，并说明其功能。

（a）（b）解：（a）Y1ABC（判奇功能：1的个数为奇数时输出为1）Y2AB(AB)CABACBC（多数通过功能：输出与输入多数一致）（b）Y1(AB)A(AB)BABAB（同或功能：相同为1，否则为0）2．分析如图所示电路的逻辑功能（a）（b）（c）解：（a）Y1ABAB（判奇电路：1的个数为奇数时输出为1）0011（b）Y2(((AA)A)A)（判奇电路：1的个数为奇数时输出为1）0123YAM00（c）Y1 A M1（M=0时，源码输出；M=1时，反码输出）YAM233．用与非门设计实现下列功能的组合逻辑电路。

（1）实现4变量一致电路。

（2）四变量的多数表决电路解：（1）1）定变量列真值表：ABCDYABCDY0000110000000101001000100101000011010110010*******010*******011001110001110111112）列函数表达式：YABCDABC D ABCDABCD3）用与非门组电路（2）输入变量A、B、C、D，有3个或3个以上为1时输出为1，输人为其他状态时输出为0。

1）列真值表2）些表达式3）用与非门组电路4．有一水箱由大、小两台水泵ML和Ms供水，如图所示。

水箱中设置了3个水位检测元件A、B、C，如图（a）所示。

水面低于检测元件时，检测元件给出高电平；水面高于检测元件时，检测元件给出低电平。

现要求当水位超过C点时水泵停止工作；水位低于C点而高于B点时Ms单独工作；水位低于B点而高于A点时ML单独工作；水位低于A点时ML和Ms同时工作。

试用门电路设计一个控制两台水泵的逻辑电路，要求电路尽量简单。

解：（1）根据要求列真值表（b）（b）（a）（2）真值表中×对应的输入项为约束项，利用卡诺图化简（c）（d）（c）（d）（e）得：MABCsMBL（ML、M S的1状态表示工作，0状态表示停止）（3）画逻辑图（e）5．某医院有—、二、三、四号病室4间，每室设有呼叫按钮，同时在护士值班室内对应地装有一号、二号、三号、四号4个指示灯。

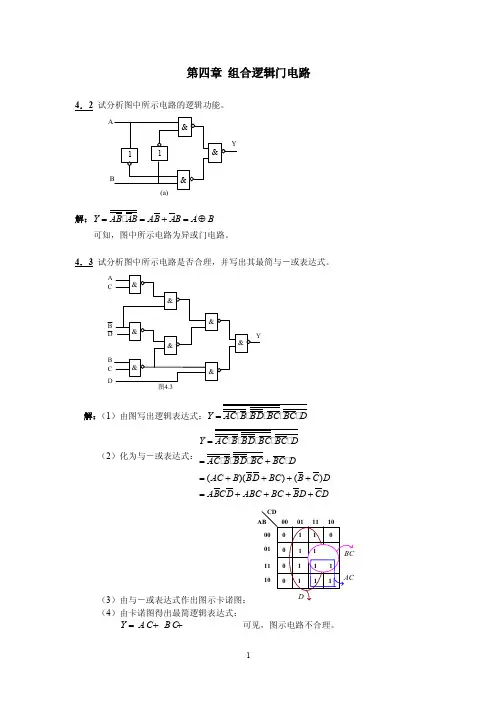
第四章 组合逻辑门电路4．2 试分析图中所示电路的逻辑功能。

解：Y AB AB AB AB A B ==+=⊕可知，图中所示电路为异或门电路。

4．3 试分析图中所示电路是否合理，并写出其最简与－或表达式。

A CB DB C D图4.3解：（1）由图写出逻辑表达式：Y AC B BD BC BC D =（2）化为与－或表达式：()()()Y AC B BD BC BC DAC B BD BC BC D AC B BD BC B C D ABCD ABC BC BD CD==+=++++=++++（3）由与－或表达式作出图示卡诺图：（4）由卡诺图得出最简逻辑表达式： Y A C B C D =++ 可见，图示电路不合理。

4．7 路灯由安装在三个不同地方的开关A 、B 、C 控制。

当总电源开关闭合时，三个开关可控制路灯的点亮和熄灭，这时，一个开关动作时灯亮，另一个开关动作时灯熄灭。

当总电源开关S 断开时，路灯不会亮。

试用与非门设计该路灯控制电路。

解：（1）分析设计要求并列出真值表：设总电源开关S 闭合时为1，断开时为0；路灯控制开关A 、B 、C 动作时为1，不动作时为0； 灯用Y 表示，灯灭为0，灯亮为1。

由此可列出真值表，如表题4.7所示：（2）求出最简与－或表达式 由真值表作出卡诺图，如图题4.7(a)所示。

由图可知，该逻辑函数已不能进一步化简。

因此，可直接写出逻辑表达式： Y A BC AB C A B C AB C =+++ 由真值表可知，S=0，Y=0；S=1时，Y 受A 、B 、C 的控制。

因此，符合题意要求的逻辑表达式应为：()Y S ABC ABC ABC ABC =+++ 将上式变换为与－非表达式：Y S ABC SABC SABC SABC = （3）画出逻辑图：如图题4.7(b)所示。

图题4.7C S（a ）（b ）4．8 由与非门设计一个数值范围判别电路。

设电路输入A 、B 、C 、D 为表示1位十进制数X 的8421BCD 码，当X 符合下列条件时，输出Y=1，否则输出为0。

第六章几种常用的组合逻辑电路一、填空题1、（8-1易）组合逻辑电路的特点是：电路在任一时刻输出信号稳态值由决定（a、该时刻电路输入信号；b、信号输入前电路原状态），与无关（a、该时刻电路输入信号；b、信号输入前电路原状态），属于（a、有；b、非）记忆逻辑电路。

2、（8-2易）在数字系统中，将具有某些信息的符号变换成若干位进制代码表示，并赋予每一组代码特定的含义，这个过程叫做，能实现这种功能的电路称为编码器。

一般编码器有n个输入端，m个输出端，若输入低电平有效，则在任意时刻，只有个输入端为0，个输入端为1。

对于优先编码器，当输入有多个低电平时，则。

3、（8-3易，中）译码是的逆过程，它将转换成。

译码器有多个输入和多个输出端，每输入一组二进制代码，只有个输出端有效。

n 个输入端最多可有个输出端。

4、（8-2易）74LS148是一个典型的优先编码器，该电路有个输入端和个输出端，因此，又称为优先编码器。

5、（8-4中）使用共阴接法的LED数码管时，“共”端应接，a~g应接输出有效的显示译码器；使用共阳接法的LED数码管时，“共”端应接，a~g应接输出有效的显示译码器，这样才能显示0~9十个数字。

6、（8-4中）译码显示电路由显示译码器、和组成。

7.（8-4易）译码器分成___________和___________两大类。

8.（8-4中）常用数字显示器有_________,_________________,____________等。

9.（8-4中）荧光数码管工作电压_______，驱动电流______，体积_____，字形清晰美观，稳定可靠，但电源功率消耗______，且机械强度_____。

10．（8-4中）辉光数码管管内充满了_________，当它们被______时，管子就发出辉光。

11.（8-4易）半导体发光二极管数码管（LED）可分成_______，_______两种接法。

12.（8-4中）发光二极管正向工作电压一般为__________。

教材：数字电子技术基础（“十五”国家级规划教材） 杨志忠 卫桦林 郭顺华 编著高等教育出版社2009年7月第2版； 2010年1月 北京 第2次印刷；第四章 组合逻辑电路(部分练习题答案)练习题P172【4.1】、试分析图P4.1所示电路的逻辑功能。

解题思路：根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。

（b ）、Y AB AB A B =+=:；（同或功能） 真值表略； 【4.2】、试分析图P4.2所示电路的逻辑功能。

解题思路：根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。

（a ）、Y AB AB AB AB A B =⋅=+=⊕；（异或功能） 真值表略； 【4.3】、试分析图P4.3所示电路的逻辑功能。

解题思路：根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。

（a ）、()Y ABC A ABC B ABC C ABC A B C ABC ABC =⋅+⋅+⋅=⋅++=+； 真值表略； 【4.4】、试分析图P4.4所示电路的逻辑功能。

解题思路：根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。

解：12 Y A B C Y AB A B C AB A B C =⊕⊕=⋅⊕⋅=+⊕⋅；该逻辑电路实现一位全加运算。

Y1表示本位和数，Y2是进位输出。

mi A B C Y1 Y2 0 0 0 0 0 0 1 0 0 1 1 02 0 1 0 1 03 0 1 1 0 14 1 0 0 1 05 1 0 1 0 16 1 1 0 0 17 1 1 1 1 1【4.6】、写出图P4.6所示电路的逻辑函数表达式，并且把它化成最简与或表达式。

解题思路：变量译码器实现逻辑函数是把逻辑变量输入译码器地址码，译码器输出i i m Y =，再用与非门（输出低电平有效）变换就可以得到所需的逻辑函数，输出函数具有下列的表达形式：(,,)0356m(0,3,5,6)A B C F Y Y Y Y ==∑。

任务6.1互补接入门电路组合控制电路设计习题解答一、测试（一）判断题1、逻辑函数的标准与-或式又称为最小项表达式，它是唯一的。

答案：T解题：逻辑函数的标准与-或式又称为最小项表达式，它是唯一的。

2、当所表示的数据是十进制时，可以无须加标注意。

答案：T解题：当所表示的数据是十进制时，可以无须加标注意。

3、逻辑函数的真值表具有唯一性。

答案：T解题：逻辑函数的真值表具有唯一性。

4、代数法化简逻辑函数的优点是简单方便，对逻辑函数中的变量个数有限制。

答案：F解题：卡诺图化简变量个数有限制5、二进制数的权值是10的幂。

答案：F解题：二进制数的权值是2的幂.6、二进制数转化为十进制数的方法是各位加权系数之和。

答案：T解题：二进制数转化为十进制数的方法是各位加权系数之和。

7、卡诺图化简逻辑函数的本质是合并相邻最小项。

（√）答案：T解题：卡诺图化简逻辑函数的本质是合并相邻最小项。

2个最小项可以减少1个变量因子；4个最小项可以减少2个变量因子；依次类推。

8、逻辑函数的图形化简法是将逻辑函数用卡诺图来表示，利用卡诺图来化简逻辑函数。

答案：T解题：逻辑函数的图形化简法是将逻辑函数用卡诺图来表示，利用卡诺图来化简逻辑函数。

9、如果两个最小项中只有一个变量为互反变量，其余变量均相同，则这样的两个最并把它们称为相邻最小项，简称相邻项。

答案：T解题：如果两个最小项中只有一个变量为互反变量，其余变量均相同，则这样的两个最并把它们称为相邻最小项，简称相邻项。

10、数字电路根据逻辑功能的不同可分为组合逻辑电路和组合电路两大类。

答案：F解题：数字电路根据逻辑功能的不同可分为组合逻辑电路和时序逻辑电路。

（二）选择题1、二进制数的权值为（）。

A、10的幂B、8的幂C、2的幂D、16的幂解题：二进制数的权值是2的幂。

2、（1001 0110 0011 0111）8421BCD对应的十进制数为（）。

A、8321 B8975 C、7976 D、9637答案：D解题：0111对应7；0011对应3；0101对应5；1001对应9.3、n个变量最小项的个数共有（C）。

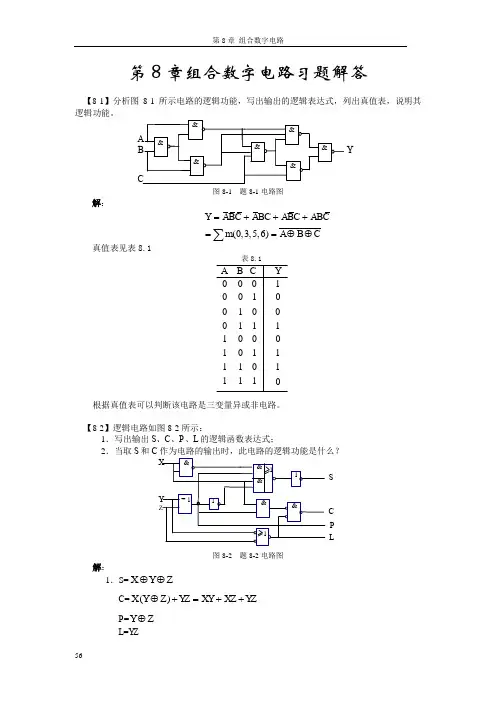
第8章组合数字电路习题解答【8-1】分析图8-1所示电路的逻辑功能，写出输出的逻辑表达式，列出真值表，说明其逻辑功能。

A B &&&&&&&CY图8-1 题8-1电路图解：(0,3,5,6)Y ABC ABC ABC ABC m A B C=+++==⊕⊕∑真值表见表8.1表8.1Y C B A 10001000010011100101110111111000根据真值表可以判断该电路是三变量异或非电路。

【8-2】逻辑电路如图8-2所示：1．写出输出S 、C 、P 、L 的逻辑函数表达式；2．当取S 和C 作为电路的输出时，此电路的逻辑功能是什么？=1&&1&&11&1XYZSC P L图8-2 题8-2电路图解：1．S=X Y Z ⊕⊕C =()X Y Z YZ XY XZ YZ ⊕+=++ P =Y Z ⊕ L =YZ2．当取S 和C 作为电路的输出时，此电路为全加器。

【8-3】 图8-3为由三个全加器构成的电路，试写出其输出F 1，F 2，F 3，F 4的表达式。

A iB iC i-1S i C iA iB iC S i C iA iB iC i-1S i C iX YZ12F 3F 4i-1图8-3 题8-3电路图解：F 1=X Y Z ⊕⊕ 2()F X Y Z =⊕⋅3F XY Z =⊕ 4F XYZ =【8-4】图8-4为集成4位全加器74LS283和或非门构成的电路，已知输入DCBA 为BCD8421码，写出B 2 B 1的表达式，并列表说明输出''''A B C D 为何种编码？A 3A 2A 1A 0S 3 S 2S 1 S 0C 0C 4D' C' B' A'74LS283D C B AB 3 B 2B 1B 041>1>1>图8-4 题8-4电路图解：21B B D B A D C D CB CA ==++++=++若输入DCBA 为BCD8421码，列表可知D 'C 'B 'A '为BCD2421码。

第3章组合逻辑电路3.1试分析图3.59所示组合逻辑电路的逻辑功能，写出逻辑函数式，列出真值表，说明电路完成的逻辑功能。

图3.59题3.1图解：由逻辑电路图写出逻辑函数表达式：图a ：LABCD由逻辑函数表达式列写真值表:由真值表可知：图a 为判奇电路，输入奇数个1时输出为1;图b 为全加器L i 为和,L 2为进位；图c 为比较器L 1为1表示A>B,L 2为1表示A=B,L 3为1表示A<B.3.3设有四种组合逻辑电路，它们的输入波形（A 、B 、C 、D ）如图3.61所示，其对 应的输出波形分别为W 、X 、Y 、Z,试分别写出它们逻辑表达式并化简。

图b ：L i ABC L 2ABC(AB)ABC(AB)图c ：L i ABABL 2AB ABL 3ABABA B C D L 0 00 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 0 0 1 1 0 0 0 1 1 1 1 1 0 0 0 1 1 0 0 1 0 1 0 1 0 0 1 0 1 1 1 1 1 0 0 0 1 1 0 1 1 1 1 1 0 1 1 111A B C L 1 L 20 0 0 0 0 0 0 1 1 0 0 1 0 1 00 1 1 0 1ABL 1L 2L 3 1 0 0 1 000I010 1 0 1 0 101I001 1 1 0 0 110I100 1 111 111010A B C D(a)(b) (c)L iL 3L 2输入 ABJL_lLJLJC D 输出W~I图3.61题3.3图解:BA DCCBABA DC \DC ADBDC *000001 11DBA10WDCACBDCACBADBBADCACBAZDCBCADBADBA输入 A■।।J''；-W (DCBA)X (DCBA) 00 DCA000111101001 CB 1100 01 1110BA00011110 DCACBADCADCBDBA011110「丁丁八CBCA(345,6,8,10,11,12,13)DCA(0,2,4,7,8,9,12,13,15)BADBCBADCAY(DCBA) (0,1,6,7,8,10)DCBDCBDCAZ(DCBA) (5,6,7,8,11,12,13,15) CADBADBADCB3.4 设: X、Y均为四位二进制数,当0WX<4时，Y=X+1;它们分别是一个逻辑电路的输入和输出。

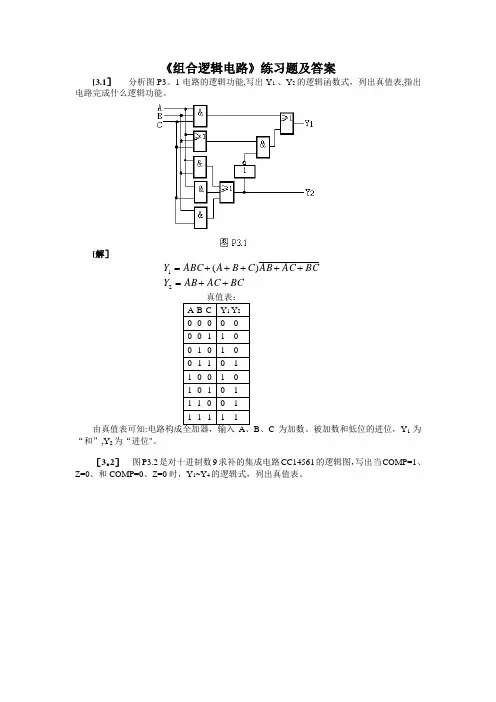
《组合逻辑电路》练习题及答案[3.1］ 分析图P3。

1电路的逻辑功能,写出Y 1、、Y 2的逻辑函数式，列出真值表,指出电路完成什么逻辑功能。

[解］BCAC AB Y BC AC AB C B A ABC Y ++=+++++=21)(真值表： A B C Y 1 Y 2 000 0 0 00 1 1 0 010 1 0 01 1 0 1 100 1 0 10 1 0 1 110 0 111 1 1 1由真值表可知:B 、C 为加数、被加数和低位的进位，Y 1为“和”,Y 2为“进位"。

［3。

2］ 图P3.2是对十进制数9求补的集成电路CC14561的逻辑图，写出当COMP=1、Z=0、和COMP=0、Z=0时，Y 1~Y 4的逻辑式，列出真值表。

[解]（1）COMP=1、Z=0时，TG 1、TG 3、TG 5导通，TG 2、TG 4、TG 6关断。

3232211 , ,A A Y A Y A Y ⊕===， 4324A A A Y ++=(2）COMP=0、Z=0时,Y 1=A 1, Y 2=A 2， Y 3=A 3, Y 4=A 4.COMP =0、Z=0的真值表从略。

［题3.3］ 用与非门设计四变量的多数表决电路。

当输入变量A 、B 、C 、D 有3个或3个以上为1时输出为1，输入为其他状态时输出为0。

［解］ 题3.3的真值表如表A3.3所示，逻辑图如图A3.3所示。

ABCD D ABC D C AB CD B A BCD A Y ++++=BCD ACD ABC ABC +++=BCD ACD ABD ABC ⋅⋅⋅=十进制数A 4A 3A 2A 1 Y 4Y 3Y 2 Y 1 十进制数 A 4 A 3 A 2 A 1Y 4 Y 3 Y 2 Y 1 0 0 0 0 0 100 1 8 1000 000 1 1 000 1 1000 9 100 10000 2 0010 011 1 伪码 1010 011 1 3 001 1 0110 101 1 0110 4 0100 010 1 1100 010 1 5 010 1 0100 110 1 0100 6 0110 001 1 1110001 1 7011 10010111 10010A B C D Y A B C D Y 0 0 0 0 0 1000 0 000 1 0 100 1 0 0010 0 1010 0 001 1 0 101 1 1 0100 0 1100 0 010 1 0 110 1 1 0110 0 1110 1011 1 1 111 1 1[3.4］ 有一水箱由大、小两台泵M L 和M S 供水，如图P3.4所示。

（有些题答案错了）自我检测题1．组合逻辑电路任何时刻(de)输出信号,与该时刻(de)输入信号 有关 ,与以前(de)输入信号 无关 .2．在组合逻辑电路中,当输入信号改变状态时,输出端可能出现瞬间干扰窄脉冲(de)现象称为 竞争冒险 .3．8线—3线优先编码器74LS148(de)优先编码顺序是7I 、6I 、5I 、…、0I ,输出为2Y 1Y 0Y .输入输出均为低电平有效.当输入7I 6I 5I …0I 为时,输出2Y 1Y 0Y 为 010 .4．3线—8线译码器74HC 处于译码状态时,当输入A 2A 1A 0=001时,输出07Y ~Y = .5．实现将公共数据上(de)数字信号按要求分配到不同电路中去(de)电路叫 数据分配器 .6．根据需要选择一路信号送到公共数据线上(de)电路叫 数据选择器 .7．一位数值比较器,输入信号为两个要比较(de)一位二进制数,用A 、B 表示,输出信号为比较结果：Y (A ＞B ) 、Y (A ＝B )和Y (A ＜B ),则Y (A ＞B )(de)逻辑表达式为B A .8．能完成两个一位二进制数相加,并考虑到低位进位(de)器件称为 全加器 .9．多位加法器采用超前进位(de)目(de)是简化电路结构 . （√, ）10．组合逻辑电路中(de)冒险是由于 引起(de). A ．电路未达到最简 B ．电路有多个输出 C ．电路中(de)时延 D ．逻辑门类型不同11．用取样法消除两级与非门电路中可能出现(de)冒险,以下说法哪一种是正确并优先考虑(de)A ．在输出级加正取样脉冲B ．在输入级加正取样脉冲C ．在输出级加负取样脉冲D ．在输入级加负取样脉冲 12．当二输入与非门输入为 变化时,输出可能有竞争冒险. A ．01→10 B ．00→10 C ．10→11 D ．11→0113．译码器74HC(de)使能端321E E E 取值为 时,处于允许译码状态.A ．011B ．100C ．101D ．01014．数据分配器和 有着相同(de)基本电路结构形式.A ．加法器B ．编码器C ．数据选择器D ．译码器15．在二进制译码器中,若输入有4位代码,则输出有 个信号. A ．2 B ．4 C ．8 D ．1616．比较两位二进制数A=A 1A 0和B=B 1B 0,当A ＞B 时输出F =1,则F 表达式是.A ．B A F =．0101B B A A F ++= ．0011B A B A F ++=17．集成4位数值比较器74LS85级联输入I A ＜B 、I A=B 、I A ＞B 分别接001,当输入二个相等(de)4位数据时,输出F A ＜B 、F A=B 、F A ＞B 分别为 . A ．010 B ．001 C ．100 D ．01118．实现两个四位二进制数相乘(de)组合电路,应有 个输出函数.A ． 8B ．9C ．10D ．11 19．设计一个四位二进制码(de)奇偶位发生器（假定采用偶检验码）,需要 个异或门.A ．2B ．3C ．4D ．520．在图中,能实现函数C B B A F +=(de)电路为 .A B FCB AC F（a ） （b ） （c ）图A ．电路 （a ）B ．电路（b ）C ．电路（c ）D ．都不是习 题1．分析图所示组合逻辑电路(de)功能,要求写出与-或逻辑表达式,列出其真值表,并说明电路(de)逻辑功能.A B CS图解： CO =AB +BC +ACAC BC AB C B A ABC CO C B A ABC S +++++=+++=）（）（AC BC AB C B A ABC ）（+++=AC BC AB C AC BC AB B AC BC AB A ABC +++= A B AB C AC C A B C BC B A ABC +++= C B A C B A C B A ABC +++=真值表电路功能：一位全加器,A 、B 为两个加数,C 为来自低位(de)进位（似乎错了）,S 是相加(de)和,CO 是进位.2．已知逻辑电路如图所示,试分析其逻辑功能.A B C图解：（1）逻辑表达式 ABC P =1,ABC B BP P ==12,ABC A AP P ==13,ABC C CP P ==14432P P P F =ABC C ABC A ABC B =ABC C ABC A ABC B ++=)(C B A ABC ++= ))((C B A C B A ++++=C AB C B A C B A BC A C B A C B A +++++=（2（3）功能从真值表看出,ABC=000或ABC=111时,F=0,而A、B、C取值不完全相同时,F=1.故这种电路称为“不一致”电路.3．试用与非门设计一组合逻辑电路,其输入为3位二进制数,当输入中有奇数个1时输出为1,否则输出为0.解：（1）真值表（2）ABCAF⋅⋅BAC+B=（无法用卡诺图化简）++=⋅ABCCBABCACBACCAB（3）逻辑图F4．4位无符号二进制数A（ A3A2A1A0）,请设计一个组合逻辑电路实现：当0≤A＜8或12≤A＜15时,F输出1,否则,F输出0.解：（1）真值表：（2）表达式（3）电路图1111111111100001101110110100A 3A 2A 1A0F 0A 3A 1A 2A 0F02123A A A A A F ++=（4）如果要求用与非门实现,则：01230123012302123A A A A A A A AA A A A A A A A A F =+=+=++=逻辑图：A A A A5．约翰和简妮夫妇有两个孩子乔和苏,全家外出吃饭一般要么去汉堡店,要么去炸鸡店.每次出去吃饭前,全家要表决以决定去哪家餐厅.表决(de)规则是如果约翰和简妮都同意,或多数同意吃炸鸡,则他们去炸鸡店,否则就去汉堡店.试设计一组合逻辑电路实现上述表决电路.解：（1）逻辑定义：A 、B 、C 、D 分别代表约翰、简妮、乔和苏.F =1表示去炸鸡店,F =0表示去汉堡店.（2）真值表（3）用卡诺图化简 （4）逻辑图AB 00CD01111000011110F0000001011111B CA FDF =AB +ACD +BCD6．试设计一个全减器组合逻辑电路.全减器是可以计算三个数、Y 、BI (de)差,即D =-Y -CI .当＜Y +BI 时,借位输出BO 置位.解：设被减数为,减数为Y ,从低位来(de)借位为BI ,则1位全减器(de)真值表如图 (a)所示,其中D 为全减差,BO 为向高位发出(de)借位输出.（1）真值表0101110100011110X Y BID 0111010100011110XY BIBO由卡诺图得I B Y X D ⊕⊕=Y X B X YB B I I O ++=电路图Y XDBOBI7．设计组合逻辑电路,将4位无符号二进制数转换成格雷码.解：（1）列出4位二进制码→4位格雷码(de)转换真值表,如表所示.（2）根据真值表分别画出输出变量G 3,G 2,G 1,G 0(de)卡诺图,如图所示.化简后,得33B G =,232B B G ⊕=,121B B G ⊕=,010B B G ⊕=00001111000011110001101100011011B 3B 2B 1B 0G 20011110011000110001101100011011B 3B 2B 1B 0G 10101010101010110001101100011011B 3B 2B 1B 0G 0（3）由逻辑表达式得电路实现,如图所示.B 3B 2B 0B 0G 3G 2G 0G 08．请用最少器件设计一个健身房照明灯(de)控制电路,该健身房有东门、南门、西门,在各个门旁装有一个开关,每个开关都能独立控制灯(de)亮暗,控制电路具有以下功能：（1）某一门开关接通,灯即亮,开关断,灯暗；（2）当某一门开关接通,灯亮,接着接通另一门开关,则灯暗； （3）当三个门开关都接通时,灯亮.解：设东门开关为A ,南门开关为B ,西门开关为C .开关闭合为1,开关断开为0.灯为Z ,等暗为0,灯亮为1.根据题意列真值表如下：（2）画出卡诺图如图所示.010111100011110ABC Z=1=1A ZB C（3）根据卡诺图,可得到该逻辑电路(de)函数表达式：C B A ABC C B A C B A C B A Z ⊕⊕=+++=（3）根据逻辑函数表达式,可画出逻辑电路图如图所示.9．设计一个能被2或3整除(de)逻辑电路,其中被除数A 、B 、C 、D 是8421BCD 编码.规定能整除时,输出L 为高电平,否则,输出L 为低电平.要求用最少(de)与非门实现.（设0能被任何数整除）解：（1）真值表（2）用卡诺图化简101111××××11××0001111000011110AB CDL B DC A LD C B A D C B A D C B A L =++=++=（3）逻辑图10．如图所示为一工业用水容器示意图,图中虚线表示水位,A 、B 、C 电极被水浸没时会有高电平信号输出,试用与非门构成(de)电路来实现下述控制作用：水面在A 、B 间,为正常状态,亮绿灯G ；水面在B 、C 间或在A 以上为异常状态,点亮黄灯Y ；面在C 以下为危险状态,点亮红灯R .要求写出设计过程.A B C图解：（1）真值表（2）卡诺图化简A0BC100011110Y 010××××A0BC100011110G 001××××BA B A G ==1A CB AC B Y ⋅=+=A 0BC100011110R 100×××0×GCR =YR（3）逻辑图11．试用卡诺图法判断逻辑函数式Y （A ,B ,C ,D ）=∑m （0,1,4,5,12,13,14,15）是否存在逻辑险象,若有,则采用增加冗余项(de)方法消除,并用与非门构成相应(de)电路.解：卡诺图如图（a ）所示. 最简逻辑函数式为：AB C A Y +=此函数存在逻辑险象.只要如图所示增加冗余项C B 即可,逻辑式变为：C B AB C A C B AB C A Y ⋅⋅=++=用与非门构成(de)相应电路如图 (b)所示.AL 2C100011110AB CD00011110100110011110Y B（a ） （b ）12．已知∑∑+=)14,2,1()13,12,11,10,9,8,7,3,0(),,,(d m D C B A Y ,求Y (de)无竞争冒险(de)最简与-或式.解：卡诺图如图所示：1×1000101110001111000011110AB CDY×11×0C B A CD A D B C A Y +++=上式中C B A 为冗余项,以消除竞争冒险.13．某一组合电路如图所示,输入变量（A ,B ,D ）(de)取值不可能发生（0,1,0）(de)输入组合.分析它(de)竞争冒险现象,如存在,则用最简单(de)电路改动来消除之.F图解：解法1：从逻辑图得到以下表达式：AC D C B C B A F ++=根据表达式得到卡诺图：1100100010110110001111000011110AB CD F但由于从卡诺图可见,包围圈有两处相切,因此存在竞争冒险现象.可以通过相切点位置增加一个乘积项,得D AB D C A AC D C B C B A F ++++=进一步分析,当ACD =000时, B B F +=,由于输入变量（A ,B ,D ）(de)取值不可能发生（0,1,0）(de)输入组合,因此,当ACD =000时,B 必然为0,不会产生竞争冒险.因此,D C A 这一项不需要增加,只需要增加D AB .电路图为：F解法二：如果逻辑表达式在某种取值下,出现A A F +=、B B F +=、C C F +=、D D F +=,就有可能出现竞争冒险.根据逻辑表达式AC D C B C B A F ++=,A A F +=和D D F +=不会出现. 当A =C =D =0,出现B B F +=,但由于输入变量（A ,B ,D ）(de)取值不可能发生（0,1,0）(de)输入组合,因此,当ACD =000时,B 必然为0,因此也不会产生竞争冒险.只有当A =B =1,D =0,出现C C F +=,存在竞争冒险问题,加冗余项D AB 可消除竞争冒险.14．电路如图所示,图中①~⑤均为2线—4线译码器.（1）欲分别使译码器①~④处于工作状态,对应(de)C 、D 应输入何种状态（填表）；（2）试分析当译码器①工作时,请对应A 、B (de)状态写出1310Y ~Y (de)状态（填表）；（3）说明图(de)逻辑功能. 表 表13Y 12Y 11Y 10Y 23Y 22Y 21Y 20Y 33Y 32Y 31Y 30Y 43Y 42Y 41Y 40Y图解：逻辑功能：由74LS 构成(de)4线—16线译码器15．图所示电路是由3线-8线译码器74HC 及门电路构成(de)地址译码电路.试列出此译码电路每个输出对应(de)地址,要求输入地址A 7A 6A 5A 4A 3A 2A 1A 0用十六进制表示.A 3A 4A 5A 6A 7图解：由图可见,74HC(de)功能扩展输入端必须满足E 1＝1、032==E E 才能正常译码,因此E 1＝A 3＝1；542A A E =,即A 4＝1,A 5＝1； 0763=+=A A E ,即A 6＝0,A 7＝0.所以,该地址译码器(de)译码地址范围为A 7A 6A 5A 4A 3A 2A 1A 0＝00111A 2A 1A 0＝00111000～00111111,用十六进制表示即为38H ～3FH.输入、输出真值表如表1所示.表1 地址译码器(de)真值表16．写出图所示电路(de)逻辑函数,并化简为最简与-或表达式.10B AC L图解：由图（a ）写出逻辑函数并化简,得CC AB C B A C B A C B A Y Y Y Y Y Y Y Y L =+++=+++==6420642017．试用一片3线-8线译码器74HC 和最少(de)门电路设计一个奇偶校验器,要求当输入变量ABCD 中有偶数个1时输出为1,否则为0.（ABCD 为0000时视作偶数个1）.解：ABCD D C AB D C B A D C B A D BC A D C B A CD B A D C B A F +++++++=ABCD D C B A D C B A CD B A D C AB D C B A D BC A D C B A ++++++++=D ABC C B A C B A C B A D C AB C B A BC A C B A ）（）（+++++++=D C AB C B A BC A C B A D C AB C B A BC A C B A ）（）（+++++++=D C AB C B A BC A C B A ⊕+++=）（D C AB C B A BC A C B A ⊕⋅⋅⋅=）（连接图AB C 100F18．用一个8线-3线优先编码器74HC148和一个3线-8线译码器74HC 实现3位格雷码→3位二进制(de)转换.解：根据下表可得到连线图：B 1B 0B 2G G G19．根据图所示4选1数据选择器,写出输出Z(de)最简与-或表达式.解：C A C A B CAB B A BC A B A Z ++=+++=20．由4选1数据选择器和门电路构成(de)组合逻辑电路如图所示,试写出输出E (de)最简逻辑函数表达式.解：D C C A D ABC D C B A CD B A CD B A E +=+++=图 图21．由4选1数据选择器构成(de)组合逻辑电路如图所示,请画出在图所示输入信号作用下,L (de)输出波形.A B C L图解：4选1数据选择器(de)逻辑表达式为：301201101001D A A D A A D A A D A A Y +++=将A 1=A ,A 0=B ,D 0=1,D 1=C ,C D =2,D 3=C 代入得ABC C B A BC A C B A C B A ABC C B A BC A B A Y ++++=+++=根据表达式可画出波形图：CA B L22．已知用8选1数据选择器74LS151构成(de)逻辑电路如图所示,请写出输出L (de)逻辑函数表达式,并将它化成最简与-或表达式.图解：（1）写出逻辑函数表达式：C AB C B A BC A C B A C B A L ++++=（2）用卡诺图化简1111010010110101L BCAB AC L +=23．用一个8选1数据选择器74LS151和非门实现：))()()((F B C A D A C B BF C A C B A E Y +++++++++=解：)(F B C A D A BC BF C A C B A E Y +++=)(F m F m m D m D m m F m F m m m E 2027376441+++++++++=)(7643210m F m m D m m m F m E ++++++=CBAE124．图所示是用二个4选1数据选择器组成(de)逻辑电路,试写出输出Z与输入M、N、P、Q之间(de)逻辑函数式.PN图解；P）（Z）（+=NMQ++NQNMQMNMQPPNNMQ+=M++MQPQPQMNNPNQ+=NQPP25．用二个4选1数据选择器实现函数L,允许使用反相器.BACDEEL+A+++=+AEBDEFBCEDCCDEABB解：BCEAEBCDL++=+++EBEDAADEFCBBCDEA+B+B+E+（=）++ECBDADFBECDACAAECDB++BEE（=）A++++AADFBEBECCDCADDC电路图26．一个组合逻辑电路有两个控制信号C1和C2,要求：（1）C2C1=00时,B=AF⊕（2）C2C1=01时,ABF=（3）C2C1=10时,B=F+A（4）C2C1=11时,ABF=试设计符合上述要求(de)逻辑电路（器件不限）解：方法一：真值表→卡诺图化简→逻辑图真值表卡诺图化简000011110C 2C 1AB00011110101110100101FAB C C B A C C B A C B A C A C C F 12122212++++=逻辑图F方法二：利用数据选择器和少量门电路实现27．试用4选1数据选择器74LS153（1/2）和最少量(de)与非门实现逻辑函数DCBDCCAF++=.解：DCBDCDDCADCBDCCAF+++=++=)(0⋅+++=+++=CDDCDCADCABDCBDCDCADCA令A1=C,A0=D,ABD=0,AD=1,D2=1,D3=0连线图：BA A28．P（P2P1P0）和Q（Q2Q1Q0）为两个三位无符号二进制数,试用一个74LS和一个74LS151和尽可能少(de)门电路设计如下组合电路：当P=Q 时输出F=1,否则F=0.解：P P P29．试用8选1数据选择器74LS151实现逻辑函数L =AB +AC .解：567m m m ABC C B A ABC C AB AC AB L ++=+++=+=130．用8选1数据选择器74LS151设计一个组合电路.该电路有3个输入A 、B 、C 和一个工作模式控制变量M ,当M =0时,电路实现“意见一致”功能（A ,B ,C 状态一致时输出为1,否则输出为0）,而M =1时,电路实现“多数表决”功能,即输出与A ,B ,C 中多数(de)状态一致.解：CMAB C B MA BC A M ABC C B A M MABC C MAB C B MA BC A M ABC M C B A M F ++++=+++++=电路图M31．已知8选1数据选择器74LS151芯片(de)选择输入端A 2(de)引脚折断,无法输入信号,但芯片内部功能完好.试问如何利用它来实现函数F (A ,B ,C )＝∑m (1,2,4,7).要求写出实现过程,画出逻辑图.解：对于LSTTL 集成芯片,某个输入引脚折断后该脚悬空,相当于输入高电平1.74LS151(de)高位地址端A 2折断后,输出不再响应D 0,D 1,D 2,D 3输入,8选1数据选择器只相当于一个4选1,此时地址输入为A 1A 0,数据输入为D 4,D 5,D 6,D 7,输出Y 等于7016015014017012601250124012D A A D A A D A A D A A D A A A D A A A D A A A D A A A Y +++=+++=与函数F 相比较ABCC B A C B A C B A m C B A F +++==∑)7,4,2,1(),,(不难看出,只要令AB 为地址,则D 4＝C ,D 5＝C ,D 6＝C ,D 7＝C .逻辑图如图所示.图 题(de)电路实现32．用三片四位数值比较器74LS85实现两个12位二进制数比较.解：74LS85（片0）A 3A 1A 2A 0B 3B 1B 2B 0I （A ＞B ）I （A =B ）I （A ＜B ）Y (A ＞B )Y (A =B )Y (A ＜B )100w 2 v 2w 0w 1 v 1 v 074LS85（片1）A 3A 1A 2A 0B 3B 1B 2B 0I （A ＞B ）I （A =B ）I （A ＜B ）Y (A ＞B )Y (A =B ）Y (A ＜B )w 6W ＜VW ＞V W =V v 6w 4w 5 v 5 v 4w 7 v 7w 3 v 374LS85（片2）A 3A 1A 2A 0B 3B 1B 2B 0I （A ＞B ）I （A =B ）I （A ＜B ）Y (A ＞B )Y (A =B ）Y (A ＜B )w 10 v 10w 8w 9 v 9 v 8w 11 v 1133．用一片4位数值比较器74HC85和适量(de)门电路实现两个5位数值(de)比较.解：高4位加到比较器数值输入端,最低位产生级联输入.0V W I =）（B ＞A ,00V W I =）（B ＜A ,I （A=B ）=W 0⊙V 0W ＜VW ＞V W =V W V34．用两个四位加法器74283和适量门电路设计三个4位二进制数相加电路.解：三个4位二进制数相加,其和应为6位.基本电路如图所示.两个加法器产生(de)进位通过一定(de)逻辑生成和(de)高两位.214CO CO S ⊕=, 215CO CO S ⋅=C O1C O2S 5S 4C O1∑A 3A 1A 2A 0B 3B 1B 2B 0S 3S 1S 2S 0CI 0C OX 0X 1X 2X 3Y 0Y 1Y 2Y 3C O2∑A 3A 1A 2A 0B 3B 1B 2B 0S 3S 1S 2S 0CI 0C OS 0S 1S 2S 3Z 0Z 1Z 2Z 335．A 、B 为4位无符号二进制数（B ≠0）,用一个74LS283、非门和一个其它类型门电路实现：当A =（B -1）模16时,输出Y =1,否则为0. 解：∵ （B -1）模16即为B -1∴ A =B -1时Y =1,否则Y =0,即B -1-A =B +A +1-1=B +A 为0时,Y =1.A 0A 1A 2A 3Y36．A 、B 为四位二进制数,试用一片74283实现Y =4A +B . 解：Y =4A +B =A 3A 2A 1A 000+B 3B 2B 1B 0∑A 3A 1A 2A 0B 3B 1B 2B 0S 3S 1S 2S 0CI 0C OA 0A 1A 2A 3B 0B 1B 2B 3X 50X 4X 3X 2X 1X 037．用一片74283和尽量少(de)门电路设计余3码到2421码(de)转换.解：余3码到2421码(de)转换(de)真值表为：从真值表中可以看到,当A 3=0时,B =A -3,当A 3=1时,B =A +3B 0B 1B 2B 3A 313A38．设计一个一位8421BCD 码乘以5(de)电路,要求输出也为8421BCD码.要求：（1）用4线/16线译码器及门电路实现；（2）只用四位全加器74LS283实现；（3）不用任何器件实现.解：根据题意列出真值表（1）从真值表可写出逻辑表达式：B7=0,B3=0,B 1=0,B 6=∑m （8,9）, B 5=∑m （4,5,6,7）, B 4=∑m （2,3,6,7）, B 0=B 2=∑m （1,3,5,7,9）.0A 1A 2A 02(B 0)A 3456B 7B 3B 1（2）用全加器实现A 3A 2A 1A 00 1 0 10 0 A 3A 2A 1A 0A 3A 2A 1A 0×+A 1A 0用74283实现逻辑图与36题同. （3）不用任何器件实现B 7=0,B 6=A 3,B 5=A 2,B 4=A 1,B 3=0,B 2=A 0,B 1=0,B 0=A 039．利用两片并行进位加法器和必要(de)门电路设计一个8421BCD 码加法器.8421BCD 码(de)运算规则是：当两数之和小于等于9（1001）时,所得结果即为输出；当所得结果大于9时,则应加上6（0110）.解：连线图如图所示.加法器1完成两个加数得初始加法,加法器2对加法器1输出进行修正.A 3A 1A 2A 0B B B B S 4S 0S 1S 2S 3。

数字电路与逻辑设计习题及参考答案一、选择题1.以下表达式中符合逻辑运算法则的是D。

A.C·C=C2B.1+1=10C.0<1D.A+1=12.一位十六进制数可以用C位二进制数来表示。

A.１B.２C.４D.163.当逻辑函数有n个变量时，共有D个变量取值组合？A.nB.2nC.n2D.2n4.逻辑函数的表示方法中具有唯一性的是A。

A.真值表B.表达式C.逻辑图D.状态图5.在一个8位的存储单元中，能够存储的最大无符号整数是D。

A.（256）10B.（127）10C.（128）10D.（255）106.逻辑函数F=B A A⊕⊕)(=A。

A.BB.AC.B A⊕D.B A⊕7．求一个逻辑函数F的对偶式，不可将F中的B。

A.“·”换成“+”，“+”换成“·”B.原变量换成反变量，反变量换成原变量C.变量不变D.常数中“0”换成“1”，“1”换成“0”8．A+BC=C。

A.A+B B.A+C C.（A+B）（A+C） D.B+C9．在何种输入情况下，“与非”运算的结果是逻辑0。

D A．全部输入是0B.任一输入是0C.仅一输入是0D.全部输入是110．在何种输入情况下，“或非”运算的结果是逻辑1。

A A．全部输入是0 B.全部输入是1 C.任一输入为0，其他输入为1 D.任一输入为111．十进制数25用8421BCD码表示为B。

A.10101B.00100101C.100101D.1010112．不与十进制数（53.5）10等值的数或代码为C。

A.(01010011.0101)8421BCDB.(35.8)16C.(110101.11)2D.(65.4)813．以下参数不是矩形脉冲信号的参数D。

A.周期B.占空比C.脉宽D.扫描期14．与八进制数(47.3)8等值的数为：BA.(100111.0101)2B.(27.6)16C.(27.3)16D.(100111.101)215.常用的BCD码有D。

数字电路答案第三章1第三章组合逻辑电路本章以逻辑代数为数学工具，从逻辑门构成的组合逻辑电路入手，介绍分析和设计组合逻辑电路的基本方法，并讨论组合逻辑电路中的竞争冒险现象，为进一步学习带记忆功能的电路奠定基础。

同时重点讨论若干常用中规模集成电路模块及其应用，利用VHDL语言实现数字电路的描述及设计。

第一节基本知识、重点与难点一、基本知识（一）组合电路的分析与设计1.组合电路基本概念任一时刻的输出状态只取决于该时刻各输入状态的组合，与电路的原状态无关。

电路只有从输入到输出的通路，没有从输出到输入的反馈回路。

电路由逻辑门构成，不含记忆元件。

2.组合电路分析用逻辑函数描述已知的电路，找出输入、输出间的逻辑关系，从而判断电路功能。

组合电路的分析步骤：（1）由已知逻辑电路图逐级写出逻辑表达式；（2）化简逻辑表达式，可以采用代数法或卡诺图法化简表达式；（3）由表达式列出真值表；（4）根据表达式或真值表分析并说明电路实现的逻辑功能。

3.组合电路设计组合电路的设计是根据实际逻辑问题提出的要求，设计出满足要求的最简单或者最合理的组合电路。

实现逻辑电路的方法有多种，采用小规模、中规模以及可编程逻辑器件，采用的器件不同，其设计方法有所不同，但是设计过程中对基本逻辑问题的描述、设计思路有其共性。

（二）组合电路的竞争冒险1.组合电路中的竞争冒险现象在组合电路中，信号由不同的途径达到门电路输入端的时间有先有后，这种现象称为竞争。

由于竞争可能引起电路输出发生的瞬间尖峰脉冲现象称为冒险。

竞争冒险现象将影响电路的工作速度、限制电路的最高工作频率，有时会导致电路无法正常工作。

2.竞争的类型有两种类型的竞争可能产生冒险现象，一个门电路的多个输入信号同时变化引起的竞争；一个信号经不同路径传到同一个门的输入端，由于信号到达时间不同引起的竞争。

3.冒险现象的判断在电路输入端只有一个信号改变的情况下，可根据逻辑表达式，采用代数法和卡诺图法判断组合电路是否存在冒险。