二次函数图像过定点的研究

初中二次函数过定点问题一、问题的重要性在初中的数学课程中，二次函数是重要的内容之一，它不仅在数学领域有广泛的应用，还在物理、经济和其他科学领域中有所涉及。

而二次函数过定点的问题，是二次函数中的一个经典问题，它能帮助我们深入理解函数的性质，提高我们的数学思维能力。

二、问题概述二次函数过定点的问题，是指在二次函数图像中，无论自变量取何值，函数值恒为定值的点的位置问题。

这种定值可以是常数，也可以是与自变量有关的表达式。

这种问题的解决需要我们对二次函数的性质有深入的理解，以及对函数图像的准确描绘。

三、解决步骤和方法1. 确定二次函数的形式：首先我们需要根据题目给出的条件，确定二次函数的形式。

通常，二次函数的形式为y=ax²+bx+c。

2. 计算定点坐标：在确定了二次函数的形式后，我们需要通过解方程来找到定点的坐标。

例如，如果定点是(m, n)，那么我们需要找到使am²+bm+c=n成立的m和n的值。

3. 描绘函数图像：根据确定的二次函数形式和定点坐标，我们可以描绘出函数的图像。

4. 验证答案：最后，我们需要验证我们的答案是否正确。

这可以通过将自变量的值代入二次函数中，看是否得到与定点相同的函数值来完成。

四、实例分析例如，若二次函数y=x²-2x-3过定点(m, n)，且无论m取何值，n总为常数，求这个定点坐标。

首先，我们可以通过整理函数的形式来找到定点的坐标：y=x²-2x-3=(x-1)²-4，这个函数的图像是一个开口向上的抛物线，顶点坐标为(1, -4)。

因此，这个二次函数过定点(1, -4)。

五、结论与展望解决二次函数过定点的问题需要我们对二次函数的性质有深入的理解和掌握，同时还需要我们具备灵活的思维能力和良好的代数运算技巧。

在解决这类问题的过程中，我们不仅可以提高我们的数学思维能力，还可以提升我们的数学素养。

在未来的学习和研究中，我们将会遇到更多与二次函数过定点类似的问题。

【九年级】函数过定点问题分析本文将阐述一下函数图象过定点的问题．学习了二次函数的顶点式与交点式之后，我们就可以完成下面两个题目了：⑴二次函数y＝a（x－1）²＋3的顶点坐标为____________．⑵二次函数y＝a（x－1）（x＋3）与x轴的交点坐标为____________ ．【答案】⑴（1，3）．⑵（1，0）和（－3，0）．【总结】我们发现两题中的二次函数解析式都有一个参数a的值是待定的，但是二次函数都会经过与a无关的定点．换句话说，也就是该定点与a 的取值无关．因此，我们可以把函数过定点的问题转化为与参数无关的问题进行解决．【典型例题】二次函数y＝ax²－2ax＋1的图象必经过点____________．【答案】（0，1）和（2，1）．【分析】因为y＝ax²－2ax＋1＝ax（x－2）＋1，所以当x（x－2）＝0，即x＝0或2时，代数式ax（x－2）＋1的取值与a无关．当x＝0或2时，y＝1．所以二次函数y＝ax²－2ax＋1的图象必经过点（0，1）和（2，1）．【变式练习】⑴二次函数y＝ax²＋bx＋1的图象必经过点____________．⑵若a－b＋c＝0，且a≠0，则二次函数y＝ax²＋bx＋c必经过点____________．⑶某二次函数y＝ax²＋（a＋c）x＋c必过定点____________．⑷（2016年广州中考压轴题改编）证明抛物线y＝mx²＋（1－2m）x＋1－3m一定经过非坐标轴上的一点P，并求出点P的坐标．【参考答案】⑴（0，1）．⑵（－1，0）．⑶（－1，0）．⑷证明：∵抛物线y＝mx²＋（1－2m）x＋1－3m，∴y＝m（x²－2x＋3）＋x＋1，因为抛物线过定点，说明在这一点的y与m无关，显然当x²－2x＋3＝0时，y与m无关，解得：x＝3或x＝－1，当x＝3，定点坐标为（3，4）；当x＝－1，定点坐标为（，0），∵P不在坐标轴上，∴P（3，4）．。

二次函数的最值与图像过定点问题对于二次函数:y=-x 2+4x-1/2(1)当x 取任意实数时,该函数有最 值,最 值是(2)当-1≤x≤1时,该函数的最大值是 ;最小值是(3)当3≤x≤4时,该函数的最大值是 ;最小值是(4)当0≤x≤3时,该函数的最大值是 ;最小值是求二次函数最值的一般方法： 1画出函数图像找对称轴； 2分清自变量范围找区间； 3数形结合找对应函数值例1、对于二次函数y=-x 2+2bx-0.5(1)若b<-1,当-1≤x≤1时,求该函数的最大或最小值(用含b 的式子表示)。

(2)若0﹤b ﹤1时,当-1≤x≤1,求该函数的最大或最小值。

1.如图,抛物线22y x x p =--与直线x y =交于点A(-1,m)、B(4,n),点M 是抛物线上的一个动点,连接OM(1)求m,n,p 。

(2)当M 为抛物线的顶点时,求M 坐标和⊿OMB 的面积；(3)当点M 在直线AB 的下方抛物线上,M 运动到何处时,⊿AMB 的面积最大。

2.抛物线y=ax 2和直线y=kx+b(k 为正常数)交于点A 和点B,其中点A 的坐标是(-2,1),过点A 作x 轴的平行线交抛物线于点E,点D 是抛物线上B,E 之间的一个动点,设其横坐标为t,经过点D 作两坐标轴的平行线分别交直线AB 于点C,M,设CD=r,MD=m.(1)根据题意可求出a= ,点E 的坐标是 ；(2)当点D 可与B,E 重合时,若k=0.5,求t 的取值范围,并确定t 为何值时,r 的值最大；(3)当点D 不与B,E 重合时,若点D 运动过程中可以得到r 的最大值,求k 的取值范围,并判断当r 为最大值时m 的值是否最大,说明理由(下图供分析参考用).yxCME AO BD24．(12分) 如图1，平面之间坐标系中，等腰直角三角形的直角边BC 在x 轴正半轴上滑动，点C 的坐标为(t ，0)，直角边AC=4，经过O ，C 两点做抛物线y 1=ax(x ﹣t)(a 为常数，a ＞0)，该抛物线与斜边AB 交于点E ，直线OA ：y 2=kx(k 为常数，k ＞0)(1)填空：用含t 的代数式表示点A 的坐标及k 的值：A_________，k=_________；(2)随着三角板的滑动，当a=14时：①请你验证：抛物线y 1=ax(x ﹣t)的顶点在函数y=﹣14x 2的图象上；②当三角板滑至点E 为AB 的中点时，求t 的值；(3)直线OA 与抛物线的另一个交点为点D ，当t≤x≤t+4，|y 2﹣y 1|的值随x 的增大而减小，当x≥t+4时，|y 2﹣y 1|的值随x 的增大而增大，求a 与t 的关系式及t 的取值范围．抛物线过定点的问题集锦解法步骤第一步：对含有变系数的项集中第二步：然后将这部分项分解因式，使其成为一个只含系数和常数的因式与一个只含x 和常数的因式之积的形式 第三步：令后一因式等于0，得到一个关于自变量x 的方程(这时系数如何变化，都“失效”了)第四步：解此方程，得到x 的值x0(定点的横坐标)，将它代入原函数式(也可以是其变式)，即得到一个y 的值y0(定点的纵坐标)，于是，函数图象一定过定点(x0，y0)； 第五步：反思回顾，查看关键点、易错点，完善解题步骤1.某二次函数y ＝ax 2－(a ＋c)x ＋c 必过定点__________2.无论m 为任何实数，二次函数y ＝x 2＋(2－m)x ＋m 的图像总过的点是（ ）A. （1，3）B. （1，0）C. （－1，3）D. （－1，0）3.不论a 取何值，抛物线y ＝－12x 2＋5－a 2x ＋2a －2 经过x 轴上一定点Q ，则点Q 坐标为 4.抛物线y ＝ax 2＋ax －2过直线y ＝mx －2m ＋2上的定点A ，求抛物线的解析式。

函数图像过定点的研究题1：2＋(k－2)x＋2k(3求证：拋物线y＝－k)x－1(k≠3)过定点，并求出定点的坐标．归纳：第一步：对含有变系数的项集中；第二步：然后将这部分项分解因式，使其成为一个只含系数和常数的因式与一个只含x和常数的因式之积的形式；第三步：令后一因式等于0，得到一个关于自变量x的方程(这时系数如何变化，都“失效”了)；第四步：解此方程，得到x的值x0(定点的横坐标)，将它代入原函数式(也可以是其变式)，即得到一个y的值y(定点的纵坐标)，于是，函数图象一定过定点(x，y)；000第五步：反思回顾，查看关键点、易错点，完善解题步骤．题2：（2001年北京市西城区中考题）无论m为任何实数，二次函数的图像总）过的点是（）0，1 31 C. 01B. ），（ A. 13 （，）（－，）（－D.巩固练习：2）﹣m）x+m的图象总是过定点为何实数，二次函数1．无论my=x（﹣（2 ）（﹣D． 1，0，10） C．（﹣1，3） 3 A．（1，） B．（2）1（a≠0），下列说法正确的有（ 2．对于关于x的二次函数y=ax）﹣（2a﹣1x﹣取何值，图象必过两定②无论取何值，此二次函数图象与x轴必有两个交点；a①无论a的增大而减小；④当1时，y随x点，且两定点之间的距离为；③当a＞0时，函数在x＜ x轴所得的线段长度必大于2．a＜0时，函数图象截 4个．．3 个 D A ．1个 B． 2个C2（m≠0）的图象发现，随﹣2mx+33.（2012?鼓楼区一模）某数学兴趣小组研究二次函数y=mx的变化，这个二次函数的图象形状与位置均发生变化，但这个二次函数的图象总经过两着m ．个定点，请你写出这两个定点的坐标：_________2的变化，这个二次函（m≠0）的图象发现，随着4．某数学小组研究二次函救y=mxm﹣3mx+2数图象的形状与位置均发生变化，但这个二次函数的图象总经过两个定点．请你写出这两个．定点的坐标：_________2，则这个函数的图象一定经过某一个﹣c=2+bx+c满足by=x5．（2009?宜宾县一模）二次函数．定点，这个定点是 _________2．的图象总是过定点 _________ y=x）﹣（2﹣mx+mm6．无论为何实数，二次函数）在函数的图象12，1）图象不经过三、四象限；（2）点（．已知一个二次函数具有性质（7的增大而增大．试写出一个满足以上性质的二次函x时，函数值y随自变量03上；（）当x＞ _________ ．数解析式：8.证明无论m为何值，函数y=mx-（4m-3)图像过定点，求出该定点坐标2．（m是常数）－6x＋1y.9（南京2011年24题7分）已知函数=mx轴上的一个定点；m为何值，该函数的图象都经过y⑴求证：不论的值．轴只有一个交点，求m⑵若该函数的图象与x，﹣），与y轴的交点为（0．已知二次函数的顶点坐标为（﹣，n﹣m），其顶点恰101（好在直线1y=x+﹣m）上（其中m、n为正数）．2（1）求证：此二次函数的图象与x轴有2个交点；（2）在x轴上是否存在这样的定点：不论m、n如何变化，二次函数的图象总通过此定点？若存在，求出所有这样的点；若不存在，请说明理由．函数图像过定点的研究题1：2＋(k－2)x＋－k)x2k－1(k≠3)过定点，并求出定点的坐标．求证拋物线y＝(3审题视角有些函数的图象具有过定点的性质，这是由函数式中的一些系数的取值特点所决定的，例如，直线y＝kx＋b(k≠0)，当b确定时，无论k取不等于0的任何值，它总过定点(0，b)；物线线y＝ax2＋bx＋c(a≠0)，当c确定时，无论a、b取何值，它总过定点(o，c)．本题中可以把函数解析式整理变形，使含字母k的项组合于一组，赋值为零，可以求的自变量的值，而后代入函数解析式，再求得相对应的函数值，即得定点的坐标．解：整理抛物线的解析式，得2＋(k－2)x＋2k－1 y＝(3－k)x2－2x－1－kx2＋＝3xkx＋2k2－2x－1－k(x2 －＝3xx－2)(k≠3)，2－x－2＝0，得x＝－1，x＝上式中令x2. 2122－x－2)，－2x－1－将它们分别代入y＝3xk(x解得y＝4，y＝7，2122－x－2)1－k(x，3x(2，7)分别代入y＝－2x －4)把点(－1，、无论k取何值，等式总成立，2＋(k－2)x＋2k－1(k≠3)上，(3，7)总在抛物线y＝－k)x 4)即点(－1，、(22＋(k－2)x＋2k－1(k≠3)过定点(－1，4)、－即拋物线y＝(3k)x(2，7)．归纳：第一步：对含有变系数的项集中；第二步：然后将这部分项分解因式，使其成为一个只含系数和常数的因式与一个只含x和常数的因式之积的形式；第三步：令后一因式等于0，得到一个关于自变量x的方程(这时系数如何变化，都“失效”了)；第四步：解此方程，得到x的值x0(定点的横坐标)，将它代入原函数式(也可以是其变式)，即得到一个y的值y(定点的纵坐标)，于是，函数图象一定过定点(x，y)；000第五步：反思回顾，查看关键点、易错点，完善解题步骤．题2：（2001年北京市西城区中考题）无论m为任何实数，二次函数的图像总过的点是（）A. （1，3）B. （1，0））0，1（－D. ）3，1（－ C.解法一、特殊值法依据：二次函数的图像随着m的取值不同，它的位置也随之变化，可见这是一个抛物线群。

专题探究二次函数与定点问题方法技巧：运用韦达定理，通过设参数、消参数等手法求出定点坐标。

一、无论参数怎么变化图象都过一个定点例1．求证上：无论a（a≠0）取何值，二次函数y=ax2－2x+a－4都经过一个定点P，并求P的坐标。

例2．已知抛物线C：y=ax2+bx－4a－2b与抛物线l：y=4ax2－2bx+c的一个交点在y轴上，求抛物线l所经过的定点坐标。

二、符合几何条件的定点例3．已知抛物线y=12x2与直线y=mx+n交于点A、B，交y轴于点C，是否存在定点C，使得OA⊥OB，若存在，求C点坐标，若不存在，说明理由。

三、对称点与定点例4．过为P(1，－2)的任一直线交抛物线y=12x2－x于A、B两点，点B与点C关于对称轴对称，连AC，求证直线AC必经过一定点，并求这个定点煌坐标。

练习：1．如图，抛物线C1：y=ax2+bx+c(a≠0)过y轴上一点(0,4)，C1与直线y=kx交于点E、F，P为y轴上一定点，过P的直线y=bx+n与直线y=kx交于点Q，若1OE+1OF=2OQ，求定点P的坐标。

2．如图，抛物线的顶点为(2，0)，且经过点(4,1)，直线y=14x与抛物线交于A、B两点。

（1）求抛物线的解析式；（2）点F为平面内一定点，M为抛物线上一动点，且点M到直线y=－1的距离与到点F的距离始终相等，求定点的坐标。

3．如图，抛物线y=12(x－1)2上任意一点P(xo，m)，过点P作直线y=(x o－1)x+b与直线x=1交于点A，对于点F（1，n），恒有PF=FA，求点F的坐标。

初中数学如何通过二次函数的参数确定其顶点坐标在初中数学中，二次函数是一个重要的概念。

它可以用来描述很多实际问题，例如抛物线的形状、物体的运动轨迹等。

二次函数的顶点是其图像的关键特征之一，因为它包含了函数的最值信息。

下面将详细介绍如何通过二次函数的参数确定其顶点坐标：二次函数的一般形式为：f(x) = ax^2 + bx + c，其中a、b、c是实数，且a不等于零。

顶点坐标可以通过以下步骤来确定：1. 确定平移项：平移是指把函数图像沿x轴或y轴方向移动。

平移的方向和距离由二次函数的参数决定。

首先，我们需要确定平移项。

平移项是二次函数中与x相关的项，即bx。

如果函数中没有平移项，即b等于零，那么二次函数的图像将不会发生平移。

2. 确定平移的方向和距离：平移的方向由平移项的符号决定。

如果b大于零，即正平移，图像将向左移动；如果b 小于零，即负平移，图像将向右移动。

平移的距离由平移项的绝对值决定。

具体来说，平移的距离等于平移项的绝对值除以2a的绝对值。

3. 计算顶点的横坐标：顶点的横坐标可以通过以下公式计算：h = -b / (2a)。

其中，h表示顶点的横坐标。

4. 计算顶点的纵坐标：顶点的纵坐标可以通过将顶点的横坐标代入二次函数中计算得出。

具体来说，顶点的纵坐标等于二次函数在顶点横坐标位置的函数值，即k = f(h) = ah^2 + bh + c。

5. 确定顶点坐标：顶点的坐标即为(h, k)，其中h为顶点的横坐标，k为顶点的纵坐标。

通过以上步骤，我们可以通过二次函数的参数a、b、c来确定其顶点坐标。

顶点是二次函数图像的关键特征，它可以帮助我们分析函数的最值、对称性以及解决实际问题。

理解如何通过二次函数的参数确定顶点坐标，可以帮助我们深入理解二次函数的性质和图像特征。

22.1.4(4.2)---过定点问题一．【知识要点】1.过定点问题二．【经典例题】1.（1）如果一个二次函数的图象经过（－1,-11）（2,8）（0,-8）三点，求出这个二次函数的解析式.（2）如果一个二次函数的顶点为(2,1)且经过点（0,3），求出这个二次函数的解析式.（3）已知二次函数的图象与x 轴交于A （—2,0）,B （6,0）两点，与y 轴交于点C （0,- 4）求二次函数解析式.2.如图,已知抛物线()20y ax bx c a =++≠的对称轴为直线x=-1,且经过A （1,0），B （0，-3）两点.(1)求抛物线的解析式;(2)在抛物线的对称轴x=-1上,是否存在点M,使它到点A 的距离与到点B 的距离之和最小,如果存在求出点M 的坐标,如果不存在请说明理由.3．如图，已知A （0，2），B （1，0），C （2，1），若抛物线y=x 2+bx+1与△ABC 的边一定有公共点，则b 的取值范围是（ ）A ．b ≤0B ．b ≤﹣2C ．b ≥0D ．b ≥﹣2三．【题库】【A 】【B 】【C 】1.对于二次函数2(21)1(0)y ax a x a a =--+-≠，有下列结论：①其图象与x 轴一定相交；②若a<0，函数在x>1时，y 随x 的增大而减小；③无论a 取何值，抛物线的顶点始终在同一条直线上；④无论a 取何值，函数图象都经过同一个点。

其中所有正确的结论是_____________ 。

（填写正确结论的序号）【D 】1．如图，已知抛物线y ＝ax 2+bx+c （a ，b ，c 为常数，a ≠0）经过点（2，0），且对称轴为直线x ＝，有下列结论：①abc ＞0；②a+b ＞0；③4a+2b+3c ＜0；④无论a ，b ，c 取何值，抛物线一定经过（，0）；⑤4am 2+4bm ﹣b ≥0．其中正确结论有（ ） A ．1个 B ．2个C ．3个D ．4个。

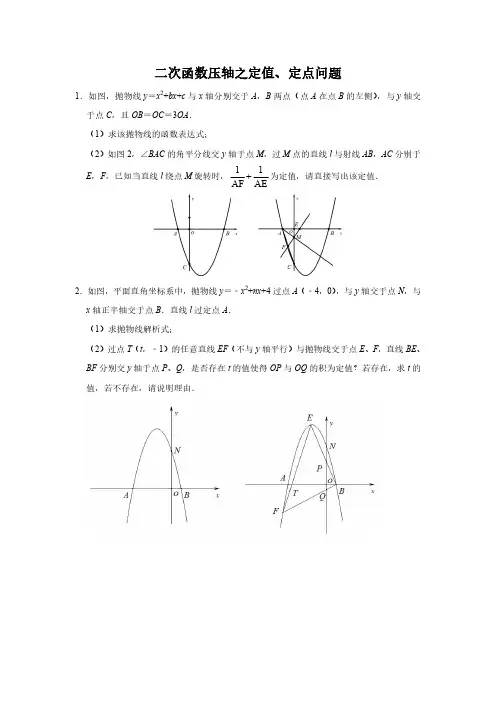
二次函数压轴之定值、定点问题1．如图，抛物线y＝x2+bx+c与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于点C，且OB＝OC＝3OA．（1）求该抛物线的函数表达式；（2）如图2，∠BAC的角平分线交y轴于点M，过M点的直线l与射线AB，AC分别于E，F，已知当直线l绕点M旋转时，11AF AE为定值，请直接写出该定值．2．如图，平面直角坐标系中，抛物线y＝﹣x2+nx+4过点A（﹣4，0），与y轴交于点N，与x轴正半轴交于点B．直线l过定点A．（1）求抛物线解析式；（2）过点T（t，﹣1）的任意直线EF（不与y轴平行）与抛物线交于点E、F，直线BE、BF分别交y轴于点P、Q，是否存在t的值使得OP与OQ的积为定值？若存在，求t的值，若不存在，请说明理由．3.如图1，已知二次函数y ＝x 2+bx +c 的图象与x 轴交于点A （﹣1，0）和点B （3，0），与y 轴的负半轴交于点C ．（1）求这个函数的解析式；（2）如图2，点T 是抛物线上一点，且点T 与点C 关于抛物线的对称轴对称，过点T 的直线TS 与抛物线有唯一的公共点，直线MN ∥TS 交抛物线于M ，N 两点，连AM 交y 轴正半轴于G ，连AN 交y 轴负半轴于H ，求OH ﹣OG4．如图1，已知抛物线的解析式为21362y x =--，直线y ＝kx ﹣4k 与x 轴交于M ，与抛物线相交于点A ，B （A 在B 的左侧）．（1）当k ＝1时，直接写出A ，B ，M 三点的横坐标：x A ＝，x B ＝，x M ＝；（2）作AP ⊥x 轴于P ，BQ ⊥x 轴于Q ，当k 变化时，MP •MQ 的值是否发生变化？若变化，求出其变化范围；若不变，求出其值；5．如图，在正方形OABC中，AB＝4，点E是线段OA（不含端点）边上一动点，作△ABE 的外接圆交AC于点D．抛物线y＝ax2﹣x+c过点O，E．（1）如图1，若抛物线恰好经过点B，求此时点D的坐标；（2）如图2，AC与BE交于点F．请问点E在运动的过程中，CF•AD是定值吗？如果是，请求出这个值，如果不是，请说明理由；6.已知顶点为A的抛物线y＝a（x﹣2）2（a≠0）交y轴于点B（0，2），且与直线l交于不同的两点M、N（M、N不与点A重合）．（1）求抛物线的解析式；（2）若∠MAN＝90°，试说明：直线l必过定点；7.如图，在直角坐标系中有Rt△AOB，O为坐标原点，OB＝1，tan∠ABO＝3，将此三角形绕原点O顺时针旋转90°，得到Rt△COD，二次函数y＝﹣x2+bx+c的图象刚好经过A，B，C三点．（1）求二次函数的解析式及顶点P的坐标；（2）过定点Q（1，3）的直线l：y＝kx﹣k+3与二次函数的图象相交于M，N两点．证明：无论k为何值，△PMN恒为直角三角形．8.已知，抛物线y＝ax2+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，点P是抛物线上一点．（1）求抛物线的解析式；（2）如图2，当点P位于第二象限时，过P点作直线AP，BP分别交y轴于E，F两点，请问CECF的值是否为定值？若是，请求出此定值；若不是，请说明理由．9.已知点P（0，﹣4）为平面直角坐标系内一点，直线l绕原点O旋转，交经过点（0，﹣2）的抛物线y＝14x2+c于M、N两点．（1）请求出该抛物线的解析式；（2）在直线l绕原点O旋转的过程中，请你研究一下（PM+MO）（PN﹣NO）是否定值？若是，请求出这个定值；若不是，请说明理由．10.如图，抛物线C：y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣12，且抛物线经过A、B两点，交x轴于另一点C,A（﹣2，0），B（0，2）；(1)求抛物线的解析式；(2)在（1）的条件下，设对称轴直线x＝﹣12与x轴交于M，点P为抛物线上对称轴左侧一点，直线PM交抛物线于另一点Q，点P关于抛物线对称轴对称点H，直线HQ交抛物线对称轴于G点，在点P运动过程中GM长是否为一定值，若为定值，请求出其值，若不为定值，请求出其变化范围．11．如图，在平面直角坐标系中，已知抛物线的顶点D为（1，﹣1），且经过点B（3，3）．（1）求这个抛物线相应的函数表达式；（2）如图1，过点D且平行于x轴的直线l，与直线OB相交于点A，过点B作直线l 的垂线，垂足为C．若点Q是抛物线上BD之间的动点（不与B、D重合），连接DQ并延长交BC于点E．如图2，连接BQ并延长交CD于点F，在点Q运动的过程中，FC（AC+EC）的值是否发生变化？若不变求出该定值，若变化说明理由．12.如图，抛物线y＝ax2+bx+c（a，b，c为常数，且a≠0）与坐标轴分别交于点A（﹣3，0），B（1，0）和点C．（1）求出a与c的数量关系式；（2）如图，若抛物线y=-x2-2x+3与直线y＝（2k1﹣2）x交于E，F两点，与直线y＝（2k2﹣2）x交于M，N两点，且k1k2＝﹣1，点P，Q分别是EF、MN的中点，求证：直线PQ必定经过一个定点，并求出该定点坐标．13.已知抛物线y＝ax2+bx+5（a≠0）经过点（4，5）．（1）若a+b＝﹣3，求抛物线y＝ax2+bx+5的解析式；（2）在（1）的条件下，经过点A(2,54)的任意直线y＝mx+n（m≠0）与（1）中的抛物线交于B，C两点，那么11AB AC的值是定值吗？如果是定值，请求出这个定值，如果不是定值，请说明理由．14.如图1，抛物线C：y＝ax2+bx﹣3与x轴的正半轴交于点B，与y轴交于点C，OB＝OC，其对称轴为直线x＝1．（1）直接写出抛物线C的解析式；（2）如图2，将抛物线C平移得到抛物线C1，使C1的顶点在原点，过点P（t，﹣1）的两条直线PM，PN，它们与y轴不平行，都与抛物线C1只有一个公共点分别为点M和点N，求证：直线MN必过定点．参考答案1.解：(1)OB=OC,C(0,c)则B(-c,0)，代入抛物线解析式得c 2-bc+c=0，c-b+1=0，即当x=-1时，y =1-b+c=0，故抛物线过点(-1，0)，故A(-1，0)，B(3，0)，C(0,-3)抛物线的解析式为y =x 2-2x -3(2)过点M 作MG||x 轴交AC 于点G ，作FP||x 轴交AM 于点P ，作CQ||x 轴，易知∆COA~∆CMG ，∆ACQ~∆AGM ，GM CG OA AC =GM AG CQ AC =，GM GM CG AG 1OA CQ AC AC+=+=即得111OA CQ GM+=，而AM 平分∠BAC ，故AC=CQ ，故111OA AC GM +=；同时CG AC GM AE =，AF GM AC CQ=即可得111AE AF GM +=，OA=1，AC=10，故11101AE AF 10+=+2.解：(1)y =-x 2-3x +4(2)存在t 的值使得OP 与OQ 的积为定值,t=-4设E(m ,-m 2-3m+4)，F(n,-n 2-3n+4)，设BE 的解析式为y =k (x -1)，将E 点坐标代入得k =-m -4，同理k =-n -4,则OP=m+4，OQ=-n-4，故OP ∙OQ=(m+4)(-n-4)=-mn-4(m+n)-16，直线CE 的解析式为y =k 1(x-t )-1，与抛物线y =-x 2-3x +4联立得x 2+(k 1+3)x-k 1t -5=0，m+n=-k 1-3,mn =-k 1t -5,OP ∙OQ=k 1t+4k 1+1=4k 1(t+4)+1，当t=-4时，OP ∙OQ 为定值，故当t=-4时,OP ∙OQ=13.解：(1)y =x 2-2x-3(3)易知T(2，-3),设直线TS 的解析式为y=m(x-2)-3，与抛物线y =x 2-2x-3联立得x 2-(m +2)x +2m =0，有两个相等实根，m 2+4m+4-8m=0，故m=2，即TS 解析式为y =2x -7,设MN 的解析式为y =2x+h ,与抛物线联立得x 17+h ，x 27+h 故7+h ，7+h )，N(2-7+h 7+h )，直线AM 解析式为y 1=k 1x+b 1，得b 1737hh +++737hh +++，同理可得773hh ++-，OH-OG=24.解：6，6,4；(2)MP ∙MQ 的值不变.y =21362x -与y =kx -4k 联立得x 2+6kx +9-24k =0,x A +x B =6k ，x A ∙x B =9-24k ,M(4，0)，MP ∙MQ=(4-x P )(4-x Q )=16-4(x A +x B )+x A x B =16+24k+9-24k=255.解：(1)易得抛物线的解析式为y =12x 2-x ，圆的直径为BE ，故∠BDE=90°，且∠BED=∠BAD=45°，作MN ⟂OA 交BC 、OA 于点M 、N ，易知∆BDM ≅∆DEN ，设DM=NE=m ，则CM=ON=m ，而OE=2，故m=1，此时D(1，3)(2)不变，CF ∙AD=16，∠DBF=∠BAD=45°，故∆ADB~∆CBF ，故CF ∙AD=AB ∙CB=166.解：(1)y =12(x -2)2(2)设直线MN 的解析式为y=kx+b ，与抛物线联立得x 2-(4+2k )x +4-2b=0，x M +x N =4+2k,x M ∙x N =4-2b ，作ME 、NF 垂直于x 轴，易知∆AME~∆NAF ，AE ME NF AF =，即有AE ∙AF=ME ∙NF ，ME=kx 1+b ，NF=kx 2+b ，AE=2-x 1,AF=x 2-2，(2-x 1)(x 2-2)=(kx 1+b)(kx 2+b)，即有4+2(x 1+x 2)-x 1x 2=k 2x 1x 2+kb (x 1+x 2)+b 2，整理得2k+b =0或2k +b -2=0,即当x =2时，y =2,所以直线l 必过定点(2,2)7.解：(1)y =-x 2+2x +3，P(1,4)(2)联立y=kx-k +3和抛物线y =-x 2+2x +3得x 2+(k-2)x-k=0,x 1+x 2=k-2,x 1x 2=-k,过点M 、N 作对称轴的垂线ME 、NF ，tan ∠PME=PE ME =221111114(23)(1)111x x x x x x --++-==---，同理tan ∠PFN=211x -，(1-x)(x2-1)=1，故tan ∠PME=tan ∠FPN,∠PME=∠FPN ，故∠MPN=90°，所以无论k 为何值，∆PMN 恒为直角三角形.8.解:(1)y =-x 2+2x +3(2)CE CF 的值为定值13，设P(t,-t 2+2t+3)，直线AP 的解析式为y =(3-t)x +3-t ，直线BP 的解析式为y =(-t-1)x +3t+3,故CE=-t ，CF=-3t ，故CE CF =139.(1)y =2124x -(2)(PM+MO)(PN-ON)为定值，设直线l 的解析式为y=kx ，与抛物线联立得x 2-4kx -8=0，设M(x 1，y 1)，N(x 2,y 2)则有x 1x 2=-8，，y 1=kx 1，故PM=|x 1OM=|x 1，同理PN=|x 2,ON=|x 2，故+|x 1)(|x 2-|x 2)=16，故(PM+MO)(PN-ON)为定值16.10.解：(1)y=-x 2-x +2(2)连接MH ，易知AMP=CMH ，设PQ 的解析式为y=kx+b 1，MH 的解析式为y=-kx+b 2,分别代入(-12，0)得b 1=12k ，b 2=12-k ，故PM 的解析式为y=kx+12k ，MH 的解析式为y=-kx-12k 与抛物线联立得x=(1)92k -+±,所以Q((1)92k -++,292k -±),同理可得H(192k -,292k --)，易知QH 的解析式为y=-x +992-当x=-12时，y=92，所以G(-12,92)，所以点P 运动过程中GM 长为定值9211.解：(1)y =x 2-2x(2)FC(AC+EC)为定值，设Q(m ,m 2-2m )，易得BF 的解析式为y=(m -1)x -3m ，故点F(311m m -+，-1)，D(1，-1)，DE 的解析式为y=(m-1)x-m ，E(3，2m-3)，FC=3-311m m -+=41m +，AC+EC=4+2m-3+1=2m+2，所以FC(AC+EC)=41m +(2m+2)=812.解：(1)c =-3a (2)联立y =-x 2-2x +3与y ＝(2k 1﹣2)x 得x 2+2k 1x -3=0所以x 1+x 2=-2k 1，y 1+y 2=-4k 12+4k 1，故P(-k 1，-2k 12+2k 1)，同理可得Q(-k 2，-2k 22+2k 2)，设直线PQ 的解析式为y=kx+b,将P 、Q 两点代入得y =(2k 1+2k 2-2)x -2,所以直线PQ 过定点(0,-2)13.解：(1)y=x 2-4x +5(3)将坐标系向右平移2个单位，向上平移1个单位，此时抛物线的解析式为y=x2，点A(0，14),设B(m,m 2),C(n,n 2)，则AB=m 2+14,AC=n 2+14，故11AB AC +=AB AC AB AC +⋅=22221211()()416m n mn m n +++++，同时BC 的解析式y=kx +14，与抛物线联立得x 2-kx -14=0，m+n=k,mn =-14，故11AB AC +=414.解：(1)y =x 2-2x -3(2)平移后的抛物线的解析式为y =x 2,设M(m,m 2),N(n,n 2)，直线PM 的解析式设为y=k 1(x-m)+m 2，PN 的解析式为y=k 2(x-n)+n 2，与抛物线联立得x2-k1x+k1m-m2=0，此时∆=0，即有k 1=2m ，PM 的解析式为y=2m(x-m)+m 2=2mx-m 2同理可得PN 的解析式为y=2n(x-n)+n 2=2nx-n 2，可得P(2m n +，mn ),mn =-1,MN 的解析式为y=(m+n)x +1,故MN 过定点(0，1)。

二次函数必过一个定点的求法
二次函数：
1、定义：二次函数是一类特殊的函数，其函数表达式为：
y=ax^2+bx+c(a≠0)。

2、特性：
（1）二次函数的图像是一个抛物线,有一个顶点和两个渐近线。

（2）当a>0时,该函数抛物线是一个开口朝上的抛物线；当a<0时，该函数抛物线是一个开口朝下的抛物线。

（3）二次函数的方程在数学上具有唯一解。

（4）二次函数的顶点可以通过两个坐标点来求出，公式为：x=-
b/2a ,y=4ac-b^2/4a。

3、应用：
（1）在物理中，二次函数的定义可以用于计算物体的加速度，描述物体在X方向上的位移与时间；
（2）在经济学中，二次函数可以用来研究产使供求关系；
（3）在工程学中，二次函数可以用来求解静力学问题，描述不同物体在不同受力条件下的运动状态；
（4）在博弈论中，二次函数可以用来研究游戏的收益情况。

4、求法：
（1）根据二次函数定义y=ax^2+bx+c，首先求出a、b、c的值；（2）根据顶点的求法，计算出顶点的坐标；
（3）根据渐近线的方程，确定抛物线的渐近线解析式。

二次函数与定点、定值问题【方法归纳】已知抛物线和满足一定条件的直线在平面直角坐标系中，直线上的线段满足一定几何条件，图中可能产生一些定点，定量关系．通常要运用几何量的关系转换成线段关系和坐标关系求解． 思路：结合二次函数，将几何向代数转化，构建方程或方程组，并归纳解题一致性．例1．已知抛物线：y ＝ax 2＋bx ＋c ，顶点坐标为原点，且过（4，8），如图，若A 、B 两点在抛物线上，且OA ⊥OB ，AB 交y 轴于H 点，求H 点的坐标．易求a ＝21，b ＝0，c ＝0，∴y ＝12x 2，设A (m ，21m 2)，B (n ，12n 2)，设AB 的解析式y ＝kx ＋b ，联立⎪⎩⎪⎨⎧+==b kx y xy 221得x 2－2kx －2b ＝0，m ＋n ＝2k ，mn ＝－2b ，又∵OA ⊥OB ，过A 点作AC 丄x 轴，BD ⊥y 轴，垂足分别为C 、D 两点，易证△AOC ∽△OBD ，∴OC AC ＝BD OD ，∴A A x y ＝B B y x -，∴m m221＝221n n -，41mn ＝－1，∴mn＝－4，∴b ＝2，∴H (0，2)．（2013年武汉中考压轴题的关键一步）方法总结：_________________________________________________ _________________________________________________ _________________________________________________【练1】抛物线y ＝21(x －1)2，顶点为M ，直线AB 交抛物线于A 、B 两点，且MA ⊥MB ，求证：直线AB 过定点．设A (x 1，y 1)，B (x 2，y 2)，易求M (1，0)，作AE ⊥x 轴，BF ⊥x 轴，△AEM ∽△BFM ，易得EM AE ＝FBMF，即111x y -＝221y x -，1211)1(21x x --＝222)1(211--x x ，∴－21(x 1－1)2＝)1(2112-x ，∴－41[x 1x 2－(x 1＋x 2)＋1]＝1，联立⎪⎩⎪⎨⎧+=-=b kx y x y 2)1(21得，21(x －1)2＝kx ＋b ，x 2－2x ＋1＝2kx ＋2b ，x 2－(2＋2k )x ＋1－2b ＝0，x 1·x 2＝1－2b ，x 1＋x 2＝2k ＋2，∴(1－2b )－(2k ＋2)＋1＝－4，k ＋b ＝2，∴y ＝kx ＋b ＝kx ＋2－k ＝k (x －1)＋2，∴AB 过定点(1，2)．例2．已知抛物线y ＝41x 2，以M (－2，1)为直角顶点作该抛物线的内接直角三角形MAB （即M ，A ，B 均在抛物线上），求证：直线AB 过定点，并求出该定点坐标．过M 作PQ ∥x 轴，AP ⊥PQ 于P ，BQ ⊥PQ 于Q ，设AB ：y ＝kx ＋b ， 由⎪⎩⎪⎨⎧+==bkx y xy 241得41x 2－kx －b ＝0，x A ＋x B ＝4k ，x A ·x B ＝－4b ， 由△APM ∽△MQB 得AP ·BQ ＝PM ·MQ ，即(y A －1)(41x B 2－1)＝－(x A ＋2)(x B ＋2)， ∴161(x A －2)(x B －2)＝－1，x A ·x B －2(x A ＋x B )＋4＝－16， ∴－4b －8k ＋4＝－16，b ＝5－2k ，∴AB ：y ＝kx ＋5－2k ＝k (x －2)＋5，过定点(2，5)．【练2】（2014武汉中考）如图，已知直线AB ：y ＝kx ＋2k ＋4于抛物线y ＝21x 2交于A 、B 两点． （1）直线AB 总经过一个定点C ，请直接写出点C 坐标； （2）若在抛物线上存在定点D 使∠ADB ＝90°，求点D 到直线AB 的最大距离．（1）C (－2，4)（2）设A (x 1，21x 12)，B (x 2，21x 22)，D (m ，21m 2)，由⎪⎩⎪⎨⎧++==42212k kx y xy 得x 2－2kx －4k －8＝0，x 1＋x 2＝2k ，x 1·x 2＝－4k －8，过D 作EF ∥x 轴，AE ⊥EF 于E ，BF ⊥EF 于F ，由△AED ∽△DFB 得AE ·BF ＝DE ·DF ，即(21x 12－21m 2)(21x 22－21m 2)＝(m －x 1)(x 2－m )，化简x 1x 2＋m (x 1＋x 2)＋m 2＝4，∴2k (m －2)＋m 2－4＝0，当m －2＝0，即m ＝2时，点D 的坐标与k 无关，∴D (2，2)，又∵C (－2，4)，∴CD ＝25，作DM ⊥AB 于M ，则DM ≤CD ＝25，∴当CD ⊥AB 时，点D 到直线AB 的距离最大，最大距离为25．例3．如图，抛物线y ＝x 2＋3顶点为P ，直线l 交抛物线于A 、B 两点，交y 轴于C 点，∠AOC ＝∠BOC ，求证：直线AB 过定点．设A (m ，m 2＋3)，B (n ，n 2＋3)，设直线AB 的解析式为y ＝kx ＋b ，⎩⎨⎧+=+=32x y bkx y ，∴kx ＋b ＝x 2＋3，x 2－kx ＋3－b ＝0，∴mn ＝3－b ，∵∠AOC ＝∠BOC ，∴tan ∠AOC ＝tan ∠BOC ，∴32+m m ＝32+-n n，∴mn 2＋3m ＝－m 2n －3n ，∴mn ＝－3，∴b ＝6，∴C (0，6)．【练3】抛物线y ＝x 2－4x ＋5，对称轴交x 轴于P 点，直线EF 交抛物线于E 、F ，交对称轴于H ，且∠EPH ＝∠FPH ，求证：EF 恒过定点．E (x 1，y 1)，F (x 2，y 2)，⎩⎨⎧+-=+=542x x y bkx y ，∴x 2－(4＋k )x ＋5－b ＝0，x 1＋x 2＝4＋k ，x 1x 2＝5－b ，tan ∠EPH ＝tan ∠FPH ，∴112y x -＝222y x -，∴(kx 1＋b)(x 2－2)＝(kx 2＋b )(2－x 1)，∴b ＋2k ＝2，y ＝kx ＋b ，∴直线过(2，2)．例4．如图，抛物线y ＝x 2－1交x 轴于A 、B 两点，直线y ＝a （a ＞0）交抛物线于M 、N ，点C 在抛物线上，且∠MCN ＝90°，点C 到MN 的距离是否为定值？若是，求出这个定值．作CH ⊥MN 于H ．则∠MCH ＝∠CNH ，Rt △MCH ∽Rt △CNH ，CH 2＝MH ·HN ，令C (x C ，t )，M (m ，m 2－1)，则N (－m ，m 2－1)，CH ＝m 2－1－t ，MH ·HN ＝(x C －x M )(x N －x C )＝－x C 2＋m 2，y C ＝x C 2－1＝t ，故x C 2＝t ＋1，－x C 2＝－t －1，即MH ·HN ＝m 2－1－t ，又CH 2＝MH ·HN ，∴(m 2－1－t )2＝m 2－1－t ，∴m 2－1－t ＝0（舍去）或m 2－1－t ＝1，即CH ＝m 2－1－t ＝1，点C 到MN 的距离是定值，这个值为1．【练4】（2015永州改）如图，抛物线：y ＝41(x －1)2，R (1，1)是对称轴l 上一点，点P 为抛物线上一个动点，PM 垂直于直线y ＝－1于M ，求PRPM的值．设P (t ，41(t －1)2)，连PR ，作PM ⊥直线y ＝－1于点M ，PM ＝41(t －1)2＋1， PR ＝222]1)1(41[)1(--+-t t ＝41(t －1)2＋1，∴PM ＝PR ，∴PRPM＝1．【课后反馈】1．如图，抛物线y ＝x 2－1交x 轴正半轴于A (1，0)，M 、N 在抛物线上，且MA ⊥NA ，试说明MN 恒过一定点，求此定点的坐标．作MP ⊥x 轴于P ，NQ ⊥x 轴于Q ，设MN ：y ＝mx ＋n ，由21y mx ny x =+⎧⎪⎨=-⎪⎩得x 2－mx －n －1＝0，x M ＋x N ＝m ，x M ·x N ＝－1－n ，tan ∠MAP ＝PA MP ＝211M M x x --＝－x M －1，tan ∠ANQ ＝AQ NQ ＝211N N x x --＝11Nx +．由∠MAP ＝∠ANQ 得－x M －1＝11Nx +，即－x M ·x N －(x M ＋x N )－1＝1，1＋n －m －1＝1，n ＝m ＋1，MN ：y ＝mx ＋m＋1＝m (x ＋1)＋1，故MN 过定点(－1，1)．2．如图，抛物线y ＝41(x －4)2－4的顶点为P ，M ，N 均在对称轴上，且PM ＝PN ，延长OM 交抛物线于点A ．求证：∠ANM ＝∠ONM ．易求P (4，－4)，设A (m ，41m 2－2m )，可求OA ：y ＝(41m －2)x ，点M 在OA 上，x ＝4时，y ＝m －8，∴M (4，m －8)，故N (4，－m )，tan ∠ONM ＝N N x y -＝4m ，tan ∠ANM ＝4A A N x y y --＝2412()4m m m m ----＝41(4)4m m m --＝4m ，故∠ANM ＝∠ONM ．3．（2016六初九下2月考T24）已知抛物线y ＝41x 2＋m 与x 轴交于A 、B 两点，与y 轴交于C 点，且OA ＝2OC ，直线y ＝kx －2k ＋4（k ≠0）与抛物线交于D 、E 两点． （1）求m 值及A 点坐标；（2）当k 取何值时，△ADE 的面积最小，并求面积的最小值；（3）若M 、N 为抛物线上两点，其以MN 为直径的圆始终经过A 点，求直线MN 经过的定点P 的坐标．（1）令x ＝0时，y ＝m ，∴OC ＝－m ，令y ＝0时，x ＝m -±2，∴OA ＝m -2， ∵OA ＝2OC ，∴m -2＝2(－m )，m ＝－1，∴A (2，0)；（2）直线y ＝kx －2k ＋4过定点(2，4)，过点A 作AF ∥y 轴交DE 于F ，∴F (2，4)， 设D (x 1，y 1)、E (x 2，y 2)，∴S △ADE ＝21×4×(x 1－x 2)＝2(x 1－x 2)， 联立⎪⎩⎪⎨⎧-=+-=141422x y k kx y ，整理得41x 2－kx ＋2k －5＝0，∴x 1＋x 2＝4k ，x 1x 2＝8k －15 ∴S △ADE ＝2212142)(x x x x -+＝84)1(2+-k ，当k ＝1时，S △ADE 有最小值，最小值为16； （3）设M (x 1，y 1)、N (x 2，y 2)， ∵∠MAN ＝90°，过点M 作ME ⊥x 轴于E ，过点N 作NF ⊥x 轴于F ，∴△MEA ∽△AFN ，∴212122y x x y -=-，y 1y 2＝(x 2－2)(2－x 1)， 即)141)(141(2121--x x )＝(x 2－2)(2－x 1)，x 1x 2＋2(x 1＋x 2)＋20＝0，设直线MN 的解析式为y ＝kx ＋b ，联立⎪⎩⎪⎨⎧-=+=1412x y bkx y ，整理得x 2－4kx －4－4b ＝0， ∴x 1＋x 2＝4k ，x 1x 2＝－4－4b ，∴－4－4b ＋2×4k ＋20＝0，2k －b ＝－4， 当x ＝－2时，－2k ＋b ＝4，∴直线MN 必过顶点(－2，4)．。

二次函数的图像和性质提高讲义一．选择题（共2小题）1．无论m为何实数，二次函数y=x2﹣（2﹣m）x+m的图象总是过定点（）A．（1，3）B．（1，0）C．（﹣1，3）D．（﹣1，0）2．对于关于x的二次函数y=ax2﹣（2a﹣1）x﹣1（a≠0），下列说法正确的有（）①无论a取何值，此二次函数图象与x轴必有两个交点；②无论a取何值，图象必过两定点，且两定点之间的距离为；③当a＞0时，函数在x＜1时，y随x的增大而减小；④当a＜0时，函数图象截x轴所得的线段长度必大于2．A．1个B．2个C．3个D．4个二．填空题（共6小题）3．已知A点坐标为（2，3），在x轴上有一点P，使得△POA为等腰三角形．则P点的个数有_________个．4．（2012•鼓楼区一模）某数学兴趣小组研究二次函数y=mx2﹣2mx+3（m≠0）的图象发现，随着m的变化，这个二次函数的图象形状与位置均发生变化，但这个二次函数的图象总经过两个定点，请你写出这两个定点的坐标：_________．5．某数学小组研究二次函救y=mx2﹣3mx+2（m≠0）的图象发现，随着m的变化，这个二次函数图象的形状与位置均发生变化，但这个二次函数的图象总经过两个定点．请你写出这两个定点的坐标：_________．6．（2009•宜宾县一模）二次函数y=x2+bx+c满足b﹣c=2，则这个函数的图象一定经过某一个定点，这个定点是_________．7．无论m为何实数，二次函数y=x2﹣（2﹣m）x+m的图象总是过定点_________．8．已知一个二次函数具有性质（1）图象不经过三、四象限；（2）点（2，1）在函数的图象上；（3）当x＞0时，函数值y随自变量x的增大而增大．试写出一个满足以上性质的二次函数解析式：_________．三．解答题（共22小题）9．（2014•曲靖模拟）如图，已知二次函数y=ax2﹣4x+c的图象与坐标轴交于点A（﹣1，0）和点C（0，﹣5）．（1）求该二次函数的解析式和它与x轴的另一个交点B的坐标．（2）在上面所求二次函数的对称轴上存在一点P（2，﹣2），连接OP，找出x轴上所有点M的坐标，使得△OPM是等腰三角形．10．已知二次函数y=ax2﹣4x+c的图象过点（﹣1，0）和点（2，﹣9）．（1）求该二次函数的解析式并写出其对称轴；（2）已知点P（2，﹣2），连结OP，在x轴上找一点M，使△OPM是等腰三角形，请直接写出点M的坐标（不写求解过程）．11．如图，已知二次函数y=ax2﹣4x+c的图象与坐标轴交于点A（﹣1，0）和点B（0，﹣5）．（1）求该二次函数的解析式；（2）已知该函数图象的对称轴上存在一点P，使得△ABP的周长最小．请求出点P的坐标．（3）在（2）的条件下，在x轴上找一点M，使得△APM是等腰三角形，请直接写出所有符合条件的点M的坐标．12．（2011•淮安）如图．已知二次函数y=﹣x2+bx+3的图象与x轴的一个交点为A（4，0），与y轴交于点B．（1）求此二次函数关系式和点B的坐标；（2）在x轴的正半轴上是否存在点P．使得△PAB是以AB为底边的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．13．已知二次函数y=（m﹣1）x2+4x+m2﹣1的图象经过原点．（1）请求出m的值及图象与x轴的另一交点的坐标；（2）若把（1）中求得的函数的图象沿其对称轴上下平行移动，使顶点移到直线上，请求出此时函数的解析式；（3）若在（1）中求得的函数的图象上，已知有一点E在x轴上，点F在抛物线上，且点E 和点F的横坐标都为﹣2，能否在抛物线的对称轴上找一点P，使得PE+PF最短？若能，请求出这个最短距离；若不能，请说明理由．14．（2012•同安区一模）已知二次函数y=﹣x2+3x+k的图象经过点C（0，﹣2），与x轴交于A、B两点（点A在点B的左边），直线x=m（m＞2）与x轴交于点D（1）在直线x=m（m＞2）上有一点E（点E在第四象限），使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似，求E点坐标（用含m的代数式表示）；（2）在（1）成立的条件下，抛物线上是否存在一点F，使得四边形ABEF为平行四边形？若存在，请求出m的值；若不存在，请说明理由．15．（2013•汕头）已知二次函数y=x2﹣2mx+m2﹣1．（1）当二次函数的图象经过坐标原点O（0，0）时，求二次函数的解析式；（2）如图，当m=2时，该抛物线与y轴交于点C，顶点为D，求C、D两点的坐标；（3）在（2）的条件下，x轴上是否存在一点P，使得PC+PD最短？若P点存在，求出P 点的坐标；若P点不存在，请说明理由．16．（2011•深圳模拟）如图，已知二次函数y=ax2+bx+c（a≠0）的图象经过点A（1，0），B （2，0），C（0，﹣2），直线x=m（m＞2）与x轴交于点D．（1）求二次函数的解析式；（2）在直线x=m（m＞2）上有一点E（点E在第四象限），使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似，求E点坐标（用含m的代数式表示）；（3）在（2）成立的条件下，抛物线上是否存在一点F，使得四边形ABEF为平行四边形？若存在，请求出F点的坐标；若不存在，请说明理由．17．（2014•南漳县模拟）已知二次函数y=ax2+bx+c（a≠0）的图象经过点A（﹣1，0），B（﹣2，0），C（0，﹣2），直线x=m（m＜﹣2）与x轴交于点D．（1）求二次函数的解析式；（2）在直线x=m（m＜﹣2）上有一点E（点E在第二象限），使得以E、B、D为顶点的三角形与以A、O、C为顶点的三角形相似，求E点坐标（用含m的代数式表示）；（3）在（2）成立的条件下，抛物线上是否存在一点F，使得四边形ABEF为平行四边形？若存在，请求出四边形ABEF的面积；若不存在，请说明理由．18．（2009•包头）已知二次函数y=ax2+bx+c（a≠0）的图象经过点A（1，0），B（2，0），C （0，﹣2），直线x=m（m＞2）与x轴交于点D．（1）求二次函数的解析式；（2）在直线x=m（m＞2）上有一点E（点E在第四象限），使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似，求E点坐标（用含m的代数式表示）；（3）在（2）成立的条件下，抛物线上是否存在一点F，使得四边形ABEF为平行四边形？若存在，请求出m的值及四边形ABEF的面积；若不存在，请说明理由．19．如图，已知直线AB与x轴交于A（6，0）点，与y轴交于B（0，10）点，点M的坐标为（0，4），点P（x，y）是折线O→A→B上的动点（不与O点、B点重合），连接OP，MP，设△OPM的面积为S．（1）求S关于x的函数表达式，并求出x的取值范围；（2）当△OPM是以OM为底边的等腰三角形时，求S的值．20．已知：二次函数y=﹣x2﹣2x+m的图象与x轴交于点A（1，0），另一交点为B，与y 轴交于点C．（1）求m的值；（2）求点B的坐标；（3）该二次函数图象上有一点P（x，y），满足S△ABP=S△ABC，试求点P的坐标．21．（2013•涉县模拟）如图，已知二次函数y=﹣x2+x+4的图象与y轴交于点A，与x轴交于B、C两点，其对称轴与x轴交于点D，连接AC．（1）点A的坐标为_________，点C的坐标为_________；（2）△ABC是直角三角形吗？若是，请给予证明；（3）线段AC上是否存在点E，使得△EDC为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由．22．（2014•闵行区三模）已知：如图，在直角坐标平面xOy中，O为原点，点A、C分别在x轴、y轴的正半轴上，四边形OABC是边长为4的正方形，点E为BC的中点，且二次函数y=﹣x2+bx+c经过B、E两点．将正方形OABC翻折，使顶点C落在二次函数图象的对称轴MN上的点G处，折痕EF交y轴于点F．（1）求二次函数y=﹣x2+bx+c的解析式；（2）求点G的坐标；（3）设点P为直线EF上的点，是否存在这样的点P，使得以P、F、G为顶点的三角形为等腰三角形？若存在，请直接写出点P的坐标；如果不存在，请说明理由．23．已知二次函数的图象经过（﹣1，3）、（1，3）、（2，6）三点．（1）求二次函数的解析式．（2）写出二次函数图象的对称轴和顶点坐标．24．已知二次函数y=x2+（m+1）x+4m﹣13．（1）求证：此二次函数与x轴有两个交点．（2）当m取不同的值时，此函数图象的位置就会不一样．但是，这些抛物线都会经过一个定点，求此定点的坐标．25．设实数a、b、c满足，求证：二次函数y=ax2+bx+c的图象过一个定点，并求这个定点．26．已知二次函数的顶点坐标为（﹣，﹣），与y轴的交点为（0，n﹣m），其顶点恰好在直线y=x+（1﹣m）上（其中m、n为正数）．（1）求证：此二次函数的图象与x轴有2个交点；（2）在x轴上是否存在这样的定点：不论m、n如何变化，二次函数的图象总通过此定点？若存在，求出所有这样的点；若不存在，请说明理由．。

二次函数直线过定点问题的求法在学习数学的过程中，二次函数和直线这两位“大咖”总是让人又爱又恨。

想想吧，二次函数就像个调皮捣蛋的小孩，总是喜欢抛出一些奇奇怪怪的问题。

而今天我们要聊的就是，怎么让一条直线经过一个固定的点，这个点就像一个聚光灯，照亮了我们的思路，嘿嘿，有意思吧？咱们得明白二次函数的形状。

它就像一个大大的碗，开口向上，或者说是一个弯弯的笑脸。

它的标准形式是 (y = ax^2 + bx + c)。

这时候，如果你让一条直线，比如 (y = mx + n)，穿过这个碗，哎呀，这可是有讲究的。

想象一下，一条直线要穿越一个碗，那绝对不是随便的事儿。

得看看这条直线是怎样在碗里游走的，有时候它会碰到碗的边缘，有时候又可能深深地扎进去。

这个过程可是非常精彩的。

而我们关注的那一个定点，假设叫它 ((x_0, y_0))，就是个特别的存在。

这个点就像是个小明星，无论直线怎么动，它都得在旁边默默注视。

要想让这条直线通过这个点，我们需要确保直线的方程在这个点成立。

换句话说，就是把这个点的坐标带入直线的方程里，如果结果成立，那就完美了，直线成功过关！不过，得注意，二次函数的曲线和直线的交点可不是只有一个，可能有两个、一个，甚至没有，这就得看具体的参数了。

想象一下，如果直线和二次函数相交的地方，就像是两个人在街头偶然碰面，兴奋得不得了。

两者会在一个地方重合，哦，那可是很有戏的。

比如说，直线和二次函数的交点要么在上面，要么在下面，甚至可能紧紧相拥在一起。

这种情况我们就得认真分析了，看看那条直线的斜率、截距等因素，如何影响它与二次函数的关系。

真是神奇。

还有个小技巧，如果我们用到求根公式，问题就迎刃而解了。

对于二次方程，咱们用判别式来判断它的交点个数，公式简单得不能再简单了。

哎呀，真是好用。

这样一来，复杂的数学问题就变得清晰明了，像阳光洒在大海上一样，金光闪闪。

你会发现，虽然公式听起来有点吓人，但其实背后有趣的故事才是最重要的。

初中数学二次函数的图像与原点的关系如何确定
确定二次函数的图像与原点的关系涉及到函数的对称性和函数值的计算。

下面将介绍如何确定二次函数的图像与原点的关系：
1. 对称性：
二次函数f(x) = ax^2 + bx + c 的图像关于直线x = -b/2a 对称。

这条直线称为二次函数的对称轴。

如果原点在对称轴上，则二次函数的图像与原点有特殊的关系。

2. 判断原点是否在对称轴上：
a. 计算二次函数的对称轴横坐标x = -b/2a。

b. 如果计算得到的对称轴横坐标为0，则原点在对称轴上。

c. 如果对称轴横坐标不为0，则原点不在对称轴上。

3. 计算函数值：
a. 当原点在对称轴上时，即对称轴横坐标为0，我们只需计算函数在原点的纵坐标。

b. 将x = 0 代入二次函数的表达式f(0) = a(0)^2 + b(0) + c = c，即得到二次函数在原点的纵坐标。

通过以上步骤，我们可以确定二次函数的图像与原点的关系。

如果原点在对称轴上，则二次函数的图像经过原点。

如果原点不在对称轴上，则需要计算二次函数在原点的函数值来确定与原点的关系。

在初中数学中，理解二次函数的对称性和计算函数值对于分析函数图像和确定函数与原点的关系非常重要。

二次函数过定点问题
二次函数过定指是怎样通过求解某二次函数满足特定条件而得到特定的解。

从图形讲，二次函数过定点可以理解为二次函数对某特定点有特殊性质，当它被满足时，我们可以用特定解解决二次函数问题。

其实当我们解决这类
问题的时候，只要我们坚持计算求解的原则，并根据这些原则确定求解方案，就能够实现所求解的目的。

而且，当解决二次函数过定点问题时，首先要了解二次函数的形式，它
是一元二次方程，一般可以写成ax^2 + bx + c = 0的形式，其中a、b、c
要满足特定的条件。

因此，我们在解决二次函数过定点问题时，要先把这个
方程的各参数确定下来，之后就可以根据它们开始分析和解决问题，而不必
从零开始，这样也能节约时间。

因此，在解决二次函数过定点问题时，我们一定要了解二次函数的形式，它是一元二次方程，通过求解并满足特定条件，我们就能够确定这个方程的
各参数，最后就能够得出特定的解。

二次函数过定点题目：当我们说一个二次函数通过定点时，通常指的是函数图像上的一个特定点。

一个一般的二次函数可以写成[f(x) = ax^2 + bx + c]，其中 (a)、(b) 和 (c) 是常数，(a \neq 0)。

通过这个函数的顶点，可以找到它的顶点坐标，并用这些信息来解决问题。

下面是三个通过定点的二次函数题目，我们可以分别来解决它们：题目1:某二次函数的图象经过点 (P(3, 7))，并且在点 (Q(-1, 3)) 处的切线斜率为 4。

求这个二次函数的解析式。

解答：首先，根据条件得出函数图象经过点 (P(3, 7))，由此可知函数图象对应的二次函数过点 (P)，因此可以列出方程 (f(3) = 7)。

这样得到 (9a + 3b + c = 7)。

另外，切线的斜率为4，说明在点 (Q(-1, 3)) 处的导数值为4。

因此可以列出方程 (f'(-1) = 4)，这将得到 (-2a + b = 4)。

最后，因为函数图象对应的二次函数是一个二次函数，所以它的导数是一个一次函数。

根据函数的导数性质，可以得到函数图象对应的二次函数在顶点处的导数值为0。

由于顶点的横坐标为 (-\frac{b}{2a})，所以有 (-\frac{b}{2a} = 3)。

解出以上方程组即可得到二次函数的解析式。

题目2:已知抛物线 (y = ax^2 + bx + c) 的顶点为 (V(-2, 5))，求 (a)、(b)、(c) 的值。

解答：给出顶点，可以直接得到 (c) 的值，也就是 (c = 5)。

另外，顶点的横坐标为 (-\frac{b}{2a} = -2)。

结合这个信息可以得到一个关于 (a) 和 (b) 的方程。

最后，利用顶点的纵坐标 (5)，也就是 (f(-2) = 5)，可以得到另外一个关于 (a) 和 (b) 的方程。

解出以上方程即可得到 (a)、(b) 的值。

题目3:已知二次函数的图像包含点 ((1, 2)) 和 ((3, 8))，求该二次函数的解析式。

函数图象过定点问题总结在初中我们学习过的函数中,有些函数的图象具有过定点的性质,如正比例函数y kx(k 0),无论k取不等于0的任何值,当x 0时,都有y 0,所以其图象是一条经过定点（0,0）即坐标原点的直线;对于一次函数y kx b(k 0),当b确定时,无论k取不等于 0的任何值,其图象总经过定点(0,b);对于二次函数y ax2bx c(a 0),当c确定时,无论a,b取何值,其图象总经过定点(0,c).针对这类函数,我们关心的是如何求出定点的坐标.常使用的方法有: （1）特殊值法;（2）分离参数法;（3）变换主元法.其中,有时候最简单的方法是特殊值法,最常用的方法是分离参数法.下面给出以上三种方法的具体介绍:特殊值法例1.无论m为任何实数,抛物线y x2(2m)x m总过的点是【】（A）(1,3)（B）(1,0)（C）(1,3)（D）(1,0)解:任意赋予m两个特殊值,不妨设m0和m 2则对应的两个函数解析式为:y x22x,y x22y x22x联立得到方程组yx22x1解之得:y3检验:把x1代入y x2(2m)x m中,发现无论m为任何实数,等式总成y3函数图象过定点问题总结第1页立.∴抛物线y x2(2 m)x m总经过定点(1,3),故应选【A】.归纳总结:1．这类函数有一个特点,那就是它们的解析式里面含有1个或2个的变系数,也可称为参数,如例1中的m,参数的值可以改变,不同的参数值对应不同的函数解析式.2.利用这类函数的图象过定点的性质,我们可以给参数（变系数）指定两个特殊值,继而得到两个具体的函数解析式,联立两个解析式为方程组,方程组的解就是定点的横坐标与纵坐标.另外,需要指出的是,若方程组的解不唯一,则定点也不唯一.分离参数法例2.求证:抛物线y(3 k)x2(k 2)x 2k 1(k3)过定点,并求出定点的坐标.解:整理得: y3x22x1k(x2x2)(k3)令x2x20解之得:x11,x22把x11,x22分别代入y3x22x1k(x2x2)得:y14,y27x11,x22分别代入该抛物线的解析式,无论k取不等于3的何值,等式把4y27y1总成立∴抛物线y (3 k)x2(k 2)x 2k 1(k 3)过定点,且定点有两个,定点坐标分别为(1,4)、(2,7).函数图象过定点问题总结第2页归纳总结:使用分离参数法的一般步骤是:（1）对含有参数的项集中;（2）对所有含参数的项进行因式分解,把参数用提公因式法提出来;（3）提出公因式后令剩下的因式等于0,得到一个关于自变量x的方程（这时参数如何变化,都“失效了”）;（4）解方程方程的解x x0是定点的横坐标,把解x x0代入解析式得到的函数值y y0是定点的纵坐标.经过以上步骤,求出定点的坐标为(x0,y0).若方程的解不唯一,则定点的个数也不唯一.变换主元法我们在七年级学习一元一次方程的时候,要把方程化为ax b的形式,其解分为三种情况:（1）当a0时,方程有唯一解:x b;a（2）当a b0时,方程的解为全体实数;（3）当a0,b0时,方程无解.把函数的解析式化为am b（m为参数,a,b为含有x,y的代数式）的形式,无论m取何值,既然函数的图象经过定点,那么令b0, 得到关于x,y的二．．．．．．．．．．．．．．．．．．．．．a元方程组（注意,不一定是二元一次方程组）,方程组的解即为定点的坐标.以上处理问题时,把参数m当做主元来处理,相当于方程ax b里面的x,这或许就是这种方法名称的由来吧!函数图象过定点问题总结第3页以上所有内容供同学们作为常识知识储备.例3.无论m为任何实数,抛物线y x2(2m)x m经过定点________. 解:∵yx2(2m)xm∴y x22x mx m∴(x1)m x22x y（＊）令x10,解之得x1 x22x y0:3y∴无论m为任何实数, x1(2m)x m y恒满足等式（＊）,即抛物线yx23恒经过定点(1,3).★1. 无论m取何值,函数y mx4m3的图象过定点________.★2. 二次函数y x2bx c满足b c2,则这个函数的图象一定经过某一个定点,这个定点是________.★3.无论k为何值直线y kx3k2必经过点________.,★4. 抛物线y(3m)x2(m2)x2m1m3经过的定点是________.★5. 某数学兴趣小组研究二次函数y mx22mx3(m0)的图象发现,随着m的变化,这个二次函数的图象形状与位置均发生变化,但这个二次函数的图象总经过两个定点,请你写出这两个定点的坐标:________________.★6. 对于二次函数y ax 2(2a1)x1(a下列说法正确的有【】0),①无论a取何值,此二次函数的图象与x轴必有两个交点;②无论a取何值,图象必过两个定点,且两个定点之间的距离为2;③当a 0时,函数在x1时,y随x的增大而减小;④当a 0时,函数图象截x轴所得线段长度必大于 2.函数图象过定点问题总结第4页（A）1个（B）2个（C）3个（D）4个函数图象过定点问题总结第5页。

二次函数的图象过定点的证法
祁福元
【期刊名称】《数学学习与研究》
【年(卷),期】2002(000)011
【总页数】2页(P15-16)
【作者】祁福元
【作者单位】山西省大同县教育局037300
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.二次函数的经典题型——二次函数图象与系数之间关系的应用 [J], 王荣;
2.几何画板在初三专题复习课中的应用——以"二次函数图象"为例 [J], 冯伟;张骅
3.二次函数的“不动点”与“稳定点”──从数学通报2139号问题谈起 [J], 魏国兵
4.基于粤教翔云平台的翻转课堂教学实践--以“二次函数y=ax^(2)的图象与性质”为例 [J], 苏国东
5.概念图指向单元整体建构课的教学策略--“二次函数图象与性质”赛课观摩有感[J], 袁健
因版权原因，仅展示原文概要，查看原文内容请购买。

第10讲 二次函数与定点方法技巧利用根与系数的关系，通过设参、消参等手段，求出定点的坐标．●题型一与参系数无关例1：关于x 的二次函数y ＝ax 2－2ax +a －4的图象经过定点P ，求点P 的坐标．例2：抛物线y ＝ax 2+b x －4a －2b 与抛物线y ＝ 4 ax 2－2b x +c 与y 轴交于同一点， 求关于x 的二次函数 y ＝ 4 ax 2－2b x +c 的图象所经过的定点的坐标．●题型二用几何条件求定点例3：已知抛物线y ＝21x 2与直线y ＝mx+n 交于点A ，点B ，直线AB 交y 轴于点C ，是否存在定点C ，使得OA ⊥OB ，若存在，求出定点C 的坐标，若不存在，说明理由．●题型三对称点与定点例4：过点P(1，－2) 的任一直线交抛物线y ＝21x 2－x 于A ，B 两点，点B 关于抛物线的对称轴x ＝1的对称点为点C ，连接AC ，求直线AC 所经过的定点的坐标．练1．如图，抛物线C ： y ＝ax 2 +b x +c(a >0)过y 轴上一点(0， 4)，C1与直线y ＝k x 交于点E ，F ， P 为y 轴上一定点，过点P 的直线y ＝b x +n 与直线y ＝k x 交于点Q ，若OQ OF OE 211=+，求定点P 的坐标．练2．如图，抛物线的顶点为(2， 0)，且经过点(4，1)， 直线y ＝41x 与抛物线交于A ， B 两点，直线l 的解析式为y ＝－1．(1)求抛物线的解析式；(2)点F 为平面内一定点，M 为抛物线上一动点，且点M到直线l 的距离与点M 到点F 的距离始终相等，求定点的坐标．3．如图，抛物线y ＝21 (x －1)2上任意一点P(x ， m)，过点P 作直线y ＝(x 0－1)x +b 与直线x ＝1交于点 A ，F(1，n)，恒有FP ＝FA ，求点F 的坐标．。