数学建模提高班专题一数学规划模型、案例及软件求解(2010410)final

一、线性规划1.简介1.1适用情况用现有资源来安排生产，以取得最大经济效益的问题。

如： （1）资源的合理利用（2）投资的风险与利用问题 （3）合理下料问题 （4）合理配料问题 （5）运 输 问 题 （6）作物布局问题（7）多周期生产平滑模型 （8）公交车调度安排 1.2建立线性规划的条件（1）要求解问题的目标函数能用数值指标来反映，且为线性函数；（2）要求达到的目标是在一定条件下实现的，这些约束可用线性等式或不等式描述。

1.3线性规划模型的构成决策变量、目标函数、约束条件。

2、一般线性规划问题 数学标准形式：目标函数：1max ==∑ njjj z cx约束条件：1,1,2,...,,..0,1,2,...,.=⎧==⎪⎨⎪≥=⎩∑nij j i j ja xb i m s t x j nmatlab 标准形式：3、可以转化为线性规划的问题 例：求解下列数学规划问题解：作変量変换1||||,,1,2,3,4,22+-===i i i ii x x x x u v i 并把新变量重新排序成一维变量[]1414,,,,,⎡⎤==⎢⎥⎣⎦Tu y u u v v v ，则可把模型转化为线性规划模型其中：[]1,2,3,4,1,2,3,4;=T c 12,1,;2⎡⎤=---⎢⎥⎣⎦Tb 111111131 - - ⎡⎤⎢⎥= - -⎢⎥⎢⎥ -1 -1 3⎣⎦A 。

利用matlab 计算得最优解：12342,0,=-===x x x x 最优值z=2。

程序如下： 略二、整数规划 1.简介数学规划中的变量(部分或全部)限制为整数时称为整数规划。

目前流行求解整数规划的方法一般适用于整数线性规划。

1.1整数规划特点1）原线性规划有最优解，当自变量限制为整数后，出现的情况有①原线性规划最优解全是整数，则整数规划最优解与线性规划最优解一致。

②整数规划无可行解。

③有可行解（存在最优解），但最优解值变差。

2）整数规划最优解不能按照实数最优解简单取整获得。

数学建模教案－线性规划模型一、问题的提出在生产管理和经营活动中经常提出一类问题，即如何合理地利用有限的人力、物力、财力等资源，以便得到最好的经济效果。

例1 若需在长为4000mm的圆钢上，截出长为698mm和518mm两种毛坯，问怎样截取才能使残料最少？初步分析可以先考虑两种“极端”的情况：（1）全部截出长为698mm的甲件，一共可截出EQ F(4000,698) »5件，残料长为510mm。

（2）全部截出长为518mm的乙件，一共可截出 E Q F(4000,518) »7件，残料长为374mm。

由此可以想到，若将 x个甲件和y 个乙件搭配起来下料，是否可能使残料减少？把截取条件数学化地表示出来就是：698 x + 518y £ 4000x ，y都是非负整数目标是使：z = EQ F(698x + 518y,4000) （材料利用率）尽可能地接近或等于1。

（尽可能地大）该问题可用数学模型表示为：目标函数： max z = EQ F(698x + 518y,4000)满足约束条件：698 x + 518y £ 4000 ， (1)x ，y都是非负整数 . (2)例2 某工厂在计划期内要安排生产I 、II两种产品，已知生产单位产品所需的设备台数及A、B两种原料的消耗，如下表所示。

该工厂每生产一件产品I可获利 2 元，每生产一件产品II可获利 3 元，问应如何安排生产计划使工厂获利最多？这问题可以用以下的数学模型来描述：设 x 1, x 2分别表示在计划期内产品I、II的产量。

因为设备的有效台数为8 ，这是一个限制产量的条件，所以在确定I 、II的产量时，要考虑不超过设备的有效台数，即可用不等式表示为：x 1 + 2x 2£ 8 .同理，因原材料A 、B的限量，可以得到以下不等式：4 x 1£ 164 x 2£ 12.该工厂的目标是在不超过所有资源限量的条件下，如何确定产量x1、x2以得到最大的利润。

数学规划模型的matlab求解数学规划模型的matlab求解数学规划模型是优化模型的一种，包括线性规划模型(目标函数和约束条件都是线性函数的优化问题);非线性规划模型(目标函数或者约束条件是非线性的函数);整数规划(决策变量是整数值得规划问题);多目标规划(具有多个目标函数的规划问题)；目标规划(具有不同优先级的目标和偏差的规划问题)动态规划(求解多阶段决策问题的最优化方法)。

数学规划模型相对比较好理解，关键是要能熟练地求出模型的解。

以下是解线性规划模型的方法：1.线性规划问题线性规划问题的标准形式为：min f'*xsub.to：A*x<b< p="">其中f、x、b、beq、lb、ub为向量，A、Aeq为矩阵。

MATLAB中，线性规划问题（Linear Programming）的求解使用的是函数linprog。

函数linprog格式x=linprog(f,A,b)%求min f'*x sub.to A*x<=b线性规划的最优解。

x=linprog(f,A,b,Aeq,beq)%等式约束，若没有不等式约束，则A=[]，b=[]。

x=linprog(f,A,b,Aeq,beq,lb,ub)%指定x的范围，若没有等式约束，则Aeq=[]，beq=[]x=linprog(f,A,b,Aeq,beq,lb,ub,x0)%设置初值x0x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options)%options为指定的优化参数[x,fval]=linprog(…)%返回目标函数最优值，即fval=f'*x。

[x,lambda,exitflag]=linprog(…)%lambda为解x的Lagrange乘子。

[x,lambda,fval,exitflag]=linprog(…)%exitflag为终止迭代的错误条件。

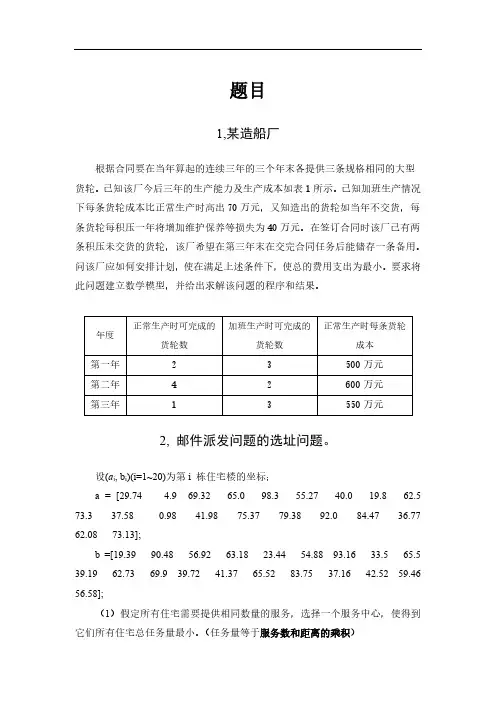
题目1,某造船厂根据合同要在当年算起的连续三年的三个年末各提供三条规格相同的大型货轮。

已知该厂今后三年的生产能力及生产成本如表1所示。

已知加班生产情况下每条货轮成本比正常生产时高出70万元，又知造出的货轮如当年不交货，每条货轮每积压一年将增加维护保养等损失为40万元。

在签订合同时该厂已有两条积压未交货的货轮，该厂希望在第三年末在交完合同任务后能储存一条备用。

问该厂应如何安排计划，使在满足上述条件下，使总的费用支出为最小。

要求将此问题建立数学模型，并给出求解该问题的程序和结果。

2, 邮件派发问题的选址问题。

设(a i, b i)(i=1~20)为第i 栋住宅楼的坐标；a = [29.74 4.9 69.32 65.0 98.3 55.27 40.0 19.8 62.573.3 37.58 0.98 41.98 75.37 79.38 92.0 84.47 36.7762.08 73.13];b =[19.39 90.48 56.92 63.18 23.44 54.88 93.16 33.5 65.539.19 62.73 69.9 39.72 41.37 65.52 83.75 37.16 42.52 59.46 56.58];（1）假定所有住宅需要提供相同数量的服务，选择一个服务中心，使得到它们所有住宅总任务量最小。

（任务量等于服务数和距离的乘积）（2）假定不同的住宅有不同的服务量，值为c=[2 1 2 4 4 2 5 1 6 1 1 1 4 2 6 2 1 2 4 5]。

重新计算服务中心的地址和服务方案。

（3）在（2）的基础上，另外假定服务中心可以设定3个，一个主中心和两个分中心，要求分配的服务量之比为2：1：1（尽可能接近这个比例），而且规定一个住宅只能由其中一家服务中心提供服务。

如何选址并且给出每条路线上的运输量。

3, 曲线拟合问题可以使用无约束或者约束优化进行描述。

为确定变量y 和x 之间的函数关系，通过实验得到n 个数据(x i ,y i )，i=1,…,n 。

数学建模10-规划类
问题
数学建模10-规划类问题
一、线性规划
MATLAB中的标准形式
计算机求解：MATLAB解法和LINGO解法
二、整数规划
变量（部分或全部）限制为整数。

其中0-1整数规划是整数规划中的特殊情形，主要适用问题有：①相互排斥的约束条件；②固定费用的问题（采用/不采用哪种生产方式）；③指派问题（指派n个人去做n 项工作，每人做且仅做一项工作，指派矩阵的含义）。

蒙特卡洛法（随机取样法）：使用计算机生成相关分布的随机数，进行多次随机模拟，尽可能找到最优解。

三、非线性规划
目标函数或约束条件中包含非线性函数。

无约束问题的MATLAB解法：（1）符号解；（2）数值解：fminunc，finsearch
（3）求函数的零点和方程组的解：roots，solve,fsolve 约束极值问题
（1）二次规划：目标函数是自变量x的二次函数，而约束条件全是线性的。

（2）罚函数法：将非线性规划问题转化为求解一系列无约束极值问题。

（3）MATLAB中求约束极值问题：fminbnd，fseminf，
fminimax，具体用法参考书中或MATLAB的help命
令。

（4）利用梯度求解约束优化问题
四、动态规划：求解决策过程最优化的数学方法，主要用
于求解以时间划分阶段的动态过程的优化问题。

五、目标规划：实际问题中，衡量方案优劣要考虑多个目
标，有主要的，有主要的，也有次要的；有最大值的，也有最小值的；有定量的，也有定性的；有相互补充的，也有相互对立的，这时可用目标规划解决。

数学建模的常用模型与求解方法知识点总结数学建模是运用数学方法和技巧来研究和解决现实问题的一门学科。

它将实际问题抽象化，建立数学模型，并通过数学推理和计算求解模型，从而得出对实际问题的理解和解决方案。

本文将总结数学建模中常用的模型类型和求解方法，并介绍每种方法的应用场景。

一、线性规划模型与求解方法线性规划是数学建模中最常用的模型之一，其基本形式为：$$\begin{align*}\max \quad & c^Tx \\s.t. \quad & Ax \leq b \\& x \geq 0\end{align*}$$其中，$x$为决策变量向量，$c$为目标函数系数向量，$A$为约束系数矩阵，$b$为约束条件向量。

常用的求解方法有单纯形法、对偶单纯形法和内点法等。

二、非线性规划模型与求解方法非线性规划是一类约束条件下的非线性优化问题，其目标函数或约束条件存在非线性函数。

常见的非线性规划模型包括凸规划、二次规划和整数规划等。

求解方法有梯度法、拟牛顿法和遗传算法等。

三、动态规划模型与求解方法动态规划是一种用于解决多阶段决策问题的数学方法。

它通过将问题分解为一系列子问题，并利用子问题的最优解构造原问题的最优解。

常见的动态规划模型包括最短路径问题、背包问题和任务分配等。

求解方法有递推法、记忆化搜索和剪枝算法等。

四、图论模型与求解方法图论是研究图及其应用的一门学科，广泛应用于网络优化、城市规划和交通调度等领域。

常见的图论模型包括最小生成树、最短路径和最大流等。

求解方法有贪心算法、深度优先搜索和广度优先搜索等。

五、随机模型与概率统计方法随机模型是描述不确定性问题的数学模型，常用于风险评估和决策分析。

概率统计方法用于根据样本数据对随机模型进行参数估计和假设检验。

常见的随机模型包括马尔可夫链、蒙特卡洛模拟和马尔科夫决策过程等。

求解方法有蒙特卡洛法、马尔科夫链蒙特卡洛法和最大似然估计等。

六、模拟模型与求解方法模拟模型是通过生成一系列随机抽样数据来模拟实际问题，常用于风险评估和系统优化。

数学规划模型及其求解简单的优化模型往往是一元或者多元无约束或者等式约束的最优化问题。

而在很多实际问题中，所能够提供的决策变量取值受到很多因素的制约，这样就产生了一般的优化模型，统称为数学规划模型。

一 线性规划线性规划是指在一组线性条件的约束下，求某一个线性函数的最值问题。

一般地，线性规划的数学模型为：min(or max) n n x c x c x c z +++= 2211i n in i i b or x a x a x a t s ),(..2211≥=≤+++m i ,,2,1 =n j x j ,,2,1,0 =≥用矩阵、向量符号，可以简化线性规划模型的表示：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=3212121212222111211,,,c c c c b b b b x x x x a a a a a a a a a A n n nn n n n n则线性规划问题可写为：x c z or ')max min(=ni x bor Ax t s i ,,2,1,0),(.. =≥≥=≤用MATLAB 实现线性规划的运算为了避免这种形式多样性带来的不便，Matlab 中规定线性规划的标准形式为min x c 'ubx lb beq x Aeq b Ax t s ≤≤=∙≤.. 其中c 和x 为n 维列向量，A 、Aeq 为适当维数的矩阵，b 、beq 为适当维数的列向量。

例如线性规划b Ax t s xc ≥..'max的Matlab 标准型为b Ax t s xc -≤--..'min求解线性规划的matlab 命令linprog 的格式：X=linprog(c,A,b)可以求解线性规划问题 min c ´x s.t. Ax <= bX=linprog(c,A,b,Aeq,beq) 可以求解线性规划问题 min c ´x s.t. Ax <= b, Aeq*x = beq X=linprog(c,A,b,Aeq,beq,lb,ub)可以对上述问题中的变量加上范围约束 lb <= X <= ub 当无下限时可设为lb=-inf 无上限时可以设定ub=inf X=linprog(f,A,b,Aeq,beq,lb,ub,X0) 给出了初始点X0 例：求解下列线性规划问题⎪⎩⎪⎨⎧≥≥+-=++-+=0,,10527532max 321321321321x x x x x x x x x x x x z编写M 文件如下：c=[-2;-3;5]; A=[-2,5,-1]; b=-10;Aeq=[1,1,1]; beq=7;lb=[0;0;0];[x,fval]=linprog(c,A,b,Aeq,beq,lb,inf)例：货机装运模型问题重述：一架货机有三个货舱：前舱、中舱和后舱。

实验一： 数学规划模型AMPL 求解一、实验目的1.熟悉启动AMPL 的方法。

2.熟悉SCITE 编辑软件的运行。

3.熟悉AMPL 基本编程。

4.熟悉AMPL 求解数学规划模型的过程。

二、实验原理1. AMPL 的启动与运行一奶制品加工厂用牛奶生产A1和A2两种奶制品，1桶牛奶可以在甲类设备上用12小时加工成3公斤A1或者在乙类设备上用8小时加工成4公斤A2，且都能全部售出，且每公斤A1获利24元，每公斤A2获利16元。

先加工厂每天能得到50桶牛奶的供应，每天工人总的劳动时间为480小时，并且甲类设备每天至多加工100公斤A1，乙类设备的加工能力没有限制，试为该厂制定一个计划，使每天的获利最大。

建模：决策变量：x 1桶牛奶生产A1 ，x 2桶牛奶生产A2 目标函数： 约束条件：AMPL 安装与设置（Windows 下）：（1）下载ampl.zip ，限制版本，带求解器cplex （解线性规划），minos （解线性或非线性规划，默认求解器）；（2）把ampl.zip 解压至一个目录下，然后找到ampl.exe 文件所在的目录，称为ampl 根目录，比如C:\ampl ；（3）把ampl 根目录设置到Windows 路径上，方法：鼠标右击我的电脑---属性—高级---点击环境变量出现环境变量窗口，在图下方的系统变量窗口找到Path 变量，把C:\ampl 增加在变量值后面（注意前面加分号），如下图；216472x x z Max +=12,0x x ≥13100x ≤12128480x x +≤1250x x +≤（1）下载文本编辑器Scite.rar并解压到安装目录，双击scite.exe,得到如下界面（2）建立模型文件：在空白窗口中输入如下代码，语言选项选择AMPL，保存为milk.modset Products ordered; #产品集合param Time{i in Products }>0; #加工时间param Quan{i in Products}>0; #单位产量param Profit{i in Products}>0; #单位利润var x{i in Products}>=0; #决策变量maximize profit: sum{i in Products} Profit [i]* Quan [i]*x[i];subject to raw: sum{i in Products}x[i] <=50;subject to time:sum{i in Products}Time[i]*x[i]<=480;subject to capacity: Quan[first(Products)]*x[first(Products)]<=100;（2）建立数据文件：新建文件, 输入如下代码, 保存为milk.datset Products:=A1 A2;param Time:=A1 12 A2 8;param Quan:=A1 3 A2 4;param Profit:=A1 24 A2 16;(3) 建立批处理文件：新建文件, 输入如下代码, 保存为milk.runmodel milk.mod;data milk.dat;option solver cplex;solve;display x;注意：模型文件、数据文件和批处理文件的文件名应该相同，保存在同一文件夹。