七年级上册数学第五章知识点参考：一元一次方程

浙教版-7年级-上册-数学-第5章《一元一次方程》分节知识点一、方程及等式1、定义：含有未知数的等式叫做方程.要点诠释：（1）判断一个式子是不是方程，只需看两点：一是等式；二是含有未知数．2、方程的解：使方程左右两边的值相等的未知数的值，叫做方程的解.要点诠释：（1）判断一个数（或一组数）是否是某方程的解，只需看两点：①它（或它们）是方程中未知数的值；②将它（或它们）分别代入方程的左边和右边，若左边等于右边，则它（或它们）是方程的解，否则不是．3、解方程：求方程的解的过程叫做解方程.4、方程的两个特征：（1）方程是等式；（2）方程中必须含有字母（或未知数）.5、建立方程：把所要求的量用字母x（或y，…）表示，根据问题中的等量关系列出方程，这一过程叫做建立方程。

要点二、一元一次方程的有关概念1、定义：只含有一个未知数（元），并且未知数的次数都是1，这样的方程叫做一元一次方程.要点诠释：（1）“元”是指未知数，“次”是指未知数的次数，一元一次方程满足条件：①是一个方程；②必须只含有一个未知数；③含有未知数的项的最高次数是1；④分母中不含有未知数．（2）一元一次方程的标准形式是：ax+b=0(其中a≠0，a,b是常数).（3）一元一次方程的最简形式是：ax＝b（其中a≠0，a,b是常数）.要点三、等式的性质1、等式的概念：用符号“=”来表示相等关系的式子叫做等式.2、等式的性质：（1）等式的性质1：等式两边加（或减）同一个数（或式子），所得结果仍是等式.即：如果，那么(c为一个数或一个式子).（2）等式的性质2：等式两边都乘（或除以）同一个数（或式子），（除数或除式不能为0），所得结果仍是等式.即：如果，那么；如果，那么.要点诠释：（1）根据等式的两条性质，对等式进行变形，等式两边必须同时进行完全相同的变形；（2）等式性质1中，强调的是整式，如果在等式两边同加的不是整式，那么变形后的等式不一定成立，如x＝0中，两边加上得x＋，这个等式不成立;（3）等式的性质2中等式两边都除以同一个数时，这个除数不能为零．二、一元一次方程的解法要点一、解一元一次方程的一般步骤变形名称具体做法注意事项去分母在方程两边都乘以各分母的最小公倍数（1）不要漏乘不含分母的项（2）分子是一个整体的，去分母后应加上括号去括号先去小括号，再去中括号，最后去大括号（1）不要漏乘括号里的项（2）不要弄错符号移项把含有未知数的项都移到方程的一边，其他项都移到方程的另一边(记住移项要变号)（2）移项要变号（2）不要丢项合并同类项把方程化成ax＝b(a≠0)的形式字母及其指数不变两边同除以未知数的系数（系数化成1）在方程两边都除以未知数的系数a，得到方程的解．不要把分子、分母写颠倒要点诠释：（1）移项的定义：把方程中的项改变符合后，从方程的一边移到另一边，这种变形叫做移项.（2）解方程时，表中有些变形步骤可能用不到，而且也不一定要按照自上而下的顺序，有些步骤可以合并简化．（3）去括号一般按由内向外的顺序进行，也可以根据方程的特点按由外向内的顺序进行.（4）当方程中含有小数或分数形式的分母时，一般先利用分数的性质将分母变为整数后再去分母，注意去分母的依据是等式的性质，而分母化整的依据是分数的性质，两者不要混淆．要点二、解特殊的一元一次方程1、含绝对值的一元一次方程（1）解此类方程关键要把绝对值化去，使之成为一般的一元一次方程，化去绝对值的依据是绝对值的意义．要点诠释：此类问题一般先把方程化为的形式，然后分类讨论：（1）当时，无解；（2）当时，原方程化为：；（3）当时，原方程可化为：或.2、含字母的一元一次方程：此类方程一般先化为一元一次方程的最简形式ax＝b，再分三种情况分类讨论：（1）当a≠0时，；（2）当a＝0，b＝0时，x为任意有理数；（3）当a＝0，b≠0时，方程无解．三、实际问题与一元一次方程（一）知识点一、用一元一次方程解决实际问题的一般步骤1、列方程解应用题的基本思路为：问题方程解答．由此可得解决此类题的一般步骤为：审、设、列、解、检验、答．要点诠释：（1）“审”是指读懂题目，弄清题意，明确哪些是已知量，哪些是未知量，以及它们之间的关系，寻找等量关系；（2）“设”就是设未知数，一般求什么就设什么为x，但有时也可以间接设未知数；（3）“列”就是列方程，即列代数式表示相等关系中的各个量，列出方程，同时注意方程两边是同一类量，单位要统一；（4）“解”就是解方程，求出未知数的值；（5）“检验”就是指检验方程的解是否符合实际意义，当有不符合的解时，及时指出，舍去即可；（6）“答”就是写出答案，注意单位要写清楚．知识点二、常见列方程解应用题的几种类型1、和、差、倍、分问题（1）基本量及关系：增长量＝原有量×增长率，现有量＝原有量+增长量，现有量＝原有量-降低量．（2）寻找相等关系：抓住关键词列方程，常见的关键词有：多、少、和、差、不足、剩余以及倍，增长率等．2、行程问题（1）三个基本量间的关系：路程=速度×时间（2）基本类型有：①相遇问题（或相向问题）：Ⅰ、基本量及关系：相遇路程=速度和×相遇时间；Ⅱ、寻找相等关系：甲走的路程+乙走的路程＝两地距离．②追及问题：Ⅰ、基本量及关系：追及路程=速度差×追及时间；Ⅱ、寻找相等关系：第一，同地不同时出发：前者走的路程＝追者走的路程；第二，同时不同地出发：前者走的路程+两者相距距离＝追者走的路程．③航行问题：Ⅰ、基本量及关系：顺流速度=静水速度+水流速度，逆流速度=静水速度－水流速度，顺水速度－逆水速度＝2×水速；Ⅱ、寻找相等关系：抓住两地之间距离不变、水流速度不变、船在静水中的速度不变来考虑．（3）解此类题的关键是抓住甲、乙两物体的时间关系或所走的路程关系，并且还常常借助画草图来分析．3、工程问题：如果题目没有明确指明总工作量，一般把总工作量设为1。

XXX版初一上册第五章一元一次方程知识点总结和例题讲解1.方程是含有未知数的等式。

2.一元一次方程是只含有一个未知数的方程，未知数的指数都是1.例如：1700+50x=1800，2（x+1.5x）=5都是一元一次方程。

3.方程的解是使方程中等号左右两边相等的未知数的值。

注：⑴方程的解和解方程是不同的概念，方程的解实质上是求得的结果，它是一个数值(或几个数值)，而解方程的含义是指求出方程的解或判断方程无解的过程。

⑵方程的解的检验方法，首先把未知数的值分别代入方程的左、右两边计算它们的值，其次比较两边的值是否相等从而得出结论。

等式的性质：1)等式两边都加上(或减去)同个数(或式子)，结果仍相等。

2)等式两边乘同一个数，或除以同一个不为0的数，结果仍相等。

移项法则：把等式一边的某项变号后移到另一边，叫做移项。

去括号法则：1.括号外的因数是正数，去括号后各项的符号与原括号内相应各项的符号相同。

2.括号外的因数是负数，去括号后各项的符号与原括号内相应各项的符号改变。

解方程的一般步骤：1.去分母(方程两边同乘各分母的最小公倍数)。

2.去括号(按去括号法则和分配律)。

3.移项(把含有未知数的项移到方程一边，其他项都移到方程的另一边，移项要变号)。

4.合并(把方程化成ax=b (a≠0)形式)。

5.系数化为1(在方程两边都除以未知数的系数a，得到方程的解x= b/a)。

一元一次方程解应用题的一般步骤：1)审题：弄清题意。

2)找出等量关系：找出能够表示本题含义的相等关系。

3)设出未知数，列出方程：设出未知数后，表示出有关的含字母的式子，然后利用已找出的等量关系列出方程。

4)解方程：解所列的方程，求出未知数的值。

5)检验，写答案：检验所求出的未知数的值是否是方程的解，是否符合实际，检验后写出答案。

一元一次方程的实际应用：1.和、差、倍、分问题：增长量=原有量×增长率，现在量=原有量+增长量。

倍数关系：通过关键词“是几倍，增加几倍，增加到几倍，增加百分之几，增长率”来表示两个数之间的倍数关系。

第五章《一元一次方程》期末复习基础知识梳理一、主要概念1．方程的概念：含有未知数的等式叫方程.2．一元一次方程的概念：只含有一个未知数，未知数的指数是1，这样的方程叫做一元一次方程.3．方程的解：使方程中等号左右两边相等的未知数的值，叫做方程的解.4．解方程：求方程的解的过程叫做解方程.5．同类项：如果两项所含字母相同，并且相同字母的指数也相同，那么这样的两项叫做同类项.二、主要性质1．等式的性质等式的性质1：等式两边加（或减）同一个数（或式子），结果仍相等.等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等.2．合并同类项法则同类项相加（减），把它们的系数相加（减）作为结果的系数，字母部分不变.3．去括号法则（1）括号外的因数是正数，去括号后各项的符号与原括号内相应各项的符号相同.（2）括号外的因数是负数，去括号后各项的符号与原括号内相应各项的符号相反.三、解一元一次方程的注意事项1．分母是小数时，根据分数的基本性质，分子、分母都扩大相同的倍数，把分母转化成整数，此时和不含分母的项无关，不要和去分母相混淆.2．去分母时，方程两边各项都乘各分母的最小公倍数，此时不含分母的项切勿漏乘，分数线相当于括号，去分母后分子各项应加括号.3．去括号时，不要漏乘括号内的项，要依据法则，不要弄错符号.4．移项时切记要变号，不要丢项，另外合并同类项和移项要灵活运用，如：有时去括号后等号的某一边或两边有同类项，可先合并，再移项，以免丢项.5．系数化为1时，不要弄错符号，分子、分母不要颠倒.6．不要生搬硬套解方程的步骤，要根据具体题目灵活运用，以便找到一个最简便的解法.四、列一元一次方程解决实际问题的步骤1．审：审题，多读几次，理清题中各量之间的关系.2．设：把题中某个未知数用字母代替，有时直接设元，有时间接设元.为了比较容易列方程或列出的方程比较简单易解，不直接把题目的问题设成未知数，而间接地把和题目中要求的问题有关的量设成未知数，即间接设元.3．找：把已知数和未知数放在一起找出一个相等的关系，有时可借助图形来找相等关系.4．列：根据等量关系列出方程.5．解：求出方程的解.6．验：检验方程的解是否符合问题的实际意义.7．答：写出答案（包括单位）巩固练习一、选择题：1. 下列各题中正确的是（ ）A. 由347-=x x 移项得347=-x xB.由231312-+=-x x 去分母得)3(31)12(2-+=-x x C.由1)3(3)12(2=---x x 去括号得19324=---x xD.由7)1(2+=+x x 移项、合并同类项得x =52．方程2－2x 4x 7312－－＝－去分母得（ ）。

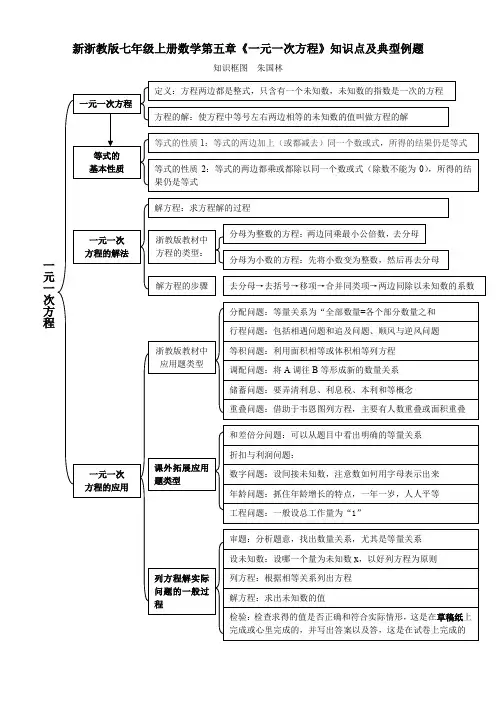
新浙教版七年级上册数学第五章《一元一次方程》知识点及典型例题知识框图朱国林关于一元一次方程概念的拓展教材中的概念：方程两边都是整式，只含有一个未知数，未知数的指数是一次的方程是一元一次方程，那么 x+2=x+3是一元一次方程吗？从概念上来看，是一元一次方程，但稍作变形，就是2=3，是不是觉得很可笑？因此，一元一次方程的概念应该是：方程两边都是整式，只含有一个未知数，未知数的指数是一次，并且能变形为ax=b （a ≠0，a 、b 均为常数）的方程是一元一次方程，也就是说，一元一次方程一定只有一个解。

关于用方程解应用题的秘诀：相关条件设未知数，剩余条件列方程考点一、判断方程是不是一元一次方程及一元一次方程概念的简单应用 考点二、关于在解方程过程中的某些变形问题，只能以选择题的形式出现 考点三、解一元一次方程考点四、列一元一次方程解与实际生活无关的题目（可以是选择题、填空题、解答题） 考点五、列一元一次方程解与实际生活有关的题目（可以是选择题、填空题、解答题）将考点与相应习题联系起来考点一、判断方程是不是一元一次方程及一元一次方程概念的简单应用 1、下列等式中是一元一次方程的是（ ）A ．3x=y-1B ．2(1)21x x -=+C ．3(x-1)= -2x-3D ．3x 2-2=3E ．11x x=+ 2、在方程23=-y x ，021=-+x x ，2121=x ，0322=--x x 中一元一次方程的个数为（ ） A ．1个 B ．2个 C ．3个 D ．4个 3、如果06312=+--a x是一元一次方程，那么=a ，方程的解为 。

（特别注意）考点二、关于在解方程过程中的某些变形问题，只能以选择题的形式出现 1、已知等式523+=b a ，则下列等式中不一定．．．成立的是（ ） （A ）;253b a =- （B ）;6213+=+b a （C ）;523+=bc ac （D ）.3532+=b a 2、解方程2631xx =+-，去分母，得（ ） （A ）133x x --= （B ）633x x --= （C ）633x x -+= （D ）133x x -+=3、下列方程变形中，正确的是（ ）（A ）方程1223+=-x x ，移项，得;2123+-=-x x （B ）方程()1523--=-x x ，去括号，得;1523--=-x x （C ）方程2332=t ，未知数系数化为1，得;1=t （D ）方程110.20.5x x --=化成101010125x x --= 考点三、解一元一次方程（1）x x 3.15.67.05.0-=-； （2）；（3）1676352212--=+--x x x ； （4）4.06.0-x 3.011.0+x .考点四、列一元一次方程，解与实际生活无关的题目（可以是选择题、填空题、解答题） 1、方程432-=+x m x 与方程6)16(21-=-x 的解相同，则m 的值为__________. 2、已知5x+3=8x －3和65a x +=37这两个方程的解是互为相反数，则a= . 3、某数的4倍减去3比这个数的一半大4，则这个数为__________.4、若与互为相反数，则的值是 .5、一个两位数，个位上的数字是十位上的数字的3倍，它们的和是12，那么这个两位数是 .6、写出一个以x=－21为解的一元一次方程7、小明在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是：11222y y -=- 怎么办呢？小明想了一想，便翻看书后答案，此方程的解是53y =-，于是很快就补好了这个常数，你能补出这个常数吗？它应是（ ） A.1 B.2 C.3 D.48、已知21=x 是方程32142m x m x -=--的根，求代数式()⎪⎭⎫ ⎝⎛---+-121824412m m m 的值.★★★已知关于x 的一元一次方程b x x +=+2301121的解为2=x ，那么关于y 的一元一次方程b y y ++=++）（）（123101121的解为 ． 考点五、列一元一次方程解与实际生活有关的题目（可以是选择题、填空题、解答题） 1、日历上竖列相邻的三个数，它们的和是39，则第一个数是（ ）A.6B.12C.13D.142、有m 辆客车及n 个人，若每辆客车乘40人，则还有10人不能上车；若每辆客车乘43人，则还有1人不能上车．有下列四个等式：①4010431m m +=-；②1014043n n ++=；③1014043n n --=；④4010431m m +=+．其中正确的是（ ） A.①② B.②④ C.②③ D.③④ 3、某商店卖出两件衣服，每件60元，其中一件赚25%，另一件亏25%，那么这两件衣服卖出后，商店是 （ ） A.不赚不亏 B.赚8元 C.亏8元 D. 赚15元4、一件商品提价25%后发现销路不是很好，欲恢复原价，则应降价（ ） A.40% B.20% C.25% D.15%5、小强比他叔叔小30岁，而两年前，小强的年龄是他叔叔的41，则小强的叔叔今年____________岁. 6、一项工程甲独做10天完成，乙的工作效率是甲的2倍，两人合做了2天未完成，剩下的工作量由乙完成，还需的天数为 ( )(A)．1 天 (B)2 天 (C)3 天 (D)4天 7、小明存入100元人民币，存期一年，年利率为2％，到期应缴纳所获利息的20％的利息税，那么小明存款到期交利息税后共得款 （ ）A.106元B.102元C.111.6元D.101.6元8、银行教育储蓄的年利率如右下表：小明现正读七年级，今年7月他父母为他在银行存款30000元，以供3年后上高中使用. 要使3年后的收益最大，则小明的父母应该采用（ ） （A ）直接存一个3年期；（B ）先存一个1年期的，1年后将利息和自动转存一个2年期； （C ）先存一个1年期的，1年后将利息和自动转存两个1年期； （D ）先存一个2年期的，2年后将利息和自动转存一个1年期.9、某酒店为招揽生意，对消费者实施如下优惠：凡订餐5桌以上，多于5桌的部分按定价的7折收费.小叶集团公司组织工会活动，预定了10桌，缴纳现金2550元，那么每桌定价是 元.10、某商店将彩电按成本价提高50%，然后在广告上写“大酬宾，八折优惠”，结果每台彩电仍获利270元，那么每台彩电成本价是___________。

第02讲_解一元一次方程知识图谱解一元一次方程知识精讲步骤 具体做法依据注意事项去分母 在方程两边同乘以各分母的最小公倍数等式性质2①不含分母的项不要漏乘 ②注意分数线有括号作用，去掉分母后，如果分子是多项式，要加括号去括号由内向外去括号，即先去小括号，再去中括号，最后去大括号 分配律，去括号法则①运用分配律去括号时，不要漏乘括号内的项②如果括号前是“－”号，去括号时，括号内各项要变号 移项 把含未知数的项都移到方程的一边（通常是左边），不含未知数的项都移到方程的另一边 等式性质1①移项必须变号②一般把含未知数的项移到左边，其他项移到右边 合并同类项把方程两边同类项分别合并，把方程化为()0ax b a =≠的形式合并同类项法则合并同类项是同类项的系数相加，字母及其指数不变未知数系数化1在方程两边同除以未知数系数a ，得到方程的解b x a =看不清楚解，不会调整等式性质2 应注意系数a 不能等于0注意：这五个步骤在解一元一次方程中，有时可能用不到，有时可能需重复用，使用时不一定严格按从（1）到（5）的顺序进行，要根据方程的特点灵活运用．例：解方程121123x x +--= 去分母：3(1)2(21)6x x +--=去括号：33426x x +-+= 移项：34632x x -=-- 合并同类项：1x -= 未知数系数化1：1x =-三点剖析一．考点：解一元一次方程．二．重难点：解一元一次方程三．易错点：1．在解方程的过程中，移项不变号；2．去括号时容易漏乘括号内的项或弄错符号．一元一次方程的解法例题1、 在解方程123123x x -+-=时，去分母正确的是（ ） A.134)1(3=+--x x B.63413=+--x xC.13413=+--x xD.6)32(2)1(3=+--x x 【答案】 D【解析】 暂无解析 例题2、 解下列方程：（1）76163x x +=-； （2）1111122x ⎛⎫--= ⎪⎝⎭（3）()()5310679x x x x --=-- （4）x 1x 3100.20.1++-=-【答案】 （1）1x =；（2）10x =；（3）335x =；（4）-3x =【解析】 去括号时，要注意考虑两个因素：一是系数，二是符号． 例题3、 解下列方程： （1）4﹣3（2﹣x ）=5x ；（2）2x 0.250.1x=0.10.030.02-+ ． 【答案】 （1）﹣1 （2）﹣186925【解析】 （1）去括号得：4﹣6+3x=5x ， 移项合并得：2x=﹣2， 解得：x=﹣1； （2）方程变形得：200x 3+2510x2-=0.1， 去分母得：400x+75﹣30x=0.6，移项合并得：370x=﹣74.4， 解得：x=﹣186925． 例题4、 仔细观察下面的解法，请回答为问题．解方程：52x 421x 3+=-﹣1 解：15x ﹣5=8x+4﹣1，15x ﹣8x=4﹣1+5， 7x=8， x=87． （1）上面的解法错误有_______处．（2）若关于x 的方程52x 421x 3+=-+a ，按上面的解法和正确的解法的得到的解分别为x 1，x 2，且x 21x 1-为非零整数，求|a|的最小值． 【答案】 （1）2（2）97【解析】 （1）上面的解法错误有2处； （2）52x 421x 3+=-+a ， 错误解法为：15x ﹣5=8x+4+a ，移项合并得：7x=9+a ， 解得：x=a 97+，即x 1=a97+； 正确解法为：去分母得：15x ﹣5=8x+4+10a ， 移项合并得：7x=9+10a ，解得：x=7a 109+，即x 2=7a109+， 根据题意得：x 2﹣1x 1=7a 109+﹣7a 9+=7a9，由7a 9为非零整数，得到|a|最小值为97．随练1、 将方程212134x x -+=-去分母，得（ ） A.4（2x ﹣1）=1﹣3（x+2） B.4（2x ﹣1）=12﹣（x+2） C.（2x ﹣1）=6﹣3（x+2） D.4（2x ﹣1）=12﹣3（x+2） 【答案】 D【解析】 去分母得：4（2x ﹣1）=12﹣3（x+2）随练2、 已知x=3是关于x 的方程x+m=2x ﹣1的解，求（m+1）2的值为__________． 【答案】 9【解析】 将x=3代入方程求出m 的值，即可求出所求式子的值． 解：将x=3代入方程得：3+m=6﹣1， 解得：m=2， 则（m+1）2=32=9 随练3、 解方程（1）4﹣x=2﹣3（2﹣x ）（2）2x 13-﹣10x 16+=2x 14+﹣1． 【答案】 （1）x=2 （2）x=16【解析】 （1）4﹣x=2﹣3（2﹣x ） 4﹣x=2﹣6+3x ，﹣x ﹣3x=2﹣6﹣4， ﹣4x=﹣8， x=2；（2）去分母得：4（2x ﹣1）﹣2（10x+1）=3（2x+1）﹣12， 8x ﹣4﹣20x ﹣2=6x+3﹣12， 8x ﹣20x ﹣6x=3﹣12+4+2， ﹣18x=﹣3， x=16． 随练4、 解方程：（1）31223x x --=+；（2）321123x x x --+=-．【答案】 （1）1118-（2）5【解析】 （1）去分母，得－12x －9＝6x ＋2 移项，得－12x －6x ＝2＋9 合并同类项，得－18x ＝11系数化为1，得1118x =-；（2）去分母，得3（x －3）＋2（2x －1）＝6（x －1）， 去括号，得3x －9＋4x －2＝6x －6， 移项，得3x ＋4x －6x ＝－6＋2＋9 合并同类项，得x ＝5．拓展1、 解方程（1）()9316x x --=（2）131125x x +--=． 【答案】 （1）12；（2）3-． 【解析】 （1）()9316x x --= 9336x x -+= 63x = 12x =． （2）131125x x +--=，()()5110231x x +-=-，551062x x +-=-，3x =-． 2、 ()212511254326x x x +-⎛⎫--=- ⎪⎝⎭．【答案】 23x =-【解析】 ()212511254326x x x +-⎛⎫--=- ⎪⎝⎭去分母（两边同乘以12）：()()2532412252x x x -⎛⎫+--=- ⎪⎝⎭，去括号：364410410x x x +-+-=-，移项：344461010x x x +-=-+-，合并同类项：32x =-，系数化为1：23x =-，∴23x =-是原方程的解．3、 解下列方程：（1）0.040.090.30.250.050.32x x x ++--=； （2）0.210.010.0310.30.04x x ---=；（3）21101211364x x x -++-=-．【答案】 （1）10921x =；（2）435x =；（3）16x =【解析】 （1）原方程等价于49325532x x x ++--=； ()()()6491032155x x x +-+=-；245430201575x x x +--=-；243015755420x x x --=--+；21109x -=-，10921x =． （2）原方程等价于2103134x x ---=．去分母，得()()42103312x x ---= 去括号，得8403912x x --+=，移项，得8312409x x -=+-，合并同类项，得543x =系数化为1，得435x =．（3）21101211364x x x -++-=-，()842026312x x x --+=+-82066312x x x --=+-，183x -=-，16x =．4、 解下列方程：（1）111246819753x ⎧⎫⎡+⎤⎛⎫+++=⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭（2）111233234324x x x x ⎧⎫⎡⎤⎛⎫----=+⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭【答案】 （1）1x =，（2）229x =-【解析】 根据一元一次方程的解题步骤即可解得．。

新赢数学 七年级数学★第五章 一元一次方程精熟掌握，考场无敌 I win ！翻转学习 有效学习 注重过程赢取中考！ 1 姓名第五章 一元一次方程1、方程含有未知数的等式叫做方程。

方程的两个条件：①含有未知数，未知数可以是一个也可以是几个，一般用x,y,z 等字母表示;②必须是等式。

2、一元一次方程只含有一个未知数，并且未知数的最高指数是1的整式方程叫做一元一次方程。

3、方程的解使方程左右两边相等的未知数的值叫做方程的解。

判断一个数是不是方程的解，可以将这个数代入方程验证，只要左、右两边方程的值相等就是该方程的解。

4、解方程求方程的解的过程。

5、等式的性质（1）等式的两边同时加上（或减去）同一个代数式，所得结果仍是等式。

（2）等式的两边同时乘以同一个数（或除以同一个不为0的数），所得结果仍是等式。

6、移项：把方程中的某一项改变符号后，从方程的一边移到另一边，这种变形叫移项。

7、解一元一次方程的一般步骤：（1）去分母；（2）去括号；（3）移项；（4）合并同类项；（5）将未知数的系数化为1 。

最终把一个一元一次方程“转化”为a x 的形式。

8、一元一次方程的应用：水箱变高了（形积变化问题：体积不变、面积不变、周长不变）；打折销售（常用公式：利润率=利润进价×100%，售价=标价×商品销售折扣=进价×（1+利润率），利润=售价—进价=进价×利润率）；“希望工程”义演（表格信息问题、多余与不足问题）；追赶小明（相遇问题、追击问题、航行问题及环形问题）。

9、用一元一次方程解决实际问题的过程：实际问题→数学问题（列一元一次方程）→解一元一次方程→数学问题的解（一元一次方程的解）→实际问题的解具体步骤：①审题：弄清题意及题中的数量关系；②设元：用字母设出未知数；③列方程：根据题意，找到等量关系，列方程；④解方程：求方程的解；⑤检验：检验所求方程的解是否符合题意；⑥作答。

第一讲 认识一元一次方程一、用合并同类项法解一元一次方程1.合并同类项：将一元一次方程中含未知数的项与常数项分别合并，使方程转化为ax ＝b (a ≠0)的形式. 要点精析：(1)要把不同的同类项分别进行合并；(2)解方程中的合并同类项和整式加减中的合并同类项一样，它们的根据都是乘法分配律，实质都是系数的合并． 例1 解下列方程：总结：(1)合并同类项的目的是将原方程转化成ax ＝b (a ≠0)的形式，依据是合并同类项的法则；(2)系数化为1的依据是等式的性质2：将方程ax ＝b (a ≠0)的两边同时除以a ，当a 为分数时，可将方程两边同时乘a 的倒数． 例2 下面解方程的结果正确的是( )A ．方程4＝3x －4x 的解为x ＝4B ．方程 x ＝ 的解为x ＝2C ．方程32＝8x 的解为x ＝D ．方程1－4＝ x 的解为x ＝－9例3 有一列数，按一定规律排列成1,－3, 9, －27, 81，－243, …，其中某三个相邻数的和是－1701， 这三个数各是多少？例4 某中学的学生自己动手整修操场，如果让八年级学生单独工作，需要6小时完成；如果让九年级学生单独工作，需要4小时完成.现在由八、九年级学生一起工作，需多少小时才能完成任务？例5 如果x ＝m 是方程 x －m ＝1的解，那么m 的值是( )A ．0B ．2C ．－2D ．－6 二、列方程解“总量＝各部分量的和”的问题1.系数化为1：方程两边同时除以未知数的系数，使一元一次方程ax ＝b (a ≠0)变形为x ＝ (a ≠0)的形式，变形的依据是等式的性质2.()51268;2x x -=-()27 2.53 1.51546 3.x x x x -+-=-⨯-⨯32131413ba122.易错警示：系数化为1时，常出现以下几种错误： (1)颠倒除数与被除数的位置； (2)忽略未知数系数的符号；(3)当未知数的系数含有字母时，不考虑系数是不是等于0的情况．例6 某校三年共购买计算机140台，去年 购买数量是前年的2倍，今年购买数量又是去年的 2倍.前年这个学校购买了多少台计算机？例7 解下列一元一次方程：(1)－x ＝3； (2)2x ＝－4； (3) x ＝－3.例8 把方程－ x ＝3的系数化为1的过程中，最恰当的叙述是( )A ．给方程两边同时乘－3B ．给方程两边同时除以－C ．给方程两边同时乘－D ．给方程两边同时除以3 三、移项比较这个方程与原方程，可以发现，这个变形相当于即把原方程中的－2改变符号后，从方程的一边移到另一边，这种变形叫移项 . 1.定义：将方程中的某些项改变符号后，从方程的一边移到另一边，这种变形叫移项．2.方法：把方程右边含有未知数的项改变符号后移到方程左边，把方程左边不含未知数的项改变符号后移到方程右边；即：“常数右边凑热闹，未知左边来报到．”用移项法解一元一次方程的一般步骤： 移项→合并同类项→系数化为1. 移项的原则： 未知项左边来报到，常数项右边凑热闹．移项的方法： 把方程中的某些项改变符号后，从方程的一边移到另一边，即移项要变号． 例9 将方程5x ＋1＝2x －3移项后，可得( ) A ．5x －2x ＝－3＋1 B ．5x －2x ＝－3－1 C ．5x ＋2x ＝－3－1 D ．5x ＋2x ＝1－3 例10解方程时，移项法则的依据是( )A ．加法交换律B ．加法结合律C ．等式的性质1D ．等式的性质212233232例2 解下列方程：(1)2x ＋6 = 1； (2) 3x ＋3 = 2x ＋7. （3）例3 已知关于x 的方程3a －x ＝ ＋3的解为2，则式子a 2－2a ＋1的值是________． 四、去括号法 去括号法则：1.如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；2.如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反． 去括号的目的是能利用移项法解方程；其实质是乘法的分配律．3.去括号必须做到“两注意”：(1)如果括号外的因数是负数时，去括号后，原括号内各项都要改变符号． (2)乘数与括号内多项式相乘时，乘数应乘以括号内每一项，不要漏乘． 4.用去括号法解一元一次方程步骤：第一步：去括号(按照去括号法则去括号)；第二步：用移项法解这个一元一次方程：移项→合并同类项→系数化为1. 例1 方程1－(2x ＋3)＝6，去括号的结果是( )A ．1＋2x －3＝6B ．1－2x －3＝6C ．1－2x ＋3＝6D ．2x －1－3＝6 例2 解方程：（1）－2(x －1) = 4. （2）4x ＋2(4x －3)＝2－3(x ＋1)．例5 解方程：2(x ＋1)－ (x －1)＝2(x －1)＋ (x ＋1)．例6 解下列方程：(1)5(x －1) = 1; (2)2－(1－x ) = －2; (3)11x ＋1 = 5(2x ＋1)； (4)4x －3(20－x ) = 3； (5)5(x ＋8)－5 = 0; (6)2(3－x ) = 9； (7)－3(x ＋3) = 24； (8)－2 (x －2) = 12. 11 3.42x x －＋2x1212五、去分母去分母的方法：方程两边同时乘所有分母的最小公倍数； 去分母的依据：等式的性质2；去分母的目的：将分数系数转化为整数系数；去分母的步骤：先找各个分母的最小公倍数,再依据等式的性质2，将方程两边同时乘这个最小公倍数． 例1 把方程3x ＋去分母，正确的是( )A ．18x ＋2(2x －1)＝18－3(x ＋1)B ．3x ＋2(2x －1)＝3－3(x ＋1)C ．18x ＋(2x －1)＝18－(x ＋1)D ．18x ＋4x －1＝18－3x ＋1例2 在解方程 时，去分母正确的是( )A ．7(1－2x )＝3(3x ＋1)－3B ．1－2x ＝(3x ＋1)－3C ．1－2x ＝(3x ＋1)－63D ．7(1－2x )＝3(3x ＋1)－63 例3 解方程：（1） （2）例4 解下列方程：课堂小结211332x x1231337x x －＋＝－111(15)(7).523x x 0.10.010.011.0.20.063x x x －－＝－34(1);23x x 11(2)1)(23);37x x （2(3);54x x11(4)(1)(1);43x x 212(5)1;34x x 11(6)(1)2(2).25x x一、合并同类项1．下列解方程的过程中，错误的是( )A ．由－4x ＋5x ＝2，得x ＝－2B ．由y ＋2y ＝2，得3y ＝2，故y ＝C ．由－2x ＋x ＝4－2，得－x ＝2，故x ＝－2D ．由0.25a －0.75a ＝0，得－0.5a ＝0，故a ＝0 2．解方程11＝x ＋6x ＋4x 的正确结果是( )A ．x ＝1B ．x ＝－1C ．x ＝2D ．x ＝－2 3．若关于x 的方程a －3ax ＝14的解是x ＝－2，则a 的值为( )A ．－14B ．－2C ．2D ．144．对于任意四个有理数a ，b ，c ，d ，定义新运算： .已知 ＝18，则x 的值为( )A ．－1B ．2C ．3D ．45．关于x 的方程3－x ＝2a 与方程x ＋3x ＝28的解相同，则a 的值为( )A ．2B ．－2C ．5D ．－5 6．解方程： (1)2x －4x ＋3x ＝5； (2) a ＋ a － a ＝－12.7．已知关于x 的方程 ＋x ＝3a －3的解为x ＝2，求(－a )2－2a ＋1的值．8．如果甲、乙、丙三村合修一条公路，计划出工84人，按3:4 : 7出工，求各村出工的人数． ①设甲、乙、丙三村分别出工3x 人、4x 人、7x 人，依题意，得3x ＋4x ＋7x ＝84；②设甲村出工x 人，依题意，得x ＋4x ＋7x ＝84； ③设乙村出工x 人，依题意，得x ＋x ＋x ＝84； ④设丙村出工x 人，依题意，得3x ＋4x ＋x ＝84. 上面所列方程中正确的有( )A ．1个B ．2个C ．3个D ．4个9．某中学的学生自己动手整修操场，如果让八年级学生单独工作，需要6 h 完成；如果让九年级学生单独工作，需要4 h 完成．现在由八、九年级学生一起工作，需多少小时才能完成任务？10．我国明代数学家程大位曾提出一个有趣的问题．有一个人赶着一群羊在前面走，另一个人牵着一只羊跟在后面，后面的人问赶羊的人说：“你这群羊有一百只吗？”赶羊的人回答：“我再得这么一群羊，再得这群羊的一半，再得这群羊的四分之一，把你牵的羊也给我，我恰好有一百只羊．”问这群羊有多少只． 1213162x二、移项1．下列变形属于移项变形的是( )A ．由 ＝3，得x －2＝12B ．由2x ＝3，得x ＝C ．由4x ＝2x －1，得4x －2x ＝－1D ．由3y －(y －2)＝3，得3y －y ＋2＝3 2．解方程3x ＋5＝8x －10的一般步骤是：(1)移项，得________________； (2)合并同类项，得____________； (3)系数化为1，得____________．3．关于x 的方程3x ＋2＝x －4b 的解是x ＝5，则b 等于( )A ．－1B ．－2C ．2D ．－34．某县由种玉米改为种优质杂粮后，今年农民人均收入比去年提高了20%，今年农民人均收入比去年的1.5倍少1 200元．问这个县去年农民人均收入多少元？若设这个县去年农民人均收入为x 元，则今年农民人均收入既可以表示为__________________，又可以表示为__________________，因此可列方程______________________________．5．(中考•荆州)为配合荆州市“我读书，我快乐”读书节活动，某书店推出一种优惠卡，每张卡售价20元，凭卡购书可享受8折优惠．小慧同学到该书店购书，她先买优惠卡再凭卡付款，结果节省了10元．若此次小慧同学不买卡直接购书，则她需付款多少元？( )A ．140元B ．150元C ．160元D ．200元 6．(中考•聊城)在如图所示的2016年6月份的月历表中，任意框出表中竖列上三个相邻的数，这三个数的和不可能是( )A ．27B ．51C ．69D ．72 7．解方程：(1)0.4x － ＝8－ x ； (2) x －3＝5x ＋ .8．如果5m ＋4与m －2互为相反数，求m 的值．9．已知|3x －6|＋(2y －8)2＝0，求2x －y 的值． 24x 321415141210．若－2x 2m ＋1y 6与 x 3m －1y 10＋4n是同类项，求m ，n 的值．11．(中考·安徽)《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八，盈三；人出七，不足四．问人数，物价各几何？译文为现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元，问共有多少人？这个物品的价格是多少？ 请解答上述问题．12．有一群鸽子和一些鸽笼，若每个鸽笼住6只鸽子，则剩余3只鸽子无鸽笼可住，若每个鸽笼住7只鸽子，则有一个鸽笼少1只鸽子．有多少只鸽子和多少个鸽笼？三、去括号1．下列解方程过程中，变形正确的是( )A ．由2x －1＝3得2x ＝3－1B ．由2x －3(x ＋4)＝5得2x －3x －4＝5C ．由－75x ＝76得x ＝D ．由2x －(x －1)＝1得2x －x ＝0 2．解方程2(x －3)－3(x －5)＝7(x －1)的步骤：(1)去括号，得____________________； (2)移项，得_______________________； (3)合并同类项，得____________； (4)系数化为1，得__________． 3．下列四组变形中，属于去括号的是( )A ．5x ＋4＝0，则5x ＝－4 B. ＝2，则x ＝6 C ．3x －(2－4x )＝5，则3x ＋4x －2＝5 D ．5x ＝2＋1，则5x ＝3 4．(中考·包头)若2(a ＋3)的值与4互为相反数，则a 的值为( )A ．1B ．C ．－5D. 5．若方程3(2x －2)＝2－3x 的解与关于x 的方程6－2k ＝2(x ＋3)的解相同，则k 的值为( )A.B ．C.D ． 7576-3x72-125989-5353-（2） （3）7．解方程： 278(x －3)－463(6－2x )－888(7x －21)＝0.8．(中考•福建)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足．问鸡兔各几何．”其大意是：“有若干只鸡和兔关在同一笼子里，它们一共有35个头，94条腿．问笼中的鸡和兔各有多少只？”试用列方程解应用题的方法求出问题的解．9．(中考·遵义)明代数学家程大位的《算法统宗》中有这样一个问题(如图)，其大意为有一群人分银子，如果每人分七两，则剩余四两：如果每人分九两，则还差八两．请问：所分的银子共有________两．(注：明代时1斤＝16两，故有“半斤八两”这个成语)．10．当m 取什么整数时，关于x 的方程 的解是正整数？四、去分母1．解方程 ，为了去分母应给方程两边同乘的最合适的数是( ) A ．6 B ．9 C ．12 D ．242．(中考·株洲)在解方程 时，方程两边同时乘6，去分母后，正确的是( )A ．2x －1＋6x ＝3(3x ＋1)B ．2(x －1)＋6x ＝3(3x ＋1)C ．2(x －1)＋x ＝3(3x ＋1)D ．(x －1)＋x ＝3(x ＋1)3．若 与 互为相反数，则x 的值为( ) A ．1B ．－1C ．D ．－24．如果方程 的解也是方程 的解，那么a 的值是( ) ()()11211.223x x x ⎡⎤--=-⎢⎥⎣⎦43126 1.345x ⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦15142323mx x ⎛⎫-=- ⎪⎝⎭3127146y y -+-=13132x x x -++=23516x -53-17236x x ++-=203a x--=5．解方程：（1） （2）（3） （4）6．在解方程3(x ＋1)－ (x －1)＝2(x －1)－ (x ＋1)时，我们可以将x ＋1，x －1各看成一个整体进行移项、合并同类项，得到 (x ＋1)＝ (x －1)，再去分母，得3(x ＋1)＝2(x －1)，进而求得x ＝－5，这种方法叫整体求解法．请用这种方法解方程：5(2x ＋3)－ (x －2)＝2(x －2)－ (2x ＋3)．7．小明在解方程 去分母时，方程右边的－1项没有乘3，因而求得的解是x ＝2，试求a 的值，并求出方程正确的解．8．已知(a ＋b )y 2－ ＋5＝0是关于y 的一元一次方程． (1)求a ，b 的值；(2)若x ＝a 是关于x 的方程 的解，求|a －b |－|b －m |的值．131.42x x x ---=-40.20.30.02.20.50.01x x x --+=()11115789.864x ⎧⎫⎡⎤-+++=⎨⎬⎢⎥⎣⎦⎩⎭1312727334121612121.156518x x x x ---+-=-+21133x x a-+=-123a y +2123626x x x mx +---+=-。

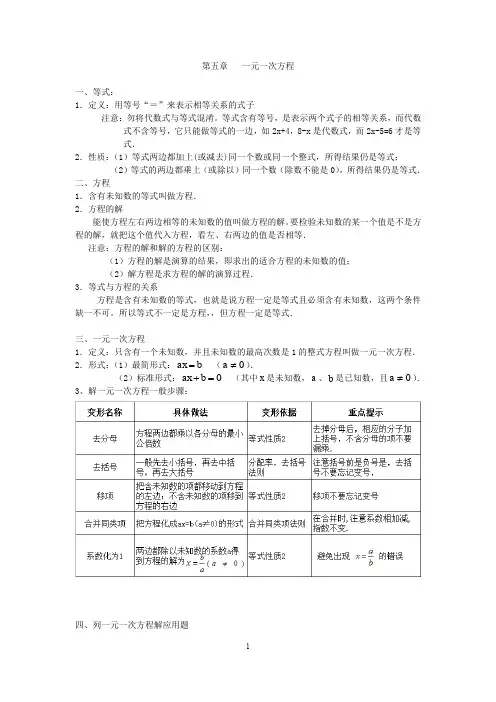
第五章 一元一次方程一、等式：1．定义：用等号“＝”来表示相等关系的式子注意：勿将代数式与等式混淆。

等式含有等号，是表示两个式子的相等关系，而代数式不含等号，它只能做等式的一边，如2x+4，8-x 是代数式，而2x-5=6才是等式．2．性质：（1）等式两边都加上(或减去)同一个数或同一个整式，所得结果仍是等式；（2）等式的两边都乘上（或除以）同一个数（除数不能是0），所得结果仍是等式．二、方程1．含有未知数的等式叫做方程．2．方程的解能使方程左右两边相等的未知数的值叫做方程的解。

要检验未知数的某一个值是不是方程的解，就把这个值代入方程，看左、右两边的值是否相等．注意：方程的解和解的方程的区别：（1）方程的解是演算的结果，即求出的适合方程的未知数的值；（2）解方程是求方程的解的演算过程．3．等式与方程的关系方程是含有未知数的等式，也就是说方程一定是等式且必须含有未知数，这两个条件缺一不可。

所以等式不一定是方程，，但方程一定是等式．三、一元一次方程1．定义：只含有一个未知数，并且未知数的最高次数是1的整式方程叫做一元一次方程．2．形式：（1）最简形式：b ax = （0≠a ）．（2）标准形式：0=+b ax （其中x 是未知数，a 、b 是已知数，且0≠a ）．3、解一元一次方程一般步骤：四、列一元一次方程解应用题1、水箱变高了——利用等积变换的思想2、打折销售商品利润= 商品售价－商品进价；利润率=商品利润÷商品进价×100%；商品售价＝标价×折扣数÷10；商品售价=商品进价×(1+利润率)。

3、“希望工程”义演工作总量＝工作时间×工作效率；工作时间＝工作总量÷工作效率；工作效率＝工作总量÷工作时间；甲的工作量＋乙的工作量＝甲乙合作的工作总量注意：工程问题常把工作总量看做“1”，解工程问题的关键是先找出单位时间内的工作效率。

1第五章一元一次方程知识归纳与题型突破（题型清单）01思维导图02知识速记一、基本概念1、等式的概念：含有等号，表示相等关系的式子2、方程的概念：含有未知数的等式3、一元一次方程的概念：（1）只含有1个未知数；（2）未知数的最高次数为1次；（3）等式两边都是整式．二、等式的性质若b a =，则c b c a +=+、c b c a -=-、bc ac =、cbc a =．特别注意：等式两边须同时乘以或除以一个不为0的数．三、解一元一次方程1、去分母（不漏乘不含分母的项，去分母应加括号）2、去括号（带着符号计算，不要漏乘）3、移项（移项要变号；未知数移到左边，常数移到右边；先后顺序不重要）4、合并同类项5、系数化为1（系数不能为0，若未知数的系数含有字母则需要讨论）四、列方程解应用题的步骤①审：审题，分析题中已知什么，求什么，明确各数量之间关系②设：设未知数（一般求什么，就设什么为x ）③找：找出能够表示应用题全部意义的一个相等关系④列：根据这个相等关系列出需要的代数式，进而列出方程⑤解：解所列出的方程，求出未知数的值⑥答：检验所求解是否符合题意，写出答案（包括单位名称）五、一元一次方程的应用（4）工程问题（①工作量=人均效率×人数×时间；②如果一件工作分几个阶段完成，那么各阶段的工作量的和=工作总量）；（5）行程问题（路程=速度×时间）；（6）等值变换问题；（7）和，差，倍，分问题；（8）分配问题；（9）比赛积分问题；（10）水流航行问题（顺水速度=静水速度+水流速度；逆水速度=静水速度-水流速度）．03题型归纳题型一判断是否是一元一次方程例题：（24-25七年级上·全国·单元测试）下列各式：①236x y -=；②2430x x --=；③()2353x x +=-；④310x+=；⑤()3425x x --．其中，一元一次方程有（）A ．1个B ．2个C ．3个D ．4个巩固训练1．（23-24七年级下·全国·期中）下列各式中，属于一元一次方程的是（）A ．6518x y -=B ．242715x x =+-C ．438x x+=D ．94x x-=2．（23-24七年级上·全国·单元测试）在方程①231325x +=，②=0，③235x y +=，④3120x+=中，一元一次方程共有（）A ．1个B ．2个C ．3个D ．4个3．（23-24七年级上·全国·单元测试）①12x x -=；②0.31x ≤；③243x x -=；④512x x =-；⑤6x =；⑥20x y +=．其中一元一次方程的个数是（）A ．2B ．3C ．4D ．5题型二根据一元一次方程的定义求参数的值例题：（24-25七年级上·黑龙江哈尔滨·阶段练习）已知1320m x --=是关于x 的一元一次方程，则m 的值是．巩固训练1．（23-24七年级上·全国·单元测试）若()1246a a x--+=-是关于x 的一元一次方程，则a =．2．（23-24七年级上·河南漯河·期中）已知关于x 的方程()||233m m x m --+=是一元一次方程，则m 的值为．3．（23-24七年级上·全国·单元测试）若关于x 的方程()21120m mx m x -+--=是一元一次方程，则m 的值为．题型三已知一元一次方程的解求参数的值例题：（23-24七年级下·全国·期中）关于x 的一元一次方程213mx x -=-有解，则m 的值为．巩固训练1．（23-24七年级上·浙江金华·期末）已知3x =是方程26ax a -=-+的解，则a =．2．（23-24七年级下·四川宜宾·期中）整式ax b +的值随着x 的取值的变化而变化，下表是当x 取不同的值时对应的整式的值：x 1-0123ax b+8-4-048则关于x 的方程8ax b +=的解是．3．（23-24七年级上·浙江·期末）若关于x 的方程30ax +=的解为2x =，则方程()130a x -+=的解为．题型四列一元一次方程例题：（23-24六年级下·全国·单元测试）设某数为x ，如果某数的2倍比它的相反数大1，那么列方程是．巩固训练1．（23-24七年级上·福建福州·期末）“x 的5倍与2的和等于x 的13与4的差”，用等式表示为2．（2024·湖南益阳·模拟预测）《孙子算经》中有一道题，原文是：今有三人共车，二车空：二人共车，九人步，问人车各几何？译文为：今有若干人乘车，每3人共乘一车，刚好每车坐满后还剩余2辆车没人坐；若每2人共乘一车，最终剩余9个人无车可乘只能步行，问共有多少人，多少辆车？设共有x 辆车，则可列方程．3．（2023·吉林长春·模拟预测）《算法统宗》是中国古代重要的数学著作，其中记载：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空，其大意为：今有若干人住店，若每间住7人，则余下7人无房可住：若每间住9人，则余下一间无人住，设店中共有x 间房，可列方程为．题型五等式的基本性质例题：（23-24七年级上·天津·期中）下列说法错误的是（）A ．若22x y -=-，则x y =B ．若25x x =，则5x =C ．若a b =，则66a b -=-D ．若2211a bc c =++，则a b =巩固训练1．（23-24七年级下·广西南宁·开学考试）下列是根据等式的性质进行变形，正确的是（）A ．若x y =，则33x y -=+B ．若a b =，则32a b =C ．若22x y=，则x y =D ．若ax ay =，则x y=2．（23-24七年级上·安徽·单元测试）下列运用等式的性质变形中正确的是（）A ．如果a b =，则a c b c +=-B ．如果23x x =，则3x =C ．如果a b =，则22a bc c =D ．如果22a b c c =，则a b =3．（22-23七年级上·山东济南·阶段练习）下列变形正确的是（）A ．4532x x -=+变形得4325x x -=-+B ．211332x x -=+变形得4633x x -=+C ．3(1)2(3)x x -=+变形得3126x x -=+D ．32x =变形得23x =4．（2024·贵州贵阳·一模）用“□”“△”“○”表示三种不同的物体，现用天平称了两次，情况如图所示．设a ，b ，c 均为正数，则能正确表示天平从左到右变化过程的等式变形为（）A ．如果a c b c +=+，那么a b =B ．如果a b =，那么a c b c +=+C ．如果22a b =，那么a b=D ．如果a b =，那么22a b=题型六解一元一次方程巩固训练题型七解一元一次方程中的错解复原问题巩固训练(2)仿照上例解方程：0.2 0.3x+题型八用一元一次方程解决实际问题例题：（2024上·辽宁大连·七年级统考期末）某车间生产一批螺钉和螺母，由一个人操作机器做需要200h完成．现计划由一部分人先做4h，然后增加5人与他们一起做6h，完成这项工作．假设这些人的工作效率相同．(1)求具体应先安排多少人工作？(2)在增加5人一起工作后，若每人每天使用机器可以生产1200个螺钉或2000个螺母，1个螺钉需要配2个螺母成为一个完整的产品，为使每天生产的螺钉和螺母刚好配套，应安排生产螺钉和螺母的工人各多少名？(3)若该车间有10台A型和11台B型机器可以生产这种产品，每台A型机器比B型机器一天多生产1个产品．已知5台A型机器一天的产品装满8箱后还剩4个，7台B型机器一天的产品装满11箱后还剩1个，且每箱装的产品数相同．某天有6台A型机器和m台B型机器同时开工，请问一天生产的产品能否恰好装满29箱．若能，请计算出m的值；若不能，请说明理由．巩固训练1．（2024上·甘肃酒泉·七年级统考期末）合肥庐阳区实验学校七（6）班为迎接学校秋季运动会计划购买30支签字笔，若干本笔记本（笔记本数量超过签字笔数量），用来奖励运动会中表现出色的运动员和志愿者，甲、乙两家文具店的标价都是签字笔8元/支、笔记本2元/本，甲店的优惠方式是签字笔打九折，笔记本打八折；乙店的优惠方式是每买5支签字笔送1本笔记本，签字笔不打折，购买的笔记本打七五折．(1)请用含x的代数式分别表示学校在甲、乙两家店购物所付的费用；(2)如果购买笔记本数量为60本，并且只在一家店购买的话，请通过计算说明，到哪家店购买更合算？(2)小亮家—年缴纳水费1180元，则小亮家这一年用水多少立方米？(3)小红家去年和今年共用水520立方米，共缴纳水费2950元，并且今年的用水量超过去年的用水量，则小红家今年和去年各用水多少立方米？第五章一元一次方程知识归纳与题型突破（题型清单）01思维导图02知识速记一、基本概念1、等式的概念：含有等号，表示相等关系的式子2、方程的概念：含有未知数的等式3、一元一次方程的概念：（1）只含有1个未知数；（2）未知数的最高次数为1次；（3）等式两边都是整式．二、等式的性质若b a =，则c b c a +=+、c b c a -=-、bc ac =、cbc a =．特别注意：等式两边须同时乘以或除以一个不为0的数．三、解一元一次方程1、去分母（不漏乘不含分母的项，去分母应加括号）2、去括号（带着符号计算，不要漏乘）3、移项（移项要变号；未知数移到左边，常数移到右边；先后顺序不重要）4、合并同类项5、系数化为1（系数不能为0，若未知数的系数含有字母则需要讨论）四、列方程解应用题的步骤①审：审题，分析题中已知什么，求什么，明确各数量之间关系②设：设未知数（一般求什么，就设什么为x ）③找：找出能够表示应用题全部意义的一个相等关系④列：根据这个相等关系列出需要的代数式，进而列出方程⑤解：解所列出的方程，求出未知数的值⑥答：检验所求解是否符合题意，写出答案（包括单位名称）五、一元一次方程的应用（4）工程问题（①工作量=人均效率×人数×时间；②如果一件工作分几个阶段完成，那么各阶段的工作量的和=工作总量）；（5）行程问题（路程=速度×时间）；（6）等值变换问题；（7）和，差，倍，分问题；（8）分配问题；（9）比赛积分问题；（10）水流航行问题（顺水速度=静水速度+水流速度；逆水速度=静水速度-水流速度）．03题型归纳题型一判断是否是一元一次方程例题：（24-25七年级上·全国·单元测试）下列各式：①236x y -=；②2430x x --=；③()2353x x +=-；④310x+=；⑤()3425x x --．其中，一元一次方程有（）A ．1个B ．2个C ．3个D ．4个【答案】A【知识点】一元一次方程的定义【分析】本题考查的是一元一次方程的定义，掌握一元一次方程的定义是解题的关键．根据一元一次方程的定义进行判定．【详解】解：①是二元一次方程，不符合题意；②是一元二次方程，不符合题意；③是一元一次方程，符合题意；④是分式方程，不符合题意；⑤是代数式，不是方程，不符合题意．故选：A ．巩固训练1．（23-24七年级下·全国·期中）下列各式中，属于一元一次方程的是（）A ．6518x y -=B ．242715x x =+-C ．438x x+=D ．94x x-=2．（23-24七年级上·全国·单元测试）在方程①231325x +=，②=0，③235x y +=，④120x+=中，一元一次方程共有（）A ．1个B ．2个C ．3个D ．4个【答案】A【知识点】一元一次方程的定义3．（23-24七年级上·全国·单元测试）①2x x -=；②0.31x ≤；③243x x -=；④512x x =-；⑤6x =；⑥20x y +=．其中一元一次方程的个数是（）A ．2B ．3C ．4D ．5题型二根据一元一次方程的定义求参数的值例题：（24-25七年级上·黑龙江哈尔滨·阶段练习）已知1320m x --=是关于x 的一元一次方程，则m 的值是．【答案】2【知识点】一元一次方程的定义【分析】本题考查了一元一次方程的概念，根据一元一次方程的定义得到11m -=，求出m 即可．【详解】解：根据题意得：11m -=，解得：2m =，故答案为：2．巩固训练1．（23-24七年级上·全国·单元测试）若()1246a a x --+=-是关于x 的一元一次方程，则a =．2．（23-24七年级上·河南漯河·期中）已知关于x 的方程()||233m m x m --+=是一元一次方程，则m 的值为．故答案为：13．（23-24七年级上·全国·单元测试）若关于x 的方程()21120m mx m x -+--=是一元一次方程，则m 的值为．【答案】1或0【知识点】一元一次方程的定义【分析】本题主要考查了一元一次方程的一般形式，只含有一个未知数，且未知数的指数是1，一次项系数不是0，这是这类题目考查的重点．根据一元一次方程的一般形式即可判定有3种情况，分别讨论①当0m ≠且10m -≠时，②当0m =且10m -≠时，③当10m -=时是否满足该方程为一元一次方程即可．【详解】解： 关于x 的方程()21120m mxm x -+--=是一元一次方程，可考虑三种情况，①当0m ≠且10m -≠时，即0m ≠且1m ≠，则211m -=，解得：1m =，此时1m ≠，故排除；②当0m =且10m -≠时，即0m =且1m ≠，∴0m =，符合条件；③当10m -=即1m =时，211m -=，符合条件；综上：m 的值为1或0，故答案为：1或0．题型三已知一元一次方程的解求参数的值例题：（23-24七年级下·全国·期中）关于x 的一元一次方程213mx x -=-有解，则m 的值为．1．（23-24七年级上·浙江金华·期末）已知3x =是方程26ax a -=-+的解，则a =．【答案】2【知识点】方程的解【分析】本题考查了方程解的定义，使方程的左右两边相等的未知数的值，叫做方程的解．将3x =代入原方程，可得出关于a 的一元一次方程，解之即可得出a 的值．【详解】解：将3x =代入原方程得326a a -=-+，解得：2a =，∴a 的值为2．故答案为：2．2．（23-24七年级下·四川宜宾·期中）整式ax b +的值随着x 的取值的变化而变化，下表是当x 取不同的值时对应的整式的值：x 1-0123ax b+8-4-048则关于x 的方程8ax b +=的解是．【答案】3x =【知识点】方程的解【分析】此题考查了方程的解，根据表格中的数据求解即可．【详解】根据题意可得，当3x =时，8ax b +=∴关于x 的方程8ax b +=的解是3x =．故答案为：3x =．3．（23-24七年级上·浙江·期末）若关于x 的方程30ax +=的解为2x =，则方程()130a x -+=的解为．题型四列一元一次方程例题：（23-24六年级下·全国·单元测试）设某数为x ，如果某数的2倍比它的相反数大1，那么列方程是．【答案】21x x =-+【知识点】列方程【分析】本题主要考查了一元一次方程的应用，数x 的2倍为2x ，相反数为x -，据此根据题意列出方程即可．【详解】解：由题意得，21x x =-+，故答案为：21x x =-+．巩固训练1．（23-24七年级上·福建福州·期末）“x 的5倍与2的和等于x 的13与4的差”，用等式表示为2．（2024·湖南益阳·模拟预测）《孙子算经》中有一道题，原文是：今有三人共车，二车空：二人共车，九人步，问人车各几何？译文为：今有若干人乘车，每3人共乘一车，刚好每车坐满后还剩余2辆车没人坐；若每2人共乘一车，最终剩余9个人无车可乘只能步行，问共有多少人，多少辆车？设共有x 辆车，则可列方程．【答案】()3229x x -=+【知识点】古代问题(一元一次方程的应用)【分析】本题考查了由实际问题抽象出一元一次方程．根据人数不变，即可得出关于x 的一元一次方程，此题得解．【详解】解：依题意，得：()3229x x -=+．故答案为：()3229x x -=+．3．（2023·吉林长春·模拟预测）《算法统宗》是中国古代重要的数学著作，其中记载：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空，其大意为：今有若干人住店，若每间住7人，则余下7人无房可住：若每间住9人，则余下一间无人住，设店中共有x 间房，可列方程为．【答案】()7791x x +=-【知识点】古代问题(一元一次方程的应用)【分析】本题考查一元一次方程的应用，理清题中的等量关系是解题的关键．由等量关系“一房七客多七客，一房九客一房空”，即可列出一元一次方程即可．【详解】解： 每间住7人，则余下7人无房可住：若每间住9人，则余下一间无人住，∴客人可表示为()77x +个，也可表示为()91x -个，()7791x x ∴+=-，故答案为：()7791x x +=-．题型五等式的基本性质例题：（23-24七年级上·天津·期中）下列说法错误的是（）A ．若22x y -=-，则x y =B ．若25x x =，则5x =C ．若a b =，则66a b -=-D ．若2211a bc c =++，则a b =【答案】B1．（23-24七年级下·广西南宁·开学考试）下列是根据等式的性质进行变形，正确的是（）A ．若x y =，则33x y -=+B ．若a b =，则32a b =C ．若22x y=，则x y =D ．若ax ay =，则x y=2．（23-24七年级上·安徽·单元测试）下列运用等式的性质变形中正确的是（）A ．如果a b =，则a c b c+=-B ．如果23x x =，则3x =C ．如果a b =，则22a b c c =D ．如果22a b c c =，则a b =3．（22-23七年级上·山东济南·阶段练习）下列变形正确的是（）A ．4532x x -=+变形得4325x x -=-+B ．211332x x -=+变形得4633x x -=+C ．3(1)2(3)x x -=+变形得3126x x -=+D ．32x =变形得23x =4．（2024·贵州贵阳·一模）用“□”“△”“○”表示三种不同的物体，现用天平称了两次，情况如图所示．设a ，b ，c 均为正数，则能正确表示天平从左到右变化过程的等式变形为（）A ．如果a c b c +=+，那么a b=B ．如果a b =，那么a c b c +=+C ．如果22a b =，那么a b=D ．如果a b =，那么22a b=【答案】A【知识点】等式的性质【分析】本题考查等式的性质，根据天平两端相等即可求得答案．【详解】解：由图形可得如果a c b c +=+，那么a b =，故选：A ．题型六解一元一次方程例题1：解方程：(1)25433x x -=-；(2)576132x x -=-+.【答案】(1)35x =(2)415x =【分析】()1方程移项合并，把x 系数化为1，即可求解；()2方程移项合并，把x 系数化为1，即可求解．【详解】（1）移项，得24353x x -+=-，合并同类项，得1023x -=-，系数化为1，得35x =．（2）移项，得756123x x -+=-，合并同类项，得5223x -=-，系数化为1，得415x =．【点睛】此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．例题2：解方程：(1)5(1)2(31)41---=-x x x ；(2)23(1)12(10.5)-+=-+x x ．题型七解一元一次方程中的错解复原问题巩固训练(2)仿照上例解方程：0.2 0.3x+【答案】(1)③④①②(2)3x=-题型八用一元一次方程解决实际问题1．（2024上·甘肃酒泉·七年级统考期末）合肥庐阳区实验学校七（6）班为迎接学校秋季运动会计划购买30支签字笔，若干本笔记本（笔记本数量超过签字笔数量），用来奖励运动会中表现出色的运动员和志愿者，甲、乙两家文具店的标价都是签字笔8元/支、笔记本2元/本，甲店的优惠方式是签字笔打九折，笔记本打八折；乙店的优惠方式是每买5支签字笔送1本笔记本，签字笔不打折，购买的笔记本打七五折．答：小红家去年和今年用水分别为245立方米、275立方米．。

初一上册数学第五章知识点参考：一元一次方程朱熹曾说过：不勤于始，将毁与中。

换句话确实是：勤于始、精于始，才能成于始。

初中在小孩求学的生涯是一个重要的承上启下时期。

详细内容请看七年级上册数学第五章知识点。

1.等式：用=号连接而成的式子叫等式.2.等式的性质：等式性质1：等式两边都加上(或减去)同一个数或同一个整式，所得结果仍是等式;等式性质2：等式两边都乘以(或除以)同一个不为零的数，所得结果仍是等式.3.方程：含未知数的等式，叫方程.4.方程的解：使等式左右两边相等的未知数的值叫方程的解;注意：方程的解就能代入!5.移项：改变符号后，把方程的项从一边移到另一边叫移项.移项的依据是等式性质1.6.一元一次方程：只含有一个未知数，同时未知数的次数是1，同时含未知数项的系数不是零的整式方程是一元一次方程.7.一元一次方程的标准形式：ax+b=0(x是未知数，a、b是已知数，且a 0).8.一元一次方程解法的一样步骤：化简方程----------分数差不多性质去分母----------同乘(不漏乘)最简公分母去括号----------注意符号变化移项----------变号(留下靠前)合并同类项--------合并后符号系数化为1---------除前面10.列一元一次方程解应用题：(1)读题分析法:多用于和，差，倍，分问题认真读题，找出表示相等关系的关键字，例如：大，小，多，少，是，共，合，为，完成，增加，减少，配套-----，利用这些关键字列出文字等式，同时据题意设出未知数，最后利用题目中的量与量的关系填入代数式，得到方程.我国古代的读书人,从上学之日起,就日诵不辍,一样在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。

什么缘故在现代化教学的今天,我们念了十几年书的高中毕业生甚至大学生,竟提起作文就头疼,写不出像样的文章呢?吕叔湘先生早在19 78年就尖锐地提出:“中小学语文教学成效差,中学语文毕业生语文水平低,……十几年上课总时数是9160课时,语文是2749课时,恰好是30%,十年的时刻,二千七百多课时,用来学本国语文,却是大多数只是关,岂非咄咄怪事!”寻根究底,其要紧缘故确实是腹中无物。

第五章一元一次方程1 认识一元一次方程第1课时知识与技能目标:在对实际问题情境的分析过程中感受方程模型的意义.过程与方法目标:1.借助类比、归纳的方式概括一元一次方程的概念,并在概括的过程中体验归纳方法,体会发现概念的喜悦.2.使学生在分析实际问题情境的活动中体会数学与现实生活的密切联系. 情感态度目标:观察、讨论等活动,养成独立思考的习惯与合作交流的意识.重点难点重点:学生在实际问题中分析、找到等量关系,准确列出方程,并总结所列方程的共同特点,归纳出一元一次方程的概念.难点:由特殊的几个方程的共同特点归纳一元一次方程的概念.教学过程一、创设情境内容1:请一位同学阅读章前图中关于“丟番图”的故事.内容2:回答以下3个问题:1.你能找到题中的等量关系并列出方程吗?2.你对方程有什么认识?3.列方程解决实际问题的关键是什么?解:设丟番图的年龄为x岁,则:x+x+x+5+x+4=x.内容3:阅读学习目标:活中等量关系的有效模型.掌握等式的基本性质,能解一元一次方程.能用一元一次方程解决一些简单的实际问题.在探索一元一次方程解法的过程中,感受转化思想.二、探究归纳内容1:让学生阅读本节教材随堂练习之前的内容.结合课本多以问题串的形式呈现内容的特点,粗读并完成书上的填空题.内容2:与学生共同分析完成教材呈现的五个情境.(1)如果设小彬的年龄为x 岁,那么“乘2再减5”就是2x-5,所以得到方程:2x-5=21. (2)小颖种了一株树苗,开始时树苗高为40 cm,栽种后每周树苗长高约5 cm,大约几周后树苗长高到1 m?如果设x 周后树苗长高到1 m,那么可以得到方程:40+5x=100.(3)甲、乙两地相距22 km,张叔叔从甲地出发到乙地,每时比原计划多行走1 km,因此提前12 min 到达乙地,张叔叔原计划每时行走多少千米?设张叔叔原计划每时行走x km,可以得到方程:22x -22x+1=.(4)根据第六次全国人口普查统计数据,截至2023年11月1日0时,全国每10万人中具有大学文化程度的人数为8 930人,与2000年第五次全国人口普查相比增长了147.30%.2000年第五次全国人口普查时每10万人中约有多少人具有大学文化程度?如果设2000年第五次全国人口普查时每10万人中约有x 人具有大学文化程度,那么可以得到方程:(1+147.30%)x=8__930.(5)某长方形操场的面积是5 850 m 2,长和宽之差为25 m,这个操场的长与宽分别是多少米?如果设这个操场的宽为x m,那么长为(x+25)m.可以得到方程x(x+25)=5__850.归纳一元一次方程的定义,了解一元一次方程的解的含义.(1)由上面的问题你得到了哪些方程?其中哪些是你熟悉的方程?与同伴进行交流.共得到五个方程.其中(1)、(2)、(4)都只有一个未知数,在小学学习时常见.(2)方程2x-5=21,40+5x=100,(1+147.30%)x=8 930有什么共同点?它们都只含有一个未知数,且未知数的指数都是1.内容4:判断下列各式是不是一元一次方程,是的打“√”,不是的打“×”.(1)-2+5=3. ( )(2)3x-1=0. ( )(3)y=3. ()(4)x+y=2. ( )(5)2x-5x+1=0. ( )(6)xy-1=0. ( )内容5:方程的解的含义:使方程左、右两边的值相等的未知数的值,叫做方程的解 2. x=2是下列方程的解吗?(1)3x+(10-x)=20.(2)2x2+6=7x.三、交流反思1.本节给出了四个知识点:等式(回顾巩固),方程(给出描述性定义),一元一次方程及一元一次的解(根).2.感觉在解决实际问题时,列方程相比小学算术法,给出的思维方式与途径更具普遍性.3.列方程的核心:实际问题“数学化”,关键是找到等量关系.四、检测反馈内容1:完成教材上的随堂练习1.根据题意,列出方程:(1)在一卷公元前1600年左右遗留下来的古埃及纸草书中,记载着一些数学问题.其中一个问题翻译过来是:“啊哈,它的全部,它的,其和等于19.”你能求出问题中的“它”吗?解:设“它”为x,则:x+x=19.(2)甲、乙两队开展足球对抗赛,规定每队胜一场得3分,平一场得1分,负一场得0分.甲队与乙队一共比赛了10场,甲队保持了不败记录,一共得了22分.甲队胜了多少场?平了多少场?解:设甲队胜了x场,则甲队平了(10-x)场.则:3x+(10-x)=22.内容2:达标练习:1.如果5x m-2=8是一元一次方程,那么m=________.2.下列各式中,是方程的是________(只填序号).①2x=1②5-4=1 ③7m-n+1 ④3(x+y)=43.下列各式中,是一元一次方程的是________(只填序号).①x-3y=1 ②x2+2x+3=0 ③x=7④x2-y=04.a的20%加上100等于x.则可列出方程:________.5.某数的一半减去该数的等于6,若设此数为x,则可列出方程________.6.一桶油连桶的重量为8千克,油用去一半后,连桶重量为4.5千克,桶内有油多少千克?设桶内原有油x千克,则可列出方程________________________.7.李颖的爸爸今年44岁,是小颖年龄的3倍还大2岁,设李颖今年x岁,则可列出方程:________________________.8.3年前,父亲的年龄是儿子年龄的4倍,3年后父亲的年龄是儿子年龄的3倍,求父子今年各是多少岁?设3年前儿子年龄为x岁,则可列出方程:________________________.五、布置作业教学反思1.此阶段的学生有比较强烈的自我发展意识，教师只有进行得当合理的诠释方可得到学生的认可.授课时要设法让学生体会运用方程建模的优越性,使众多实际问题“数学化”的重要数学模型成为学生学习后续知识的自觉选择.2.让学生在简单的背景问题中,一点一滴地体会分析已知量、未知量之间的数量关系,对列方程的帮助,真正做到分解难点、降低难度、突破难点的目的.3.学生的读书仍然停留在表面上的阅读,还须继续坚持和及时引导.从学生的年龄特点和认知特点来看，初中阶段是智力和心理发展的关键阶段。

初一上册数学知识点之一元一次方程1.通过处理实际问题，让学生体验从算术方法到代数方法是一种进步;2.初步学会如何查找问题中的相等关系，列出方程，了解方程的概念;3.培养学生猎取信息，分析问题，处理问题的能力。

二、重点从实际问题中查找相等关系;建立列方程解决实际问题的思想方法，学会合并同类项，会解ax+bx= c类型的一元一次方程。

三、难点从实际问题中查找相等关系;分析实际问题中的差不多量和未知量，找出相等关系，列出方程，使学生逐步建立列方程解决实际问题的思想方法。

四、知识框架五、知识点、概念总结1.一元一次方程：只含有一个未知数，同时未知数的次数是1，同时含未知数项的系数不是零的整式方程是一元一次方程。

2.一元一次方程的标准形式：ax+b=0(x是未知数，a、b是已知数，且a 0)。

3.条件：一元一次方程必须同时满足4个条件：(1)它是等式;(2)分母中不含有未知数;(3)未知数最高次项为1;(4)含未知数的项的系数不为0.4.等式的性质：等式的性质一：等式两边同时加一个数或减去同一个数或同一个整式，等式仍旧成立。

等式的性质二：等式两边同时扩大或缩小相同的倍数(0除外)，等式仍旧成立。

等式的性质三：等式两边同时乘方(或开方)，等式仍旧成立。

解方程差不多上依据等式的这三个性质等式的性质一：等式两边同时加一个数或减同一个数，等式仍旧成立。

5.合并同类项(1)依据：乘法分配律(2)把未知数相同且其次数也相同的相合并成一项;常数运算后合并成一项(3)合并时次数不变，只是系数相加减。

6.移项(1)含有未知数的项变号后都移到方程左边，把不含未知数的项移到右边。

(2)依据：等式的性质(3)把方程一边某项移到另一边时，一定要变号。

7.一元一次方程解法的一样步骤：使方程左右两边相等的未知数的值叫做方程的解。

一样解法：(1)去分母：在方程两边都乘以各分母的最小公倍数;(2)去括号：先去小括号，再去中括号，最后去大括号;(记住如括号外有减号的话一定要变号)(3)移项：把含有未知数的项都移到方程的一边，其他项都移到方程的另一边;移项要变号(4)合并同类项：把方程化成ax=b(a0)的形式;(5)系数化成1：在方程两边都除以未知数的系数a，得到方程的解x=b /a.8.同解方程假如两个方程的解相同，那么这两个方程叫做同解方程。

精选初一上册数学第五单元知识点：一元一
次方程性质
等式的性质一：等式两边同时加一个数或减去同一个数或同一个整式，等式仍然成立。

等式的性质二：等式两边同时扩大或缩小相同的倍数(0除外)，等式仍然成立。

等式的性质三：等式两边同时乘方(或开方)，等式仍然成立。

解方程都是依据等式的这三个性质等式的性质一：等式两边同时加一个数或减同一个数，等式仍然成立
小编为大家精心推荐的初一上册数学第五单元知识点还满意吗?相信大家都会仔细阅读，加油哦!
2015最新初一上册数学第四章知识点总结：几何图形分类
列方程解应用题的方法知识点总结：七年级上册数学（精选）。