气体的流速计算伯努利方程 (2)

浅析气体动力学原理——伯努利方程例解气体动力学作为一门研究物体运动的科学，是研究物理学的重要组成部分。

在气体动力学中有许多定律，伯努利方程是其中最基础也最重要的定律之一。

本文将对伯努利方程的原理及其在例题中的解法进行浅析。

一、伯努利方程原理伯努利方程（Bernoulli equation），又称为贝纳方程，是气体动力学的基本方程，由拉丁物理学家Daniel Bernoulli于1738年发现，他发现在一个恒定的系统中，当沿着系统上流动的流体（一般情况下是气体）改变速度和高度，其内能总量是不变的，这一定律叫做伯努利定律。

伯努利方程可以概括为：P +γV +gh = k（γ是气体的比容系数，V是气体流速，h是气体高度，P是气体压强，g是重力加速度，k是常数）式中，其中P +γV体现了气体的动能，gh表示气体的位能，两者之和即为气体的总能量，而k则表示该总能量在系统中是恒定的。

二、伯努利方程在例题中的解法1.设有一个气体在一定的容器中，容器的高度是 h1，而此时气体的压强为P1，流速为V1，则由伯努利方程可知：P1 +γV1 +gh1 = k2.气体流出容器时，留下来的气体高度为h2，压强为P2，流速为V2，由伯努利方程可知：P2 +γV2 +gh2 = k3.上面两公式代入可得：P1 +γV1 +gh1 = P2 +γV2 +gh24.两边中的P1,V1,h1分别消去可得：P2 =γ(V2 - V1) +(h2 - h1)5.此可以看出，当流体从一个容器流出到另一容器时，流体的压强受其高度的变化以及流体的流速变化的影响。

三、结论伯努利方程是气体动力学中重要的基础定律，它描述了在一定系统中流体运动时总能量保持不变的定律。

本文通过一个具体的例子，讲解了伯努利方程的原理及其在例题中的解法，从而使我们对伯努利方程有了更深的理解。

不可压缩气‎流的伯努利‎方程公式及意义‎由于气流的‎密度同外部‎空气的密度‎是相同的数‎量级，在用相对压‎强进行计算‎时，需要考虑外‎部大气压在‎不同高度的‎差值。

下面为气流‎伯努利方程‎：气流的密度‎为ρ，外部空气的‎密度为ρa‎，p1、p2为1-1、2-1断面上的‎静压，ρυ1^2/2、ρυ2^2/2是动压，（ρa-ρ）g是单位体‎积气体所受‎的有效浮力‎，（z2-z1）是气体沿浮‎力方向升高‎的距离，（ρa-ρ）g（z2-z1）是1-1断面相对‎于2-2断面单位‎体积气体的‎位能（称为位压），pw是压强‎损失。

当气流的密‎度与外界空‎气的密度相‎同时或两计‎算点的高度‎相同时，上式可以简‎化为：其中静压和‎动压之和称‎为总压。

当气流的密‎度远大于外‎界空气的密‎度时，此时相当于‎液体总流前‎一式中的ρ‎a可忽略不‎计，认为各点的‎当地大气压‎相同，可以简化为‎：注意事项（1）动能修正系‎数动能修正系‎数α为实际‎动能与按平‎均速度计算‎的动能的比‎值，α值反映了‎断面速度分‎布的不均匀‎程度。

由于气体的‎动力黏度值‎较小，过流断面速‎度梯度小，实际的气流‎运动的速度‎分布比较均‎匀，接近于断面‎平均流速。

所以，气体运动中‎的动能修正‎系数常常取‎1.0。

（2）气流能量方‎程应采用压‎强量纲能量方程用‎于液体时，因液体中水‎头概念很直‎观具体，采用长度量‎纲很方便。

但是气体流‎动则不同，由于气体重‎度γ很小，压强一般比‎较大，水头概念不‎明确。

所以一般采‎用压强量纲‎。

（3）气流能量方‎程应采用绝‎对压强其原因是：方程中两个‎过流断面之‎间的高差比‎较大时，由于不同高‎度大气压强‎不同，而导致两断‎面相对压强‎的起算基准‎不同。

因此，将总流能量‎方程的两端‎，直接代入该‎断面处得相‎对压强值进‎行计算，必定会产生‎误差。

有能量输入‎或输出的伯‎努利方程总流伯努利‎方程是在两‎过流断面间‎除水头损失‎之外，再无能量输‎入或输出的‎条件下导出‎的。

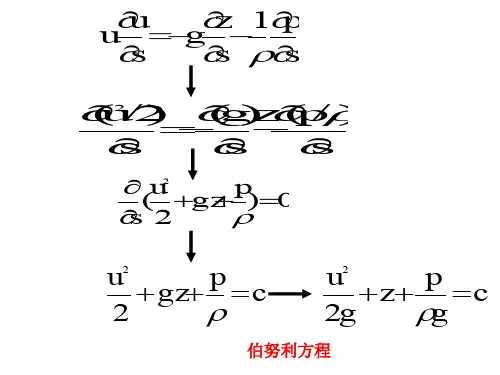
压力与流速的计算公式压力和流速是流体力学中常用的两个物理量，它们的计算公式主要依赖于流体的类型以及流体在管道、管道中的速度和流量等因素。

下面将分别介绍压力和流速的计算公式。

1.压力的计算公式：压力是指单位面积上的力，计算压力时需要考虑垂直于所选面积的力的大小。

压力可以用下述公式计算：P=F/A其中，P表示压力，F表示作用在面积上的力，A表示所选面积。

在流体力学中，压力计算的常见公式有：(1) 托利密度定律（Torr或mmHg）：P=h*ρ*g其中，P表示压力，h表示液体的柱状高度，ρ表示液体的密度，g 表示重力加速度。

注：托利密度定律适用于非粘稠流体（如水）的静态压力计算。

(2)理想气体状态方程：P=n*R*T/V其中，P表示压力，n表示气体的摩尔数，R表示气体常数，T表示气体的温度（单位为开尔文），V表示气体的体积。

注：理想气体状态方程只适用于理想气体（假设气体分子之间没有相互作用）。

(3)伯努利方程：P1+1/2*ρ*v1^2+ρ*g*h1=P2+1/2*ρ*v2^2+ρ*g*h2其中，P1和P2表示两个位置的压力，ρ表示流体密度，v1和v2表示两个位置的流速，g表示重力加速度，h1和h2表示两个位置的高度差。

注：伯努利方程适用于光滑无粘扰的流体。

2.流速的计算公式：流速是指单位时间内通过一些截面的流体体积，常用的流速计算公式有：(1)流量公式：Q=A*v其中，Q表示流量，A表示截面积，v表示流速。

(2)泊肃叶定理：A1*v1=A2*v2其中，A1和A2表示两个截面的面积，v1和v2表示在两个截面上的流速。

(3)管道柱塞流速公式：v=(2*g*h)^0.5其中，v表示流速，g表示重力加速度，h表示所测得的压头。

(4)流动能量方程：(P1/ρ)+(v1^2/2g)+h1=(P2/ρ)+(v2^2/2g)+h2其中，P1和P2表示两个截面的压力，ρ表示密度，v1和v2表示两个截面的流速，h1和h2表示两个截面的高度。

1、流速计算：按照伯努利方程，假设条件为水平管，管口为大气压。

则p1+ρ1gz1+(1/2)*ρ1v1^2=p2+ρ2gz2+(1/2)*ρ2v2^2由于ρ1gz1=ρ2gz2；v1=0；p2=0.1MPa；ρ2为水的密度=1000kg/m3；p1=1.1MPa(管道内的绝对压力）；公式化简为：p1=p2+(1/2)*ρ2v2^2按照已知条件计算得出v2=44.72m/s这是管道敞口端的计算流速，实际中不会有这么高，因为管道敞口端压力不一定是大气压。

2、流量计算：Q=ρ.s.v2=1000*3.14/4*0.2*0.2*44.72=1404 kg/s每小时的出水量=1404*3600/1000=5054（吨）这个计算值明显偏大，但是计算结果是这样，我无奈。

根据我实际中见到的自来水管道的水量估算，压力为4公斤，管径为DN40，每小时最大的流量大概16吨。

按照这个比例折下来你的管子每小时流量大概为1000吨。

DN15、DN25、DN50管径的截面积分别为：DN15：15²*3.14/4=176.625平方毫米，合0.0177平方分米。

DN25：25²*3.14/4=490.625平方毫米，合0.0491平方分米。

DN50：50²*3.14/4=1962.5平方毫米，合0.1963平方分米。

设管道流速为V=4米/秒，即V=40分米/秒，且1升=1立方分米，则管道的流量分别为（截面积乘以流速）：DN15管道：流量Q=0.0177*40=0.708升/秒，合2.55立方米/小时。

DN25管道：流量Q=0.0491*40=1.964升/秒，合7.07立方米/小时。

DN50管道：流量Q=0.1963*40=7.852升/秒，合28.27立方米/小时。

注：必须给定流速才能计算流量，上述是按照4米/秒计算的。

任何气体流量的计算都可以用密度乘速度乘面积来计算，你给的条件中面积已经知道了，密度可以通过压力和温度来计算(用理想气体公式或者查表)，速度虽然计算不出来，但是可以用两个公式解方程得到。

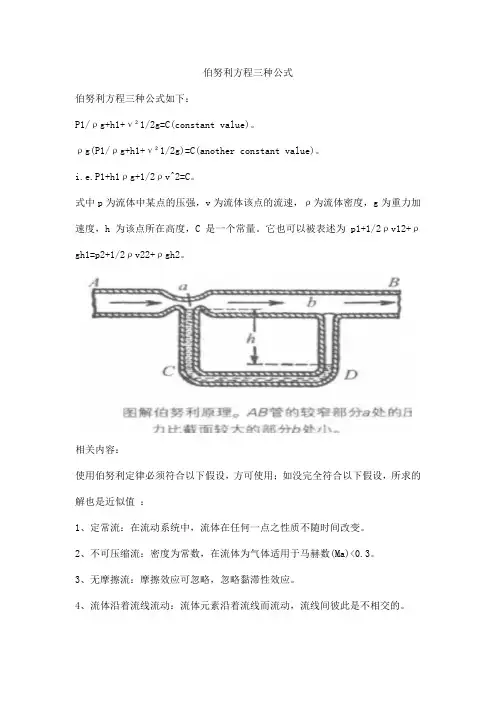
伯努利方程三种公式
伯努利方程三种公式如下：
P1/ρg+h1+ν²1/2g=C(constant value)。

ρg(P1/ρg+h1+ν²1/2g)=C(another constant value)。

i.e.P1+h1ρg+1/2ρv^2=C。

式中p为流体中某点的压强，v为流体该点的流速，ρ为流体密度，g为重力加速度，h为该点所在高度，C是一个常量。

它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。

相关内容：
使用伯努利定律必须符合以下假设，方可使用；如没完全符合以下假设，所求的解也是近似值：
1、定常流：在流动系统中，流体在任何一点之性质不随时间改变。

2、不可压缩流：密度为常数，在流体为气体适用于马赫数(Ma)<0.3。

3、无摩擦流：摩擦效应可忽略，忽略黏滞性效应。

4、流体沿着流线流动：流体元素沿着流线而流动，流线间彼此是不相交的。

气体流速与压力的计算公式咱们在生活中啊，经常会碰到跟气体流速和压力有关的事儿。

比如说，吹气球的时候，你使劲吹气，气球里的气体流速变快，压力也跟着变化。

这气体流速与压力之间，可是有着神秘的计算公式呢！咱们先来说说伯努利方程，这可是理解气体流速和压力关系的关键。

它就像是一把神奇的钥匙，能打开气体世界的秘密大门。

伯努利方程是这样的：p + 1/2ρv² + ρgh = 常量。

这里的“p”代表压力，“ρ”是气体的密度，“v”是气体的流速，“h”是高度，“g”是重力加速度。

就拿咱们常见的吹风机来说吧。

吹风机的口子越小，风出来的速度就越快。

这时候，根据伯努利方程，口子那里的压力就会变小。

我记得有一次，我在家用吹风机吹头发，不小心把风口对准了一块小纸片，结果那小纸片一下子就被吸进了风口里。

当时我就特别好奇，为啥纸片会被吸进去呢？后来一琢磨，这不就是因为气体流速快了，压力变小，外面的大气压就把纸片给推进去了嘛！再比如说，飞机能飞起来，也跟这个原理有关。

飞机的机翼上面是弧形的，下面是平的。

当空气流过机翼时，上面的气体流速快，压力小；下面的流速慢，压力大。

这样就产生了一个向上的升力，飞机就能飞起来啦。

还有在工厂的通风系统里，也是利用这个原理来控制气流的。

通过调整管道的粗细和形状，改变气体的流速和压力，让空气能够有效地流通。

在汽车设计中，也得考虑气体流速和压力的关系。

汽车的外形设计可不是随便搞的，得让气流能够顺畅地流过车身，减少阻力，这样不仅能提高车速，还能节省燃油呢。

咱们平时吹泡泡的时候也能感受到。

你轻轻地吹，泡泡慢悠悠地变大，这时候气体流速慢，压力相对稳定。

要是你猛地一吹，泡泡可能一下子就破了，因为气体流速太快，压力变化太大。

总之啊，气体流速与压力的计算公式在咱们生活中到处都能派上用场。

了解了它，就能更好地理解身边的很多现象，是不是还挺有趣的？所以说，别小看这个看似复杂的公式，它可是藏在我们日常生活的方方面面呢。

伯努利方程的应用伯努利方程对于流动体系除了掌握体系的对于流动体系，除了掌握体系的物料衡算关系以外，还必须找出体系各种形式能量之间的转换关系系各种形式能量之间的转换关系。

伯努利(Bernoulli)方程：描述了流体流动过程中各种形式能量之间的转换关系，是流体在定常流动情。

是热力学第一Daniel Bernoulli ，1700-1782况下的能量衡算式是热力学第定律对流体流动过程的具体描述。

流动系统的能量流动系统的能量：流动系统的能量流动系统的能量：(3) 动能：流体以一定的速度运动时便具有一定的动能，大时所需要的功小等于流体从静止加速到流速v时所需要的功。

(4) 静压能：流体进入划定体积时需要对抗压力所做的功。

流体进入划定体积时需要对抗压力所做的功若质量为m的流体体积为，某截面处的静压强为p，截面面积为A，则将质量为m的流体压入划定体积的功为：则将质量为的流体压入划定体积的功为质量为能量还可以通过其他外界条件与流动系统进行交换，包括：：流体通过换热器吸热或放热Q e吸热时为正，放热时为负。

：泵等流体输送机械向系统做功W em 的流体交换热量=m Q e流体接受外功为正流体对外作功为负作功为负的流体所接受的功= mW e以截面两边同除以m单位质量流体稳定流动过程的总能量衡算式，流动系统的力学第一定律表达式系统内能变化系统内能变化：是单位质量流体从截面1-1到截面是单位质量流体从截面1-1到截面2-2流体通过环境直接获得的热量，Q e(1)流体通过环境直接获得的热量流体流动时需克服阻力做功，因而消耗机械能转化为热量，若流体等温流动，这部分热量则散失到系统外部。

设单位流体因克服阻力而损失的，则则不可压缩流体ρ=const=0无外加功W e=0理想流体，Σhf伯努力方程努力方程的有关伯努力方程的讨论(1)伯努力方程的适用条件：不可压缩的理想流体做定常流动而无外功输入的情况，选取截面符合缓变流条件。

单位质量流体在任一截面上所具有的势能、动能和静压能之和是一常数。

伯努利方程计算流速伯努利方程是流体力学中的重要定律，它描述了在稳态流动中，流体在不同位置上的速度、压力和高度之间的关系。

通过应用伯努利方程，我们可以计算出流体的流速。

本文将介绍伯努利方程的基本原理，并给出一些应用实例。

伯努利方程的基本原理是基于能量守恒定律。

在没有外力作用的情况下，流体的总能量在流动过程中保持不变。

伯努利方程表示了流体在不同位置上的总能量相等。

伯努利方程的数学表达式如下：P + 1/2ρv^2 + ρgh = constant其中，P表示压力，ρ表示流体的密度，v表示流体的速度，g表示重力加速度，h表示流体元素所在位置的高度。

根据伯努利方程，我们可以计算流体的流速。

以水流为例，我们可以通过测量流体的压力和高度差来计算流速。

假设我们有一个水箱，水箱上方有一个小孔，水从小孔中流出。

我们可以测量水箱的高度和小孔处的压力，根据伯努利方程计算出水流的速度。

我们测量水箱的高度差，记作Δh。

然后，我们测量小孔处的压力，记作P。

假设水的密度为ρ，重力加速度为g。

根据伯努利方程，我们可以得到以下等式：P + 1/2ρv^2 + ρgh = constant由于小孔处的速度非常小，我们可以忽略1/2ρv^2这一项。

此外，我们将参考点设为水箱底部，即Δh为小孔处的高度差。

根据这些假设，我们可以简化伯努利方程为：P + ρgh = constant将P和ρgh的值代入上述方程，我们可以解出水流的速度v。

除了上述实例，伯努利方程还可以应用于其他许多情况。

例如，在空气动力学中，伯努利方程可以用于计算飞机在不同位置上的空速。

在涡流流量测量中，伯努利方程可以用于计算流体的流速。

此外，在水力工程中，伯努利方程可以用于计算水流的速度和压力。

伯努利方程是流体力学中的重要定律，可以用于计算流体的流速。

通过测量流体的压力和高度差，并应用伯努利方程，我们可以准确地计算出流体的速度。

除了上述实例，伯努利方程还可以应用于各种不同的情况中。

伯努利方程（Bernoulli equation）伯努利方程（Bernoulli equation）理想正压流体在有势彻体力作用下作定常运动时，运动方程（即欧拉方程）沿流线积分而得到的表达运动流体机械能守恒的方程。

因著名的瑞士科学家D.伯努利于1738年提出而得名。

对于重力场中的不可压缩均质流体，方程为p+ρgz+(1/2)*ρv^2=C式中p、ρ、v分别为流体的压强、密度和速度；z 为铅垂高度；g为重力加速度。

上式各项分别表示单位体积流体的压力能 p、重力势能ρg z和动能(1/2)*ρv ^2，在沿流线运动过程中，总和保持不变，即总能量守恒。

但各流线之间总能量（即上式中的常量值）可能不同。

对于气体，可忽略重力，方程简化为p+(1/2)*ρv ^2＝常量(p0)，各项分别称为静压、动压和总压。

显然，流动中速度增大，压强就减小；速度减小，压强就增大；速度降为零，压强就达到最大(理论上应等于总压)。

飞机机翼产生举力，就在于下翼面速度低而压强大，上翼面速度高而压强小，因而合力向上。

据此方程，测量流体的总压、静压即可求得速度，成为皮托管测速的原理。

在无旋流动中，也可利用无旋条件积分欧拉方程而得到相同的结果但涵义不同，此时公式中的常量在全流场不变，表示各流线上流体有相同的总能量，方程适用于全流场任意两点之间。

在粘性流动中，粘性摩擦力消耗机械能而产生热，机械能不守恒，推广使用伯努利方程时，应加进机械能损失项。

图为验证伯努利方程的空气动力实验。

补充：p1+1/2ρv1^2+ρgh1=p2+1/2ρv2^2+ρgh2（1）p+ρgh+(1/2)*ρv^2=常量（2）均为伯努利方程其中ρv^2/2项与流速有关，称为动压强，而p和ρgh称为静压强。

伯努利方程揭示流体在重力场中流动时的能量守恒。

由伯努利方程可以看出，流速高处压力低，流速低处压力高。

图II.4-3为一喷油器，已知进口和出口直径D1=8mm，喉部直径D2=7.4mm，进口空气压力p1=0.5MPa，进口空气温度T1=300K，通过喷油器的空气流量qa=500L/min （ANR），油杯内油的密度ρ=800kg/m3。

流体力学流速计算公式一、伯努利方程推导流速公式（理想不可压缩流体定常流动）1. 伯努利方程。

- 对于理想不可压缩流体作定常流动时，在同一条流线上有p+(1)/(2)ρ v^2+ρ gh = C（p是流体压强，ρ是流体密度，v是流速，h是高度，C是常量）。

- 假设水平流动（h_1 = h_2），则方程变为p_1+(1)/(2)ρ v_1^2=p_2+(1)/(2)ρ v_2^2。

- 由此可推导出流速公式v_2=√(v_1^2)+(2(p_1 - p_2))/(ρ)。

2. 适用条件。

- 理想流体（无粘性），实际流体在粘性较小时可近似使用。

- 不可压缩流体，像水在大多数情况下可视为不可压缩流体，气体在低速流动时也可近似为不可压缩流体。

- 定常流动，即流场中各点的流速等物理量不随时间变化。

3. 示例。

- 已知水管中某点1处的压强p_1 = 2×10^5Pa，流速v_1 = 1m/s，另一点2处的压强p_2 = 1.5×10^5Pa，水的密度ρ = 1000kg/m^3。

- 根据v_2=√(v_1^2)+(2(p_1 - p_2))/(ρ)，将数值代入可得：- v_2=√(1^2)+frac{2×(2×10^{5-1.5×10^5)}{1000}}- 先计算括号内的值：2×(2×10^5-1.5×10^5)=2×5×10^4=10^5。

- 则v_2=√(1 + 100)= √(101)≈10.05m/s。

二、连续性方程推导流速公式（不可压缩流体定常流动）1. 连续性方程。

- 对于不可压缩流体的定常流动，有S_1v_1 = S_2v_2（S_1、S_2分别是流管中两个截面的面积，v_1、v_2是相应截面处的流速）。

- 由此可推导出流速公式v_2=(S_1)/(S_2)v_1。

2. 适用条件。

- 不可压缩流体，如液体或低速流动的气体。

伯努利原理的应用计算1. 引言伯努利原理是流体力学领域中重要的原理之一。

它描述了沿着流体流动方向发生的压强变化和速度变化之间的关系。

伯努利原理在各个领域中都有广泛的应用，如航空、汽车工程、水力工程等。

本文将介绍伯努利原理的应用计算方法，并结合实际案例进行具体说明。

2. 伯努利原理的原理简介伯努利原理是指在沿着流体流动方向上，速度增加时压强就要降低，速度减小时压强就要增加。

这是因为在流体流动中，速度增加意味着动能增加，而动能的增加必须以压强的降低为代价，从而保持整体能量守恒。

3. 伯努利原理的应用计算方法伯努利原理可以用于各种流动问题的计算，下面将介绍几种常见应用计算方法。

3.1 管道中的流速计算当流体通过管道时，可以利用伯努利方程计算不同位置处的流速。

假设流体从入口到出口在水平方向流动，并忽略摩擦损失和其他外界影响，可以使用以下公式计算流速：v = sqrt(2*(P1-P2)/ρ)其中，v表示流速，P1表示入口处的压强，P2表示出口处的压强，ρ表示流体的密度。

3.2 飞机升力的计算飞机的升力是由差压产生的，而差压可以通过伯努利原理计算得到。

假设飞机在飞行过程中，上表面和下表面的气压分别为P1和P2，飞机的升力可以通过以下公式计算：L = 1/2 * ρ * v * A * (P1 - P2)其中，L表示升力，ρ表示空气的密度，v表示飞机的速度，A表示飞机的翼展面积。

3.3 涡轮机动力计算涡轮机是一种制造动力的装置，其动力来源于喷气式发动机的燃烧产生的高速气流。

涡轮机的动力可以通过伯努利方程计算得到。

假设涡轮机中气流的速度为v1，出口的速度为v2，则动力可以通过以下公式计算：P = 1/2 * ρ * (v2^2 - v1^2) * A其中，P表示动力，ρ表示气体的密度，A表示气流的截面积。

4. 应用实例为了进一步说明伯努利原理的应用计算方法，以下将给出一些具体的应用实例。

4.1 气球的上升力计算气球的上升力由于气球内部的气体比外界气体密度小所产生的浮力。

气体的流速计算伯努利方程20210711093808一、伯努利方程概述伯努利方程是流体力学中描述流体流动的基本方程之一，它反映了在流体流动过程中，速度、压力和高度之间的关系。

对于气体而言，伯努利方程同样适用，可以用来计算气体的流速。

伯努利方程的基本形式如下：P + 1/2ρv^2 + ρgh = 常数其中，P为气体压力，ρ为气体密度，v为气体流速，g为重力加速度，h为气体所处的高度。

二、气体流速计算1. 已知条件要计算气体流速，我们需要知道气体的压力、密度、重力加速度和高度。

这些参数可以通过实验测量得到，或者根据气体的性质和所处环境进行估算。

2. 计算步骤(1) 确定气体压力P、密度ρ、重力加速度g和高度h的数值。

(2) 将这些数值代入伯努利方程，求解气体流速v。

(3) 分析计算结果，确保流速值在合理范围内。

三、实际应用伯努利方程在气体流速计算中有着广泛的应用，例如：1. 气体管道输送：在气体输送过程中，利用伯努利方程可以计算管道中气体的流速，从而确定管道的设计参数，如直径、壁厚等。

2. 气体喷射：在气体喷射设备中，利用伯努利方程可以计算喷射气体的流速，从而优化喷射效果。

3. 气体风机：在气体风机的设计和运行中，利用伯努利方程可以计算气体流速，从而提高风机效率。

4. 气体扩散：在气体扩散过程中，利用伯努利方程可以计算气体流速，从而分析气体扩散的规律。

伯努利方程在气体流速计算中具有重要的作用。

通过合理应用伯努利方程，我们可以更好地理解和解决气体流动问题，为工程实践提供有力支持。

气体的流速计算伯努利方程20210711093808四、伯努利方程的适用条件伯努利方程在应用时需要满足一定的条件，以确保计算的准确性。

这些条件包括：1. 流体不可压缩：伯努利方程适用于不可压缩流体，即流体密度在流动过程中保持不变。

对于气体而言，当气体流速较低，压力变化不大时，可以近似认为气体是不可压缩的。

2. 流动是稳定的：伯努利方程适用于稳定的流动，即流体的速度、压力和高度随时间保持不变。

伯努利方程计算气体流速好啦，今天我们来聊聊一个有趣又实用的话题——伯努利方程。

这可不是个听起来让人打瞌睡的数学公式，而是一个关于气体流速的神奇工具。

想象一下，夏天的某个下午，你在公园里享受微风拂面的感觉，突然意识到风是如何流动的。

嘿，没错，这就跟伯努利方程有关！咱们得知道伯努利方程是什么。

简单来说，它描述了流体在运动时的行为。

想象一下，流体就像一群在河里嬉戏的小鱼，随着河水的流动，它们的速度、压力和高度都会互相影响。

就像那些鱼在水中游来游去，流体也是一样的道理。

压力高的地方，流体的速度就会慢一些；压力低的地方，流体的速度就会快一些。

这就像你在拥挤的地铁里，推推搡搡，难免慢下来，而当人少的时候，你就能像飞一样冲出去。

好啦，接下来我们就得拿这个方程来计算气体的流速。

想象一下你在一个有风扇的房间，风扇的风吹得你发丝飞扬，感觉简直不要太爽！这时，如果我们能用伯努利方程来算一算，风扇的风速大概有多快，那可真是酷毙了。

风速的计算并不复杂，只需要知道几个参数：气体的密度、流速以及压力。

听起来很高大上，但其实这就像你在做一顿丰盛的晚餐，准备好食材就行了。

在这里，咱们得引入一个小公式。

伯努利方程的经典形式是这样的：P + 0.5ρv² +ρgh = 常数。

别担心，这看起来复杂，但其实每一部分都有它自己的意思。

P是压力，ρ是气体的密度，v是流速，而h是高度。

就像咱们去超市购物，得把不同的物品放进购物车里，最后再结账，才能知道总共花了多少钱。

我们就可以通过公式来进行计算了。

比如说，假设你想知道在某个点上气体的流速。

只需要知道那个地方的压力和气体的密度，然后再用公式计算一下，就能得到流速啦！这就像你在玩拼图游戏，找到所有的拼图块，最后拼出一个完整的图案。

简简单单，轻轻松松！这个方程在实际生活中有什么应用呢？嘿，真不少呢！比如飞机飞起来的原理。

飞机的翅膀设计得特别巧妙，能够在飞行时创造出不同的压力，这样就可以让飞机在空中翱翔。