第二讲(空间数据模型)
- 格式：pptx
- 大小：14.46 MB
- 文档页数：35
下载文档原格式
合集下载
(第二讲)数据库(第二章：关系数据库的基本概念)
表2-5 学生表 XS_Sex XS_Age ZY_Id
类型 char(10) char(10) char(2) Int char(4) 学号，主码 姓名：字符类型
说明
性别：只能为男或女 年龄：整形 所在专业编号，外码，参照专业表
4. 选课表（XK_Tab）：记录学生的选课结果，对于任意一门课，每 个学生一年最多只能选一次，因此用课程编号、学号和年份联合作为 选课表的主码。选课表通过学号参照学生表，通过课程编号参照课程 表。
2. 课程表（KC_Tab）：存放多门课程，主码为课程编号。
表2-4 课程表（KC_Tab）
列名 KC_Id KC_Name KC_KC_Id KC_Point
类型 char(4) char(50) char(4) Float
说明 课程编号，主码 课程名称 先修课课程编号 课程的学分
3. 学生表（XS_Tab）：记录学生的基本信息，主码为学号，通过专业 编号参照专业表。
2.3 关系模型规范化
关系模型规范化的目的是为了消除存储异常，减少数据冗余， 保证数据的完整性和存储效率。 关系数据库中的关系是要满足一定的规范化要求的。对于不 同规范化程度，可以使用“范式”来衡量。满足最低要求的为I范 式。。在I范式的基础上，进一步满足一些要求的为II范式，以次 类推。一般情况下，在实践中关系模式满足3范式就基本可以。
元素的每一个值 di 叫作一个分量。关系模型中要求每一 个分量必须属于某种基本数据类型，如整形或字符串型。
关系：笛卡尔积的子集就是一个关系。
R( D1 , D2 ,, Dn )
这里R表示关系的名字，n是关系的目或度。
例: 我们给出如下三个域： D1 =导师集合。导师={王新，赵阳} D2=专业集合。专业={计算机，通信} D3=学生集合。学生={（张三，101），（李四，201）} 则笛卡尔积为： D1XD2XD3={（王新，计算机，张三，101）， （王新，计算机，李四，201），
类型 char(10) char(10) char(2) Int char(4) 学号，主码 姓名：字符类型
说明
性别：只能为男或女 年龄：整形 所在专业编号，外码，参照专业表
4. 选课表（XK_Tab）：记录学生的选课结果，对于任意一门课，每 个学生一年最多只能选一次，因此用课程编号、学号和年份联合作为 选课表的主码。选课表通过学号参照学生表，通过课程编号参照课程 表。
2. 课程表（KC_Tab）：存放多门课程，主码为课程编号。
表2-4 课程表（KC_Tab）
列名 KC_Id KC_Name KC_KC_Id KC_Point
类型 char(4) char(50) char(4) Float
说明 课程编号，主码 课程名称 先修课课程编号 课程的学分
3. 学生表（XS_Tab）：记录学生的基本信息，主码为学号，通过专业 编号参照专业表。
2.3 关系模型规范化
关系模型规范化的目的是为了消除存储异常，减少数据冗余， 保证数据的完整性和存储效率。 关系数据库中的关系是要满足一定的规范化要求的。对于不 同规范化程度，可以使用“范式”来衡量。满足最低要求的为I范 式。。在I范式的基础上，进一步满足一些要求的为II范式，以次 类推。一般情况下，在实践中关系模式满足3范式就基本可以。
元素的每一个值 di 叫作一个分量。关系模型中要求每一 个分量必须属于某种基本数据类型，如整形或字符串型。
关系：笛卡尔积的子集就是一个关系。
R( D1 , D2 ,, Dn )
这里R表示关系的名字，n是关系的目或度。
例: 我们给出如下三个域： D1 =导师集合。导师={王新，赵阳} D2=专业集合。专业={计算机，通信} D3=学生集合。学生={（张三，101），（李四，201）} 则笛卡尔积为： D1XD2XD3={（王新，计算机，张三，101）， （王新，计算机，李四，201），
第二讲 面板数据回归模型
第二讲 面板数据回归模型2.1面板数据回归模型的一般形式 面板数据模型的一般形式如下：it Kk kit ki it u x y +=∑=1β （2.1）其中，N ,,,,i "321=，表示N 个个体；T ,,,,t "321=，表示已知的T 个时点。
it y 是被解释变量对个体i 在t 时的观测值；kit x 是第k 个非随机解释变量对于个体i 在t 时的观测值；ki β是待估计的参数；it u 是随机误差项。
用矩阵表示为i i i i =+Y X βU （N ,,,,i "321=） （2.1’）其中，121i i i iT T y y y ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#Y ，112111222212i i Ki i i Ki i iTiTKiT T K x x x x x x x x x ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦""##"#"X ， 121×⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=K Ki i i i βββ#β，121i i iiT T u u u ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#U .2.2 面板数据回归模型的分类通常，对模型（2.1）将做许多限制性假设，使其成为不同类型的面板数据回归模型。
一般来说，常用的面板数据回归模型有如下九种模型，下面分别介绍它们。
1混合回归模型从时间上看，不同个体之间不存在显著性差异；从截面上看，不同截面之间也不存在显著性差异，那么就可以直接把面板数据混合在一起，用普通最小二乘法（OLS ）估计参数。
即估计模型12Kit k kit it k y x u ββ==++∑ （2.2）=+Y X U β （2.2’）其中，121N NT ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#Y Y Y Y ，12N NT K×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#X X X X ，121×⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=K K βββ#β，121N NT ×⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦#U U U U .实际上，混合回归模型（Pooled Regression Models ）假设了解释变量对被解释变量的影响与个体无关。
第二讲 面板数据线性回归模型
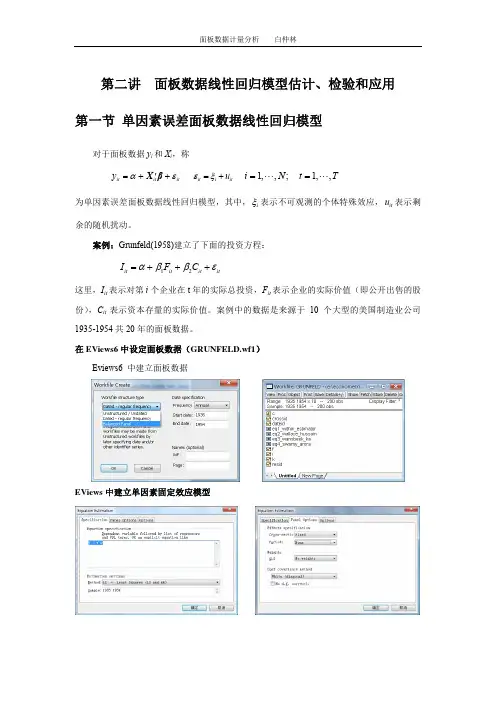
第二讲 面板数据线性回归模型估计、检验和应用 第一节 单因素误差面板数据线性回归模型对于面板数据y i 和X i ，称it it it y αε′=++X βit i it u εξ=+ 1,,;1,,i N t T ==""为单因素误差面板数据线性回归模型，其中，i ξ表示不可观测的个体特殊效应，it u 表示剩余的随机扰动。
案例：Grunfeld(1958)建立了下面的投资方程：12it it it it I F C αββε=+++这里，I it 表示对第i 个企业在t 年的实际总投资，F it 表示企业的实际价值（即公开出售的股份），C it 表示资本存量的实际价值。
案例中的数据是来源于10个大型的美国制造业公司1935-1954共20年的面板数据。
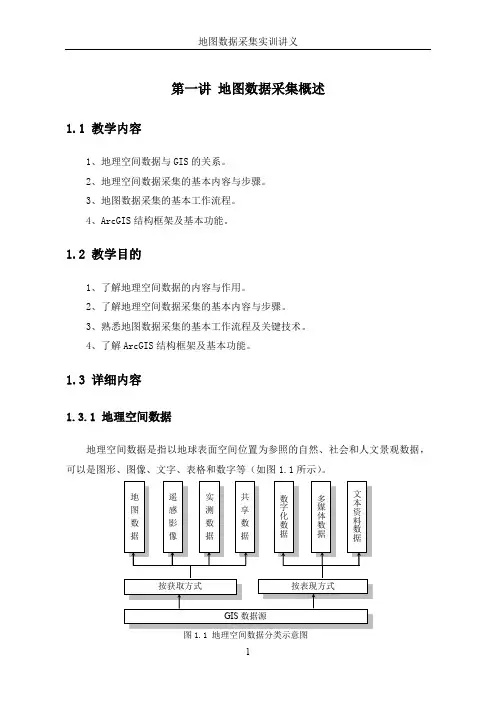
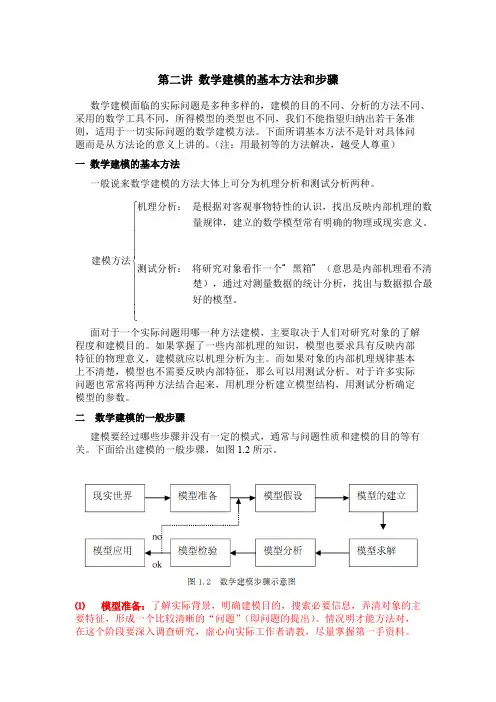
在EViews6中设定面板数据（GRUNFELD.wf1）Eviews6 中建立面板数据EViews 中建立单因素固定效应模型1.1 混合回归模型1 面板数据混合回归模型 假设1 ε ~ N (0, σ2I NT )对于面板数据y i 和X i ，无约束的线性回归模型是y i = Z i δi + εi i =1, 2, … , N(4.1)其中'i y = ( y i 1, … , y iT )，Z i = [ ιT , X i ]并且X i 是T×K 的，'i δ是1×(K +1)的，εi 是T×1的。
注意：各个体的回归系数δi 是不同的。
如果面板数据可混合，则得到有约束模型y = Z δ + ε(4.2)其中Z ′ = ('1Z ,'2Z , … ,'N Z )，u ′ = ('1ε,'2ε, … ,'N ε)。
2 混合回归模型的估计当满足可混合回归假设时，()1''ˆZ Z Z Y −=δ在假设1下，对于Grunfeld 数据，基于EViews6建立的混合回归模型3 面板数据的可混合性检验假设检验原理：基于OLS/ML 估计，对约束条件的检验。
第二讲 数学建模的作用及案例
产生了众多的边缘学科。就以生物数学这一新学科来说吧，
种国际学术杂志名称。这表明各学科正在利用数学方法和
数学成果来加速本学科的发展。数学模型还物化于各种高
新科技之中，从家用电物工程，高科技的高精度、
高速度、高安全、高质量、高效率等特点无一不是通过数
断完善，直到获得满意结果。
模型应用：模型应用是数学建模的宗旨，也是对模型 的最客观、最公正的检验。因此，一个成功的数学模型， 必须根据建模的目的，将其用于分析、研究和解决实际问 题，充分发挥数学模型在生产和科研中的特殊作用。
构造模型
建模准备
建模假设
否
模型求解
模型应用
是
模型检验
是
模型分析
四、建模案例
统论中提出的机理分析法和系统辩识法来说，它们是构造 数学模型的两种基本方法。机理分析法是在对事物内在机
理分析的基础上，利用建模假设所给出的建模信息或前提
条件来构造模型；系统辨识法是对系统内在机理一无所知 的情况下，利用建模假设或实际对系统的测试数据所给出 的事物系统的输入、输出信息来构造模型。随着计算机科 学的发展，计算机模拟有力地促进了数学建模的发展，也
成预制品供你在建模时使用。模型的这种非预制性使得 建模本身常常事先没有答案的问题。在建立新的模型的 过程中甚至会伴随着新的数学方法或数学概念的产生。
6）模型的条理性 从建模的角度考虑问题可以使人们对现实对象的分 析更全面、更具体、更深入、更具条理性，这样即使建 立的模型由于种种原因尚未达到使用的程度，对问题的 研究也是有利的。 7）模型的艺术性 建模的方法与其他一些数学方法，如方程解法、规 划问题解法等是根本不相同的，无法归纳出若干条普遍 适应的建模准则和技巧。曾有人说过，建模目前与其说 是一门技术，不如说是一种艺术，是艺术性很强的技巧 。经验、想象力、洞察力、判断力以及直觉、灵感等在 建模过程中起的作用往往比一些具体的数学知识更大。
6.2数据库(second)
① 无法用递归和嵌套的方式来描述复杂 关系的层次和网状结构，模拟和操作 复杂地理对象的能力较弱； ② 用关系模型描述本身具有复杂结构和 涵义的地理对象时，需对地理实体进 行不自然的分解，导致存储模式、查 询途径及操作等方面均显得语义不甚 合理； ③ 由于概念模式和存储模式的相互独立 性，及实现关系之间的联系需要执行 系统开销较大的联接操作，运行效率 不够高。
(1)基本思想和基本概念
• 面向对象的方法就是以接近人类通常 思维方式的思想，将客观世界的一切 实体模型化为对象。每一种对象都有 各自的内部状态和运动规律，不同对 象之间的相互联系和相互作用就构成 了各种不同的系统。 • 在面向对象的方法中，对象、方法的独立模块， 可以认为是数据和行为的统一体。如一个 城市、一棵树均可作为地理对象。对于一 个对象，应具有如下特征： 具有一个唯一的标识，以表明其存在的独 立性； 具有一组描述特征的属性，以表明其在某 一时刻的状态； 具有一组表示行为的操作方法，用以改变 对象的状态。
消息与方法
•
消息——对对象进行操作的
请求，是连接对象与外部世界 的唯一通道。 • 方法——对对象的所有操作， 如对对象的数据进行操作的函 数、指令、例程等。
(2)面向对象的特性
抽象性 封装性 多态性
(3)面向对象数据模型的 四种核心技术
象归纳或映射为一个公共类的过程。对象和类的 关系是“实例”(instance-of)的关系。 • 概括是把几个类中某些具有部分公共特征的属性 和操作方法抽象出来，形成一个更高层次、更具 一般性的超类的过程。 • 聚集是将几个不同类的对象组合成一个更高级的 复合对象的过程。术语“复合对象”用来描述更 高层次的对象， • 联合是将同一类对象中的几个具有部分相同属性 值的对象组合起来，形成一个更高水平的集合对 象的过程。
数字高程模型第二讲DEM数据组织与管理
在TIN模型中;基本的结构元素有三角形顶点 边 面 它们之间存在着点与线 点与面 线与面 面与 面等拓扑关系 通过组成三角形的三顶点可完整地 表达三角形的构成以及三角形顶点 三角形边 三角 形之间的拓扑关系
这种结构只需要两个文件：三角形顶点坐标文件和组 成三角形三顶点用点在坐标文件中的序号表示文件
ArcView DEM 文本文件格式
2行程编码结构
对于一幅DEM;常常在行或列方向上相邻的若干点具 有相同的高程值;因而从第一列开始;在格网单元数值发生 变化时一次纪录该值以及重复的个数;应用时利用重复个 数恢复DEM矩阵 对DEM每一行均按上述结构组织;则实现 DEM行程编码方案
行程编码实际上是一种栅格数据的压缩方案;能有效地 减少数据存储量;特别在平坦地区
3块状编码结构
块状编码方案是将行程编码方案从一维扩展到二维的 情况;它采用方形区域作为纪录单元;每个纪录单元包括相 邻的若干栅格 数据结构是由纪录单元的初始位置行列号 格网单元高程值和方形区域半径正方形区域的边长;采用 格网间距倍数表示所组成的单元组 整个DEM数据文件由 该单元组组成;根据初始位置和区域半径可恢复高程矩阵
● 镶嵌数据模型按照网格形状可分为规则镶 嵌数据模型和不规则镶嵌数据模型;镶嵌模型的典 型应用是地形曲面模拟;即数字高程模型;其中基 于正方形网络的镶嵌数据模型为栅格DEM;而基于 不规则镶嵌数据模型为不规则三角网DEM
2 2 2规则镶嵌数据模型 ● 所谓规则镶嵌数据模型;就是用规则的小面
块集合来逼近不规则分布的地形曲面 在二维空间 中可以有多种可能的规则格网划分方法;如图1
ＴＩＮ
坐标表
三角形表
ＴＩＮ模型基本链表结构
这种结构简单但拓扑关系是隐含的;不利于TIN模型的检索与应 用 因此围绕着拓扑关系的描述产生了多种TIN的数据结构
这种结构只需要两个文件：三角形顶点坐标文件和组 成三角形三顶点用点在坐标文件中的序号表示文件
ArcView DEM 文本文件格式
2行程编码结构
对于一幅DEM;常常在行或列方向上相邻的若干点具 有相同的高程值;因而从第一列开始;在格网单元数值发生 变化时一次纪录该值以及重复的个数;应用时利用重复个 数恢复DEM矩阵 对DEM每一行均按上述结构组织;则实现 DEM行程编码方案
行程编码实际上是一种栅格数据的压缩方案;能有效地 减少数据存储量;特别在平坦地区
3块状编码结构
块状编码方案是将行程编码方案从一维扩展到二维的 情况;它采用方形区域作为纪录单元;每个纪录单元包括相 邻的若干栅格 数据结构是由纪录单元的初始位置行列号 格网单元高程值和方形区域半径正方形区域的边长;采用 格网间距倍数表示所组成的单元组 整个DEM数据文件由 该单元组组成;根据初始位置和区域半径可恢复高程矩阵
● 镶嵌数据模型按照网格形状可分为规则镶 嵌数据模型和不规则镶嵌数据模型;镶嵌模型的典 型应用是地形曲面模拟;即数字高程模型;其中基 于正方形网络的镶嵌数据模型为栅格DEM;而基于 不规则镶嵌数据模型为不规则三角网DEM
2 2 2规则镶嵌数据模型 ● 所谓规则镶嵌数据模型;就是用规则的小面
块集合来逼近不规则分布的地形曲面 在二维空间 中可以有多种可能的规则格网划分方法;如图1
ＴＩＮ
坐标表
三角形表
ＴＩＮ模型基本链表结构
这种结构简单但拓扑关系是隐含的;不利于TIN模型的检索与应 用 因此围绕着拓扑关系的描述产生了多种TIN的数据结构
第二讲--2 工程设计集成分系统
了描述各个组成面素的信息的面表。即曲面是由哪些基
本曲线构成。
三． 曲面生成方法
1.对于一般常用的曲面，可以采用几种简化曲面生成
的方法。
1)线性拉伸面(平移表面) 这是一种将某曲线，沿固 定方向拉伸，而产生的曲面的方法。
2）直纹面
给定两条相似的NURBS曲线或其它曲线，
它们具有相等的次数，和相等的节点个数，将两条曲
线上的对应的节点用直线连接，就形成了直纹曲面。
3）旋转面
将指定的曲线，绕旋转轴，旋转一个
角度，所生成的曲面就是旋转曲面。
4）扫描面
扫描面构造方法很多，其中应用最多、最
有效的方法是沿导向曲线（也有称它为控制线）扫描
而形成曲面，它适用于创建有相同构形规律的表面。
5）边界曲面
在4条连接直线或多义线间建立一个三维表面
2 工程设计集成分系统
CIMS工程设计集成分系统(CIMS／EDIS) 是指用计算机辅助产品设计、制造准备及 产品性能测试等产品开发各过程的系统。 随着计算机应用日益广泛，在EDIS中也相 继出现了多个计算机辅助子系统，包括计 算机辅助设计(CAD)、计算机辅助工艺规程 制定(CAPP)和计算机辅助加工制造及监控 (CAM)。
（5）软件设计技术 如窗口界面设计、 软件工具、软件工程规范等。 近十多年来，由于先进制造技术 的快速发展，带动了先进设计技术的同 步发展，使传统CAD技术有了很大的扩 展，将这些扩展的CAD技术总称为“现 代CAD技术”。
值得指出的是：不应该将CAD与计算机绘图、 计算机图形学混淆起来。 计算机绘图的内涵；计算机绘图是使用 图形软件和硬件进行绘图及有关标注的一种 方法和技术，以摆脱繁重的手工绘图为其主 要目标。 计算机图形学（computer graphics，CG） 的内涵：计算机图形学是研究通过计算机将 数据转换为图形，并在专用设备上显示的原 理、方法和技术的科学. CG的研究内容有以下四个方面：
Part1-地图数据采集及建库
按表现方式
图 1.1 地理空间数据分类示意图 1
地图数据采集实训讲义 地理空间数据是 GIS 所表达的现实世界经过模型抽象的实质性内容，是 GIS 能 够正确发掘、展示、分析地理现象与地理过程的基础。 不同用途的 GIS，其地理空间数据的种类、精度都是不同的，但基本上都包括三 种互相联系的数据类型： 1、几何图形数据 即几何坐标，标识地理实体和地理现象在某个已知坐标系（如大地坐标系、直 角坐标系、极坐标系、自定义坐标系）中的空间位置，可以是经纬度、平面直角坐 标、极坐标，也可以是矩阵的行、列数等。 2、空间关系数据 即拓扑关系，表示点、线、面实体之间的空间联系，如网络结点与网络线之间 的枢纽关系，边界线与面实体间的构成关系，面实体与岛或内部点的包含关系等。 空间拓扑关系对于地理空间数据的编码、录入、格式转换、存贮管理、查询检索和 模型分析都有重要意义，是地理信息系统的特色之一。 3、非几何属性数据 即常说的非几何属性或简称属性，是与地理实体和地理现象相联系的地理变量 或地理意义。属性分为定性和定量的两种，前者包括名称、类型、特性等，后者包 括数量和等级，定性描述的属性如岩石类型、土壤种类、土地利用类型、行政区划 等；定量的属性如面积、长度、土地等级、人口数量、降雨量、河流长度、水土流 失量等。GIS 的分析、检索和表示主要是通过属性的操作运算实现的，因此，属性的 分类系统、量算指标对 GIS 系统的功能有较大的影响。
图 1.4 ArcGIS9 体系一览图
1、Desktop GIS Desktop GIS 包含诸如 ArcMap、ArcCatalog、ArcToobox 以及 ArcGlobe 等在内 的用户界面组件，其功能可分为三个级别： ArcView 、 ArcEditor 和 ArcInfo ，而
第二讲-几何建模
HalfEdge e;
e e->opp()
e->start() = e->opp()->end();
e->start()
class HalfEdge { HalfEdge *opp; Vertex *end; Face *left; HalfEdge *next; };
HalfEdge e;
e->left()
Non-Manifold
Closed Manifold
Open Manifold
拓扑
v = 12 f = 14 e = 25 c=1 g=0 b=1 图的亏格(genus)：handle的数目。 在沿其撕裂后，能够使图保持连通 的封闭路径的最大数目的一半
Euler-Poincare 公式 v+f-e = 2(c-g)-b
• • • • 将一个隐式的曲面转换为三角网格 在3D网格（grid）上定义的隐式曲面 在每个立方体（cube）中根据8个顶点的标量值来确定重构曲面 一般用于医学数据
点云
深度图像
网格（Mesh）
– – – – – 图形学中最常用的表达 简单 可表达复杂形状 图形硬件支持 一般为三角网格
为什么是三角网格
网格的数据结构是否优秀
• 构建数据结构的时间复杂度
• 进行一个查询操作的时间复杂度 • 进行一个网格编辑操作的时间复杂度（更 新数据结构） • 空间复杂度
数据结构举例
• 面列表（ List of faces）
• 邻接矩阵（Adjacency matrix） • 半边结构（Half-edge）
一个实际的文件例子 .obj文件
All neighboring vertices
edge
e e->opp()
e->start() = e->opp()->end();
e->start()
class HalfEdge { HalfEdge *opp; Vertex *end; Face *left; HalfEdge *next; };
HalfEdge e;
e->left()
Non-Manifold
Closed Manifold
Open Manifold
拓扑
v = 12 f = 14 e = 25 c=1 g=0 b=1 图的亏格(genus)：handle的数目。 在沿其撕裂后，能够使图保持连通 的封闭路径的最大数目的一半
Euler-Poincare 公式 v+f-e = 2(c-g)-b
• • • • 将一个隐式的曲面转换为三角网格 在3D网格（grid）上定义的隐式曲面 在每个立方体（cube）中根据8个顶点的标量值来确定重构曲面 一般用于医学数据
点云
深度图像
网格（Mesh）
– – – – – 图形学中最常用的表达 简单 可表达复杂形状 图形硬件支持 一般为三角网格
为什么是三角网格
网格的数据结构是否优秀
• 构建数据结构的时间复杂度
• 进行一个查询操作的时间复杂度 • 进行一个网格编辑操作的时间复杂度（更 新数据结构） • 空间复杂度
数据结构举例
• 面列表（ List of faces）
• 邻接矩阵（Adjacency matrix） • 半边结构（Half-edge）
一个实际的文件例子 .obj文件
All neighboring vertices
edge
07-《3S技术-第二讲-3S的结构与组成》幻灯片
中电兴发科技集团公司
地理信息系统知识
三.3S的系统结构：
在探讨3S的系统结构之前，先要对“系统结构”有一个明确的认识。 对于“系统结构”这个概念，人们在认知上往往容易将其与“系统组成”、“拓 扑结构”这两个概念混淆。这是因为，系统结构与组成系统的内部各个要素之间有着 必然的逻辑的和物理的关系，而拓扑结构又恰恰是数学的图论分支中专门分析图形之 间逻辑关系的学科。但系统结构不是系统组成，更不是拓扑结构，三者的根本区别在 于：系统结构是逻辑性结构，拓扑结构仅只考虑图形要素之间的逻辑关系，而系统组 成则是物理性结构。 系统结构是从自然的或人工的系统目的出发，按照一定规则组织起来的、相互关 联的系统元素的集合，一般指系统内部各组成要素之间的相互联系、相互作用的方式 或秩序，用来表述对系统中各个组成要素之间的逻辑级别，各级要素之间界点、界线、 界面的逻辑划分和物理含义的定义，并对各级要素之间上、下的功能进行分配。系统 结构就是体系架构。 任何系统都是由相互关联的更小系统(子系统)或基本要素构成，因此各级组成要 素内部也都有自己的系统结构。基本要素是指不需要再加以分解和追究其内部结构的 基本成份，这种情况下也可以称之为组成元素。 一个计算机系统，其系统结构就是各组成要素在时间或空间上排列的秩序(顺序) 与组合的具体形式，其基本特点有五：关联性、相对性、稳定性、兼容性、开放性。 系统结构有多种逻辑形式，按其功能框架的不同与组织形式的不同，可以分为六 种基本形式，即主从式结构、层次化结构、模块化结构、树体型结构、网络化结构、 复合式结构。
中电兴发科技集团公司
地理信息系统知识
1.主从式结构(PSA，Principal-Subordinate Architecture)： 谈及主从式结构，人们会 立即联想起类如Master-Slave (M/S，集散型模式)、Client/ Server(C/S,客户端-服务器)、 Browser/Server(B/S，浏览器 -服务器)等主从式架构系统。 实际上M/S、C/S、B/S等 号称“主从式结构”的系统都 是一些用于系统构建的逻辑模 型，能够用来构建一个面向对 象的应用系统，它们都是从主 从式结构(PSSA)中引伸出来的 具体应用性模型系统，并不能 代表主从式结构本身。 那么，真正的主从式结构 的逻辑模型是什么呢？其逻辑 模型图为→
地理信息系统知识
三.3S的系统结构：
在探讨3S的系统结构之前，先要对“系统结构”有一个明确的认识。 对于“系统结构”这个概念，人们在认知上往往容易将其与“系统组成”、“拓 扑结构”这两个概念混淆。这是因为，系统结构与组成系统的内部各个要素之间有着 必然的逻辑的和物理的关系，而拓扑结构又恰恰是数学的图论分支中专门分析图形之 间逻辑关系的学科。但系统结构不是系统组成，更不是拓扑结构，三者的根本区别在 于：系统结构是逻辑性结构，拓扑结构仅只考虑图形要素之间的逻辑关系，而系统组 成则是物理性结构。 系统结构是从自然的或人工的系统目的出发，按照一定规则组织起来的、相互关 联的系统元素的集合，一般指系统内部各组成要素之间的相互联系、相互作用的方式 或秩序，用来表述对系统中各个组成要素之间的逻辑级别，各级要素之间界点、界线、 界面的逻辑划分和物理含义的定义，并对各级要素之间上、下的功能进行分配。系统 结构就是体系架构。 任何系统都是由相互关联的更小系统(子系统)或基本要素构成，因此各级组成要 素内部也都有自己的系统结构。基本要素是指不需要再加以分解和追究其内部结构的 基本成份，这种情况下也可以称之为组成元素。 一个计算机系统，其系统结构就是各组成要素在时间或空间上排列的秩序(顺序) 与组合的具体形式，其基本特点有五：关联性、相对性、稳定性、兼容性、开放性。 系统结构有多种逻辑形式，按其功能框架的不同与组织形式的不同，可以分为六 种基本形式，即主从式结构、层次化结构、模块化结构、树体型结构、网络化结构、 复合式结构。
中电兴发科技集团公司
地理信息系统知识
1.主从式结构(PSA，Principal-Subordinate Architecture)： 谈及主从式结构，人们会 立即联想起类如Master-Slave (M/S，集散型模式)、Client/ Server(C/S,客户端-服务器)、 Browser/Server(B/S，浏览器 -服务器)等主从式架构系统。 实际上M/S、C/S、B/S等 号称“主从式结构”的系统都 是一些用于系统构建的逻辑模 型，能够用来构建一个面向对 象的应用系统，它们都是从主 从式结构(PSSA)中引伸出来的 具体应用性模型系统，并不能 代表主从式结构本身。 那么，真正的主从式结构 的逻辑模型是什么呢？其逻辑 模型图为→
第二讲：数学建模的基本方法和步骤
数学模型法是一种通过数学语言和符号描述现实对象内在规律的方法，其一般步骤包括模型准备、模型假设、模型的建立、模型求解、模型分析、模型检验和模型应用。在模型准备阶段，需要了解实际背景，明确建模目的，并搜集必要信息。模型假设阶段则需根据对象特征和建模目的，作出合理简化假设。接下来，在模型的建立阶段，使用数学语言和符号描述对象内在规律，构建数学结构。完成模型建立后，利用各种数学方法、软件和计算机技术对模型进行求解，并对求解结果进行数学分析，误差分析、稳定性分析等。之后，将求解和分析结果与实际现象、数据进行比较，检验模型的合理性与适用性。最后，根据问题的性质、建模目的及最终结果，进行模型的应用。值得注意的是，这些步骤并非一成不变，建模过程中应灵活调整，不拘泥于形式。
02第二讲 数据融合系统的结构形式
nust自动化学院智能信息处理技术4数据融合系统的构成nust自动化学院智能信息处理技术21数据融合系统的主要结构形式1集中式融合系统2无反馈的分布式融合系统3有反馈的分布式融合系统4有反馈的全并行融合系统nust自动化学院智能信息处理技术1集中式融合系统nust自动化学院智能信息处理技术特点
第二讲 数据融合系统结构形式
42
融合层次的优缺点比较
43
数据融合分类-按融合判决方式
分类：硬判决、软判决 指数据处理活动中用于信号检测、目标识别的 判决方式。 应用： 每个传感器内部或信息融合中心都既可以选用 硬判决方式，也可选用软判决方式。
44
1）硬判决
特点： ①设置有确定的预置判决门限，只有数据样本 特征量达到或超过预置门限时，系统才作出判决断 言；
38
3、决策级融合
特点： 1)是一种高层次融合，其结果为检测、控制、 指挥、决策提供依据； 2)从具体决策问题出发，充分利用特征级融合 的最终结果，直接针对具体决策目标，融合结果直 接影响决策水平。
39
主要优点
1)融合中心处理代价低，具有很高灵活性； 2)通信量小，抗干扰能力强； 3)当一个或几个传感器出现错误时，通过适当融 合，系统还能获得正确结果，具有容错性； 4)对传感器的依赖性小，传感器可以是同质的， 也可以是异质的； 5)能有效反映环境或目标各侧面不同类型信息。
5
2、无反馈的分布式融合系统
6
主要特点
每个传感器都要进行滤波，称为局部滤波。
送给融合中心的数据是当前的状态估计，融合中 心利用各个传感器所提供的局部估计进行融合， 最后给出融合结果，即全局估计。
分布式融合系统所要求的通信开销小，融合中心 计算机所需的存储容量小，且其融合速度快，但 其性能不如集中式融合系统。
第二讲 数据融合系统结构形式
42
融合层次的优缺点比较
43
数据融合分类-按融合判决方式
分类：硬判决、软判决 指数据处理活动中用于信号检测、目标识别的 判决方式。 应用： 每个传感器内部或信息融合中心都既可以选用 硬判决方式，也可选用软判决方式。
44
1）硬判决
特点： ①设置有确定的预置判决门限，只有数据样本 特征量达到或超过预置门限时，系统才作出判决断 言；
38
3、决策级融合
特点： 1)是一种高层次融合，其结果为检测、控制、 指挥、决策提供依据； 2)从具体决策问题出发，充分利用特征级融合 的最终结果，直接针对具体决策目标，融合结果直 接影响决策水平。
39
主要优点
1)融合中心处理代价低，具有很高灵活性； 2)通信量小，抗干扰能力强； 3)当一个或几个传感器出现错误时，通过适当融 合，系统还能获得正确结果，具有容错性； 4)对传感器的依赖性小，传感器可以是同质的， 也可以是异质的； 5)能有效反映环境或目标各侧面不同类型信息。
5
2、无反馈的分布式融合系统
6
主要特点
每个传感器都要进行滤波，称为局部滤波。
送给融合中心的数据是当前的状态估计，融合中 心利用各个传感器所提供的局部估计进行融合， 最后给出融合结果，即全局估计。
分布式融合系统所要求的通信开销小，融合中心 计算机所需的存储容量小，且其融合速度快，但 其性能不如集中式融合系统。
第2讲 房室模型
用MatLab 软件编制程序如下:
19
function f=fun1(t,x); r1 =1; r2 =0.5; r3 =0.6; lambda1 =0.1; lambda2 =0.02; lambda3=0.06; mu=0.1; f=[ x(1)*(r1 - lambda1*x(2)); x(2)*(- r2 + lambda2*x(1) - mu*x(3)); x(3)*(- r3 + lambda3*x(2)) ]; [t, x] = ode45 ('fun1', [0, 20], [100, 40, 6]); subplot(1,2,1) plot(t,x(:,1),'- ',t,x(:,2),'- .',t,x(:,3),':') legend('x1(t)','x2(t)','x3(t)') grid subplot(1,2,2) plot3(x(:,1),x(:,2),x(:,3)) grid
由较大的 ti , c1 (ti ) 用最小二乘法定A,
t t ~ c1 (t ) c1 (t ) Ae Be
由较小的
~ ti , c1 (ti )用最小二乘法定B,
10
再估计参数: k12 , k21, k13
t , c1 , c2 0
D0 k13V1 0 c1 (t )dt
dx1 x1 ( r1 1 x2 ) dt
比例系数λ1 反映哺乳动物掠取植物的能力。
(1)
14
哺乳动物离开植物无法生存, 设它独自存在时死亡率 为r2, 即 x2(t) = -r2 x2, 而植物的存在又为哺乳动物提供了 食物, 植物的存在相当于使哺乳动物的死亡率降低, 且促使 哺乳动物增长, 设这种作用与植物的数量成正比, 则有:
第二讲 模型简介
什么是数学建模？ 数学建模就是用数学语言描述实际现象的过 程。可以直观的理解为数学建模是让一个纯粹 数学家变成物理学家、生物学家、经济学家甚 至是心理学家等等的过程。
引子——测量上高问题
问题：小明站在一个小山丘上，想要测量这个 山丘的高度。他站在山边，采取了最原始的方 法：从小山丘向下丢一小石子，5s 后他听到了 从小山丘下传来的回音。请各位尝试建立数学 模型估计小山丘的高度 模型一： 运用自由落体公式来计算：
约 l2 : 12x1 8x2 480 束 12x1 8x2 480 l4 条 3x1 100 l3 : 3x1 100 件 c l4 : x1 0, l5 : x2 0 x1 , x2 0 目标 函数
分析：上述模型是最简单最理想的自由落体模 型并没有考虑其他可能影响测量的因素。
引子——测量上高问题
模型二： 在模型一的基础上我们增加了考虑的因 素，增加了人的肉眼反应时间，通过查 阅资料得知人的反应时间约为1秒。
分析：此结果较模型一而言更接近实际 情况，属于修正的自由落体模型。
引子——测量上高问题
建模的一般步骤：
建模其实没有固定的模式，具体问题需要具 体分析，当然建模的过程也有其共性，一般来 说可以分为以下几个步骤： 1. 形成问题 2. 简化和假设 3. 模型构建 4. 模型的求解 5. 检验和评价 6. 模型的改进
模型的分类
大大小小的模型总计可达三十多种以上，如果再 加上算法的话可能有成百上千种，因此我们需要在 自己的脑子里对数学模型有一定的分类，以便自己 在以后的问题中遇到了能够很好地找到并利用。
模型分析与假设
PMCAD建模
五.结构整体模型的输入
1.【轴线输入】
2.【网格生成】
3.【楼层定义】 PMCAD主菜单1： 建筑模型与荷载输入 4.【荷载输入】 5.【楼面恒活】 6.【设计参数】 7.【楼层组装】 8.【保存文件】
China University of Petroleum
1.轴线输入：轴线可以是与墙、梁等长的线段（推荐），也
二、基本术语：
轴线──即建筑平面图上的轴线。它是确定建筑的墙、柱、梁位 臵的线段，也叫定位轴线。
网格线──平面图中通过墙、柱、梁的轴线。
网格──网格线交织后被交点分割成的线段。
节点──网格线的交点、线段的端点、圆弧的圆心点。
结构标准层—结构布臵相同、荷载布臵(不包括楼面均布荷载) 相同的相邻楼层； 荷载标准层—楼面均布恒载和活载相同的楼层。
可以是一整条建筑轴线，各标准层轴线网格可不同。 绘制轴线的基本方法： －－－－－－－－－－－－－－－－－－－－－－－－－ 节点 圆环 正交轴网 两点直线 圆弧 斜交轴网 平行直线 三点圆弧 折线 矩形 辐射线 －－－－－－－－－－－－－－－－－－－－－－－－－ 轴线命名 轴线显示
China University of Petroleum
China University of Petroleum
3.楼层定义:各层平面布臵的核心 偏心对齐：
– 柱上下齐：当上下柱尺寸不同时（边对齐、中心对齐)
– 梁与柱齐：可使梁与柱的某一边自动对齐
构件查询与修改
– 对已输入在平面上的内容可随时用光标指点，自动弹
出TIP条显示构件截面尺寸、偏心等信息 – 对光标停留处构件按鼠标右键，可随时对该构件的布 臵编辑修改
并把这些构件布臵在平面网格和节点上。 •各结构层主要设计参数，如楼板厚度、混凝土强度等级等。 •输入作用在梁、墙、柱和节点上的恒、活荷载。 •定义楼面荷载标准层和各层上的楼面恒、活均布面荷载。 •根据结构标准层、荷载标准层和各层层高，楼层组装出总层数 •设臵设计参数、材料信息、风荷信息和抗震信息等。 •对上一步所建模型进行检查，发现错误并提示用户。根据上下 层结构布臵状况作上下层构件连接。
第02讲-创建有限元模型 [黑白版]
第二讲创建有限元模型第二讲目的及学习内容（续）第讲Part F. 单元属性定义材料属性、单元类型以及实常数.Part G. 划分网格划分网格的主要步骤；使用默认设置对几何模型划分网格；单元尺寸大小. Part H: 模型建立后的检查Part I. 修改有限元模型Part IPart J: 直接生成有限元模型Part K: Select选择和部件Part A.Part A实体建模的概念实体模型(Solid modeling)及有限元模型S lid d li)建模的最终目的是：获得正确可靠的有限元网格模型←保证网格具有正确的形状，单元大小合适、密度分布合理，适合于施加边界条件和荷载，保证变形前后都具有合理单元形状，场量（变形、应力）分布描述清晰。
——这是优秀有限元分析的有合理单元形状，场量（变形应力）分布描述清晰关键所在。
ANSYS的建模功能非常强大。
的建模功能非常强大ANSYS提供了两种建模方法——实体模型和有限元直接模型◆实体模型。
指的是几何实体（点、线、面和体）——建模时先建立实体模型指的是几何实体（点线面和体），再利用ANSYS提供的分网工具划分为有限元模型；◆有限元直接模型。
包括节点和单元——建模时，直接建立节点并利用节点创建单元，从而直接获得有限元模型。
建单元从而直接获得有限元模型实体建模和有限元直接建模各有优缺点。
实体模型四种实体图元–体(3D模型) 由面围成，代表三维实体。
–面(表面) 由线围成。
代表实体表面、平面形状、壳、三维曲面。
–线(可以是空间曲线) 以关键点为端点，代表物体的边。
–关键点(位于3D空间) 代表物体的角点。
•硬点：属于关键点，在网格划分中必须要划分成结点的关键点。
属于关键点在网格划分中必须要划分成结点的关键点AreasKeypointsLinesAreaVolume——点适合于建立规则的图元。
12 6 Y 34X Z 5通过Autocad导入几何实体模型Autocad的空间建模功能非常强大，可以利用它来建立更为复杂的几何实体模型。
2011新生研讨课第二讲
1.人类与计算
1911年， Hollerith制表机公司与其他公司合并成立 了计算制表-记录设备公司，并于1924年命名为IBM 公司 1936年，英国数学家Alan Turing发表“论可计算数 及其在判定问题中的应用”论文，提出了著名的理 论计算机模型-图灵机 1938年，德国Konrad Zuse建成了采用二进制机械 式计算机Z1 1941年，Zuse建成了继电器计算机Z3并用了符点数 的表示
所谓计算就是计算者（人或机器）对一条两端可无限延长的纸带上 的一串0和1执行指令，一步一步地改变纸带上的0或1，经过有限步 骤，最后得到一个满足预先规定的符号串的变换过程。 可计算性=图灵可计算性。 丘奇-图灵论点：即直观的能行可计算函数等同于一般递归函数、可 λ定义函数和图灵机可计算函数。 结论：任一过程是能行的（能够具体表现在一个算法中），当且仅 当它能够被一台图灵机实现。
2.计算模型与电子计算机
2.计算模型与电子计算机
巨型化 1974年美国伊利诺斯州立大学研制成功了阵列巨型机ILLIAC－IV 1975年，Amdahl公司研制成Amdahl 470V/6型计算机 日本富士通（Fujitsu）公司生产出FACOM (Fujitsu Automatic COMputer)M-190机 中国银河-I/II/III巨型计算机—1亿/10亿/100亿次计算，面向工程 应用和大规模数据处理，分布式共享存储结构，64位字长 中国的曙光“星云”3000万亿次 IBM“红杉系统”这部超级计算机拥有逾160万个微型处理器，分 布在96部雪柜大小的巨箱内,需要3422平方英尺的地方安装。虽 然体积庞大，但由于微型处理器变得愈来愈小兼威力大增，每年 只消耗6000瓦的电源，即相当于500个美国家庭的耗电量，因此 非常具能源效益。 速度每秒2千万亿次。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
将连续空间离散化，即用二维铺盖或划分覆盖整个连续空 间。方格、三角形和六角形可完整地铺满一个平面，是栅 格数据模型中最常用的规则覆盖。
25
基于栅格的空间模型把空间看作像元（Pixel）的划分， 每个像元的值表明了在已知类中现象的分类情况。
荒地 1 湖泊 2 湿地 3 树林 4
栅格数据模型
26
栅格数据模型
地理编码是项目世界中地理要素的另一重要特征。
15
项目世界与地理空间世界的关系
16
地理要素在信息世界的实现 • 点世界（Points World） • 几何体世界（Geometry World） • 地理要素世界（Featቤተ መጻሕፍቲ ባይዱre World） • 要素集合世界（Feature Collection World）
根据对地理实体从现实世界到计算机内部表示的不 断抽象，GIS空间数据模型由概念数据模型、逻辑数据 模型和物理数据模型3个有机联系的层次组成。
20
• 概念数据模型 是关于空间实体及实体间联系的抽象概念集。
• 逻辑数据模型 根据概念数据模型确定的空间实体及相互关系，
具体地表达数据项、记录等之间的关系，因而可以有 若干不同的实现方法。（如结构化模型、关系模型） • 物理数据模型
在GIS中只有概念世界中一个简化的子集才是兴趣所在。 这个子集叫做地理空间世界。
地理空间世界 11
现实世界与地理空间世界的联系
在地理空间世界中，地理要素被抽象为点、线、面、 体。如河流被看作线，地形被看作等高线多边形的简化， 而森林被看作多边形。
12
• 维度世界（Dimensional World） 维度世界是对地理空间世界的抽象，它通过在欧氏空间
一个二维场就是在二维空间中任何已知的地点上，都 有一个表现这一现象的值；而一个三维场就是在三维空间 中对于任何位置来说都有一个值。
23
场模型可以表示为如下的数学公式： z(s))或f(x,y) 上式表示了从空间域到某个值域的映射，其中z为
空间位置可度量的函数，s表示空间中的位置。
24
• 栅格数据模型 栅格数据模型是场模型在信息系统中的具体实现。它
17
二、空间数据模型
18
• 数据模型 以一定方式组织数据，通过足够的抽象性和概括
性，对客观事物及其联系的进行描述,是连接现实世界 和计算机世界的桥梁。
• 空间数据模型 是关于现实世界中空间实体及其相互联系的概念，
它为空间数据的组织和空间数据库的设计提供基本方 法。
19
基于计算机的地理信息系统不能直接作用于现实世 界，必须采用一定的空间数据模型对现实世界进行数 据描述。
地理信息系统及应用
云南大学信息学院 梁虹
第二讲 空间数据模型
2
为了能够利用信息系统来描述现实 世界，必须对现实世界进行建模。对于 地理信息系统而言，其结果就是空间数 据模型。
空间数据模型是整个GIS理论中最 为核心的内容。
3
一、现实世界抽象
4
OGC：
（OpenGIS Consortium） 美国的OpenGIS协会。
描述数据在计算机中的物理组织、存储路径和数据 库结构。
21
空间数据模型的 三个层次
22
目前GIS常用的空间数据模型（概念模型）有场（Field） 模型、要素（Feature）模型和网络（Network）模型。 • 场模型
场模型用于描述在一定空间内具有连续分布特点的地 理现象。例如，空气中污染物指数、地表的温度、土壤的 湿度、森林植被等。
6
• 点世界（Points World） • 几何体世界（Geometry World） • 地理要素世界（Feature World） • 要素集合世界（Feature Collection World） 九层模型中，前五个模型是对现实世界的抽象，并不 在计算机软件中被实现；后四个模型是现实世界的数学和 符号化模型，将在软件中被实现。
道路 1 河流 2 建筑 3 空地 4
§行 §列 §单元格大小 §分辨率
27
栅格数据模型中，每个像元具有固定的尺寸和位置， 其位置由像元所处的行号和列号决定。
由于栅格模型是用规则的“栅格块”来表现连续的自 然现象，且每个像元具有相同的值，因此分类之间的界限 被迫采用沿着栅格像元的边界线。这可能造成对现象的分 布的误解，其程度则取决于像元的大小（分辨率）。分辨 率的大小决定了栅格模型与现实世界的接近程度。
OpenGIS：
（Open Geodata Interoperation Specification） 开放的地理数据互操作规范
5
OpenGIS定义了从现实世界到地理要素集合世界的转换模 型，即将地理对象的抽象过程分为如下9个层次： • 现实世界（Real World） • 概念世界（Conceptual World） • 地理空间世界（Geospatial World） • 尺度世界（Dimensional World） • 项目世界（Project World）
7
8
• 现实世界（Real World） 现实世界是所有客观事物（Fact）的集合。
现实世界
9
• 概念世界（Conceptual World） 概念世界是人类自然语言的世界，人类了解且认识其所
命名的事物，因此这些事物构成了“语言的世界”。
概念世界
10
• 地理空间世界（Geospatial World） 对于GIS来讲，自然语言的概念世界并不是充分抽象的，
中进行工具测量获取要素的尺度。如距离、面积、方位等。
指北针
维度世界 13
• 项目世界（Project World） 项目世界是维度世界的进一步抽象，它将地理世界抽象
为针对特殊应用领域的具体实现。
制图员、地籍管理员和道路管理人员视角的项目世界
14
在项目世界中，空间参照系统（Spatial Reference System）的概念被引入，最常见的参照系统是环绕地球表 面建立的坐标系统（经纬度）；此外，还有其它的间接的 参照系统，例如线性参照系统可以用一个参数标识出一条 线（如高速公路）上的一个点位。
OGC是一个非赢利性组织，目的是促进采用新的技术 和商业方式来提高地理信息处理的标准化和互操作性。 OGC会员主要包括GIS相关的计算机硬件和软件制造商（包 括ESRI, Intergraph,MapInfo等知名GIS软件开发商）， 数据生产商以及一些高等院校，政府部门等，其技术委员 会负责具体标准的制定工作。
25
基于栅格的空间模型把空间看作像元（Pixel）的划分， 每个像元的值表明了在已知类中现象的分类情况。
荒地 1 湖泊 2 湿地 3 树林 4
栅格数据模型
26
栅格数据模型
地理编码是项目世界中地理要素的另一重要特征。
15
项目世界与地理空间世界的关系
16
地理要素在信息世界的实现 • 点世界（Points World） • 几何体世界（Geometry World） • 地理要素世界（Featቤተ መጻሕፍቲ ባይዱre World） • 要素集合世界（Feature Collection World）
根据对地理实体从现实世界到计算机内部表示的不 断抽象，GIS空间数据模型由概念数据模型、逻辑数据 模型和物理数据模型3个有机联系的层次组成。
20
• 概念数据模型 是关于空间实体及实体间联系的抽象概念集。
• 逻辑数据模型 根据概念数据模型确定的空间实体及相互关系，
具体地表达数据项、记录等之间的关系，因而可以有 若干不同的实现方法。（如结构化模型、关系模型） • 物理数据模型
在GIS中只有概念世界中一个简化的子集才是兴趣所在。 这个子集叫做地理空间世界。
地理空间世界 11
现实世界与地理空间世界的联系
在地理空间世界中，地理要素被抽象为点、线、面、 体。如河流被看作线，地形被看作等高线多边形的简化， 而森林被看作多边形。
12
• 维度世界（Dimensional World） 维度世界是对地理空间世界的抽象，它通过在欧氏空间
一个二维场就是在二维空间中任何已知的地点上，都 有一个表现这一现象的值；而一个三维场就是在三维空间 中对于任何位置来说都有一个值。
23
场模型可以表示为如下的数学公式： z(s))或f(x,y) 上式表示了从空间域到某个值域的映射，其中z为
空间位置可度量的函数，s表示空间中的位置。
24
• 栅格数据模型 栅格数据模型是场模型在信息系统中的具体实现。它
17
二、空间数据模型
18
• 数据模型 以一定方式组织数据，通过足够的抽象性和概括
性，对客观事物及其联系的进行描述,是连接现实世界 和计算机世界的桥梁。
• 空间数据模型 是关于现实世界中空间实体及其相互联系的概念，
它为空间数据的组织和空间数据库的设计提供基本方 法。
19
基于计算机的地理信息系统不能直接作用于现实世 界，必须采用一定的空间数据模型对现实世界进行数 据描述。
地理信息系统及应用
云南大学信息学院 梁虹
第二讲 空间数据模型
2
为了能够利用信息系统来描述现实 世界，必须对现实世界进行建模。对于 地理信息系统而言，其结果就是空间数 据模型。
空间数据模型是整个GIS理论中最 为核心的内容。
3
一、现实世界抽象
4
OGC：
（OpenGIS Consortium） 美国的OpenGIS协会。
描述数据在计算机中的物理组织、存储路径和数据 库结构。
21
空间数据模型的 三个层次
22
目前GIS常用的空间数据模型（概念模型）有场（Field） 模型、要素（Feature）模型和网络（Network）模型。 • 场模型
场模型用于描述在一定空间内具有连续分布特点的地 理现象。例如，空气中污染物指数、地表的温度、土壤的 湿度、森林植被等。
6
• 点世界（Points World） • 几何体世界（Geometry World） • 地理要素世界（Feature World） • 要素集合世界（Feature Collection World） 九层模型中，前五个模型是对现实世界的抽象，并不 在计算机软件中被实现；后四个模型是现实世界的数学和 符号化模型，将在软件中被实现。
道路 1 河流 2 建筑 3 空地 4
§行 §列 §单元格大小 §分辨率
27
栅格数据模型中，每个像元具有固定的尺寸和位置， 其位置由像元所处的行号和列号决定。
由于栅格模型是用规则的“栅格块”来表现连续的自 然现象，且每个像元具有相同的值，因此分类之间的界限 被迫采用沿着栅格像元的边界线。这可能造成对现象的分 布的误解，其程度则取决于像元的大小（分辨率）。分辨 率的大小决定了栅格模型与现实世界的接近程度。
OpenGIS：
（Open Geodata Interoperation Specification） 开放的地理数据互操作规范
5
OpenGIS定义了从现实世界到地理要素集合世界的转换模 型，即将地理对象的抽象过程分为如下9个层次： • 现实世界（Real World） • 概念世界（Conceptual World） • 地理空间世界（Geospatial World） • 尺度世界（Dimensional World） • 项目世界（Project World）
7
8
• 现实世界（Real World） 现实世界是所有客观事物（Fact）的集合。
现实世界
9
• 概念世界（Conceptual World） 概念世界是人类自然语言的世界，人类了解且认识其所
命名的事物，因此这些事物构成了“语言的世界”。
概念世界
10
• 地理空间世界（Geospatial World） 对于GIS来讲，自然语言的概念世界并不是充分抽象的，
中进行工具测量获取要素的尺度。如距离、面积、方位等。
指北针
维度世界 13
• 项目世界（Project World） 项目世界是维度世界的进一步抽象，它将地理世界抽象
为针对特殊应用领域的具体实现。
制图员、地籍管理员和道路管理人员视角的项目世界
14
在项目世界中，空间参照系统（Spatial Reference System）的概念被引入，最常见的参照系统是环绕地球表 面建立的坐标系统（经纬度）；此外，还有其它的间接的 参照系统，例如线性参照系统可以用一个参数标识出一条 线（如高速公路）上的一个点位。
OGC是一个非赢利性组织，目的是促进采用新的技术 和商业方式来提高地理信息处理的标准化和互操作性。 OGC会员主要包括GIS相关的计算机硬件和软件制造商（包 括ESRI, Intergraph,MapInfo等知名GIS软件开发商）， 数据生产商以及一些高等院校，政府部门等，其技术委员 会负责具体标准的制定工作。