浙教版八年级数学下册4.2(1)证明导学案

证明教学目标：1、继续学习证明的方法和表述。

2、通过探求，让学生归纳和掌握证明的两种思考方法。

注重对证明思路的启发，提倡证明方法的多样性。

3、并初步形成解题思路的思考途径。

——书写证明思路框图。

重点与难点： 本节教学的重点是如何分析证明的途径。

难点：难点是例6的证明，要用逆向思维的思考方法。

教学设想： 课本在教学中应注意在证明思路和方法上对学生的引导，帮助学生分析辅助线的添加、辅助图形的构造。

在这个过程中，原来在进行图形的折叠、拼摆等探索图形性质时所使用的方法对证明的思路也是很重要的，教师应注意引导启发。

很多图形性质及结论的证明的方法和途径是不唯一的，辅助线的添加方法也是多样的。

因此，教师在教学时要注意引导学生探索证明的不同方法，提倡证明方法的多样性，并引导学生在与他人的交流中比较证明方法的异同，提高逻辑思维水平。

在命题的探索和证明过程中，蕴涵着一些数学思想方法，如由特殊到一般的归纳思想方法、类比的思想方法、转化的思想方法、反证法的思想方法、分析法的思想方法等，教学中应注重这些思想方法的强化和渗透，有意识的引导学生去领会这些思想方法并运用在问题的解决过程中。

并注意培养学生逆向思维、逻辑思维等能力。

教学过程：一、例5教学例5 已知:如图，AD 是△ABC 的高，E 是AD上一点.AD=BD ，DE=DC ，求证:∠1=∠C.⌒B CDE 1A 想一想:（1）由已知AD 是△ABC 的高，可以得到什么?（2）由已知AD =BD ，DE =DC ，∠BDE = ∠ADC = Rt ∠，可以得到什么结论?（3）据此，你能得到∠1=∠C 吗?∟对于学生来说，主要是解题思路的寻求，在本题的学习之前，学生已经初步掌握对几何图形进行分析的基本方法——分解图形。

因此，教学中可要求对学生进行图形的分解（如下图）。

然后结合下图来分析理解题意。

总结：1、要证明一个结论，可以从已知出发，推出可能的结果，并与证明的结论比较，直至推出要证明的结论。

洪塘中学师生共用导学稿课题：《4.4.2平行四边形的判定定理》课型：新授课时间：4月4日主备人：审核人：八年级备课组编号：26班级姓名_____________一、学习目标1. 掌握平行四边行的判定定理“对角线互相平分的四边形是平行四边形”.2. 会运用“对角线互相平分的四边形是平行四边形”判断一个四边形是不是平行四边形.3. 会综合运用平行四边形的性质定理和判定定理解决简单的几何问题.重点：平行四边形的判定定理“对角线互相平分的四边形是平行四边形”难点：综合运用平行四边形的判定定理和性质定理二、预习领航1.想一想:(1)利用两个全等的三角形拼成一个平行四边形是利用什么原理呢?(2)平行四边形的性质有哪些？(3)平行四边形的判定方法有哪几种？定理3: 对角线互相平分的四边形也是平行四边形求证：四边形ABCD是平行四边形三、新知导学3.如图□ABCD中，E、F是对角线BD上的两点，且∠BAE=∠DCF求证：(1)BE=DF (2)四边形AFEC是平行四边形4.请用一把刻度尺画出一个平行四边形。

（不能推平行线，不能用直尺的平行的两边）四、课内练习5. 在□ABCD 中，顶点A 、C 与对角线BD 的距离________．6. 在□ABCD 中，周长为16，∠B 为锐角，对角线AC ⊥AB ，AC ＝4cm ，则AB ＝_____，S □ABCD ＝______.7. M 是△ABC 的AB 边上的中点，连接CM 并延长到D ，使MD ＝CM ，则AD 与BC_______________，BD 与AC________________．8. 四边形ABCD 的对角线AC,BD 相交于点O,OA=OC,OB=OD 则AB 与CD 的位置是____________ 9. 判断(1)四个内角都相等的四边形是平行四边形（ ） (2)一组对边平行且相等的四边形是平行四边形（ ） (3)一组对边平行，另一组对边相等的四边形是平行四边形 （ ） (4)对角线互相平分的四边形是平行四边形（ ） (5)一组对角相等，一组对边平行的四边形是平行四边形（ ）(6)一组对角相等，一组对边相等的四边形是平行四边形（ ）10. BD 是□ABCD 的对角线，点E,F 在BD 上，要使四边形AECF是平行四边形，还需要增加的一个条件是_______________________________.11. 如图四边形ABDE 和四边形AFCD 都是平行四边形，若AF ⊥ED ，若AG=3cm ，DG=4cm, □ABED 的面积为36，则四边形ABCD 的周长是___________12. 如图:□ABCD 中,O 是AD,BC 的交点,点N ,M,G,H 分别是OA,OB,OC,OD 上一点,且AN=DH,BM=CG则四边形MNHG 是平行四边形吗?13. 已知在直角坐标系中, 四边形 ABCD 四个顶点的坐标分别为A(2,3--), B (1, -1), C(2,3), D (-1, 1). 以点A, B, C, D 为顶点的四边形是不是平行四边形? 请给出证明.D BE G AC FB DC O NM G H。

第四章证明与命题复习课一、教学目标：1、了解定义、命题、定理的含义，会区分命题的条件（题设）和结论。

2、会在简单情况下判断一个命题的真假。

理解反例的作用，知道利用反例可证明一个命题是错误的。

3、了解证明的含义，理解证明的必要性，体会证明的过程要步步有据。

4、会根据一些基本事实证明简单命题。

5、通过实例，体会反证法的含义。

了解反证法的基本步骤。

6、初步会综合运用命题、证明以及相关知识解决简单的实际问题。

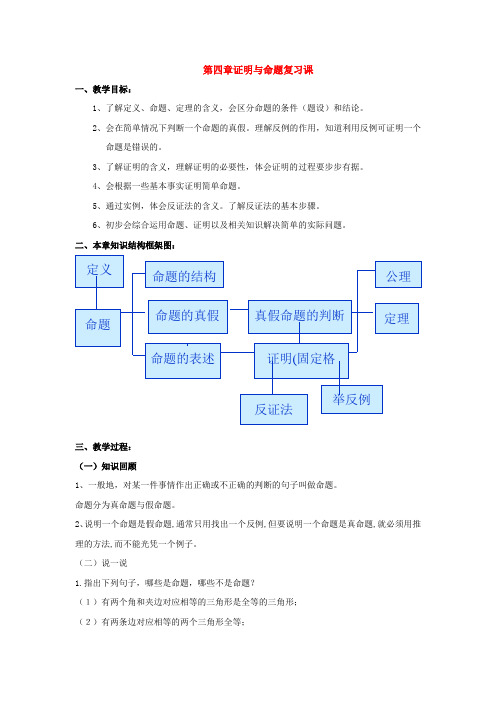
二、本章知识结构框架图：三、教学过程：（一）知识回顾1、一般地，对某一件事情作出正确或不正确的判断的句子叫做命题。

命题分为真命题与假命题。

2、说明一个命题是假命题,通常只用找出一个反例,但要说明一个命题是真命题,就必须用推理的方法,而不能光凭一个例子。

（二）说一说1.指出下列句子，哪些是命题，哪些不是命题？（１）有两个角和夹边对应相等的三角形是全等的三角形；（２）有两条边对应相等的两个三角形全等；（３）作∠Ａ的平分线；（４）若ａ＝ｂ 则 a 2= b 2（5） 同位角相等吗?2.说出一个已学过定理:说出一个已学过公理:3、下列把命题改写成“如果……，那么……”的形式。

并判断下列命题的真假.（1）不相等的角不可能是对顶角.（2）垂直于同一条直线的两直线平行；（3）两个无理数的乘积一定是无理数.（三）练一练1. 用反例证明下列命题是假命题：(1) 若x(５-x)=0，则x=0；(2) 等腰三角形一边上的中线就是这条边上的高；(3) 相等的角是内错角；（4）若x ≠2,则分式 有意义.（四）例题分析例1求证:全等三角形对应角的平分线相等.证明命题的一般步骤:(1)根据题意,画出图形;(2)用符号语言写出“已知”和“求证”;(3)分析证明思路;(4) 写出证明过程;例2已知：如图，△ABC 中,∠C=2∠B ，∠BAD=∠DAC.求证：AB=AC+CD42 x x还有其他方法吗？AAEB DC BD C(第三题) (第二题)例3已知：如图D,E分别是BC,AB上的一点,BC、BD的长度之比为3:1, △ECD的面积是△ABC的面积的一半.求证： BE=3AE例4、已知：如图，直线AB，CD，EF在同一平面内，且AB ∥ EF，CD ∥ EF，求证：AB ∥ CD。

八年级数学下册 4.2《证明》学案（2）浙教版4、2 证明 (2)【学习目标】1、进一步体会证明的含义；２、探索并理解三角形内角和定理的几何证明；３、进一步熟练证明的方法和表述；４、体验从实验几何向推理几何的过渡【学习过程】1、复习证明的一般格式和表述，①按题意画出图形；②分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论；A ③在“证明”中写出推理过程、2、例3、求证：三角形三内角和等于180CB分析：（1）并根据条件和结论画出图形，写出已知:求证:（2）之前是用实验方法加以说明:将纸片三角形顶角剪下，随意将它们拼凑在一起。

（3）请同学们思考：如何通过添加辅助线的方法把三个角拼在一起，________线容易产生相等的角？1、在证明三角形内角和定理时，小明的想法是把三个角“凑”到A处，他过点A作直线DE//BC，（如图）。

他的想法可行吗？请证明:请同学们再思考，除了选三角形顶点作平行线之外，还有没有其他方法?问：三角形内角和外角之间有什么关系？_________________________________________________________ _____________________________________________练习：书上做一做例4、已知：如图，AD是∠BAC的角平分线，BC⊥AD于点O，AC⊥DC于点C、求证：（1）⊿ABC是等腰三角形；（2）∠D=∠B、点拨：（1）要证明⊿ABC是等腰三角形，只需证明什么？________________________（2）证明两边相等或两角相等常用的方法是什么？____________ 图中能否找到以AB，AC为对应边的全等三角形？是____________⊿ABO与⊿ACO全等吗？______应该满足什么条件？____________ （3）要证明∠D=∠B，你能找到合适的全等三角形吗？是____________ 根据已知AC⊥DC，能得到∠D与三角形中哪个角互余？____________ 根据已知BC⊥DA，能得到∠B与三角形中哪个角互余？____________ 小结：此题是由结论出发寻求解题思路，这是常用的一种数学方法――分析法、当堂练习：书上作业题证”三角形三内角和等于180”的其它方法:1、证明：作BC的延长线CD，过点C作射线CE//AB，证明：2、可在BC边上任意取一点P，作PD∥AB，交AC于点D；作PE∥AC，交AB于点E。

浙教版初中数学
重点知识精选掌握知识点，多做练习题，基础知识很重要！
浙教版初中数学和你一起共同进步学业有成！
课题4.2平行四边形及其性质(2)
备课组：八数主备人：孙慧日期：2015.4.14 执教者：
学习目标1、会用平行线的“夹在两条平行线间的平行线段和垂线段相等”的性质。

2、了解两条平行线间的距离的意义，能度量两条平行线间的距离。

重
点
难
点
重点：夹在两条平行线间的平行线段相等
难点：例2及运用同（等）底等（同）高原理进行等积变形课前自学　课中交流课堂教学设计
一、【知识链接】
//CD,
夹在两条平行线间的垂线段相等．
AB=
课本
、课本 1
课前自学　课中交流课堂教学设计
图，三棱柱上、下底面是一个等腰直角三角形，腰长为
现要将这个三棱柱通过宽为
若把它改成一个以
(2)，若把它改成一个以请画图说明．
教师不光要传授知识，还要告诉学生学会生活。

数学思维可以让他们更理性地看待人生。

瑞安市新纪元实验学校三学循环导学案学科数学课题 4.6反证法授课教师
学习水平知识目标细化识
记
领
悟
运
用
分
析
综
合
评
价
目标一反证法的基本步骤√
目标二理解反证法证明问题的合理性√
目标三√
重、难点本节教学的重点是反证法的含义和步骤．
课本“合作学习”要求用两种方法完成平行线的传递性的证明，有较高难度，是本节教学的
难点．
导学过程设计
自学
认真阅读教材P100---P101,通过阅读课本，掌握反证法的定义及其步骤。

2.写出下列各结论的反面：
（1）a//b；（2）a≥0；
（3）b是正数；（4）a⊥b
3.求证：在同一平面内,如果一条直线和两条平行直线中的一条相交,那么和另一条也相交。

已知：如图，a∥b，c与a相交于点P
求证：c与b相交
议学
1.反证法的步骤有哪些？
2.宜用反证法证明的题型有哪些？
悟学提高
如图，在△ABC中,若∠C是直角，那么∠B一定是锐角.
课后练习
1、写出下列各结论的反面：
（1）a//b
a
b
c
P。

“体验型课堂”学习方案数学（八年级下册）班级：姓名：学号：___ 命题者：徐巧波审核者：裘爱尔4.2证明（3）【学习导言】我能完成简单的证明题吗？我会通过逆向思维的思考方式去完成证明？课前尝试：尝试体验（对话课本，记下问题，尝试练习）【对话课本】阅读教材79页到80页【记下重点与问题】[记下问题]【尝试练习】1．1.如图，在△ABC中，CF⊥AB于点F，点D在BC上，DE⊥AB于点E，若∠1=∠2，求证：FG∥BC．证明：∵CF⊥AB，DE⊥AB（已知），∴∠BED=90°，∠BFC=90°（）.∴∠BED=∠BFC．∴ED∥FC（）．∴∠1=∠BCF（）．又∵∠1=∠2（已知），∴∠2=∠BCF．∴FG∥BC（）．2.如图，在四边形ABCD中，点E和F在DC上，DF=EC，AD=BC，∠D=∠C.求证：△AED•≌△BFC．•课内对话：合作体验（检评预习，审视问题，独立练习，纠错反审）【检评预习】同桌交换学案，检查评价批语：【审视问题】审视下面的学习要点，思考提出的问题（1）书写证明过程要注意些什么？（2）证明题应如何分析？【尝试例题】例1 已知：AD是V ABC的高，E是AD上一点，若AD=BD，DE=DC，求证: ∠1=∠C.例2 已知：如图，AD是三角形纸片ABC的高，将纸片沿直线EF 折叠，使点A与点D重合。

求证：EF P BC【独立练习】1．如图，在△ABC中，AB=AC，D和E是线段BC上的两点，AD=AE，求证：BD=CE．2．如图，AC=AB，∠1=∠2，E为AD上一点，求证△DCE≌△DBE.3.如图，在等边三角形ABC中，D，E，F分别是BC，AC，AB上的点，且AF=BD=CE.求证：△DEF是等边三角形．课后反审：反审体验（审查错误原因，检查练习，完成作业）【反思审查】再仔细审查学案，用红笔作出示意。

【作业练习】作业本（1）4.2(3)。

4.2平行四边形及其性质
班级＿＿＿姓名＿＿＿＿第＿＿小组
操作：画出平行四边形ABCD的对角线AC和BD，它们交于点O。

你能得到那些线段相等？你能证明你的猜想吗？
结论：平行线的性质：
应用：
（1）在口ABCD中，AC和BD交于点O，AB=4，△AOB的周长为16，则AC+BD= 。

（2）已知O是口ABCD两条对角线的交点，AC=24cm，BC=38cm，OD=28cm，则⊿OBC的周长为__________。

（3）如图，口ABCD的对角线AC，BD相交于点O。

已知AB=5cm，
△AOB的周长和△BOC的周长相差3cm，则AD的长为__________。

（4）有没有这样的平行四边形，它的两条对角线长分别为14cm
和20cm，它的一边长为18cm?为什么?若平行四边形的边长为
xcm，则x的取值范围为多少？
课内练习
1、如图：四边形ABCD是平行四边形，AB=10，AD=8，AC⊥BC，求BD。

2、已知：如图，口ABCD的对角线AC，BD交于点O。

过点O作
直线EF，分别交AB，CD于点E，F。

求证：OE=OF。

变式：已知：如图，口ABCD的对角线AC，BD交于点O。

过点O作直线EF，分别交AB、CD的延长线于点E，F。

OE还与OF相等吗？
小结：。