新课标高三理科数学下期考前练习题

2021年高三下学期理科数学测试题（5）一、选择题（本大题共10小题，每小题5分，共50分，1、已知全集，集合1|{},0)1)(2(|{-=>-+=x B x x x A ≤则（C U B ）为A ．B ．≥C ．D ．≥2、已知直线平面，直线平面，给出下列命题:（1）（2） （3） （4）其中正确命题的序号是A 、（1）（2）（3）B 、（2）（3）（4）C 、（2）（4）D 、（1）（3）3、将函数的图象按向量平移后，得到的图象，则 （ ）A ．=（1，2）B ．=（1，－2）C ．=（－1，2）D ．=（－1，－2）4、等差数列的公差，若与的等比中项，则（ ）A ．2B ．4C ．6D ．85、设随机变量～B(2,p), ～B(4,p),若，则的值为A .B . C. D .6、设命题P ：底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥；命题Q ：在中是22cos ()cos ()2424A B ππ+<+成立的必要非充分条件, 则（ ） A ．P 真Q 假 B ．P 且Q 为真 C ．P 或Q 为假 D ．P 假Q 真7、设不等式组x 1x-2y+30y x ≥⎧⎪≥⎨⎪≥⎩所表示的平面区域是,平面区域是与关于直线对称,对于中的任意一点A 与中的任意一点B, 的最小值等于( )A ．B ．4C ．D ．28、半径为的球的直径垂直于平面，垂足为，是平面内边长为的正三角形，线段、分别与球面交于点、，那么、两点间的球面距离是（ ）A. B C D9、设,.定义一种向量积：12121122(,)(,)(,)a b a a b b a b a b ⊗=⊗=.已知,点在的图象上运动,点在的图象上运动,且满足 (其中为坐标原点),则的最大值及最小正周期分别为（ ）A ．，B ．，C ．， Ｄ．，10、已知椭圆的离心率为，过右焦点且斜率为的直线与相交于两点．若，则（ ）（A ）1 （B ） （C ） （D ）2二、填空题（本大题共5小题，每小题5分，共25分。

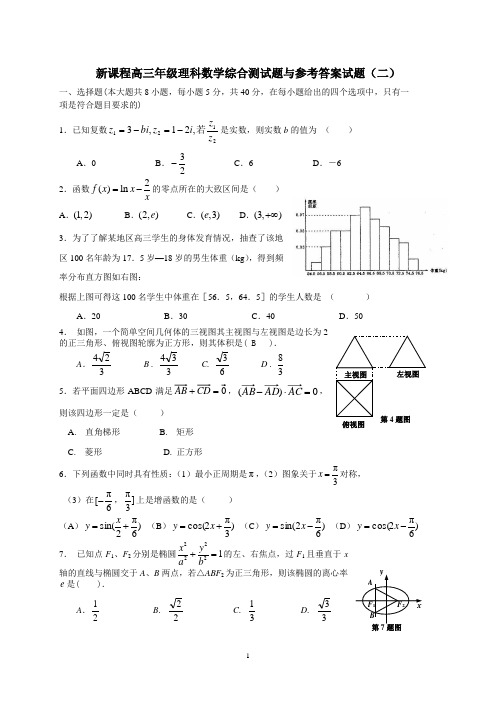
新课程高三年级理科数学综合测试题与参考答案试题（二）一、选择题(本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一 项是符合题目要求的)1．已知复数2121,21,3z z i z bi z 若-=-=是实数，则实数b 的值为 （ ）A ．0B ．23-C ．6D ．－62．函数2()ln f x x x=-的零点所在的大致区间是（ ） A ．(1,2) B ．(2,)e C ．(,3)e D ．(3,)+∞ 3．为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17．5岁—18岁的男生体重（kg ），得到频率分布直方图如右图：根据上图可得这100名学生中体重在［56．5，64．5］的学生人数是 （ ）A ．20B ．30C ．40D ．504． 如图，一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形，则其体积是( B )．A ．324 B . 334 C. 63D . 385．若平面四边形ABCD 满足=+，0)(=⋅-AC AD AB ，则该四边形一定是（ ）A. 直角梯形B. 矩形C. 菱形D. 正方形6．下列函数中同时具有性质：（1）最小正周期是π，（2）图象关于3π=x 对称， （3）在6π[-，]3π上是增函数的是（ ） （A ）)6π2sin(+=x y （B ）)3π2cos(+=x y （C ）)6π2sin(-=x y （D ）)6π2cos(-=x y7． 已知点F 1、F 2分别是椭圆22221x y a b+=的左、右焦点，过F 1且垂直于x轴的直线与椭圆交于A 、B 两点，若△ABF 2为正三角形，则该椭圆的离心率e 是( )．A ．21 B . 22 C . 31 D . 33俯视图8．图中阴影部分的面积S 是h 的函数)0(H h ≤≤，则该函数的大致图象是 （ ）二、填空题：（本大题共7小题，每小题5分，其中9－12为必做题，13－15为选做题，13－15题只需选做2小题．共30分．） 9．已知点P 是圆054:22=---+ay x y x C 上任意一点，P 点关于直线012=-+y x 的对称点也在圆C 上，则实数a = .10.已知⎰=⎪⎩⎪⎨⎧∈-∈+=20)(]2,1(2]1,0[12)(dx x f x xx x x f ，则 。

新高三数学测试题及答案一、选择题（每题4分，共40分）1. 若函数f(x) = x^2 - 6x + 8，则f(3)的值为：A. -1B. 1C. 9D. 11答案：B2. 已知等差数列{a_n}中，a_1 = 2，公差d = 3，求a_5的值。

A. 14B. 17C. 20D. 23答案：A3. 圆的方程为(x - 2)^2 + (y - 3)^2 = 9，圆心坐标为：A. (2, 3)B. (-2, -3)C. (0, 0)D. (3, 2)答案：A4. 函数y = sin(x) + cos(x)的值域为：A. [-1, 1]B. [-√2, √2]C. [0, 2]D. [1, 2]答案：B5. 已知集合A = {1, 2, 3}，B = {2, 3, 4}，则A∩B =：A. {1}B. {2, 3}C. {3, 4}D. {1, 2, 3}答案：B6. 已知向量a = (3, 4)，b = (-4, 3)，则向量a与向量b的夹角θ满足：A. cosθ = 1/7B. cosθ = -1/7C. cosθ = 7/√50D. cosθ = -7/√50答案：A7. 函数y = x^3 - 3x^2 + 4x的导数y'为：A. 3x^2 - 6x + 4B. x^2 - 3x + 4C. 3x^2 - 6x + 1D. x^2 - 3x + 2答案：A8. 已知复数z = 2 + 3i，求|z|的值。

A. √13B. √19C. √7D. √17答案：A9. 已知双曲线方程为x^2/9 - y^2/16 = 1，求其渐近线方程。

A. y = ±(4/3)xB. y = ±(3/4)xC. y = ±(16/9)xD. y = ±(9/16)x答案：A10. 已知等比数列{b_n}中，b_1 = 2，公比q = 2，求b_4的值。

A. 16B. 32C. 64D. 128答案：A二、填空题（每题4分，共20分）1. 已知函数f(x) = x^3 - 3x^2 + 2，求f'(x) = _______。

一、选择题（本大题共12小题，每小题5分，共60分）1. 下列函数中，在区间（0，+∞）上单调递增的是（）A. y = -2x + 1B. y = x^2 - 2xC. y = 2^xD. y = log2x2. 已知函数f(x) = ax^2 + bx + c，若f(1) = 2，f'(2) = 0，则f(x)的对称轴方程为（）A. x = -1B. x = 1C. x = 2D. x = 33. 设等差数列{an}的前n项和为Sn，若S5 = 20，S10 = 60，则数列{an}的公差d为（）A. 1B. 2C. 3D. 44. 在极坐标系中，点P(ρ, θ)的直角坐标为（x, y），若ρ = 5，θ = π/6，则点P到原点的距离为（）A. 2.5B. 5C. 10D. 255. 已知向量a = (1, 2)，向量b = (2, 3)，则向量a与向量b的夹角余弦值为（）A. 1/5B. 2/5C. 3/5D. 4/56. 函数f(x) = |x - 1| + |x + 1|的最小值为（）A. 0B. 1C. 2D. 37. 若等比数列{an}的公比为q，且q ≠ 1，若a1 + a2 + a3 = 6，a1 + a2 + a3 + a4 = 24，则q的值为（）A. 2B. 3C. 4D. 68. 已知函数f(x) = x^3 - 3x^2 + 2x，若f(x)在x = 1处取得极小值，则f'(1) = （）A. -2B. -1C. 0D. 19. 若复数z满足|z - 1| = |z + 1|，则复数z在复平面上的几何位置为（）A. 位于实轴上B. 位于虚轴上C. 位于第一象限D. 位于第二象限10. 设函数f(x) = x^3 - 3x^2 + 4x，若f'(x) = 0，则f(x)的极大值为（）A. 1B. 2C. 3D. 411. 在三角形ABC中，已知角A、B、C的对边分别为a、b、c，若a = 3，b = 4，c = 5，则sinA + sinB + sinC的值为（）A. 6B. 8C. 10D. 1212. 已知函数f(x) = e^x + 2，若f(x)在x = 0处取得极小值，则f'(0) = （）A. 1B. eC. e^2D. e^3二、填空题（本大题共8小题，每小题5分，共40分）13. 已知等差数列{an}的首项为a1，公差为d，若a1 + a2 + a3 = 12，则数列{an}的通项公式为______。

高考新课标理科数学押题试卷（试题及答案）整理高考新课标理科数学押题试卷（试题及答案）数学解题肯定要清楚，函数或方程或不等式的题目，先直接思索后建立三者的联系。

首先考虑定义域，其次使用“三合肯定理”。

下面是我为大家整理的高考新课标理科数学押题卷，盼望对您有所关心!高考新课标理科数学押题试题高考新课标理科数学押题答案数学解题方法1、解决肯定值问题主要包括化简、求值、方程、不等式、函数等题，基本思路是：把含肯定值的问题转化为不含肯定值的问题。

详细转化方法有：①分类争论法:依据肯定值符号中的数或式子的正、零、负分状况去掉肯定值。

①零点分段争论法：适用于含一个字母的多个肯定值的状况。

①两边平方法：适用于两边非负的方程或不等式。

①几何意义法：适用于有明显几何意义的状况。

2、因式分解依据项数选择方法和根据一般步骤是顺当进行因式分解的重要技巧。

因式分解的一般步骤是：提取公因式选择用公式十字相乘法分组分解法拆项添项法3、配方法利用完全平方公式把一个式子或部分化为完全平方式就是配方法，它是数学中的重要方法和技巧。

4、换元法解某些简单的特型方程要用到“换元法”。

换元法解方程的一般步骤是：设元→换元→解元→还元5、待定系数法待定系数法是在已知对象形式的条件下求对象的一种方法。

适用于求点的坐标、函数解析式、曲线方程等重要问题的解决。

其解题步骤是：①设①列①解①写6、简单代数等式简单代数等式型条件的使用技巧：左边化零，右边变形。

①因式分解型：(-----)(----)=0两种状况为或型①配成平方型：(----)2+(----)2=0两种状况为且型7、数学中两个最宏大的解题思路(1)求值的思路列欲求值字母的方程或方程组(2)求取值范围的思路列欲求范围字母的不等式或不等式组8、化简二次根式基本思路是：把√m化成完全平方式。

9、观看法10、代数式求值方法有：(1)直接代入法(2)化简代入法(3)适当变形法(和积代入法)留意：当求值的代数式是字母的“对称式”时，通常可以化为字母“和与积”的形式，从而用“和积代入法”求值。

2021-2022年高三下学期理科数学测试题（9）一、选择题：本大题共10小题，每小题5分，共50分。

1．设集合，，则（）A． B． C． D．2．设复数且，则复数z的虚部为（）A．-1 B．0 C．1 D．3．直线与直线互相垂直，则a的值为（）A．-2 B．-1 C．1 D．2 4．“”是“数列为递增数列”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5.有编号分别为1、2的2个红球、2个黑球、2个白球，从中任取2个，则取出的编号与颜色互不相同的概率为（）A．B．C．D．6.已知等比数列的前10项的积为32，则以下命题为真命题的是（）A．数列的各项均为正数B．数列中必有小于的项C．数列的公比必是正数D．数列中的首项和公比中必有一个大于17．F1、F2是双曲线的左右焦点，P是曲线上任意一点，则|PF1|+|PF2|的值不可以是（）A．xx B．25 C．10 D．48．在中，，AB=2，AC=1，E，F为边BC的三等分点，则（）A．B．C．D．9．已知函数满足，且直线与的图象有5个交点，则这些交点的纵坐标之和为（）A．10 B．5 C．4 D．310．球O的球面上有四点S，A，B，C，其中O，A，B，C四点共面，ABC是边长为2的正三角形，面SAB⊥面ABC，则棱锥S—ABC的体积的最大值为（）A．B．C．D．二、填空题：本大题共5小题，每小题5分，共25分。

把答案填在答题卡中对应题号后的横线上。

11．某时段内共有100辆汽车经过某一雷达地区，时速频率分布直方图如下图所示，则时速超过60km/h 的汽车数量为 辆。

12．存在两条直线与双曲线相交于四点A ，B ，C ，D ，且四边形ABCD 为正方形，则双曲线的离心率的取值范围为__________。

13．设、都是锐角，且，，则=14．已知平面向量满足：||||||1,0OA OB OC OA OB ===⋅=，若，则的最大值是 。

全国卷理科数学模拟试题一第Ⅰ卷一 选择题：本题共12题，每小题5分，共60.在每小题给出的四个选项中，有且只有一个是正确的.1．设集合{1,2,3,4},{1,2,3},{2,3,4}U M N ===，则)(N M C U = （ ） A.{1,2} B.{2,3} C.{2,4} D.{1,4} 2.复数131iZ i -=+的实部是（ ） A ． 2 B ． 1C ．1-D ．4-3.设0.8log 0.9a =， 1.1log 0.9b =，0.91.1c =,则a ，b ， c 的大小关系是 ( ) （A ）a b c <<（B ）a c b << （C ）b a c <<（D ）c a b <<4．如图，在66⨯的方格纸中，若起点和终点均在格点的向量,,a b c 满足,(,)c xa yb x y R =+∈，则x y +=A ．0B ． 1C ．5D ．1355.下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程ˆｙ＝3-5x ,变量x 增加一个单位时,y 平均增加5个单位; ③回归方程ˆˆˆｙ＝bx+a 必过（x,y) ④有一个2×2列联表中,由计算得2k =13.079,则有99%的把握确认这两个变量间有关系.其中错误的个数是( )(A)0 (B)1 (C)2 (D)3P(2k ≥0k )0.50 0.40 0.25 0.15 0.10 0.05 0. 025 0.010 0k0.4550.7081.3232.0722.7063.8415. 0246.635a b c6．执行如图的程序框图，输出的S 值是（ ） A ．23-B ．23C ．0D ．37．等差数列{a n }中，a 1+a 2+…+a 50＝200，a 51+a 52+…+a 100＝2700，则a 1等于( ) A ．－1221 B ．－21．5 C ．－20．5 D ．－208．下列命题中正确的是（ ）A ．若p q ∨为真命题，则p q ∧为真命题B ．“0a >，0b >”是“2b aa b+≥”的充分必要条件 C ．命题“若2320x x -+=，则1x =或2x =”的逆否命题为“若1x ≠或2x ≠，则2320x x -+≠”D ．命题:p R x ∃∈，使得210x x +-<，则:p ⌝R x ∀∈，使得210x x +-≥9．设等比数列{}n a 的前n 项和为n S ．则“10a >”是“32S S >”的（ ） （A ）充分而不必要条件 （B ）必要而不充分条件 （D ）既不充分又不必要条件 （C ）充要条件10.某四棱柱的三视图如图所示，该几何体的各面中互相垂直的面的对数是（ ）A ．2B ．4C ．6D ．811.设Q P ,分别为()2622=-+y x 和椭圆11022=+y x 上的点，则Q P ,两点间的最大距离是（ ）.52A B.246+ C.27+ D.2612.已知函数2,1,()1,1,x ax x f x ax x ⎧-+≤=⎨->⎩若1212,,x x x x ∃∈≠R ，使得12()()f x f x =成立，则实数a 的取值范围是 ( ) （A ）2a （B ）2a （C ）22a （D ）2a 或2a第II 卷本卷包括必考题和选考题两部分。

2023年高考-数学（理科）考试备考题库附带答案第1卷一.全考点押密题库(共50题)1.(单项选择题)(每题 5.00 分) 已知A，B 是球 O 的球面上两点，∠AOB = 90° ，C为该球面上的动点。

若三棱锥 O - ABC 体积的最大值为36，则球 O 的表面积为A. 36πB. 64πC. 144πD. 256π正确答案：C,2.(填空题)(每题 5.00 分) 已知圆锥的顶点为S，母线SA，SB所成角的余弦值为7/8,SA与圆锥底面所成角为45°.若△SAB的面积为5√15，则该圆锥的侧面积为.正确答案：40√2π，3.(单项选择题)(每题 5.00 分) 记SN.为等差数列αN}的前n项和.若3S3=S2+S4，α=2,则α5= {A. -12B. -10C. 10D. 12正确答案：B,4.(填空题)(每题5.00 分) 已知函数f(x)=2sinx+sin2x，则f(x)的最小值是_______?正确答案：-3√3/2，5.(单项选择题)(每题 5.00 分) 双曲线x2/α2-y2/b2=1(α>0,b>0)的离心率为√3，则其渐近线方程为A. y=±√2xB. y=±√3xC. y=±√2/2xD. y=±√3/2x正确答案：A,6.(单项选择题)(每题 5.00 分) 已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为A. 3√3/4B. 2√3/3C. 3√2/4D. √3/2正确答案：A,7.(单项选择题)(每题 5.00 分) 已知集合A=x∣x2-x-2>0}，则CRA={A. x∣-12}{D. {x∣x≦-1}∪{x∣x≧2}正确答案：B,8.(单项选择题)(每题 5.00 分) 在△ABC中，cos C/2=√5/5,BC=1,AC=5,则AB=A. 4√2B. √30C. √29D. 2√5正确答案：A,9.(填空题)(每题 5.00 分) 某髙科技企业生产产品 A 和产品 B 需要甲、乙两种新型材料。

2024届陕西省高三下学期高考数学（理科）模拟检测试题（十模）第Ⅰ卷（选择题 共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知集合，则（ ）{}{}212,30A x x B x x x =-≤≤=-+>∣∣A B = A ．B ．C ．D ．R(]0,2[)1,0-[)1,3-2．定义运算，则满足（i 为虚数单位）的复数在复平面内a b ad bc c d =-i01i 2iz -=--z 对应的点在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知菱形的边长为1，，则（ABCD 60,,,AB a BC b AC A c ∠=︒=== 2a b c ++=）A B C D 4．黄地绿彩云龙纹盘是收藏于中国国家博物馆的一件明代国宝级瓷器．该龙纹盘敞口，弧壁，广底，圈足．器内施白釉，外壁以黄釉为地，刻云龙纹并填绿彩，美不胜收．黄地绿彩云龙纹盘可近似看作是圆台和圆柱的组合体，其口径，足径，高，22.5cm 14.4cm 3.8cm 其中底部圆柱高，则黄地绿彩云龙纹盘的侧面积约为（）（附：的值取3，0.8cm π）5≈A ．B ．C ．D ．2300.88cm2311.31cm2322.24cm2332.52cm5．已知函数是奇函数，则（ ）()()2021x x bf x a ab +=+≠-A ．B ．C ．D ．1a b +=1a b -=-21a b +=21a b -=-6．2024年中国足球乙级联赛陕西联合的主场火爆，一票难求，主办方设定了三种不同的票价分别对应球场三个不同的区域，五位球迷相约看球赛，则五人中恰有三人在同一区域的不同座位方式共有（ ）A ．30种B ．60种C ．120种D ．240种7．设是坐标原点，在区域内随机取一点，记该点为，则直线的O (){},1x y x y +≤P OP 倾斜角不大于的概率为（ ）3π4A ．B ．C ．D ．345812148．一个几何体的三视图如图所示，如果该几何体的顶点都在球的球面上，那么球的表O O 面积是（）A ．B ．C ．D ．2π4π8π16π9．在平面直角坐标系中，圆的方程为，若直线上存在一xOy C 2240x y y +-=1y kx =-点，使过点所作的圆的两条切线相互垂直，则实数的值不可能是（ ）P P kA ．－1B ．C ．D 14-1210．2024年1月九省联考的数学试卷出现新结构，其中多选题计分标准如下：①本题共3小题，每小题6分，满分18分；②每道小题的四个选项中有两个或三个正确选项，全部选对得6分，有选错的得0分；③部分选对得部分分（若某小题正确选项为两个，漏选一个正确选项得3分；若某小题正确选项为三个，漏选一个正确选项得4分，漏选两个正确选项得2分）．已知在某次新结构数学试题的考试中，小明同学三个多选题中第一小题确定得满分，第二小题随机地选了两个选项，第三小题随机地选了一个选项，则小明同学多选题所有可能总得分（相同总分只记录一次）的中位数为（ ）A ．9B ．10C ．11D ．1211．已知抛物线的焦点为，准线为，过的直线与()2:20C y px p =>F l F 交于两点，为的中点，且于点的垂直平分线交轴于点，C ,A BD AB DM l ⊥,M AB x N四边形的面积为，（ ）DMFN p =A ．B ．C ．D ．12．已知函数，对，有()()π2sin 0,2f x x ωϕωϕ⎛⎫=+><⎪⎝⎭x ∀∈R ，，且函数在上单调递增，ππ1212f x f x ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭()π02f x f x ⎛⎫+-= ⎪⎝⎭()f x π,010⎛⎫- ⎪⎝⎭则的值为（ ）ωA ．3或9B ．3C ．9D ．6第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题卷中相应的横线上．）13．已知双曲线的左右焦点分别为，曲线上的点()2222:10,0x y C a b a b -=>>12,F F C 满足，，则双曲线的离心率为______．M 1212π0,6F M F M MF F ⋅=∠=14．如图，四边形是圆柱的轴截面，是底面圆周上异于的一点，则下面结论ABCD E ,A B 中正确的序号是_____．（填序号）①；②；③平面；④平面平面．AE CE ⊥BE DE ⊥DE ⊥BCE ADE ⊥BCE15．已知大屏幕下端离地面3.5米，大屏幕高3米，若某位观众眼睛离地面1.5米，则这B 位观众在距离大屏幕所在的平面多远，可以获得观看的最佳视野？（最佳视野是指看到屏幕上下夹角的最大值）______米．16．已知函数，函数有两个极值点．若()()21ln 2x f x mx x mx =-+-()()g x f x ='12,x x ，则的最小值是______．110,e x ⎛⎤∈ ⎥⎝⎦()()12g x g x -三、解答题：本大题共5小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）“村超”是贵州省榕江县举办的“和美乡村足球超级联赛”的简称．在2023年火爆“出圈”后，“村超”热度不减．2024年1月6日，万众瞩目的2024年“村超”新赛季在“村味”十足的热闹中拉开帷幕，一场由乡村足球发起的“乐子”正转化为乡村振兴的“路子”，为了解不同年龄的游客对“村超”的满意度，某组织进行了一次抽样调查，分别抽取年龄超过35周岁和年龄不超过35周岁各200人作为样本，每位参与调查的游客都对“村超”给出满意或不满意的评价．设事件“游客对“村超”满意”，事件“游客年龄不超过35周岁”，A =B =据统计，．()()48,515P AB P B A ==∣∣（1）根据已知条件，填写下列列联表并说明理由；22⨯年龄满意不满意合计年龄不超过35周岁年龄超过35周岁合计（2）由（1）中列联表数据，分析是否有的把握认为游客对“村超”的满意度与年22⨯99%龄有关联？附：．()()()()()22,n ad bc K n a b c d a b c d a c b d -==+++++++参考数据：()20P K k ≥0.100.050.0250.0100.0050.0010k 2.7063.8415.0246.6357.87910.82818．（本小题满分12分）如图，已知正方体的棱长为2，E ，F 分别为1111ABCD A B C D -的中点．1,AD CC （1）已知点满足，求证B ，E ，G ，F 四点共面；G 14DD DG =（2）求平面BA 1C 1与平面BEF 所成的锐二面角的余弦值．19．（本小题满分12分）数列的前项的最大值记为，即{}n a n n M ；前项的最小值记为，即，令{}12max ,,,n n M a a a =⋅⋅⋅n n m {}12min ,,,n n m a a a =⋅⋅⋅，并将数列称为的“生成数列”．n n n p M m =-{}n p {}n a （1）设数列的“生成数列”为，求证：；{}n p {}n q n n p q =（2）若，求其生成数列的前项和．23n n a n =-{}n p n20．（本小题满分12分）已知椭圆2222:1(0)x y C a b a b +=>>分别为下顶点为，右顶点为的面积为．12,F F A 1,B ABF △1+（1）求椭圆的方程．C （2）设不过原点的直线交椭圆于M ，N 两点，且直线OM ，MN ，ON 的斜率依次成等O C 比数列，求面积的取值范围．MON △21．（本小题满分12分）已知函数，曲线π())e ,0,2x f x x a ϕϕ-⎛⎫=+-+∈ ⎪⎝⎭在点处的切线与轴平行或重合．()y f x =(0,(0))f x （1）求的值；ϕ（2）若对恒成立，求的取值范围；0,()0x f x ∀≥≤a （3）利用下表数据证明：．1571πsin103314k k =<∑π314e π314e 78π314e 78π314e79π314e79π314e-1.0100.9902.1820.458 2.2040.454四．选做题：请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题计分，做答时请写清题号。