2012年德化一中毕业班质量检查试卷数学(理)参考解答及评分标准

初中毕业生学业测试数学试卷2012.5试 题 卷 Ⅰ一、选择题（每小题3分，共36分，在每小题给出的四个选项中，只有一项符合题目要求） 1． –3的相反数是（ ▲ ）A.13B.3C.31- D.3- 2．方程x 2 = 2x 的解是（ ▲ ）A.x=2B.x 1=2-，x 2= 0C.x 1=2，x 2=0D.x = 03．已知甲、乙两组数据的平均数相等，若甲组数据的方差2s 甲＝0.055，乙组数据的方差2s 乙＝0.105，则（ ▲ ）A.甲组数据比乙组数据波动大B.乙组数据比甲组数据波动大C.甲组数据与乙组数据的波动一样大D.甲、乙两组数据的数据波动不能比较 4．据某网站报道：一粒废旧纽扣电池可以使600吨水受到污染．某校团委四年来共回收废旧纽扣电池3500粒，若这3500粒废旧纽扣电池可以使m 吨水受到污染．用科学记数法表示m 为（ ▲ ）A.2.1×105B.2.1×10－5 C.2.1×106 D.2.1×10－65．在一定条件下，若物体运动的路程s （米）与时间t （秒）的关系式为252s t t =+，则当4t =时，该物体所经过的路程为（ ▲ ）A.28米B.48米C.68米D.88米6．某城市进行旧城区人行道的路面翻新，准备对地面密铺彩色地砖，有人提出了4种地砖 的形状供设计选用：①正三角形，②正四边形，③正五边形，④正六边形．其中不能进行密 铺的地砖的形状是（ ▲ ）.A.①B.②C.③D.④7．某物体的三视图如右图，那么该物体形状可能是（ ▲ ） A.长方体 B.圆锥体 C.立方体 D.圆柱体8．若弧长为6π的弧所对的圆心角为60°，则这条弧所在的圆的半径为（ ▲ ）．A.6B.36C.312D.189．在的Rt △ABC 中，∠C ＝90°，cosA ＝51，则tanA ＝（ ▲ ）A.62B.26C.562D.2410．如图，AB ∥CD ，则图中∠1、∠2、∠3关系一定成立的是（ ▲ ） A.∠1＋∠2＋∠3＝180° B.∠1＋∠2＋∠3＝360°C.∠1＋∠3＝2∠2D.∠1＋∠3＝∠211．如图，若正△A 1B 1C 1内接于正△ABC 的内切圆，则11A B AB的值为（ ▲ ） A.12C.13第7题321E DBA 第10题12．如图平面上有两个全等的正十边形ABCDEFGHIJ 、A′B′C′D′E′F′G′H′I′J′，其中A 点与A′点重合，C 点与C′点重合．求∠BAJ′的度数为何？（ ▲ ） A 、96B 、108C 、118D 、126试 题 卷 Ⅱ二、填空题（每小题3分，共18分）13．分解因式：12-x = ▲ ．14．不等式 5x －9≤3（x ＋1）的解集是 ▲ ． .15．将抛物线2x y ＝的图象向右平移1个单位，则平移后的抛物线的解析式为 ▲ ． 16．已知⊙O 1和⊙O 2外切，且圆心距为10c m ，若⊙O 1半径为3c m ，则⊙O 2的半径为 ▲ c m ．17.已知函数1+-=x y 的图象与x 轴、y 轴分别交于点C 、B ，与双曲线xky =交于点A 、D ，若AB+CD= BC ，则k 的值为 ▲ ．18．如图，△ABC 的面积为126，D 是BC 上的一点，且BD ∶CD ＝2∶1，DE ∥AC 交AB 于点E ，延长DE 到F ，使FE ∶ED ＝2∶1连结CF 交AB 于点G ，则△CDF 的面积为 ▲ ．三、解答题（本大题有7小题，共66分）19．（本题5分）计算：0121(()(2)2-+---20．（本题7分）解方程：2532112x x x+=--第17题第12题第18题GFEDCBA21．（本题8分）实验探究：甲、乙两个不透明的纸盒中分别装有形状、大小和质地完全相同的两张和三张卡片．甲盒中的两张卡片上分别标有数字1和2，乙盒中的三张卡片分别标有数字3、4、5．小红从甲盒中随机抽取一张卡片，并将其卡片上的数字作为十位上的数字，再从乙盒中随机抽取一张卡片，将其卡片上的数字作为个位上的数字，从而组成一个两位数．（1）请你画出树状图或列表，并写出所有组成的两位数；（2）求出所组成的两位数是奇数的概率．22．（本题10分）某校有三个年级，各年级的人数分别为七年级600人，八年级540人，九年级565人，学校为了解学生生活习惯是否符合低碳观念，在全校进行了一次问卷调查，若学生生活习惯符合低碳观念，则称其为“低碳族”；否则称其为“非低碳族”，经过统计，将全校的低碳族人数按照年级绘制成如下两幅统计图：（1）根据图①、图②，计算八年级“低碳族”人数，并补全上面两个统计图；（2）小丽依据图①、图②提供的信息通过计算认为，与其他两个年级相比，九年级的“低碳族”人数在本年级全体学生中所占的比例较大，你认为小丽的判断正确吗？请说明理由。

2012年普通高等学校招生全国统一考试理科数学（必修+选修II ）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，第I 卷第1至2页，第II 卷第3至第4页.考试结束，务必将试卷和答题卡一并上交. 第I 卷注意事项：全卷满分150分，考试时间120分钟. 考生注意事项：1.答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码.请认真核准该条形码上的准考证号、姓名和科目.2.没小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.在试题卷上作答无效．．．．．．．．．.3.第I 卷共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 一、选择题1、 复数131ii-++= A 2+I B 2-I C 1+2i D 1- 2i 【解析】i ii i i i i i 21242)1)(1()1)(31(131+=+=-+-+-=++-，选C. 【答案】C2、已知集合A ＝{1.3.m }，B ＝{1，m} ,AB ＝A, 则m=A 0或3B 0或3C 1或3D 1或3 【解析】因为A B A = ,所以A B ⊆,所以3=m 或m m =.若3=m ，则}3,1{},3,3,1{==B A ,满足A B A = .若m m =，解得0=m 或1=m .若0=m ，则}0,3,1{},0,3,1{==B A ，满足A B A = .若1=m ，}1,1{},1,3,1{==B A 显然不成立，综上0=m 或3=m ，选B.【答案】B3 椭圆的中心在原点，焦距为4 一条准线为x=-4 ，则该椭圆的方程为A 216x +212y =1B 212x +28y =1C 28x +24y =1D 212x +24y =1 【解析】椭圆的焦距为4，所以2,42==c c 因为准线为4-=x ，所以椭圆的焦点在x 轴上，且42-=-c a ，所以842==c a ，448222=-=-=c a b ，所以椭圆的方程为14822=+y x ，选C.【答案】C4 已知正四棱柱ABCD- A 1B 1C 1D 1中 ，AB=2，CC 1=22 E 为CC 1的中点，则直线AC 1与平面BED 的距离为 A 2 B3 C 2 D 1【解析】连结BD AC ,交于点O ，连结OE ，因为E O ,是中点，所以1//AC OE ,且121AC OE =，所以BDE AC //1，即直线1AC 与平面BED 的距离等于点C 到平面BED 的距离，过C 做OE CF ⊥于F ,则CF 即为所求距离.因为底面边长为2，高为22，所以22=AC ,2,2==CE OC ,2=OE ,所以利用等积法得1=CF ，选 D.【答案】D（5）已知等差数列{a n }的前n 项和为S n ，a 5=5，S 5=15，则数列的前100项和为(A)100101 (B) 99101(C) 99100 (D) 101100 【解析】由15,555==S a ,得1,11==d a ，所以n n a n =-+=)1(1，所以111)1(111+-=+=+n n n n a a n n ，又1011001011110111001312121111110110021=-=-++-+-=+ a a a a ，选A.【答案】A（6）△ABC 中，AB 边的高为CD ，若a ·b=0，|a|=1，|b|=2，则(A) （B ） (C) (D)【解析】在直角三角形中，521===AB CA CB ，，,则52=CD ,所以5454422=-=-=CD CA AD ,所以54=AB AD ,即b a b a AB AD 5454)(5454-=-==，选D. 【答案】D（7）已知α为第二象限角，33cos sin =+αα，则cos2α= (A) 5-3 （B ）5-9 (C) 59 (D)53【解析】因为33cos sin =+αα所以两边平方得31cos sin 21=+αα，所以032cos sin 2<-=αα，因为已知α为第二象限角，所以0cos ,0sin <>αα，31535321cos sin 21cos sin ==+=-=-αααα，所以)sin )(cos sin (cos sin cos 2cos 22ααααααα+-=-==3533315-=⨯-，选A. 【答案】A（8）已知F 1、F 2为双曲线C ：x ²-y ²=2的左、右焦点，点P 在C 上，|PF 1|=|2PF 2|，则cos ∠F 1PF 2= (A)14 （B ）35 (C)34 (D)45【解析】双曲线的方程为12222=-y x ，所以2,2===c b a ，因为|PF 1|=|2PF 2|，所以点P 在双曲线的右支上，则有|PF 1|-|PF 2|=2a=22,所以解得|PF 2|=22，|PF 1|=24，所以根据余弦定理得432422214)24()22(cos 2221=⨯⨯-+=PF F ,选C. 【答案】C（9）已知x=ln π，y=log 52，21-=ez ，则(A)x ＜y ＜z （B ）z ＜x ＜y (C)z ＜y ＜x (D)y ＜z ＜x【解析】1ln >=πx ，215log 12log 25<==y ，ee z 121==-，1121<<e ，所以x z y <<，选D.【答案】D(10) 已知函数y ＝x ²-3x+c 的图像与x 恰有两个公共点，则c ＝ （A ）-2或2 （B ）-9或3 （C ）-1或1 （D ）-3或1【解析】若函数c x x y +-=33的图象与x 轴恰有两个公共点，则说明函数的两个极值中有一个为0，函数的导数为33'2-=x y ，令033'2=-=x y ，解得1±=x ，可知当极大值为c f +=-2)1(，极小值为2)1(-=c f .由02)1(=+=-c f ，解得2-=c ，由02)1(=-=c f ，解得2=c ，所以2-=c 或2=c ，选A.【答案】A（11）将字母a,a,b,b,c,c,排成三行两列，要求每行的字母互不相同，每列的字母也互不相同，则不同的排列方法共有（A ）12种（B ）18种（C ）24种（D ）36种【解析】第一步先排第一列有633=A ，在排第二列，当第一列确定时，第二列有两种方法，如图，所以共有1226=⨯种，选A.【答案】A（12）正方形ABCD 的边长为1，点E 在边AB 上，点F 在边BC 上，AE ＝BF ＝73.动点P 从E 出发沿直线喜爱那个F 运动，每当碰到正方形的方向的边时反弹，反弹时反射等于入射角，当点P 第一次碰到E 时，P 与正方形的边碰撞的次数为 （A ）16（B ）14（C ）12(D)10【解析】结合已知中的点E,F 的位置，进行作图，推理可知，在反射的过程中，直线是平行的，那么利用平行关系，作图，可以得到回到EA 点时，需要碰撞14次即可. 【答案】B2012年普通高等学校招生全国统一考试理科数学（必修+选修Ⅱ） 第Ⅱ卷 注意事项：1.答题前，考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，然后贴好条形码.请认真核准条形码上得准考证号、姓名和科目.2.第Ⅱ卷共2页，请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，在试题卷上作答无效．．．．．．．．. 3.第Ⅱ卷共10小题，共90分.二.填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上. （注意：在试题卷上作答无效．．．．．．．．．） （13）若x ，y 满足约束条件则z=3x-y 的最小值为_________.【解析】做出做出不等式所表示的区域如图，由y x z -=3得z x y -=3，平移直线x y 3=，由图象可知当直线经过点)1,0(C 时，直线z x y -=3的截距最 大，此时z 最小,最小值为1-3=-=y x z . 【答案】1-（14）当函数取得最大值时，x=___________.【解析】函数为)3sin(2cos 3sin π-=-=x x x y ，当π20<≤x 时，3533πππ<-≤-x ，由三角函数图象可知，当23ππ=-x ，即65π=x 时取得最大值，所以65π=x . 【答案】65π=x （15）若的展开式中第3项与第7项的二项式系数相等，则该展开式中的系数为_________.【解析】因为展开式中的第3项和第7项的二项式系数相同，即62n n C C =，所以8=n ，所以展开式的通项为k k k kk k x C xxC T 288881)1(--+==，令228-=-k ，解得5=k ，所以2586)1(x C T =，所以21x的系数为5658=C .【答案】56（16）三菱柱ABC-A 1B 1C 1中，底面边长和侧棱长都相等， BAA 1=CAA 1=60°则异面直线AB 1与BC 1所成角的余弦值为____________.【解析】如图设,,,1c AC b AB a AA ===设棱长为1，则,1b a AB +=b c a BC a BC -1+=+=，因为底面边长和侧棱长都相等，且01160=∠=∠CAA BAA 所以21=•=•=•c b c a b a ，所以3)(21=+=b a AB ，2)-(21=+=b c a BC ，2)-()(11=+•+=•b c a b a BC AB ，设异面直线的夹角为θ，所以36322cos 1111=⨯=•=BC AB BC AB θ. 【答案】36 三.解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.（17）（本小题满分10分）（注意：在试卷上作答无效．．．．．．．．．．．） △ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，已知cos （A-C ）＋cosB=1，a=2c ，求c.（18）（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．）如图，四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD，AC=22，PA=2，E是PC上的一点，PE=2EC.（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A-PB-C为90°，求PD与平面PBC所成角的大小.19. （本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．）乒乓球比赛规则规定：一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换.每次发球，胜方得1分，负方得0分.设在甲、乙的比赛中，每次发球，发球方得1分的概率为0.6，各次发球的胜负结果相互独立.甲、乙的一局比赛中，甲先发球. （Ⅰ）求开始第4次发球时，甲、乙的比分为1比2的概率；（Ⅱ）表示开始第4次发球时乙的得分，求的期望.（20）（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．）设函数f（x）=ax+cosx，x∈[0，π].（Ⅰ）讨论f（x）的单调性；（Ⅱ）设f（x）≤1+sinx，求a的取值范围.21.（本小题满分12分）（注意：在试卷上作答无效．．．．．．．．）已知抛物线C：y=(x+1)2与圆M：（x-1）2+(12y )2=r2(r＞0)有一个公共点，且在A处两曲线的切线为同一直线l.（Ⅰ）求r；（Ⅱ）设m、n是异于l且与C及M都相切的两条直线，m、n的交点为D，求D到l的距离.22（本小题满分12分）（注意：在试卷上作答无效．．．．．．．．）函数f(x)=x2-2x-3，定义数列{x n}如下：x1=2，x n+1是过两点P（4,5）、Q n(x n,f(x n))的直线PQ n 与x轴交点的横坐标.（Ⅰ）证明：2 x n＜x n+1＜3；（Ⅱ）求数列{x n}的通项公式.。

泉州市安溪永春德化三县结盟2012 届高中毕业班联考数学试题（理科）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，本卷满分150 分，测试时间 120 分钟。

第 I 卷（选择题，共50分）一、选择题：本大题共10 小题，每题 5 分，共50 分。

在每题给出的四个选项中，只有一项为哪一项切合题目要求的。

1．在复平面内，复数1 2i对应的点位于（）iA．第一象限B．第二象限C．第三象限D．第四象限2．以下命题中，真命题是（）A．x R, x2x B．命题“若x1,则 x2 1 ”的抗命题C．x R, x2x D．命题“若x y, 则 sin x sin y ”的逆否命题3．设M平面内的点 (a,b) , Nf (x) f (x) a cos2 x bsin2 x，给出M 到N的映射 f : (a, b) f (x) a cos 2x b sin 2x ，则点 (1,3) 的象 f ( x) 的最小正周期为() A．B．C．D． 2244. 设 m，n 是平面内的两条不一样直线，l1，l 2是平面内的两条订交直线，则/ /的一个充足而不用要条件是（）．．．．．．．．A. m / /且 l1 / /B. m / /l1且n / /l2C. m / /且n / /D.m / / 且 n / /l2 5．函数f ( x) e x ax 存在与直线 2x y0平行的切线，则实数 a 的取值范围是（）A ．,2B ．,2C．(2,)D．2,6．对一位运动员的心脏跳动检测了8 次，获得以下表所示的数据：检测次数12345678检测数据 a i（次/分钟）3940424243454647上述数据的统计剖析中，一部分计算见如右图所示的程序框图（此中 a 是这8个数据的平均数），则输出的的值是（ ）A ． 6B ． 7C ． 8D ． 567．已知等比数列 { a n } 的前 6 项和为 621，且 12 a 2成S4a2, a,等差数列，则 a n =（ ）A ． 3 2n 1B ． 2n 13C ． 3 2nD ． 3 21 n8. 某所学校计划招聘男教师 x 名，女教师 y 名， x 和 y 须知足2x y5,拘束条件x y 2, 则该校招聘的教师人数最多是 ( )（）x 6.A ． 6B ． 8C ． 10D ． 139. 如图，正方形 ABCD 的极点 A (0 ，2 2y) ，B (，0) ，D22极点 C D 位于第一象限，直线 l ： x ＝ t(0 ≤ t ≤ 2) 将正方形 ABCD 分红两部分，记位于直线 l 左边暗影 AC部分的面积为f ( t ) ，则函数 S ＝ f ( t ) 的图象大概是 ( )OB2 xlSS S S 1111O2tO2tO2 tO 2tABCD10．以下四个函数：① f (x)sin x ② f ( x)x 22x 1③ f ( x)x 34x 2④ f ( x) log 1 x2性质 A ：存在不相等的实数x 1 、 x 2 ，使得f ( x 1)f (x 2 )f ( x 1x 2 )22性质 B ：对随意 0x 1 x 2 1,总有 f ( x 1 ) f ( x 2 )以上四个函数中同时知足性质 A 和性质 B 的函数个数为（ ）A ．1 个B ．2 个C ．3 个D ．4 个第Ⅱ卷 （非选择题，共 100 分）二、填空题：本大题共5 小题，每题 4 分，共 20 分，把答案填写在答题卡的相应地点。

A B CD德化县2012年初中毕业班数学综合练习卷（满分：150分；考试时间：120分钟）友情提示：所有答案必须填写在答题卡相应的位置上一、选择题(每小题3分，共21分) 每小题有四个答案，其中有且只有一个答案是正确的．请在答题卡上相应题目的答题区域内作答, 答对的得3分，答错、不答或答案超过一个的一律得0分． 1. 6的相反数是( )A ．6B ．6-C ． 16-D ．162.下列各式，正确的是( )A ．12≥-B ． 23-≥-C ．23≥D ． 23≥3. 9的平方根是( )A.C. ±3D. 34. 如图是五个相同的正方体组成的一个几何体，它的左视图是( )5. 某品牌的复读机每台进价是400元，标价为480元， “五²一”期间搞活动打 9折促销， 则销售1台复读机的利润是( )元 A ．32 B ．48 C ．80 D ．1006. 设从泉州到福州乘坐汽车所需的时间是t (小时)，汽车的平均速度为v (千米/时)，则下面大致能反映v 与t 的函数关系的图象是( )7. 如图，边长为1的正方形ABCD 绕点A 逆时针旋转45º得到正方形AB ′C ′D ′，边B ′C ′与CD 交于点O ，则四边 形AB ′OD 的周长是( )A ． 2B ．2 2C ．1＋ 2D ．3二、填空（每小题4分，共40分）在答题卡上相应题目的答题区域内作答． 8. 计算：42a a ⋅=_________． 9. 化简=---ba b ba a ．10. 因式分解：2m m -=____________________．11. 质量检验部门抽样检测出某品牌电器的次品率为5%，某 经销商现有该种电器1000件，估计其中次品有______件.12. 如图，直线l 1//l 2，则α为_____________． 13. 据统计, 2012年福建省参加新型农村合作医疗的人数为24490000人，将“24 490 000”这个数用科学记数法可表示为_______________. 14. 在半径为6cm 的圆中，60°的圆心角所对的弧等于 cm ． 15. 六边形的内角和．．．等于 度． 16. 如图，直线y kx b =+经过(21)A ，，(12)B --，两点，则不等式122x kx b >+>-的解集为 ．17. 如图，在反比例函数y ＝xk （x>0）的图象经过点A ，B（点A 在B 的上方）．过点A 分别作AD ⊥x 轴，AH ⊥y 轴，垂足分别为D ，H ；过点B 分别作BF ⊥x 轴，BE ⊥y 轴， 垂足分别为E ，F ，AD 与BE 交于点G ．①比较大小：A H O D S 四边形 BEO F S 四边形；（填“>,=,<”） ②若:O D D G =2：1，则:A G B G =___________.三、解答题（共89分）在答题卡上相应题目的答题区域内作答.18.（9分）计算：1203)1(28|2|)3(-÷-+⨯--+-π19. （9分）先化简，再求值:)8()3(2---x x x ，其中42-=x .l 1l 2 50°70°α20. （9分）在学校组织的知识竞赛中，每班参加比赛的人数相同，成绩分为A 、B 、C 、D 四个等级，其中相应等级的得分 依次记为100分、90分、80分、70分．学校将某年级的一 班和二班的成绩整理并绘制成如右边的两个统计图：请你根 据图表提供的信息解答下列问题：（1）此次竞赛中二班参加比赛的人数为 ；并将下面的表格补充完整：（2）请你从B 级以上（包括B 级）的人数的角度来比较一班和二班的成绩．21.（9分）如图，已知：点B 、F 、C 、E 在一条直线上，FB =CE ，AC =DF ．能否由上面的已知条件证明AB ∥ED ？如果能，请给出证明；如果不能，请从①AB=ED ；②BC=EF ③∠ACB=∠DFE ．三个条件中选择一个合适的．．．．．加到已知条件中，使AB ∥ED 成立，并给出证明．22.（9分）一个不透明的口袋中装有红、黄、绿三种颜色的小球（它们除颜色不同外其余都相同），其中红球2个，黄球1个，从中任意摸出1球是红球的概率是21．(1)求口袋中绿球的个数；(2)第一次从袋中任意摸出1球（不放回），第二次再任意摸出1球，请你用画树状图或列表的方法表示所有等可能的结果，并求两次都摸到红球的概率．23.（9分）如图，点C 在以AB 为直径的⊙O 上，点D 在AB 的延长线上，B C D A ∠=∠． (1)求证：CD 为⊙O 的切线；(2).若CD=4，⊙O 的半径为3,求BD 的值.24.（9分）某小区准备新建50个停车位，以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位需0.5万元；新建3个地上停车位和2个地下停车 位需1.1万元.(1)该小区新建1个地上停车位和1个地下停车位各需多少万元？(2)若该小区预计投资金额超过10万元而不超过11万元，则共有几种建造方案？DEADOB25.（13分）如图，在直角坐标中，直线3y kx =-，分别与x 轴，y 轴交于B （3，0）、C ，过B 、C 两点的抛物线2y ax bx c =++与x 轴交于另一 点A （点A 在B 左边），且3ABC S = (1)求k 的值；(2)求抛物线的解析式；(3)点P 在抛物线上，且A C P ∠=45°，求P 点的坐标．26.（13分）如图，在直角坐标系中，⊙O 的圆心O 在坐标原点，直径AB=8，点P 是直径AB 上的一个动点（点P 不与A 、B 两点重合）， 过点P 的直线PQ 的解析式为y x m =+，当直线PQ 交y 轴于Q ，交⊙O 于C 、D 两点时，过点C 作CE ⊥x 轴交⊙O 于点E ，过点E 作EG ⊥y 轴于G ，过点C 作 CF ⊥y 轴于F ，连接DE ．（1）填空：C P B ∠=________°；（2）试探究：在P 点运动过程中，22PD PC +的值是否会发生变化？若变化，请说明理由；如果 不变化，请求出这个值；（3）如果点P 在射线．．AB 上运动，当△PDE 的面积为4时，请你求出CD 的长度．四、附加题（共10分）在答题卡上相应题目的答题区域内作答．友情提示：请同学们做完上面考题后，再认真检查一遍，估 计一下你的得分情况．如果你全卷得分低于90分（及格线），则 本题的得分将计入全卷总分，但计入后全卷总分最多不超过90 分；如果你全卷总分已经达到或超过90分，则本题的得分不计入全卷总分．1．（5分）单项式32x 的系数是__________.2．（5分）如图，直线AB 上有一点O ，且OC ⊥OD ，则12∠+∠=_________°.21DCBOA德化县2012年初中毕业班数学综合练习卷参考答案及评分意见说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分意见”的精神进行评分．（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分． 一、选择题（每小题3分，共21分）1. B ；2. C ；3. C ；4. D ；5. A ；6. A ；7. B. 二、填空题（每小题4分，共40分）8. 6a ； 9. 1； 10. (1)m m -； 11.50； 12.120； 13. 72.44910⨯； 14.2π； 15. 720；16. 12x -<<；17. ①= ②1：2三、解答题（共89分）18．18．解：原式=1243+-+ ……………………………8分 =2 ………………………………………9分 19．解：原式=22698x x x x -+-+=29x + ………………6分当4x =-时，原式=24)9⨯+=1 ……9分20．(1)二班参赛人数为25人一班众数：90；平均分：87.6；二班中位数：80 ……6分(2)一班B 级以上：18人；二班B 级以上：12人 所以一班成绩较好. ……………………………………9分21．答：不能. ……………………………………………3分选①：AB=ED 证明：∵BF=CE∴BC=EF∴在A B C ∆和D E F ∆中BC EF AB D E AC D F =⎧⎪=⎨⎪=⎩∴A B C ∆≌D E F ∆（SSS ） ∴∠B=∠E ∴AB ∥DE …………………………9分22．（1）解：122112÷--=（个）…………………………4分（2）图略 …………………………………………………………6分∴P =红16…………………………………………………………9分23．(1)证明：连结OC ，则∠OBC=∠OCB∵AB 是直径 ∴∠ACB =90° ∴∠A+∠ABC=90° 又∵∠BCD=∠A∴∠OCB+∠BCD=90° ∴∠OCD=90°即OC ⊥CD又∵点C 在⊙O 上 ∴CD 是⊙O 的切线………………4分 (2) ∵∠BCD=∠A, ∠D=∠D ∴△BCD ∽△CAD ∴C D B D D AD C=，即2CD AD BD =⋅又∵CD=4,AO=OB=3 ∴16=(BD+6)BD 解得：BD=2……9分24．（1）解：设新建一个地上停车位需x 万元，新建一个地下停车位需y 万元依题意得0.532 1.1x y x y +=⎧⎨+=⎩ 解得⎩⎨⎧==4.01.0y x答：略…………………………………………………4分﹙2﹚设新建m 个地上停车位，则10<0.1m ＋0.4(50－m) ≤11 解得 30≤m ＜3100,因为m 为整数，所以m ＝30或m ＝31或m ＝32或m ＝33,对应的50－m ＝20或50－m ＝19或50－m ＝18或50－m ＝17所以，有四种建造方案…………………………………………9分25．解：（1）∵直线B C 经过B （3，0）∴330k -= 解得：1k =……………………………3分 （2）由(1)可知：直线B C ：3y x =- 当0x =时，3y =- ∴(0,3)C -即3c =-又∵3ABC S = ∴AB=2 ∴(1,0)A 由题意，得309330a b a b +-=⎧⎨+-=⎩解得14a b =-⎧⎨=⎩，∴抛物线的解析式为243y x x =-+- ……………………8分OO(3)∵(3,0)B ，(0,3)C - ∴O B =O C =3 ∴O C B=O BC =45∠∠︒∴BC=如图，延长C P 交x 轴于点Q 又∵45A C P ∠=︒ ∴OCA BCQ ∠=∠ 在Rt △OAC 中，OA=1，OC=3∴tan ∠OCA=O A O C =13，∴tan ∠OCQ=13过B 点作BD ⊥BC 交CQ 于点D ，则45QBD ∠=︒∴在Rt △BDC 中，BD= tan ∠OCQ ⋅ BC=13⨯又∵∠BQD=∠CQA ∴△BQD ∽△CQA∴BQ BD C QAC===设BQ=n ，则在Rt △OCQ 中，222(3)3)n ++= 解得：132n =-（负值，舍去），23n =，即BQ=3∴OQ=6 ∴(6,0)设直线C P 的解析式为3y kx =- ∴630k -= ∴12k =∴直线C P 的解析式为132y x =-设P 1(,3)2m m - ∴212433m m m =-+--解得：10m =（舍去），272m = 当272m =时，132m -=54-∴P 75(,)24-………………………………………13分26．（1）C P B ∠=45︒………………………3分 （2）不变∵AB 垂直平分CE ，∴PC=PE，且45C P B E P H ∠=∠=︒，22222,PE CD PD PC PD PE DE ∴⊥∴+=+=45,90,,PCH DEDO EO DE ∠=︒∴=︒∴⊥∴==2232PD PC ∴+=…………………………………8分（3）当点P 在直径AB 上时，114228PD E S PD PE PD PC PD PC =⨯=⨯=∴⨯=又2232PD PC +=22()321648CD PD PC CD ∴=+=+=∴=当点P 在AB 延长线上，同理可得：22()3216164C D PD PC C D ∴=-=-=∴=综上，CD的长为4………………………………13分四、附加题： 1.2 2.90。

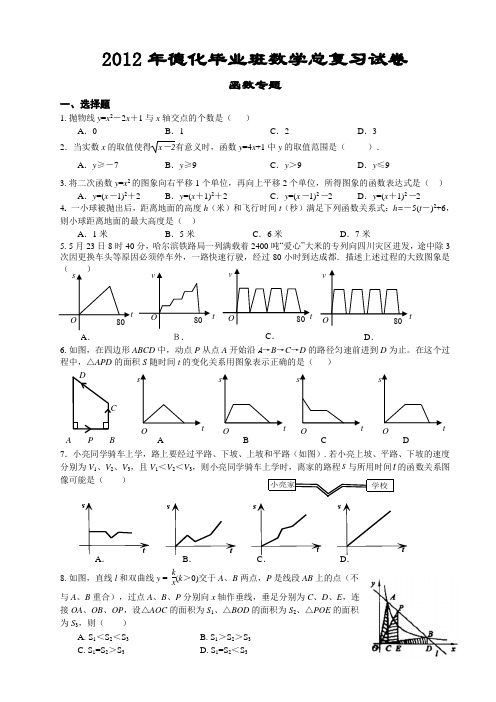
2012年德化毕业班数学总复习试卷函数专题一、选择题1.抛物线y =x 2－2x ＋1与x 轴交点的个数是（ ）A ．0B ．1C ．2D ．32．当实数x 的取值使得x －2有意义时，函数y =4x +1中y 的取值范围是（ ）．A ．y ≥－7B ．y ≥9C ．y ＞9D ．y ≤93.将二次函数y =x 2的图象向右平移1个单位，再向上平移2个单位，所得图象的函数表达式是（ ） A ．y =(x －1)2＋2 B ．y =(x ＋1)2＋2 C ．y =(x －1)2－2 D ．y =(x ＋1)2－24. 一小球被抛出后，距离地面的高度h （米）和飞行时间t （秒）满足下列函数关系式：h=－5(t －)2+6，则小球距离地面的最大高度是（ ）A ．1米B ．5米C ．6米D ．7米5.5月23日8时40分，哈尔滨铁路局一列满载着2400吨“爱心”大米的专列向四川灾区进发，途中除3次因更换车头等原因必须停车外，一路快速行驶，经过80小时到达成都．描述上述过程的大致图象是（ ）6.如图，在四边形ABCD 中，动点P 从点A 开始沿A →B →C →D 的路径匀速前进到D 为止。

在这个过程中，△APD 的面积S 随时间t 的变化关系用图象表示正确的是（ ）7．小亮同学骑车上学，路上要经过平路、下坡、上坡和平路（如图）.若小亮上坡、平路、下坡的速度分别为V 1、V 2、V 3，且V1＜V 2＜V 3，则小亮同学骑车上学时，离家的路程s 与所用时间t 的函数关系图像可能是（ ）A ．B ．C ．D ．8.如图，直线l 和双曲线y = kx (k ＞0)交于A 、B 两点，P 是线段AB 上的点（不与A 、B 重合），过点A 、B 、P 分别向x 轴作垂线，垂足分别为C 、D 、E ，连接OA 、OB 、OP ，设△AOC 的面积为S 1、△BOD 的面积为S 2、△POE 的面积为S 3，则（ ）A .S 1＜S 2＜S 3B .S 1＞S 2＞S 3C .S 1=S 2＞S 3D .S 1=S 2＜S 3s tOAs tOBs tOCstODst 80O v t 80 O v t 80 O t v O A ． Ｂ． C ． D ． 80 DCBP A 学校小亮家s t s ts ttsOlB ´ xyA B PO ´二、填空题9.一次函数y=－3x ＋6中，y 的值随x 值增大而 .10.在平整的路面上某型号汽车急刹车后仍将滑行的距离s （米）与刹车的速度v （千米/时）有这样的关系s = v 2300，当汽车紧急刹车仍滑行27米时，•汽车刹车前的速度是 _________．11.已知A (x 1，y 1)，B (x 2，y 2)都在反比例函数y = 6x的图象上，若x 1x 2=－3，则y 1y 2的值为.12．若一个反比例函数的图象位于二、四象限，则它的解析式可能是 ．（写出一个即可） 13. 根据如图所示的计算程序，若输入的值x =－1，则输出的值y =．14．函数y = 2x 与1y x =-的图象的交点坐标为（a ，b ），则1a －1b 的值为__________．15.如图，是二次函数y=ax 2+bx+c 图象的一部分，其对称轴为直线x =1，若其与x 轴一交点为A （3，0），则由图象可知，不等式ax 2+bx+c ＜0的解集是 . 16.如图，将一块直角三角板OAB 放在平面直角坐标系中，B (2，0)，∠AOB =60°，点A 在第一象限，过点A 的双曲线为y = kx .在x 轴上取一点P ，过点P 作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ´B ´. （1）当点O ´与点A 重合时，点P 的坐标是 ； （2）设P (t ，0)，当O ´B ´与双曲线有交点时，t 的取值范围是 .三、解答题17. 已知一次函数y=kx ―4，当x =2时，y=―3． （1）求一次函数的解析式；（2）将该函数的图象向上平移6个单位，求平移后的图象与x 轴交点的坐标．18. （1）请在坐标系中画出二次函数y=x 2―2x 的大致图象；（2）根据方程的根与函数图象的关系，将方程x 2―2x=1的根在图上近似的表示出来(描点)；（3）观察图象，直接写出方程x 2―2x=1的根.(精确到0.1)19.某商店经营一种小商品，进价为2.5元，据市场调查，销售单价是13.5元时平均每天销售量是500件，而销售价每降低1元，平均每天就可以多售出100件。

2012中考总复习质量监控数学学科试卷（一）评分标准及参考答案2012.5一、选择题（本题共32分，每小题4分）1. C2. D3. B4. A5. D6. B7. B8. B二、填空题（本题共16分，每小题4分）9. 3(m ＋3)(m －3) 10. x ≥2 11. b ＜0 12. 441三、解答题（本题共52分，13-18题每小题6分，19、20题每小题8分）13. 解：原式=1－22＋4＋3×33 ………………………………………………………4分 =5－22＋3 .………………………………………………………………6分14.解：原式=()()()322232+-+÷+-a a a a a －21+a ………………………………………………2分 =()()()223232-++⋅+-a a a a a －21+a ………………………………………………3分 =22+a －21+a ………………………………………………………………4分 =21+a …………………………………………………………………………5分 当a =22-时，原式=22 ………………………………………………………6分 15. 解：解①，得x ≤3， ……………………………………………………………………1分解②，得x ＞－1. …………………………………………………………………3分 ∴不等式组的解集是－1＜x ≤3.……………………………………………………4分其中整数解有0，1，2，3. ………………………………………………………6分16. 证明：∵AB BD ⊥于点B ,ED BD ⊥于点D ，∴∠ABC =∠EDC =90°. …………………………………………………………1分 又∵∠ACB =∠ECD ， ……………………………………………………………2分 BC =DC ， ………………………………………………………………………3分 ∴△ABC ≌△EDC . ……………………………………………………………4分 ∴AB =ED. ………………………………………………………………………6分17. 解：设甲种感恩册单价为x 元，则乙种感恩册的单价为（x －8）元. …………………1分 依题意，得 30x + 10(x －8)=800. …………………………………………………3分 解得 x =22. …………………………………………………………………5分 ∴x －8=14（元）. …………………………………………………………6分答：甲种感恩册单价为22元，乙种感恩册的单价为14元.18. 解：（1）在Rt △DCB 中，sin ∠DCB =CD BD =54， 设BD =4x ，CD =5x ，∵BD 2+BC 2=CD 2，即(4x )2+81=(5x )2.解得x =3， ………………………………………………………………………2分∴CD =15. ………………………………………………………………………3分BD =12. ……………………………………………………………………………4分（2）如图，过点E 作EF ⊥AB ，交BA 的延长线于点F ．∵∠EAB =120°，∴∠EAF =60°．∴AF =AE •cos ∠EAF =1.8×21=0.9（米）．. …………………5分 ∴FB =AF +AD +DB =0.9+2+12=14.9（米）．……………………6分即灯的顶端E 距离地面14.9米．19. （1）证明：∵BE ∥CD ，AB ⊥CD ，∴AB ⊥BE .又∵AB 为⊙O 直径，∴BE 是⊙O 的切线. ………………………………………………………2分（2）∵AB 为⊙O 直径，AB ⊥CD ，∴CM =21CD =21×10=5， …………………………………………………………… 3分 ∵BC =BD ，∴∠BAC =∠BCD . ……………………………………………………………………5分 ∵tan ∠BCD =21，∴21 CM BM .∴BM =21CM =25. …………………………………………………………………6分 ∵=AM CM tan ∠BAC =tan ∠BCD =21， ∴AM =10.……………………………………………………………………………7分 ∴⊙O 的直径AB =AM +BM =10+25=225. …………………………………………8分 20. （1）PQ PE 33=. …………………………………………………………………2分 （2）①当340≤≤x 时，即点P 在线段ED 上时， x PE ED PD 334-=-=，x QM 21=， ∴x x QM PD y 21)334(2121⋅-=⋅⋅=. 即x x y +-=2123（340≤≤x ）. ……………………………………………………5分 ②当34>x 时，即点P 在ED 的延长线上时，433-=-=x ED PE PD ，x QM 21=， ∴x x QM PD y 21)433(2121⋅-=⋅⋅=. 即x x y -=2123（34>x ）. ……………………………………………………………8分Q。

德化县2012年初中毕业班物理综合练习（二）
参考答案
一、选择题（本大题共22小题，每小题2分，计44分）
1-5 BCBAA 6-10 DCDBB 11-15 DCDAD 16-20 CADCC 21-22 AB
二、填空、作图题（本大题共2小题，每空1分，每图1分，计6分）
24．略
三、简答题（本题计4分）
25.示例：问：电热暖手宝内的液体为什么选择水做材料？
答：这是因为水的比热容比较大且沸点相对较高、便宜易得无污染
四、实验、探究题（本大题共6小题，每空1分，共28分）
26．（1）B 2.44～2.48 (2)略
27．（1）大小方向（2）同一直线
（3）减小因为木板摩擦力对小车运动状态的影响
28. (1)右端水平便于力臂的测量 (2) 1.5 下
29.（1）便于确定像的位置（2）靠近不变（3）不能虚
30.（1）电压电流 (2)断开左滑动变阻器错为下（或上）两接线柱接入电路
（3）0.3 左电压一定时，导体中的电流与导体的电阻成反比
31. （1）用磅秤测出人的质量m
（2）用卷尺测出从教学楼地面到教室所在楼层的高度h
（3）人一次爬楼对自己做的功W＝mgh
五、计算题（本大题共3小题，每小题6分，计18分）
32．解：（1）5.5X10-2Kg （2）0.55N
33．解：（1）2×106Pa （2）10000 W (3) 28.5%
34. 解（1）110 W 176 W
(2) 6600J
(3) 39600J。

德化县2012年秋期中质量跟踪检测八年级数学科试题（满分：150分；考试时间：120分钟）友情提示：所有答案必须填写到答题卡相应的位置上.一、选择题（每小题3分，共21分）：每小题有四个答案,其中有且只有一个答案是正确的．请在答题卡上相应题目的答题区域内作答,答对的得3分,答错或不答一律得0分． 1.4的算术平方根是（ ） A. 2-B.2C. 2±D.4±2.下列运算正确的是（ ）A ．257()a a =B ．824a a a ÷=C ．325a a a ⋅=D ．224a a a +=3.下列变形属于因式分解的是（ ） A ．()21(1)1x x x +=－－B. 2a b ab a ÷=C ．2211()42x x x ++=+ D ．23643(2)4x x x x +=+－－ 4.下列各组数不能作为直角三角形三边长的是（ ） A ．674，，B ．121620，，C ．72425，，D．1，5.下列多项式中能用平方差公式分解因式的是（）A ．22()a b +-B ．2520m mn -C ．22x y --D ．29x -+6.如图，以图中的直角三角形三边为边长向外作三个正方形M 、P 、Q ，且正方形M 、P 的面积分别为225和81，则正方形Q 的面积是 ( )A. 144B.196C.12D.137.如图所示,小方格都是边长为1的正方形，则四边形ABCD 的面积是（ ） A.56B.23.5 C.25 D.12.5二、填空题（每小题4分，共40分）：在答题卡上相应题目的答题区域内作答． 8. 8-的立方根是___________．第7题图第6题图QP M9.9的平方根是.10. 比较大小: 2____3 (填“>、 =、 < ”)． 11. 因式分解：33a b -=_______________． 12. 请写出一个负．无理数：． 13. 计算：(32)ab a a -÷=________________． 14. 计算：23(24)x x x --+=．15. 若103)()2(2--=+⋅+x x m x x ，则=m ．16. 如图,在数轴上的点A B C D ，，，表示数2123-，，，， 则表示42-的点P 应在线段____（填“AB ”、“BC ”或“CD ”）上．17.如图，等腰1Rt OAA 的直角边OA 长为1． (1)则斜边1OA 的长是____________；(2)若以1A 为直角顶点，1OA 为直角边按顺时针方向作等腰12Rt OA A ；再以2A 为直角顶点，2OA 为直角边按顺时针方向作等腰23Rt OA A ；按此作法进行下去，得到34OA A ，45OA A ，…，则6OA 的长是．三、解答题（共89分）：在答题卡上相应题目的答题区域内作答． 18.（9分）计算：23() a a ab ⋅⋅-19.（9分）因式分解：322x x x -+20.（9分）先化简，再求值：2(3)(4)(2)x x x +---, 其中5x =第17题A 4A 3A 2A 1OA第16题图21．（9分）地球的质量约为245.9810⨯千克，木星的质量约为271.910⨯千克．问木星的质量约是地球的多少倍? （结果精确到个位）22.（9分）已知长方形的长为24cm ，宽为6cm ，求与这个长方形面积相等的正方形的边长．23．（9分）如图，在ABD 中，90A ∠=︒，3AB =，4AD =，12BC =，13DC =，(1)求BD 的长；(2)求四边形ABCD 的面积.24.（9分）如图，在正方形网格中，有三个格点A B C 、、，且每个小正方形的边长为1，在AC 延长线上有一格点．．D ，连结BD ．(1)如果AC CD =，则ABD 是________三角形(按边分类)； (2)当ABD 是以BD 为底的等腰三角形，求ABD 的周长．25.（12分）如图（1）所示，边长为a 的大正方形中有一个边长为b 的小正方形，如图（2）是由图（1）中阴影部分拼成的一个长方形。

德化一中2012届毕业班考前适应性考试数学（理）试卷第Ⅰ卷（选择题 共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．sin 225的值是（★★★）．A ．B ．C ．D2．已知变量x y 、满足条件1,2,0,x y x y ≥⎧⎪≤⎨⎪-≤⎩则x y +的最小值是（★★★）．A ． 4B ． 3C ． 2D ．13．在递减等差数列}{n a 中，若150a a +=，则n S 取最大值时n 等于（★★★）．A ． 2B ． 3C ． 4D ．2或3 4．下列命题中，真命题的个数有（★★★）．①21,04x x x ∀∈-+R ≥；②21x >的充分条件是1x >；③函数2x y -=是单调递增函数；④3y x =和3log y x =互为反函数．A ． 0个B ． 1个C ． 2个D ．3个 5．某流程图如右图所示，现输入如下四个函数，则可以输出函数的是（★★★）．A ． 2()f x x =B ． 1()f x x=C ． ()ln 26f x x x =+-D ．()sin f x x =6．由两个完全相同的正四棱锥组合而成的空间几何体的正(主)视图、侧(左)视图、俯视图都相同，其图形如右图所示，其中视图中ABCD 四边形是边长为1的正方形，则该几何体的体积为（★★★）． A ．B ．C ．D ．7．双曲线22221(0,0)x y a b a b-=>>的两条渐近线将平面划分为“上、下、左、右”四个区域（不1AA含边界），若点(1,2)在“上”区域内，则双曲线离心率e的取值范围是（★★★）．A．)+∞B．)+∞C．D．8．若某同学连续三次考试的名次（第一名为1，第二名为2，以此类推且没有并列名次情况）不超过3，则称该同学为班级的尖子生．根据甲、乙、丙、丁四位同学过去连续3次考试名次数据，推断一定不是．．尖子生的是（★★★）．A．甲同学：均值为2，中位数为2 B．乙同学：均值为2，方差小于1C．丙同学：中位数为2，众数为2 D．丁同学：众数为2，方差大于19．如图，在正方体1111ABCD A B C D-中，若平面11A BCD上一动点P到1AB和BC的距离相等，则点P的轨迹为（★★★）．A．椭圆的一部分B．圆的一部分C．一条线段D．抛物线的一部分10．将方程tan0x x+=的正根从小到大地依次排列为12,,,,na a a，给出以下不等式：①12n na aπ+<-<；②12n na aππ+<-<；③122n n na a a++>+；④122n n na a a++<+；其中，正确的判断是（★★★）．A．①③B．①④C．②③D．②④第Ⅱ卷（非选择题共100分）二、填空题:本大题共5小题，每小题4分，共20分．把答案填在答题卡相应位置．11．已知复数z a bi=+（其中i为虚数单位，a b∈R、），若||1a≤且||1b≤，则||1z≤的概率为★★★★★．12．已知52345012345(1)x a a x a x a x a x a x-=+++++，则12345a a a a a++++的值等于★★★★★．13．在△ABC中，60A∠=，1b=，ABCS=，则AB AC等于★★★★★．14．已知函数32()()f x x ax bx a b=-++∈R、的图象如图所示，它与x轴在原点相切，且x轴与函数图象所围成的区域（如图阴影部分）的面积为112，则a等于★★★★★．15．类比数学归纳法的证题思路，如果要证明对于任意的(n∈--Z Z表示负整数集），命题()p n都成立，可先证明命题(1)p-成立，然后在假设命题()()p k k∈-Z成立的基础上，证明命题★★★★★成立即可．第9题图三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤． 16．（本小题满分13分）如图，在底面为平行四边形的四棱锥P ABCD -中，,AB AC PA ⊥⊥面ABCD ，3,5AP AB AD ===，点E 是PD 的中点．（Ⅰ）求证：PB ∥平面AEC ；（Ⅱ）求直线AB 与平面EAC 所成角大小．17．（本小题满分13分）ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，若函数21()4f x x mx =+-为偶函数，且(cos )02Bf =．（Ⅰ）求角B 的大小；（Ⅱ）若△ABC，求△ABC 的周长． 18．（本小题满分13分）随机变量X 的分布列如下表如示，若数列{}n p 是以1p 为首项，以q 为公比的等比数列，则称随机变量X 服从等比分布，记为1(,)Q p q ．现随机变量1(,2)15XQ ．(Ⅰ)求n 的值并求随机变量X 的数学期望EX ；（Ⅱ）甲乙两人举行乒乓球比赛，已知甲赢得每一局比赛的概率都等于)2(≤X P ，比赛采用三局两胜制（即在三局比赛中，只要有一方赢得两局比赛，就取得胜利，比赛也就随之结束了），求甲在比赛中赢的局数比输的局数多的概率． 19．（本小题满分13分）已知抛物线22(0)y px p =>的焦点为F ，A 是抛物线上横坐标为4且位于x 轴上方的点，A 到抛物线准线的距离等于5．过A 作AB 垂直于y 轴，垂足为B ，OB 的中点为M ．（Ⅰ）求抛物线方程；（Ⅱ）过M 作MN FA ⊥，垂足为N ，求点N 的坐标；（Ⅲ）以M 为圆心，MB 为半径作圆M ，当(,0)K m是x 轴上一动点时，判断直线AK 与圆M 的位置关系．PBCA DE20．（本小题满分14分）某公司有价值a 万元的一条流水线，要提高该流水线的生产能力，就要对其进行技术改造，从而提高产品附加值，改造需要投入，假设附加值y （万元）与技术改造投入x （万元）之间的关系满足：①y 与a x -和x 的乘积成正比；②2a x =时，2y a =；③02()xt a x ≤≤-，其中t 为常数，且[0,1]t ∈．(Ⅰ)设()y f x =，求()f x 表达式，并求()y f x =的定义域； （Ⅱ）求出附加值y 的最大值，并求出此时的技术改造投入．21．本题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题记分．作答时，先用2B 铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中． （1）（本小题满分7分）选修4－2：矩阵与变换已知矩阵1021M ⎛⎫= ⎪⎝⎭．（Ⅰ）请写出矩阵Ｍ对应的变换f 的变换公式；（Ⅱ）从变换的角度说明矩阵Ｍ可逆吗？如果可逆，请用求逆变换的方式求出对应的逆矩阵1M -．（2）（本小题满分7分) 选修4—4：极坐标与参数方程在直角坐标平面内，以坐标原点O 为极点，x 轴的非负半轴为极轴建立极坐标系． 已知点A 、B 的极坐标分别为(1,0)、(1,)2π，曲线C 的参数方程为cos ,(sin x r y r ααα=⎧⎨=⎩为参数，0r >）．（Ⅰ）求直线AB 的直角坐标方程；（Ⅱ）若直线AB 和曲线C 只有一个交点，求r 的值．（３）（本小题满分7分）选修4—5: 不等式证明选讲已知正实数a 、b 、c 满足条件3a b c ++=，(Ⅰ) 3≤；（Ⅱ）若c ab =，求c 的最大值．德化一中2012届毕业班考前适应性考试数学（理）试卷参考解答及评分标准一、选择题：1．B 2．C 3．D 4．C 5．D 6．C 7．D 8．D 9．D 10．D 二、填空题 11．4π； 12． －1 ； 13． 1 ； 14． －1； 15．(1)p k -.三、解答题16．证明： （Ⅰ）连结BD 交AC 于点O ，并连结EO ， 四边形ABCD 为平行四边形∴O 为BD 的中点 又E 为PD 的中点 ∴在PDB ∆中EO 为中位线，PB EO //AEC EO AEC PB 面面⊂⊄,∴AEC PB 面// ．…………………5分（Ⅱ）以A 为原点，AC ,AB ,AP 分别为,,x y z 轴建立空间直角坐标系，则(0,0,0),(0,3,0),(4,0,0)A B C ，(4,3,0)D -，(0,0,3)P ，33(2,,)22E -，则AB =(0,3,0)，33(2,,)22AE =-,AC =(4,0,0), ……………………………………7分设平面EAC 一个法向量(,,)n x y z =，则00n AE n AC ⎧⋅=⎪⎨⋅=⎪⎩，即33(,,)(2,,)022(,,)(4,0,0)0x y z x y z ⎧⋅-=⎪⎨⎪⋅=⎩， 令1y =，得0,1x z ==，所以(0,1,1)n =．………………………………………………9分 设直线AB 与平面EAC 所成角为α，则||sin |cos ,|||||32AB n AB n AB n α⋅=<>===⋅， 又[0,]2πα∈，所以求直线AB 与平面EAC 所成角等于4π．……………………………13分 17． 解：（Ⅰ）∵41)(2-+=mx x x f 是偶函数， ∴()()f x f x =-，即221144x mx x mx +-=--，∴0m =………………………………2分 PBCADE又(cos)02B f =，∴21cos 24B =，即1cos 124B +=， ∴1cos 2B =-，又(0,)B π∈∴23B π=．………………………………………………5分（Ⅱ）∵△ABC的外接圆半径为3， ∴根据正弦定理2sin bR B =得，23sin 3b π=，7b =．…………………………7分又1sin 2ABC S ac B ∆==，∴15ac =． …………………………………………9分 在△ABC 中，根据余弦定理得，2222cos b a c ac B =+-，即22230cos493a c π+-=，2234a c += …………11分 ∴222()264a c a c ac +=++=，∴8a c +=，∴△ABC 的周长等于15．……………………………………………………………………13分18．解：(Ⅰ)依题意得，数列{}n p 是以115为首项，以2为公比的等比数列， ………1分 所以121(12)1512n n n S p p p -=+++=-=1 …………………………………………………3分 解得n=4．…………………………………………………………………………………………5分EX 2312341222234123415151515p p p p =+++=⨯+⨯+⨯+⨯()012311222324215=⨯+⨯+⨯+⨯ …………………………………………………………6分 4915=………………………………………………………………………………………………7分 （Ⅱ）由(Ⅰ)知随机变量X 的分布列为设“甲在第)3,2,1(=i i 局取胜”为事件i A ， 依题意，51152151)2()(=+=≤=X P A P i ……………………………………………………9分 设“甲在比赛中赢的局数比输的局数多”为事件A ，则事件A 等价32132121A A A A A A A A ++， ……………………………………………………11分则125135154515151545151)()()()(32132121=⨯⨯+⨯⨯+⨯=++=A A A P A A A P A A P A P …13分 19． 解:（Ⅰ）抛物线.2,524,222=∴=+-==p p p x px y 于是的准线为∴抛物线方程为24y x =．…………………………………………………………………… 3分 （Ⅱ）∵点A 的坐标是(4,4)， 由题意得B (0,4)，M (0,2)，又∵F (1,0)， ∴,43,;34-=∴⊥=MN FA k FA MN k ………5分 则FA 的方程为4(1)3y x =-，MN 的方程为.432x y -=-解方程组84(1)8453,(,)4355254x y x N y y x ⎧⎧==-⎪⎪⎪⎪∴⎨⎨⎪⎪=-=-⎪⎪⎩⎩得．…………8分(Ⅲ）由题意得，圆M 的圆心是点(0,2)，半径为2． ……………………………………9分 当4m =时，直线AK 的方程为4x =，此时，直线AK 与圆M 相离；…………………10分 当4m ≠时，直线AK 的方程为),(44m x my --= 即为,04)4(4=---m y m x 圆心(0,2)M 到直线AK 的距离2)4(16|82|-++=m m d ，令1,2>>m d 解得∴1m >当时，直线AK 与圆M 相离； 当1m =时，直线AK 与圆M 相切； 当1<m 时，直线AK 与圆M 相交． ……………………………………………………………………13分 20． 解：设()y k a x x =-，当2a x =时，2y a =，可得：4k =，∴4()y a x x =-……2分 由02()x t a x ≤≤-得02()2()xa x x t a x ⎧≥⎪-⎪⎨⎪≤⎪-⎩（1）（2）………………………………………………3分 又0x ≥所以由（1）得0,0a x x a -><<即 ………………………………………………4分 所以（2）可化为22()12atx a x t x t≤-∴≤+ …………………………………………………5分 因为[0,1]t ∈，所以212ata t<+ …………………………………………………………………6分综上可得函数()f x 定义域为2[0,]12att+，其中t 为常数，且[0,1]t ∈．……………………7分 （2）4()y a x x =-224()2a x a =--+ ………………………………………………………9分当2122at a t ≥+时，即112t ≤≤，2ax =时，2max y a = ……………………………………11分 当2122at a t <+，即102t ≤<，4()y a x x =-在2[0,]12at t+上为增函数 ∴当212at x t=+时，2max 28(12)a t y t =+ …………………………………………………13分 答：当112t ≤≤，投入2ax =时，附加值y 最大，为2a 万元； 当102t ≤<，投入212at x t=+时，附加值y 最大，为228(12)a t t +万元 …………………14分21． ⑴矩阵与变换 解：（Ⅰ）假设1021M ⎛⎫=⎪⎝⎭把任一点(),x y 变成()','x y ， 则'10'21x x y y ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭''2x xy x y=⎧∴⎨=+⎩ ················································································································· ３分 （Ⅱ）从变换的角度看，变换f 是可逆的．由（Ⅰ）得矩阵Ｍ对应的变换f 是y 轴方向上的切变变换．因为变换f 把每个点在横坐标不变的情况下，纵坐标变为原来纵坐标加上横坐标的２倍，所以它的逆变换1f-应该是把每个点在横坐标不变的情况下，纵坐标变为原来纵坐标减去横坐标的２倍． ·············································································································· ５分''2x xy x y=⎧∴⎨=-+⎩ ····················································································································· ６分 ∴11021M -⎛⎫=⎪-⎝⎭． ·············································································································· 7分 （2）极坐标与参数方程解：（Ⅰ）∵点A 、B 的极坐标分别为(1,0)、(1,)2π，∴点A 、B 的直角坐标分别为(1,0)、(0,1)， ································································· 2分 ∴直线AB 的直角坐标方程为10x y +-=． ······································································ 4分（Ⅱ）由曲线C 的参数方程cos ,(sin x r y r ααα=⎧⎨=⎩为参数）化为普通方程为222x y r +=， ·· 5分 ∵直线AB 和曲线C 只有一个交点，∴直线AB 与圆C 相切∴半径r == ································································································ 7分 ⑶不等式证明选讲解：(Ⅰ)由柯西不等式得2()(111)a b c ≤++++ 代入已知 3a b c ++=29∴+≤3+≤当且仅当1a b c ===取等号． ………………………………………………………………3分（Ⅱ）由ab b a 2≥+得3c +≤，若c ab =，则3c +≤，()()013≤-+c c ，所以1≤c ，1≤c ，当且仅当1a b ==时，c 有最大值1．………………………………7分。