《一元一次方程》全章复习与巩固(提高)知识讲解初一数学知识导学

一元一次方程复习讲义1．方程的有关概念2．等式的基本性质3．解一元一次方程的基本步骤：4.应用一元一次方程解决实际问题的一般步骤（1)审 （2）找 （3）设 （4)列 (5）解 （6）验 （7）答1．下列方程是一元一次方程的有哪些? x+2y=9 x 2－3x=111=x x x 3121=- 2x=1 3x –5 3+7=10 x 2+x=12、解下列方程:⑴ 103.02.017.07.0=--x x ⑵16110312=+-+x x⑶03433221=-+++++x x x ⑷2362132432⎪⎭⎫ ⎝⎛+--=+--x x x x x(5)｜5x 一2｜＝33、8=x 是方程a x x 2433+=- 的解，又是方程 ()[]b x b x x x +=⎥⎦⎤⎢⎣⎡---913131的解，求 b4、小张在解方程1523=-x a （x 为未知数)时，误将 - 2x 看成 2x 得到的解为3=x ，请你求出原来方程的解5、已知关于x 的方程 ()()x n x m 121232+=-+无穷多解，求m 、n1、(本题7分）按要求完成下面题目：323221+-=--x x x解:去分母，得424136+-=+-x x x ……① 即 8213+-=+-x x ……②移项，得 1823-=+-x x ……③合并同类项，得 7=-x ……④∴ 7-=x ……⑤上述解方程的过程中，是否有错误？答：__________；如果有错误，则错在__________步。

如果上述解方程有错误,请你给出正确的解题过程：2、（本题7分）请阅读下列材料:让我们来规定一种运算：bcad dc ba -=，例如：5432=2×5－3×4=10－12=－2. 按照这种运算的规定，若2121x x-=23，试用方程的知识求x 的值。

3、检修一处住宅区的自来水管,甲单独完成需要14天，乙单独完成需18天，丙单独完成需要12天。

复习一元一次方程综合提高相关概念与性质：一元一次方程的定义1．一元一次方程的概念只含有一个未知数，并且未知数的最高次数是1，且未知数的系数不等于0的方程叫做一元一次方程。

2．一元一次方程的形式标准形式：0ax b+=〔其中0a≠，a，b是数〕的形式叫一元一次方程的标准形式．最简形式：方程ax b=〔0a≠，a，b为数〕叫一元一次方程的最简形式．【注意】任何一元一次方程都可以转化为最简形式或标准形式，所以判断一个方程是不是一元一次方程，可以通过变形为最简形式或标准形式来验证．如方程22216x x x++=-是一元一次方程．如果不变形，直接判断就出会现错误．等式的概念用等号“＝〞来表示相等关系的式子，叫做等式．1.在等式中，等号左、右两边的式子，分别叫做这个等式的左边、右边．等式可以是数字算式，可以是公式、方程，也可以是用式子表示的运算律、运算法如此．2.等式的性质等式的性质1：等式两边都加上〔或减去〕同一个数或同一个整式，所得结果仍是等式．假如a b=，如此a m b m±=±；等式的性质2：等式两边都乘以〔或除以〕同一个数〔除数不能是0〕或同一个整式，所得结果仍是等式．假如a b=，如此am bm=，a bm m=(0)m≠．【注意】〔1〕在对等式变形过程中，等式两边必须同时进展．即：同时加或同时减，同时乘以或同时除以，不能漏掉某一边．〔2〕在等式变形中，以下两个性质也经常用到：①等式具有对称性，即：如果a b=，那么b a=．②等式具有传递性，即：如果a b=，b c=，那么a c=．一元一次方程的解法1．解一元一次方程的一般步骤〔1〕去分母：在方程的两边都乘以各分母的最小公倍数．【注意】不要漏乘不含分母的项，分子是个整体，含有多项式时应加上括号． 〔2〕去括号：一般地，先去小括号，再去中括号，最后去大括号．【注意】不要漏乘括号里的项，不要弄错符号．〔3〕移项：把含有未知数的项都移到方程的一边，不含未知数的项移到方程的另一边．【注意】①移项要变号；②不要丢项．〔4〕合并同类项：把方程化成ax b =的形式．【注意】字母和其指数不变． 〔5〕系数化为1：在方程的两边都除以未知数的系数a 〔0a ≠〕，得到方程的解b x a=．【注意】不要把分子、分母搞颠倒． 2、一元一次方程实际应用提升练习题型一：1.如下各式中：①3x +；②2534+=+；③44x x +=+；④12x =；⑤213x x ++=； ⑥44x x -=-；⑦23x =；⑧2(2)3x x x x +=++．哪些是一元一次方程＿＿＿＿。

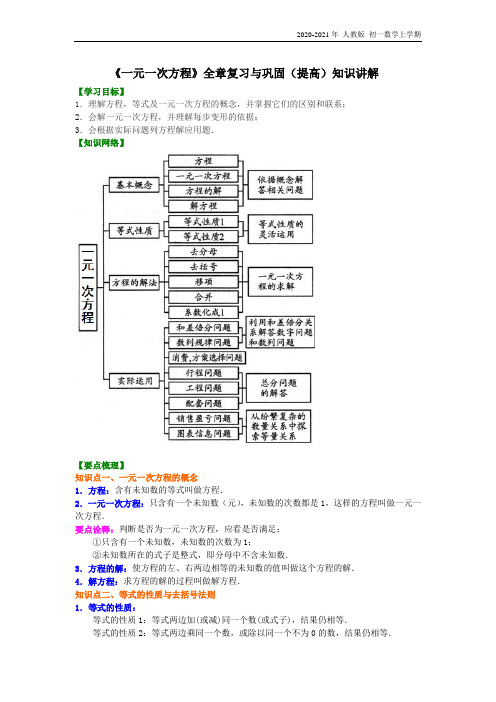
《一元一次方程》全章复习与巩固（提高）知识讲解【学习目标】1．理解方程，等式及一元一次方程的概念，并掌握它们的区别和联系；2．会解一元一次方程，并理解每步变形的依据；3．会根据实际问题列方程解应用题．【知识网络】【要点梳理】知识点一、一元一次方程的概念1．方程：含有未知数的等式叫做方程．2．一元一次方程：只含有一个未知数（元），未知数的次数都是1，这样的方程叫做一元一次方程．要点诠释：判断是否为一元一次方程，应看是否满足：①只含有一个未知数，未知数的次数为1；②未知数所在的式子是整式，即分母中不含未知数．3．方程的解：使方程的左、右两边相等的未知数的值叫做这个方程的解．4．解方程：求方程的解的过程叫做解方程．知识点二、等式的性质与去括号法则1．等式的性质：等式的性质1：等式两边加(或减)同一个数(或式子)，结果仍相等．等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等．2．合并法则：合并时，把系数相加(减)作为结果的系数，字母和字母的指数保持不变．3．去括号法则：（1）括号外的因数是正数，去括号后各项的符号与原括号内相应各项的符号相同．（2）括号外的因数是负数，去括号后各项的符号与原括号内相应各项的符号相反． 知识点三、一元一次方程的解法解一元一次方程的一般步骤：(1)去分母：在方程两边同乘以各分母的最小公倍数．(2)去括号：依据乘法分配律和去括号法则，先去小括号，再去中括号，最后去大括号．(3)移项：把含有未知数的项移到方程一边，常数项移到方程另一边．(4)合并：逆用乘法分配律，分别合并含有未知数的项及常数项，把方程化为ax ＝b(a ≠0)的形式．(5)系数化为1：方程两边同除以未知数的系数得到方程的解b x a=(a ≠0)． (6)检验：把方程的解代入原方程，若方程左右两边的值相等，则是方程的解；若方程左右两边的值不相等，则不是方程的解．知识点四、用一元一次方程解决实际问题的常见类型1.行程问题：路程＝速度×时间2.和差倍分问题：增长量＝原有量×增长率3.利润问题：商品利润＝商品售价－商品进价4.工程问题：工作量＝工作效率×工作时间，各部分劳动量之和＝总量5.银行存贷款问题：本息和＝本金+利息，利息＝本金×利率×期数6.数字问题：多位数的表示方法：例如：32101010abcd a b c d =⨯+⨯+⨯+.【典型例题】 类型一、一元一次方程的相关概念1．已知方程(3m-4)x 2-(5-3m)x-4m ＝-2m 是关于x 的一元一次方程，求m 和x 的值．【思路点拨】若一个整式方程经过化简变形后，只含有一个未知数，并且未知数的次数都是1，系数不为0，则这个方程是一元一次方程．【答案与解析】解：因为方程(3m-4)x 2-(5-3m)x-4m ＝-2m 是关于x 的一元一次方程，所以3m-4＝0且5-3m ≠0．由3m-4＝0解得43m =，又43m =能使5-3m ≠0，所以m 的值是43． 将43m =代入原方程，则原方程变为485333x ⎛⎫--⨯= ⎪⎝⎭，解得83x =-． 所以43m =，83x =-． 【总结升华】解答这类问题，一定要严格按照一元一次方程的定义．方程(3m-4)x 2-(5-3m)x-4m ＝-2m 2是关于x 的一元一次方程，就是说x 的二次项系数3m-4＝0，而x 的一次项系数5-3m ≠0，m 的值必须同时符合这两个条件．举一反三：【变式】下面方程变形中，错在哪里：(1)方程2x=2y两边都减去x+y，得2x-(x+y)=2y-(x+y), 即x-y=-(x-y).方程 x-y=-(x-y)两边都除以x-y, 得1=-1.（2）3721223x xx-+=+，去分母，得3(3-7x)=2(2x+1)+2x，去括号得：9-21x=4x+2+2x.【答案】（1）答：错在第二步，方程两边都除以x-y.（2）答：错在第一步，去分母时2x项没乘以公分母6.2.如果5(x+2)＝2a+3与(31)(53)35a x a x+-=的解相同，那么a的值是________．【答案】7 11【解析】由5(x+2)＝2a+3，解得275ax-=．由(31)(53)35a x a x+-=，解得95x a=-．所以27955aa-=-，解得711a=．【总结升华】因为两方程的解相同，可把a看做已知数，分别求出它们的解，令其相等，转化为求关于a的一元一次方程．举一反三：【变式】（2015•温州模拟）已知3x=4y，则= ．【答案】．解：根据等式性质2，等式3x=4y两边同时除以3y，得：=．类型二、一元一次方程的解法3．（2016春•淅川县期中）解方程﹣=．【思路点拨】方程整理后，去分母，去括号，移项合并，把x系数化为1，即可求出解．【答案与解析】解：原方程可化为6x﹣=，两边同乘以6得36x﹣21x=5x﹣7，解得：x=﹣0.7．【总结升华】此题考查了解一元一次方程，注意第一步用到的是分数的基本性质：分子和分母扩大相同的倍数，分数的值不变.举一反三：【变式1】解方程26752254436z z z z z +---++=- 【答案】解：把方程两边含有分母的项化整为零，得267522544443366z z z z z +++-=--+． 移项，合并同类项得：1122z =，系数化为1得：z ＝1． 【变式2】解方程： 0.10.050.20.05500.20.54x x +--+=. 【答案】解：把方程可化为：0.520.550254x x +--+=， 再去分母得：232x =-解得：16x =-4．解方程3{2x-1-[3(2x-1)+3]}＝5．【答案与解析】解：把2x-1看做一个整体．去括号，得：3(2x-1)-9(2x-1)-9＝5．合并同类项，得-6(2x-1)＝14． 系数化为1得：7213x -=-，解得23x =-． 【总结升华】把题目中的2x-1看作一个整体，从而简化了计算过程．本题也可以考虑换元法：设2x-1＝a ，则原方程化为3[a-(3a+3)]＝5．类型三、特殊的一元一次方程的解法1．解含字母系数的方程5.解关于x 的方程：11()(2)34m x n x m -=+ 【思路点拨】这个方程化为标准形式后，未知数x 的系数和常数都是以字母形式出现的，所以方程的解的情况与x 的系数和常数的取值都有关系．【答案与解析】解：原方程可化为：(43)462(23)m x mn m m n -=+=+当34m ≠时，原方程有唯一解：4643mn m x m +=-； 当33,42m n ==-时，原方程无数个解； 当33,42m n =≠-时，原方程无解； 【总结升华】解含字母系数的方程时，一般化为最简形式ax b =，再分类讨论进行求解，注意最后的解不能合并，只能分情况说明．2．解含绝对值的方程6. 解方程|x-2|＝3．【答案与解析】解：当x-2≥0时，原方程可化为x-2＝3，得x＝5．当x-2＜0时，原方程可化为-(x-2)＝3，得 x＝-1．所以x＝5和x＝-1都是方程|x-2|＝3的解．【总结升华】如图所示，可以看出点-1与5到点2的距离均为3，所以|x-2|＝3的意义为在数轴上到点2的距离等于3的点对应的数，即方程|x-2|＝3的解为x＝-1和x＝5．举一反三：【变式1】若关于x的方程230x m-+=无解，340x n-+=只有一个解，450x k-+=有两个解，则,,m n k的大小关系为： ( )A. m n k>> B.n k m>> C.k m n>> D.m k n>>【答案】A【变式2】若9x=是方程123x m-=的解，则__m=；又若当1n=时，则方程123x n-=的解是．【答案】1； 9或3．类型四、一元一次方程的应用7．李伟从家里骑摩托车到火车站，如果每小时行30千米，那么比火车开车时间早到15分钟；若每小时行18千米，则比火车开车时间迟到15分钟，现在李伟打算在火车开车前10分钟到达火车站，求李伟此时骑摩托车的速度应是多少?【思路点拨】本题中的两个不变量为：火车开出的时间和李伟从家到火车站的路程不变．【答案与解析】解：设李伟从家到火车站的路程为y千米，则有：151530601860y y+=-，解得：452y=由此得到李伟从家出发到火车站正点开车的时间为4515213060+=(小时)．李伟打算在火车开车前10分钟到达火车站时，设李伟骑摩托车的速度为x千米/时, 则有：452271010116060yx===--(千米/时)答：李伟此时骑摩托车的速度应是27千米/时．【总结升华】在解决问题时，当发现某种方法不能解决问题时，应该及时变换思维角度，如本题直接设未知数较难时，应迅速变换思维的角度，合理地设置间接未知数以寻求新的解决问题的途径和方法．8.（2015春•万州区校级月考）一项工程，甲单独做要10天完成，乙单独做要15天完成，两人合做4天后，剩下的部分由乙单独做，还需要几天完成？【答案与解析】解：设乙还需x天完成，由题意得4×（+）+=1，解得x=5．答：乙还需5天完成．【总结升华】本题考查了一元一次方程的应用，解决问题的关键是找到所求的量的等量关系．当题中没有一些必须的量时，为了简便，可设其为1．举一反三：【变式】某商品进价2000元，标价4000元，商店要求以利润率不低于20%的售价打折出售，售货员最低可以打几折出售此商品？【答案】解：设售货员可以打x折出售此商品，得：⨯=+40000.12000(120%),xx=解得： 6.答：售货员最低可以打六折出售此商品．。

一元一次方程的解法（提高）知识讲解【学习目标】1. 熟悉解一元一次方程的一般步骤，理解每步变形的依据；2. 掌握一元一次方程的解法，体会解法中蕴涵的化归思想；3. 进一步熟练掌握在列方程时确定等量关系的方法. 【要点梳理】要点诠释：（1）解方程时，表中有些变形步骤可能用不到，而且也不一定要按照自上而下的顺序，有些步骤可以合并简化．(2) 去括号一般按由内向外的顺序进行，也可以根据方程的特点按由外向内的顺序进行. （3）当方程中含有小数或分数形式的分母时，一般先利用分数的性质将分母变为整数后再去分母，注意去分母的依据是等式的性质，而分母化整的依据是分数的性质，两者不要混淆．要点二、解特殊的一元一次方程1.含绝对值的一元一次方程解此类方程关键要把绝对值化去，使之成为一般的一元一次方程，化去绝对值的依据是绝对值的意义．要点诠释：此类问题一般先把方程化为ax b c +=的形式，再分类讨论：(1)当0c <时，无解；（2）当0c =时，原方程化为：0ax b +=；（3）当0c >时，原方程可化为：ax b c +=或ax b c +=-. 2.含字母的一元一次方程此类方程一般先化为最简形式ax ＝b ，再分三种情况分类讨论： （1）当a ≠0时，b x a=；（2）当a ＝0，b ＝0时，x 为任意有理数；（3）当a ＝0，b ≠0时，方程无解． 【典型例题】类型一、解较简单的一元一次方程1．关于x的方程2x﹣4=3m和x+2=m有相同的解，则m的值是（）A.10 B.-8 C.-10 D.8【答案】B．【解析】解：由2x﹣4=3m得：x=；由x+2=m得：x=m﹣2由题意知=m﹣2解之得：m=﹣8．【总结升华】根据题目给出的条件，列出方程组，便可求出未知数．举一反三：【变式】下列方程的解法对不对?如果不对，错在哪里?应当怎样改正?3x+2＝7x+5解：移项得3x+7x＝2+5，合并得10x＝7．，系数化为1得710x=．【答案】以上的解法是错误的，其错误的原因是在移项时没有变号，也就是说将方程中右边的7x移到方程左边应变为-7x，方程左边的2移到方程右边应变为-2．正确解法：解：移项得3x-7x＝5-2，合并得-4x＝3，系数化为1得34x=-．类型二、去括号解一元一次方程2. 解方程：112 [(1)](1) 223x x x--=-．【答案与解析】解法1：先去小括号得：11122[]22233x x x-+=-．再去中括号得：1112224433x x x-+=-．移项，合并得：5111212x-=-．系数化为1，得：115x=．解法2：两边均乘以2，去中括号得：14(1)(1)23x x x--=-．去小括号，并移项合并得：51166x-=-，解得：115x=．解法3：原方程可化为：112 [(1)1(1)](1) 223x x x-+--=-．去中括号，得1112(1)(1)(1) 2243x x x-+--=-．移项、合并，得51(1)122x--=-．解得115x=．【总结升华】解含有括号的一元一次方程时，一般方法是由内到外或由外到内逐层去括号，但有时根据方程的结构特点，灵活恰当地去括号，以使计算简便．例如本题的方法3：方程左、右两边都含(x-1)，因此将方程左边括号内的一项x变为(x-1)后，把(x-1)视为一个整体运算．3．解方程：111111110 2222x⎧⎫⎡⎤⎛⎫----=⎨⎬⎪⎢⎥⎝⎭⎣⎦⎩⎭．【答案与解析】解法1：(层层去括号)去小括号11111110 2242x⎧⎫⎡⎤----=⎨⎬⎢⎥⎣⎦⎩⎭．去中括号1111110 2842x⎧⎫----=⎨⎬⎩⎭．去大括号111110 16842x----=．移项、合并同类项，得115168x=，系数化为1，得x＝30．解法2：(层层去分母)移项，得11111111 2222x⎧⎫⎡⎤⎛⎫---=⎨⎬⎪⎢⎥⎝⎭⎣⎦⎩⎭．两边都乘2，得1111112 222x⎡⎤⎛⎫---=⎪⎢⎥⎝⎭⎣⎦．移项，得111113 222x⎡⎤⎛⎫--=⎪⎢⎥⎝⎭⎣⎦．两边都乘2，得11116 22x⎛⎫--=⎪⎝⎭．移项，得111722x⎛⎫-=⎪⎝⎭，两边都乘2，得11142x-=．移项，得1152x=，系数化为1，得x＝30．【总结升华】此题既可以按去括号的思路做，也可以按去分母的思路做．举一反三：【变式】解方程11111641 2345x⎧⎫⎡⎤⎛⎫--+=⎨⎬⎪⎢⎥⎝⎭⎣⎦⎩⎭．【答案】解：方程两边同乘2，得1111642 345x⎡⎤⎛⎫--+=⎪⎢⎥⎝⎭⎣⎦．移项、合并同类项，得111162 345x⎡⎤⎛⎫--=-⎪⎢⎥⎝⎭⎣⎦．两边同乘以3，得11166 45x⎛⎫--=-⎪⎝⎭．移项、合并同类项，得1110 45x⎛⎫-=⎪⎝⎭．两边同乘以4，得110 5x-=．移项，得115x=，系数化为1，得x＝5．类型三、解含分母的一元一次方程4．（2016春•淅川县期中）解方程﹣=．【思路点拨】方程整理后，去分母，去括号，移项合并同类项，把x系数化为1，即可求出解．【答案与解析】解：原方程可化为6x﹣=，两边同乘以6，得36x﹣21x=5x﹣7，移项合并，得10x=-7解得：x=﹣0.7．【总结升华】此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把未知数系数化为1，求出解．举一反三：【变式】解方程0.40.90.30.210.50.3y y++-=．【答案】解：原方程可化为49321 53y y++-=．去分母，得3(4y+9)-5(3+2y)＝15．去括号，得12y+27-15-10y＝15．移项、合并同类项，得2y＝3．系数化为1，得32y =． 类型四、解含绝对值的方程5．解方程：3|2x|-2＝0 ．【思路点拨】将绝对值里面的式子看作整体，先求出整体的值，再求x 的值． 【答案与解析】解：原方程可化为：223x = ． 当x ≥0时，得223x =，解得：13x =， 当x ＜0时，得223x -=，解得：13x =-，所以原方程的解是x ＝13或x ＝13-．【总结升华】此类问题一般先把方程化为ax b c +=的形式，再根据（ax b +）的正负分类讨论，注意不要漏解．举一反三：【变式】（2014秋•故城县期末）已知关于x 的方程mx+2=2（m ﹣x ）的解满足方程|x ﹣|=0，则m 的值为（ ）A. B. 2 C.D.3【答案】B解：∵|x﹣|=0，∴x=，把x 代入方程mx+2=2（m ﹣x ）得：m+2=2（m ﹣）， 解之得：m=2.类型五、解含字母系数的方程6. 解关于x 的方程：1mx nx -= 【答案与解析】解：原方程可化为：()1m n x -=当0m n -≠，即m n ≠时，方程有唯一解为：1x m n=-； 当0m n -=，即m n =时，方程无解．【总结升华】解含字母系数的方程时，先化为最简形式ax b =，再根据x 系数a 是否为零进行分类讨论．【高清课堂：一元一次方程的解法388407解含字母系数的方程】 举一反三：【变式】若关于x 的方程(k-4)x =6有正整数解，求自然数k 的值.【答案】解：∵原方程有解，∴40k-≠原方程的解为：64xk=-为正整数，∴4k-应为6的正约数，即4k-可为：1，2，3，6∴k为：5，6，7，10答：自然数k的值为：5，6，7，10.附录资料：方程的意义（基础）知识讲解【学习目标】1．正确理解方程的概念，并掌握方程、等式及算式的区别与联系；2. 正确理解一元一次方程的概念，并会判断方程是否是一元一次方程及一个数是否是方程的解；3. 理解并掌握等式的两个基本性质.【要点梳理】【高清课堂：从算式到方程一、方程的有关概念】要点一、方程的有关概念1．定义：含有未知数的等式叫做方程.要点诠释：判断一个式子是不是方程，只需看两点：一.是等式；二.是含有未知数．2．方程的解：使方程左右两边的值相等的未知数的值，叫做方程的解.要点诠释：判断一个数（或一组数）是否是某方程的解，只需看两点：①.它（或它们）是方程中未知数的值；②将它（或它们）分别代入方程的左边和右边，若左边等于右边，则它们是方程的解，否则不是．3．解方程：求方程的解的过程叫做解方程.4．方程的两个特征：（1）.方程是等式；（2）.方程中必须含有字母（或未知数）.【高清课堂：从算式到方程二、一元一次方程的有关概念】要点二、一元一次方程的有关概念定义：只含有一个未知数（元），并且未知数的次数都是1，这样的方程叫做一元一次方程.要点诠释：“元”是指未知数，“次”是指未知数的次数，一元一次方程满足条件：①首先是一个方程;②其次是必须只含有一个未知数;③未知数的指数是1;④分母中不含有未知数．【高清课堂：从算式到方程三、解方程的依据——等式的性质】要点三、等式的性质1．等式的概念：用符号“=”来表示相等关系的式子叫做等式.2．等式的性质：等式的性质1：等式两边加（或减）同一个数（或式子），结果仍相等.即：如果，那么 (c为一个数或一个式子) .等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等.即：如果，那么；如果，那么.要点诠释：（1）根据等式的两条性质，对等式进行变形，等式两边必须同时进行完全相同的变形； (2) 等式性质1中，强调的是整式，如果在等式两边同加的不是整式，那么变形后的等式不一定成立，如x＝0中，两边加上得x＋，这个等式不成立;(3) 等式的性质2中等式两边都除以同一个数时，这个除数不能为零．【典型例题】类型一、方程的概念1．下列各式哪些是方程？①3x-2＝7；②4+8＝12；③3x-6；④2m-3n＝0；⑤3x2-2x-1＝0；⑥x+2≠3；⑦251x=+；⑧28553x x-=．【答案与解析】解：②虽是等式，但不含未知数；③不是等式；⑥表示不等关系，故②、③、⑥均不符合方程的概念．①、④、⑤、⑦、⑧符合方程的定义，所以方程有：①、④、⑤、⑦、⑧．【总结升华】方程的判断必须看两点，一个是等式，二是含有未知数．当然未知数的个数可以是一个，也可以是多个．举一反三：【变式】下列四个式子中，是方程的是（）A. 3+2=5B. x=1C. 2x﹣3＜0D. a2+2ab+b2 【答案】B．2．（2015春•孟津县期中）下列方程中，以x=2为解的方程是（）A. 4x﹣1=3x+2B. 4x+8=3（x+1）+1C. 5（x+1）=4（x+2）﹣1D. x+4=3（2x﹣1）【答案】C．【总结升华】检验一个数是不是方程的解，根据方程解的概念，只需将所给字母的值分别代入方程的左右两边，若两边的值相等，则这个数就是此方程的解，否则不是．举一反三：【变式】下列方程中，解是x=3的是( )A．x+1＝4 B．2x+1＝3 C．2x-1＝2 D．217 3x+=类型二、一元一次方程的相关概念3．（2016春•南江县期末）在下列方程中①x 2+2x=1，②﹣3x=9，③x=0，④3﹣=2，⑤=y+是一元一次方程的有（ ）个．A ．1B ．2C ．3D ．4【思路点拨】根据一元一次方程的定义：只含有一个未知数，并且未知数的最高次数是1次的整式方程，可以逐一判断. 【答案】B.【解析】解：①x 2+2x=1，是一元二次方程；②﹣3x=9，是分式方程；③x=0，是一元一次方程；④3﹣=2，是等式，不是方程；⑤=y+是一元一次方程；一元一次方程的有2个，故选：B ． 【总结升华】本题考查了一元一次方程的定义，解决本题的关键是熟记一元一次方程的定义．举一反三：【变式】下列方程中是一元一次方程的是__________（只填序号）． ①2x-1＝4；②x ＝0；③ax ＝b ；④151x-=-． 【答案】①②.类型三、等式的性质4．用适当的数或整式填空，使所得的结果仍为等式，并说明根据等式的哪一条性质，以及怎样变形得到的． (1)如果41153x -=，那么453x =+________； (2)如果ax+by ＝-c ，那么ax ＝-c +________； (3)如果4334t -=，那么t ＝________． 【答案与解析】解： (1). 11；根据等式的性质1，等式两边都加上11； (2).（-by ）； 根据等式的性质1，等式两边都加上-by ； (3).916-； 根据等式的性质2，等式两边都乘以34-． 【总结升华】先从不需填空的一边入手，比较这一边是怎样变形的，再根据等式的性质，对另一边也进行同样的变形．举一反三：【变式】下列说法正确的是( )．A ．在等式ab ＝ac 两边都除以a ，可得b ＝c.B ．在等式a ＝b 两边除以c 2+1，可得2211a bc c =++. C ．在等式b ca a=两边都除以a ，可得b ＝c.D．在等式2x＝2a-b两边都除以2，可得x＝a-b.【答案】B.类型四、设未知数列方程5．根据问题设未知数并列出方程：一次考试共有25道选择题，做对一道得4分，做错或不做一道倒扣1分．若小明想考80分，他要做对多少道题？【答案与解析】解：设小明要做对x道题，则有(25-x)道做错或没做的题，依题意有：4x-(25-x)×1＝80．可以采用列表法探究其解显然，当x＝21时，4x-(25-x)×1＝80．所以小明要做对21道题．【总结升华】根据题意设出合适的未知量，并根据等量关系列出含有未知量的等式．举一反三：【变式】根据下列条件列出方程．(l)x的5倍比x的相反数大10；(2)某数的34比它的倒数小4；(3)甲、乙两人从学校到公园，走这段路甲用20分钟，乙用30分钟，如果乙比甲早5分钟出发，问甲用多少时间追上乙？【答案】(1)5x-(-x)＝10；(2)设某数为x，则1344xx-=；(3)设甲用x分钟追上乙，由题意得11(5)3020x x+=．。

初一数学一元一次方程知识梳理与练习巩固第二讲 一元一次方程✍知识网络1.定义：在一个方程中,如果只含有一个未知数，且未知数的最高次数是1的整式方程叫做一元一次方程。

（linear equation in one ）一般形式：ax+b=0（a 、b 为常数，a ≠0）。

一元一次方程只有一个解。

一元一次方程的最终结果(方程的解)是x=a 的形式2.性质：一元一次方程的“等式的性质1”和“等式的性质2” 1）.等式两边同时加或减一个相同数，等式两边相等。

（如果a=b ，那么a ±c=b ±c 。

）2）.等式两边同时乘或除以一个相同数（0除外），或一个整式,等式两边相等。

（如果a=b ，那么ac=bc 。

如果a=b ，c ≠0，那么a/c=b/c 。

）解法是通过移项将未知数移到一边，再把常数移到一边(等式基本性质1，注意符号!)，然后两边同时除以未知数系数(化系数为1,等式基本性质2)，即可得到未知数的值。

3.一般解法：1）去分母 方程两边同时乘各分母的最小公倍数。

2）去括号 一般先去小括号，在去中括号，最后去大括号。

但顺序有时可依据情况而定使计算简便。

可根据乘法分配律。

3）移项 把方程中含有未知数的项移到方程的另一边，其余各项移到方程的另一边移项时别忘记了要变号。

4）合并同类项 将原方程化为ax=b(a ≠0)的形式。

5）系数化1 方程两边同时除以未知数的系数，得出方程的解。

✍例题精选例1.3 1.50.2x --0.20.10.03x -=2.5例2．解方程：312-x -12110+x =412+x -1例3.已知关于x 的方程3a-x=2x +3的解是4，则（-a ）2-2a ＝ 例4.当m= 时，方程5x+4=4x-3和方程2(x+1)-m=-2(m-2)的解相同；当n= 时，代数式4n+8与3n-10的值互为相反数。

例5.已知关于x 的方程2a(x-1)=(5-a)x+3b 有无数多解，试求a 、b 的值。

2019年初一年级巩固数学知识点之一元一次方程完成了小学阶段的学习，进入紧张的初中阶段。

这篇2019年初一年级巩固数学知识点之一元一次方程，是查字典数学网特地为大家整理的，欢迎阅读~一元一次方程1.等式：用=号连接而成的式子叫等式.2.等式的性质：等式性质1：等式两边都加上(或减去)同一个数或同一个整式，所得结果仍是等式;等式性质2：等式两边都乘以(或除以)同一个不为零的数，所得结果仍是等式.3.方程：含未知数的等式，叫方程.4.方程的解：使等式左右两边相等的未知数的值叫方程的解;注意：方程的解就能代入!5.移项：改变符号后，把方程的项从一边移到另一边叫移项.移项的依据是等式性质1.6.一元一次方程：只含有一个未知数，并且未知数的次数是1，并且含未知数项的系数不是零的整式方程是一元一次方程.7.一元一次方程的标准形式：ax+b=0(x是未知数，a、b是已知数，且a0).8．一元一次方程解法的一般步骤：化简方程----------分数基本性质去分母----------同乘(不漏乘)最简公分母去括号----------注意符号变化移项----------变号(留下靠前)合并同类项--------合并后符号系数化为1---------除前面10．列一元一次方程解应用题：(1)读题分析法:多用于和，差，倍，分问题仔细读题，找出表示相等关系的关键字，例如：大，小，多，少，是，共，合，为，完成，增加，减少，配套-----，利用这些关键字列出文字等式，并且据题意设出未知数，最后利用题目中的量与量的关系填入代数式，得到方程.(2)画图分析法:多用于行程问题一般说来，“教师”概念之形成经历了十分漫长的历史。

杨士勋（唐初学者，四门博士）《春秋谷梁传疏》曰：“师者教人以不及，故谓师为师资也”。

这儿的“师资”，其实就是先秦而后历代对教师的别称之一。

《韩非子》也有云：“今有不才之子……师长教之弗为变”其“师长”当然也指教师。

第三章一元一次方程知识要点梳理一.元一次方程及解的概念1、一元一次方程的概念只含有一个未知数，并且未知数的次数都是1的方程叫做一元一次方程。

一元一次方程的标准形式是：ax+b=0(其中x是未知数，a,b是已知数，且a≠0)。

2、方程的解使方程左右两边的值相等的未知数的值叫做方程的解注意：（1）一元一次方程必须满足的3个条件：只含有一个未知数；未知数的次数是1次；整式方程．（2）判断一个数是否是某方程的解：将其代入方程两边，看两边是否相等．二.方程变形——解方程的重要依据1、等式的基本性质（也叫做方程的同解原理）等式的性质1：等式两边加（或减）同一个数（或式子），结果仍相等。

即：如果，那么；(c为一个数或一个式子)。

等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等。

即：如果，那么；如果，那么2、分数的基本的性质分数的分子、分母同时乘以或除以同一个不为0的数，分数的值不变。

即：（其中m≠0）注：分数的基本的性质主要是用于将方程中的小数系数（特别是分母中的小数）化为整数，如方程：－=1.6，将其化为的形式：－=1.6。

方程的右边没有变化，这要与“去分母”区别开。

三.解一元一次方程的一般步骤1、解一元一次方程的基本思路通过对方程变形，把含有未知数的项归到方程的一边，把常数项归到方程的另一边，最终把方程“转化”成x＝a的形式。

2、解一元一次方程的一般步骤是变形名称具体做法变形依据去分母在方程两边都乘以各分母的最小公倍数等式基本性质2去括号先去小括号，再去中括号，最后去大括号去括号法则、分配律移项把含有未知数的项都移到方程的一边，其他项都等式基本性质1移到方程的另一边(记住移项要变号)合并同类项把方程化成ax＝b(a≠0)的形式合并同类项法则等式基本性质2系数化成1 在方程两边都除以未知数的系数a，得到方程的解x＝注意：(1) 解方程时应注意：①解方程时，表中有些变形步骤可能用不到，并且也不一定按照自上而下的顺序，要根据方程形式灵活安排求解步骤。

七年级数学上册知识点思维导
图、考点梳理一元一次方程
七年级数学上册知识点思维导图、考点梳理——一元一次方程_问题
1.列方程时，要先设字母表示未知数，然后根据问题中的相等关系，写出还有未知数的等式——方程。

2.含有一个未知数(元素)且该未知数的次数为1的方程称为一元线性方程。

3.利用等价关系分析实际问题中的数量关系，列出方程，是用数学方法解决实际问题的一种方法。

4.等式1的性质:等式两边加(或减)相同的数(或公式)，结果仍然相等。

5.等式的性质2:当等式两边都乘以同一个数，或者除以一个不为0的数，结果仍然相等。

6.将等式一边的变化符号移动到另一边叫做移项。

7.应用：行程问题：s=v×t
工程问题：工作总量=工作效率×时间
盈亏问题：利润=售价－成本利率=利润÷成本×100％
售价=标价×折扣数×10％储蓄利润问题：利息=本金×利率×时间本息和=本金+利息
end。