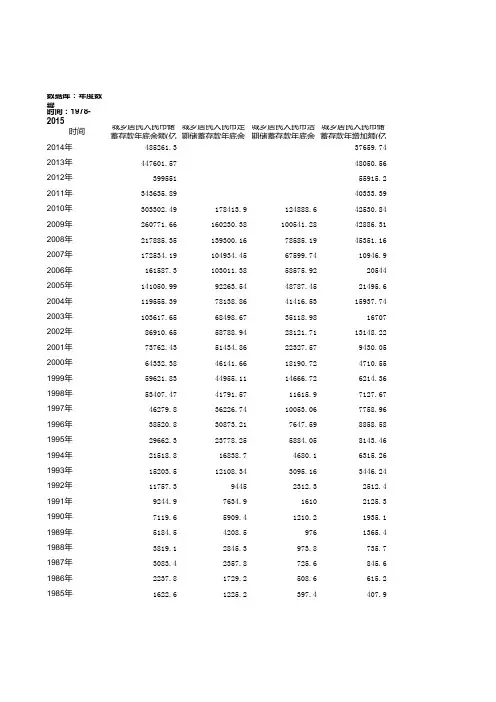
各地区城乡居民人民币储蓄存款 (年底余额)

山东省临沂市高职单招2021-2022学年职业技能模拟试卷及答案学校:________ 班级:________ 姓名:________ 考号:________一、单选题(100题)1.研究耐盐碱的海水稻.有助于突破我国18亿亩有限的耕地资源约束，并在很大程度上缓解人类水资源、可耕地和粮食三夫危机。

下列关于海水稻的说法，错误的是（）A.野生耐盐碱水稻的出现,是长期自然选择的结果B.水稻的耐盐性和不耐盐性属于相对性状C.通过杂交水稻技术，可以增加海水稻的优势D.海水稻的细胞壁可以阻止盐碱等分子的进入，因此可以达到耐盐碱的目的2.依次填入下列各句括号中的词语，最恰当的一组是(). ①想想看，哪一个伟大的作家不是学问()又积极劳动的人呢？②有女儿在身边，她能得到一丝（）。

③那月色()了我多年内心的创伤，所有的仇恨在一瞬间消融了。

A.广博、安抚、安慰B.渊博、安慰、抚慰C.渊博、抚慰、安抚D.广博、安慰、安抚3.李鸿章认为，要改变中国贫弱的现状，“必先求富，而后才能自强”。

下列企业体现“求富”这一思想的是（）A.天津机器局B.上海机器织布局C.福州船政局D.江南机器制造总局4.一块木板切掉一半后，保持不变的物理量是()A.重力B.体积C.密度D.质量5.下列不属于学习型组织的要素是()A.建立远景B.自我超越C.个人学习D.系统思考6.下列句子中有语病的一项是：()A.原始思维具有拟人化倾向，以具体意向间的类比关系为基础，目的在于揭示某种诉诸我们感官的经验状态。

B.在新形势下，我们应该树立新的文化发展观，推进文化体制创新，挖掘特色文化内涵，着力开发富有时代精神和地方特色的文化产品。

C.素质可以理解为人在先天条件的基础上，在家庭、社会的影响下，经过后天的教育所形成的稳定的心理品格。

D.在经济全球化与文化多元化的时代趋势下，人文社会科学的地位正日益凸现和扩大，每一个有责任感的学者，必将以独立的思考，来回应社会、时代提出的问题。

2015普通高等学校招生全国统一考试(重庆卷)数学(文史类)一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合{1,2,3},{1,3}A B ==，则A B ∩= （ ） A.{2} B.{1,2} C.{1,3} D. {1,2,3} 【参考答案】C.【测量目标】集合的运算.【试题分析】由交集的定义得{1,3}A ∩=B . 故选C.2. “1x =”是“2210x x -+=”的 （ ） A. 充要条件 B. 充分不必要条件 C.必要不充分条件 D. 既不充分也不必要条件 【参考答案】A. 【测量目标】充要条件.【试题分析】由“1x =”显然能推出“2210x x -+=”，故条件是充分的；又由“2210x x -+=”可得2(1)01x x -=⇒=，所以条件也是必要的；故选A.3. 函数22()log (23)f x x x =+-的定义域是 （ ）A.[—3,1]B.（—3,1）C.(,3]-∞-∞∩[1,+)D. (,3)-∞-∞∪(1,+) 【参考答案】D.【测量目标】函数的定义域与二次不等式.【试题分析】由2230(3)(1)0x x x x +->⇒+->解得3x <-或1x >； 故选D.4. 重庆市2013年各月的平均气温（°C ）数据的茎叶图如下第4题图则这组数据中的中位数是 ( ) A. 19 B. 20 C. 21.5 D.23 【参考答案】B.【测量目标】茎叶图与中位数.【试题分析】由茎叶图知，第六第七个数据均为20，所以中位数为20 故选B.5. 某几何体的三视图如图所示，则该几何体的体积为第5题图A.123+πB.136π C.73π D.52π【参考答案】B. 【测量目标】三视图.【试题分析】由三视图可知该几何体是由一个底面半径为1，高为2的圆柱，再加上一个半圆锥：其底面半径为1，高也为1；构成的一个组合体，故其体积为221132166ππ⨯1⨯+⨯π⨯1⨯=；故选B. 6. 若11tan ,tan()32a ab =+=,则tan b =( ) A.17 B.16 C.57D. 56【参考答案】A.【测量目标】正切差角公式.【试题分析】11tan()tan 123tan tan[()]111tan()tan 7123a b a b a b a a b a -+-=+-===+++⨯；故选A.7. 已知非零向量,a b r r 满足||4||,(2)b a a a b =+r r r r r且⊥则a r 与b r 的夹角为 （ ）A.3π B.2πC.23πD.56π【参考答案】C.【测量目标】向量的数量积运算及向量的夹角.【试题分析】由已知可得2=0a a b a a b ⋅⇒+⋅=r r r r r r（2+）02；设a r 与b r 的夹角为θ，则有22||||||cos 0a a b θ+⋅=⇒r r r 222||1cos 24||a a θ=-=-r r ，又因为[0,]θ∈π，所以23θπ=； 故选C.8. 执行如下图所示的程序框图，则输出s 的值为 （ ）第8题图A.34 B.56 C.1112D. 2524【参考答案】D. 【测量目标】程序框图.【试题分析】初始条件：s =0,k =0;第1次判断0<8,是，k =2,s =11022+=； 第2次判断2<8,是，k =4,s =113244+=；第3次判断4<8,是，k =6, s =31114612+=；第4次判断6<8,是，k =6,s =1112512824+=； 第5次判断8<8,否，输出s =2524.9. 设双曲线22221(0,0)x y a b a b-=>>的右焦点是F ，左、右顶点分别是12,A A ,过F 做12A A 的垂线与双曲线交于B ，C 两点，若12A B A C ⊥,则双曲线的渐近线的斜率为 （ ）A.12±B.2±C.1±D.【参考答案】C.【测量目标】双曲线的几何性质.【试题分析】由已知得右焦点F （c ,0）（其中222,0c a b c =+>）,2212(,0),(,0),(,),(,)b b A a A a B c C c a a --;从而21(,)b A B c a a =+-uuu r ，22(,)b A C c a a =-uuu r ，又因为12A B A C ⊥,即22()()()()0b b c a c a a a -⋅++-⋅=；化简得2211b ba a=⇒=±，即双曲线的渐进线的斜率为1±；故选C.10. 若不等式组2022020x y x y x y m +-≤⎧⎪+-≥⎨⎪-+≥⎩,表示的平面区域为三角形，且其面积等于43，则m 的值为 （ ）A.3-B. 1C.43D.3 【参考答案】B. 【测量目标】线性规划. 【试题分析】第10题图如图，由于不等式组2022020x y x y x y m +-≤⎧⎪+-≥⎨⎪-+≥⎩,表示的平面区域为三角形ABC ，且其面积等于43，再注意到直线AB ：x +y -2=0与直线BC :x -y +2m =0互相垂直，所以三角形ABC 是直角三角形；易知，A （2，0），B （1-m ,m +1）,C(2422,33m m -+); 从而11224=|22||1||22|||2233ABC m S m m m ++⋅+-+⋅=△，化简得：2(1)4m +=，解得m =-3,或m =1；检验知当m =-3时，已知不等式组不能表示一个三角形区域，故舍去；所以m =1; 故选B.二、填空题：本大题共5小题，每小题5分，共25分.把答案填写在答题卡相应位置上.11．复数(12i)i +的实部为________. 【参考答案】-2【测量目标】复数运算.【试题分析】由于(1+2i)i=i+22i =-2+i,故知其实部为-2.12. 若点P （1，2）在以坐标原点为圆心的圆上，则该圆在点P 处的切线方程为___________. 【参考答案】x +2y -5=0 【测量目标】圆的切线.【试题分析】由点P （1，2）在以坐标原点为圆心的圆上知此圆的方程为：225x y +=，所以该圆在点P 处的切线方程为125x y ⨯+⨯=，即x +2y -5=0.13. 设△ABC 的内角A ，B ，C 的对边分别为,,a b c ,且12,cos 4a C ==-，3sin 2sin A B =,则c =________. 【参考答案】4【测量目标】正弦定理与余弦定理.【试题分析】由3sin 2sin A B =及正弦定理知：3a =2b ,又因为a =2,所以b =3； 由余弦定理得：22212cos 49223()164c a b ab C =+-=+-⨯⨯⨯-=，所以c =4; 14. 设,0,5ab a b >+=,________. 【参考答案】【测量目标】基本不等式.【试题分析】由2ab ≤22a b +两边同时加上22a b +得2()a b +≤222()a b +两边同时开方得：a b +0a >,0b >）且当且仅当a =b 时取“=”）；==13a b +=+，即73,22a b ==时，“=”成立）15. 在区间[0,5]上随机地选择一个数p ，则方程22320x px p ++-=有两个负根的概率为________. 【参考答案】23. 【测量目标】复数运算.【试题分析】方程22320x px p ++-=有两个负根的充要条件是21212=4p 4(32)020320p x x p x x p ⎧--≥⎪+=-<⎨⎪=->⎩V 即213p <≤或2p ≥；又因为[0,5]p ∈，所以使方程22320x px p ++-=有两个负根的p 的取值范围为2(,1][2,5]3∪，故所求的概率2(1)(52)23503-+-=-.三、解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤.16．(本小题满分13分，（1）小问7分，（2）小问6分) 已知等差数列{}n a 满足3a =2，前3项和3S =92. （1）求{}n a 的通项公式；（2）设等比数列{}n b 满足11b a =，415b a =，求{}n b 前n 项和n T . 【测量目标】(1)数列的通项公式；(2) 等比数列的前n 项和.【试题分析】（1）设{}n a 的公差为d ，则由已知条件得1132922,322a d a d ⨯+=+= 化简得11322,2a d a d +=+=解得111,2a d ==, 故通项公式112n n a -=+，即12n n a +=.(2)由（1）得14151511,82b b a +====. 设{}n b 的公比为q ,则3418b q b ==,从而q =2.故{}n b 的前n 项和 1(1)1(12)21112n n n n b q T q -⨯-===---. 17．(本小题满分13分，（1）小问10分，（2）小问3分)随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款（年底余额）如下表：（1）求y 关于t 的回归方程ˆˆˆybt a =+ （2）用所求回归方程预测该地区2015年（t =6）的人民币储蓄存款.附：回归方程ˆˆˆybt a =+中 1122211()(),()ˆ.nni i i ii i n ni i i i x x y y x y nxyb x x x nx ay bx ====⎧---⎪⎪==⎨--⎪⎪=-⎩∑∑∑∑【测量目标】：线性回归方程. 【试题分析】(1)列表计算如下ii ti y2i ti i t y1 1 5 1 52 2 6 4 123 3 7 9 214 4 8 16 325 5 10 25 50 ∑153655120这里111151365,3,7.255n n i i i i n t t y y n n =========∑∑ 又22211555310,120537.212.nnny iny i i i i l tnt l t y nt y ===-=-⨯==-=-⨯⨯=∑∑从而12ˆˆˆ1.2,7.2 1.23 3.610ny ny l b a y bt l ====-=-⨯=.故所求回归方程为ˆ 1.2 3.6yt =+. (2)将t =6代入回归方程可预测该地区2015年的人民币储蓄存款为ˆ 1.26 3.610.8y=⨯+= 18．(本小题满分13分，（1）小问7分，（2）小问6分)已知函数21()sin 22f x x x =. (1)求f （x ）的最小周期和最小值；(2)将函数f （x ）的图象上每一点的横坐标伸长到原来的两倍，纵坐标不变，得到函数g (x )的图象.当x ∈[,]2ππ时，求g (x )的值域.【测量目标】(1)三角函数的性质和恒等变换；(2)正弦函数的图象及性质. 【试题分析】(1) 211()sin 2sin 2(1cos 2)222f x x x x x =-=-+1sin 22sin(2)22232x x x π=--=--. ,因此()f x 的最小正周期为π，最小值为22+-.(2)由条件可知：()sin()3g x x π=-.当[,]2x π∈π时，有[,]363x ππ2π-=，从而sin()3x π-的值域为1[,1]2，那么sin()3x π--的值域为.故g()x 在区间[,]2ππ上的值域是. 19．(本小题满分12分，（1）小问4分，（2）小问8分) 已知函数32()()f x ax x a =+∈R 在x =43-处取得极值. (1)确定a 的值；(2)若()()e x g x f x =，讨论的单调性.【测量目标】(1)导数与极值；(2)导数与单调性. 【试题分析】 (1)对()f x 求导得2()32f x ax x '=+因为f (x )在43x =-处取得极值，所以4()03f '-=， 即16416832()09333a a ⨯+⨯-=-=,解得12a =.(2)由(1)得，321()e 2x g x x x ⎛⎫=+⎪⎝⎭, 故232323115()2e e 2e 2222x x x g x x x x x x x x ⎛⎫⎛⎫⎛⎫'=+++=++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=1(1)(4)e 2x x x x ++令()0g x '=，解得0,14x x x ==-=-或. 当4x <-时，()0g x '<,故g (x )为减函数； 当41x -<<-时，()0g x '>,故g (x )为增函数； 当10x -<<时，()0g x '<,故g (x )为减函数； 当0x >时，()0g x '>,故g (x )为增函数；综上知g (x )在(,4)-∞-和(-1,0)内为减函数，(4,1)(0,)--+∞和内为增函数. 20．(本小题满分12分，（1）小问5分，（2）小问7分) 如图，三棱锥P-ABC 中，平面PAC ⊥平面ABC ，∠ABC =2π，点D 、E 在线段AC 上，且AD =DE =EC =2，PD =PC =4，点F 在线段AB 上，且EF //BC .(1)证明：AB ⊥平面PFE.(2)若四棱锥P-DFBC 的体积为7，求线段BC 的长.第20题图【测量目标】(1)空间线面垂直关系；(2)锥体的体积；(3)方程思想.【试题分析】（1）证明：如图.由DE =EC ，PD =PC 知，E 为等腰△PDC 中DC 边的中点，故PE ⊥AC ，又平面PAC ⊥平面ABC ，平面PAC ∩平面ABC =AC ，PE ⊂平面PAC ，PE ⊥AC ，所以PE ⊥平面ABC ，从而PE ⊥AB .因,2ABC EF BC π∠=∥,故AB ⊥EF . 从而AB 与平面PEF 内两条相交直线PE ，EF 都垂直， 所以AB ⊥平面PFE .(2)解：设=BC x ,则在直角△ABC 中，AB =从而1122ABC S AB BC =⋅=△由EF ∥BC 知23AF AE AB AC ==，得△AEF ∽△ABC ,故224==39AEF ABC S S △△（）， 即49AEF ABC S S =△△. 由12AD AE =,11421==22999AFD AFE ABC ABC S S S S =⋅=△△△△从而四边形DFBC的面积为117=2918DFBC ABC ADF S S S =-=△△.由(1)知，PE ⊥平面ABC ，所以PE 为四棱锥P-DFBC 的高. 在直角△PEC 中,PE ==体积11773318P DFBC DFBC V S PE -=⋅⋅=⨯=, 故得42362430x x -+=，解得22927x x ==或，由于x >0，可得3x x ==或所以3BC =或BC =21、(本小题满分12分，（1）小问5分，（2）小问7分)如图，椭圆22221x y a b +=（a >b >0）的左右焦点分别为12,F F ,且过2F 的直线交椭圆于P ,Q 两点，且PQ ⊥1PF .(1)若1||2PF =，2||2PF =，求椭圆的标准方程. (2)若|PQ |=1||PF λ，且34≤λ≤43，试确定椭圆离心率的取值范围.第21题图【测量目标】(1)椭圆的标准方程；(2)椭圆的定义；(3)函数与方程思想. 【试题分析】标准文案大全 (1)由椭圆的定义，122||||(2(24a PF PF =+=+=,故a =2.设椭圆的半焦距为c ，由已知12PF PF ⊥，因此122||c F F ====c =从而1b == 故所求椭圆的标准方程为2214x y +=. (2)如图，由11,||||PF PQ PQ PF λ=⊥,得11|||QF PF ==由椭圆的定义,1212||||2,||||2PF PF a QF QF a +=+=,进而11||||||4PF PQ QF a ++=于是1(1||4PF a λ+=解得1||PF =21||2||PF a PF =-=由勾股定理得222221212||||(2)4|PF |PF F F c c +===,从而2224c ⎛⎫+=, 两边除以24a2e =,若记1t λ=+，则上式变成22224(2)111842t e t t +-⎛⎫==-+ ⎪⎝⎭. 由34≤43λ≤，并注意到1λ+λ的单调性，得3≤t ≤4，即11143t ≤≤，进而212e ≤≤59，即2e ≤。

第2节 一元线性回归模型及其应用知识点一 一元线性回归模型称⎩⎪⎨⎪⎧Y ＝bx ＋a ＋e ，E (e )＝0，D (e )＝σ2为Y 关于x 的一元线性回归模型．其中Y 称为因变量或响应变量，x 称为自变量或解释变量，a 称为截距参数，b 称为斜率参数；e 是Y 与bx ＋a 之间的随机误差，如果e ＝0，那么Y 与x 之间的关系就可以用一元线性函数模型来描述． 知识点二 最小二乘法将y ^＝b ^x ＋a ^称为Y 关于x 的经验回归方程，也称经验回归函数或经验回归公式，其图形称为经验回归直线，这种求经验回归方程的方法叫做最小二乘法，求得的b ^，a ^叫做b ，a 的最小二乘估计，其中，a ^＝y －b ^x .也可以表示为，这样更便于实际计算。

思考1 经验回归方程一定过成对样本数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )中的某一点吗？ 答案 不一定．思考2 点(x ，y )在经验回归直线上吗？ 答案 在． 知识点三 残差与残差分析 1．残差对于响应变量Y ，通过观测得到的数据称为观测值，通过经验回归方程得到的y ^称为预测值，观测值减去预测值称为残差． 2．残差分析残差是随机误差的估计结果，通过对残差的分析可以判断模型刻画数据的效果，以及判断原始数据中是否存在可疑数据等，这方面工作称为残差分析． 知识点四 对模型刻画数据效果的分析 1．残差图法在残差图中，如果残差比较均匀地集中在以横轴为对称轴的水平带状区域内，则说明经验回121()()ˆ()niii nii x x y y bx x ==--=-∑∑1221ˆni ii nii x y nx ybxnx==-=-∑∑归方程较好地刻画了两个变量的关系．2．残差平方和法：残差平方和∑ni ＝1(y i －y ^i )2越小，模型的拟合效果越好． 3．R 2法：可以用R 2＝1－∑ni ＝1（y i －y ^i ）2∑ni ＝1（y i －y －）2来比较两个模型的拟合效果，R 2越大，模型拟合效果越好，R 2越小，模型拟合效果越差．思考 利用经验回归方程求得的函数值一定是真实值吗？ 答案 不一定，他只是真实值的一个预测估计值．1．求经验回归方程前可以不进行相关性检验．( × )2．在残差图中，纵坐标为残差，横坐标可以选为样本编号．( √ ) 3．利用经验回归方程求出的值是准确值．( × )4．残差平方和越小，线性回归模型的拟合效果越好．( √ ) 5．R 2越小，线性回归模型的拟合效果越好．( × )一、求经验回归方程例1 某研究机构对高三学生的记忆力x 和判断力y 进行统计分析，得下表数据：(1)请画出上表数据的散点图；(2)请根据上表提供的数据，用最小二乘法求出y 关于x 的经验回归方程y ^＝b ^x ＋a ^；(3)试根据求出的经验回归方程，预测记忆力为9的同学的判断力．解 (1)散点图如图所示：1221ˆni ii nii x y nx ybxnx==-=-∑∑(2)＝6＋8＋10＋124＝9，＝2＋3＋5＋64＝4， ＝62＋82＋102＋122＝344，＝6×2＋8×3＋10×5＋12×6＝158，＝158－4×9×4344－4×92＝1420＝0.7，a ^＝y －b ^x ＝4－0.7×9＝－2.3，故经验回归方程为y ^＝0.7x －2.3.(3)由(2)中经验回归方程可知，当x ＝9时，y ^＝0.7×9－2.3＝4，即预测记忆力为9的同学的判断力为4.反思感悟 求经验回归方程可分如下四步来完成 (1)列：列表表示x i ，y i ，x 2i ，x i y i . (2)算：计算，，，，(3)代：利用公式求出，再由求出的值； (4)写：写出经验回归方程．跟踪训练1 随着我国经济的发展，居民储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款(年底余额)如下表：121()n x x x x n=+++121()n y y y y n=+++2222121nin i xx x x ==+++∑11221n i in n i x yx y x y x y ==++∑1221ˆni ii nii x y nx ybxnx==-=-∑∑121()n x x x x n=+++121()n y y y y n=+++11221ni in n i x yx y x y x y ==++∑2222121ni n i x x x x ==+++∑1221ˆni ii ni i x y nx ybx nx==-=-∑∑ˆbˆˆa y bx =-ˆa(1)求y 关于t 的经验回归方程y ^＝b ^t ＋a ^；(2)用所求经验回归方程预测该地区2021年(t ＝7)的人民币储蓄存款． 解 (1)由题意可知，n ＝5，t ＝1n ∑=51i i t ＝155＝3，＝365＝7.2.又∑=ni t12i＝55，∑=ni i yt 1i＝120，计算得，b ^＝1.2，a ^＝y －b ^t ＝7.2－1.2×3＝3.6.故所求经验回归方程为y ^＝1.2t ＋3.6.(2)将t ＝7代入y ^＝1.2t ＋3.6，可得y ^＝1.2×7＋3.6＝12(千亿元)， 所以预测该地区2021年的人民币储蓄存款为12千亿元． 二、线性回归分析例2 已知某种商品的价格x (单位：元)与需求量y (单位：件)之间的关系有如下一组数据：求y 关于x 的经验回归方程，并借助残差平方和和R 2说明回归模型拟合效果的好坏． 解 x ＝15×(14＋16＋18＋20＋22)＝18，y ＝15×(12＋10＋7＋5＋3)＝7.4，＝142＋162＋182＋202＋222＝1 660，＝14×12＋16×10＋18×7＋20×5＋22×3＝620，所以＝620－5×18×7.41 660－5×182＝－1.15，a ^＝7.4＋1.15×18＝28.1，所以所求经验回归方程是y ^＝－1.15x ＋28.1. 列出残差表：所以∑ni ＝1(y i －y ^i )2＝0.3，∑=n1i (y i －y)2＝53.2，R 2＝1－∑ni ＝1（y i －y ^i ）2∑ni ＝1（y i －y －）2≈0.994，所以回归模型的拟合效果很好．121()n y y y y n =+++2222121ni n i xx x x ==+++∑11221n iin n i x yx y x y x y ==++∑1221ˆni ii nii x y nx ybxnx==-=-∑∑反思感悟 刻画回归效果的三种方法(1)残差图法，残差点比较均匀地落在水平的带状区域内说明选用的模型比较合适．(2)残差平方和法：残差平方和∑ni ＝1(y i －y ^i )2越小，模型的拟合效果越好． (3)R 2法：R 2＝1－∑ni ＝1 （y i －y ^i ）2∑ni ＝1（y i －y －）2越接近1，表明模型的拟合效果越好． 跟踪训练2 为研究重量x (单位：克)对弹簧长度y (单位：厘米)的影响，对不同重量的6个物体进行测量，数据如下表所示：(1)作出散点图并求经验回归方程； (2)求出R 2; (3)进行残差分析． 解 (1)散点图如图 .x ＝16×(5＋10＋15＋20＋25＋30)＝17.5，y ＝16×(7.25＋8.12＋8.95＋9.90＋10.9＋11.8)≈9.487，＝2 275，＝1 076.2，计算得，b ^≈0.183，a ^≈6.285， 所求经验回归方程为y ^＝0.183x ＋6.285. (2)残差表如下：所以∑=ni 1(y i －y ^i )2≈0.013 18，∑=ni 1(y i －y )2≈14.678 3.2222121nini xx x x ==+++∑11221ni i n n i x y x y x y x y ==++∑所以R 2≈1－0.013 1814.678 3≈0.999 1，所以回归模型的拟合效果很好．(3)由残差表中的数值可以看出第3个样本点的残差比较大，需要确认在采集这个数据的时候是否有人为的错误，如果有，则需要纠正数据，重新建立回归模型；由表中数据可以看出残差点比较均匀地落在宽度不超过0.15的狭窄的水平带状区域中，说明选用的线性回归模型的精度较高，由以上分析可知，弹簧长度与重量成线性关系． 三、非线性回归例3 下表为收集到的一组数据：(1)作出x 与y 的散点图，并猜测x 与y 之间的关系； (2)建立x 与y 的关系，预报回归模型并计算残差； (3)利用所得模型，预测x ＝40时y 的值．解 (1)作出散点图如图，从散点图可以看出x 与y 不具有线性相关关系，根据已有知识可以发现样本点分布在某一条指数函数型曲线y ＝c 12e c x 的周围，其中c 1，c 2为待定的参数．(2)对两边取对数把指数关系变为线性关系，令z ＝ln y ，则有变换后的样本点应分布在直线z ＝bx ＋a (a ＝ln c 1，b ＝c 2)的周围，这样就可以利用经验回归模型来建立y 与x 之间的非线性经验回归方程了，数据可以转化为求得经验回归方程为z ^＝0.272x －3.849， ∴y ^＝e 0.272x－3.849.残差表如下：(3)当x ＝40时，y ^＝e 0.272×40－3.849≈1 131.反思感悟 非线性回归问题的处理方法 (1)指数函数型y ＝e bx ＋a ①函数y ＝e bx＋a的图象，如图所示；②处理方法：两边取对数得ln y ＝ln e bx ＋a ，即ln y ＝bx ＋a .令z ＝ln y ，把原始数据(x ，y )转化为(x ，z )，再根据线性回归模型的方法求出a ，b . (2)对数函数型y ＝b ln x ＋a①函数y ＝b ln x ＋a 的图象，如图所示；②处理方法：设x ′＝ln x ，原方程可化为y ＝bx ′＋a ， 再根据线性回归模型的方法求出a ，b . (3)y ＝bx 2＋a 型处理方法：设x ′＝x 2，原方程可化为y ＝bx ′＋a ，再根据线性回归模型的方法求出a ，b . 跟踪训练3 为了研究甲型H1N1中的某种细菌随时间x 变化的繁殖个数y ，收集数据如下：求y 关于x 的非线性经验回归方程． 解 作出散点图如图(1)所示．由散点图看出样本点分布在一条指数型曲线y ＝c e bx 的周围，则ln y ＝bx ＋ln c . 令z ＝ln y ，a ＝ln c ，则z ＝bx ＋a .相应的散点图如图(2)所示．从图(2)可以看出，变换后的样本点分布在一条直线附近，因此可以用经验回归方程来拟合．由表中数据得到经验回归方程为z ^＝0.69x ＋1.115.因此细菌的繁殖个数y 关于天数x 的非线性经验回归方程为y ^＝e 0.69x ＋1.115.1．如果两个变量之间的线性相关程度很高，则其R 2的值应接近于( ) A ．0.5 B ．2 C ．0 D ．1 答案 D解析 R 2越接近于1，相关程度越高，故选D.2．对变量x ，y 进行回归分析时，依据得到的4个不同的回归模型画出残差图，则下列模型拟合精度最高的是( )答案 A解析 用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适，带状区域的宽度越窄，说明模型的拟合精度越高．3．工人工资y (元)与劳动生产率x (千元)的相关关系的经验回归方程为y ^＝50＋80x ，下列判断正确的是( )A ．劳动生产率为1 000元时，工人工资为130元B ．劳动生产率提高1 000元时，工人工资平均提高80元C ．劳动生产率提高1 000元时，工人工资平均提高130元D ．当月工资为250元时，劳动生产率为2 000元 答案 B解析 因为经验回归方程的斜率为80，所以x 每增加1，y 平均增加80，即劳动生产率提高1 000元时，工人工资平均提高80元．4．两个变量的散点图如图，可考虑用如下函数进行拟合比较合理的是( )A ．y ＝a ·x bB ．y ＝a ＋b ln xC ．y ＝a ·e bxD ．y ＝a ·e bx答案 B解析 由散点图可知，此曲线类似对数函数型曲线，因此可用函数y ＝a ＋b ln x 模型进行拟合． 5．(多选)对于经验回归方程y ^＝b ^x ＋a ^(b ^>0)，下列说法正确的是( ) A ．当x 增加一个单位时，y ^的值平均增加b ^个单位 B ．点(x ，y )一定在y ^＝b ^x ＋a ^所表示的直线上 C ．当x ＝t 时，一定有y ＝b ^t ＋a ^D ．当x ＝t 时，y 的值近似为b ^t ＋a ^答案 ABD解析 经验回归方程是一个模拟函数，它表示的是一系列离散的点大致所在直线的位置及其大致变化规律，所以有些散点不一定在经验回归直线上．6．某地区近10年居民的年收入x 与年支出y 之间的关系大致符合y ^＝0.8x ＋0.1(单位：亿元)，预计今年该地区居民收入为15亿元，则今年支出估计是________亿元． 答案 12.1解析 将x ＝15代入y ^＝0.8x ＋0.1，得y ^＝12.1.7．若经验回归直线方程中的回归系数b ^＝0，则样本相关系数r ＝________. 答案 0解析 样本相关系数与()()nniii ix x y y x y nx yr ---==∑∑的分子相同，故r ＝0.8．某品牌服装专卖店为了解保暖衬衣的销售量y (件)与平均气温x (℃)之间的关系，随机统计了连续四旬的销售量与当旬平均气温，其数据如表：由表中数据算出经验回归方程y ^＝b ^x ＋a ^中的b ^＝－2，样本点的中心为(10,38)． (1)表中数据m ＝________；(2)气象部门预测三月中旬的平均气温约为22 ℃，据此估计，该品牌的保暖衬衣在三月中旬的销售量约为________件． 解析 (1)由y ＝38，得m ＝40.(2)由a ^＝y －b ^x 得a ^＝58，故y ^＝－2x ＋58，当x ＝22时，y ^＝14，故三月中旬的销售量约为14件．9．已知变量x ，y 有如下对应数据：(1)作出散点图；(2)用最小二乘法求关于x ，y 的经验回归方程． 解 (1)散点图如图所示．(2)x ＝1＋2＋3＋44＝52，y ＝1＋3＋4＋54＝134， ∑=ni i yx 1i＝1＋6＋12＋20＝39，∑=ni x12i＝1＋4＋9＋16＝30，121()()ˆ()niii nii x x y y bx x ==--=-∑∑＝39－4×52×13430－4×⎝⎛⎭⎫522＝1310，a ^＝134－1310×52＝0，所以y ^＝1310x 即为所求的经验回归方程．10．由某种设备的使用年限x i (年)与所支出的维修费y i (万元)的数据资料算得如下结果，∑=ni ix12＝90，∑=ni i iy x1＝112，∑=n i i x 1＝20，∑=ni i y 1＝25.(1)求所支出的维修费y 关于使用年限x 的经验回归方程y ^＝b ^x ＋a ^； (2)①判断变量x 与y 之间是正相关还是负相关； ②当使用年限为8年时，试估计支出的维修费是多少？ 解 (1)∵∑=ni ix1＝20，∑=ni iy1＝25，∴x ＝15∑=ni i x 1＝4，y ＝15∑=ni i y1i ＝5，∴＝112－5×4×590－5×42＝1.2，a ^＝y －b ^x ＝5－1.2×4＝0.2. ∴所求经验回归方程为y ^＝1.2x ＋0.2.(2)①由(1)知b ^＝1.2>0，∴变量x 与y 之间是正相关． ②由(1)知，当x ＝8时，y ^＝1.2×8＋0.2＝9.8， 即使用年限为8年时，支出的维修费约是9.8万元．11．设两个变量x 和Y 之间具有线性相关关系，它们的样本相关系数是r ，Y 关于x 的经验回归方程的回归系数为b ^，回归截距是a ^，那么必有( ) A.b ^与r 的符号相同 B.a ^与r 的符号相同 C.b ^与r 的符号相反 D.a ^与r 的符号相反答案 A1221ˆni ii ni i x y nx ybx nx==-=-∑∑1221ˆniii ni i x y nx ybx nx==-=-∑∑解析 b ^与r 的符号相同．12．恩格尔系数是食品支出总额占个人消费支出总额的比重．据某机构预测，n (n ≥10)个城市职工购买食品的人均支出y (千元)与人均月消费支出x (千元)具有线性相关关系，且经验回归方程为y ^＝0.4x ＋1.2，若其中某城市职工的人均月消费支出为5千元，则该城市职工的月恩格尔系数约为( )A ．60%B ．64%C ．58%D ．55% 答案 B解析 把x ＝5代入经验回归方程y ^＝0.4x ＋1.2中，得y ^＝0.4×5＋1.2＝3.2，则该城市职工的月恩格尔系数约为3.25＝0.64＝64%，故选B.13．(多选)设某大学的女生体重y (单位：kg)与身高x (单位：cm)具有线性相关关系．根据一组样本数据(x i ，y i )(i ＝1,2，…，n )，用最小二乘法建立的经验回归方程为y ^＝0.85x －85.71，则下列结论中正确的是( ) A ．y 与x 具有正的线性相关关系B ．经验回归方程过样本点的中心(x ，y )C ．若该大学某女生身高增加1 cm ，则其体重约增加0.85 kgD ．若该大学某女生身高为170 cm ，则可判定其体重必为58.79 kg 答案 ABC解析 A ，B ，C 均正确，是经验回归方程的性质，D 项是错误的，经验回归方程只能预测学生的体重，应为大约58.79 kg.14．某数学老师身高176 cm ，他爷爷、父亲和儿子的身高分别是173 cm,170 cm,182 cm.因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为________ cm. 答案 185解析 因为儿子的身高与父亲的身高有关，所以设儿子的身高为Y (单位：cm)，父亲身高为X (单位：cm)，根据数据列表：由表中数据，求得回归系数b ^＝1，a ^＝3. 于是儿子身高与父亲身高的关系式为Y ＝X ＋3， 当X ＝182时，Y ＝185.故预测该老师的孙子的身高为185 cm.15．已知变量y 关于x 的非线性经验回归方程为y ^＝e b ^x－0.5，其一组数据如下表所示：若x ＝5，则预测y 的值可能为( ) A ．e 5 B ．112e C ．e 7 D ．152e 答案 D解析 将式子两边取对数，得到ln y ^＝b ^x －0.5， 令z ＝ln y ^，得到z ＝b ^x －0.5， 列出x ，z 的取值对应的表格如下：则x ＝1＋2＋3＋44＝2.5，z ＝1＋3＋4＋64＝3.5，∵(x ，z )满足z ＝b ^x －0.5， ∴3.5＝b ^×2.5－0.5，解得b ^＝1.6， ∴z ＝1.6x －0.5，∴y ^＝e 1.6x －0.5，当x ＝5时，y ^＝e1.6×5－0.5＝152e .16．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：(1)求经验回归方程y ^＝b ^x ＋a ^，其中b ^＝－20；(2)预计在今后的销售中，销量与单价仍然服从(1)中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？(利润＝销售收入－成本) 解 (1)由于x ＝16×(8＋8.2＋8.4＋8.6＋8.8＋9)＝8.5，y ＝16×(90＋84＋83＋80＋75＋68)＝80.所以a ^＝y －b ^x ＝80＋20×8.5＝250， 从而经验回归方程为y ^＝－20x ＋250.(2)设工厂获得的利润为L 元，依题意得L ＝x (－20x ＋250)－4(－20x ＋250)＝－20x 2＋330x －1 000＝－20(x －8.25)2＋361.25.故当单价定为8.25元时，工厂可获得最大利润．。

高考冲刺作业（80）2020年3月20日 （回归分析、独立性检验）考点1线性回归分析提示：由最小二乘法得回归直线方程：（认真阅读、深刻理解）y a bx =+，其中1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑，a y bx =-.有时这样表述：对于一组数据11(,)u v ，22(,)u v ，L ，(,)n n u v ，其线性回归方程v u αβ=+的斜率和截距的最小二乘估计分别为：121()()()nii i nii uu v v uu β==--=-∑∑，v u αβ=-.1.（2015·重庆卷·文理）随着我国经济的发展，居民的储蓄存款逐年增长.设（Ⅰ）求y 关于t 的回归方程y bt a =+； 1.2 3.6y t =+（Ⅱ）用所求回归方程预测该地区2015年（6t =）的人民币储蓄存款. 10.8 2.已知x ，y 的取值如下表所示：如果y 与x 呈线性相关，且线性回归方程为 3.5y bx =+，则b = . 0.5b = 3.（2011·陕西卷·理科）设11(,)x y ，22(,)x y ，L ，(,)n n x y 是变量x 和y 的n 个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是 DA.x 和y 的相关系数为直线l 的斜率B.x 和y 的相关系数在0到1之间C.当n为偶数时，分布在l两侧的样本点的个数一定相同D.直线l过点(,)x y Array4.已知x，y的取值如下表根据上表提供的数据，求出y关于x的线性回归直线方程为0.80.4y x=+,那么表中t的值为 CA.4.8B.5.2C.5.5D.5.65.设有一个线性回归方程为3 2.5y x=-,则变量x增加一个单位时 C A.y平均增加2.5个单位 B.y平均增加1个单位C.y平均减少2.5个单位D.y平均减少1个单位6.（2015·福建卷）为了解某社区居民的家庭年收入与年支出的关系，随机调查=+，其中0.76b=，a y bx社区一户收入为15万元家庭年支出为 BA.11.4万元B.11.8万元C.12.0万元D.12.2万元7.对四组变量,x y进行相关性检验，r是相关系数，已知①0.96r=，r=，②0.30③0.99r=-，④0.48r=-.则,x y线性相关程度最高的两组是 .8.（2010·湖南卷·文科）某商品销售量y（件）与销售价格x（元/件）负相关，则其回归方程可能是 AA.$10200=-- D.$10200y x=+ y xy x=-+ B.$10200y x=+ C.$10200考点2可线性化回归分析1.（2015·全国卷Ⅰ·文理）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x （单位：千元）对年销售量y （单位：t ）和年利润z （单位：千元）的影响，对近8年的年宣传费i x 和年销售量i y (1,2,,8)i =L 数据作了初步处理，得到下面的散点图及一些统计量的值.表中i w =8118i i w w ==∑.（Ⅰ）根据散点图判断，y a bx =+与y c =+哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型？（给出判断即可，不必说明理由） （Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y 关于x 的回归方程； （Ⅲ）已知这种产品的年利率z 与x ，y 的关系为0.2z y x =-.根据（Ⅱ）的结果回答下列问题：（i ）年宣传费49x =时，年销售量及年利润的预报值是多少？ （ii ）年宣传费x 为何值时，年利率的预报值最大？解析：（Ⅰ）根据散点图判断，y c =+y 关于年宣传费x 的回归方程类型；年宣传费／千元（Ⅱ）根据（Ⅰ）的判断结果，令w =y c d ω=+，81821()()()iii ii w w y y d w w ==--==-∑∑108.8681.6=，56368 6.8100.6c y d ω=+=-⨯=，所以100.668y ω=+，于是y 关于x的回归方程是：100.6y =+（Ⅲ）（i ）由0.2z y x =-及当49x =时，100.6y =+，0.2576.6z =⨯-4966.32=，年销售量576.6千元及年利润的预报值是66.32千元.（ii ）由0.2z y x =-及100.6y =+0.2(100.6z x x =⨯+-=-+20.04+t =，2()13.620.04h t t t =-++，当 6.8t =，即46.24x =时，年利率的预报值最大.2.已知某种细菌的适宜生长温度为1025C C o o :，为了研究该种细菌的繁殖数量y （单位：个）随温度x （温度：C o ）变化的规律，收集数据如下：对数据进行初步处理后，得到了一些统计量的值，如下表所示：其中，ln i i k y =，7117i i k k ==∑.参考数据： 5.5245e ≈.（Ⅰ）绘出y 关于x 的散点图，并根据散点图判断，y a bx =+与21c x y c e =哪一个适宜作为该种细菌的繁殖数y 关于温度x 的回归方程类型？（给出判断即可，不必说明理由）（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y 关于x 的回归方程（结果精确到0.1）.（Ⅲ）当温度为25C o 时，该种细菌繁殖数量的预报值为多少？ 解析：（Ⅰ）根据散点图可知：21c x y c e =比较合适；（Ⅱ）由（Ⅰ）知，21c x y c e =得12ln ln y c c x =+，即2k m c x =+，712721()()()iii ii x x kk c x x ==--=-∑∑20.50.1830.2112=≈≈， 3.80.183180.5m k bx =-=-⨯≈，即1ln 0.5c =，所以 ln 0.50.2y x =+，于是y 关于x 的回归方程是：0.50.2x y e +=.（Ⅲ）当25x =时，0.50.225 5.5245y e e +⨯==≈，即当温度为25C o 时，该种细菌繁殖数量的预报值为245.3.噪音污染已经成为影响人们身体健康和生活质量的严重问题，为了了解声音强度D （单位：分贝）与声音能量I （单位：2/W cm ）之间的关系，将测量得到的声音强度i D 和声音能量i I （1,2,,10i =L ）数据作了初步处理，得到下面的散点图即一些统计量的值.（Ⅰ）根据散点图判断，D c dI =+与lg D a b I =+哪一个适宜作为声音强度D 关于声音能量I 的回归方程类型？（Ⅱ）根据表中数据，建立D 关于I 的回归方程；（Ⅲ）当声音强度大于60分贝时，属于噪音，会产生噪音污染，城市中某点P 共DIg g g gg g g ggg 1020 10 0 20 30 30 40 50 40 50 60受到两个声源的影响，这两个声音能量分别为1I ，2I ，且10121410I I +=.已知点P 的声音能量等于1I 和2I 声音能量之和，请根据（Ⅰ）中回归方程，判断点P 是否受到噪音污染的干扰，并说明理由.参考数据：其中表中lg i i W I =，101110i i W W ==∑，截距的最小二乘估计分别为：v u αβ=-，121()()()nii i nii uu v v uu β==--=-∑∑.解析：（Ⅰ）根据散点图可知，lg D a b I =+适宜作为声音强度D 关于声音能量I 的回归方程；（Ⅱ）由（Ⅰ）知，lg D a b I =+，D a bW =+,1011021()()5.1100.51()iii ii W W D D b W W ==--===-∑∑， 45.710(11.5)160.7a D bW =-=-⨯=，所以D 关于I 的回归方程为：160.710lg D I =+（Ⅲ）点P 的声音能量等于1I 和2I 声音能量之和，101212121410()()I I I I I I I -=+=++ 10102112410[5()]109I I I I --=++≥⨯，10min 160.710lg(109)60.710lg 960D -=+⨯=+>，P 会受到噪音污染的干扰.4．2019年12月以来，湖北省武汉市持续开展流感及相关疾病监测，发现多起病毒性肺炎病例，均诊断为病毒性肺炎/肺部感染，后被命名为新型冠状病毒肺炎（ 2019Corona Virus Disease ， 2019COVID ），简称“新冠肺炎”．下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图．为了预测在未采取强力措施下，后期的累计确诊人数，建立了累计确诊人数y 与时间变量t 的两个回归模型，根据1月15日至1月24日的数据（时间变量t 的值依次1，2，L ，10），建立模型y c dt =+和 1.5t y a b =+⋅.（Ⅰ）根据散点图判断，$y c dt =+和$ 1.5t y a b =+⋅哪一个适宜作为累计确诊人数y 与时间变量t 的回归方程类型？(给出判断即可，不必说明理由)； （Ⅱ）根据（Ⅰ）的判断结果及附表中数据，建立y 关于t 的回归方程； （Ⅲ）以下是1月25日至1月29日累计确诊人数的真实数据，根据（Ⅱ）的结果时间1月25日 1月26日 1月27日 1月28日 1月29日 累计确诊人数的真实数据19752744451559747111①当1月25日至1月27日这3天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于0.1，则认为模型可靠，请判断（Ⅱ）的回归方程是否可靠？②2020年1月24日在人民政府的强力领导下，全国人民共同采取了强力的预防“新冠肺炎”的措施，若采取措施5天后，真实数据明显低于预测数据，则认为防护措施有效，请判断预防措施是否有效？附：对于一组数据11(,)u v ，22(,)u v ，L ，(,)n n u v ，其回归线v u αβ=+的斜率和截距的最小二乘估计分别为：121()()()nii i nii uu v v uu β==--=-∑∑，v u αβ=-参考数据：其中 1.5it i ω=，101110i i ωω==∑.解析：（Ⅰ）根据散点图可知：$ 1.5t y a b =+⋅适宜作为累计确诊人数y 与时间变t 的回归方程类型；（Ⅱ）令 1.5tω=，$y a b ω=+⋅，1011021()()()iii ii y y bωωωω==--=-∑∑$101102211010i ii ii y yωωωω==-=-∑∑，215470010193902076401019-⨯⨯==-⨯，390201910a y b ω=-=-⨯=，$1020y ω=+⋅，即 $1020 1.5t y =+⨯；（Ⅲ）①当11t =时，111.5100=，10201002010y =+⨯=，201019753519752010-=0.0170.1≈<，当12t =时，121.5150=，10201503010y =+⨯=，301027442744-=2660.0970.12744≈<，当13t =时，131.5225=，10202254510y =+⨯=，451045154515-50.14515=<.所以（Ⅱ）的回归方程可靠； ②当15t =时，$10150y =,远大于7111，所以防护措施有效．考点3独立性检验构造随机变量（卡方统计量）统计量2χ（也可表示2K），来判断“两个分类变量有关联”的方法称为独立性检验.其中22()()()()()n ad bca b c d a c b dχ-=++++，n a b c d=+++.1.（2010·课标全国卷·文科）为调查某地区老年人是否需要志愿者提供帮助，（Ⅰ）估计该地区老年人中，需要志愿提供帮助的老年人的比例；（Ⅱ）能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？解：（Ⅰ）调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中需要帮助的老年人的比例的估计值为7014% 500=.（Ⅱ）22500(4027030160)9.96720030070430K⨯⨯-⨯=≈⨯⨯⨯.由于9.967 6.635>所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.2.（2014·辽宁卷）某大学餐饮中心为了了解新生的饮食习惯，在全校一年级学（Ⅰ）根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；（Ⅱ）已知在被调查的北方学生中有5名数学系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取3人，求至多有1人喜欢甜品的概率.22100(60102010)100 4.7627030802021K ⨯⨯-⨯==≈⨯⨯⨯, 710p =.3.（2018·全国卷Ⅲ·文理科）某工厂为了提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20名工人，第一组工人用第一种生产方式，第二组工人用第二种生产方式.根据工人完成生产任务的工作时间（单位：min ）绘制了如下茎叶图：（Ⅰ）根据茎叶图判断哪种生产方式的效率更高？并说明理由.（Ⅱ）求40名工人完成生产任务所需的时间的中位数m ，并将完成生产任务所（Ⅲ）根据（Ⅱ）中列联表，能否有99％把握认为两种生产方式的效率有差异？ 解析：（Ⅰ）第二中生产方式效率更高.（Ⅱ）7981802m +==.（Ⅲ）2240(151555)10 6.63520202020K ⨯⨯-⨯==>⨯⨯⨯.所以有99％把握认为两种生产方式的效率有差异.4.（2019·全国卷Ⅰ·文科）某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面列联表：（Ⅰ）分别估计男、女顾客对该商场服务满意的概率；（Ⅱ）能否有95%的把握认为男、女顾客对该商场服务的评价有差异？第一种生产方式第二种生产方式 8 8765 56 8 90 1 2 2 3 4 5 6 6 8 1 4 4 5 099 7 6 2 9 8 7 7 6 5 4 3 3 2 2 1 1 0 0解析：（Ⅰ）由调查数据，男顾客中对该商场服务满意的比率为400.850=，因此男顾客对该商场服务满意的概率的估计值为0.8．女顾客中对该商场服务满意的比率为300.650=，因此女顾客对该商场服务满意的概率的估计值为0.6．22100(40203010) 4.76250507030K ⨯⨯-⨯=≈⨯⨯⨯．由于4.762 3.841>，故有95％的把握认为男、女顾客对该商场服务的评价有差异. 5.（2017·全国卷Ⅱ·文科）淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取100个网箱，测量各箱水产品的产量（单位：kg ）某频率直方图如下：（Ⅰ）设两种养殖方法的箱产量相互独立，记A 表示事件：“旧养殖法的箱产量低于50kg ”，估计A 的概率；0.62（Ⅱ）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖22200(62663438)15.70510010096104K ⨯⨯-⨯=≈⨯⨯⨯.6.（2017·全国卷Ⅱ·文科）淡水养殖场进行某水产品的新、旧网箱养殖方法的/kg旧养殖法kg新养殖法产量对比，收获时各随机抽取100个网箱，测量各箱水产品的产量（单位：kg ）某频率直方图如下：（Ⅰ）设两种养殖方法的箱产量相互独立，记A 表示事件：旧养殖法的箱产量低于50kg ，新养殖法的箱产量不低于50kg ，估计A 的概率；（Ⅱ）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖（Ⅲ）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到0.01）7.（2013·福建卷）某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关，现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分为5组：)[50,60，)[60,70，)[70,80，)[80,90，)[90,100， 分别加以统计，得到如图所示的频率分布直方图.（Ⅰ）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的概率；（Ⅱ）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完/kg旧养殖法kg新养殖法成列联表，并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”？710p =,22100(45152515)25 1.797030604014K ⨯⨯-⨯==≈⨯⨯⨯.没有把握.8.（2010·辽宁卷·理科）为了比较注射A ,B 两种药物后产生的皮肤疱疹的面积，选200只家兔做实验，将这200只家兔随机地分成两组.每组100只，其中一组注射药物A ，另一组注射药物B .下表1和表2分别是注射药物A 和药物B 后的实验结果.（疱疹面积单位：2mm ）（Ⅰ）完成下面频率分布直方图，并比较注射两种药物后疱疹面积的中位数大小；（Ⅱ）完成下面22⨯列联表，并回答能否有99.9％的把握认为“注射药物A 后的25周岁以上组25周岁以下组注射药物A 后皮肤疱疹面积的频率分布直方图注射药物B 后皮肤疱疹面积的频率分布直方图22200(70653530)24.5610010010595K ⨯⨯-⨯=≈⨯⨯⨯,210.828K >.有99.9％的把握认为“注射药物A 后的疱疹面积与注射药物B 后的疱疹面积有差异”.。

精选全文完整版（可编辑修改）2022年锦州师范高等专科学校单招职业技能考试试题及答案解析毕业院校：__________ 姓名：__________ 考场：__________ 考号：__________一、选择题1．当红、橙、黄、绿、青、蓝、紫七种光会聚一点时，该点呈()。

A.黄色B.绿色C.红色D.白色答案：D2．跳舞草会随着音乐连续摆动叶片，形似跳舞，这说明生物()A.需要营养B.能进行呼吸C.能生长和繁殖D.能对外界刺激作出反应答案：D3．如图所示是一款恒温加热保暖手套，配有专门的电池和充电配件，使用时可三挡智能调温。

以下对于该手套温度控制系统分析不恰当的是()A.执行器可以选择电热丝B.三档温度调节，说明该控制系统为手动控制C.外界环境温度是该控制系统的干扰因素D.手套的温度控制可以采用闭环控制方式答案：B4．下列关于计算机基本功能和特征的说法正确的是()A.虽然人工智能的发展使得计算机的功能变得空前强大，但某些问题的解决还需要人的参与B.计算机的基本功能是存储数据C.计算机可以在极短的时间内解决所有计算问题D.计算机处理问题有较高的准确性，运算速度快的计算机准确性更高答案：A5．东晋以少胜多战胜前秦的一次战役是()A.城濮之战B.官渡之战C.淝水之战D.赤壁之战答案：C6．中国革命和建设的基本立足点是()。

A.艰苦奋斗B.实事求是C.独立自主D.争取外援答案：C7．《西游记》的作者生活在()。

A.宋朝B.元朝C.明朝D.清朝答案：C8．三只小松鼠小芳、小松和点点住在同一棵大松树上，一天它们在一起玩智力游戏，小芳说:今天我们三个有的吃了松子;小松说:今天我们三个有的没吃松子;点点说:今天我没吃松子。

已知它们三个中只有一个说的是真的，则以下判断正确的是()A.全吃了B.全没吃C.有的吃了D.有的没吃答案：A9．“早上起床窗帘自动打开、出门上班家里电器自动节能、下班到家即洗热水澡、睡眠空调温度智能控......”，随着5G时代来临，全场景智能化家居逐渐成为有稳定工作的新生代租客的选择。

1．2函数的概念和性质1．2.1对应、映射和函数第二课时函数的概念在现实生活中，我们可能会遇到下列问题：(1)某地区城乡居民人民币储蓄存款(年底余额)随时间的变化如下表：(2)一物体从静止开始下落，下落的距离y(m)与下落时间x(s)之间近似地满足关系式y＝4.9x2.若一物体下落2 s，你能求出它下落的距离吗？(3)下图为某市一天24小时内的气温变化图．①上午6时的气温约是多少？全天的最高、最低气温分别是多少？②在什么时刻，气温为0℃？③在什么时段内，气温在0℃以上？如何用集合语言来阐述上述3个问题的共同特点？1．函数的定义设A，B是两个非空的数集，如果按照某种对应法则f，对于集合A中的任何一个数x，在集合B中都有唯一的数y和它对应，这样的对应f叫作定义于A取值于B的函数，记作f：A→B或者y＝f(x)(x∈A，y∈B)．2．函数的定义域、值域在函数的定义中，集合A叫作函数的定义域，与x∈A对应的数y叫x的像，记作y＝f(x)，由所有x∈A的像组成的集合叫作函数的值域．3．函数的三要素为定义域，对应法则，值域．举出几个有关函数的例子，并用定义加以描述，指出函数的定义域和值域．[提示](1)下表记录了几个不同气压下水的沸点.，值域是{81,100,121,152,179}．(2)如图是匀速直线运动路程s随时间变化的函数关系图，它的定义域是{t|t≥0}，值域是{s|s≥0}．[例1](1)A＝R，B＝{x|x>0}，f：x→y＝|x|；(2)A＝Z，B＝Z，f：x→y＝x2；(3)A＝R，B＝Z，f：x→y＝x；(4)A＝[－1,1]，B＝{0}，f：x→y＝0.[思路点拨]可根据函数的定义直接判断．[解](1)A中的元素0在B中没有对应元素，故不是A到B的函数；(2)对于集合A中的任意一个整数x，按照对应关系f：x→y＝x2，在集合B中都有唯一一个确定的整数x2与其对应，故是集合A到集合B的函数；(3)A中元素负数没有平方根，故在B中没有对应的元素且x不一定为整数，故此对应关系不是A到B的函数；(4)对于集合A中任意一个实数x，按照对应关系f：x→y＝0，在集合B中都有唯一一个确定的数0与它对应，故是集合A到集合B的函数.1．若集合A ＝{x |0≤x ≤2}，B ＝{y |0≤y ≤3}，则下列图形给出的对应中能构成从A 到B 的函数f ：A →B 的是( )解析：选D A 中的对应不满足函数的存在性，即存在x ∈A ，但B 中无与之对应的y ；B 、C 均不满足函数的唯一性，只有D 正确．2．下列对应或关系式中是A 到B 的函数的是( )A ．A ＝R ，B ＝R ，x 2＋y 2＝1 B ．A ＝{1,2,3,4}，B ＝{0,1}，对应关系如图：C ．A ＝R ，B ＝R ，f ：x →y ＝1x －2D ．A ＝Z ，B ＝Z ，f ：x →y ＝2x －1解析：选B A 错误，x 2＋y 2＝1可化为y ＝±1－x 2，显然对任意x ∈A ，y 值不唯一．B 正确，符合函数的定义．C 错误，2∈A ，在B 中找不到与之相对应的数．D 错误，－1∈A ，在B 中找不到与之相对应的数.[例2] 已知f (x )＝1－x1＋x(x ≠－1)．求： (1)f (0)及f ⎝⎛⎭⎫ f ⎝⎛⎭⎫12的值； (2)f (1－x )及f (f (x ))．[思路点拨] 将f (x )中的x 分别赋值或式子，代入1－x1＋x 中化简即得．[解] (1)f (0)＝1－01＋0＝1，f ⎝⎛⎭⎫12＝1－121＋12＝13， ∴f ⎝⎛⎭⎫f ⎝⎛⎭⎫12＝f ⎝⎛⎭⎫13＝1－131＋13＝12. (2)f (1－x )＝1－(1－x )1＋(1－x )＝x2－x (x ≠2)．f (f (x ))＝f ⎝ ⎛⎭⎪⎫1－x 1＋x ＝1－1－x 1＋x 1＋1－x 1＋x ＝x (x ≠－1).3．已知函数f (x )＝x 2－2x ，求： (1)f (－2)； (2)f ⎝⎛⎭⎫1＋1x (x ≠0)； (3)若f (x )＝3，求x 的值． 解：(1)f (－2)＝(－2)2－2·(－2)＝8. (2)f ⎝⎛⎭⎫1＋1x ＝⎝⎛⎭⎫1＋1x 2－2⎝⎛⎭⎫1＋1x＝⎝⎛⎭⎫1＋1x ⎝⎛⎭⎫1＋1x －2 ＝⎝⎛⎭⎫1＋1x ⎝⎛⎭⎫1x －1＝1x2－1(x ≠0)． (3)若f (x )＝3，则x 2－2x ＝3，x ＝－1或x ＝3.1．若f (x )＝1x 的定义域为M ，g (x )＝|x |的定义域为N ，令全集U ＝R ，则M ∩N ＝( ) A ．M B ．N C ．∁R MD ．∁R N解析：选A M ＝{x |x >0}，N ＝R ，∴M ∩N ＝M . 2．下列图形中，不可能是函数y ＝f (x )的图象的是( )解析：选B 根据函数的存在性和唯一性(定义)可知，B 不正确． 3．下列各对函数中，图象完全相同的是( ) A ．y ＝x 与y ＝(3|x |)3 B ．y ＝(x )2与y ＝|x | C ．y ＝xx 与y ＝x 0D ．y ＝x ＋1x 2－1与y ＝1x －1解析：选C 若函数的图象相同，则是相同的函数．对于A ，y ＝(3|x |)3＝|x |，所以对应关系不同；对于B ，y ＝(x )2＝x (x ≥0)，所以两函数定义域与对应关系均不同；对于C ，y ＝xx ＝1(x ≠0)，而y ＝x 0＝1(x ≠0)，定义域与对应关系均相同，是相同的函数；对于D ，y ＝x ＋1x 2－1＝x ＋1(x ＋1)(x －1)＝1x －1，其中x 2≠1，即x ≠±1，而y ＝1x －1中x ≠1，定义域不同，不是相同函数．4．已知f (x )＝11＋x，g (x )＝x 2＋2，则f (2)＝________，f [g (2)]＝________. 解析：f (2)＝11＋2＝13，g (2)＝22＋2＝6， ∴f [g (2)]＝f (6)＝11＋6＝17.答案：13 175．已知函数f (x )＝x 2－x ，若f (a )＝2，则a 的值是________． 解析：f (a )＝(a )2－a ＝2.即(a －2)(a ＋1)＝0，a ＝4. 答案：4通过这节课的学习，你对函数符号“y ＝f (x )”有了哪些新的认识？对应关系f 是表示定义域和值域的一种对应关系，与所选择的字母无关．符号y ＝f (x )是“y 是x 的函数”的数学表示，应理解为：x 是自变量，它是对应关系所施加的对象；f 是对应关系，它既可以是解析式，也可以是图象、表格或文字描述．y ＝f (x )仅仅是函数符号，不能理解为“y 等于f 与x 的乘积”．f (x )与f (a )的区别与联系：f (a )表示当x ＝a 时函数f (x )的值，是一个常量，而f (x )是自变量x 的函数，表示的是变量．虽然f (x )＝x 2和f (x －1)＝x 2等号右边的表达式都是x 2，但是，由于f 施加的对象不同(一个为x ，而另一个为x －1)，因此两个函数的解析式是不同的．一、选择题1．设集合M ＝{x |0≤x ≤2}，N ＝{y |0≤y ≤2}，给出如下四个图形，其中能表示从集合M 到集合N 的函数关系的是( )解析：选D 由函数的定义可以判断只有D 正确．2．函数f (x )定义在区间[－2,3]上，则y ＝f (x )的图象与直线x ＝2的交点个数为( ) A ．0 B ．1 C ．2D ．不确定解析：选B ∵2∈[－2,3]，由函数的定义可知，y ＝f (x )的图象与x ＝2只能有一个交点． 3．集合A ＝{x |0≤x ≤4}，B ＝{y |0≤y ≤2}，下列不表示从A 到B 的函数是( ) A ．f ：x →y ＝12xB ．f ：x →y ＝13xC ．f ：x →y ＝23xD ．f ：x →y ＝x解析：选C 对选项C ，当x ＝4时，y ＝83>2不合题意，故选C.4．下列说法错误的是( )A ．函数定义域中的任一元素在其值域中都有它的对应B ．函数的定义域是无限集，则值域也是无限集C ．定义域与对应关系确定后，函数值域也就确定了D ．若函数的定义域只有一个元素，则值域也只有一个元素 答案：B 二、填空题5．已知函数f (x )＝x 2＋|x －2|，则f (1)＝________. 解析：∵f (x )＝x 2＋|x －2|， ∴f (1)＝12＋|1－2|＝1＋1＝2. 答案：26．若f (2x )＝x 3，则f (1)＝________. 解析：令2x ＝1，则x ＝12，∴f (1)＝(12)3＝18.答案：18三、解答题7．已知函数f (x )＝x 2＋x －1，求： (1)f (2)； (2)f ⎝⎛⎭⎫1x ＋1；(3)若f (x )＝5，求x 的值． 解：(1)f (2)＝4＋2－1＝5. (2)f ⎝⎛⎭⎫1x ＋1＝⎝⎛⎭⎫1x ＋12＋⎝⎛⎭⎫1x ＋1－1 ＝1x 2＋3x＋1. (3)f (x )＝5，即x 2＋x －1＝5. 由x 2＋x －6＝0得x ＝2或x ＝－3. 8．已知函数f (x )＝x 21＋x 2.(1)求f (2)＋f ⎝⎛⎭⎫12，f (3)＋f ⎝⎛⎭⎫13的值；(2)求证：f (x )＋f ⎝⎛⎭⎫1x 是定值；(3)求f (2)＋f ⎝⎛⎭⎫12＋f (3)＋f ⎝⎛⎭⎫13＋…＋f (2 019)＋f ⎝⎛⎭⎫12 019的值． 解：(1)∵f (x )＝x 21＋x 2，∴f (2)＋f ⎝⎛⎭⎫12＝221＋22＋⎝⎛⎭⎫1221＋⎝⎛⎭⎫122＝1， f (3)＋f ⎝⎛⎭⎫13＝321＋32＋⎝⎛⎭⎫1321＋⎝⎛⎭⎫132＝1. (2)证明：f (x )＋f ⎝⎛⎭⎫1x ＝x21＋x 2＋⎝⎛⎭⎫1x 21＋⎝⎛⎭⎫1x 2 ＝x 21＋x 2＋1x 2＋1＝x 2＋1x 2＋1＝1. (3)由(2)知f (x )＋f ⎝⎛⎭⎫1x ＝1， ∴f (2)＋f ⎝⎛⎭⎫12＝1，f (3)＋f ⎝⎛⎭⎫13＝1， f (4)＋f ⎝⎛⎭⎫14＝1，…，f (2 019)＋f ⎝⎛⎭⎫12 019＝1. ∴f (2)＋f ⎝⎛⎭⎫12＋f (3)＋f ⎝⎛⎭⎫13＋…＋f (2 019)＋f ⎝⎛⎭⎫12 019＝2 018.。

2020-2021武汉市高一数学下期末试题(附答案)一、选择题1．ABC 中，已知sin cos cos a b cA B C==，则ABC 为（ ） A ．等边三角形B ．等腰直角三角形C ．有一个内角为30°的直角三角形D ．有一个内角为30°的等腰三角形2．如图，在ABC 中，90BAC ︒∠=，AD 是边BC 上的高，PA ⊥平面ABC ，则图中直角三角形的个数是（ ）A ．5B ．6C ．8D ．103．已知不等式()19a x y x y ⎛⎫++ ⎪⎝⎭≥对任意实数x 、y 恒成立，则实数a 的最小值为（ ） A ．8 B ．6 C ．4 D ．24．已知ABC ∆是边长为4的等边三角形，P 为平面ABC 内一点，则•()PA PB PC +的最小值是（） A ．6-B ．3-C ．4-D ．2-5．如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示成x 的函数()f x ，则()y f x =在[0,]π上的图象大致为（ ）A ．B ．C ．D ．6．已知数列{}n a 的前n 项和22n S n n =+，那么它的通项公式是（ ）A ．21n a n =-B ．21n a n =+C ．41n a n =-D ．41n a n =+7．有5支彩笔（除颜色外无差别），颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔，则取出的2支彩笔中含有红色彩笔的概率为 A ．45B ．35C ．25D ．158．函数()lg ||f x x x =的图象可能是（ ）A ．B ．C ．D ．9．1()xf x e x=-的零点所在的区间是（ ） A ．1(0,)2B ．1(,1)2C ．3(1,)2D ．3(,2)210．下列四个正方体图形中，A ，B 为正方体的两个顶点，M ，N ，P 分别为其所在棱的中点，能得出//AB 平面MNP 的图形的序号是（ ）A ．①③B ．②③C ．①④D ．②④11．若tan()24πα+=，则sin cos sin cos αααα-=+（ ）A ．12B ．2C ．2-D ．12-12．如图，在△ABC 中, 13AN NC =,P 是BN 上的一点,若29AP m AB AC −−→−−→−−→=+,则实数m 的值为( )A ．B ．C ．19D ．二、填空题13．奇函数()f x 对任意实数x 都有(2)()f x f x +=-成立，且01x 时，()21x f x =-，则()2log 11f =______.14．若三点1(2,3),(3,2),(,)2A B C m --共线，则m 的值为 ． 15．某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200,400,300,100件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取________ 件.16．设a ，b ，c 分别为ABC ∆内角A ，B ，C 的对边.233a b c-=，则222a cb ac+-的取值范围为______. 17．若,2παπ⎛⎫∈⎪⎝⎭，1sin 43πα⎛⎫+= ⎪⎝⎭，则sin α=_________18．等边ABC ∆的边长为2，则AB 在BC 方向上的投影为________．19．在200m 高的山顶上，测得山下一塔顶与塔底的俯角分别是30°,60°，则塔高 为20．在圆x 2＋y 2＋2x ＋4y －3＝0上且到直线x ＋y ＋1＝0的点共有________个．三、解答题21．已知函数f （x ）是定义在R 上的偶函数，且当x ≥0时，f （x ）＝x 2﹣2x ． （1）求f （0）及f （f （1））的值； （2）求函数f （x ）的解析式；（3）若关于x 的方程f （x ）﹣m ＝0有四个不同的实数解，求实数m 的取值范围， 22．随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款（年底余额）如下表：（Ⅰ）求y 关于t 的回归方程^^^t yb a =+（Ⅱ）用所求回归方程预测该地区2015年（6t =）的人民币储蓄存款.附：回归方程^^^t yb a =+中1122211()(),{().n niii ii i nni i i i x x y y x y nxyb x x x nx a y bx ====---==--=-∑∑∑∑23．已知矩形ABCD 的两条对角线相交于点20M （，），AB 边所在直线的方程为360x y --=，点11T -（，）在AD 边所在直线上. （1）求AD 边所在直线的方程； （2）求矩形ABCD 外接圆的方程.24．如图，在三棱柱111ABC A B C -中，侧棱垂直于底面，1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ； （3）求三棱锥E ABC -体积．25．记n S 为等差数列{}n a 的前n 项和，已知17a =-，315S =-． （1）求{}n a 的通项公式； （2）求n S ，并求n S 的最小值．26．ABC ∆中，三个内角,,A B C 的对边分别为,,a b c ，若(cos ,cos )m B C =，(2,)n a c b =+，且m n ⊥.（1）求角B 的大小；（2）若7b =，8a c +=，求ABC ∆的面积.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【解析】 【分析】 【详解】因为sin cos cos a b c A B C==，所以sin sin sin sin cos cos 4A B C B C A B C π==∴== , 即ABC 为等腰直角三角形.故选：B .2．C解析：C 【解析】 【分析】根据线面垂直得出一些相交直线垂直，以及找出题中一些已知的相交直线垂直，由这些条件找出图中的直角三角形．【详解】①PA ⊥平面ABC ，,,,PA AB PA AD PA AC PAB ∴⊥⊥⊥∴∆,,PAD PAC ∆∆都是直角三角形；②90,BAC ABC ︒∠=∴是直角三角形； ③,,AD BC ABD ACD ⊥∴∆∆是直角三角形；④由,PA BC AD BC ⊥⊥得BC ⊥平面PAD ，可知：,,BC PD PBD PCD ⊥∴∆∆也是直角三角形.综上可知：直角三角形的个数是8个，故选C ．【点睛】本题考查直角三角形个数的确定，考查相交直线垂直，解题时可以充分利用直线与平面垂直的性质得到，考查推理能力，属于中等题．3．C解析：C 【解析】 【分析】由题意可知，()min 19a x y x y ⎡⎤⎛⎫++≥⎢⎥ ⎪⎝⎭⎣⎦，将代数式()1a x y x y ⎛⎫++ ⎪⎝⎭展开后利用基本不等式求出该代数式的最小值，可得出关于a 的不等式，解出即可. 【详解】()11a ax yx y a x y y x ⎛⎫++=+++⎪⎝⎭. 若0xy <，则0yx<，从而1ax y a y x +++无最小值，不合乎题意；若0xy >，则0yx>，0x y >.①当0a <时，1ax ya y x+++无最小值，不合乎题意； ②当0a =时，111ax y y a y x x +++=+>，则()19a x y x y ⎛⎫++ ⎪⎝⎭≥不恒成立；③当0a >时，()()21121211a ax y ax yx y a a a a a x y y xy x ⎛⎫++=+++≥⋅++=++=+ ⎪⎝⎭，当且仅当=y ax 时，等号成立.所以，()219a +≥，解得4a ≥，因此，实数a 的最小值为4.故选：C. 【点睛】本题考查基本不等式恒成立问题，一般转化为与最值相关的不等式求解，考查运算求解能力，属于中等题.4．A解析：A 【解析】 【分析】建立平面直角坐标系，表示出点的坐标，利用向量坐标运算和平面向量的数量积的运算，求得最小值，即可求解. 【详解】由题意，以BC 中点为坐标原点，建立如图所示的坐标系， 则(0,23),(2,0),(2,0)A B C -，设(,)P x y ，则(,23),(2,),(2,)PA x y PB x y PC x y =--=---=--， 所以22()(2)(23)(2)2432PA PB PC x x y y x y y •+=-⋅-+-⋅-=-+222[(3)3]x y =+--，所以当0,3x y ==时，()PA PB PC •+取得最小值为2(3)6⨯-=-， 故选A.【点睛】本题主要考查了平面向量数量积的应用问题，根据条件建立坐标系，利用坐标法是解答的关键，着重考查了推理与运算能力，属于基础题.5．B解析：B 【解析】 【分析】计算函数()y f x =的表达式，对比图像得到答案. 【详解】 根据题意知：cos cos OM OP x x ==M 到直线OP 的距离为：sin cos sin OM x x x = 1()cos sin sin 22f x x x x ==对应图像为B 故答案选B 【点睛】本题考查了三角函数的应用，意在考查学生的应用能力.6．C解析：C 【解析】分类讨论：当1n =时，11213a S ==+=，当2n ≥时，221(2)2(1)141n n n a S S n n n n n -⎡⎤=-=+--+-=-⎣⎦， 且当1n =时：1414113n a -=⨯-== 据此可得，数列的通项公式为：41n a n =-. 本题选择C 选项.7．C解析：C 【解析】选取两支彩笔的方法有25C 种，含有红色彩笔的选法为14C 种，由古典概型公式，满足题意的概率值为142542105C p C ===. 本题选择C 选项. 考点：古典概型名师点睛：对于古典概型问题主要把握基本事件的种数和符合要求的事件种数，基本事件的种数要注意区别是排列问题还是组合问题，看抽取时是有、无顺序，本题从这5支彩笔中任取2支不同颜色的彩笔，是组合问题，当然简单问题建议采取列举法更直观一些.8．D解析：D 【解析】 【分析】分析函数()y f x =的定义域、奇偶性及其在()0,1上的函数值符号，可得出结论. 【详解】函数()lg f x x x =的定义域为{}0x x ≠，定义域关于原点对称，()()lg lg f x x x x x f x -=--=-=-，函数()y f x =为奇函数，排除A 、C 选项；当01x <<时，lg 0x <，此时()lg 0f x x x =<，排除B 选项. 故选：D. 【点睛】本题考查由函数的解析式选择函数图象，一般分析函数的定义域、奇偶性、单调性、零点以及函数值符号，考查推理能力，属于中等题.9．B解析：B 【解析】 函数f （x ）=e x ﹣1x 是（0，+∞）上的增函数，再根据f （12）=e ﹣2＜0，f （1）=e ﹣1＞0，可得f （12）f （1）＜0，∴函数f （x ）=e x ﹣1x 的零点所在的区间是（12，1），故选B ．点睛：判定函数的零点所在区间，只需计算区间端点处的函数值，并判断是否异号，只要异号，则区间内至少有一个零点存在.10．C解析：C 【解析】 【分析】用面面平行的性质判断①的正确性.利用线面相交来判断②③的正确性，利用线线平行来判断④的正确性. 【详解】对于①，连接AC 如图所示，由于//,//MN AC NP BC ，根据面面平行的性质定理可知平面//MNP 平面ACB ，所以//AB 平面MNP .对于②，连接BC 交MP 于D ，由于N 是AC 的中点，D 不是BC 的中点，所以在平面ABC 内AB 与DN 相交，所以直线AB 与平面MNP 相交.对于③，连接CD ，则//AB CD ，而CD 与PN 相交，即CD 与平面PMN 相交，所以AB 与平面MNP 相交.对于④，连接CD ，则////AB CD NP ，由线面平行的判定定理可知//AB 平面MNP .综上所述，能得出//AB 平面MNP 的图形的序号是①④. 故选：C 【点睛】本小题主要考查线面平行的判定，考查空间想象能力和逻辑推理能力，属于基础题.11．D解析：D 【解析】 由tan()24πα+=有tan 112,tan 1tan 3ααα+==-，所以11sin cos tan 1131sin cos tan 1213αααααα---===-+++，选D.点睛：本题主要考查两角和的正切公式以及同角三角函数的基本关系式，属于中档题。

绝密★启用前湖南省永州市八县普通高中(祁阳、宁远、道县、东安、新田、蓝山、江华、江永) 2021届高三毕业班上学期12月新高考联考检测数学试题2020年12月本试卷共4页，22题。

全卷满分150分。

考试用时120分钟。

注意事项：1.答题前，先将自己的姓名、考号等填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2.选择题的作答：选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3.填空题和解答题的作答：用签字笔直接写在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4.考试结束后,请将本试题卷和答题卡一并上交。

一、单项选择题：本题共8小题,每小题5分,共40分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1.已知集合A＝{x|y＝lg(x＋1)},B＝{x|x2＋4x≤0},则A∩B＝A.[－4,＋∞)B.[－4,－1)C.(－1,0]D.[－4,0)2.复数＝1332izi+=-在复平面上对应的点在A.第一象限B.第二象限C.第三象限D.第四象限3.玉璧是我国传统的玉礼器之一,也是“六瑞”之一,象征着吉祥等寓意,穿孔称作“好”,边缘器体称作“肉”。

《尔雅·释器》“肉倍好谓之壁,好倍肉谓之瑷,肉好若一谓之环”,一般把体形扁平、周边圆形、中心有一上下垂直相透的圆孔的器物称为璧。

如图所示,某玉璧通高2.5cm,孔径8cm、外径18cm,则该玉璧的体积为A .158.5π cm 3B .160.5π cm 3C .162.5π cm 3D .164.5π cm 34.已知等差数列{a n }的前n 项和为S n ,若S 4＝22,a 6＝16,则a 3＝A.3B.4C.5D.75.已知(x 2xn 展开式中,所有项的二项式系数的和为32,则其展开式中的常数项为A.60B.－60C.80D.－806.声音的等级f(x)(单位：dB)与声音强度x(单位：W/m 2)满足f(x)＝10×lg 12110x -⨯。