图乘法原理

三、注意事项： 注意事项：
1.若 Aω与 1.若 取负值
yc
在杆件的同侧，取正值；反之， 在杆件的同侧，取正值；反之，
2.当图乘法的适用条件不满足时的处理方法： 当图乘法的适用条件不满足时的处理方法： 当图乘法的适用条件不满足时的处理方法 a）曲杆或EI=EI（x）时，只能用积分法求位移； ）曲杆或 只能用积分法求位移； （ ） b）当EI分段为常数或单位弯矩图、荷载弯矩图均非 ） 分段为常数或单位弯矩图、 分段为常数或单位弯矩图 直线时， 直线时，应分段图乘再叠加 3.yc应取自直线图中。若两图均为直线图形，也可 应取自直线图中。若两图均为直线图形， 图的面积乘其形心所对应的M 用 M 图的面积乘其形心所对应的 P 图的竖标来计 算。
2
yc = h
1 2 ql 2 = × × ×l×h ∆ CD = ∑ EI EI 3 8 qhl 3 = (→ ← ) 12 EI
ω yc
为常数，求刚架A点的竖向位 例 3. 已知 EI 为常数，求刚架 点的竖向位 并绘出刚架的变形曲线。 移 ∆ Ay ，并绘出刚架的变形曲线。
F
解：作荷载内力图和单位荷载内力图
M=1
M P图
∆ CV
300 × 6 2 = × ×6× 2 2 3 1 2 − × 6 × 45 × 3 = 6660 3
6
M A图
Fp=1
M C图
为常数， 例 5. 已知 EI 为常数，求 ∆Cy 。 q
A
l 2
C
B
l 2
解：作荷载内力图和单位荷载内力图
ql 2 2
A
ql 2 8
C
l 2
1
B A
二、图乘法原理
MM P 图乘法求位移的一般 ds 表达式为 ∫ EI 1 ∆=∑ Aω yC 1 = ∫ MM P ds EI EI

材料力学图乘法材料力学图乘法是材料力学中的一种重要计算方法，它可以帮助工程师和科研人员快速准确地计算材料的性能参数，为材料的设计和应用提供重要参考。

在材料力学图乘法中，我们需要了解一些基本概念和计算步骤，下面将对材料力学图乘法进行详细介绍。

首先，我们需要了解什么是材料力学图。

材料力学图是用来描述材料在外力作用下的性能变化规律的图表，通常包括应力-应变曲线、拉伸性能曲线、压缩性能曲线等。

通过材料力学图，我们可以直观地了解材料在不同应力下的应变变化情况，从而评估材料的力学性能。

接下来，我们来介绍材料力学图乘法的计算步骤。

首先，我们需要准备两个材料的力学图，分别记为A和B。

然后，我们将这两个力学图进行叠加，即将A图的应力-应变曲线与B图的应力-应变曲线进行对应相乘。

这样，我们就可以得到一个新的力学图，用来描述两种材料叠加后的性能。

在进行材料力学图乘法计算时，我们需要注意一些细节。

首先，要保证A图和B图的坐标轴尺度一致，这样才能进行准确的叠加计算。

其次，要注意叠加计算的顺序，通常是先进行应力的叠加，然后再进行应变的叠加。

最后，要对叠加后的新力学图进行分析，得出叠加后材料的性能参数，如弹性模量、屈服强度、断裂强度等。

通过材料力学图乘法，我们可以更加深入地了解材料的性能特点。

例如，当我们需要设计一个复合材料结构时，可以通过材料力学图乘法来评估不同材料叠加后的性能，从而选择合适的材料组合方案。

另外，材料力学图乘法还可以帮助我们预测材料在复杂加载条件下的性能表现，为工程实践提供重要参考。

总之，材料力学图乘法是材料力学中一种重要的计算方法，它可以帮助我们快速准确地评估材料的性能参数，为材料的设计和应用提供重要参考。

通过深入学习和应用材料力学图乘法，我们可以更好地理解材料的性能特点，为工程实践和科研工作提供有力支持。

希望本文的介绍能够帮助大家更好地掌握材料力学图乘法的基本原理和计算方法，为相关领域的工作提供帮助。

W12 W21
二、 位移互等定理
在任一线性变形体系中，由荷载FP1引起的 与荷载FP2相应的位移影响系数δ21等于由荷载 FP2引起的与荷载FP1相应的位移影响系数δ12。
即
δ12= δ21
FP1
12
FP 2
12
11
21
状态I
12
22
状态II
由功的互等定理可得： FP112 FP221

1 81 2
4
21
20
y2

( 4 3
12) 3

3
y3

1 2
(1 1 /
2)

3 4
B

1 EI
(1 y1
2 y2
3 y3 )

1 EI
(64 1 2
4
20 3

32 3 ) 34
1 (32 80 8) 13.33 ( )
Ma2 16EI
21

21
/
F

a2 16EI
12

12
/M

a2 16EI
12 21
例2 验证位移互等定理。
FP1=5kN.m 1
EI 4m
2
1
Δ21
1m
FP2=3kN
Δ12
2
EI
4m
1m
3 5
11
1
解：
11
1 10
21

EI

2
5
4
1 3
3EI
12

1 EI
和量纲 (W FP1FP2 ) 上仍然保持相等。

实用文档
CL12TU35
解：
ql2
vB
1 EI
l
ql2
3 2
3l 4
2
ql4 8E I 实用文档
ql2
B
1 EI
l
ql2
3 2
1
2
ql3 顺时针
6EI
实用文档
例：试用图乘法求图示悬臂梁中点C 处的铅垂位移。
实用文档
CL12TU36
解：
vC
1 EI
l2 8
m
ml2 8E I 实用文档
max
1 2lql2 EI3 8
1 2
ql3
24E I
实用文档
ql2 / 8
例：试用图乘法求所示简支梁的最大 挠度和最大转角。
实用文档
CL12TU33
解：
vmaxE2I212l P 4l6l
Pl3 48E I 实用文档
Pl /4 l/4
max E1I21lP 4l 21
Pl2 16E I
实用文档
Pl /4
例：试用图乘法求所示简支梁C截面的 挠度和A、B截面的转角。
实用文档
CL12TU34
解：
vC
1 EI
l2 8
m
2
ml 2
16E I
l/4
实用文档
A
1 EI
ml 2
13
ml 顺时针
6EI 实用文档
B
1 EI
ml 2
23
ml 逆时针
3EI 实用文档
例：试用图乘法求所示悬臂梁自由端 B的挠度和转角。
CE 1IX 2 al2 3X2 a21q 1l232 1 0

分析： 分析： 在直杆结构中总是直线。 M在直杆结构中总是直线。 满足上式推导中f(x)的条件 满足上式推导中f(x)的条件 f(x)
y0 o A
MM P 1 ∆ = ∑∫ ds = ωy 0 EI EI
武汉理工大学土木工程与建筑学院 结构力学教研室 李保德副教授
MM P 1 ds = ∑ ωy 0 ∆ = ∑∫ EI EI
1 1 2 ω 3 = × qL 2 8 3 y3 = L 4
C
B L/2
1 L 1 2 ω1 = × × qL 3 2 8
1 L 1 2 ω 2 = × × y2 = L 6
∆B =
1 (ω1 y1 + ω 2 y 2 + ω 3 y3 ) EI
41qL4 = 384 EI
武汉理工大学土木工程与建筑学院
结构力学教研室
李保德副教授
3. 常见图形的面积和形心
武汉理工大学土木工程与建筑学院
结构力学教研室
李保德副教授
注意: 注意:
标准抛物线
武汉理工大学土木工程与建筑学院
结构力学教研室
李保德副教授
4. 图乘的一般方法
两图均是直线图形，y0可取其中的任一图形
ω
y0
y0
ω
武汉理工大学土木工程与建筑学院
武汉理工大学土木工程与建筑学院
C
B L/2
∆B =
1 ωM P y EI
1 1 2 PL3 = × L × PL × L = EI 2 3 EI
B
MP
或
1 ∆B = ωM y EI
1 1 2 PL3 = × L × L × PL = EI 2 3 EI
M
结构力学教研室
李保德副教授

与数值法的比较
数值法通过计算机模拟得出结果，适用于复杂问题但需要专业软件；图乘法简单易行，但计算能力有限。
05
CHAPTER
图乘法的发展趋势与展望
航空航天领域
随着航空航天技术的不断发展，图乘法在分析飞行器结构、优化设计等方面将有更广泛的应用。
1
2
3
图乘法在多物理场耦合分析方面具有优势，未来研究将进一步深化其在流固耦合、热固耦合等领域的应用。
直观易懂
图乘法在处理某些复杂问题时，可以简化计算过程，提高解题效率。
计算简便
图乘法适用于多种类型的力学问题，尤其在解决平面问题和旋转问题时表现出色。
适实际实验获取数据，真实度高但受实验条件限制；图乘法不受实验条件限制，但结果依赖于绘图精度。
与解析法的比较
解析法通过数学公式解析问题，精确度高但计算复杂；图乘法在保持一定精确度的同时，简化了计算过程。
详细描述
02
CHAPTER
图乘法的基本原理
图乘法涉及到代数运算，包括线性代数和矩阵运算等。
代数基础
几何基础
微积分基础
图乘法涉及到几何图形，如平面图形和立体图形等。
图乘法涉及到微积分的知识，如微分和积分等。
03
02
01
图乘法可以用于结构分析，通过计算结构的位移和应力等参数，评估结构的性能。
结构分析
在机械结构分析中，图乘法常用于计算机械零件的应力和变形。通过将机械零件各部分离散化，并利用图乘法计算各部分产生的内力和变形，可以得出整个机械零件的受力状态和变形情况。这对于确保机械零件的安全性和稳定性至关重要。
总结词
详细描述
04
CHAPTER
图乘法的优缺点分析
图乘法通过图形直观地展示力学问题，使得学生更容易理解。

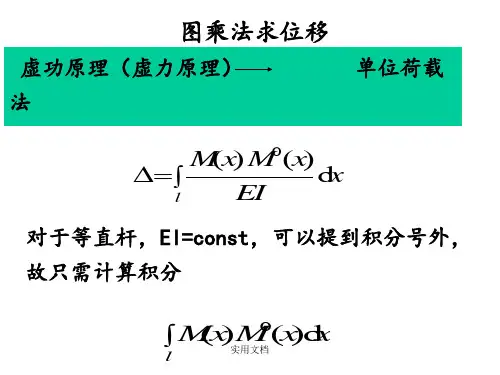
图乘法原理图乘法原理是指在数学中，两个图形的面积可以通过它们的长和宽的乘积来计算。

这个原理在几何学和代数学中都有广泛的应用，可以帮助我们更好地理解图形的性质和相互之间的关系。

首先，让我们来看一个简单的例子，假设有一个长为3米，宽为4米的矩形，我们可以通过计算长和宽的乘积来得到它的面积，即3米×4米=12平方米。

这个例子就展示了图乘法原理的基本概念，即通过乘法来计算图形的面积。

在几何学中，图乘法原理可以帮助我们计算各种不规则图形的面积。

比如，一个不规则的四边形，我们可以将它分割成几个简单的图形，然后分别计算它们的面积，最后将它们加起来就得到了整个图形的面积。

这个方法在实际问题中非常有用，可以帮助我们计算各种复杂图形的面积，从而更好地理解它们的特性。

在代数学中，图乘法原理也有着重要的应用。

比如，在矩阵乘法中，两个矩阵的乘积可以通过它们对应元素的乘积来计算。

这个过程实质上就是在应用图乘法原理，通过乘法来计算两个图形的相关性。

矩阵乘法在计算机图形学、工程学和物理学等领域都有着广泛的应用，它可以帮助我们更好地理解复杂系统之间的关系。

除此之外，图乘法原理还可以帮助我们理解概率和统计学中的一些概念。

比如，在概率计算中，两个事件同时发生的概率可以通过它们各自发生的概率相乘来计算，这也是在应用图乘法原理。

通过这种方法，我们可以更好地理解概率事件之间的关系，从而更准确地进行概率计算。

总的来说，图乘法原理是数学中一个非常重要的概念，它在几何学、代数学、概率和统计学等领域都有着广泛的应用。

通过理解图乘法原理，我们可以更好地解决各种与图形、矩阵、概率事件相关的问题，从而提高我们的数学素养和解决问题的能力。

希望本文对读者能够有所帮助，谢谢阅读！。

EI
E1I1 E2 I 2 E3 I3
Ei Ii
对于等直杆有
Δ

1 EI
l M ( x)M ( x)dx
M(x)
MC
EI
ω
C
即 积分可用M(x)图的面积 ω 和与M(x)
xc
x
图形心C对应的 Mc 的乘积来代替
M(x)
当M图为正弯矩时，
Δ MC
EI
ω应代以正号. 当M图为负弯矩时， ω应代以负号.
（3）图 M 图 M P中至少有一个是直线
图形。
3、图乘法公式
KP
Ap yc EI
M M P ds EI
←杆轴为直线
M M P dx EI
←杆段EI为常数
1 EI
M M Pdx
(M x tan α)
1
EI x tan α M Pdx

tan α EI
注意
有时M(x)图为连续光滑曲线，而 M(x) 为折线，则应以 折线的转折点为界，把积分分成几段，逐段使用图乘法， 然后求其和.
例1 求CV , EI等于常数。
解：
2kN/m
作 M 图 MP 图，如右图所示。 A 2m C 2m B
分段：M ，M P 分为AC、CB两段。16
分块： M P图的AC段分为两块。
还记得 吗？
（3）同侧弯矩图相乘为正，反之为负；
（4）拱、曲杆结构和连续变截面的结构只能通过积 分的方式求解；
（5）应用图乘法首先熟练掌握常用图形面积及形心 位置。
几中常见图形的面积和形心的计算公式
a
b
C
lb
la
3

图乘法原理
图乘法原理是指在进行图的乘法运算时，将两个图的每个顶点对都连接起来，形成一个新的图。

这个新图的顶点由两个原始图的顶点组成，边由两个原始图的边组成。

具体而言，设图G1=(V1,E1)和图G2=(V2,E2)是两个图，其中
V1和V2分别是G1和G2的顶点集合，E1和E2分别是G1和G2的边集合。

那么图乘法原理定义了一个新的图G=(V,E)，
其中V=V1×V2，即G的顶点是由G1和G2的顶点对组成的。

而E是由所有G1和G2的边连接起来的，即对于每个
(u,v)∈V1×V2，如果存在(u1,v1)∈E1和(u2,v2)∈E2满足u=u1，v=v2，那么(u,v)∈E。

通过图乘法原理，我们可以将两个图的结构进行组合，得到一个新的图。

这个新图中的顶点保留了原来两个图的顶点的属性，而边则是两个图的边的组合。

在实际应用中，图乘法原理可以用于表示两个图之间的关系，例如社交网络中的用户之间的关注关系和互动关系等。

总之，图乘法原理是一种用于将两个图进行乘法运算的方法，通过将两个图的顶点对连接起来，形成一个新的图。

它可以用于表示两个图之间的关系，在图论和网络分析领域有着广泛的应用。

2、求ΔCV ① MP图如图(b)所示。 ② 单位弯矩图M如图(d)所示。 ③ 计算A、yC。 2×l/2=ql3/24 A=2/3×1/8ql yC=5/8×l/4=5l/32 ④ 计算ΔCV ΔCV=2(1/EI*A*yC)= 5ql4/384EI (↓)
【课后作业】习题8-6（用图乘法）
【预习】：静定结构的位计算习题课
三、几个规则图形的面积和形心位置
顶点：指曲线上切线平行于底边的点 标准抛物线：指顶点在中点或端点的抛物线
四、图乘法技巧
1、图形分解图乘 当图形的面积和形心不 便确定时，可以将其分 解成几个简单的图形， 分别与另一图形相应的 纵坐标相乘。
（1）梯-梯同侧组合（三角形为特殊情况）
（2）、梯-梯同侧组合：
剪力与轴力项能用图乘法？
3、图乘法求位移的一般表达式
注意：
y [1]. c
应取自直线图中。 [2].若 A 与 yc 在杆件的同侧, 取正值;反之,取负值（不是MP与M 图位于杆件同侧或异侧）。 [3]. 如图形较复杂，可分解为几个简 单图形。
二、图乘法步骤 (1) 画出结构在实际荷载作用下的弯 矩图（荷载弯矩图）MP； (2) 根据所求位移选定相应的虚拟力 状态，画出单位弯矩图M(注：M图不标 单位）； (3) 分段计算一个弯矩图形的面积A 及其形心所对应的另一个弯矩图形的竖 标yC； (4) 将A、yC代入图乘法公式计算所 求位移。
解：1、求φA ① 实际荷载作用 下的弯矩图MP如图(b) 所示。 ② 在A端加单位力 偶m=1，其单位弯矩图M 如图(c)所示。
③ MP图面积及其形心 对应M图竖标分别为：
A=2/3*l*1/8*ql2=ql3/12 yC=1/2 ④ 计算φA φA=1/EI*A*yC =1/EI*ql3/12*1/2=ql3/24 EI

4.5 图乘法原理1. 教学要求正确理解图乘法和应用条件以及图乘法的含义，能够利用图乘法计算梁、刚架的位移，理解各种弯矩图的叠加并能够根据叠加进行图乘。

2. 教学内容4.5.1 图乘法及应用条件4.5.2 常见图形的面积和形心4.5.3 图乘法的几个具体问题4.5.4 图乘法应用举例4.5.1 图乘法及应用条件（1）问题的提出梁和刚架位移的公式：积分计算复杂，在已知荷载和虚设单位力作用下的弯矩图下，能否找到更好的方法。

（2）公式推导图4.9为某直杆段AB 的两个弯矩图，其中Mi 图为直线，抗弯刚度EI 为常数：图4.9在多个杆件情况下，式中：A 是Mx 图的面积；y0是在Mx 图形心C 对应处的Mi 图标距（3）应用条件：杆件应是等截面直杆；两个图形中至少有一个是直线，标距y0 应取自直线图形中。

（4）正负号规定：面积A 与标距y0 在同一侧时，两者乘积取正号；反之取负号。

4.5.2 常见图形的面积和形心常见图形的形心和面积（图4.10）。

图4.10以上图形的抛物线均为标准抛物线：抛物线的顶点处的切线都是与基线平行4.5.3 应用图乘法时的几个具体问题(1) 如果两个图形都是直线图形，标距可任取自其中一个图形（图4.11）。

图4.11(2) 如果有一个图形为折线，则应分段考虑（图4.12）图4.12(3) 如果图形比较复杂，应根据弯矩图的叠加原理将图形分解为几个简单图形，分项计算后再进行叠加图4.13图4.13（图4.13b中A1与y1的乘积为负值；图4.13c中抛物线为非标准曲线）。

4.5.4 图乘法应用举例例5：试计算图4.14悬臂梁B 点和C点的竖向位移、B点的转角位移，EI 为常数。

图4.14解: （1）虚设单位荷载，作实际状态和虚设单位荷载的弯矩图（B 点和C点的竖向位移、B点的转角位移分别为图4.15a、b和c)。

图4.152）实际荷载弯矩图中计算面积，单位荷载弯矩图中计算竖标, 代入公式，图乘。

1c图，
q
C
B
2.θb M02f图，
2 1 2 ql 3 ω 2 = × ql ⋅ l = 3 8 12 1 M 20 c = 2
l 2 1 ql 8
2
M 1
l 5 5l M = × = 4 8 32 2 ω 1 ⋅ M 10c fc = EI
0 1c
l 4
M
0 1
θb = −
ω ⋅ M 20c
EI
2 ql 3 5l = × × EI 24 32 5 ql 4 = (↓ ) 384 EI
1
M
0 2
1 ql 3 1 =− × × EI 12 2 ql 3 =− 24 EI
1
外伸梁右端挠度
P A C D
Pl 4
B
ω 1 ⋅M 10c
1 Pl l Pl 3 =− × ×l× = − 2 4 8 64 1 Pl l 2 Pl 3 = × ×l× × = 2 4 4 3 48
l 2
l Pl 4

1
l 4
2
解：
ω 2 ⋅M 20c
ω 3 ⋅M 30c

2

Pl l l Pl 3 = × × = 4 4 8 128
3
Pl 4
1
M 图
fb =
B
A
D
1 0 ( −ω 1 ⋅M 10c + ω 2 ⋅M 2 c +ω 3 ⋅M 30c ) EI
l 4
M
0
Pl 3 1 1 1 5 Pl 3 = + + (↓ ) (− )= EI 64 48 128 384 EI
C dA
令M ( x) dx = dA

FN FPb M FQ 状态II FPa
M ds ds EI FN ds ds EA
ds 0
kFQ GA
ds
令状态I的平衡力系在状态II的位移上做虚功，得到：
0 ds FN ds W12 FP M ds FQ FQ kFQ FN FN M M ds ds ds EI GA EA
yc
几中常见图形的面积和形心的计算公式
a b 顶点
C
lb 3
C
5l 8
la 3
3l 8
l
l
三角形
l h AP 2
二次抛物线
2 Ap h l 3
顶点
c
顶点
( n 1) l n2
c
l n2
3l/4 l
l/4
l
二次抛物线
l h Ap 3
N 次抛物线
lh n1
3. 图形相乘的几种情况
1
作业：
4-3 (a)；(c)
§4-5 互等定理
互等定理适用于线性变形体系，即体系产生的 是小变形，且杆件材料服从虎克定律。
一、 功的互等定理
功的互等本质上是虚功互等。
下图给出状态I和状态II。
FP1 2 FP
FPa
FPb
A
1 2 a b
a
b
B
A
1 2 B a 1 b 2
所以
即
F F
P P
11 FP 2 FP 2 FPa a FPb b
在任一线性变形体系中，第一状态的外力 在第二状态的位移上所做的虚功W12等于第二状 态的外力在第一状态的位移上所做的虚功W21。

实例分析：圆轴扭转内力计算
第一段
M1 = (T1 + T2) × L/2
第二段
M2 = (T2 + T1) × L/2
实例分析：圆轴扭转内力计算
01
4. 比较M1和M2的大小，取较大 者作为圆轴内的最大扭矩。
02
5. 根据扭矩的正负号，绘制扭矩 图。
Part
04
组合变形图乘法
组合变形基本概念及分类
者联系起来，从而求解结构位移。
图乘法适用条件及限制
适用条件Βιβλιοθήκη 01载荷作用下，结构的变形是线性的，即变 形量与载荷成正比。
03
02
结构变形符合小变形假设，即变形量与结构 尺寸相比很小。
04 限制
图乘法只适用于线性弹性问题，对于非线 性问题或塑性变形问题不适用。
05
06
在应用图乘法时，需要保证图形函数的准 确性，否则会影响计算结果的精度。
Part
02
弯曲内力图乘法
弯曲内力基本概念
01
02
03
弯曲内力
指构件在受到外力作用时， 其内部产生的抵抗弯曲变 形的力。
剪力
作用于构件横截面上的内 力，其方向与构件轴线垂 直。
弯矩
作用于构件横截面上的内 力偶矩，其大小等于该截 面左侧或右侧所有外力对 截面形心的力矩之和。
弯曲内力图乘法求解步骤
图乘法优点总结
直观性
图乘法通过图形表示结构 中的力学元素和它们之间 的关系，使得分析结果更 直观，易于理解和解释。
高效性
相较于数值分析方法，图 乘法能够更快地给出结构 分析的近似解，适用于初 步设计和快速评估。
适用性广
图乘法可应用于各种不同 类型的结构，包括静定结 构和超静定结构，具有较 广泛的适用性。

2、图乘法原理 y
d A =MPdx
A MP
A 面积
形心 C MP图 B
dx
O
x

M xtgα
yC
yC=xCtg
B
A
xC
x
由此可知，计算位移的积分就等于一 个弯矩图的面积A乘以其形心所对应的 另一个直线弯矩图上的竖标yC，再除以 EI，于是积分运算转化为数值乘除运 算，此法即称图乘法。
剪力与轴力项能用图乘法？
3、图乘法求位移的一般表达式
注意：
yc [1].
应取自直线图中。 [2].若 A 与 yc 在杆件的同侧, 取正值;反之,取负值（不是MP与M 图位于杆件同侧或异侧）。 [3]. 如图形较复杂，可分解为几个简 单图形。
二、图乘法步骤 (1) 画出结构在实际荷载作用下的弯 矩图（荷载弯矩图）MP； (2) 根据所求位移选定相应的虚拟力 状态，画出单位弯矩图M(注：M图不标 单位）； (3) 分段计算一个弯矩图形的面积A 及其形心所对应的另一个弯矩图形的竖 标yC； (4) 将A、yC代入图乘法公式计算所 求位移。
【预习】：静定结构的位计算习题课
解：1、求φA ① 实际荷载作用 下的弯矩图MP如图(b) 所示。 ② 在A端加单位力 偶m=1，其单位弯矩图M 如图(c)所示。
③ MP图面积及其形心 对应M图竖标分别为：
A=2/3*l*1/8*ql2=ql3/12 yC=1/2 ④ 计算φA φA=1/EI*A*yC =1/EI*ql3/12*1/2=ql3/24 EI
（3）异侧组合
（4）非规则抛物线图形
由区段叠加法作的弯矩图 ，其弯矩 图可以看成一个直线弯矩图和一个规 则抛物线图形的叠加 。
MB

力学图乘法算位移力学图乘法是一种常用的求解机械系统位移的方法。

它的基本思想是通过对机械系统的力学图进行乘法运算，来求解系统的位移。

这种方法在机械工程领域中广泛使用，特别是在求解复杂机械系统的位移时，力学图乘法尤为有用。

首先，我们来解释一下什么是力学图。

力学图是一种表示机械系统力学关系的图形。

它由若干个节点和若干条边组成。

每个节点表示一个机械单元，每条边表示两个机械单元之间的力学关系。

通过对力学图进行乘法运算，我们可以得到机械系统中每个机械单元的位移。

力学图乘法的具体过程如下：1. 首先，我们需要建立机械系统的力学图。

这一步通常是由工程师来完成的，需要结合机械系统的设计图纸和力学原理进行建模。

2. 接下来，我们需要求解机械系统的基底矩阵。

基底矩阵是指机械系统中每个机械单元在基底坐标系下的位移矩阵。

这一步通常需要解决机械系统的边界条件，即确定某些机械单元的位移是已知的。

通常情况下，我们可以在机械系统的力学图中选择一些节点作为基底，并将其位移设定为零。

3. 然后，我们需要求解机械系统的力学图矩阵。

力学图矩阵是指机械系统中每个机械单元与基底之间的力学关系的矩阵。

这一步通常是通过对力学图进行乘法运算来完成的。

4. 最后，我们需要计算机械系统的总位移矩阵。

总位移矩阵是指机械系统中每个机械单元在基底坐标系下的位移矩阵之和。

这一步通常是通过对基底矩阵和力学图矩阵进行乘法运算来完成的。

通过这几步运算，我们就可以得到机械系统中每个机械单元的位移。

力学图乘法是一种高效的求解机械系统位移的方法，在机械工程领域中广泛使用。

然而，力学图乘法也有一些局限性。

首先，力学图乘法只适用于线性系统。

如果机械系统存在非线性因素，则力学图乘法就无法正确求解系统的位移了。

其次，力学图乘法只能求解机械系统的位移，无法求解其他力学量，如弹性力矩、转矩等。

总之，力学图乘法是一种常用的求解机械系统位移的方法，它的优点是简单易懂、计算量小，但是也有一些局限性，在求解复杂机械系统的位移时可能存在不足。

各种直线形乘直线形，都可以用该公式处理。如竖标在基×4×3+6×3－4×2）=15
（1）
2
（2）
3
4
4
6
6
3 2
9
9
S = 9/6 ×（2×6×2+2×4×3－6×3－4×2）= 33
（3）
2
6
3 S = 9/6×（－2×6×2+2×0×3 +6×3－0×2） = －9
C为实际状态的支座位移， R C 为反力虚功。
当 R 与实际支座位移C的方向一致时其乘
积取正，相反时取负。
此外，上式右边前面还有一个负号， 不可漏掉。
例
DB = EI 3
2
l l= 4 8EI
二、图乘技巧
1、当图乘法的适用条件不满足时的处理方法（分段）
P
1
A
EI
BA
EI
B
C
C
l/2
Pl/4 l/2
l/2
l/4 l/2
Dc
=
2
1 EI

1 2

l 2

Pl 4

2 3

l 4
=
Pl 3 48 EI
a）曲杆或 EI=EI （ x）时，只能用积 分法求位移；
y0 ω
③ S=ωy0 （×）
ω y0
⑥ S=ωy0 （√ ）
三、练习 图乘法的步骤
例1
[1] 设虚拟状态； [2] 画 M P 图；M 图； [3] 图乘求位移。
例2
三、 静定结构由于支座位移所引起的位移
静定结构由于支座移动并不产生内力也无变形，只发生刚体位移。 如图 a所示静定结构,其支座发生水平位移C1 、竖向位移C2 和转角C3， 现要求由此引起的任一点沿任一方向的位移，例如求k点竖向位移ΔK