计量经济学实验二 一元线性回归 2

计量经济学上机实验上机实验一：一元线性回归模型实验目的：EViews软件的基本操作实验内容：对线性回归模型进行参数估计并进行检验上机步骤：中国内地2011年中国各地区城镇居民每百户计算机拥有量和人均总收入一．建立工作文件：1.在主菜单上点击File\New\Workfile；2.选择时间频率，A3.键入起始期和终止期，然后点击OK；二．输入数据:1.键入命令：DATA Y X2.输入每个变量的统计数据；3.关闭数组窗口（回答Yes）;三．图形分析：1.趋势图：键入命令PLOT Y X2.相关图：键入命令 SCAT Y X 散点图：趋势图：上机结果：Yˆ11.958+0.003X=s (βˆ) 5.6228 0.0002t (βˆ) 2.1267 11.9826prob 0.0421 0.00002=0.831 R2=0.826 FR=143.584 prob(F)=0.0000上机实验二：多元线性回归模型实验目的：多元回归模型的建立、比较与筛选，掌握基本的操作要求并能根据理论对分析结果进行解释实验内容：对线性回归模型进行参数估计并进行检验上机步骤：商品的需求量与商品价格和消费者平均收入趋势图：散点图：上机结果:i Yˆ=132.5802-8.878007X1-0.038888X2s (βˆ) 57.118 4.291 0.419t (βˆ) 2.321 -2.069 -0.093prob 0.0533 0.0773 0.9286 R2=0.79 R2=0.73 F =13.14 prob(F)=0.00427三：非线性回归模型实验目的：EViews软件的基本操作实验内容：对线性回归模型进行参上机步骤：我国国有独立核算工业企业统计资料一．建立工作文件：1.在主菜单上点击File\New\Workfile；2.选择时间频率，A3.键入起始期和终止期，然后点击OK；二．输入数据:1.键入命令：DATA Y L K2.输入每个变量的统计数据；3.关闭数组窗口（回答Yes）;三．图形分析：1.趋势图：键入命令PLOT Y K L2.相关图：键入命令 SCAT Y K L四．估计回归模型：键入命令LS Y C K L上机结果：Y =4047.866K1.262204L-1.227157s (βˆ) 17694.18 0232593 0.759696t (βˆ) 0.228768 5.426669 -1.615325prob 0.8242 0.0004 0.1407R2=0.989758 R2=0.987482 F=434.8689 prob(F)=0.0000上机实验四：异方差实验目的：：掌握异方差的检验与调整方法的上机实现实验内容：我国制造工业利润函数行业销售销售行业销售销售实验步骤：一．检验异方差性1．图形分析检验：1) 观察Y、X相关图：SCAT Y X2) 残差分析:观察回归方程的残差图LS Y C X在方程窗口上点击Residual按钮；2． Goldfeld-Quant检验：SORT XSMPL 1 10LS Y C X（计算第一组残差平方和）SMPL 19 28LS Y C X（计算第二组残差平方和）计算F统计量，判断异方差性3．White检验：SMPL 1 28LS Y C X在方程窗口上点击：View\Residual\Test\White Heteroskedastcity 由概率值判断异方差性。

《计量经济学》实验报告一元线性回归模型
三、实验步骤（简要写明实验步骤）
1、数据的输入、编辑
2、图形分析与描述统计分析
3、数据文件的存贮、调用
4、一元线性回归的过程
点击view中的Graph-scatter-中的第三个获得
在上方输入ls y c x回车得到下图
在上图中view处点击view-中的actual，Fitted，Residual中的第一个得到回归残差
打开Resid中的view-descriptive statistics得到残差直方图
打开工作文件第二个中的structure将workfiels选中第一个，将右边改为16个
之后打开工作文件xy右键双击，open-as grope
在回归方程中有Forecast，残差立为yfse，点击ok后自动得到下图
在上方空白处输入ls y c s---之后点击proc 中的forcase 根据
公式)|(0^
0X Y Y E 得到2015估计量
四、实验结果及分析（将本问题的回归模型写出，并作出经济意义检。

计量经济学试验（完整版）-—李子奈ﻬ目录实验一一元线性回归ﻩ错误!未定义书签。

一实验目得..................................... 错误!未定义书签。

二实验要求.................................... 错误!未定义书签。

三实验原理ﻩ错误!未定义书签。

四预备知识ﻩ错误!未定义书签。

五实验内容ﻩ错误!未定义书签。

六实验步骤..................................... 错误!未定义书签。

1、建立工作文件并录入数据................... 错误!未定义书签。

2、数据得描述性统计与图形统计: .............. 错误!未定义书签。

3、设定模型，用最小二乘法估计参数：ﻩ错误!未定义书签。

４、模型检验: ............................... 错误!未定义书签。

5、应用：回归预测：ﻩ错误!未定义书签。

实验二可化为线性得非线性回归模型估计、受约束回归检验及参数稳定性检验............................... 错误!未定义书签。

一实验目得：ﻩ错误!未定义书签。

二实验要求..................................... 错误!未定义书签。

三实验原理..................................... 错误!未定义书签。

四预备知识.................................... 错误!未定义书签。

五实验内容ﻩ错误!未定义书签。

六实验步骤ﻩ错误!未定义书签。

实验三多元线性回归...................... 错误!未定义书签。

一实验目得..................................... 错误!未定义书签。

三实验原理ﻩ错误!未定义书签。

四预备知识.................................... 错误!未定义书签。

第二章经典单方程计量经济学模型：一元线性回归模型一、内容提要本章介绍了回归分析的基本思想与基本方法。

首先，本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始，建立了回归分析的基本思想。

总体回归函数是对总体变量间关系的定量表述，由总体回归模型在若干基本假设下得到，但它只是建立在理论之上，在现实中只能先从总体中抽取一个样本，获得样本回归函数，并用它对总体回归函数做出统计推断。

本章的一个重点是如何获取线性的样本回归函数，主要涉及到普通最小二乘法（OLS）的学习与掌握。

同时，也介绍了极大似然估计法（ML）以及矩估计法（MM）。

本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断，即进行所谓的统计检验。

统计检验包括两个方面，一是先检验样本回归函数与样本点的“拟合优度”，第二是检验样本回归函数与总体回归函数的“接近”程度。

后者又包括两个层次：第一，检验解释变量对被解释变量是否存在着显著的线性影响关系，通过变量的t检验完成；第二，检验回归函数与总体回归函数的“接近”程度，通过参数估计值的“区间检验”完成。

本章还有三方面的内容不容忽视。

其一，若干基本假设。

样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。

其二，参数估计量统计性质的分析，包括小样本性质与大样本性质，尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。

Goss-markov定理表明OLS估计量是最佳线性无偏估计量。

其三，运用样本回归函数进行预测，包括被解释变量条件均值与个值的预测，以及预测置信区间的计算及其变化特征。

二、典型例题分析例1、令kids表示一名妇女生育孩子的数目，educ表示该妇女接受过教育的年数。

生育率对教育年数的简单回归模型为β+μβkids=educ+1（1）随机扰动项μ包含什么样的因素？它们可能与教育水平相关吗？（2）上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。

XX实验指导书《计量经济学》编写人：XX实验一 EViews软件的基本操作【实验目的】通过上机试验，了解EViews软件特点、工作窗口的组成、充分掌握EViews软件的基本操作、熟悉数据处理、统计分析（图形分析）【实验内容】EViews是专门用于从事数据分析、回归分析和预测的工具，使用EViews可以迅速从数据中找出统计关系，并用得到的关系去预测数据的未来值。

最小二乘估计是估计变量间线形关系中相互作用与影响的有效方法，在数据分析中有很重要的作用。

本次试验内容包括：进行EViews的一些基本操作来熟悉这个软件。

实验内容以表1-1所列出的税收收入和国内生产总值的统计资料为例进行操作。

表1-1 我国税收与GDP统计资料单位：亿元资料来源：《中国统计年鉴1999》【实验步骤】一、数据的输入、编辑与序列生成㈠创建工作文件⒈菜单方式启动EViews软件之后，进入EViews主窗口。

在主菜单上依次点击File/New/Workfile，即选择新建对象的类型为工作文件，将弹出一个对话框，由用户选择数据的时间频率（frequency）、起始期和终止期。

其中， Annual——年度 Monthly——月度Semi-annual——半年 Weekly——周Quarterly——季度 Daily——日Undated or irregular——非时序数据选择时间频率为Annual（年度），再分别点击起始期栏（Start date）和终止期栏（End date），输入相应的日前1985和1998。

然后点击OK按钮，将在EViews软件的主显示窗口显示相应的工作文件窗口。

工作文件窗口是EViews的子窗口，工作文件一开始其中就包含了两个对象，一个是系数向量C （保存估计系数用），另一个是残差序列RESID（实际值与拟合值之差）。

⒉命令方式在EViews软件的命令窗口中直接键入CREATE命令，也可以建立工作文件。

命令格式为：CREATE 时间频率类型起始期终止期则以上菜单方式过程可写为：CREATE A 1985 1998㈡输入Y、X的数据⒈DATA命令方式在EViews软件的命令窗口键入DATA命令，命令格式为：DATA <序列名1> <序列名2>…<序列名n>本例中可在命令窗口键入如下命令：DATA Y X将显示一个数组窗口，此时可以按全屏幕编辑方式输入每个变量的统计资料。

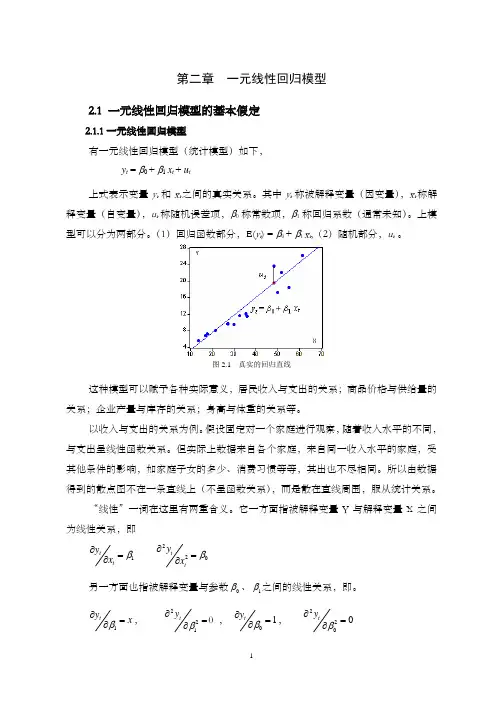
第二章 一元线性回归模型2.1 一元线性回归模型的基本假定2.1.1一元线性回归模型有一元线性回归模型（统计模型）如下， y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。

其中y t 称被解释变量（因变量），x t 称解释变量（自变量），u t 称随机误差项，β0称常数项，β1称回归系数（通常未知）。

上模型可以分为两部分。

（1）回归函数部分，E(y t ) = β0 + β1 x t ,（2）随机部分，u t 。

图2.1 真实的回归直线这种模型可以赋予各种实际意义，居民收入与支出的关系；商品价格与供给量的关系；企业产量与库存的关系；身高与体重的关系等。

以收入与支出的关系为例。

假设固定对一个家庭进行观察，随着收入水平的不同，与支出呈线性函数关系。

但实际上数据来自各个家庭，来自同一收入水平的家庭，受其他条件的影响，如家庭子女的多少、消费习惯等等，其出也不尽相同。

所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周围，服从统计关系。

“线性”一词在这里有两重含义。

它一方面指被解释变量Y 与解释变量X 之间为线性关系，即1tty x β∂=∂220tt y x β∂=∂另一方面也指被解释变量与参数0β、1β之间的线性关系，即。

1ty x β∂=∂，221ty β∂=∂0 ，1ty β∂=∂，2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同，消费习惯不同，不同地域的消费指数不同，不同家庭的外来收入不同等因素。

所以在经济问题上“控制其他因素不变”是不可能的。

随机误差项u t 正是计量模型与其它模型的区别所在，也是其优势所在，今后咱们的很多内容，都是围绕随机误差项u t 进行了。

回归模型的随机误差项中一般包括如下几项内容： （1）非重要解释变量的省略， （2）数学模型形式欠妥， （3）测量误差等，（4）随机误差（自然灾害、经济危机、人的偶然行为等）。

目录一、加载工作文件 (7)二、选择方程 (7)1.作散点图 (7)2.进行因果关系检验 (9)三、一元线性回归 (10)四、经济检验 (12)五、统计检验 (13)六、回归结果的报告 (15)七、得到解释变量的值 (15)八、预测应变量的值 (17)实验二一元线形回归模型的估计、检验和预测实验目的：掌握一元线性回归模型的估计、检验和预测方法。

实验要求：选择方程进行一元线性回归，进行经济、拟合优度、参数显著性和方程显著性等检验，预测解释变量和应变量。

实验原理：普通最小二乘法，拟合优度的判定系数R2检验和参数显著性t检验等，计量经济学预测原理。

实验步骤：已知广东省宏观经济部分数据如表2-1所示，要根据这些数据研究和分析广东省宏观经济，建立宏观计量经济模型，从而进行经济预测、经济分析和政策评价。

实验二~实验十二主要都是用这些数据来完成一系列工作。

表2-1 广东省宏观经济数据续上表续上表一、加载工作文件广东省宏观经济数据已经制成工作文件存在盘中，命名为GD01.WF1，进入EViews后选择File/Open打开GD01.WF1。

二、选择方程根据广东数据（GD01.WF1）选择收入法国国内生产总值（GDPS）、财政收入（CS）、财政支出（CZ）和社会消费品零售额（SLC），分别把①CS作为应变量，GDPS作为解释变量；②CZ作为应变量，CS作为解释变量；③SLC作为应变量，GDPS作为解释变量进行一元线性回归分析。

1.作散点图从三个散点图（图2-1~图2~3）可以看出，三对变量都呈现线性关系。

图2-1 图2-2图2-3 2.进行因果关系检验从三个因果关系检验可以看出，GDPS是CS的因；CS不是CZ 的因；GDPS不是SLC的因。

但根据理论CS是CZ的因，GDPS是SLC的因，可能是由于指标设置问题。

所以还是把CS作为应变量，GDPS作为解释变量；CZ作为应变量，CS作为解释变量；SLC作为应变量，GDPD作为解释变量进行一元线性回归分析。

实验二一元线性回归模型2.1 实验目的掌握一元线性回归模型的基本理论，一元线性回归模型的建立、估计、检验及预测的方法，以及相应的EViews软件操作方法。

2.2 实验内容建立中国消费函数模型。

以表2.1中国的收入与消费的总量数据为基础，建立中国消费函数的一元线性回归模型。

表2.1数据来源：2004年中国统计年鉴，中国统计出版社2.3 实验步骤2.3.1 散点相关图分析将表1.1的GDP设为变量X，总消费设为Y，建立变量X和Y的相关图，如图2.1所示。

可以看X和Y之间呈现良好的线性关系。

可以建立一元线性回归模型。

2.3.2 估计线性回归模型在数组窗口中点击Proc\Make Equation ，如果不需要重新确定方程中的变量或调整样本区间，可以直接点击OK 进行估计。

也可以在EViews 主窗口中点击Quick\Estimate Equation ，在弹出的方程设定框（见图2.2）内输入模型：Y C X 或 Y = C (1) + C (2) * X图2.2图2.3还可以通过在EViews 命令窗口中键入LS 命令来估计模型，其命令格式为：LS 被解释变量 C 解释变量系统将弹出一个窗口来显示有关估计结果（如图2.3 所示）。

因此，我国消费函数的估计式为：ˆY2329.4010.547*X =+St 1191.923 0.014899t 1.95 36.71R 2=0.99 s.e.=2091s.e .是回归函数的标准误差，即σˆ=)216(ˆ2-∑t u。

R 2是可决系数。

R 2 = 0.99,说明上式的拟合情况好，y t 变差的99%由变量x t 解释。

因为t = 36.71> t 0.05 (15) = 2.13，所以检验结果是拒绝原假设β1 = 0，即总消费和GDP 之间存在线性回归关系。

上述模型的经济解释是，GDP 每增长1 亿元，我国消费将总额将增加0.547亿元。

图2.42.3.3 残差图在估计方程的窗口选择View\ Actual, Fitted,Residual\Actual, Fitted,Residual Table，得到相应的残差图2.4。

《计量经济学》上机实验参考答案实验一：线性回归模型的估计、检验和预测（3 课时）实验设备：个人计算机，计量经济学软件Eviews，外围设备如U 盘。

实验目的：（1）熟悉Eviews 软件基本使用功能；（2）掌握一元线性回归模型的估计、检验和预测方法；正态性检验；（3）掌握多元线性回归模型的估计、检验和预测方法；（4）掌握多元非线性回归模型的估计方法；（5）掌握模型参数的线性约束检验与参数的稳定性检验。

实验方法与原理：Eviews 软件使用，普通最小二乘法（OLS），拟合优度评价、t 检验、F 检验、J-B 检验、预测原理。

实验要求：（1）熟悉和掌握描述统计和线性回归分析；（2）选择方程进行一元线性回归；（3）选择方程进行多元线性回归；（4）进行经济意义检验、拟合优度评价、参数显著性检验和回归方程显著性检验；（5）掌握被解释变量的点预测和区间预测；（6）估计对数模型、半对数模型、倒数模型、多项式模型模型等非线性回归模型。

实验内容与数据1（第2 章思考与练习：三、简答、分析与计算题第12 小题）：12. 表1 数据是从某个行业的5 个不同的工厂收集的，请回答以下问题：ˆˆˆˆ（1）估计这个行业的线性总成本函数：yˆt= b0 + b1 x t ；（2）b0 和b1 的经济含义是什么？；（3）估计产量为10 时的总成本。

表1 某行业成本与产量数据参考答案：(1)总成本函数(标准格式)：yˆt = 26.27679 + 4.25899xts = (3.211966) (0.367954)t = (8.180904) (11.57462)R 2 = 0.978098 S.E = 2.462819 DW =1.404274 F =133.9719ˆˆ(2) b0 =26.27679 为固定成本，即产量为0 时的成本；b1 =4.25899 为边际成本，即产量每增加1 单位时，总成本增加了4.25899 单位。

计量经济学第二章一元线性回归模型第二章一元线性回归模型第一节一元线性回归模型及其古典假定第二节参数估计第三节最小二乘估计量的统计特性第四节统计显著性检验第五节预测与控制第一节回归模型的一般描述（1）确定性关系或函数关系：变量之间有唯一确定性的函数关系。

其一般表现形式为：一、回归模型的一般形式变量间的关系经济变量之间的关系，大体可分为两类：（2.1)（2）统计关系或相关关系：变量之间为非确定性依赖关系。

其一般表现形式为：(2.2)例如：函数关系：圆面积S =统计依赖关系/统计相关关系：若x和y之间确有因果关系，则称(2.2)为总体回归模型，x(一个或几个）为自变量（或解释变量或外生变量），y为因变量（或被解释变量或内生变量），u为随机项，是没有包含在模型中的自变量和其他一些随机因素对y的总影响。

一般说来，随机项来自以下几个方面：1、变量的省略。

由于人们认识的局限不能穷尽所有的影响因素或由于受时间、费用、数据质量等制约而没有引入模型之中的对被解释变量有一定影响的自变量。

2、统计误差。

数据搜集中由于计量、计算、记录等导致的登记误差；或由样本信息推断总体信息时产生的代表性误差。

3、模型的设定误差。

如在模型构造时，非线性关系用线性模型描述了；复杂关系用简单模型描述了；此非线性关系用彼非线性模型描述了等等。

4、随机误差。

被解释变量还受一些不可控制的众多的、细小的偶然因素的影响。

若相互依赖的变量间没有因果关系，则称其有相关关系。

对变量间统计关系的分析主要是通过相关分析、方差分析或回归分析(regression analysis)来完成的。

他们各有特点、职责和分析范围。

相关分析和方差分析本身虽然可以独立的进行某些方面的数量分析，但在大多数情况下，则是和回归分析结合在一起，进行综合分析，作为回归分析方法的补充。

回归分析(regression analysis)是研究一个变量关于另一个（些）变量的具体依赖关系的计算方法和理论。

第2章 一元线性回归模型一、单项选择题1、变量之间的关系可以分为两大类。

A 函数关系与相关关系B 线性相关关系和非线性相关关系C 正相关关系和负相关关系D 简单相关关系和复杂相关关系 2、相关关系是指。

A 变量间的非独立关系B 变量间的因果关系C 变量间的函数关系D 变量间不确定性的依存关系 3、进行相关分析时的两个变量。

A 都是随机变量B 都不是随机变量C 一个是随机变量，一个不是随机变量D 随机的或非随机都可以 4、表示x 和y 之间真实线性关系的是。

A 01ˆˆˆt tY X ββ=+ B 01()t t E Y X ββ=+ C 01t t t Y X u ββ=++ D 01t t Y X ββ=+5、参数β的估计量ˆβ具备有效性是指。

A ˆvar ()=0βB ˆvar ()β为最小C ˆ()0ββ－＝ D ˆ()ββ－为最小 6、对于01ˆˆi i i Y X e ββ=++，以σˆ表示估计标准误差，Y ˆ表示回归值，则。

A i i ˆˆ0Y Y 0σ∑＝时，（－）＝B 2iiˆˆ0Y Y σ∑＝时，（－）＝0 C ii ˆˆ0Y Y σ∑＝时，（－）为最小 D 2iiˆˆ0Y Yσ∑＝时，（－）为最小 7、设样本回归模型为i 01i i ˆˆY =X +e ββ+，则普通最小二乘法确定的i ˆβ的公式中，错误的是。

A ()()()i i 12iX X Y -Y ˆX X β--∑∑＝B()i iii122iin X Y -X Y ˆn X -X β∑∑∑∑∑＝C ii122iX Y -nXY ˆX -nXβ∑∑＝ D i i ii12xn X Y -X Y ˆβσ∑∑∑＝8、对于i 01i iˆˆY =X +e ββ+，以ˆσ表示估计标准误差，r 表示相关系数，则有。

A ˆ0r=1σ＝时， B ˆ0r=-1σ＝时， C ˆ0r=0σ＝时， D ˆ0r=1r=-1σ＝时，或 9、产量（X ，台）与单位产品成本（Y ，元/台）之间的回归方程为ˆY 356 1.5X -＝，这说明。