4.程序框图的画法习题课

A．计算小于 100 的奇数的连乘积 B．计算从 1 开始的连续奇数的连乘积 C．从 1 开始的连续奇数的连乘积，当乘积大于或等于 100 时，计算奇数的个数 D．计算 1×3×5×…×n≥100 时的最小的 n 值 解析：选 D 这是一个直到型循环结构，S＝1×3×5×…，判断条件是 S≥100？，输 出的是 i，所以表示的是 S＝1×3×5×…×n≥100 时的最小的 n 值，故选 D. 7．执行如图所示的程序框图，若输出的 a 值大于 2 015，那么判断框内的条件应为 ________．
先判断条件，若条件满足，则执行 循环体，否则终止循环.
(3)设计算法程序框图的步骤
①用自然语言表述算法步骤．
②确定每一个算法步骤所包含的逻辑结构，并用相应的程序框图表示，得到该步骤的程
序框图．
③将所有步骤的程序框图用流程线连接起来，并加上终端框，得到表示整个算法的程序
框图．
1
[问题思考]
(1)循环结构中一定包含条件结构吗？ 提示：循环结构是在一些算法中从某处开始，按照一定条件反复执行处理某一步骤，因 此循环结构一定包含条件结构． (2)循环结构中的判断框中的条件是唯一的吗？ 提示：不是，在具体的程序框图设计时，这里的条件可以不同，但不同表示应该有共同 的确定的结果． (3)举例说明循环结构适用哪些常见的计算？ 提示：循环结构主要用在一些有规律的重复计算中，如累加求和，累乘求积等问题．
6
(1)两种循环的转化易弄错，如讲 1； (2)控制循环的条件易弄错，如讲 2(3)．
课下能力提升(四) [学业水平达标练] 题组 1 循环结构及两种循环结构 1．下列框图是循环结构的是( )
A．①② B．②③ C．③④ D．②④ 答案：C 2．一个完整的程序框图至少包含( ) A．起止框和输入、输出框 B．起止框和处理框 C．起止框和判断框 D．起止框、处理框和输入、输出框 解析：选 A 一个完整的程序框图至少包括起止框和输入、输出框，故选 A. 3．(2016·安徽巢湖检测)如图所示是一个循环结构的算法，下列说法不正确的是( )

否 否
n是质数
循直环到结型构循 环结构
条件结构
结束
例3. 某高中男子体育小组的50m跑成绩(单位:s)为: 6.4, 6.5, 7.0, 6.8, 7.1, 7.3, 6.9, 7.4, 7.5.
设计一个算法,从这些成绩中搜出小于6.8s的成绩.
算法分析:
第一步, n=1.
第二步, 输入一个成绩r,判断r与6.8的大小.若 r≥6.8,则执行下一步;若r<6.8,则输出r,并执行下 一步.
97.有三个人是我的朋友爱我的人.恨我的人.以及对我冷漠的人。 爱我的人教我温柔；恨我的人教我谨慎；对我冷漠的人教我自立。――[J·E·丁格] 98.过去的事已经一去不复返。聪明的人是考虑现在和未来，根本无暇去想过去的事。――[英国哲学家培根] 99.真正的发现之旅不只是为了寻找全新的景色，也为了拥有全新的眼光。――[马塞尔·普劳斯特] 100.这个世界总是充满美好的事物，然而能看到这些美好事物的人，事实上是少之又少。――[罗丹] 101.称赞不但对人的感情，而且对人的理智也发生巨大的作用，在这种令人愉快的影响之下，我觉得更加聪明了，各种想法，以异常的速度接连涌入我的脑际。――[托尔斯泰] 102.人生过程的景观一直在变化，向前跨进，就看到与初始不同的景观，再上前去，又是另一番新的气候――。[叔本华] 103.为何我们如此汲汲于名利，如果一个人和他的同伴保持不一样的速度，或许他耳中听到的是不同的旋律，让他随他所听到的旋律走，无论快慢或远近。――[梭罗] 104.我们最容易不吝惜的是时间，而我们应该最担心的也是时间；因为没有时间的话，我们在世界上什么也不能做。――[威廉·彭] 105.人类的悲剧，就是想延长自己的寿命。我们往往只憧憬地平线那端的神奇【违禁词，被屏蔽】，而忘了去欣赏今天窗外正在盛开的玫瑰花。――[戴尔·卡内基] 106.休息并非无所事事，夏日炎炎时躺在树底下的草地，听着潺潺的水声，看着飘过的白云，亦非浪费时间。――[约翰·罗伯克] 107.没有人会只因年龄而衰老，我们是因放弃我们的理想而衰老。年龄会使皮肤老化，而放弃热情却会使灵魂老化。――[撒母耳·厄尔曼] 108.快乐和智能的区别在于：自认最快乐的人实际上就是最快乐的，但自认为最明智的人一般而言却是最愚蠢的。――[卡雷贝·C·科尔顿] 109.每个人皆有连自己都不清楚的潜在能力。无论是谁，在千钧一发之际，往往能轻易解决从前认为极不可能解决的事。――[戴尔·卡内基] 110.每天安静地坐十五分钟·倾听你的气息，感觉它，感觉你自己，并且试着什么都不想。――[艾瑞克·佛洛姆] 111.你知道何谓沮丧---就是你用一辈子工夫，在公司或任何领域里往上攀爬，却在抵达最高处的同时，发现自己爬错了墙头。－－[坎伯] 112.「伟大」这个名词未必非出现在规模很大的事情不可；生活中微小之处，照样可以伟大。――[布鲁克斯] 113.人生的目的有二：先是获得你想要的；然后是享受你所获得的。只有最明智的人类做到第二点。――[罗根·皮沙尔·史密斯] 114.要经常听.时常想.时时学习，才是真正的生活方式。对任何事既不抱希望，也不肯学习的人，没有生存的资格。

一般地，一个算法的程序框图有以下几个步骤：
第一步：用自然语言表述算法步骤. 第二步：确定每一个算法步骤所包含的逻辑结构，并 用相应的程序框图表示，得到该步骤的程序框图.
第三步：将所有步骤的程序框图用流程线连接起 来， 并加上终端框，得到表示整个算法的程序框图.
2020/5/1
1
14
P19)设计一个用有理指数幂逼近无理指数幂 5 2的算法，并 估计 5 2 的近似值，画出算法的程序框图.
2020/5/1
a 300?
直到型循环结构
1
7
开始
n 2005
a 200
t 0.05a
aat
n n1
否
a 300?
是
输出 n
结束
2020/5/1
直 到 型 循 环 结 构
当 型 循 环 结 构
1
开始 n 2005 a 200
n n1
aat
a 300?
否
输出 n
结束
t 0.05a
是
2020/5/1
1
1
知识回顾
1、顺序结构
由若干个依次执行的步骤组成的结构.它是任何 一个算法都离不开的结构.
步骤n
步骤n＋1
2020/5/1
1
2
知识回顾
(2)条件结构
满足条件？
是
步骤A
否
步骤B
满足条件？ 否
是
步骤A
2020/5/1
1
3
知识回顾
(3)循环结构
循环结构分为当型循环结构和直到型循环结构
含零点的区间为 [m,b].将新得到的含零点的区间仍记为[a,b].
第五步：判断 [a,b] 的长度是否小于d或f(m)是否等于0． 若是，则m是方程的近似值；否则，返回第三步．

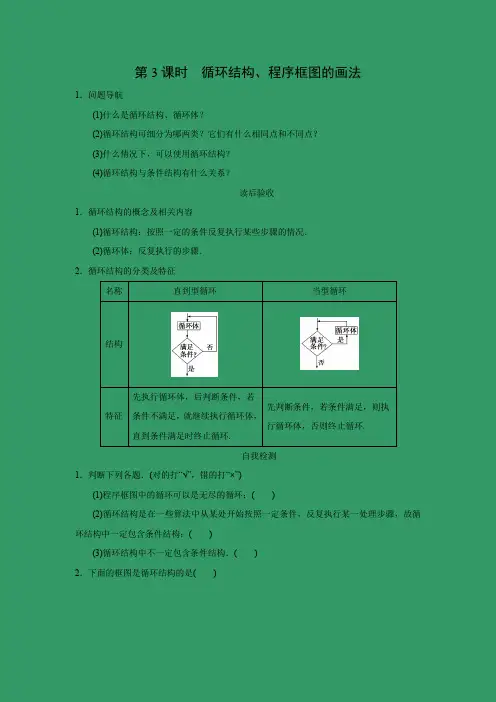
第3课时循环结构、程序框图的画法1．问题导航(1)什么是循环结构、循环体？(2)循环结构可细分为哪两类？它们有什么相同点和不同点？(3)什么情况下，可以使用循环结构？(4)循环结构与条件结构有什么关系？读后验收1．循环结构的概念及相关内容(1)循环结构：按照一定的条件反复执行某些步骤的情况．(2)循环体：反复执行的步骤．2．循环结构的分类及特征名称直到型循环当型循环结构特征先执行循环体，后判断条件，若条件不满足，就继续执行循环体，直到条件满足时终止循环.先判断条件，若条件满足，则执行循环体，否则终止循环.自我检测1．判断下列各题．(对的打“√”，错的打“×”)(1)程序框图中的循环可以是无尽的循环；()(2)循环结构是在一些算法中从某处开始按照一定条件，反复执行某一处理步骤，故循环结构中一定包含条件结构；()(3)循环结构中不一定包含条件结构．()2．下面的框图是循环结构的是()A．①②B．②③C．③④D．②④3．运行如图所示的程序框图，输出的结果为________．4．举例说明循环结构适用哪些常见的计算？名师点睛1．算法的基本逻辑结构有三种，即顺序结构、条件结构和循环结构．其中顺序结构是最简单的结构，也是最基本的结构，循环结构必然包含条件结构，所以这三种基本逻辑结构是相互支撑的，它们共同构成了算法的基本结构，无论怎样复杂的逻辑结构，都可以通过这三种结构来表达．2．两种循环结构的相同点：从两种不同形式的循环结构可以看出，循环结构中一定包含条件结构，用于确定何时终止执行循环体．3．如果算法问题里涉及的运算进行了许多次重复的操作，且先后参与运算的数之间有相同的规律，就可引入变量循环参与运算(我们称之为循环变量)，应用于循环结构．在循环结构中，要注意根据条件设计合理的计数变量、累加和累乘变量等，特别要求条件的表述要恰当、精确．题型探究探究一循环结构程序框图的设计例1 设计一个算法，求13＋23＋…＋993＋1003的值，并画出程序框图． 跟踪训练1．(1)如图所示程序框图输出的结果是( )A ．8B ．9C ．10D ．11(2)设计求1×2×3×4×…×2 015的程序框图． 探究二利用循环结构求满足条件的数值例2 求满足1＋12＋13＋14＋…＋1n >2的最小正整数n ，写出算法，并画出程序框图．跟踪训练2．(1)某程序框图如图所示，则该程序的算法功能是________．(2)已知1＋2＋3＋4＋…＋i ≤200，画出求i 的最大值的程序框图．探究三循环结构的实际应用例3 某工厂2014年生产小轿车200万辆，技术革新后预计每年的生产能力比上一年增加5%，问最早哪一年该厂生产的小轿车数量超过300万辆？写出解决该问题的一个算法，并画出相应的程序框图．跟踪训练3．(1)小红今年12岁，她父亲比她大25岁，设计程序框图，计算出几年后她父亲比她的年龄大一倍，那时他们两人的年龄各是多少？(2)某城市现有人口总数为100万人，如果年自然增长率为1.2%，试解答下列问题：①写出该城市人口数y(万人)与年份x(年)的函数关系式；②用流程图表示如下算法：计算大约多少年以后该城市人口将达到120万人．当堂检测1.如图所示的程序框图中，语句“S＝S×n”将被执行的次数是()A．4 B．5C．6 D．72．如图所示的程序框图表示的算法功能是()A．计算小于100的奇数的连乘积B．计算从1开始的连续奇数的连乘积C．从1开始的连续奇数的连乘积，当乘积大于或等于100时，计算奇数的个数D．计算1×3×5×…×n≥100时的最小的n值3．如图所示的程序框图的输出结果为－18，那么在判断框中①表示的条件应该是()A．i≥9? B．i≥8?C．i≥7? D．i≥6?4．如图是一个算法流程图，则输出的n的值是________．参考答案自我检测1.【解析】程序框图中的循环，必须是有限循环；循环结构一定包含条件结构．【答案】(1)×(2)√(3)×2.【解析】选C.由循环结构的特点知③④是循环结构，其中①是顺序结构，②是条件结构．【答案】C3.【解析】n＝1；S＝1＋0＝1，n＝2；S＝3，n＝3；S＝6，n＝4；S＝10，n＝5；S＝15，n ＝6；S＝21，n＝7；S＝28，n＝8.【答案】284.解：循环结构主要用在一些有规律的重复计算中，如累加求和，累乘求积等问题．例1 解：算法如下：第一步，使S＝0.第二步，使I＝1.第三步，使S＝S＋I3.第四步，使I＝I＋1.第五步，若I≤100，则返回第三步；否则，输出S，算法结束．程序框图如图所示．跟踪训练1．（1）【解析】选D.当i＝11时，不满足条件即输出．【答案】D（2）解：程序框图如图所示：例2 解：算法如下：第一步，S＝0；第二步，i ＝1； 第三步，S ＝S ＋1i ；第四步，i ＝i ＋1；第五步，若S ＞2，则输出i －1，否则返回第三步，循环结束． 程序框图如图所示：跟踪训练2．(1)【解析】由程序框图可知，输出的i 是满足1×3×5×7×…×n >50 000的最小正整数n .【答案】求满足1×3×5×7×…×n >50 000的最小正整数n (2)解：程序框图如图所示．例3解：算法如下：第一步，令n ＝0，a ＝200，r ＝0.05； 第二步，T ＝ar (计算年增量)； 第三步，a ＝a ＋T (计算年产量)；第四步，如果a ≤300，那么n ＝n ＋1，返回第二步；否则执行第五步； 第五步，N ＝2014＋n ；第六步，输出N.程序框图如图所示：跟踪训练3．(1)解：程序框图如图所示．(2)解：①y＝100(1＋1.2%)x；②程序框图如图：1.【解析】选B.由程序框图知：S＝1×2×3×…×n.又1×2×3×4×5＝120＜200，1×2×3×4×5×6＝720＞200.故语句“S＝S×n”被执行了5次．【答案】2.【解析】选D.这是一个直到型循环结构，S＝1×3×5×…，判断条件是S≥100？，输出的是i，所以表示的是S＝1×3×5×…×n≥100时的最小的n值，故选D.【答案】D3.【解析】选A.当S＝6，i＝1时，m＝－2×1＋6＝4，S＝6＋4＝10；当i＝2时，m＝－2×2＋6＝2，S＝10＋2＝12；当i＝3时，m＝－2×3＋6＝0，S＝0＋12＝12；当i＝4时，m＝－2×4＋6＝－2，S＝－2＋12＝10；当i＝5时，m＝－2×5＋6＝－4，S＝－4＋10＝6；当i＝6时，m＝－2×6＋6＝－6，S＝－6＋6＝0；当i＝7时，m＝－2×7＋6＝－8，S＝－8＋0＝－8；当i＝8时，m＝－2×8＋6＝－10，S＝－10－8＝－18.故判断条件为：i≥9？，故选A.【答案】A4.【解析】由算法流程图可知：第一次循环：n＝1，2n＝2<20，不满足要求，进入下一次循环；第二次循环：n＝2，2n＝4<20，不满足要求，进入下一次循环；第三次循环：n＝3，2n＝8<20，不满足要求，进入下一次循环；第四次循环：n＝4，2n＝16<20，不满足要求，进入下一次循环；第五次循环：n＝5，2n＝32>20，满足要求，输出n＝5.【答案】5。

高一数学《程序框图习题课》
36、如果我们国家的法律中只有某种 神灵， 而不是 殚精竭 虑将神 灵揉进 宪法， 总体上 来说， 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日，便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持，法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例，它们 迅速累 聚，进 而变成 法律。 ——朱 尼厄斯
40、学而不思则罔，思而不学则殆。——孔子
40、人类法律，事物有规律，这是不 容忽视 的。— —爱献 生
ห้องสมุดไป่ตู้
谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳

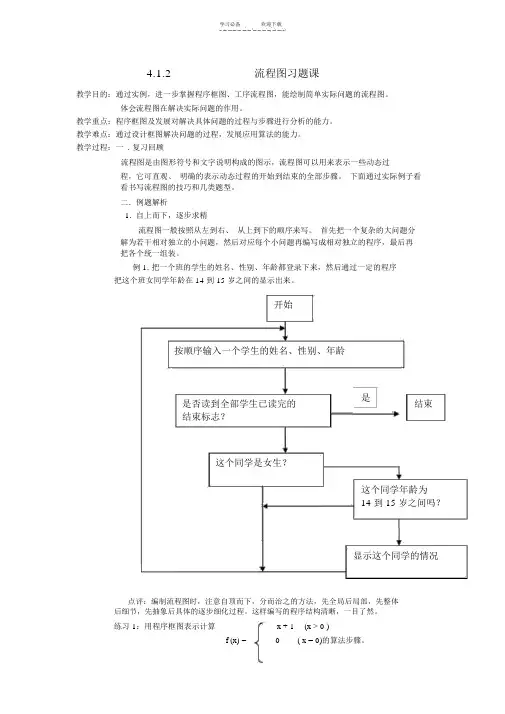
学习必备欢迎下载4.1.2流程图习题课教学目的：通过实例，进一步掌握程序框图、工序流程图，能绘制简单实际问题的流程图。

体会流程图在解决实际问题的作用。

教学重点：程序框图及发展对解决具体问题的过程与步骤进行分析的能力。

教学难点：通过设计框图解决问题的过程，发展应用算法的能力。

教学过程：一 . 复习回顾流程图是由图形符号和文字说明构成的图示，流程图可以用来表示一些动态过程，它可直观、明确的表示动态过程的开始到结束的全部步骤。

下面通过实际例子看看书写流程图的技巧和几类题型。

二．例题解析1.自上而下，逐步求精流程图一般按照从左到右、从上到下的顺序来写。

首先把一个复杂的大问题分解为若干相对独立的小问题，然后对应每个小问题再编写成相对独立的程序，最后再把各个统一组装。

例 1. 把一个班的学生的姓名、性别、年龄都登录下来，然后通过一定的程序把这个班女同学年龄在 14 到 15 岁之间的显示出来。

开始按顺序输入一个学生的姓名、性别、年龄是否读到全部学生已读完的是结束结束标志？这个同学是女生？这个同学年龄为14 到 15 岁之间吗？显示这个同学的情况点评：编制流程图时，注意自顶而下，分而治之的方法，先全局后局部，先整体后细节，先抽象后具体的逐步细化过程。

这样编写的程序结构清晰，一目了然。

练习 1：用程序框图表示计算x + 1(x > 0 )f (x) =0( x = 0)的算法步骤。

— x + 1( x < 0)2．明确步骤，搞清各步骤之间的关系用流程图表示前，首先明确分几步，及各步骤之间的关系，才能够清晰的表达比较复杂的系统各部分之间的关系，这有利于交流思想。

例 2. 要在一规划区域内建工厂，试画出该工厂由拆迁、设计、购买设备、、厂房建设、设备安装到试车生产的工序流程图。

（各工序名称、工序代号、紧前工序如图）（注：紧前工序，即与该工序相衔接的前一工序）。

工序代号工序名称紧前工序A拆迁—B工程设计—C土建设计BD设备采购BE厂房土建 A , CF设备安装 D , EG设备测试FH试车生产G分析：按照工序要求，据题意， A 、 B 可同时进行， C 、 D 可同时进行，因此，A与 B ，C 与 D ，可设计为平行工序。

活页作业(四)循环结构程序框图的画法(25分钟，60分)一、选择题(每小题5分，共25分)1．如图所示，是一个循环结构的算法，下列说法不正确的是()A．①是循环变量初始化，循环就要开始B．②为循环体C．③是判断是否继续循环的终止条件D．①可以省略不写解析：①为循环变量初始化，必须先赋值才能有效控制循环，不可省略．故选D．答案：D2．图中所示的程序框图，表达式为()A．11＋2＋3＋…＋99B．11＋2＋3＋…＋100C．199D．1 100解析：由程序框图可知前面求的是1＋2＋3＋…＋99，最后输出的为前面的和的倒数，故选A．答案：A3．(2016·高考北京卷)执行如图所示的程序框图，输出S的值为()A ．8B ．9C ．27D ．36解析：借助循环结构进行运算求解． k ＝0，s ＝0，满足k ≤2； s ＝0，k ＝1，满足k ≤2； s ＝1，k ＝2，满足k ≤2；s ＝1＋23＝9，k ＝3，不满足k ≤2，输出s ＝9． 答案：B4．(2014·高考新课标全国卷Ⅱ)执行如图所示的程序框图，如果输入的x ，t 均为2，那么输出的S ＝( )A ．4B ．5C ． 6D ．7解析：x ＝2，t ＝2，M ＝1，S ＝3，k ＝1； k ≤t ，M ＝11×2＝2，S ＝2＋3＝5，k ＝2；k ≤t ，M ＝22×2＝2，S ＝2＋5＝7，k ＝3；3>2，不满足条件，输出S ＝7． 答案：D5．(2015·高考重庆卷)执行如图所示的程序框图，若输出k 的值为8，则判断框内可填入的条件是( )A ．s ≤34B ．s ≤56C ．s ≤1112D ．s ≤2524解析：根据程序框图表示的算法求解．由s ＝0，k ＝0满足条件，则k ＝2，s ＝12，满足条件；k ＝4，s ＝12＋14＝34，满足条件；k＝6，s ＝34＋16＝1112，满足条件；k ＝8，s ＝1112＋18＝2524，不满足条件，输出k ＝8.所以应填s ≤1112．答案：C二、填空题(每小题5分，共15分)6．(2016·高考山东卷)执行如图的程序框图，若输入的a ，b 的值分别为0和9，则输出的i 的值为________．解析：利用循环结构的知识进行求解．第1次循环：a ＝0＋1＝1，b ＝9－1＝8，a <b ，此时i ＝2； 第2次循环：a ＝1＋2＝3，b ＝8－2＝6，a <b ，此时i ＝3； 第3次循环：a ＝3＋3＝6，b ＝6－3＝3，a >b ，此时i ＝3． 答案：37．根据条件把图中的程序框图补充完整，求区间[1,1 000]内所有奇数的和． (1)处填____________；(2)处填__________．解析：求[1,1 000]内所有奇数的和，初始值i ＝1，S ＝0，并且i <1 000，所以(1)应填S ＝S ＋i ，(2)为i ＝i ＋2．答案：(1)S ＝S ＋i (2)i ＝i ＋28．(2015·高考安徽卷)执行如图所示的程序框图(算法流程图)，输出的n 为________．解析：结合程序框图逐一验证求解．执行第一次判断：|a －1.414|＝0.414>0.005，a ＝32，n ＝2；执行第二次判断：|a －1.414|＝0.086>0.005，a ＝75，n ＝3；执行第三次判断：|a －1.414|＝0.014>0.005，a ＝1712，n ＝4；执行第四次判断：|a －1.414|<0.005，输出n ＝4． 答案：4三、解答题(每小题共10分，共20分)9．设计程序框图，求出12×⎝⎛⎭⎫－23×34×⎝⎛⎭⎫－45×…×99100的值． 解：程序框图如图所示．10．已知函数f(x)＝3x，求f{f[f(x)]}．画出输入x求函数值的程序框图．解：算法如下．第一步，输入x．第二步，i＝1．第三步，若i≤3，则执行第四步；否则，执行第七步．第四步，y＝3x．第五步，x＝y．第六步，i＝i＋1，返回第三步．第七步，输出y．程序框图如图所示．(20分钟，40分)一、选择题(每小题5分，共10分)1．(2015·高考天津卷)阅读如图所示的程序框图，运行相应的程序，则输出S的值为()A．－10B．6C．14D．18解析：先识别程序框图的功能，再结合循环结构与条件结构求解．S＝20，i＝1，i＝2i＝2，S＝S－i＝20－2＝18，不满足i>5；i＝2i＝4，S＝S－i＝18－4＝14，不满足i>5；i＝2i＝8，S＝S－i＝14－8＝6，满足i>5；故输出S＝6．答案：B2．运行如图所示的程序框图，若输出的结果是7，则判断框中的横线上可以填入的最大整数为()A．7 B．8C．9 D．10解析：在循环体内部，执行运算s＝s＋i，i＝i＋2，可知当执行完第三次循环后s＝1＋3＋5＝9，i＝7，所以第三次循环是最后一次循环，返回判断条件时，应不满足判断条件，退出循环，即s＝9时，不满足判断条件．故答案为9．答案：C二、填空题(每小题5分，共10分)3．某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，根据如图所示的程序框图，若其中4位居民的月均用水量(单位：t)分别为1,1.5,1.5,2，则输出的结果s 为________________．解析：第一(i ＝1)步，s 1＝s 1＋x 1＝0＋1＝1，s ＝1，i ＝2； 第二(i ＝2)步，s 1＝s 1＋x 2＝1＋1.5＝2.5，s ＝2.52，i ＝3；第三(i ＝3)步，s 1＝s 1＋x 3＝2.5＋1.5＝4，s ＝43，i ＝4；第四(i ＝4)步，s 1＝s 1＋x 4＝4＋2＝6，s ＝14×6＝32，i ＝5，不满足i ≤4，输出s ＝32．答案：324．按下列程序框图运算：规定：程序运行到“判断结果是否大于244”为1次运算，若x ＝5，则运算进行________________次才停止．解析：第一次运算得13，第二次运算得37，第三次运算得109，第四次运算得325，大于244，程序终止，故运算进行4次．答案：4三、解答题(每小题10分，共20分)5．设计一个算法求满足10＜x 2＜1 000的所有正整数，并画出程序框图． 解：算法步骤如下． 第一步，x ＝1．第二步，如果x 2＞10，那么执行第三步；否则执行第四步． 第三步，如果x 2＜1 000，那么输出x ；否则结束程序． 第四步，x ＝x ＋1，转到第二步． 程序框图如图．6．运行如图所示的程序框图．(1)若输入x 的值为2，根据该程序的运行过程完成下面的表格，并求输出的i 与x 的值.第i 次 i ＝1 i ＝2 i ＝3 i ＝4 i ＝5 x ＝2×3i(2)解：(1)第i 次 i ＝1 i ＝2 i ＝3 i ＝4 i ＝5 x ＝2×3i61854162486因为(2)由输出i 的值为2，则程序执行了循环体2次，即⎩⎪⎨⎪⎧3x ≤168，9x >168，解得563<x ≤56．所以输入x 的取值范围是563<x ≤56．。

高中数学人教A版必修3第一章第1节《 程序框 图》习 题课课 件（共 35张PP T）
(3) 注意控制循环的变量的步长是 多少，比如例3中i=i+1,还是i=i+2，循环变量 的步长对输出结果也是有影响的。
高中数学人教A版必修3第一章第1节《 程序框 图》习 题课课 件（共 35张PP T）
高中数学人教A版必修3第一章第1节《 程序框 图》习 题课课 件（共 35张PP T）
开始 i=1 S=0
i<3？
否
输出S 结束
i=i+2 S=S+i
是
解析：
初始i=1,s=0 进入循环：i=1<3满足条件,
s=0+1=1，i=1+2=3
检验：i=3<3不满足条件,循环终止
输出s=1
高中数学人教A版必修3第一章第1节《 程序框 图》习 题课课 件（共 35张PP T）
(2) 循环结构中的循环次数要严格 把握，区分“≤”与“＜”,“≥”与“＞”， 不要出现多一次或少一次的错误，比如例2中前 者i=3时退出循环，输出s=3；后者i=4时才退出 循环，输出s=6。
高中数学人教A版必修3第一章第1节《 程序框 图》习 题课课 件（共 35张PP T）
高中数学人教A版必修3第一章第1节《 程序框 图》习 题课课 件（共 35张PP T）
程序框图的习题课 （循环结构）
制作人：王元忠
循环结构是高考命题的一个热点问题，多以选择
题、填空题的形式呈现，试题难度不大，多为容易题 或中档题。高考对循环结构的考查主要有以下三个命 题角度： （1）已知程序框图，求输出的结果； （2）完善程序框图； （3）判断程序框图的功能。
新疆 王新敞

人教a版必修三分层训练2（第3课时）程序框图的画法（含答第3课时循环结构、程序框图的画法一、基础达标1．运行如图程序框图，输出的结果为()A．15C．28答案C解析n＝1，S＝1＋0＝1；n＝2，S＝3；n＝3，S＝6；n＝4，S＝10；n＝5，S＝15；n＝6，S＝21；n＝7，S＝28.n＝8时，不满足n≤7，因此输出S＝28.2．执行如图所示的程序框图，输出的S值为()B．21D．36A．2答案CB．4C．8D．16解析利用程序框图的算法特点求解．当k＝0时，满足k<3，因此S＝1某20＝1；当k＝1时，满足k<3，因此S＝1某21＝2；当k＝2时，满足k<3，因此S＝2某22＝8；当k＝3时，不满足k<3，因此输出S＝8.3．(2022·山东高考)执行两次如图所示的程序框图，若第一次输入的a的值为－1.2，第二次输入的a的值为1.2，则第一次、第二次输出的a的值分别为()A．0.2，0.2C．0.8，0.2答案C解析若第一次输入的a的值为－1.2，满足上面一个判断框条件a＜0，第1次循环，a＝－1.2＋1＝－0.2，第2次判断后循环，a＝－0.2＋1＝0.8，第3次判断，满足上面一个判断框的条件退出上面的循环，进入下面的循环，不满足下面一个判断框条件a≥1，退出循环，输出a＝0.8；第二次输入的a的值为1.2，不满足上面一个判断框条件a＜0，退出上面的循环，进入下面的循环，满足下面一个判断框条件a≥1，第1次循环，a＝1.2－1＝0.2，第2次判断后不满足下面一个判断框的条件退出下面的循环，输出a＝0.2.故选C.B．0.2，0.8D．0.8，0.84．如图是求某1，某2，，某10的乘积S的程序框图，图中空白框中应填入的内容为()A．S＝S某(n＋1)C．S＝S某n答案D解析赋值框内应为累乘积，累乘积＝前面项累乘积某第n项，即S＝S某某n.5．(2022·深圳高一检测)某程序框图如图所示，若输出的S＝57，则判断框内为A．k>4C．k>6答案A解析当k＝1时，k＝k＋1＝2，S＝2某1＋2＝4；当k＝2时，k＝k＋1＝3，S＝2某4＋3＝11；当k＝3时，k＝k＋1＝4，S＝2某11＋4＝26；当k＝4时，k＝k＋1＝5，S＝2某26＋5＝57.此时S＝57，循环结束，k＝5，所以判断框中应为“k>4？”．B．S＝S某某n＋1D．S＝S某某n()B．k>5D．k>76．阅读如图所示的程序框图，运行相应的程序，输出的值等于______．答案－3解析第一次循环：＝1，k＝1<4，＝2某1－1＝1，k＝1＋1＝2；第二次循环：k＝2<4，＝2某1－2＝0，k＝2＋1＝3；第三次循环：k＝3<4，＝2某0－3＝－3，k＝3＋1＝4；当k＝4时，k<4不成立，循环结束，此时＝－3.7．有十件商品，设计一个算法，计算其平均价，并画出程序框图．解我们用一个循环依次输入10个数，再用一个变量存放数的累加和，在求出10个数的和后，除以10，就得到10件商品的平均价．算法：第一步，S＝0，i＝1.第二步，输入P.第三步，S＝S＋P.第四步，i＝i＋1.第五步，判断i是否大于10，若不大于10，转入第二步，若i>10，退出循环，执行第六步．S第六步，A＝10.第七步，输出A.程序框图如图所示．二、能力提升8．(2022·重庆高考)执行如图所示的程序框图，如果输出S＝3，那么判断框内应填入的条件是()A．k≤6答案B解析k＝2，＝1某log23＝log23；k＝3，＝log23某log34＝log24；k＝4，＝log24某log45＝log25；k＝5，＝log25某log56＝log26；k＝6，＝log26某log67＝log27；k＝7，＝log27某log78＝log28＝3，停止，说明判断框内应填k≤7？.9．(2022·青岛高一检测)根据条件把图中的程序框图补充完整，求区间[1，1000]内所有奇数的和，(1)处填________；(2)处填________．B．k≤7C．k≤8D．k≤9答案(1)S＝S＋i(2)i＝i＋2解析求[1，1000]内所有奇数和，初始值i＝1，S＝0，并且i<1000，所以(1)应填S＝S＋i，(2)为i＝i＋2.10．某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中n位居民的月均用水量分别为某1，，某n(单位：吨)．根据如图所示的程序框图，若n＝2，且某1，某2分别为1，2，则输出的结果S为________．1答案4解析当i＝1时，S1＝1，S2＝1；当i＝2时，S1＝1＋2＝3，S2＝1＋22＝5，111此时S＝2(5－2某9)＝4.i的值变成3，从循环体中跳出，输出S的值为4.111111．用循环结构书写求1＋2＋3＋4＋＋1000的算法，并画出相应的程序框图．解相应的算法如下：第一步，S＝0，i＝1；1第二步，S＝S＋i；第三步，i＝i＋1；第四步，i＞1000是否成立，若成立执行第5步，否则重复执行第二步；第五步，输出S.相应的算法框图如图所示．三、探究与创新12．画出求满足12＋22＋32＋＋n2>106的最小正整数n的程序框图．解程序框图如下：13．以下是某次考试中某班15名同学的数学成绩：72，91，58，63，84，88，90，55，61，73，64，77，82，94，60.要求将80分以上的同学的平均分求出来．画出程序框图．解用条件结构来判断成绩是否高于80分，用循环结构控制输入的次数，同时引进两个累加变量S、m，分别计算高于80分的成绩的总和S和人数m.程序框图如图所示．。

中学教师课时教案备课人授课时间课题1．1．2程序框图与算法的基本逻辑结构（习题课）课标要求 1.掌握程序框图的概念； 2.会用通用的图形符号表示算法；3.掌握画程序框图的基本规则，能正确画出程序框图；教学目标知识目标通过设计流程图来表达解决问题的过程，了解流程图的三种基本逻辑结构：顺序、条件分支、循环。

理解掌握三种基本逻辑结构，能设计简单的流程图。

技能目标通过模仿、操作和探索，抽象出算法的过程，培养抽象概括能力、语言表达能力和逻辑思维能力。

情感态度价值观通过算法实例，体会构造的数学思想方法；培养学生学习兴趣，增强学好数学的信心；通过学生的积极参与、大胆探索，培养学生的探索精神和合作意识。

重点综合运用框图知识正确地画出程序框图难点综合运用这些知识正确地画出程序框图。

教学过程及方法问题与情境及教师活动学生活动一．复习(1)请大家回忆顺序结构，并用程序框图表示.顺序结构是由若干个依次执行的步骤组成的,这是任何一个算法都离不开的基本结构.框图略.(2)请大家回忆条件结构，并用程序框图表示.在一个算法中，经常会遇到一些条件的判断，算法的流程根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构(3)请大家回忆循环结构，并用程序框图表示.在一些算法中要求重复执行同一操作的结构称为循环结构即从算法某处开始，按照一定条件重复执行某一处理过程.重复执行的处理步骤称为循环体.循环结构有两种形式：当型循环结构和直到型循环结构.二．问题讲解(一）顺序结构13.画出求坐标平面内两点baA,，dcB,之间距离的程序框图。

问题与情境及教师活动学生活动(二)条件结构14、y 与x 之间的函数关系式为：79.49.1702.1x x x xy 。

请你设计一个输入用水量、输出应缴费额的算法，画出程序框图。

教学过程及方法问题与情境及教师活动学生活动（三）循环结构13. 2000年某地森林面积为10002km，且每年增长%5，到哪一年该地森林面积超过20002km。

4.程序框图的画法习题课
第 2 页
第 3 页
一．复习
(1)请大家回忆顺序结构，并用
程序框图表示.
顺序结构是由若干个依次执
行的步骤组成的,这是任何一个算
法都离不开的基本结构.框图略.
(2)请大家回忆条件结构，并用
程序框图表示.
在一个算法中，经常会遇到
一些条件的判断，算法的流程根据
条件是否成立有不同的流向.条件
问题与情境及教师活动学生活动
第 4 页
第 5 页
(二)条件结构
14、y 与x 之间的函数关系式为：
()()
⎩
⎨
⎧>-≤≤=79.49.1702.1x x x x y 。

请你设计一个输入用水量、输出应缴费额的算法，画出程序框图。

教
问题与情境及教师活动
学生活动
学过程及方法（三）循环结构
13. 2019年某地森林面积为10002km，
且每年增长%5，到哪一年该地森
林面积超过20192km。

请设计一个
算法，并画出程序框图。

教学小结（1）进一步熟悉三种逻辑结构的应用，理解算法与程序框图的关系.
（2）根据算法步骤画出程序框图.
课
后
反
思
第 6 页。

程序框图习题课 参考答案一、会读流程图1.如图（1）为循环体中的__当型__循环，它换成另外一种__直到型__循环的框图.2.写出如图(2)的算法功能__求乘积为624的相邻两个偶数__.3.指出程序框图的运算结果: 当箭头指向①处时,输出sum=__5_；指向②处时,输出sum=__15__.4.观察所给程序框图,写出它所表示的函数.5.如图所示是某一算法的程序框图，根据该框图指出这一算法的功能. 求和201614121++++= S 二、会写流程图（一）、条件结构练习1. 设计一个求任意数的绝对值的算法,并画出程序框图.⎪⎩⎪⎨⎧≤<≤<≤=)100005000(,50)5000100(,01.0)100(,1x x x xy2. 画出一个求3个实数中最小数的程序框图.3. 闰年是指年份能被4整除但不能被100整除,或者能被400整除的年份.编写一个程序框图,判断输入的年份是否为闰年.（二）循环结构练习关注易错点：①关注变量的初始值，理解两种变量的意义：计数变量（循环变量、步进变量）和累加（累乘）变量。

②关注“S=S+i ”和“i=i+1”先后顺序的影响（初始值的影响、循环次数的影响、输出结果的影响）。

③判断条件是否具备“=”。

④当型与直到型分别是什么时候继续循环，什么时候结束循环。

怎样改为当型循环？误右侧程序框图是否有错的最小正整数求满足?,1021.16222n n >+++左图1应该输出1-i ，左图2应该初始化为1=S2. 已知30021≤+++i ，画出求解i 的最大值的过程的程序框图如右图. 问题：输出处横线应该填__2-i _.变1：若改为sum<300, 输出处横线应该填__1-i _.变2：若改变i=i+1与sum=sum+i 的顺序，输出处横线应该填__1-i _.（初始化要改为1=sum ）变3：在变2的条件下，要输出i ，判断框内应该填_ sum<300_.3. 设计一个求1+2+4+7+…+46的算法,并画出相应的程序框图.见左侧（变差数列的设计）4. 课本P20页B 组第2题.（略）。

直到型循环在执行了 一次循环体之后,对控制循 环条件进行判断,当条件不 满足时执行循环体,直到条 件满足终止循环.(反复执行 循环体,直到条件满足)
当型循环在每次执 行循环体前对循环条件 进行判断,当条件满足时 执行循环体,不满足则停 止;(当条件满足时反复 执行循环体)
循环体
否 满足条件? 是 满足条件? 否 是
算法框图如右，应该在空格位置 填入什么条件？ 分析：空格位置判断条件，应该 考虑循环的终止条件是什么？ 应该填入：i>10？
第二步，确定区间[a，b]。
第四步，若f (a) f (m) < 0，则含零点的区间为[a，m]； 否则，含零点的区间为[m，b]。将新得到的含零点的区 间仍记为[a，b]。 第五步，判断[a，b]的长度是否小于d或f (m)是否等于0。 若是，则m是方程的近似解；否则，返回第三步。
请画出其程序框图。
i i1 S Si
Y
循环变量
i 1 S0
循环终止条件
i 100 ? N 输出 S
结束
循环结构的三要素 循环变量,循环体、循环的终止条件.
循环结构的设计步骤
(1)确定循环结构的循环变量和初始条件; (2)确定算法中需要反复执行的部分,即循环体； (3)确定循环的终止条件.
开始
i=1
循环体
求1+2+3+ … +100
第一步:令 i 1, S 0 第二步:若 i 100成立,则执行第三步；否则,输出S, 结束算法. 第三步: S S i 第四步:i
i1
,返回第二步.
开始
计数变量:用于记录循环次数,同时 还用于判断循环是否终止. 累加变量:用于输出结果,一般与 计数变量同步执行,累加一次,计 数一次. 循环体

答案：3序框图，
如果输入的x＝0，y＝1， n＝1，则输出x，y的值 满足( ) B．y＝3x
A．y＝2x
C．y＝4x
D．y＝5x
【答案】
C
例7(2016· 课标全国Ⅲ)
执行下面的程序框图， 如果输入的a＝4， b＝6，那么输出的 n＝( A． 3 C． 5 ) B．4 D． 6
例 4 ．执行如图所示的框
图，已知集合A＝{x|框图中 输出的x值}，集合B＝{y|框 图中输出的 y 值 }，全集U ＝ Z，Z为整数集，则当x＝－ 1 时， ( ∁ UA ) ∩ B ＝ _____.
答案 {－3，－1，7，9}
例5：某算法的
程序框图如图所
示，若输出结果 为 3 ，则可输入的 实数 x 的个数共有 _____个．
【答案】 A
)
例11：执行如图所示
的程序框图，若输入
的x的值为2，则输出
的y的值为（ ） A． 2 C．11
【答案】 D
B．5 D．23
例12：执行如图所示
的程序框图，输出的
S的值是________．
2 -1 答案： 2
A．i<10
【答案】
B．i>10 D．i>20
C．i<20
B
例 9：某程序框图如图所示，若该程 9 序运行后输出的值是 ，则（ 5
A．a＝4 C．a＝6 B．a＝5 D．a＝7
）
【答案】
A
例10：执行下面的
程序框图，如果输
入的t∈[－1,3]，
则输出的s属于(
A．[－3,4] B．[－5,2] C．[－4,3] D．[－2,5]
解析 第一次循环：a＝2，b＝4，a＝6，s＝6，n＝1； 第二次循环：a＝－2，b＝6，a＝4，s＝10，n＝2； 第三次循环：a＝2，b＝4，a＝6，s＝16，n＝3；

第3课时循环结构、程序框图的画法1.一个完整的程序框图至少包含()A．起止框和输入、输出框B．起止框和处理框C．起止框和判断框D．起止框、处理框和输入、输出框2.如图所示是一个循环结构的算法，下列说法不正确的是()A．①是循环变量初始化，循环就要开始B．②为循环体C．③是判断是否继续循环的终止条件D．①可以省略不写3.执行如图所示的程序框图，输出的S值为()A．2 B．4C．8 D．164．如图所示，程序框图(算法流程图)的输出结果是()A．34 B．55C．78 D．895．执行如图所示的程序框图，若m＝5，则输出的结果为()A．4B．5C．6D．86．阅读如图所示的框图，运行相应的程序，输出S的值为________．7．如果执行如图所示的程序框图，输入x＝4.5，则输出的数i＝________．8．执行如图所示的程序框图，若输出的a值大于2 015，那么判断框内的条件应为________．9．设计一个算法，求表达式12＋22＋32＋…＋102的值，并画出程序框图．10．有一列数1，1，2，3，5，8，…，其规律是从第3个数开始，后一个数等于前两个数的和，画出计算这列数前20个数的和的程序框图．11．设计一个求满足10<x2<1 000的所有正整数x的值的程序框图．参考答案1.【解析】选A.一个完整的程序框图至少包括起止框和输入、输出框，故选A.【答案】A2.【解析】选D.①为循环变量初始化，必须先赋值才能有效控制循环，不可省略．故选D.【答案】D3.【解析】选C.框图执行如下：k＝0，S＝1；S＝1，k＝1；S＝2，k＝2；S＝8，k＝3.所以输出S的值为8.【答案】84.【解析】选B.当输入x＝1，y＝1，执行z＝x＋y及z≤50，x＝y，y＝z后，x，y，z的值依次对应如下：x＝1，y＝1，z＝2；x＝1，y＝2，z＝3；x＝2，y＝3，z＝5；x＝3，y＝5，z＝8；x＝5，y＝8，z＝13；x＝8，y＝13，z＝21；x＝13，y＝21，z＝34；x＝21，y＝34，z＝55.由于55≤50不成立，故输出55.故选B.【答案】B5.【解析】选B.由程序框图可知，k＝0，P＝1.第一次循环：因为k＝0＜5，所以P＝1×30＝1，k＝0＋1＝1.第二次循环：因为k＝1＜5，所以P＝1×31＝3，k＝1＋1＝2.第三次循环：因为k＝2＜5，所以P＝3×32＝33，k＝2＋1＝3.第四次循环：因为k＝3＜5，所以P＝33×33＝36，k＝3＋1＝4.第五次循环：因为k＝4＜5，所以P＝36×34＝310，k＝4＋1＝5.此时满足判断框内的条件，输出结果为z＝log9 310＝5.故选B.【答案】B6.【解析】S＝0，n＝3，S＝0＋(－2)3＝－8，n＝3－1＝2≤1不成立；故S＝－8＋(－2)2＝－4，n＝2－1＝1≤1成立．故输出S的值为－4.【答案】－47.【解析】第一次执行循环体时，i＝1，x＝3.5；第二次执行循环体时，i＝2，x＝2.5；第三次执行循环体时，i＝3，x＝1.5；第四次执行循环体时，i＝4，x＝0.5＜1.输出i＝4，结束．【答案】48.【解析】第一次循环：k＝1，a＝1，满足条件，所以a＝4×1＋3＝7，k＝1＋1＝2.SGKS87第二次循环：a＝7＜2 015，故继续循环，所以a＝4×7＋3＝31，k＝2＋1＝3.第三次循环：a＝31＜2 015，故继续循环，所以a＝4×31＋3＝127，k＝3＋1＝4.第四次循环：a＝127＜2 015，故继续循环，所以a＝4×127＋3＝511，k＝4＋1＝5.第五次循环：k＝511＜2 015，故继续循环，所以a＝4×511＋3＝2 047，k＝5＋1＝6.由于a＝2 047＞2 015，故不符合条件，输出a值．所以判断框内的条件是“k≤5？”．【答案】k≤5?9. 解：算法如下：第一步，令S＝0，i＝1.第二步，判断i是否小于或等于10，若是，则执行第三步；若否，则输出S.第三步，令S＝S＋i2，并令i＝i＋1，然后返回第二步．程序框图如图：10. 解：程序框图如图所示：11.解：可以从最小的正整数1开始进行判断，判断是否满足10<x2<1 000.若满足，则输出x 的值；若不满足，则对1进行累加后再进行判断，依次下去，直到x2≥1 000为止，结束程序．程序框图如图所示：。

第3课时 循环结构、程序框图的画法一、选择题1.下面关于当型循环结构和直到型循环结构的说法，不正确的是( )A.当型循环结构是先判断后循环，条件成立时执行循环体，条件不成立时结束循环B.直到型循环结构要先执行循环体再判断条件，条件成立时结束循环，条件不成立时执行循环体C.设计程序框图时，两种循环结构可以根据需要选其中的一个，两种结构也可以相互转化D.当型循环体和直到型循环体在执行时都至少要执行一次2.执行如图所示的程序框图，输出的S 的值的为( )A.1B.23C.1321D.610987第2题图 第3题图3.执行如图所示的程序框图，输出的S 的值为( )A.2B.4C.8D.164.阅读如图所示的程序框图，则输出n 与z 的值分别是( )A.2、20B.3、20C.3、26D.2、265.执行如图所示的程序框图，如果输入的N ＝10，那么输出的S 等于( )A.1＋12＋13＋…＋110B.1＋12！＋13！＋…＋110！C.1＋12＋13＋…＋111D.1＋12！＋13！＋…＋111！(注：n ！＝1×2×3×…×n )第5题图 第6题图6.如图是求x 1，x 2，…，x 10的乘积S 的程序框图，图中空白框中应填入的内容为() A.S ＝S ×(n ＋1) B.S ＝S ×x n ＋1C.S ＝S ×nD.S ＝S ×x n7.下图是计算1＋12＋13＋…＋1999的值的一个程序框图，判断框里应填( )A.i <999?B.i >999?C.i <1 000?D.i >1 000?第7题图第8题图8.相传古代的印度国王要奖赏国际象棋的发明者，问他需要什么.发明者说：陛下，在国际象棋的第一个格子里面放1粒麦子，在第二个格子里面放2粒麦子，第三个格子里面放4粒麦子，以后每个格子中的麦粒数都是它前一个格子中麦粒数的二倍，依此类推(国际象棋棋盘共有64个格子)，如图所示的程序框图就是计算国王共需付出多少粒麦子的.则空白处理框里应填()A.sum＝sum＋iB.sum＝sum＋2iC.sum＝sum＋i2D.sum＝sum＋2i二、填空题9.如图所示的程序框图运行后，输出的结果为______.第9题图第10题图10.阅读如图所示的程序框图，运行相应的程序.若输入m的值为2，则输出的结果i＝________.11.根据如图所示的程序框图，若n＝2，且x1，x2分别为1,2，则输出的结果S为________.三、解答题12.如图所示的程序框图，(1)输入x＝－1，n＝3，则输出的数S是多少？(2)该程序框图是什么型？试把它转化为另一种结构.13.某工厂2005年的年生产总值为200万元，技术革新后预计以后每年的年生产总值都比上一年增长5%，设计一个程序框图，输出预计年生产总值超过300万元的最早年份.答案精析1.D [当型循环先判断后循环，如果一开始条件就不满足，则循环体一次都不执行.]2.C [执行第一次循环后S ＝23，i ＝1；执行第二次循环后，S ＝1321，i ＝2≥2，退出循环体，输出S 的值为1321.] 3.C [当k ＝0时，满足k <3，因此S ＝1×20＝1；当k ＝1时，满足k <3，因此S ＝1×21＝2；当k ＝2时，满足k <3，因此S ＝2×22＝8；当k ＝3时，不满足k <3，因此输出S ＝8.]4.D5.B [k ＝1，T ＝11，S ＝1， k ＝2，T ＝11×2＝12！，S ＝1＋12！， k ＝3，T ＝11×2×3＝13！，S ＝1＋12！＋13！， …由于N ＝10，即k >10时结束循环，共执行10次.所以输出的S ＝1＋12！＋13！＋ (110).] 6.D 7.C 8.D9.20解析 由于5≥4，所以s ＝5，a ＝4，又∵4≥4也成立，∴第二次经过循环体时，s ＝5×4＝20，此时a ＝3，而a ＝3≥4不成立，∴输出的s 的值为20.10.411.14解析 当i ＝1时，S 1＝1，S 2＝1，此时S ＝0；当i ＝2时，S 1＝1＋2＝3，S 2＝1＋22＝5，此时S ＝12(5－12×9)＝14. i 的值变成3，从循环体中跳出，输出S 的值为14.12.解(1)当n＝3时，i＝3－1＝2，满足i≥0，故S＝6×(－1)＋2＋1＝－3；执行i＝i－1后i的值为1，满足i≥0，故S＝(－3)×(－1)＋1＋1＝5；再执行i＝i－1后i的值为0，满足i≥0，故S＝5×(－1)＋0＋1＝－4；继续执行i＝i－1后i的值为－1，不满足i≥0，故输出S＝－4.(2)原图是当型循环.改为直到型如图：13.解算法分析：先写出解决本例的算法步骤：第一步，输入2005年的年生产总值.第二步，计算下一年的年生产总值.第三步，判断所得的结果是否大于300，若是，则输出该年的年份；否则，返回第二步.设a为某年的年生产总值，t为年生产总值的年增长量，n为年份，则n的初始值为2005，a 的初始值为200，循环体为t＝0.05a，a＝a＋t，n＝n＋1.用“a>300”是否成立来控制循环.程序框图如图：。

题型三：程序框图的补充
1、求1-1000内所有奇 数的和。设计的算法框 图如右，应该在空格位 置填入什么条件？
分析：空格位置是循 环体部分，应考虑需 要量重复执行的步骤 是什么？以及步骤的 执行顺序如何？
应该填入：S=S+i i=i+2
例题讲解
题型三：程序框图的补充 2、求 1 1 1 .... 1 的值。设计
n=1
S=0
3、循环体执行多少次？
4、这个程序框图解决了什么实际问题？
n=n+1
n≤100？ 否
输出S
结束
S=S-n×n
S=S+n×n
是
是
n是偶数?
否
求12-22+32-42+…+992-1002的值.
例题讲解
题型二：程序框图的阅读与理解
练习1：如右图，该程序图表 示的算法的功能是什么？
例题讲解
程序框图的画法
例题讲解
题型一：设计算法解决实际问题
例1、用程序框图表示用二分法求方程x2-2=0的近似解的算法。 哪些步骤可以用顺序结构 表示？如何表示？
f(x)=x2-2输入精确度d来自和初始值a，bm ab 2
例题讲解
题型一：设计算法解决问题
例1、用程序框图表示用二分法求方程x2-2=0的近似解的算法。
2 4 6 20
的算法框图如右，应该在空格位 置填入什么条件？
分析：空格位置判断条件，应该 考虑循环的终止条件是什么？
应该填入：i>10
； 兴发娱乐 ；
趁此机会.何愁孙公子不肯赐教.弟子几个也不认得.他就是小道会的总舵主韩志国.二十年前的英气雄风.骂道：“小丫头有多大本领？”说罢又坐了下去.焦直急忙叫道：“洪二弟.康熙皇帝非常宠爱他