大学物理第3章动量与冲量

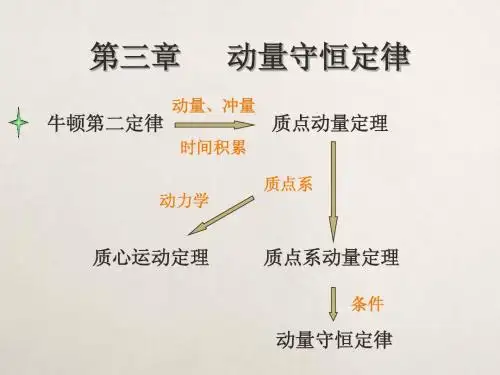
动量、冲量及动量守恒定律动量和动量定理一、动量1．定义：运动物体的质量和速度的乘积叫动量；公式p＝m v；2．矢量性：方向与速度的方向相同．运算遵循平行四边形定则．3．动量的变化量(1)定义：物体在某段时间内末动量与初动量的矢量差(也是矢量)，Δp＝p′－p(矢量式)．(2)动量始终保持在一条直线上时的运算：选定一个正方向，动量、动量的变化量用带有正负号的数值表示，从而将矢量运算简化为代数运算(此时的正负号仅代表方向，不代表大小)．4．与动能的区别与联系：(1)区别：动量是矢量，动能是标量．(2)联系：动量和动能都是描述物体运动状态的物理量，大小关系为E k＝p22m或p＝2mE k.二、动量定理1．冲量(1)定义：力与力的作用时间的乘积．公式：I＝Ft．单位：牛顿·秒，符号：N·s．(2)矢量性：方向与力的方向相同．2．动量定理(1)内容：物体在一个运动过程中始末的动量变化量等于它在这个过程中所受力的冲量．(2)公式：m v′－m v＝F(t′－t)或p′－p＝I．3．动量定理的应用碰撞时可产生冲击力，要增大这种冲击力就要设法减少冲击力的作用时间．要防止冲击力带来的危害，就要减小冲击力，设法延长其作用时间．（缓冲）题组一对动量和冲量的理解1.关于物体的动量，下列说法中正确的是() A．运动物体在任一时刻的动量方向，一定是该时刻的速度方向B．物体的动能不变，其动量一定不变C．动量越大的物体，其速度一定越大D．物体的动量越大，其惯性也越大2.如图所示，在倾角α＝37°的斜面上，有一质量为5 kg的物体沿斜面滑下，物体与斜面间的动摩擦因数μ＝0.2，求物体下滑2s的时间内，物体所受各力的冲量．(g取10 m/s2，sin 37°＝0.6，cos 37°＝0.8)3．(2014·西安高二期末)下列说法正确的是() A．动能为零时，物体一定处于平衡状态B．物体受到恒力的冲量也可能做曲线运动C．物体所受合外力不变时，其动量一定不变D．动能不变，物体的动量一定不变4.如图所示，质量为m的小滑块沿倾角为θ的斜面向上滑动，经过时间t1速度为零然后又下滑，经过时间t2回到斜面底端，滑块在运动过程中受到的摩擦力大小始终为F1.在整个过程中，重力对滑块的总冲量为()A．mg sin θ(t1＋t2) B．mg sin θ(t1－t2) C．mg(t1＋t2) D．05．在任何相等时间内，物体动量的变化总是相等的运动可能是()A．匀速圆周运动B．匀变速直线运动C．自由落体运动D．平抛运动题组二动量定理的理解及定性分析1跳远时，跳在沙坑里比跳在水泥地上安全，这是由于()A．人跳在沙坑的动量比跳在水泥地上的小B．人跳在沙坑的动量变化比跳在水泥地上的小C．人跳在沙坑受到的冲量比跳在水泥地上的小D．人跳在沙坑受到的冲力比跳在水泥地上的小2．一个小钢球竖直下落，落地时动量大小为0.5 kg·m/s，与地面碰撞后又以等大的动量被反弹．下列说法中正确的是()A．引起小钢球动量变化的是地面给小钢球的弹力的冲量B．引起小钢球动量变化的是地面对小钢球弹力与其自身重力的合力的冲量C．若选向上为正方向，则小钢球受到的合冲量是－1 N·sD．若选向上为正方向，则小钢球的动量变化是1 kg·m/s3.如图所示，一铁块压着一纸条放在水平桌面上，当以速度v抽出纸条后，铁块掉到地面上的P点，若以2v速度抽出纸条，则铁块落地点为()A．仍在P点B．在P点左侧C．在P点右侧不远处D．在P点右侧原水平位移的两倍处题组三动量定理的有关计算1．一辆轿车强行超车时，与另一辆迎面驶来的轿车相撞，两车车身因相互挤压，皆缩短了0.5 m，据测算两车相撞前速度约为30 m/s，则：(1)假设两车相撞时人与车一起做匀减速运动，试求车祸中车内质量约60 kg的人受到的平均冲力是多大？(2)若此人系有安全带，安全带在车祸过程中与人体的作用时间是1 s，求这时人体受到的平均冲力为多大？动量守恒定律一、系统、内力与外力1．系统：相互作用的两个或多个物体组成一个力学系统．2．内力：系统中，物体间的相互作用力．3．外力：系统外部物体对系统内物体的作用力．二、动量守恒定律1．内容：如果一个系统不受外力或者所受外力的矢量和为零，这个系统的总动量保持不变．2．表达式：对两个物体组成的系统，常写成：p1＋p2p1′＋p2′或m1v1＋m2v2m1v1′＋m2v2′．3．成立条件(1)系统不受外力作用．(2)系统受外力作用，但合外力为零．三、动量守恒定律的普适性动量守恒定律是一个独立的实验规律，它适用于目前为止物理学研究的一切领域．四、对动量守恒定律的理解1．研究对象相互作用的物体组成的系统．2．动量守恒定律的成立条件(1)系统不受外力或所受合外力为零．(2)系统受外力作用，合外力也不为零，但合外力远远小于内力．此时动量近似守恒．(3)系统所受到的合外力不为零，但在某一方向上合外力为零，则系统在该方向上动量守恒．3．动量守恒定律的几个性质(1)矢量性．公式中的v1、v2、v1′和v2′都是矢量，只有它们在同一直线上，并先选定正方向，确定各速度的正、负(表示方向)后，才能用代数方法运算．(2)相对性．速度具有相对性，公式中的v1、v2、v1′和v2′应是相对同一参考系的速度，一般取相对地面的速度．(3)同时性．相互作用前的总动量，这个“前”是指相互作用前的某一时刻，v1、v2均是此时刻的瞬时速度；同理，v1′、v2′应是相互作用后的同一时刻的瞬时速度．例1如图所示，A、B两物体质量之比m A∶m B＝3∶2，原来静止在平板小车C上，A、B间有一根被压缩的弹簧，地面光滑．当弹簧突然释放后，则()A．若A、B与平板车上表面间的动摩擦因数相同，A、B组成系统的动量守恒B．若A、B与平板车上表面间的动摩擦因数相同，A、B、C组成系统的动量守恒C．若A、B所受的摩擦力大小相等，A、B组成系统的动量守恒D．若A、B所受的摩擦力大小相等，A、B、C 组成系统的动量守恒针对训练下列情形中，满足动量守恒条件的是()A．用铁锤打击放在铁砧上的铁块，打击过程中，铁锤和铁块的总动量B．子弹水平穿过放在光滑桌面上的木块的过程中，子弹和木块的总动量C．子弹水平穿过墙壁的过程中，子弹和墙壁的总动量D．棒击垒球的过程中，棒和垒球的总动量1．把一支弹簧枪水平固定在小车上，小车放在光滑水平地面上，枪射出一颗子弹时，关于枪、弹、车，下列说法正确的是()A．枪和弹组成的系统动量守恒B．枪和车组成的系统动量守恒C．枪弹和枪筒之间的摩擦力很小，可以忽略不计，故二者组成的系统动量近似守恒D．枪、弹、车三者组成的系统动量守恒2.木块a和b用一根轻弹簧连接起来，放在光滑水平面上，a紧靠在墙壁上．在b上施加向左的水平力使弹簧压缩，如图所示．当撤去外力后，下列说法正确的是()A．a尚未离开墙壁前，a和b组成的系统动量守恒B．a尚未离开墙壁前，a和b组成的系统动量不守恒C．a离开墙壁后，a和b组成的系统动量守恒D．a离开墙壁后，a和b组成的系统动量不守恒五、动量守恒定律简单的应用1．动量守恒定律不同表现形式的表达式的含义(1)p＝p′：(2)Δp1＝－Δp2(3)Δp＝0 (4)m1v1＋m2v2＝m1v1′＋m2v2′2．应用动量守恒定律的解题步骤(1)确定相互作用的系统为研究对象；(2)分析研究对象所受的外力；(3)判断系统是否符合动量守恒条件；(4)规定正方向，确定初、末状态动量的正、负号；(5)根据动量守恒定律列式求解．例2将两个完全相同的磁铁(磁性极强)分别固定在质量相等的小车上，水平面光滑．开始时甲车速度大小为3 m/s，乙车速度大小为2 m/s，方向相反并在同一直线上，如图所示．(1)当乙车速度为零时，甲车的速度多大？方向如何？(2)由于磁性极强，故两车不会相碰，那么两车的距离最小时，乙车的速度是多大？方向如何？题组一对动量守恒条件的理解1．关于系统动量守恒的条件，下列说法中正确的是()A．只要系统内存在摩擦力，系统的动量就不可能守恒B．只要系统中有一个物体具有加速度，系统的动量就不守恒C．只要系统所受的合外力为零，系统的动量就守恒D．系统中所有物体的加速度都为零时，系统的总动量不一定守恒2.如图所示，物体A的质量是B的2倍，中间有一压缩弹簧，放在光滑水平面上，由静止同时放开两物体后一小段时间内() A．A的速度是B的一半B．A的动量大于B的动量C．A受的力大于B受的力D．总动量为零3.在光滑水平面上A、B两小车中间有一弹簧，如图所示，用手抓住小车并将弹簧压缩后使小车处于静止状态．将两小车及弹簧看成一个系统，下面说法正确的是()A．两手同时放开后，系统总动量始终为零B．先放开左手，再放开右手后，动量不守恒C．先放开左手，后放开右手，总动量向左D．无论何时放手，两手放开后，在弹簧恢复原长的过程中，系统总动量都保持不变，但系统的总动量不一定为零题组二动量守恒定律的简单应用4．在高速公路上发生一起交通事故，一辆质量为1 500 kg向南行驶的长途客车迎面撞上了一辆质量为3 000 kg向北行驶的卡车，碰撞后两辆车接在一起，并向南滑行了一小段距离后停下，根据测速仪的测定，长途客车碰前以20 m/s的速率行驶，由此可判断卡车碰撞前的行驶速率()A．小于10 m/s B．大于20 m/s，小于30 m/sC．大于10 m/s，小于20 m/s D．大于30 m/s，小于40 m/s5．将静置在地面上质量为M(含燃料)的火箭模型点火升空，在极短时间内以相对地面的速度v0竖直向下喷出质量为m的炽热气体．忽略喷气过程重力和空气阻力的影响，则喷气结束时火箭模型获得的速度大小是( )A. m M v 0B. M m v 0C. M M －mv 0 D. m M －mv 0 6．质量为M 的木块在光滑水平面上以速度v 1向右运动，质量为m 的子弹以速度v 2水平向左射入木块，要使木块停下来，必须使发射子弹的数目为(子弹留在木块中不穿出)( )A.（M ＋m ）v 1m v 2B.M v 1（M ＋m ）v 2C.M v 1m v 2D.m v 1M v 27．质量为M 的小船以速度v 0行驶，船上有两个质量均为m 的小孩a 和b ，分别静止站在船头和船尾．现小孩a 沿水平方向以速率v (相对于静止水面)向前跃入水中，然后小孩b 沿水平方向以同一速率v (相对于静止水面)向后跃入水中，则小孩b 跃出后小船的速度方向________，大小为________(水的阻力不计)．题组三 综合应用8．光滑水平面上一平板车质量为M ＝50 kg ，上面站着质量m＝70 kg的人，共同以速度v0匀速前进，若人相对车以速度v＝2 m/s向后跑，问人跑动后车的速度改变了多少？。

物理学中的动量定理与冲量动量定理和冲量是物理学中重要的概念，它们帮助我们理解物体运动的原理和特性。

动量定理描述了作用力对物体运动的影响，而冲量则量化了力的作用时间。

本文将介绍动量定理和冲量的基本概念，并探讨它们在现实生活中的应用。

1. 动量定理的基本原理动量是物体运动的一个基本量，定义为物体的质量乘以其速度。

动量定理指出，当一个物体受到外力作用时，其动量的变化率等于作用于它的力的大小和方向。

换句话说，力是动量的源泉，它可以改变物体运动的状态。

按照牛顿第二定律，物体动量的变化率等于所受力的大小和方向。

当力作用时间很短，即力的作用瞬间完成时，这个变化量称为冲量。

冲量的大小等于力乘以时间，方向与力相同。

动量定理和冲量的关系在研究碰撞、运动中的力学问题时具有重要的作用。

2. 动量定理与碰撞动量定理在研究碰撞问题时特别有用。

碰撞是两个或多个物体之间发生的相互作用。

根据动量守恒定律，碰撞前后物体的总动量保持不变。

通过动量定理，我们可以计算碰撞过程中物体的变化动量，并推导出碰撞中的力学规律。

例如，当一个物体以一定的速度撞击另一个静止的物体时，根据动量定理，前者的动量将传递给后者，使其运动起来。

这种碰撞过程可以用冲量来表示，冲量的大小等于撞击力的大小乘以撞击时间。

通过分析冲量的大小和方向，我们可以推测碰撞后物体的运动状态。

3. 冲量与安全气囊冲量的概念在保护人类安全方面起到了重要的作用。

汽车上的安全气囊就是利用冲量原理来减缓碰撞产生的力。

当车辆发生碰撞时，安全气囊可以迅速膨胀，形成一个软垫，减缓乘客身体的冲击力。

安全气囊能够延长碰撞的时间，从而减小冲量的大小，降低身体受伤的可能性。

4. 动量定理与运动物体力学动量定理不仅适用于碰撞问题，还可以用于研究运动物体的力学特性。

例如，在空中飞行的飞机需要改变方向和速度，可以利用动量定理来分析推力和阻力的平衡。

又如，在运动中的火箭可以利用冲量调整自己的速度和轨道。

动量定理提供了理论基础，帮助我们理解和解决这些复杂的运动问题。

冲量与动量定律冲量和动量定律是描述物体运动与相互作用之间关系的重要物理定律。

本文将详细介绍冲量和动量定律的概念、公式及其应用。

一、冲量的概念与计算公式冲量是指力作用在物体上的时间积分，表示物体受到外力作用的效果。

冲量的计算公式如下：I = ∫F·dt其中，I表示冲量，F表示作用在物体上的力，t表示力作用的时间。

二、动量的概念与计算公式动量是物体运动状态的量度，是物体的质量与速度的乘积。

动量的计算公式如下：p = mv其中，p表示动量，m表示物体质量，v表示物体的速度。

三、冲量定律冲量定律是描述力对物体产生效果的物理定律。

根据冲量定律，当物体受到冲量时，其动量的变化量等于冲量，即Δp = I。

这表明，当物体受到外力作用时，它的动量将发生变化。

冲量定律的一种常见应用是描述弹性碰撞过程中的动量变化。

在弹性碰撞中，物体之间发生反弹或折返的情况较为常见。

根据冲量定律，当物体受到碰撞力作用时，其动量的变化量等于碰撞力在时间上的积分。

通过计算碰撞过程中的冲量，可以得到物体在碰撞后的速度和方向等信息。

四、动量定律动量定律是描述物体运动状态变化的物理定律。

根据动量定律，当外力作用于物体时，物体的动量将发生改变。

动量定律可以表达为F = Δp/Δt，其中F表示作用在物体上的力，Δp表示物体动量的变化量，Δt表示时间的变化量。

动量定律的一个重要应用是在解释力的作用过程中物体速度改变的原因。

根据动量定律，当物体受到外力作用时，它的动量将发生变化，从而导致速度的变化。

通过分析力对物体动量的改变，可以推导出物体速度的变化规律。

五、冲量与动量定律的应用举例1. 火箭发射：在火箭发射过程中，燃料喷射产生的冲量会使火箭获得一个巨大的动量，从而推动火箭向上运动。

2. 球类运动：例如足球的射门，球员踢球时给予球一个冲量，改变球的动量，使其向球门飞去。

3. 弹性碰撞：当两个弹性物体碰撞时，根据冲量定律和动量定律可以计算出碰撞后物体的速度和方向变化。

第三单元 牛顿定律 动量和冲量[课本内容] 马文蔚，第四版，上册 [30]-[50]，[58]-[65] [典型例题]例3-1．桌面上有一块质量为M 的木板，木板上放一个质量为的物体。

物体和木板之间、木板与桌面之间的滑动摩擦系数为，静止摩擦系数为。

现在要使木板从物体F至少多大？解：例3-2．质量分别为m 和M 的滑块A 和B ，叠放在光滑水平面上，如图．A 、B 间的静摩擦系数为μS ，滑动摩擦系数为μk ,系统原先处于静止状态．今将水平力F 作用于B 上，要使A 、B 间不发生相对滑动，应有 。

(ans .)例3-3．图中所示的装置中，略去一切摩擦力以及滑轮和绳的质量，且绳不可伸长，则质量为m 1的物体的加速度a 1= __________.解：对m 1：T 1=m 1a 1对m 2： m 2g －T 2=m 2a 2又 T 2=2T 1， a 1=2a 2 ………例3-4．质量为m 的平板A ，用竖立的弹簧支持而处在水平位置，如图．从平台上投掷一个质量也是m 的球B ，球的初速为v ，沿水平方向．球由于重力作用下落，与平板发生完全弹性碰撞。

假定平板是光滑的．则与平板碰撞后球的运动方向应为(A) A 0方向． (B) A 1方向．(C) A 2方向． (D) A 3方向． ［ ］ 提示：竖直方向上动量守恒，m B v By =m A v A 。

B 与A 碰后只有A 2方向速度。

所以选A 。

例3-5．三个物体A 、B 、C 每个质量都是M 。

B 、C 靠在一起，放在光滑水平桌面上，两者间连有一段长为0. 4m 的细绳，原先放松着B 的另一侧用一跨过桌边的定滑轮的细绳与A 相连(如图)。

滑轮和绳子的质量及轮轴上的摩擦不计，绳子不可伸长。

问：(1) A 、B 起动后，经多长时间C 也开始运动?(2) C 开始运动时速度的大小是多少? (取g=10m ·s -2)解：（1）设绳中张力为T ，分别对A 、B 列动力学方程解得设B 、C 之间绳长为，在时间t 内B 物体作匀加速运动，有m k μS μg M m F Ma g M m mg F mamg k s k s s ))(()(++=⇒⎩⎨⎧=+--≥μμμμμmg M M m F s)(+≤μa M T g M A A =-a M T B =)/(B A A M M g M a +=M M M B A == g a 21=∴l 4/2221gt at l ==12 3（2）B 和C 之间绳子刚拉紧时，A 和B 所达到的速度为令B 、C 间拉紧后，C 开始运动时A 、B 、C 三者的速度大小均为V ，由动量定理（T AB 为AB 间绳中张力，T BC 为BC 间绳中张力）得例3-6． 如图，用传送带A 输送煤粉，料斗口在A 上方高h=0.5m 处，煤粉自料斗口自由落在A 上，设料斗口连续卸煤的流量为q m =40kg/s ，A 以v=2.0m/s 的水平速度匀速向右移动。

动量与冲量的关系的推导与应用动量（Momentum）和冲量（Impulse）是力学中的重要概念，它们之间存在着密切的关系。

本文将通过推导和实际应用来阐述动量与冲量的关系，并探讨它们在物理学中的应用。

一、动量（Momentum）动量是一个物体运动状态的物理量，是描述物体运动“活力”的属性。

根据牛顿第二定律，物体的加速度与作用力成正比，与物体质量成反比。

因此，我们可以定义动量为物体质量乘以其速度：动量 = 质量 ×速度动量的单位是千克·米/秒（kg·m/s），通常用大写字母"P"表示。

二、冲量（Impulse）冲量是力在一定时间内作用于物体上的效果，是力对物体的作用时间的累积。

按照牛顿第二定律，力等于物体质量乘以其加速度。

因此，我们可以将冲量定义为力与时间的乘积：冲量 = 力 ×时间冲量的单位是牛·秒（N·s），通常用大写字母"I"表示。

三、动量与冲量的关系在物理学中，动量和冲量之间存在着紧密的数学关系。

根据牛顿第二定律和动量的定义，可以推导出动量变化的公式：动量变化 = 质量 ×加速度 ×时间 = 力 ×时间 = 冲量由此可见，冲量等于物体的动量变化。

也可以用数学公式表示为：I = ΔP其中，I代表冲量，ΔP代表动量变化。

四、动量与冲量的应用动量和冲量的理论在物理学中有着广泛的应用。

1. 碰撞问题在碰撞问题中，动量和冲量理论可以用来解释物体碰撞发生后的运动状态。

当两个物体发生完全弹性碰撞时，根据动量守恒定律，可以推导出碰撞前后两个物体的动量分别为：m1u1 + m2u2 = m1v1 + m2v2其中，m1和m2分别为物体1和物体2的质量，u1和u2为碰撞前两个物体的速度，v1和v2为碰撞后两个物体的速度。

2. 飞行物体对于飞行物体，如火箭、导弹等，动量和冲量理论可以用来计算其运动过程中所受的力和加速度。

物理动量与冲量物理学中，动量（momentum）是描述物体运动状态的重要物理量，而冲量（impulse）则是力在时间上的积累。

本文将介绍物理动量与冲量的概念、性质以及它们在各领域的应用。

一、物理动量的定义与性质动量是物体质量和速度乘积的物理量，可以用公式表示为：动量（p）= 质量（m） ×速度（v）动量是一个矢量量，即具有大小和方向。

根据牛顿第二定律，物体所受合外力的改变率等于动量的改变率，即：F = dp/dt根据上述公式可以得知，物体的动量可以通过改变其质量或速度来进行调控。

例如，一个物体的质量增加，则相同大小的速度下其动量也相应增加。

二、冲量的定义与性质冲量是力在时间上的积累，可以用公式表示为：冲量（I）= F × Δt其中，F为作用力的大小，Δt为作用时间的变化。

冲量是一个矢量量，它的方向与力的方向相同。

牛顿第二定律可以改写为：F = d(mv)/dt = mdv/dt = madt/dt = ma = mΔv / Δt可见，冲量等于力乘以作用时间，同时也等于质量乘以速度的变化量。

三、动量守恒定律动量守恒定律是物理学中的重要定律之一，它表明在一个孤立系统中，总动量保持不变。

动量守恒定律可以用公式表示为：Σp初= Σp末这意味着在一个系统中，任何物体的动量之和在发生碰撞或相互作用前后保持不变。

四、冲量与动量守恒定律的应用1. 碰撞实验动量守恒定律在碰撞实验中起到关键作用。

例如，在双球碰撞实验中，可以通过测量碰撞前后两球的速度和质量来验证动量守恒定律，并计算出碰撞的冲量。

2. 运动力学动量与冲量在运动力学中也有广泛应用。

在分析物体的运动状态和力学问题时，常常利用动量定理和冲量-时间定理简化计算过程。

这些定理可以有效地描述物体受力、运动和力学系统的行为。

3. 工程应用动量守恒定律和冲量的概念在工程领域中也有实际应用。

例如，在汽车碰撞实验中，研究动量和冲量的变化可以帮助设计更安全的汽车结构，以减少碰撞对车辆和乘客造成的伤害。

第3章动量守恒定律和能量守恒定律习题一选择题3-1 以下说法正确的是[ ]（A）大力的冲量一定比小力的冲量大（B）小力的冲量有可能比大力的冲量大（C）速度大的物体动量一定大（D）质量大的物体动量一定大解析：物体的质量与速度的乘积为动量，描述力的时间累积作用的物理量是冲量，因此答案A、C、D均不正确，选B。

3-2 质量为m的铁锤铅直向下打在桩上而静止，设打击时间为t∆，打击前锤的速率为v，则打击时铁捶受到的合力大小应为[ ]（A）mvmgt+∆（B）mg（C）mvmgt-∆（D）mvt∆解析：由动量定理可知，F t p mv∆=∆=，所以mvFt=∆，选D。

3-3 作匀速圆周运动的物体运动一周后回到原处，这一周期内物体[ ] （A）动量守恒,合外力为零（B）动量守恒,合外力不为零（C）动量变化为零,合外力不为零, 合外力的冲量为零（D）动量变化为零,合外力为零解析：作匀速圆周运动的物体运动一周过程中，速度的方向始终在改变，因此动量并不守恒，只是在这一过程的始末动量变化为零，合外力的冲量为零。

由于作匀速圆周运动，因此合外力不为零。

答案选C。

3-4 如图3-4所示，14圆弧轨道(质量为M)与水平面光滑接触，一物体（质量为m）自轨道顶端滑下，M与m间有摩擦，则[ ]（A ）M 与m 组成系统的总动量及水平方向动量都守恒,M 、m 与地组成的系统机械能守恒（B ）M 与m 组成的系统动量不守恒, 水平方向动量守恒，M 、m 与地组成的系统机械能不守恒（C ）M 与m 组成的系统动量不守恒, 水平方向动量不守恒，M 、m 与地组成的系统机械能守恒（D ）M 与m 组成系统的总动量及水平方向动量都守恒，M 、m 与地组成的系统机械能不守恒解析：M 与m 组成的系统在水平方向上不受外力，在竖直方向上有外力作用，因此系统水平方向动量守恒，总动量不守恒,。

由于M 与m 间有摩擦，m 自轨道顶端滑下过程中摩擦力做功，机械能转化成其它形式的能量，系统机械能不守恒。