下载文档原格式
粒子物理学中的粒子寿命与稳定性粒子物理学研究的是构成宇宙的基本物质及其相互作用规律。
在这个领域中，粒子的寿命和稳定性是一个重要的研究方向。
本文将探讨粒子的寿命和稳定性对于粒子物理学的意义以及相关研究的进展。
一、粒子寿命的定义与测量方法1.1 粒子寿命的定义粒子的寿命指的是从其生成到衰变所经历的时间间隔。
在粒子物理学中，通常使用平均寿命来描述一个粒子的寿命。
1.2 粒子寿命的测量方法粒子寿命的测量方法主要有两种：直接寿命测量与间接寿命测量。
直接寿命测量通过粒子轨迹的观测来确定粒子寿命。
而间接寿命测量则通过测量粒子衰变产物的能谱来获得粒子的寿命信息。
二、粒子寿命的重要性2.1 粒子寿命与基本相互作用粒子的寿命与其参与的基本相互作用有密切的关系。
例如，正电子是电子的反粒子，其寿命非常短暂，约为2.2微秒，这是因为正电子会与电子进行湮灭反应，释放能量。
而稳定的粒子，如电子和光子，寿命则非常长久，几乎可以认为是无限的。
2.2 粒子寿命与物质的稳定性粒子的寿命还与物质的稳定性密切相关。
例如，质子和中子是构成原子核的基本粒子，它们的寿命非常长，可以稳定存在于原子核中。
而高能粒子的寿命很短，靠着高能环境中的相互作用来维持其稳定性。
三、粒子稳定性的研究进展3.1 稳定性的理论模型粒子稳定性的研究离不开理论模型的发展。
目前已经提出了多种粒子稳定性的理论模型，如弱相互作用理论、标准模型等。
这些模型通过数学计算和实验验证，揭示了不同粒子的稳定性来源和衰变规律。
3.2 粒子稳定性的实验研究粒子稳定性的实验研究通常利用大型粒子加速器和探测器进行。
科学家通过观测和测量粒子的衰变产物和能谱，对粒子的稳定性进行研究。
这些实验为粒子物理学的发展和理论验证提供了重要的实验依据。
四、应用与展望4.1 应用领域粒子物理学的研究不仅仅是为了拓展基础科学的前沿，还有着重要的应用价值。
例如，粒子寿命的研究对于医学放射诊断技术的改进和发展具有重要的指导作用。
少子寿命测量方法都包括非平衡载流子的注入和检测两个基本方面。
最常用的注入方法是光注入和电注入，而检测非平衡载流子的方法很多，如探测电导率的变化，探测微波反射或透射信号的变化等，这样组合就形成了许多寿命测试方法，如：直流光电导衰减法；高频光电导衰减法；表面光电压法；微波光电导衰减法等。
WT-2000PV 采用微波光电导衰减法测试少子寿命。
微波光电导衰退法(Microwave photoconductivity decay)测试少子寿命，主要包括激光注入产生电子-空穴对和微波探测信号这两个过程。
904nm 的激光注入（对于硅，注入深度大约为30μm）产生电子-空穴对，导致样品电导率的增加，当撤去外界光注入时，电导率随时间指数衰减，这一趋势间接反映少数载流子的衰减趋势，从而通过微波探测电导率随时间变化的趋势就可以得到少数载流子的寿命。
μ-PCD测试得到的是少子有效寿命，它会受到两个因素影响：体寿命和表面寿命。
测得的少子寿命可由下式表示：（2-1）式中：τdiff 为少子从样品体内扩散到表面所需时间；τsurf 为由于样品表面复合产生的表面寿命；τmeas 为样品的测试寿命；d 为样品厚度；Dn，Dp 分别为电子和空穴的扩散系数；S 为表面复合速度。
（图2-1）不同的表面复合速率下，体寿命和测试寿命的关系由式（2-1）可知，表面寿命对测试寿命有很大影响，使其偏离体寿命，图2-1是体寿命与测试寿命的关系。
在样品厚度一定的情况下，即扩散寿命一定，如果表面复合速率很大，则在测试高体寿命样品时，测试寿命值与体寿命值就会偏差很大；而对于低体寿命的样品，不会使少子寿命降低很多。
因此我们需对样品表面进行钝化，降低样品的表面复合速率。
从图2-1我们可以看到，对于表面复合速率S为1cm/s，或10cm/s的样品，即使在1000μs数量级的体寿命，测试寿命还是与体寿命偏差很小。
即当样品的表面复合速率为10cm/s或更小的情况下，对于1000μs数量级高体寿命的样品，测试寿命也能用来表示体寿命。
少子寿命测量方法都包括非平衡载流子的注入和检测两个基本方面。
最常用的注入方法是光注入和电注入，而检测非平衡载流子的方法很多，如探测电导率的变化，探测微波反射或透射信号的变化等，这样组合就形成了许多寿命测试方法，如：直流光电导衰减法；高频光电导衰减法；表面光电压法；微波光电导衰减法等。
WT-2000PV 采用微波光电导衰减法测试少子寿命。
微波光电导衰退法(Microwave photoconductivity decay)测试少子寿命，主要包括激光注入产生电子-空穴对和微波探测信号这两个过程。
904nm 的激光注入（对于硅，注入深度大约为30μm）产生电子-空穴对，导致样品电导率的增加，当撤去外界光注入时，电导率随时间指数衰减，这一趋势间接反映少数载流子的衰减趋势，从而通过微波探测电导率随时间变化的趋势就可以得到少数载流子的寿命。
μ-PCD测试得到的是少子有效寿命，它会受到两个因素影响：体寿命和表面寿命。
测得的少子寿命可由下式表示：（2-1）式中：τdiff 为少子从样品体内扩散到表面所需时间；τsurf 为由于样品表面复合产生的表面寿命；τmeas 为样品的测试寿命；d 为样品厚度；Dn，Dp 分别为电子和空穴的扩散系数；S 为表面复合速度。
（图2-1）不同的表面复合速率下，体寿命和测试寿命的关系由式（2-1）可知，表面寿命对测试寿命有很大影响，使其偏离体寿命，图2-1是体寿命与测试寿命的关系。
在样品厚度一定的情况下，即扩散寿命一定，如果表面复合速率很大，则在测试高体寿命样品时，测试寿命值与体寿命值就会偏差很大；而对于低体寿命的样品，不会使少子寿命降低很多。
因此我们需对样品表面进行钝化，降低样品的表面复合速率。
从图2-1我们可以看到，对于表面复合速率S为1cm/s，或10cm/s的样品，即使在1000μs数量级的体寿命，测试寿命还是与体寿命偏差很小。
即当样品的表面复合速率为10cm/s或更小的情况下，对于1000μs数量级高体寿命的样品，测试寿命也能用来表示体寿命。
μ子寿命测量实验孙腊珍;吴雨生;李澄【摘要】根据粒子的平均寿命测量原理,采用大面积塑料闪烁探测器和可编程逻辑器件设计了宇宙线μ子寿命测量的实验教学装置,使用该装置可实现对宇宙μ子寿命的直接测量. 通过该实验,可使学生对高能物理理论、高能粒子探测器、高能粒子探测技术和数据获取、处理有整体的理解和认识. 本文从实验教学内容和教学方法上对μ子寿命测量实验进行了探讨.【期刊名称】《物理实验》【年(卷),期】2010(030)002【总页数】4页(P1-3,19)【关键词】宇宙线μ子;寿命测量;高能粒子探测器【作者】孙腊珍;吴雨生;李澄【作者单位】中国科学技术大学,近代物理系,安徽,合肥,230026;中国科学技术大学,近代物理系,安徽,合肥,230026;中国科学技术大学,近代物理系,安徽,合肥,230026【正文语种】中文【中图分类】O572.3231 引言宇宙线中的μ子主要是由宇宙线中的π介子衰变(π-→μ-+¯νμ,π+→μ++νμ)产生的.大部分的μ子产生在约15 km的高空,由于μ子不参与强相互作用,因而具有较强的穿透力.海平面上μ子的通量近似为1～2 cm-2·min-1,平均能量约为4 GeV[1-2].μ子带有1个单位的电荷,其质量为105.658 M eV/c2,平均寿命约2.197μs[3].对μ子寿命进行测量具有重要的物理意义,例如:可以利用μ子寿命的精确值来确定粒子物理标准模型中的费米耦合常数 G F;在实验室对μ子的观测和寿命测量也是对狭义相对论的时间膨胀效应的有力验证.在高能粒子物理实验中,传统的粒子衰变寿命测量方法是直接测量衰变事例的时间分布,计算出粒子的寿命.实验上通常采用延迟符合法测量μ子平均衰变寿命,该方法至少需要2个探测器以及相关的逻辑电路和数据处理系统,这就使得实验装置复杂,并且仪器设备所需费用较高.中国科学技术大学近代物理系高能物理研究室的教师将科研成果经过精炼,核心提取,并采用大面积塑料闪烁探测器和可编程程序逻辑器件,自行设计了专门的电子学电路和探测系统,研制了既简便又大量减少仪器费用的μ子寿命测量装置,实现了对宇宙线μ子寿命直接测量[4],测量精度达到实验要求.2 实验原理宇宙线中的μ子通过塑料闪烁体时,主要的能量损失方式是电离能损,并伴随库仑散射.高能量μ子可直接从闪烁体中穿出,并在径迹周围产生电子及荧光光子等次级粒子;一些较低能量μ子在闪烁体中停止后,可以自由衰变,也可能与物质的原子核发生作用被俘获而消失.其发生衰变如下:衰变中产生的电子(e)继续与闪烁体发生作用损失能量,并使闪烁体分子激发,而电子反中微子(¯νe)和μ子中微子(νμ)直接穿出.塑料闪烁体中受激发的分子在极短的时间内(约10-10 s)退激发并发射荧光(荧光波长在350～500 nm之间),荧光通过光电倍增管光电转换放大而输出电信号,这个信号将作为μ子的“到达”信号.当停止在闪烁体内的μ子发生衰变,产生的电子被闪烁探测器探测,形成μ子“衰变”的信号.“到达”探测器的信号与μ子“衰变”的信号的时间间隔,即为μ子1次衰变的寿命.由于微观粒子的衰变具有一定的统计性,因此实验上是通过测量时间差的分布,进而计算得到μ子的平均寿命[5-6].宇宙线中μ子的通量很低,每次击中探测器的事例可以看成单μ子事例.设μ子的平均寿命为τ,第 i个μ子的产生时间为 ti,则相对公共的时间零点,μ子在时刻t衰变概率[3]为如果第i个μ子到达闪烁探测器的时刻为 Ti,那么时间间隔ΔT内,这个μ子衰变的概率是:式中 K=e-(Ti-ti)/τ.如果实验共测量到M个μ子衰变事例,则在时间差ΔT以内,衰变的总μ子数N为式中可见在ΔT时间内μ子衰变数随时间同样服从指数规律.实验上通过记录确定时间间隔内的μ子衰变事例数,利用指数函数拟合方法,可以求得μ子衰变的平均寿命τ.3 实验装置根据μ子寿命测量实验原理,自行设计制作了大面积闪烁探测器(探测面积450 cm2),如图1所示.实验使用的塑料闪烁体的发光衰减时间约为3 ns,与微秒量级的μ子衰变时间相比很小,可以保证时间差测量的相对准确性.图1 实验装置系统框图整个实验测量装置由塑料闪烁探测器[6]、高压电源、数据获取系统以及计算机和分析软件4部分组成.宇宙线中μ子入射到塑料闪烁体,经光电倍增管、放大器、甄别器、可编程逻辑电路(FPGA),最后通过USB接口把数据输入计算机处理.图2是测量装置的照片.2套测量装置共用1个闪烁体和高压电源.图2 μ子寿命测量装置4 实验内容首先将高压电源线(红色)与探测器连接,探测器信号线(黑色)与信号处理仪器测量面板上的信号输入端连接,USB接口线与计算机相应接口连接.将各部件电源线接好,检查无误后,打开高压电源和信号处理仪器电源,并将探测器工作高压设置为-600 V,记录电压及电流值.1)用示波器观测放大器输出信号,并记录放大信号特征(幅度、上升时间,噪声信号);观测甄别器输出信号,记录甄别器输出信号特征(信号宽度、频率).2)调节仪器面板上的电阻以选择合适的阈电压,使得去除放大器输出信号中包含的噪声信号.其方法是将阈电压从0.01～0.5 V连续变化,取10个测量点,作μ子计数-阈电压曲线,并得出合适的阈电压值.3)打开计算机,执行数据获取软件:m uon.tcl,获取μ子的衰变信号,要求累积数据时间足够长(实验安排测量 3～4 h),存储数据文件(自备U盘拷贝数据文件).学生完成实验后,要求利用O rigin软件处理数据,计算μ子的平均寿命,打印出实验曲线和实验结果,如图3所示.可选取感兴趣的相关问题进行探讨:a.在地面参考系观测,运动的μ子(速率为0.998c)到达地面的平均寿命是多少?与实验测量的结果是否矛盾?b.该实验是如何保证测量的2个信号恰是同一μ子的到达与衰变信号?c.解释实验测量的μ子衰变寿命曲线具有一定分布的物理原因.图3 衰变事例-时间关系曲线d.比较所测数据与 100 h数据结果(由实验室提供)的差别.实验测量误差可能有哪些来源,如何减少这些误差?e.1948年,我国科学家张文裕发现负μ子可以取代电子被原子核捕获形成μ原子,分析μ氢原子与氢原子在原子半径、结合能方面的差异.设想是否可以用μ氘原子实现聚变反应?对问题b的探讨:学生可以利用 GEAN T4软件[4]对入射μ子在探测器中的衰变概率进行模拟.估计测量事例率,分析偶然事例对实验的影响.μ子的测量实验中,对每个事例设置20μs的测量时间窗,只取到达信号与衰变信号时间间隔小于这个窗的事例.对实验进行模拟,宇宙射线的μ子在晶体中衰变比率约2×10-3,而μ子的事例率约为10 Hz,μ子的衰变计数率在每分钟几个左右.伪事例的概率,即20μs内连续有2个无时间关联的μ信号的概率约10-4量级,所以可以认为,经可编程逻辑判选后,所测量输出的数据几乎都是μ子沉积在闪烁体内并且发生衰变的事例.对问题d的探讨:学生可获取不同时期(例如:10 h,1 d,7 d等)的多组数据,用适当的统计方法处理实验数据,并对结果进行统计置信度分析,使学生认识数据的随机性和统计性.学生通过查阅参考书、计算机模拟或实验和数据分析,对感兴趣的问题进行探讨,可进一步理解μ子寿命测量的实验原理,加深对爱因斯坦相对论中时间膨胀效应的理解.同时给出实验条件,写出实验报告.图3给出的是累积收集了18 296个衰变事例的实验结果.由测量数据拟合得到的实验值为τ=(2 124.6±9.6)ns,与文献[2]中给出的μ子静止平均寿命参考值(2 197.03±0.04)ns相近.由于测量时间所限,事例率及事例总样本数偏低,精度略显不足.5 结束语自行研制的μ子寿命测量实验装置相对比较精简,是一个较典型的基本粒子探测实验,测量方法新颖可靠,同时利用宇宙线开设高能粒子物理实验,既节省了经费,又解决了使用放射源开设核物理实验的辐射防护问题.学生通过此实验,加深了对高能粒子物理理论理解,并对高能粒子探测器、宇宙线的探测方法、相关电子学和数据获取与处理等方面有比较系统的了解.参考文献:【相关文献】[1] Coan T E,Ye J.M uon physics user manual[Z].v050201.0.[2] Particle Data Group.Cosmic ray muon detection[Z].Review of Particle Physics,Regentsof the U-niversity of Califo rnia.2006.[3] Lundy R A.Precision measurement of theμ+lifetime[J].Phys.Rev.,1962,125:1 686-1 696.[4] 吴雨生.宇宙线muon寿命测量实验的Geant4模拟[D].合肥:中国科学技术大学,2008.[5] 谢一冈,陈昌,王曼,等.粒子探测器与数据获取[M].北京:科学出版社,2003:171-220.[6] 汪晓莲,李澄,邵明,等.粒子探测技术[M].合肥:中国科学技术大学出版社,2009:232-274.[7] 林延畅,陈少敏,高原宁,等.μ子寿命测量与高能物理实验创造性人才的培养[J].实验技术与管理2008,25(9):19.。
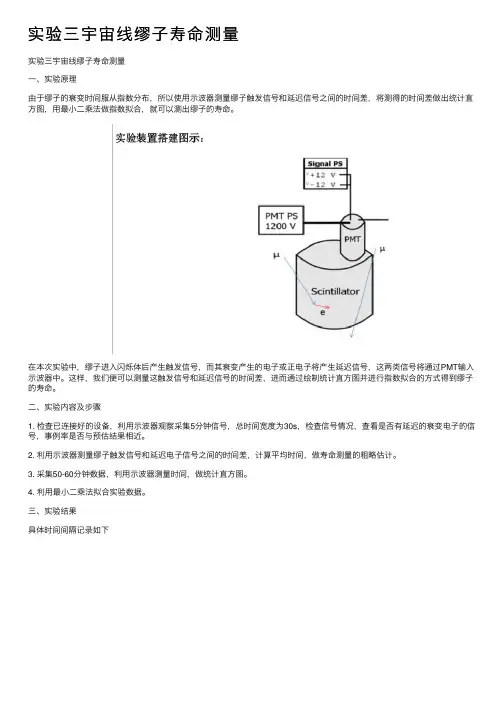
实验三宇宙线缪⼦寿命测量实验三宇宙线缪⼦寿命测量⼀、实验原理由于缪⼦的衰变时间服从指数分布，所以使⽤⽰波器测量缪⼦触发信号和延迟信号之间的时间差，将测得的时间差做出统计直⽅图，⽤最⼩⼆乘法做指数拟合，就可以测出缪⼦的寿命。
在本次实验中，缪⼦进⼊闪烁体后产⽣触发信号，⽽其衰变产⽣的电⼦或正电⼦将产⽣延迟信号，这两类信号将通过PMT输⼊⽰波器中。
这样，我们便可以测量这触发信号和延迟信号的时间差，进⽽通过绘制统计直⽅图并进⾏指数拟合的⽅式得到缪⼦的寿命。
⼆、实验内容及步骤1. 检查已连接好的设备，利⽤⽰波器观察采集5分钟信号，总时间宽度为30s，检查信号情况，查看是否有延迟的衰变电⼦的信号，事例率是否与预估结果相近。
2. 利⽤⽰波器测量缪⼦触发信号和延迟电⼦信号之间的时间差，计算平均时间，做寿命测量的粗略估计。
3. 采集50-60分钟数据，利⽤⽰波器测量时间，做统计直⽅图。
4. 利⽤最⼩⼆乘法拟合实验数据。
三、实验结果具体时间间隔记录如下统计结果如下：统计直⽅图如下：使⽤MATLAB中的Curve Fitting Tool进⾏拟合，结果如下：General model: f(x) = a*exp(-b*x)+cCoefficients (with 95% confidence bounds):a = 12.54 (10.09, 15)b = 0.4673 (0.3316, 0.6031)c = 1.126e-08 (fixed at bound)Goodness of fit:SSE: 3.572R-square: 0.9381Adjusted R-square: 0.9278RMSE: 0.7715可得缪⼦寿命τ=1/b=1/0.4673=2.14µs，与缪⼦的静⽌寿命较为接近。
四、实验思考1. 如何初始检查信号的质量？将PMT输出的信号直接输⼊⽰波器中进⾏观察。
2. 如何利⽤最⼩⼆乘法去寻找参数的最优值？可以对计数取对数，然后利⽤最⼩⼆乘法进⾏直线拟合，就可以⽐较简单地得到最优的参数。
- 7 -高 新 技 术０ 引言在地球表面可以探测到的宇宙射线就是μ子，μ子产生于离地面15 km 的高空，其速度接近光速。
工作人员一般使用多个探测器对μ子进行观测，对其寿命进行测量，并利用延迟符合的方法测量其衰变的时间分布，该方法成本较高。
为了在降低实验成本的同时，可以方便快捷地测量出宇宙线μ子的寿命，研究人员经过研究和改进，发明出融合NaI（Tl）闪烁体探测器、时间甄别器、时间幅度转换器以及多道分析器的简单方法（1种利用大面积塑料闪烁探测器配上可编程的程序逻辑器件）去测量μ子的寿命。
该方法不仅成本较低，而且还能保证实验结果具有极高的准确性。
研究人员在实验室测量的μ子寿命也是以闪烁体探测为基础而开展的，所用到的实验设备是宇宙线测量装置CRP3。
１ μ子的寿命及实验室探测原理１．１ μ子寿命μ子是1种在粒子碰撞中产生的亚原子粒子。
更恰当的说法是它的电荷等于电子的电荷，其质量是电子的200多倍。
因此，它通常被认为是1个重电子。
然而，与电子不同，μ子寿命很短，会很快衰变为其他粒子，通常是1个电子和一些中微子。
实验表明，它们的平均寿命（或者说半衰期）是2.2 μm 。
也就是说，如果研究人员从1 000个μ子开始，在2 μm 之后，预计会剩下大约500个 μ子。
再过2 μm ，将剩下250个μ子等。
μ介子是1个不稳定的基本粒子，即μ子会被分解为其他粒子。
在罗西（Rossi）进行关于μ子衰变的开创性实验时，已知的其他基本“粒子”是光子、电子及其反粒子（正电子）、质子、中子和中微子。
从那时起，已经发现了数10种粒子和反粒子，其中大多数是不稳定的粒子。
实际上，在所有被观测为孤立实体的粒子中，寿命比μ介子长的只有光子、电子、质子、中子、中微子及其反粒子。
甚至中子在自由时也会遭受β衰变，其半衰期为15 min [1]。
１．２ μ子寿命的探测原理研究人员在该实验中使用的是实验室的宇宙线测量装置CRP3。
当宇宙线粒子在该装置的闪烁体中停止衰变时，CRP3的探测器会将信号传给该实验装置的读出电子学系统。
μ子寿命测量
摘要：利用塑料闪烁体探测μ子，测量μ子的衰变时间分布，利用计算机模拟泊松过程来分析造成测量结果本底的原因，对比多种处理μ子寿命的方法，得到在本实验条件下最合理的实验结果。
关键词：宇宙线μ子；寿命测量；本底；泊松分布
引言：μ子是大自然最基本的粒子之一，地球上的生物每时每刻都受到μ子的照射。
μ子最早于1937年被J.C.Street 和E.C.Stevenson 发现1)，后来物理学家通过各种不同的方法对其进行了探测，得到其基本寿命为：（2197.03±0.04）ns 。
μ子寿命服从指数分布，当时间逐渐增大，单位时间内衰变的μ子数应该趋于0，但实验测得的结果却是趋于一个常数，本文将利用计算机模拟泊松过程来验证该本底是由两个相继到来的μ子产生的偶然符合事件造成的，并在此基础上采取恰当的方式来计算μ子的平均寿命。
实验原理：
一、实验中使用的μ子来源。
地球上的生物每时每刻都受到μ子的照射，μ子产生与大15km 的高空，由原始宇宙射线与大气中的原子核相互作用产生，海平面上μ子的通量近似为2212min cm --,这就是实验中用于探测的μ子源。
二、μ子在塑料闪烁体中发生的过程及探测原理
μ子在进入塑料闪烁体后首先主要通过电离能损和库仑散射损失能量，并使闪烁体分子发出荧光，高能μ子能直接从闪烁体中穿出，而能量较低的μ子将静止在闪烁体内，发生衰变：e e v v μμ--
→++，衰变产生的电子具有较高的能量会使闪烁体分子激发，在退激发时发出荧光，v e -与v μ则直接穿出。
图1 μ子探测原理图
上图为μ子探测原理图，μ 子从高层大气穿透下来，进入塑料闪烁体，产生的光脉冲进入PMT ，倍增过后通过一个线性放大器线性放大，随后经过一个甄别器的筛选，输出到FPGA 进行鉴定，最后在PC 上显示出来。
其中甄别器的工作原理是筛选高于其阈值的信号输出，而FPGA 的功能是记录满足其时间设定的两个脉冲之间的时间间隔,本实验中只有时间差小于20000ns 的信号才会被当做μ子衰变信号，该时间差才会被当做μ子的衰变时间被记录。
三.μ子的寿命服从指数分布，即有
()t f t e λλ-= （1）
对确定在t 0时刻前不会衰变的N 0个μ子，在t 0后按以确定时间长度T 划分时间区间，则第k 个时间区间对应的时间是(t 0+(k-1)T ，t 0+kT],设在此区间内衰变的μ子数为N(k),则有
000000(t )00(1)()(1)e t kT t t kT t T t k T t N k N e dt N e e λλλλλλ+--+-+--==-⎰ (2)
当以区间末对应的时间点作为自变量x ，对应区间内衰减的μ子数作为N(k)，两者满足指数函数关系：
()x N k Ae
λ-= （3） 其中A 为常数，00(1)t T A N e e λλλ=-，对（3）式两边同时取对数，得
ln(())N k C x λ=- (4)
其中ln C A =,为一常数。
故实验中即可以用指数函数拟合N(k)~x 关系，也可以用线性拟合ln(N(k))~x 关系来求得衰变速率λ，从而利用1/τλ=可求得μ子的平均寿命。
实验中对μ子到来的计数过程为一泊松过程，即相邻两个μ子之间的时间t ∆服从指数分布， ()n t f t n e μμ-∆∆= （5）
其中n μ为实验中μ子到来的速率。
实验装置：
图
2
实
验仪
器
上图中黑色的铝制圆柱里面，包含了塑料闪烁体，PMT ，以及高压电源；MUON PHIYSICS 子箱里面包含了放大器以及甄别器
实验结果与分析：
1.实验中探测μ子的总时间为1651225s,探测到的μ子总数为4836812个，其中有12493个μ子发生了衰变。
μ子计数率4836812==2.931651225
n μ个/s
对μ子衰变时间的统计结果如表1所示，注意到随着t 的增大，
各时间区间内衰变的μ子数目并不趋于0，而是近似为一个常数，为了看出造成此本底的原因，下面用计算机模拟μ子的计数过程
表1 对μ子衰变时间的统计结果
统计区间/ns 衰变μ子数
（0,40] 66
(40,1040]
4605 (1040,2040]
2832 (2040,3040]
1793 (3040,4040]
1135 (4040,5040]
693 (5040,6040]
446 (6040,7040]
276 (7040,8040]
188 (8040,9040]
125 (9040,10040]
91 (10040,11040]
46 (11040,12040] 39
(12040,13040] 29
(13040,14040] 26
(14040,15040] 23
(15040,16040] 28
(16040,17040] 7
(17040,18040] 19
(18040,19040] 13
(19040,20000] 13
图3 模拟μ子到达的程序框图，其中函数g(x 0)=-1/n μ*ln(x 0)
当模拟N=4836812个μ子到达后，模拟得到的总时间（即所有x 相加）为1651347.5，与实验探测到N 个μ子到达花费的总时间1651225s 非常接近，可见用泊松分布模拟μ子的到达是合理的。
由模拟结果（见表二）可见，由于μ子以2.93个/s 的速率到达，当到达的μ子数目足够多时，也会有一定数目的μ子到达时间间隔很短，小于设定的判别时间，且在到达时间上μ 子是均匀分布的，对比模拟得到的本底与实验测得的结果（表1）对比，可看出结果中的本底与模拟得到的本底
水平相当，表明确实是相邻μ子到达时间在小于20000ns 内也是均与分布的造成结果中的本底。
重复模拟产生N 个μ子的过程100次得到1000ns 内本底的平均值为14.18ns. 3.由于仪器在探测到信号后需要一定的恢复时间才能重
新探测信号，故只统计40ns 后衰变的μ子（不包括40ns ）,
为减小统计涨落造成的影响，以2000ns 为时间间隔统计衰变的μ子，并用指数函数/0x y Ae y τ-=+拟合统计得到的结果（图4），得到的结果为(2107.68.4)ns τ=± Adj R-square 为0.9991，与理论值的偏差为4.07%
表2 模拟的本底分布
图4 指数拟合统计结果
时间区间末/ns 偶然符合的事件数 偶然符合的事件数
1000 10 11
2000 20 21 3000 13 10 4000 18 14 5000 11 12
6000
11 17 7000
10 17 8000
15 14 9000
14 8 10000
19 14 11000
13 18 12000
10 13 13000
12 9 14000
16 10 15000
10 8 16000
14 11 17000
18 14 18000
12 8 19000
18 17 20000
12 7 平均值 13.8 12.65
表3 指数拟合结果
由上表拟合的结果可以看到，拟合的本底值为28.20与计算机模拟100次得到的平均本底值28.36（14.18*2）非常接近，进一步验证了用泊松过程的可行性。
τ=±，与μ子寿命的理论值实验中得到的μ子寿命为(2123.258.48)ns
τ=±相比较，偏差为3.37%。
(2197.030.04)ns
总结：本次实验利用计算机模拟泊松分布成功地解释了衰变μ子计数的均匀本底，并利用重复该过程100次得到的平均本底值，并选取恰当的统计区间来统计衰变的μ子数，利用指数函数拟合处理统计结果，求得μ子的平均寿命，并将其与μ子理论寿命相比较，得到的实τ=±，与理论值偏差为3.37%。
验结果为(2123.258.48)ns
由于本实验中探测时间不够长，探测到的μ子衰变实例较少，限制了实验的精度。
参考文献:
1> Coan.T.E, Ye J . Muon Physics:V050201.0[EB/OL].[2008-12-04]
2>吴雨生.一种简便的μ子寿命测量实验设计.中国科学技术大学学报.2010.6.第40卷第6期。
