华南理工大学 大学物理 课后习题气体动理论,习题九

第7章 气体动理论练习题一、选择题1、若理想气体的体积为V ，压强为p ，温度为T ，一个分子的质量为m ，R 是摩尔气体常量，k 称为玻耳兹曼常量，则该理想气体的分子数为[ B ](A) pV/m. (B) pV/(kT).(C) pV/(RT). (D) pV/(mT).2、下列各式中哪一式表示气体分子的平均平动动能？（式中M 为气体的质量，m 为气体分子质量，N 为气体分子总数目，n 为气体分子数密度，mol M 为摩尔质量，A N 为阿伏加得罗常量）[ A ] (A)pV M m 23. (B) pV M M mol 23. (C) npV 23. (D) pV N MM A 23mol . 3、根据经典的能量按自由度均分原理，每个自由度的平均能量为[ C ](A) kT /4. (B)kT /3.(C) kT /2. (D)kT.4、在20℃时，单原子理想气体的内能为[ D ](A)部分势能和部分动能. (B)全部势能. (C)全部转动动能.(D)全部平动动能. (E)全部振动动能.5、如果氢气和氦气的温度相同，摩尔数也相同，则[ B ](A)这两种气体的平均动能相同. (B)这两种气体的平均平动动能相同.(C)这两种气体的内能相等. (D)这两种气体的势能相等.6、在一密闭容器中，储有A 、B 、C 三种理想气体，处于平衡状态．A 种气体的分子数密度为n 1，它产生的压强为p 1，B 种气体的分子数密度为2n 1，C 种气体的分子数密度为3 n 1，则混合气体的压强p 为［D ］(A) 3 p 1． (B) 4 p 1．(C) 5 p 1． (D) 6 p 1．7、在容积V ＝4×10-3 m 3的容器中，装有压强P ＝5×102 Pa 的理想气体，则容器中气体分子的平动动能总和为［B ］(A) 2 J ． (B) 3 J ．(C) 5 J ． (D) 9 J ．8、若室内生起炉子后温度从15℃升高到27℃，而室内气压不变，则此时室内的分子数减少了［B ］(A) 0.500． (B) 400.(B) 900． (D) 2100．9、麦克斯韦速率分布曲线如图所示，图中A 、B 两部分面积相等，则该图表示［ D ］(A) 0v 为最概然速率．(B) 0v 为平均速率．(C) 0v 为方均根速率．(D) 速率大于和小于0v 的分子数各占一半.0 v二、填空题 1、有一个电子管，其真空度（即电子管内气体压强）为1.0×10-5 mmHg ，则27 ℃ 时管内单位体积的分子数为_________________ ．(玻尔兹曼常量k ＝1.38×10-23 J/K , 1 atm=1.013×105 Pa =76 cmHg )解：nkT p =故3001038.176010013.1100.12355⨯⨯⨯⨯⨯⨯==--kT p n =3.2×1017 /m 32、图示曲线为处于同一温度T 时氦（原子量4）、氖（原子量20）和氩（原子量40）三种气体分子的速率分布曲线。

第十一章气体动理论习题详细答案一、选择题1、答案：B解：根据速率分布函数()f v的统计意义即可得出。

()f v表示速率以v为中心的单位速率区间内的气体分子数占总分子数的比例，而dvvNf)(表示速率以v为中心的dv速率区间内的气体分子数，故本题答案为B。

2、答案：A解：根据()f v的统计意义和pv的定义知，后面三个选项的说法都是对的，而只有A不正确，气体分子可能具有的最大速率不是pv，而可能是趋于无穷大，所以答案A正确。

3、答案：Armsv=据题意得222222221,16H O H HH O O OT T T MM M T M===，所以答案A正确。

4、由理想气体分子的压强公式23kp nε=可得压强之比为：Ap∶Bp∶Cp＝n A kAε∶n B kBε∶n C kCε＝1∶1∶15、氧气和氦气均在标准状态下，二者温度和压强都相同，而氧气的自由度数为5，氦气的自由度数为3，将物态方程pV RTν=代入内能公式2iE RTν=可得2iE pV=，所以氧气和氦气的内能之比为5 : 6，故答案选C。

6、解：理想气体状态方程PV RTν=，内能2iU RTν=(0mMν=)。

由两式得2U iPV=，A、B两种容积两种气体的压强相同，A中，3i=；B中，5i=，所以答案A正确。

7、由理想气体物态方程'mpV RTM=可知正确答案选D。

8、由理想气体物态方程pV NkT=可得气体的分子总数可以表示为PVNkT=，故答案选C。

9、理想气体温度公式21322k m kTευ==给出了温度与分子平均平动动能的关系，表明温度是气体分子的平均平动动能的量度。

温度越高，分子的平均平动动能越大，分子热运动越剧烈。

因此，温度反映的是气体分子无规则热运动的剧烈程度。

由于k ε是统计平均值，因而温度具有统计意义，是大量分子无规则热运动的集体表现，对个别分子或少数分子是没有意义的。

故答案选B 。

10、因摩尔数相同的氢气和氦气自由度数不同，所以由理想气体的内能公式2i E RT ν=可知内能不相等；又由理想气体温度公式21322k m kT ευ==可知分子的平均平动动能必然相同，故答案选C 。

气体动理论练习1一、选择题1. 在一密闭容器中，储有A、B、C三种理想气体，处于平衡状态。

A种气体的分子数密度为n1，它产生的压强为p1，B种气体的分子数密度为2n1，C种气体的分子数密度为3n1，则混合气体的压强p为( )A. 3p1;B. 4p1;C. 5p1;D. 6p1.2. 若理想气体的体积为V，压强为p，温度为T，一个分子的质量为m，k为玻尔兹曼常量，R为普适气体常量，则该理想气体的分子数为( )A. pVm⁄； B. pVkT⁄； C. pV RT⁄； D. pV mT⁄。

3. 一定量某理想气体按pV2=恒量的规律膨胀，则膨胀后理想气体的温度( )A. 将升高；B. 将降低；C. 不变；D. 升高还是降低，不能确定。

二、填空题1. 解释下列分子动理论与热力学名词：(1) 状态参量：；(2) 微观量：；(3) 宏观量：。

2. 在推导理想气体压强公式中，体现统计意义的两条假设是：(1) ；(2) 。

练习2一、选择题1. 一个容器内贮有1摩尔氢气和1摩尔氦气，若两种气体各自对器壁产生的压强分别为p1和p2，则两者的大小关系是( )A. p1>p2；B. p1<p2；C. p1=p2；D. 不能确定。

2. 两瓶不同种类的理想气体，它们的温度和压强都相同，但体积不同，则单位体积内的气体分子数为n，单位体积内的气体分子的总平动动能为E kV⁄，单位体积内的气体质量为ρ，分别有如下关系( )A. n不同，E kV⁄不同，ρ不同；B. n不同，E kV⁄不同，ρ相同；C. n相同，E kV⁄相同，ρ不同；D. n相同，E kV⁄相同，ρ相同。

3. 有容积不同的A、B两个容器，A中装有刚体单原子分子理想气体，B中装有刚体双原子分子理想气体，若两种气体的压强相同，那么，这两种气体的单位体积的内能E A和E B的关系( )A. E A<E B；B. E A>E B；C. E A=E B；D.不能确定。

气体动理论习题、答案及解法一、 选择题1. 一定量氢气（视为刚性分子的理想气体），若温度每升高1K ，其内能增加20.8J ，则该氢气的质量为 【 B 】 （A ）1.0⨯10kg 3- (B)2.0⨯10kg 3-(C)3.0⨯10kg 3- (D)4.0⨯10kg 3-参考答案：T R i M E ∆⎪⎭⎫⎝⎛=∆2μ 5=i 刚性双原子的自由度为()kg 100.2131.851028.202233--⨯=⨯⨯⨯⨯⨯=∆⋅∆=T iR E M μ2. 有一瓶质量为m 的氢气（是作刚性双原子分子的理想气体），温度为T ，则氢分子的平均动能 【 B 】 （A ）kT 23 （B ）kT 25 （C ） RT 23 （D ）RT 25参考答案：kT i2=ε 5=i 刚性双原子的自由度为 3. 有两瓶气体，一瓶是氦气，另一瓶是氢气（均视为刚性分子理想气体），若它们的压强、体积、温度均相同，则氢气的内能是氦气的 【 C 】 （A ）21倍 （B ）32倍 （C ）35倍 （D ）2倍参考答案：T R i M E ⎪⎭⎫⎝⎛=2μ RT M pV μ= 3522222==⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛=e e e H H H H H H i i T R i M T R i M E E μμ4. A 、B 、C3个容器中皆装有理想气体，它们的分子数密度之比为A n ：Bn ：C n =4：2：1，而分子的平均平动动能之比为4:2:1::=C B A εεε，则它们的压强之比C B A p p p :::为 【 A 】（A ）1：1：1 （B)1：2；2 （C ）1：2；3 （D ）1：2；4参考答案：εn p 32=1:1:132:32:32:::==C C B B A A C B A n n n p p p εεε 5. 2g 氢气与2g 氦气分别装在两个容器相等的封闭容器内，温度也相同（氢气分子视为刚性双原子分子），氢气与氦气内能之比eH H E E 2为（A ）31 （B ）35 （C ）310 (D)316 【 C 】参考答案：T R i M E ⎪⎭⎫⎝⎛=2μ31010231045223322222=⨯⨯⨯⨯==⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛=--H H H H H H H H H H e e e e e i i T R i M T R i M E E μμμμ 6.1mol 的单原子分子理想气体，在1atm 的恒定压强下，从c 0︒加热到c 100︒，则气体的内能改变了 【 D 】（A ）0.25J 103⨯ （B ）J 105.03⨯ （C ）J 100.13⨯ （D ）J 1025.13⨯ 参考答案：T R i M E ∆⎪⎭⎫⎝⎛=∆2μ ()()J 1025.127337331.82323⨯=-⨯⨯=∆⎪⎭⎫ ⎝⎛=∆T R i M E μ7. 在容积为3210m -的容器中，装有质量g 100的气体，若气体分子的方均根速率为1200-⋅s m ，则气体的压强为 【B 】 （A ）Pa 1067.05⨯ （B ）Pa 1033.15⨯ （C ）Pa 1066.25⨯ （D ）Pa 1099.35⨯参考答案：μRTv 32=RT MpV μ= ()Pa 1033.131522⨯=⎪⎭⎫ ⎝⎛⨯=v V M p8. 如图1所示的两条()v ~v f 曲线分别表示氢气和氧气在同一温度下的麦克斯）（1-韦速率分布曲线。

大学物理（气体动理论）习题答案8-1 目前可获得的极限真空为Pa 1033.111-⨯，，求此真空度下3cm 1体积内有多少个分子?(设温度为27℃)[解] 由理想气体状态方程nkT P =得 kT V NP =，kT PV N =故 323611102133001038110110331⨯=⨯⨯⨯⨯⨯=---...N (个)8-2 使一定质量的理想气体的状态按V p -图中的曲线沿箭头所示的方向发生变化，图线的BC 段是以横轴和纵轴为渐近线的双曲线。

(1)已知气体在状态A 时的温度是K 300=A T ，求气体在B 、C 、D 时的温度。

(2)将上述状态变化过程在 T V -图(T 为横轴)中画出来，并标出状态变化的方向。

[解] (1)由理想气体状态方程PV /T ＝恒量，可得：由A →B 这一等压过程中BBA A T V T V = 则 6003001020=⋅=⋅=A AB B T V V T (K) 因BC 段为等轴双曲线，所以B →C 为等温过程，则==B C T T 600 (K)C →D 为等压过程，则CCD D T V T V = 3006004020=⋅=⋅=C CD D T V V T (K) (2)8-3 有容积为V 的容器，中间用隔板分成体积相等的两部分，两部分分别装有质量为m 的分子1N 和2N 个, 它们的方均根速率都是0υ，求： (1)两部分的分子数密度和压强各是多少?(2)取出隔板平衡后最终的分子数密度和压强是多少?010203040[解] (1) 分子数密度 VNV N n VN V N n 2222111122====由压强公式：231V nm P =， 可得两部分气体的压强为 VV mN V m n P VV mN V m n P 3231323120220222012011====(2) 取出隔板达到平衡后，气体分子数密度为 VN N V N n 21+==混合后的气体，由于温度和摩尔质量不变，所以方均根速率不变，于是压强为：VV m N N V nm P 3)(31202120+==8-4 在容积为33m 105.2-⨯的容器中，储有15101⨯个氧分子，15104⨯个氮分子，g 103.37-⨯氢分子混合气体，试求混合气体在K 433时的压强。

第11单元 气体动理论一、选择题【C 】1.在标准状态下, 若氧气（视为刚性双原子分子的理想气体）和氦气的体积比2121=V V ，则其内能之比21/E E 为： (A) 1/2 (B) 5/3 (C) 5/6 (D) 3/10【B 】2.若理想气体的体积为V ，压强为p ，温度为T ，一个分子的质量为m ，k 为玻耳兹曼常量，R 为摩尔气体常量，则该理想气体的分子数为(A) pV/m (B) pV/(kT) (C) pV/(RT) (D) pV/(mT)【D 】3.一定量的理想气体贮于某一容器中，温度为T ，气体分子的质量为m ．根据理想气体的分子模型和统计假设，分子速度在x 方向的分量平方的平均值 (A) m kT v x 32= (B)m kT v x 3312= (C) m kT v x 32= (D)mkT v x =2 【解析】m kT v 32=，222231v v v v z y x ===，故mkT v x =2。

【变式】一定量的理想气体贮于某一容器内，温度为T ，气体分子的质量为m 。

根据理想气体分子模型和统计假设，分子速度在x 方向分量的平均值为（ ） 0 D. π38 . C π831 B. π8 A.==⋅==x x x x mkT m kT m kT v v v v 解：在热平衡时，分子在x 正反两个方向上的运动是等概率的，故分子速度在x 方向分量的平均值为零。

所以答案选D 。

【D 】4.若)(v f 为气体分子速率分布函数，N 为分子总数，m 为分子质量，则)(21221v Nf mv v v ⎰ d v 的物理意义是(A) 速率为v 2的各分子的总平均动能与速率为v 1的各分子的总平均动能之差(B) 速率为v 2的各分子的总平动动能与速率为v 1的各分子的总平动动能之和(C) 速率处在速率间隔v 1~ v 2之内的分子的平均平动动能(D) 速率处在速率间隔v 1~ v 2之内的分子平动动能之和 【D 】5.在一密闭容器中，储有A 、B 、C 三种理想气体，处于平衡状态，A 种气体的分子数密度为1n ，它产生的压强为1p ，B 种气体的分子数密度为12n ，C 种气体的分子数密度为3n 1，则混合气体的压强p 为(A)31p (B)41p 1p (D)61p【A 】6.两种不同的理想气体，若它们的最概然速率相等，则它们的(A) 平均速率相等，方均根速率相等 (B) 平均速率相等，方均根速率不相等．(C) 平均速率不相等，方均根速率相等 (D) 平均速率不相等，方均根速率不相等．【解析】根据nkT p =，321n n n n ++=，得到1132166)(p kT n kT n n n p ==++=。

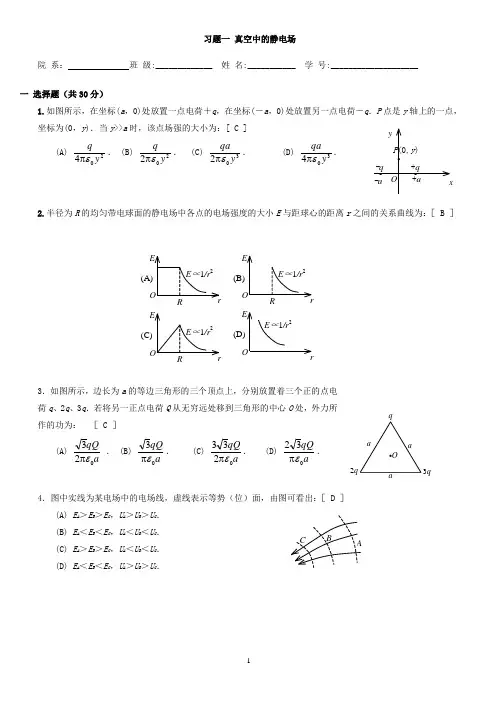
习题一 真空中的静电场院 系： 班 级:_____________ 姓 名:___________ 学 号:____________________一 选择题（共30分）1.如图所示，在坐标(a ，0)处放置一点电荷＋q ，在坐标(－a ，0)处放置另一点电荷－q ．P 点是y 轴上的一点，坐标为(0，y )．当y >>a 时，该点场强的大小为：[ C ] (A)204y q επ． (B)202y q επ． (C)302y qa επ． (D) 304yqa επ．2.半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为：［ B ］3．如图所示，边长为a 的等边三角形的三个顶点上，分别放置着三个正的点电荷q 、2q 、3q ．若将另一正点电荷Q 从无穷远处移到三角形的中心O 处，外力所作的功为： ［ C ］(A) a qQ 023επ ． (B) a qQ 03επ． (C) a qQ 0233επ． (D) aqQ 032επ．4．图中实线为某电场中的电场线，虚线表示等势（位）面，由图可看出：［ D ］ (A) E A ＞E B ＞E C ，U A ＞U B ＞U C ． (B) E A ＜E B ＜E C ，U A ＜U B ＜U C ． (C) E A ＞E B ＞E C ，U A ＜U B ＜U C ． (D) E A ＜E B ＜E C ，U A ＞U B ＞U C ．E Or(D) E ∝1/r 23q2q5．半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为： ［ B ］6．在边长为a 的正方体中心处放置一电荷为Q 的点电荷，则正方体顶角处的电场强度的大小为： (A)2012a Q επ． (B) 206a Q επ． (C) 203a Q επ． (D) 20aQεπ． ［C ］7．图示为一具有球对称性分布的静电场的E ～r 关系曲线．请指出该静电场是由下列哪种带电体产生的． (A) 半径为R 的均匀带电球面． [ B ］(B) 半径为R 的均匀带电球体．(C) 半径为R 的、电荷体密度为＝A r (A 为常数)的非均匀带电球体． (D) 半径为R 的、电荷体密度为＝A/r (A 为常数)的非均匀带电球体．8．选无穷远处为电势零点，半径为R 的导体球带电后，其电势为U 0，则球外离球心距离为r 处的电场强度的大小为(A) 302r U R ． (B) R U 0． (C) 20r RU ． (D) r U 0． ［ C ］9. 设有一“无限大”均匀带正电荷的平面．取x 轴垂直带电平面，坐标原点在带电平面上，则其周围空间各点的电场强度E随距平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负)：［C ］10. 一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的：(A) 2倍． (B) 22倍． (C) 4倍． (D) 42倍． ［ B ］E O rE ∝1/rE Or(D) E ∝1/rR E Or(C) E ∝1/rE Or(A) E ∝1/rO R rE E ∝1/r 2OxE (A)OxE (C)OxE (B)OxE (D)E ∝1/|x|E ∝x11．如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd的电场强度通量等于：(A) 06εq ． (B) 012εq ． (C) 024εq ． (D) 048εq． ［ C ］二 填空题1.电荷分别为q 1，q 2，q 3的三个点电荷分别位于同一圆周的三个点上，如图所示．设无穷远处为电势零点，圆半径为R ，则b 点处的电势U ＝___________ ． ()32102281q q q R++πε2.图中所示以O 为心的各圆弧为静电场的等势（位）线图，已知U 1＜U 2＜U 3，在图上画出a 、b 两点的电场强度的方向，并比较它们的大小．E a ＝ E b (填＜、＝、＞)．3.两根相互平行的“无限长”均匀带正电直线1、2，相距为d ，其电荷线密度分别为λ1和λ2如图所示，则场强等于零的点与直线1的距离a 为_____________ ．d 211λλλ+4.如图所示,两同心带电球面，内球面半径为r 1＝5 cm ，带电荷q 1＝3×10-8C ；外球面半径为r 2＝20 cm ， 带电荷q 2＝－6×10­8C ，设无穷远处电势为零，则空间另一电势为零的球面半径r ＝ __________________．10 cm5．已知某静电场的电势函数U ＝a ( x 2+ y )，式中a 为一常量，则电场中任意点的电场强度分量E x ＝－2ax ，E y ＝ －a ，E z ＝ 0．6．如图所示．试验电荷q ，在点电荷+Q 产生的电场中，沿半径为R 的整个圆弧的3/4圆弧轨道由a 点移到d 点的过程中电场力作功为 0 ；从d 点移到无穷远处的过程中，电场力作功为qQ / (4πε0R )．7.一个带电荷q 、半径为R 的金属球壳，壳内是真空，壳外是介电常量为ε 的无限大各向同性均匀电介质，则此球壳的电势U =________________．Rqεπ48．在点电荷q 的电场中，把一个－1.0×10-9C 的电荷，从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处，克服电场力作功 1.8×10-5 J ，则该点电荷q ＝-2×10-7库伦．(真空介电常量0＝8.85×10-12C 2·N -1·m -2)A b caq2 q 1 q 3OOU 1U 2U 3abλ2a d 12q 1 q 2 r 1r 2+Q R q d∞三 计算题1.厚度为d 的“无限大”均匀带电导体板两表面单位面积上电荷之和为σ．试求图示离左板面距离为a 的一点与离右板面距离为b 的一点之间的电势差．解：选坐标如图．由高斯定理，平板内、外的场强分布为：E = 0 (板内) )2/(0εσ±=x E (板外)1、2两点间电势差⎰=-2121d x E U U x x x d b d d d a d 2d 22/2/02/)2/(0⎰⎰+-+-+-=εσεσ )(20a b -=εσ 2.一环形薄片由细绳悬吊着，环的外半径为R ，内半径为R /2，并有电荷Q 均匀分布在环面上．细绳长3R ，也有电荷Q 均匀分布在绳上，如图所示,试求圆环中心O 处的电场强度(圆环中心在细绳延长线上)．解：先计算细绳上的电荷在O 点产生的场强．选细绳顶端作坐标原点O ，x 轴向下为正．在x 处取一电荷元 d q = d x = Q d x /(3R ) 它在环心处的场强为 ()20144d d x R qE -π=ε ()20412d x R R xQ -π=ε 整个细绳上的电荷在环心处的场强()203020116412RQx R dx R Q E R εεπ=-π=⎰ 圆环上的电荷分布对环心对称，它在环心处的场强E 2=0由此，合场强 i R Qi E E20116επ== 方向竖直向下．3.电荷Q (Q ＞0)均匀分布在长为L 的细棒上，在细棒的延长线上距细棒中心O 距离为a 的P 点处放一电荷为q (q ＞0 )的点电荷，求带电细棒对该点电荷的静电力． 解：沿棒方向取坐标Ox ，原点O 在棒中心处．求P 点场强： ()()20204d 4d d x a xx a q E -π=-π=ελε 3分 ()⎰--π=2/2/204d L L x a xE ελ()2202/2/0414L a Qx a L L -π=-⋅π=-εελ 4分 方向沿x 轴正向. 点电荷受力：==qE F ()2204πL a qQ-ε 方向沿x 轴正方向． 3分1σda1σd abxOO R 3RR /2E 1xR3R x xOPL+Q OaP O L/2L/2d x d q a。